Abstract
In underground engineering such as tunnel engineering, the condition of surrounding rock such as water-containing jointed rock mass is a common engineering geology. For broken, water-containing surrounding rock, the reasonable measures to prevent and drain water has always been a key issue. Based on the statistical information of the structural surface of the surrounding rock of the Hongtuzhang tunnel, DIPS software was used to classify the structural plane of the tunnel. Based on the statistical analysis of the occurrence, size, and density of the structural plane, the two-dimensional structural plane network model of the rock mass was established, and the permeability tensor (K1 = 1.61 × 10−6 m/s, K2 = 5.78 × 10−7 m/s) was calculated. Consider the worst orientation, the permeability tensor (K1 = 1.61 × 10−6 m/s) was selected to calculate the grouting design. Based on the theory of limited discharge, the influence of parameters of permeability coefficient ratio n and thickness of grouting layer Tg on the tunnel water inflow and lining external water pressure was analyzed. The recommended value of tunnel drainage was 3.0 m3/m∙d, then the corresponding grouting circle parameters were put forward (permeability coefficient ratio n = 100, thickness of grouting layer Tg = 8 m).
1. Introduction
The jointed rock mass is composed of rock blocks and fractures. There are obvious differences in the water conductivity of these two media. Therefore, the jointed rock mass has the characteristics of a dual medium of pores and fractures. Compared with the soil, the seepage characteristics of the rock mass are quite different. The seepage of jointed rock mass has the following characteristics [1,2,3]:
- (1)
- Non-uniform permeability coefficient;
- (2)
- The permeability coefficient has obvious anisotropy;
- (3)
- Difficulty from the type definition of permeable medium;
- (4)
- Permeability and stress state interact significantly;
- (5)
- Permeability coefficient is difficult to determine;
- (6)
- There is a big difference between the generalized flow velocity and the actual flow velocity of the equivalent continuum model.
Based on the above-mentioned characteristics of jointed rock mass seepage, it is of great significance to the study of rock mass seepage. Former scholars studied the seepage flow in a single fracture and proposed the equal-width smooth fracture model and the groove flow model [3]. The channel model of fluid flow was proposed by Tsang [4]. Because the fracture width at each point of the fracture is not uniform, the fracture width changes under the action of external force, and the fracture is closed but there are still small fractures similar to the groove between the fracture walls where seepage can still occur. Boussinesq [5] first proposed the cubic law of liquid flow in parallel-plate fractures, namely the flow rate through the fractures of equal width are proportional to the third power of the fracture width, which is also the basis for studying rock hydraulics. Since the actual fracture surface is not smooth and equal width, many scholars later corrected the roughness of the fracture.
The research on the permeability coefficient of fractured rock masse has obtained abundant achievements. Based on the water pressure test in borehole, Louis [6] obtained the empirical formula of the negative exponential relationship between the permeability coefficient of the rock mass and the normal stress. Snow [7] proposed a formula for calculating the distribution of permeability coefficients with normal stress for multiple groups of parallel fractures. Joneso [8], Kranz [9] and Gale et al. [10] studied rocks with different lithologies and proposed empirical formulas for permeability coefficients of granite, marble, basalt, and other rocks. Zhang and Sanderson et al. [11] used the fractal dimension to describe the connectivity and compactness of fracture network and found that the deformability, and the overall permeability of fractured rock masses increase greatly with increasing fracture density. Sun and Zhao et al. [12] analyzed the influence of anisotropic permeability of fractured rock mass on underground oil storage caverns by the numerical simulation method, and it is found that as the anisotropy of permeability increases, the stability of the rock around the cave crown decreases. Alireza Baghbanan and Lanru Jing [13] found that when small stress ratios (K ¼ horizontal/vertical stress) are applied at the model boundaries, the overall permeability of the fracture network is generally decreased. However, the contribution from a few large fractures of higher hydraulic conductivity prevents a drastic reduction of the overall permeability, compared with models that assume uniform fracture apertures.
The seepage theory and numerical calculation of fractured rock masses have also been researched and explored. Through experiments on the relationship between rock mass seepage and stress with the consideration of the seepage direction, Yanqing Wu [14] put forward the fractal geometric relationship between rock fracture stress and seepage, and the corresponding seepage formulas for fractured rock masses with stress in different directions. Jie Liu [15] integrated and analyzed the nonlinear seepage characteristics of single fractures and cross fractures in rock mass and proposed a nonlinear seepage calculation model for cross fractures. Moreover, the author carried out the application and verification of nonlinear seepage calculations in fracture networks. Through deducing the calculation formula for the seepage force of groundwater in the surrounding rock of a high-pressure tunnel, Zongjian Wang et al. [16] obtained the expression of the permeability coefficient of the surrounding rock with the effect of seepage force in consideration and investigated the influence of the variation of seepage force on the permeability coefficient of the surrounding rock.
From the above research results, it can be seen that the current seepage analysis and research of fractured rock masses mostly focus on the study of the permeability coefficient of the rock mass and the numerical simulation calculation of the seepage flow of the rock mass. However, it is relatively rare to combine the seepage flow of fractured rock mass with the waterproof characteristics and drainage of tunnel engineering for water-rich broken surrounding rock to determine a reasonable grouting method. The grouting technology can effectively limit the seepage of groundwater; meanwhile, fill and reinforce surrounding rocks with loose fracture can effectively preventing the occurrence of unfavorable disasters. Therefore, grouting reinforcement is often used in tunnels with water-rich, fractured rock masses to limit the flow of groundwater for the purpose of improving the stability of surrounding rock [17]. How to determine reasonable grouting parameters, design the best grouting scheme for the tunnel, and know which grouting technology to use are all issues worthy of study. In view of this, this paper carries out discrete fracture network modeling on the measured data of the rock mass structure of the Hongtuzhang tunnel, discusses the anisotropy of the fractured rock mass based on fracture hydraulics, and determines the permeability tensor of the fractured rock mass; Investigation on the effect of the limited discharge grouting layer of the Hongtuzhang tunnel on the water-bearing fractured rock mass and lining structure is important, and to propose the parameters of the limited discharge grouting circle has important theoretical and practical application significance for the construction of the Hongtuzhang tunnel.
2. Establishment of Discrete Fracture Network
2.1. Seepage Characteristics of Fractured Rock Mass
Due to the randomness of fracture distribution in fractured rock mass, the permeability of fractured aquifer medium is anisotropic. D. T. Snow [18] proposed the permeability tensor theory in the 1960s.
The Darcy’s law of isotropic permeable medium is:
That is, the flow velocity ui in a certain direction is proportional to the hydraulic gradient Ji in that direction. The proportional coefficient is the permeability coefficient, and the k value is a constant independent of the direction.
In fractured rock mass, the water conductivity of rock mass is much smaller than that of fractures distributed in it. Therefore, fractures are the main channels for seepage of fractured rock mass. According to the different occurrence distribution, the fractures with similar occurrences are classified into the same group. If the fractures are relatively developed, the anisotropic equivalent permeability medium can be obtained by equivalently averaging the permeability of fractures in rock mass. At this point, the flow velocity in one direction is proportional not only to the hydraulic gradient in that direction, but also to the hydraulic gradient in other directions, that is:
where kij is the permeability tensor, denoted as [K]. In the global coordinate system, it can be expressed as
The permeability tensor can be determined by the geometric parameters of the fracture.
- (1)
- One-dimensional problemFor the one-dimensional problem, it is assumed that the crack direction is parallel to the x-axis, the crack is smooth, the gap width is a, and the spacing between the cracks is b. The hydraulic gradient in the fracture is Jx, and the flow velocity is:the permeability coefficient is:
- (2)
- Two-dimensional problemFor the n group of fractures whose width is a and spacing is b, the maximum hydraulic gradient on the plane is set to J. The angle between the normal direction of fracture and x-axis is α, and the components are nx = cosα and ny = sinα, respectively. The hydraulic gradient components are Jx and Jy, and the equivalent continuous medium permeability tensor is:the general matrix form of writing is:
- (3)
- Three-dimensional problemFor the three-dimensional problem, there are n groups of cracks with fixed occurrences, the same crack spacing, and infinite extension. The general matrix form of the permeability tensor is:where the actual fracture, occurrence, spacing and other parameters are randomly distributed, and the size is not infinite extension, so the permeability tensor needs to be further determined according to the actual situation of fracture geometric parameters.
2.2. Engineering Hydrogeology of Hongtuzhang Tunnel Site
The Hongtuzhang tunnel is located in Tangxi Town, Fengshun County and Guotian Town, Wuhua County, passing through the location of Baxiang Mountain in the Lianhua Mountain Range. The tunnel site area is mainly affected by three geological structural zones, namely the Lianhuashan fault zone, the Lianhuashan fault-associated NW-trending fault, and the Tongziyang compound syncline fold. Figure 1 shows the Hongtuzhang tunnel and the structural spatial distribution map.

Figure 1.
Spatial distribution of Hongtuzhang tunnels and structures.
The ZK93 + 240 − ZK93 + 315 section as the research object of this paper, mainly composed of Yanshanian slightly weathered granite. It is inferred that there are developed faults, joints, and fractured zones in this part. Within the fault and the influence range of the fault, the rocks are weathered and broken. The integrity of the rock is poor, and it is easy to fall off and collapse. Geological disasters such as water seepage and water inrush may occur in the rainy season. According to the geological survey report, the sections K91 + 900 − K92 + 050, K92 + 450 − K92 + 550, and K93 + 200 − K93 + 650 through the faults (F0–4, F2–7, F2–8) may connect the Huangmian Lake reservoir with the proposed tunnel, which will affect the tunnel construction. F2–8 fault passes through the ZK93 + 240 − ZK93 + 315 section. The surrounding rock is broken, and it is easy to form a block. Structural fissure water is formed along the fault, and the amount of water is large, so water gushing may exist.
2.3. Establishment of Two-Dimensional Structural Plane Network
- (1)
- Joint grouping
The Dips software can be used to visually divide the fissures of similar occurrence on the stereographic projection isodensity map. According to the measured data, the structural plane is divided into three groups according to the occurrence. A few cracks are scattered outside the dominant joint group. To ensure that the simulated occurrence results are not too scattered, they are ignored. In order to finally have a relatively reasonable statistical law, the final determination of the structural plane grouping situation is shown in Figure 2. The number and average occurrence of structural planes in each group are shown in Table 1. According to the grouping situation, it can be seen that the average inclination angle of each group of structural planes is equivalent, which is about 73°, and the tendency is quite different.
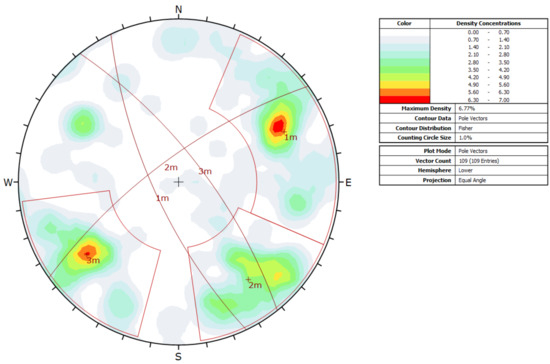
Figure 2.
Stereoscopic projection isodensity map of structural plane occurrence and division of structural plane dominant groups.

Table 1.
Structural plane division and occurrence information.
In each section, the different included angles between the structural plane and the section will cause the distribution of the structural plane on the section to be different, so the following assumptions are cited in the two-dimensional network simulation of the random structural plane of the rock mass:
- 1.
- In the designated generation domain, the two-dimensional structural surface traces are located at the same probability; that is, the structural surfaces are uniformly distributed within the generation domain.
- 2.
- In the two-dimensional random discontinuity network model, the structural surface trace is like the fracture trace length of the fractured rock mass, represented by a line segment. The angle between the counterclockwise direction of the x-axis and the trace is called the direction angle θ, which is the parameter for determining the occurrence distribution of the structural plane trace in the two-dimensional model. The direction angle is determined by the occurrence of the three-dimensional structural plane (inclination α and inclination angle β) and the azimuth angle γ of the section plane:
According to Equation (9) and the statistical results of the structural plane of the sample, the vertical section is taken, and the relationship between the calculated direction angle and the inclination and inclination angle is shown in Table 2.

Table 2.
Direction angle conversion results of structural planes in each group.
- (2)
- Dimension of structural plane
To generate the cracks, the diameter parameters of the cracks and their distribution form need to be obtained. In the case that it is difficult to obtain the crack diameter directly, to generate cracks in the structural plane model, what is needed is the distribution of crack diameters. Cacas [19] used the statistical data of the trace length directly for the crack diameter. Although the distribution of the diameter is not directly related to the distribution of the trace length, the error between the trace length and the diameter can be ignored, because of the error and uncertainty in the measurement. The results of numerical simulation experiments confirm that the difference between the two distributions is small. At the same time, some scholars discussed the relationship between the two distributions of trace length and fracture diameter. Robertson [20] gave the expression of the relationship between trace length and diameter:
where A′ is the fracture area calculated based on the trace length, and A is the average area of the fracture.
Using the measured data of the structural surface trace length to fit the probability distribution types of each group of structural surface sizes, the fitting results of the probability distribution types of each group of structural surface trace lengths can be obtained, and the results are shown in Table 3.

Table 3.
Probability distribution type fitting results of structural surface trace length.
- (3)
- Estimation of structural plane density
The relationship between surface density and bulk density can be obtained through the spatial connection between discontinuity and section. The Kulatilake–Wu estimation conversion algorithm [21] is established based on this, and the conversion relationship between surface density and bulk density is:
where E(λa) is the expected value of the surface density of the structure, E(λν) is the expected value of the surface density of the structure, E(D) is the expected value of the diameter of the structure surface, and E|sinν| is the sine value of the angle between the direction of the structural plane and the direction of the sampling plane.
The surface density of three groups of structural planes can be calculated by calculating the obtained bulk density. The calculation results are shown in Table 4.

Table 4.
Probability distribution type fitting results of structural surface trace length.
- (4)
- Calculation of rock mass range
In the calculation of the permeability tensor, considering the size effect to ensure the reasonableness of the calculation range boundary, a fracture network model larger than the calculation range of the seepage flow is usually generated; that is, the fracture network model is divided into a generation domain and an analysis domain. The former is the range of all fractures, and the latter is the calculation area of seepage. The former is usually twice the size of the latter. For seepage analysis of fractured rock mass, an analysis domain that is greater than or equal to the size of the characterizing element must be adopted, and the size of the characterizing element is usually 3 to 4 times the size of the fractured rock mass [22].
According to the above-mentioned statistical analysis of the structural plane direction angle and surface density data and each group of trace length data, the initial geometric parameters of the two-dimensional structural plane network model to be established are obtained. The average value of the three groups of crack trace length is 1.6867 m, so the structural plane network model analysis domain size is determined to be 5 m × 5 m, and the generated domain should be 10 m × 10 m; then, the number of structural planes in each group are as follows: 155, 150, and 151. The two-dimensional structural plane discrete fracture network generated by MATLAB is shown in Figure 3.

Figure 3.
Schematic diagram of two-dimensional structural plane network model.
3. Calculation of Permeability Tensor
3.1. Mathematical Model of Seepage
Assumptions about the study of structural plane network seepage are as follows:
- (1)
- The liquid flows unidirectionally in the fracture network;
- (2)
- The opening degree of the fissure remains unchanged at all times, and the rock mass does not deform;
- (3)
- The seepage–stress coupling effect is not considered.
Based on the principle of water balance at the intersection of structural surfaces, a mathematical calculation model for steady flow seepage is established, and the seepage boundary conditions are set to analyze and calculate the model.
For the two-dimensional fracture network stable seepage problem, Yanqing Wu [14] derives the corresponding calculation model based on the principle of water balance at the intersection of structural planes. Figure 4 is a schematic diagram of the equilibrium domain of the fracture unit.
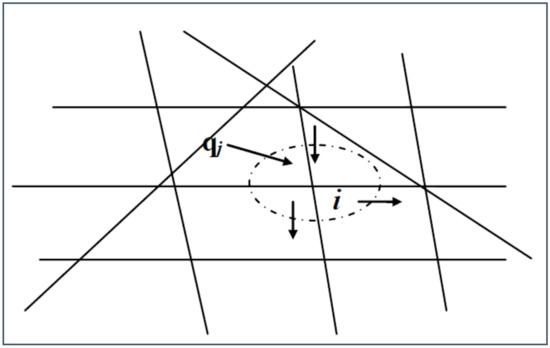
Figure 4.
Schematic diagram of the equilibrium domain of the fracture unit.
In Equation (12), the cohesion matrix can be obtained according to the relationship between the intersection points of structural plane trace lines, and the diagonal matrix can be obtained according to the gap width matrix and other parameters. The hydraulic boundary conditions are set for the two-dimensional structural plane network model, and the solutions of the other three unknowns can be obtained by determining the values of the three unknowns.
Figure 5 shows the hydraulic boundary conditions. The upper and lower boundaries and the left and right boundaries of the structural plane network model are head boundaries. The upper and lower boundaries change according to the gradient. The left and right boundaries of the model are fixed head boundaries. Under this hydraulic boundary condition, the known conditions are as follows: internal node water source Q1, and the left and right boundary water head H3. The unknown quantities are the node head vector H1, the head flow Q2 at the upper and lower boundary of the model, and the head flow Q3 at the left and right boundary of the model.
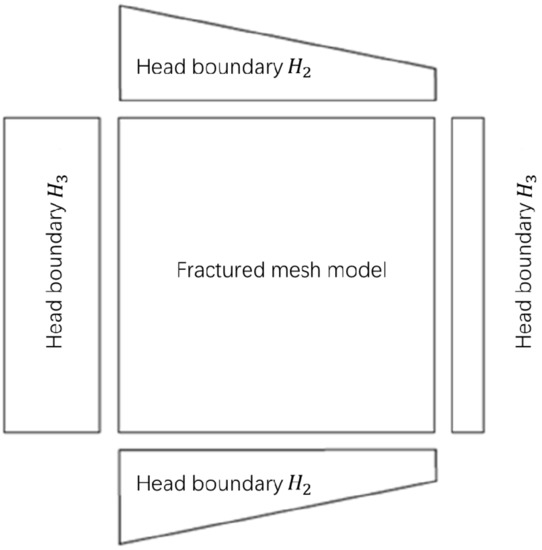
Figure 5.
Schematic diagram of boundary conditions.
From Equation (12), the water head vector of internal node can be obtained as:
where,,
Substituting the obtained into the second and third formulas in Equation (13), the formula for can be obtained as:
The upper and lower boundary flow formula is:
According to Darcy’s law, when the analysis domain is square, the permeability coefficient in the gradient direction is:
3.2. Calculation of Permeability Tensor
According to the established mathematical model and the calculation principle derived above, this paper uses MATLAB to program the corresponding calculation program according to the calculation principle. Through the above steps, the flow value in the direction of the hydraulic gradient can be obtained, and the corresponding permeability coefficient can be further obtained.
In the two-dimensional problem, the permeability tensor Kij is a second-order symmetric tensor, and the permeability coefficient along the gradient direction is:
where, Kg is the permeability coefficient along the gradient direction, νi is the flow velocity, and ni is the unit vector in the gradient direction.
Applying Darcy’s law, the relationship between seepage flow velocity and hydraulic gradient can be obtained:
That is:
In the polar coordinate system with as the variable along the gradient direction, there are:
In the solution of the two-dimensional structural plane network, the same boundary conditions are used, and then the two-dimensional stable seepage mathematical model is used to derive the permeability coefficient of the model in different directions by changing the angle. The angle of 30° is selected as the change gradient of the angle for calculation, and the permeability coefficients in 12 gradient directions are obtained.
Then, draw the reciprocal of the square root of the 12 permeability coefficients and the corresponding rotation angle in the polar coordinate system, with a total of 12 points. These 12 points can be fitted into a penetration ellipse by the least square method.
According to the size and direction of the main axis of the ellipse, the main permeability values K1 and K2 and the main direction of permeability of the fractured rock mass are derived, where the main direction of infiltration refers to the angle between the principal axis of infiltration and the positive x direction.
Equation (22) is the equation for solving the permeability tensor:
Using the structural plane network model established above, the network in the analysis domain is taken every 30° direction to calculate the permeability coefficient of the gradient in each direction. The schematic diagram is shown in Figure 6. The results obtained by calculation based on the boundary conditions given above are shown in Table 5.
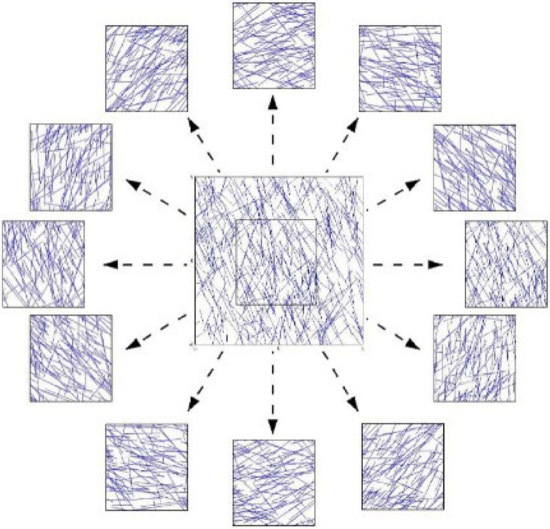
Figure 6.
Schematic diagram of structural plane network model and its rotation along the coordinate axis.

Table 5.
Calculation results of permeability coefficient and permeability ellipse radius.
According to the penetration ellipse radius in the 12 gradient directions obtained from the calculation results, the penetration ellipse is fitted according to the least square method. The calculation results and the fitting ellipse are plotted on the same polar coordinate diagram. In Figure 7, the circle represents the penetration ellipse radius in each direction obtained from the calculation, and the red dotted line represents the fitting ellipse.
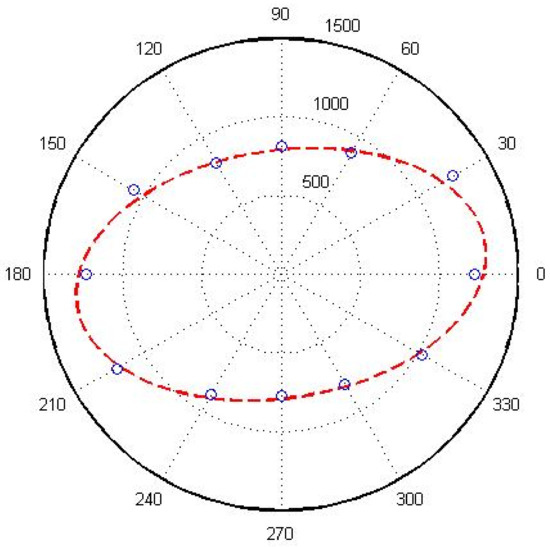
Figure 7.
Penetration ellipse fitting diagram of structural plane network model.
The main permeability coefficient can be calculated by the value of the long and short axes obtained by least squares fitting, respectively, as K1 = 1.61 × 10−6 m/s and K2 = 5.78 × 10−7 m/s. According to Equation (7), the penetration tensor can be obtained as:
Due to the discreteness of the samples, it is necessary to generate multiple samples for analysis. By changing the seed value, different fracture networks can be generated, and multiple sets of permeability tensors can be obtained. According to the calculated main permeability coefficient (K1 = 1.61 × 10−6 m/s, K2 = 5.78 × 10−7 m/s), considering the most unfavorable azimuth, K1 = 1.61 × 10−6 m/s is selected for the grouting design calculation.
4. Tunnel Grouting Limited Discharge Design
4.1. Forecast of the Water Inflow of the Hongtuzhang Tunnel
It is effective to use the method of grouting circle to carry out “limited discharge” of groundwater. In terms of engineering measures, it is reasonable to completely block the seepage of groundwater. From the perspective of ecological environment and economic benefits, all discharge is not allowed. In order to achieve the limited discharge of groundwater, it is necessary to reasonably determine the parameters of the grouting circle, such as the thickness of the grouting circle and the permeability coefficient of the grouting circle. Otherwise, the grouting circle will not be able to effectively prevent the groundwater from penetrating behind the lining. When the system cannot remove the groundwater behind the lining in time, the water pressure acting on the lining will continue to increase, which will bring huge hidden dangers to the safety of the tunnel.
When the tunnel is below the groundwater level, the tunnel tends to experience the infiltration of groundwater. Assuming that the cross section of the tunnel is circular, without considering the anisotropy of the surrounding rock, at this time, the groundwater seepage satisfies the seepage continuity equation and Darcy’s law, and the far water potential is constant as H, as shown in Figure 8. In the figure, H is the total head, r0 is the radius of the tunnel, r1 is the radius of the tunnel after lining, rg is the sum of the tunnel radius Tg after grouting and the radius of the tunnel after lining r1, r2 is the far field radius, and ks is the permeability coefficient of the surrounding rock.
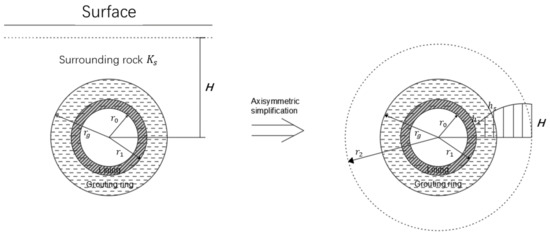
Figure 8.
Simplified schematic diagram of circular tunnel.
- (1)
- After the excavation of the tunnel and before the construction of the lining structure, according to the Darcy law, there are:Considering the boundary conditions r = r1, h1 = 0, r = H and h1 = H, then the flow before the construction of the lining structure can be calculated as:Substituting the above equation into Darcy law, the water head of surrounding rock can be obtained:
- (2)
- After the lining support is implemented, the hydraulic potential field of the surrounding rock changes from h1 to h2, and within the lining range (r = r0 − r1), there is:According to the boundary conditions r = r0 and h2l = 0, we can get:Within the grouting range (r = r1 − rg), there are:According to the boundary conditions r = rg and h2g = h2g′, we can get:Within the range of surrounding rock (r = rg − H), there are:According to the boundary conditions r = H and h2m = H, we can get:At the junction of the grouting circle and the surrounding rock (r = rg), according to the continuity of the hydraulic potential, h2g = h2r, substituting Equation (31) into Equation (29), the hydraulic potential within the grouting circle can be obtained as:According to the continuity equation, when r = , the calculation results of Equations (27) and (32) should be the same. Thus, the flow rate after lining construction is obtained, and the external water pressure of the lining is:The axisymmetric problem can be used to simplify the deep-buried tunnel with a high water level.If grouting is not considered, the water inflow of the tunnel in Equation (33) can be expressed as:According to the geological survey report, the water level elevation of Huangmian Lake Reservoir is about 988 m, the design floor elevation of this section of the tunnel is about 304–316 m, and the height difference is 659–684 m, so H = 670 m. In the calculation, = 6 m and = 6.5 m, the lining is impermeable concrete, and the permeability coefficient = 1.74 × 10−9 m/s.
4.2. Optimal Design Calculation of Permeable Grouting Circle
According to the calculation of permeability coefficient of surrounding rock, K2 = 5.78 × 10−7 m/s is selected for the design calculation of surrounding rock grouting in consideration of the most unfavorable azimuth.
- 1.
- After the hole is excavated.
At this time, r1 = r0, and the boundary conditions are introduced into Equation (24), and the water inflow of the surrounding rock of the Hongtuzhang tunnel is calculated to be 126.17 m3/(m∙d).
- 2.
- Only considering lining, not grouting.
At this time = and = , and the boundary conditions are introduced into Equation (36); the water inflow of the surrounding rock is calculated to be 7.42 m3/(m∙d), and the external water pressure of the lining of the surrounding rock of Hongtuzhang Tunnel is 6.18 MPa. The water inflow of the tunnel and the external water pressure of the lining exceed the design value, so the tunnel curtain grouting is required.
- 3.
- Carry out curtain grouting for the tunnel without considering the lining.
When only the lining is considered, and the grouting is not considered, the tunnel water influx and the external water pressure of the lining are too large, so curtain grouting is required for the tunnel. First consider the tunnel water influx when curtain grouting is performed on the tunnel without lining measures. The relationship between the water inflow of the tunnel and the thickness of the grouting ring without considering the lining is shown in Figure 9. In the figure, Q is the tunnel water influx, Tg is the thickness of the grouting circle, and n is the ratio of permeability coefficient (n = Kr/Kg is the ratio of permeability coefficient of surrounding rock and grouting circle). It can be seen from the figure that the water inflow of the tunnel is reduced after grouting. The water inflow of the tunnel decreases with the increase of the thickness of the grouting circle. When the thickness of the grouting circle is the same, the water inflow decreases with the decrease of the permeability coefficient of the grouting circle.
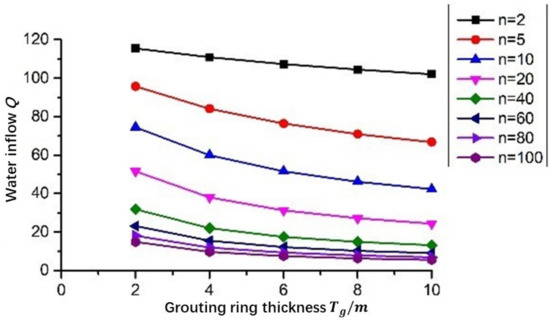
Figure 9.
The relationship curve between the water inflow and the thickness of the grouting circle after grouting in the surrounding rock.
- 4.
- When curtain grouting and lining the tunnel.
When the curtain grouting and lining are considered at the same time, the relationship between the tunnel water influx and the thickness of the grouting ring is shown in Figure 10. It can be seen from the figure that when grouting and lining support are constructed at the same time, the water inflow of the tunnel decreases with the increase of the thickness of the grouting circle. When the thickness of the grouting circle is the same, the water inflow decreases with the decrease of the permeability coefficient of the grouting circle. According to relevant specifications, the drainage volume of the tunnel in this project should be controlled within 3.0 m3/(m∙d). At this time, the designed permeability coefficient ratio n and the thickness of the grouting ring Tg are not up to the requirements.
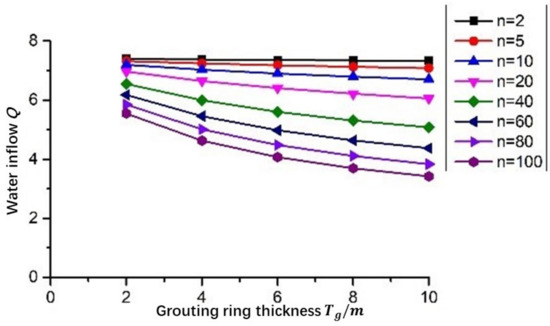
Figure 10.
The relationship curve between the water inflow and the thickness of the grouting circle after grouting and lining in the surrounding rock.
When the curtain grouting and lining are considered at the same time, the relationship between the external water pressure of the tunnel lining and the thickness of the grouting ring is shown in Figure 11. It can be seen from the figure that when grouting and lining support are constructed at the same time, the external water pressure of the tunnel lining decreases with the increase of the thickness of the grouting circle. When the thickness of the grouting circle is the same, the water inflow decreases with the decrease of the permeability coefficient of the grouting circle. According to relevant specifications, the external water pressure of the Hongtuzhang tunnel lining cannot exceed 0.8 MPa. At this time, the designed permeability coefficient ratio n and the thickness Tg of the grouting ring cannot meet the requirements.
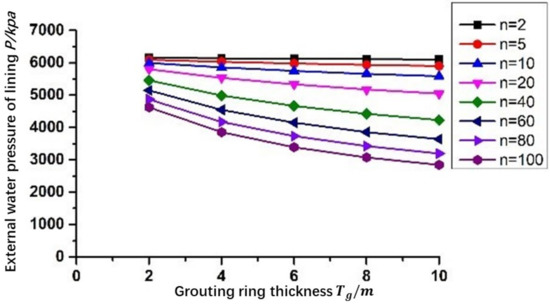
Figure 11.
The relationship curve between the external water pressure of the lining and the thickness of the grouting circle after grouting and lining in the surrounding rock.
- 5.
- Grouting and lining after draining and depressurizing the tunnel.
According to the above analysis, after only grouting and lining are used, when the water inflow of the tunnel meets the requirements, the external water pressure of the tunnel lining is relatively high, and there is a long-term operational safety hazard. Therefore, it is recommended to drain and depressurize the tunnel before grouting and lining. The recommended drainage volume of the tunnel is 3.0 m3/m∙d. The variation of the lining external water pressure reduction coefficient with grouting and with and without considering drainage is shown in Figure 12. It can be seen from Figure 12 that considering the drainage conditions of the tunnel, the reduction coefficient of the external water pressure of the lining is greatly reduced, and the stability of the surrounding rock of the tunnel is higher.
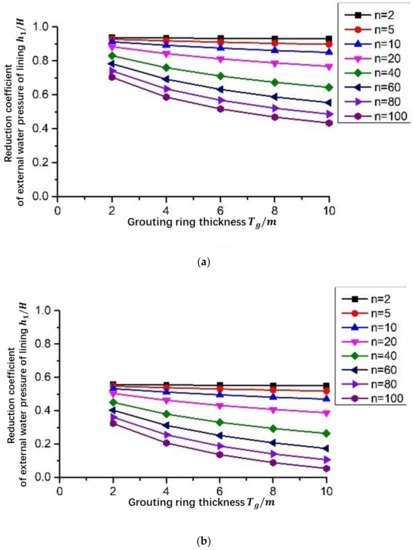
Figure 12.
The relationship curve between reduction coefficient of the external water pressure of the lining and the thickness of the grouting circle after grouting and lining in the surrounding rock. (a) Without considering tunnel drainage; (b) Considering tunnel drainage.
At this time, grouting and lining are carried out after the tunnel is drained. The thickness of the grouting circle is Tg = 8 m, and the parameter of the grouting circle is n = 100; that is, when the permeability coefficient of the grouting circle kg = 1.61 × 10−8 m/s, the requirements can be met. At this time, the drainage volume of the tunnel is 0.69 m3/(m∙d), and the external water pressure of the lining is 0.58 MPa.
5. Conclusions
Based on the Hongtuzhang tunnel project, this paper establishes a structural surface network model to calculate the permeability tensor by studying the statistical information of the structural surface of the regional rock mass and calculates the influence of grouting on the water inflow and the external water pressure of the lining according to the limited discharge theory. The main conclusions are as follows:
- (1)
- The permeability of fractured rock mass has obvious anisotropy. Through statistical analysis of the structural plane information of fractured rock masses, the structural planes are grouped and statistically analyzed for the occurrence, trace length, density, and other parameters of the structural planes, and a two-dimensional discrete fracture network model of the rock mass is established, and the dimensional permeability tensor is calculated. The two main permeability coefficients were calculated as K1 = 1.61 × 10−6 m/s and K2 = 5.78 × 10−7 m/s, respectively. Considering the most unfavorable orientation, K1 = 1.61 × 10−6 m/s was selected for grouting design calculation. Before grouting the lining, the water inflow of the tunnel was 126.17 m3/(m∙d).
- (2)
- Grouting has a significant impact on the tunnel water inflow and the external water pressure of the lining. Grouting is an effective measure to deal with the tunnel water inrush. As the thickness of the grouting ring increases, the water inflow of the tunnel and the external water pressure of the lining decrease accordingly. With the same thickness of the grouting ring, the lower the permeability coefficient of the grouting ring, the smaller the water influx of the tunnel and the external water pressure of the lining.
- (3)
- According to the theoretical calculation of limited discharge, it is recommended that the tunnel should be grouted and lined after drainage. The recommended drainage volume of the tunnel is 3.0 m3/m∙d, the thickness of the grouting circle is Tg = 8m, and the permeability coefficient of the grouting circle kg = 1.61 × 10−8 m/s. Then, the water inflow of the tunnel is 0.69 m3/(m∙d), and the external water pressure of the tunnel lining is 0.58 MPa.
Author Contributions
Methodology, L.Z., X.L. (Xiaoqing Li); software, L.Z., X.L. (Xingwei Lian); validation, D.H., J.Z. and X.L. (Xiaoqing Li); formal analysis, X.L. (Xiaoqing Li); investigation, L.Z., X.L. (Xingwei Lian); resources, X.L. (Xiaoqing Li), J.Z.; data curation, L.Z.; writing—original draft preparation, L.Z.; writing—review and editing, X.L. (Xingwei Lian); visualization, X.L. (Xingwei Lian), L.Z.; supervision, X.L. (Xiaoqing Li), D.H., L.Z.; project administration, J.Z., L.Z.; funding acquisition, X.L. (Xiaoqing Li), L.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The work presented in this paper was supported by the National Natural Science Foundation of China (No. 51808203).
Acknowledgments
The research is supported by Guangdong Poly Long Highway Engineering company ltd. We would like to acknowledge the anonymous reviewers who played a significant role in shaping and improving the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ye, F.; Duan, J.-C.; Fu, W.-X.; Yuan, X.-Y. Permeability Properties of Jointed Rock with Periodic Partially Filled Fractures. Geofluids 2019, 2019, 4039024. [Google Scholar] [CrossRef]
- Tan, W.; Wang, P. Experimental Study on Seepage Properties of Jointed Rock-Like Samples Based on 3D Printing Techniques. Adv. Civ. Eng. 2020, 2020, 9403968. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.T.; Yang, T.H.; Xu, T.; Yu, Q.L.; Liu, H.L. A Model of Anisotropic Property of Seepage and Stress for Jointed Rock Mass. J. Appl. Math. 2013, 2013, 420536. [Google Scholar] [CrossRef]
- Tsang, Y.W.; Tsang, C.F. Channel model of flow through fractured media. Water Resour. Res. 1987, 23, 467–479. [Google Scholar] [CrossRef] [Green Version]
- Boussinesq, M.; Gardon, J. Relationships between the prevalence and intensity of Loa loa infection in the Central province of Cameroon. Ann. Trop. Med. Parasitol 2001, 95, 495–507. [Google Scholar] [CrossRef] [PubMed]
- Louis, C. Rock hydraulics. In Rock Mechanics; Springer: Vienna, Austria, 1972; pp. 299–387. [Google Scholar]
- Snow, D.T. Rock fracture spacings, openings, and porosities. J. Soil Mech. Found. Div. 1968, 94, 73–91. [Google Scholar] [CrossRef]
- Jones, F.O., Jr. A laboratory study of the effects of confining pressure on fracture flow and storage capacity in carbonate rocks. J. Pet. Technol. 1975, 27, 21–27. [Google Scholar] [CrossRef]
- Kranzz, R.L.; Frankel, A.D.; Engelder, T.; Scholz, C.H. The permeability of whole and jointed Barre granite. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1979, 16, 225–234. [Google Scholar] [CrossRef]
- Gale, J.E. The effects of fracture type (induced versus natural) on the stress-fracture closure-fracture permeability relationships. In Proceedings of the 23rd US Symposium on Rock Mechanics (USRMS), Berkeley, CA, USA, 25–27 August 1982. [Google Scholar]
- Zhang, X.; Sanderson, D.J. Numerical study of critical behaviour of deformation and permeability of fractured rock masses. Mar. Pet. Geol. 1998, 15, 535–548. [Google Scholar] [CrossRef]
- Sun, J.; Zhao, Z. Effects of anisotropic permeability of fractured rock masses on underground oil storage caverns. Tunn. Undergr. Space Technol. 2010, 25, 629–637. [Google Scholar] [CrossRef]
- Baghbanan, A.; Jing, L. Stress effects on permeability in a fractured rock mass with correlated fracture length and aperture. Int. J. Rock Mech. Min. Sci. 2008, 45, 1320–1334. [Google Scholar] [CrossRef]
- Wu, Y.-Q. Research on the relationship between stress and seepage in fractured rock mass. Hydrogeol. Eng. Geol. 1995, 6, 30–35. [Google Scholar]
- Liu, J. Two-Dimensional Nonlinear Seepage Characteristics and Model of Rock Mass Fracture Network. Ph.D. Thesis, Shandong University, Jinan, China, 2019. [Google Scholar]
- Wang, Z.-J.; Li, Z.; Lu, L. Research on the distribution of permeability coefficient of surrounding rock based on seepage force. Chin. J. Undergr. Space Eng. 2018, 14, 131–136. [Google Scholar]
- Li, X.-Q. Tunnel Engineering Technology; China Building Industry Press: Beijing, China, 2011. [Google Scholar]
- Snow, D. The frequency and apertures of fractures in rock. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1970, 7, 23–40. [Google Scholar] [CrossRef]
- Cacas, M.C.; Ledoux, E.; de Marsily, G.; Tillie, B.; Barbreau, A.; Durand, E.; Feuga, B.; Peaudecerf, P. Modeling fracture flow with a stochastic discrete fracture network: Calibration and validation: 1. The flow model. Water Resour. Res. 1990, 26, 479–489. [Google Scholar] [CrossRef]
- Robertson, A.M. Interpretation of Geological Factors for Use in Slope Theory. 1970, pp. 55–71. Available online: https://xueshu.baidu.com/usercenter/paper/show?paperid=a2184df5579e38086d413c9e34c879e6 (accessed on 14 November 2021).
- Kulatilake, P.H.S.W.; Wu, T.H. Estimation of mean trace length of discontinuities. Rock Mech. Rock Eng. 1984, 17, 215–232. [Google Scholar] [CrossRef]
- Zhang, G.-K.; Xu, W.-Y. Fracture network simulation and REV scale research. Rock Soil Mech. 2008, 29, 1675–1680. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).