Using the General Regression Neural Network Method to Calibrate the Parameters of a Sub-Catchment
Abstract
:1. Introduction
2. Materials and Methods
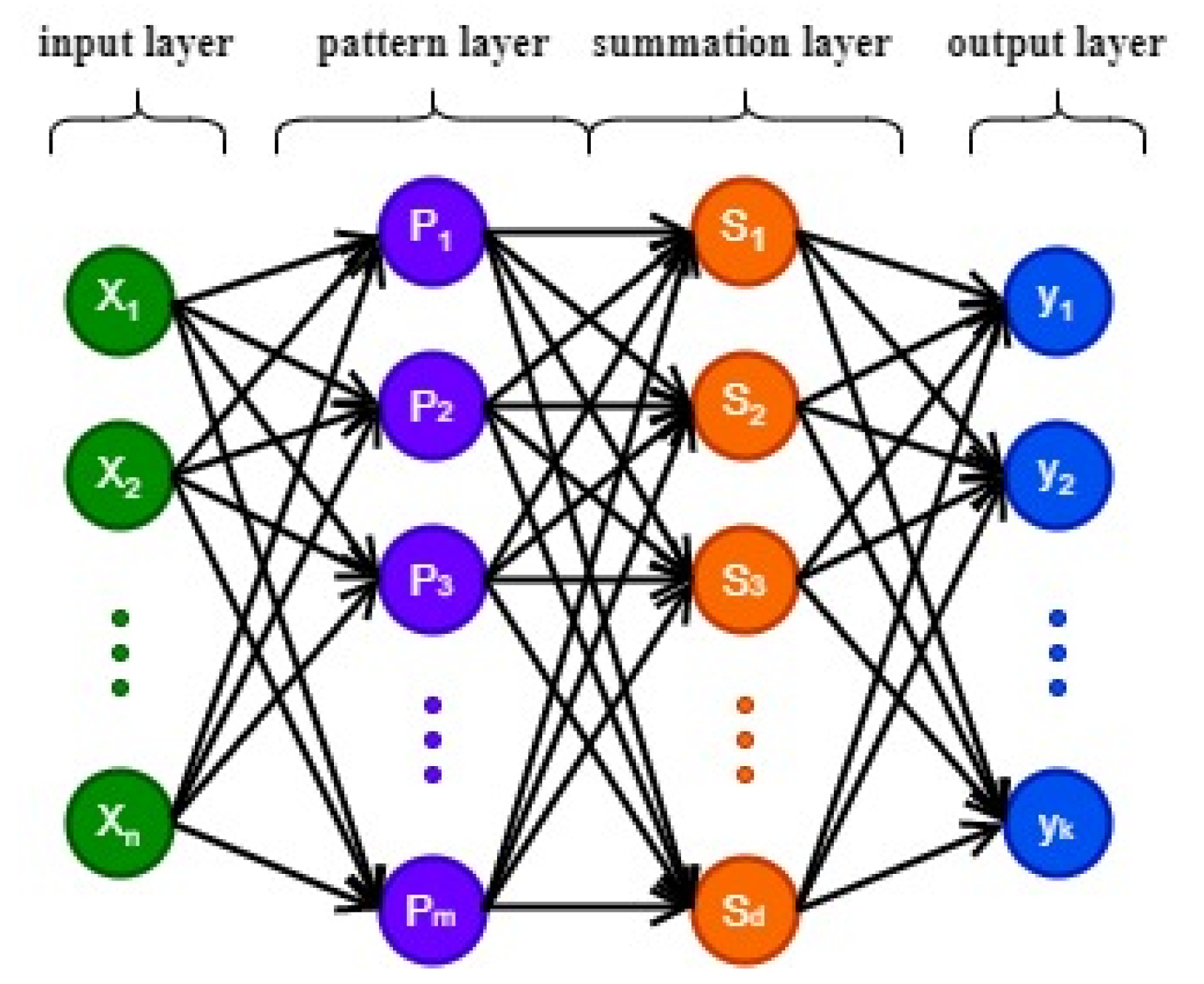
2.1. General Regression Neural Network
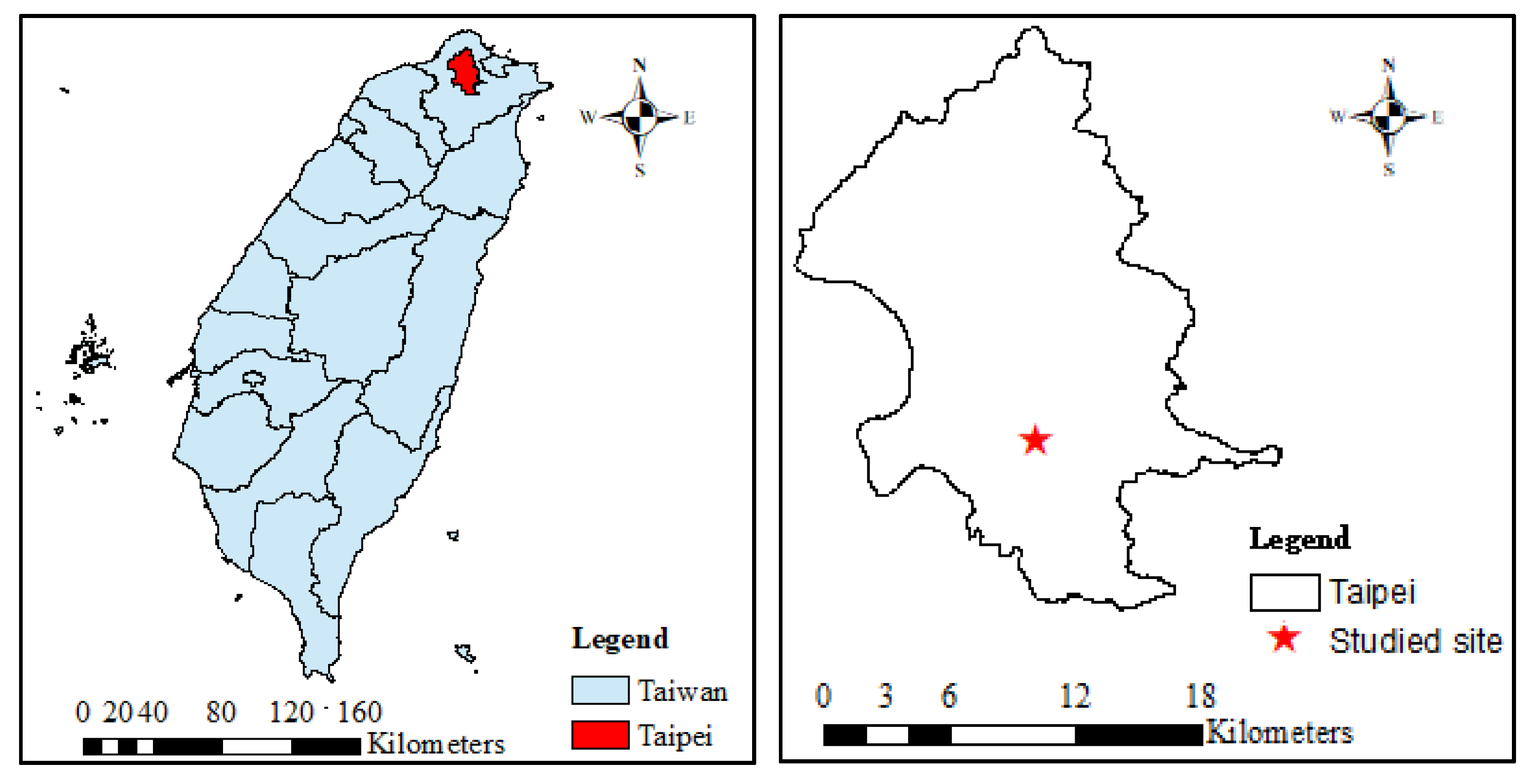
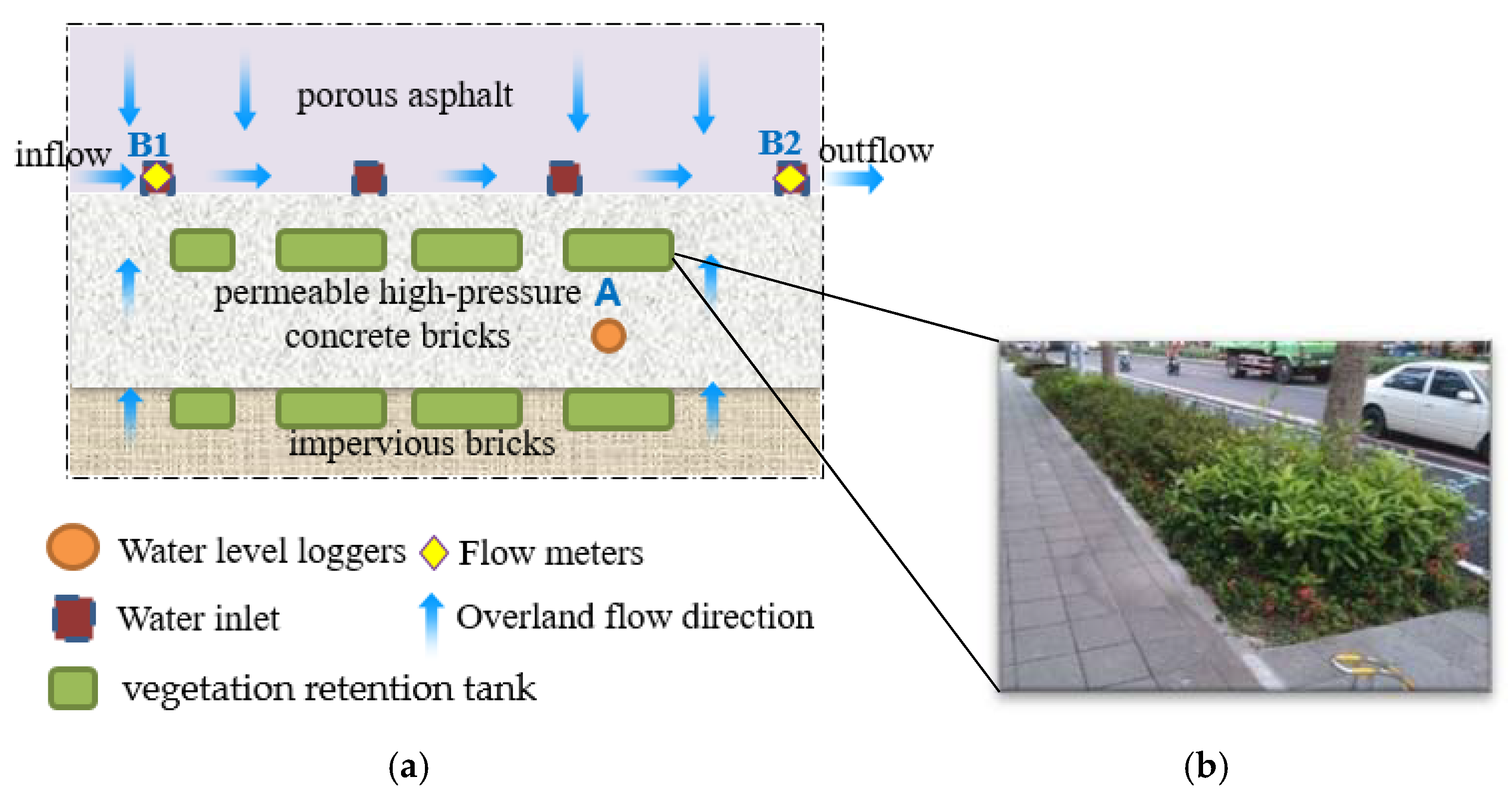
2.2. Case Study
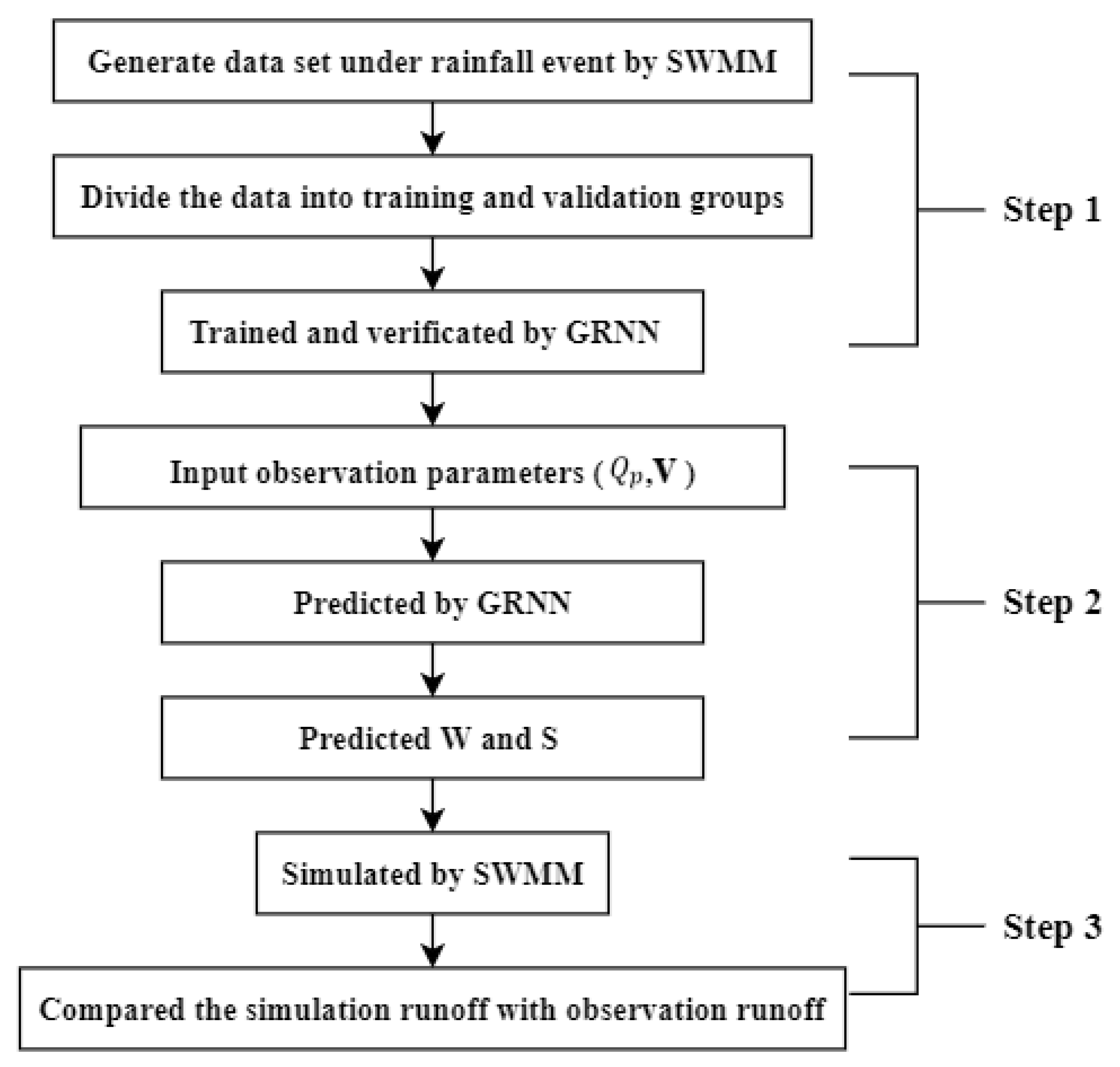
2.3. Method
2.4. Performance Criteria
- 1.
- Root-Mean-Square ErrorRoot-mean-square error (RMSE) is used to measure the deviation between the observed value and the true value and is defined aswhere is the input parameter, is the output or simulated parameter, and is the total number of input parameters. The RMSE range is between 0 and +∞.
- 2.
- Mean Absolute Percentage ErrorThe mean absolute percentage error (MAPE) is used to measure the relative error between the average test value and the real value of the test set and is defined aswhere the MAPE is between 0 and +∞. A calculated value close to zero reflects good fit in the prediction. However, it is worth noting that the formula cannot be used when the actual value is equal to zero because the denominator cannot be divided by zero.
- 3.
- Nash–Sutcliffe Efficiency CoefficientThe Nash–Sutcliffe efficiency coefficient (NSE) is defined aswhere is the average value of input parameters. The NSE range is between 1 and −∞, with calculated values close to 1 reflecting better fit for the prediction.
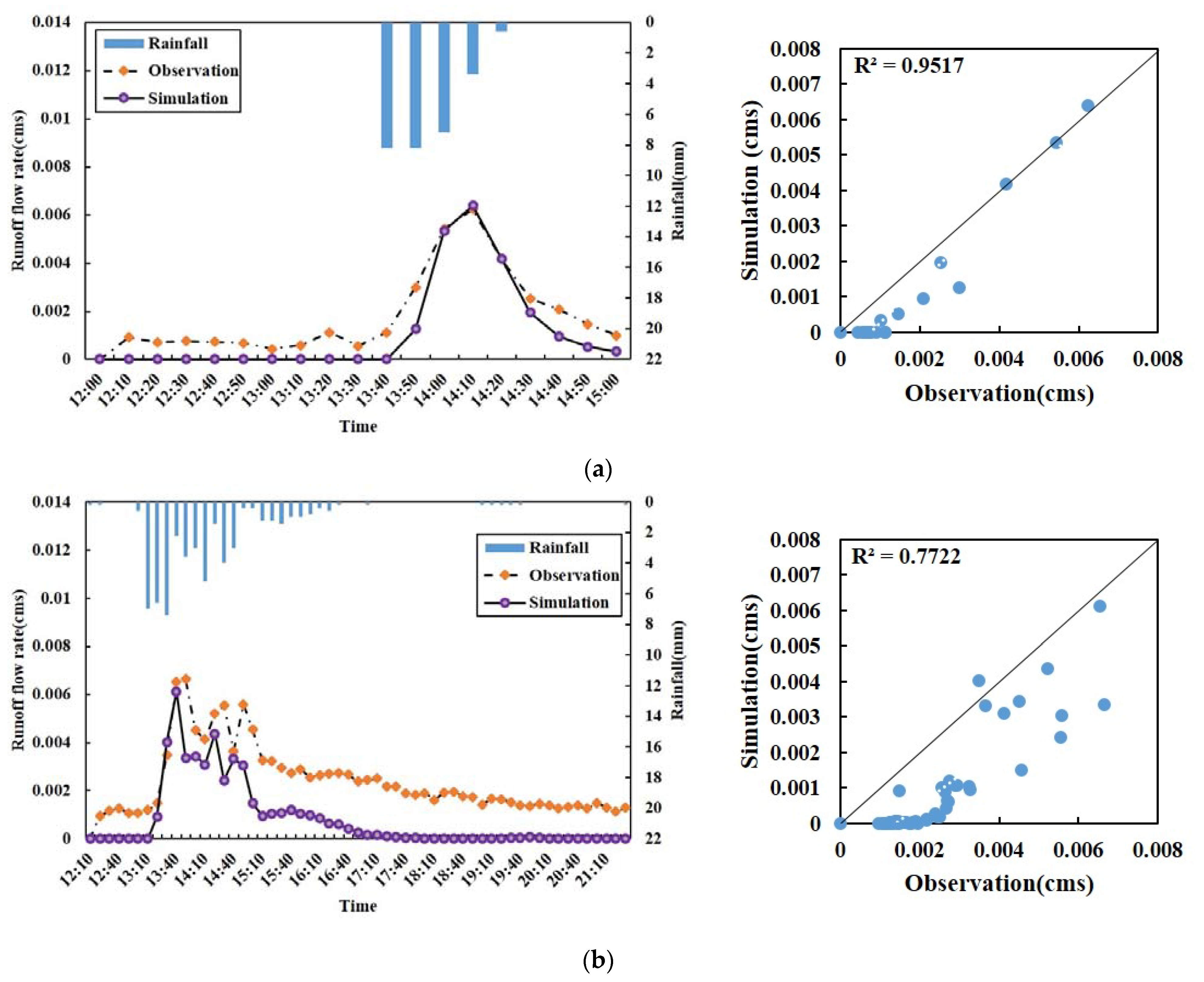
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhan, W.; Chui, T.F.M. Evaluating the life cycle net benefit of low impact development in a city. Urban For. Urban Green. 2016, 20, 295–304. [Google Scholar] [CrossRef]
- Baek, S.; Ligaray, M.; Pachepsky, Y.; Chun, J.A.; Yoon, K.-S.; Park, Y.; Cho, K.H. Assessment of a green roof practice using the coupled SWMM and HYDRUS models. J. Environ. Manag. 2020, 261, 109920. [Google Scholar] [CrossRef]
- Jiang, C.; Li, J.; Li, H.; Li, Y.; Zhang, Z. Low-impact development facilities for stormwater runoff treatment: Field monitoring and assessment in Xi’an area, China. J. Hydrol. 2020, 585, 124803. [Google Scholar] [CrossRef]
- Jia, H.; Lu, Y.; Yu, S.L.; Chen, Y. Planning of LID–BMPs for urban runoff control: The case of Beijing Olympic Village. Sep. Purif. Technol. 2012, 84, 112–119. [Google Scholar] [CrossRef]
- Degtyareva, O.; Degtyarev, G.; Togo, I.; Terleev, V.; Nikonorov, A.; Volkov, Y. Analysis of Stress-strain State Rainfall Runoff Control System–Buttress Dam. Procedia Eng. 2016, 165, 1619–1628. [Google Scholar] [CrossRef]
- Tedoldi, D.; Chebbo, G.; Pierlot, D.; Kovacs, Y.; Gromaire, M.-C. Impact of runoff infiltration on contaminant accumulation and transport in the soil/filter media of Sustainable Urban Drainage Systems: A literature review. Sci. Total. Environ. 2016, 569-570, 904–926. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Cai, Y.; Wang, J. A simulation-based real-time control system for reducing urban runoff pollution through a stormwater storage tank. J. Clean. Prod. 2018, 183, 641–652. [Google Scholar] [CrossRef]
- Ahmadi, M.; Moeini, A.; Ahmadi, H.; Motamedvaziri, B.; Zehtabiyan, G.R. Comparison of the performance of SWAT, IHACRES and artificial neural networks models in rainfall-runoff simulation (case study: Kan watershed, Iran). Phys. Chem. Earth Parts A/B/C 2019, 111, 65–77. [Google Scholar] [CrossRef]
- Srivastava, A.; Kumari, N.; Maza, M. Hydrological Response to Agricultural Land Use Heterogeneity Using Variable Infiltration Capacity Model. Water Resour. Manag. 2020, 34, 3779–3794. [Google Scholar] [CrossRef]
- Srivastava, A.; Sahoo, B.; Raghuwanshi, N.S.; Singh, R. Evaluation of Variable-Infiltration Capacity Model and MODIS-Terra Satellite-Derived Grid-Scale Evapotranspiration Estimates in a River Basin with Tropical Monsoon-Type Climatology. J. Irrig. Drain. Eng. 2017, 143, 04017028. [Google Scholar] [CrossRef] [Green Version]
- Tsihrintzis, V.A.; Hamid, R. Runoff quality prediction from small urban catchments using SWMM. Hydrol. Process. 1998, 12, 311–329. [Google Scholar] [CrossRef]
- Costabile, P.; Costanzo, C.; Ferraro, D.; Macchione, F.; Petaccia, G. Performances of the New HEC-RAS Version 5 for 2-D Hydrodynamic-Based Rainfall-Runoff Simulations at Basin Scale: Comparison with a State-of-the Art Model. Water 2020, 12, 2326. [Google Scholar] [CrossRef]
- Hossain, S.; Hewa, G.A.; Wella-Hewage, S. A Comparison of Continuous and Event-Based Rainfall–Runoff (RR) Modelling Using EPA-SWMM. Water 2019, 11, 611. [Google Scholar] [CrossRef] [Green Version]
- Paul, P.K.; Kumari, N.; Panigrahi, N.; Mishra, A.; Singh, R. Implementation of cell-to-cell routing scheme in a large scale conceptual hydrological model. Environ. Model. Softw. 2018, 101, 23–33. [Google Scholar] [CrossRef]
- Niazi, M.; Nietch, C.; Maghrebi, M.; Jackson, N.; Bennett, B.R.; Tryby, M.; Massoudieh, A. Storm Water Management Model: Performance Review and Gap Analysis. J. Sustain. Water Built Environ. 2017, 3, 04017002. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cheng, Y.-Y.; Lo, S.-L.; Ho, C.-C.; Lin, J.-Y.; Yu, S.L. Field Testing of Porous Pavement Performance on Runoff and Temperature Control in Taipei City. Water 2019, 11, 2635. [Google Scholar] [CrossRef] [Green Version]
- Tsai, L.-Y.; Chen, C.-F.; Fan, C.-H.; Lin, J.-Y. Using the HSPF and SWMM Models in a High Pervious Watershed and Estimating Their Parameter Sensitivity. Water 2017, 9, 780. [Google Scholar] [CrossRef] [Green Version]
- Chang, T.-Y.; Chen, H.; Fu, H.-S.; Chen, W.-B.; Yu, Y.-C.; Su, W.-R.; Lin, L.-Y. An Operational High-Performance Forecasting System for City-Scale Pluvial Flash Floods in the Southwestern Plain Areas of Taiwan. Water 2021, 13, 405. [Google Scholar] [CrossRef]
- Chang, H.-K.; Lin, Y.-J.; Lai, J.-S. Methodology to set trigger levels in an urban drainage flood warning system–An application to Jhonghe, Taiwan. Hydrol. Sci. J. 2017, 63, 31–49. [Google Scholar] [CrossRef]
- Del Giudice, G.; Padulano, R. Sensitivity Analysis and Calibration of a Rainfall-Runoff Model with the Combined Use of EPA-SWMM and Genetic Algorithm. Acta Geophys. 2016, 64, 1755–1778. [Google Scholar] [CrossRef] [Green Version]
- Hamouz, V.; Muthanna, T.M. Hydrological modelling of green and grey roofs in cold climate with the SWMM model. J. Environ. Manag. 2019, 249, 109350. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Yang, Z.; Han, D.; Huang, G.; Zhu, Q. A Framework for Automatic Calibration of SWMM Considering Input Uncertainty. Hydrol. Earth Syst. Sci. Discuss. 2020, 1–25. [Google Scholar] [CrossRef]
- Beven, K.; Freer, J. Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environ-mental systems using the GLUE methodology. J. Hydrol. 2001, 249, 11–29. [Google Scholar] [CrossRef]
- Biondi, D.; De Luca, D. Performance assessment of a Bayesian Forecasting System (BFS) for real-time flood forecasting. J. Hydrol. 2013, 479, 51–63. [Google Scholar] [CrossRef]
- Krzysztofowicz, R. Bayesian system for probabilistic river stage forecasting. J. Hydrol. 2002, 268, 16–40. [Google Scholar] [CrossRef]
- Srinivasulu, S.; Jain, A. A comparative analysis of training methods for artificial neural network rainfall–runoff models. Appl. Soft Comput. 2006, 6, 295–306. [Google Scholar] [CrossRef]
- Kumar, A.R.S.; Sudheer, K.P.; Jain, S.K.; Agarwal, P.K. Rainfall-runoff modelling using artificial neural networks: Comparison of network types. Hydrol. Process. 2005, 19, 1277–1291. [Google Scholar] [CrossRef]
- Asadi, H.; Shahedi, K.; Jarihani, B.; Sidle, R.C. Rainfall-Runoff Modelling Using Hydrological Connectivity Index and Artificial Neural Network Approach. Water 2019, 11, 212. [Google Scholar] [CrossRef] [Green Version]
- Yadav, A.K.; Chandola, V.K.; Singh, A.; Singh, B.P. Rainfall-Runoff Modelling Using Artificial Neural Networks (ANNs) Model. Int. J. Curr. Microbiol. Appl. Sci. 2020, 9, 127–135. [Google Scholar] [CrossRef]
- Kumari, N.; Acharya, S.C.; Renzullo, L.J.; Yetemen, O. Applying rainfall ensembles to explore hydrological uncertainty. In Proceedings of the 23rd International Congress on Modelling and Simulation, Canberra, Australia, 1–6 December 2019; pp. 1070–1076. [Google Scholar] [CrossRef]
- Apaydin, H.; Feizi, H.; Sattari, M.T.; Colak, M.S.; Shamshirband, S.; Chau, K.-W. Comparative Analysis of Recurrent Neural Network Architectures for Reservoir Inflow Forecasting. Water 2020, 12, 1500. [Google Scholar] [CrossRef]
- Erkan, M.; Turan, M. Ali Yurdusev, River flow estimation from upstream flow records by artificial intelligence methods. J. Hydrol. 2009, 369, 71–77. [Google Scholar] [CrossRef]
- Lee, J.; Lee, J.E.; Kim, N.W. Estimation of Hourly Flood Hydrograph from Daily Flows Using Artificial Neural Network and Flow Disaggregation Technique. Water 2020, 13, 30. [Google Scholar] [CrossRef]
- Wan, H.; Bian, J.; Wu, J.; Sun, X.; Wang, Y.; Jia, Z. Prediction of Seasonal Frost Heave Behavior in Unsaturated Soil in Northeastern China Using Interactive Factor Analysis with Split-Plot Experiments and GRNN. Water 2019, 11, 1587. [Google Scholar] [CrossRef] [Green Version]
- Ghritlahre, H.K.; Prasad, R.K. Exergetic performance prediction of solar air heater using MLP, GRNN and RBF models of artificial neural network technique. J. Environ. Manag. 2018, 223, 566–575. [Google Scholar] [CrossRef] [PubMed]
- Izonin, I.; Tkachenko, R.; Verhun, V.; Zub, K. An approach towards missing data management using improved GRNN-SGTM en-semble method. Eng. Sci. Technol. Int. J. 2020. [Google Scholar] [CrossRef]
- First, M.; Turan, M.E.; Yurdusev, M.A. M.; Turan, M.E.; Yurdusev, M.A. Comparative analysis of neural network techniques for predicting water consumption time series. J. Hydrol. 2010, 384, 46–51. [Google Scholar] [CrossRef]
- Behrouz, M.S.; Zhu, Z.; Matott, L.S.; Rabideau, A.J. A new tool for automatic calibration of the Storm Water Management Model (SWMM). J. Hydrol. 2020, 581, 124436. [Google Scholar] [CrossRef]
- Talei, A.; Chua, L.H.C.; Quek, C.; Jansson, P.-E. Runoff forecasting using a Takagi–Sugeno neuro-fuzzy model with online learning. J. Hydrol. 2013, 488, 17–32. [Google Scholar] [CrossRef]
- Alizadeh, M.J.; Kavianpour, M.R.; Kisi, O.; Nourani, V. A new approach for simulating and forecasting the rainfall-runoff process within the next two months. J. Hydrol. 2017, 548, 588–597. [Google Scholar] [CrossRef]
- He, X.; Luo, J.; Zuo, G.; Xie, J. Daily Runoff Forecasting Using a Hybrid Model Based on Variational Mode Decomposition and Deep Neural Networks. Water Resour. Manag. 2019, 33, 1571–1590. [Google Scholar] [CrossRef]
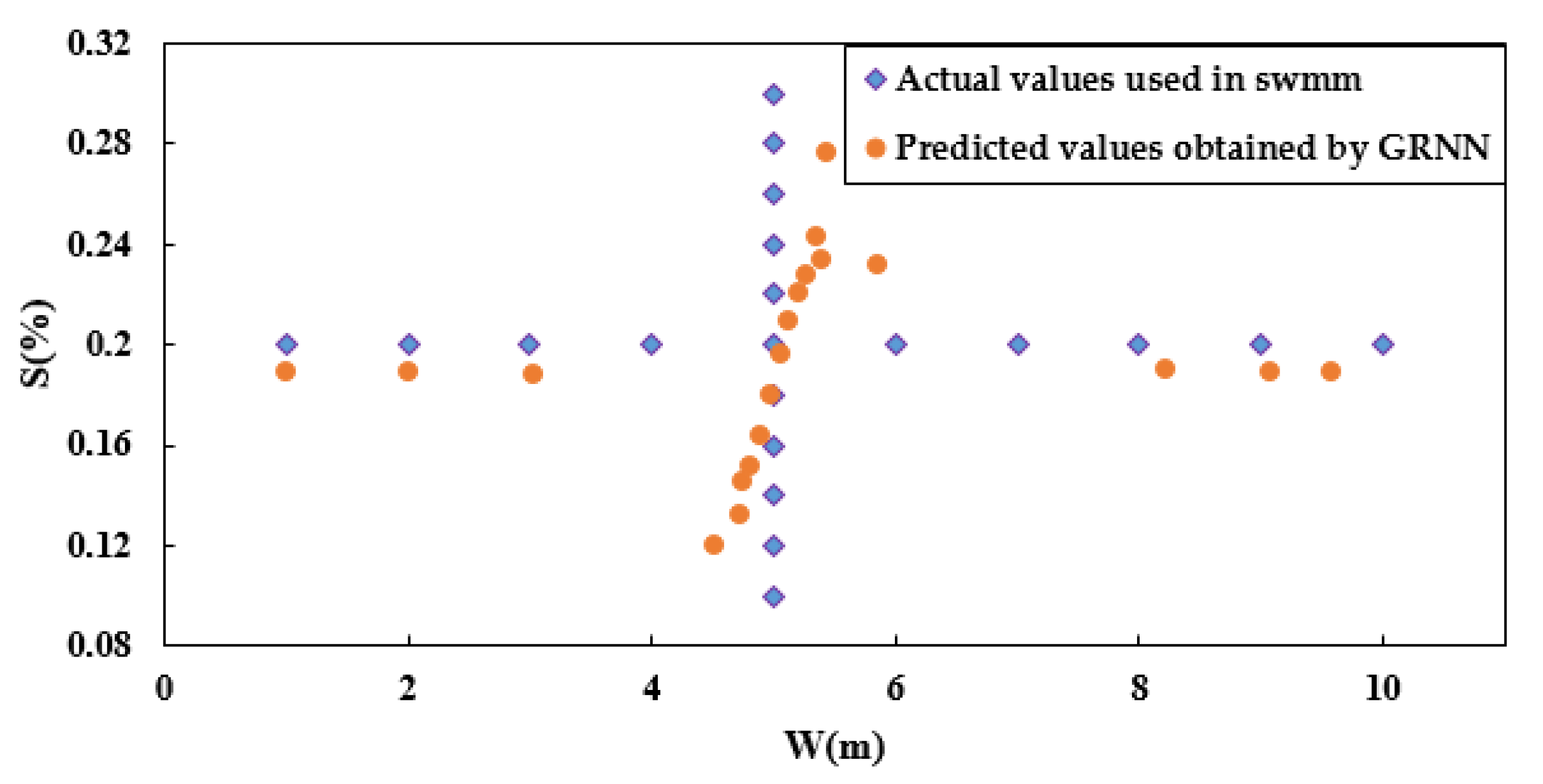
| Parameters | Sub-Catchment 1 | Sub-Catchment 2 |
|---|---|---|
| Area (ha) | 0.058694 | 0.01006 |
| Width (m) | 1–10, Basic value: 5 | 8 |
| Slope (%) | 0.1–0.3, Basic value: 0.2 | 0.1 |
| Imprev (%) | 27.23 | 0 |
| N-Imprev | 0.012 | — |
| N-perv | 0.012 | 0.04 |
| Destore Imprev (mm) | 5 | — |
| Destore–Perv (mm) | 5 | 0.2 |
| Infil. Model | Horton | Horton |
| Zero Imperv (%) | — | — |
| Hyperparameter | Value |
|---|---|
| The number of neurons in input layer | 2 |
| The number of neurons in pattern layer | 18 |
| The number of neurons in summation layer | 2 |
| The number of neurons in output layer | 2 |
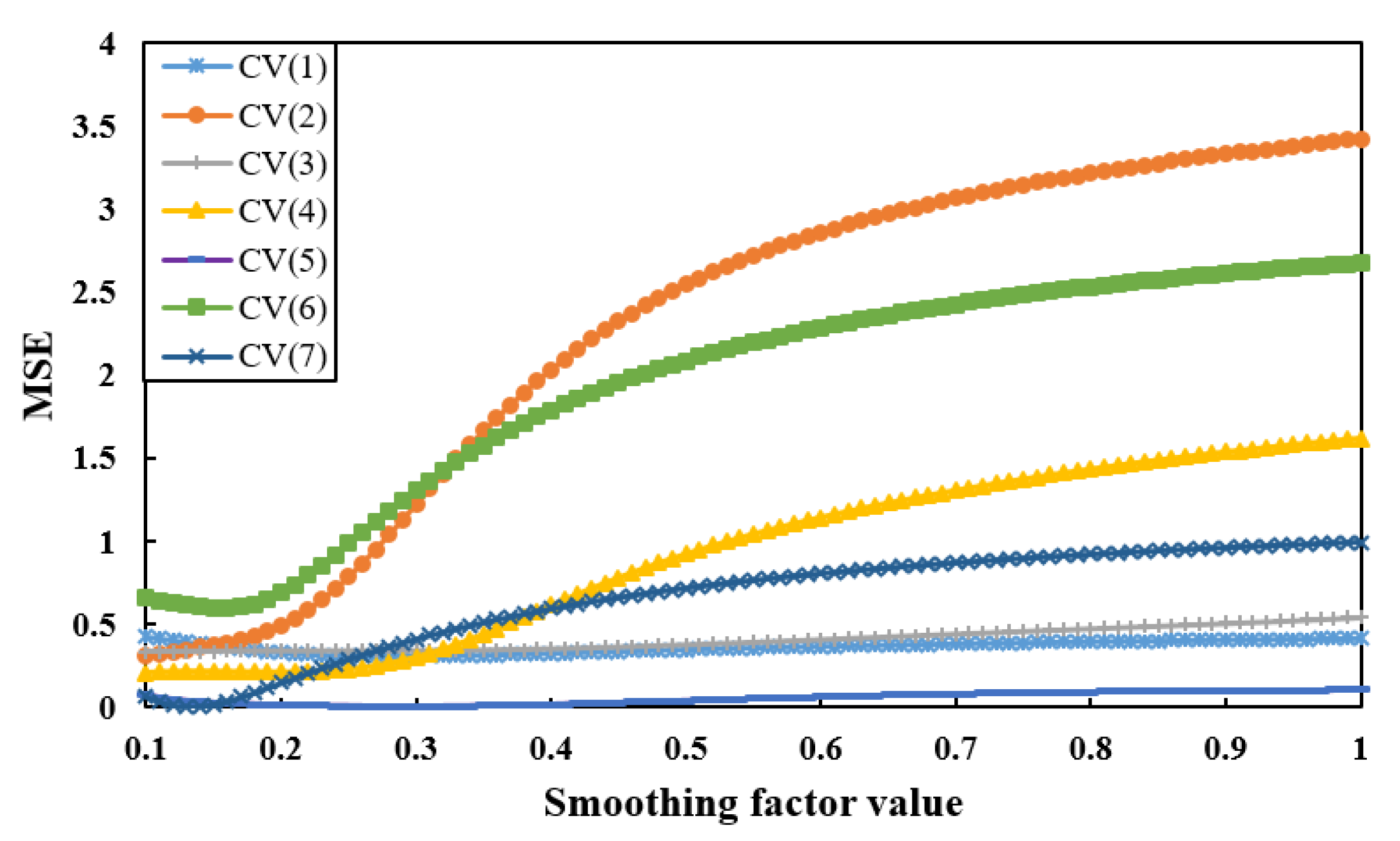
| Smoothing factor | 0.13 |
| Parameter | RMSE | MAPE | NSE |
|---|---|---|---|
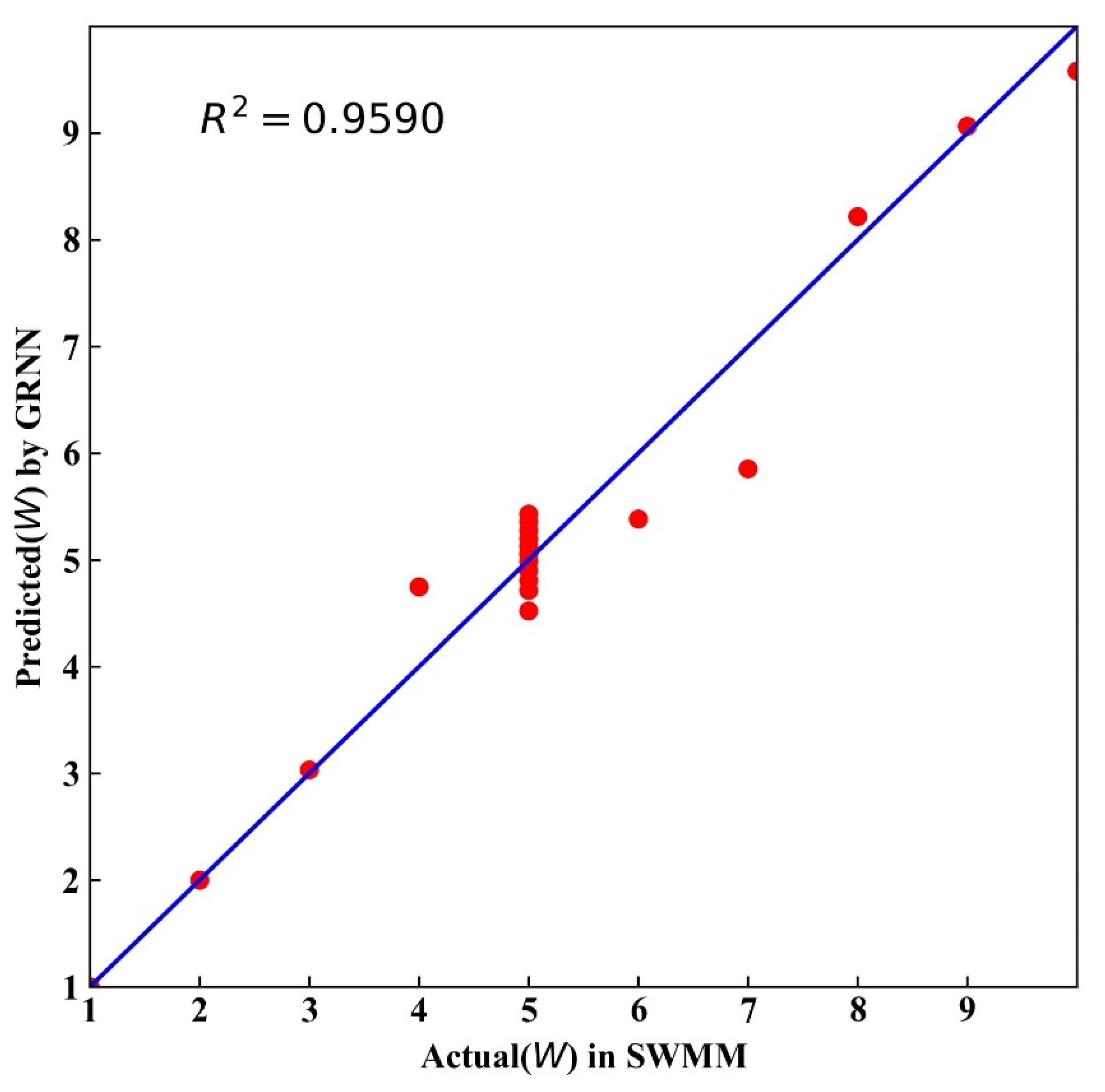
| W | 0.3946 | 5.04% | 0.9950 |
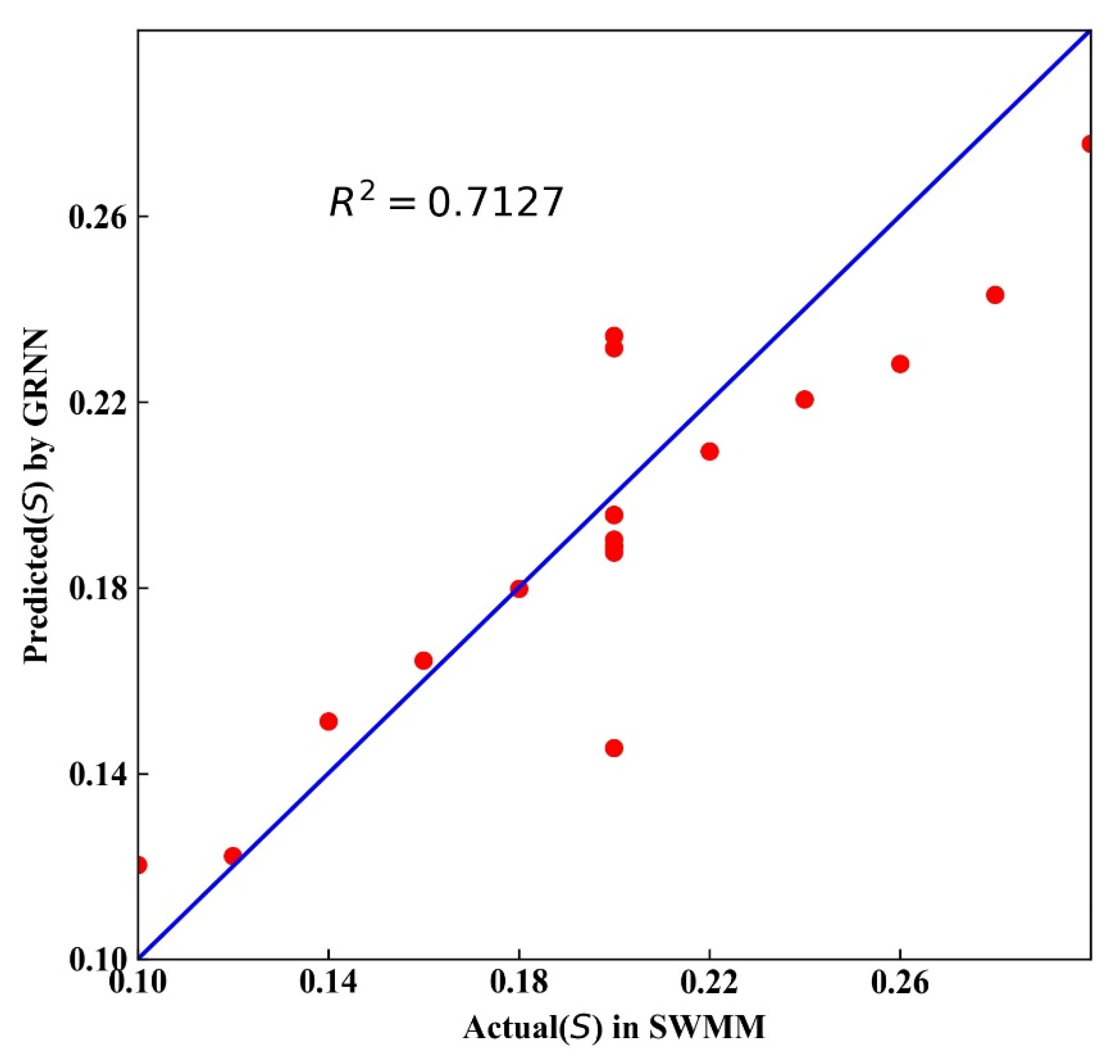
| S | 0.0219 | 8.78% | 0.9878 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Q.-C.; Hsu, T.-H.; Lin, J.-Y. Using the General Regression Neural Network Method to Calibrate the Parameters of a Sub-Catchment. Water 2021, 13, 1089. https://doi.org/10.3390/w13081089
Cai Q-C, Hsu T-H, Lin J-Y. Using the General Regression Neural Network Method to Calibrate the Parameters of a Sub-Catchment. Water. 2021; 13(8):1089. https://doi.org/10.3390/w13081089
Chicago/Turabian StyleCai, Qing-Chi, Tsung-Hung Hsu, and Jen-Yang Lin. 2021. "Using the General Regression Neural Network Method to Calibrate the Parameters of a Sub-Catchment" Water 13, no. 8: 1089. https://doi.org/10.3390/w13081089







