Changes of Streamflow Caused by Early Start of Growing Season in Nevada, United States
Abstract
:1. Introduction
2. Materials and Data
2.1. Study Regions
2.2. Weather Forcing Data
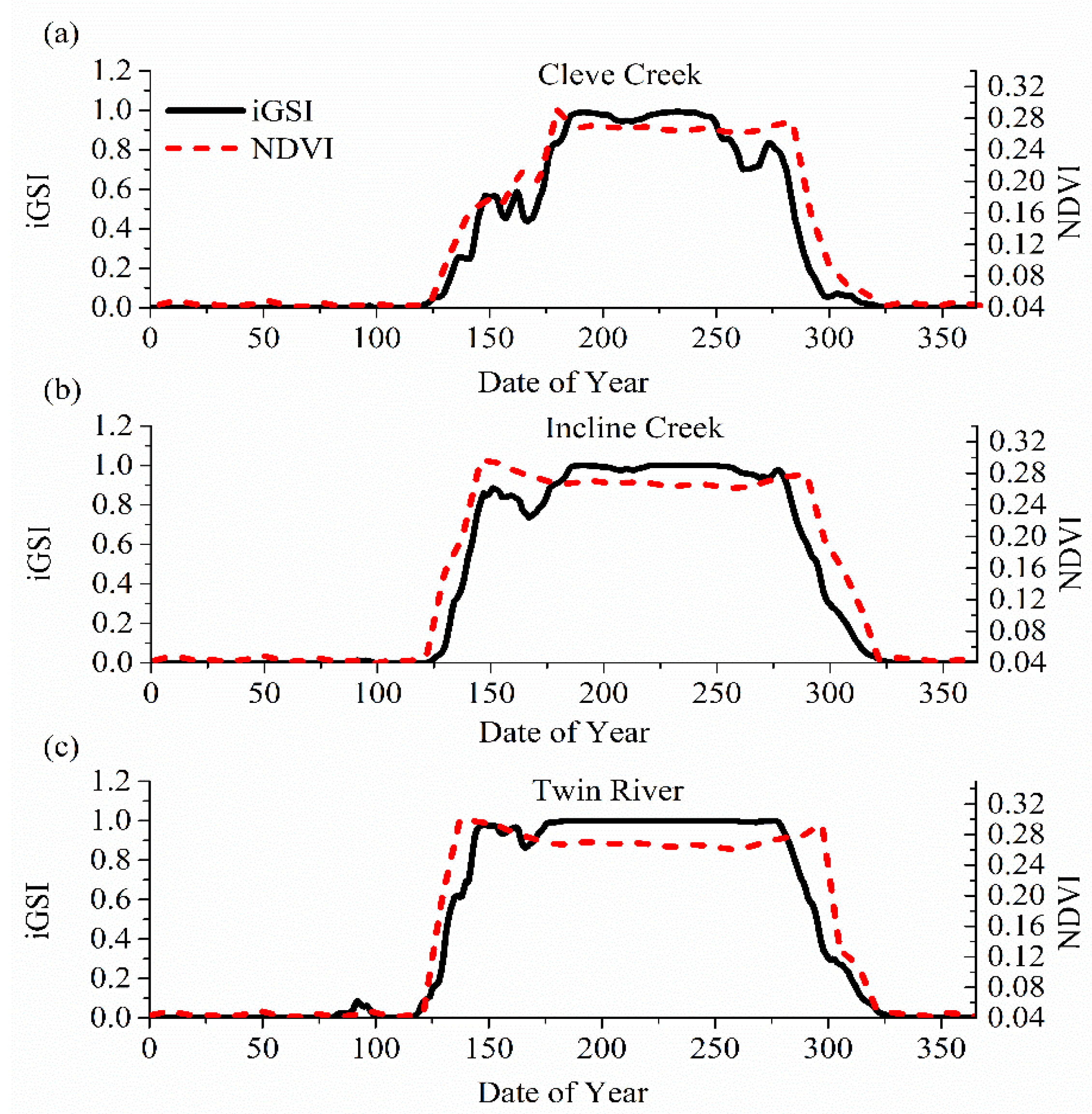
2.3. Estimating Start of Growing Season (SOS)
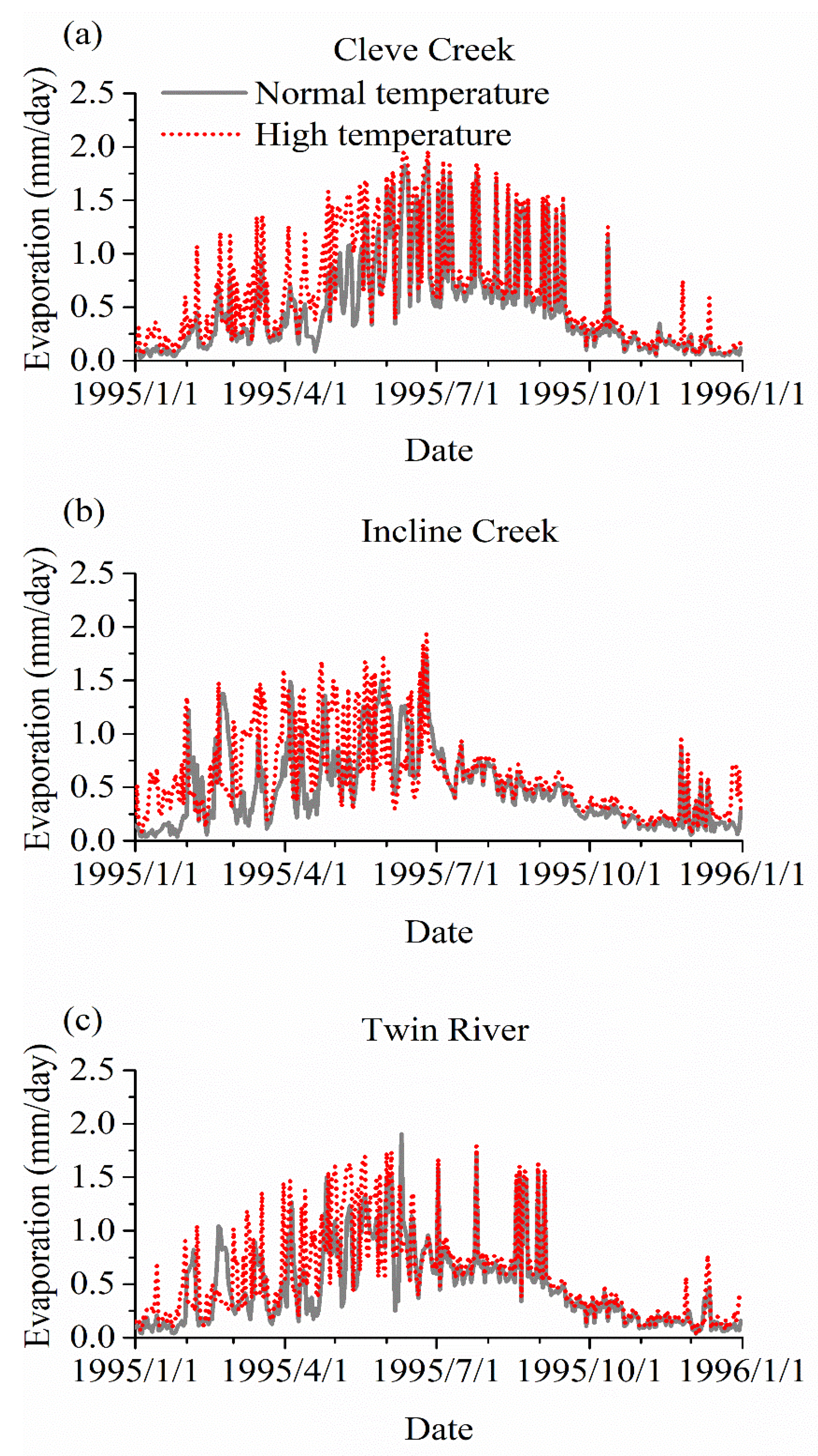
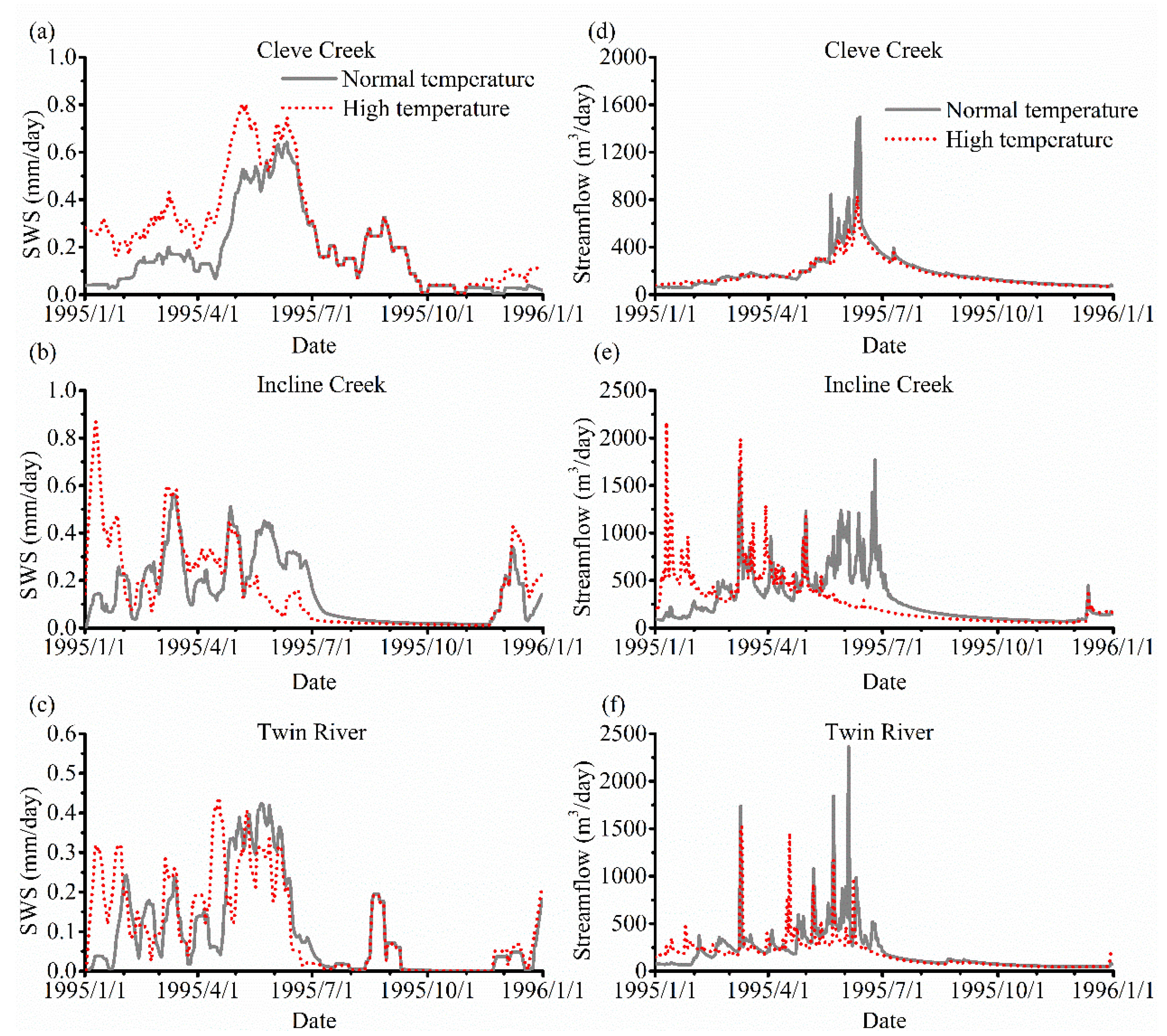
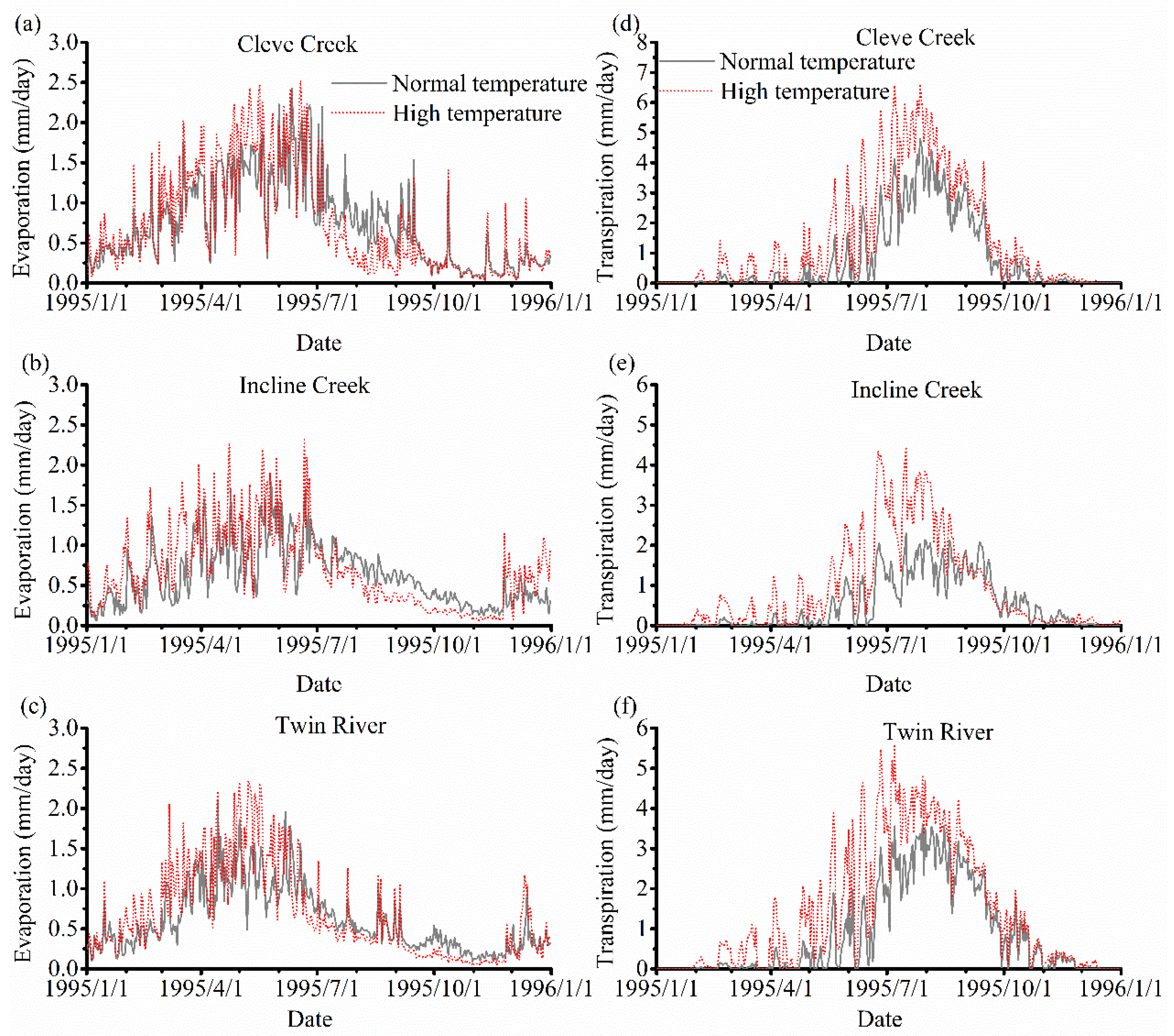
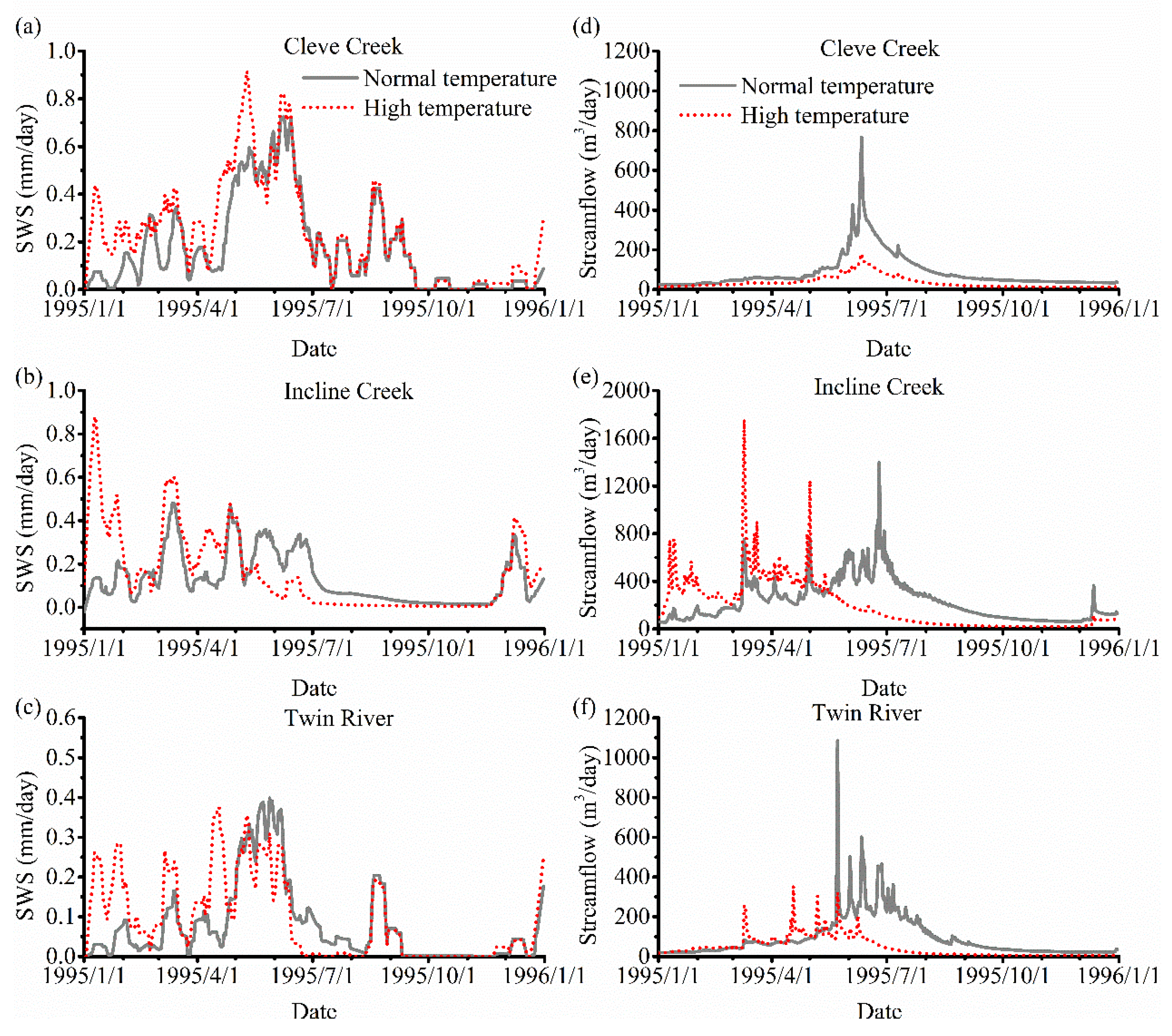
3. Results
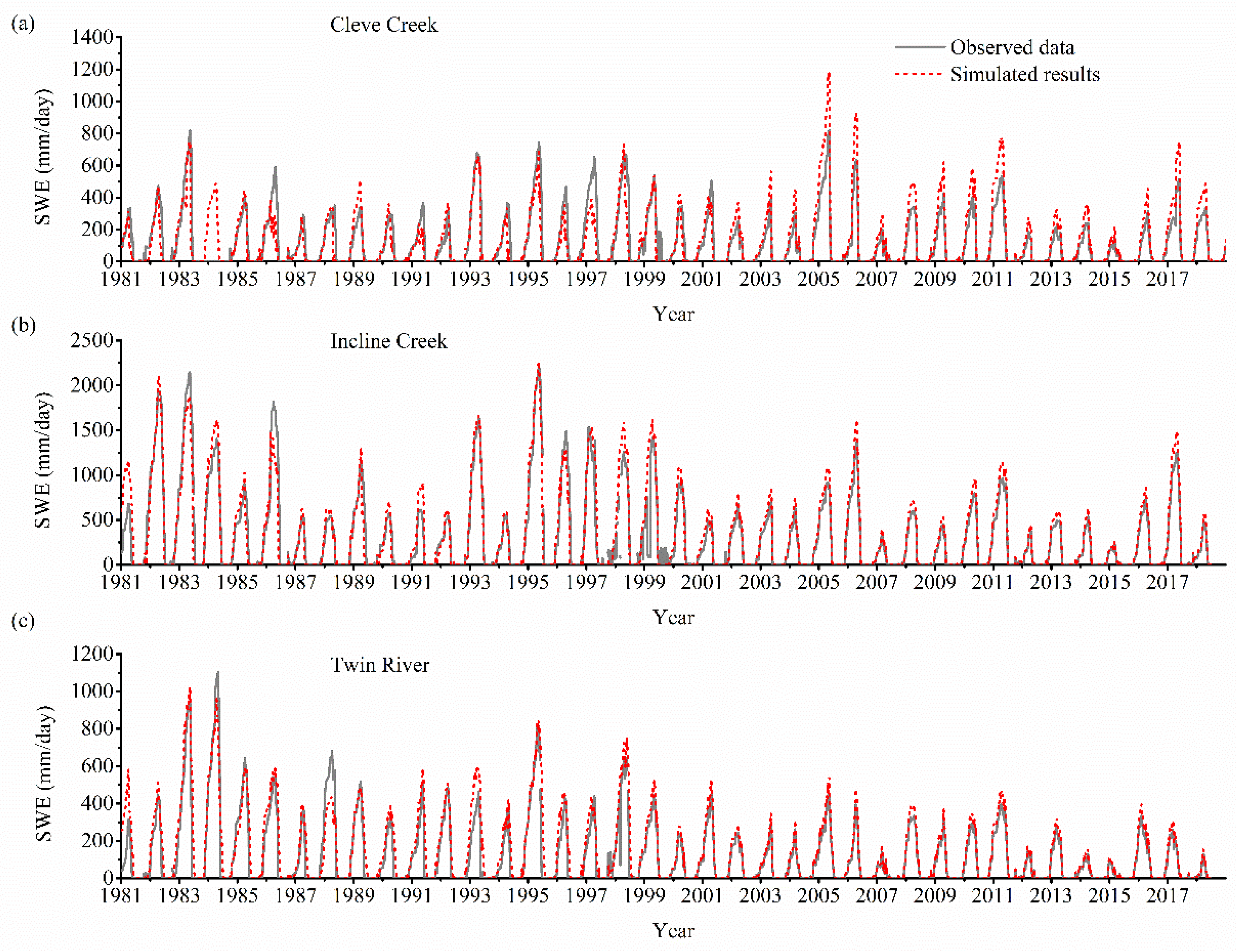
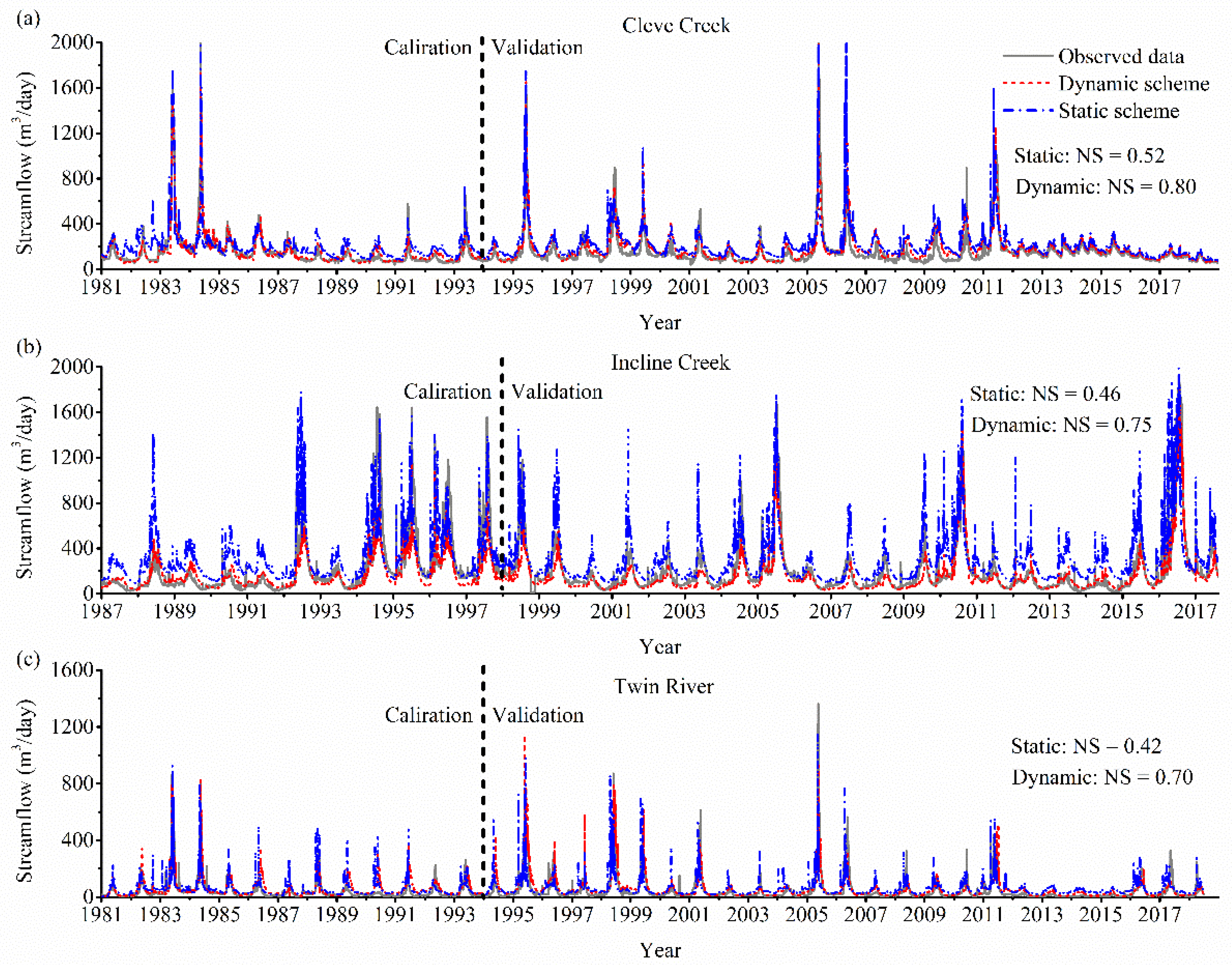
3.1. Model Validation
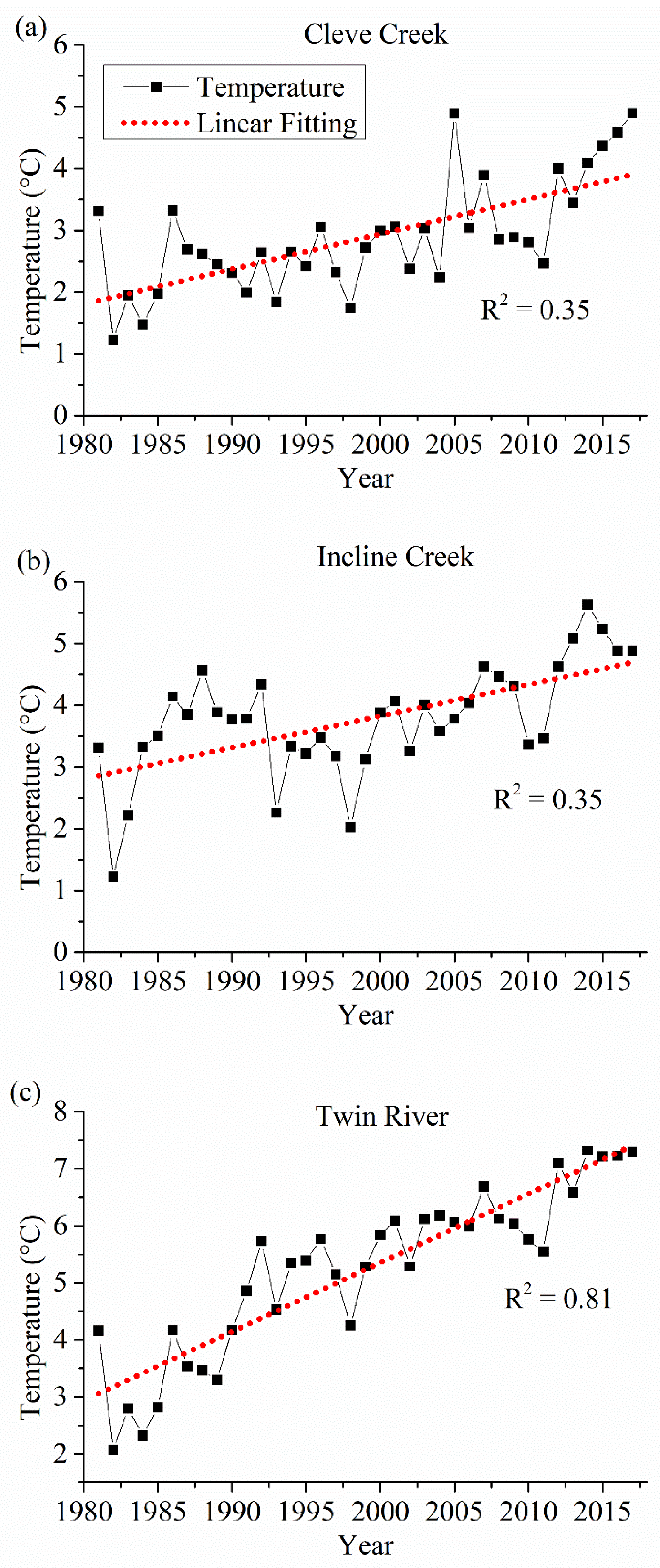
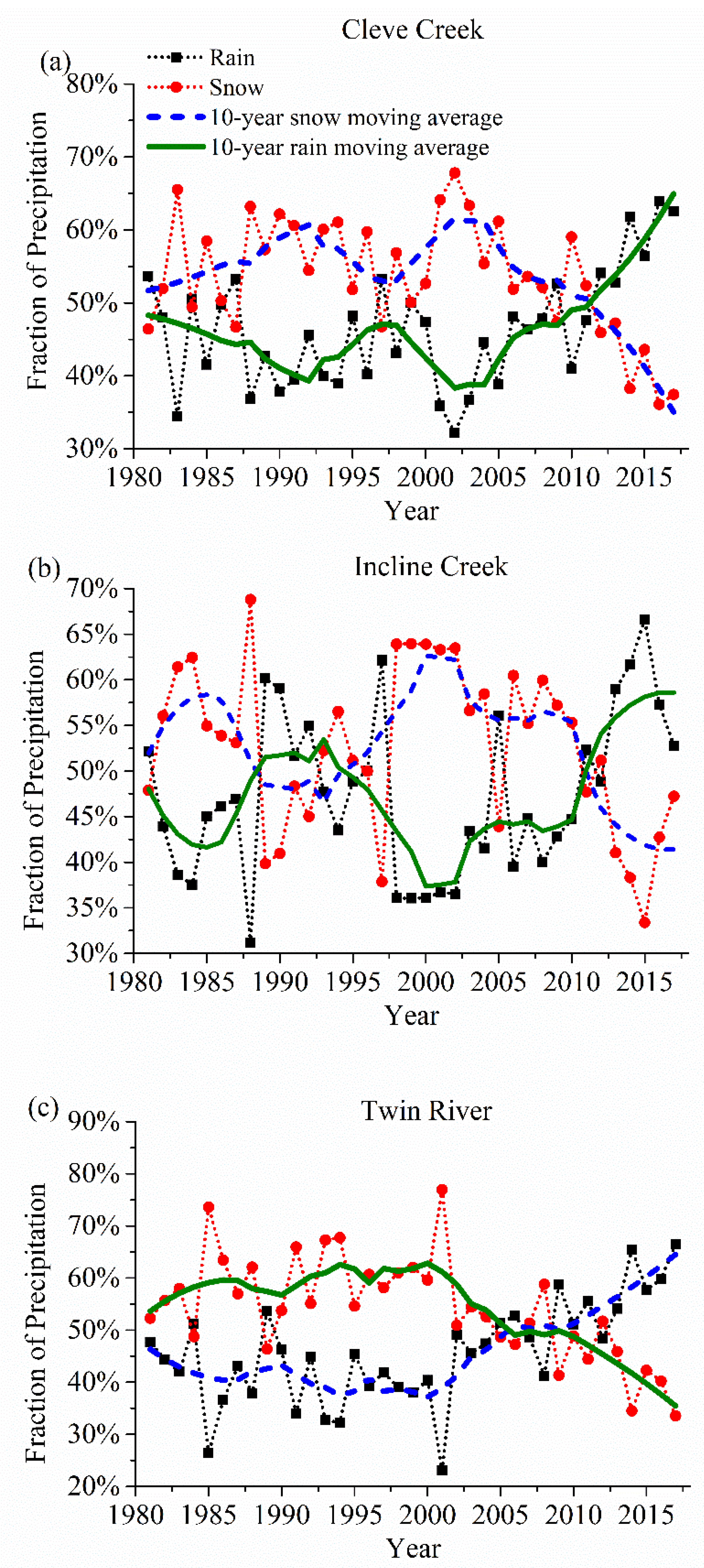
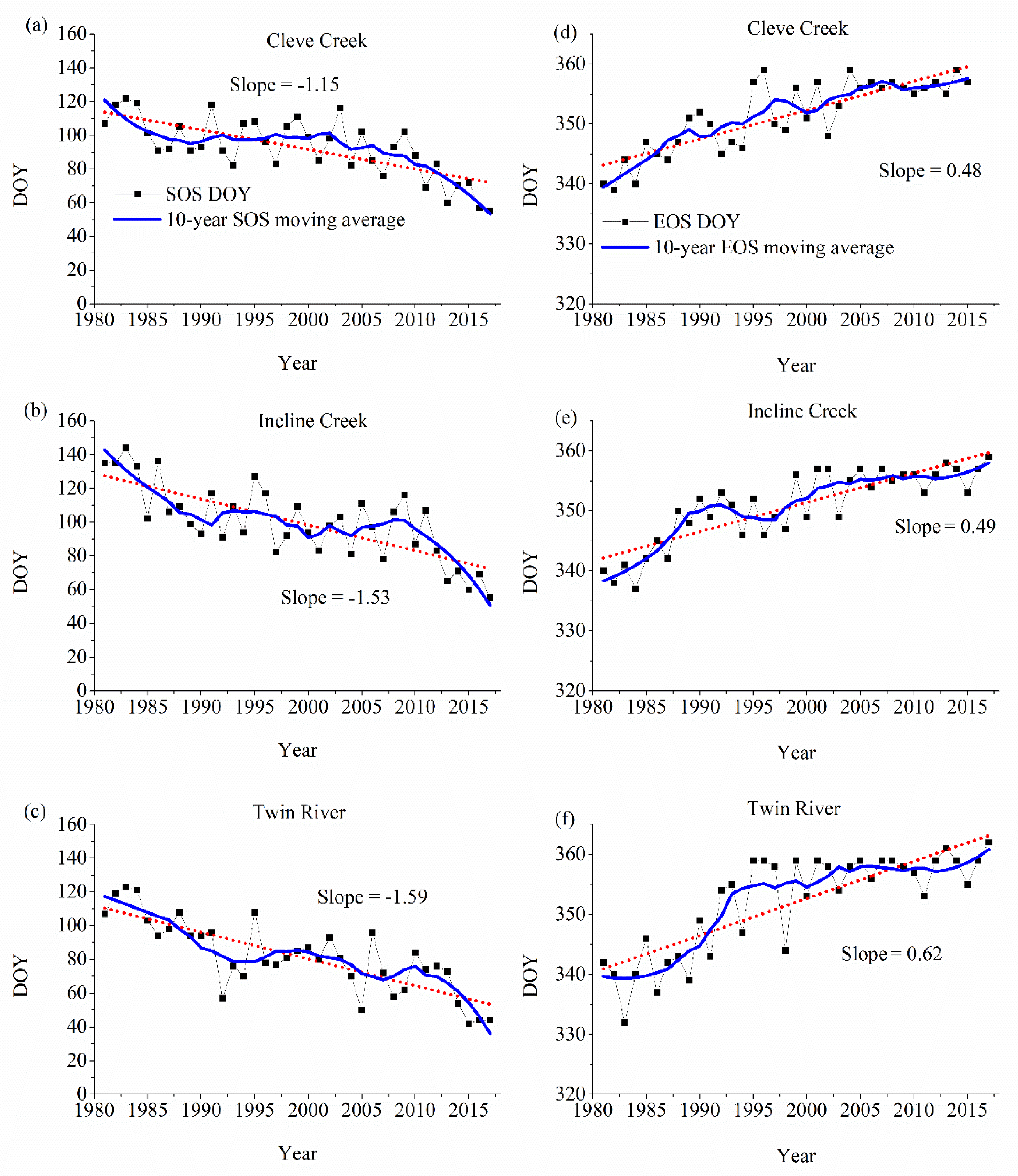
3.2. Changes in SOS and End of Growing Season (EOS)
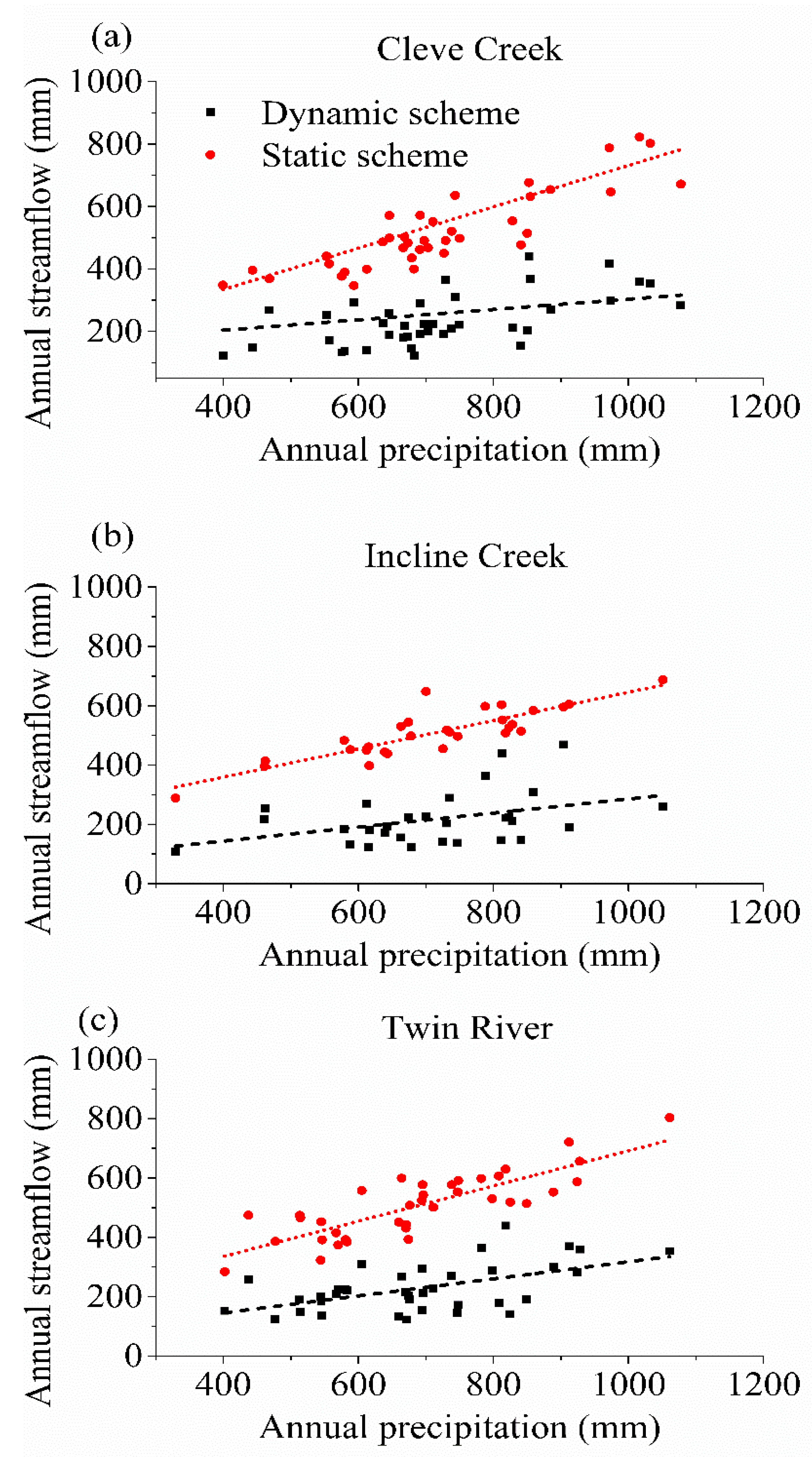
3.3. The Impact of Varying SOS
4. Discussion
4.1. Drivers of the Vegetation Phenological Variations
4.2. The Effect of Vegetation Phenology on Evapotranspiration (ET) and Streamflow
4.3. Long-Term Influence of Early SOS
4.4. Future Work
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Enzminger, T.L.; Small, E.E.; Borsa, A.A. Accuracy of Snow Water Equivalent Estimated From GPS Vertical Displacements: A Synthetic Loading Case Study for Western U.S. Mountains. Water Resour. Res. 2018, 54, 581–599. [Google Scholar] [CrossRef]
- Serreze, M.C.; Clark, M.P.; Armstrong, R.L.; McGinnis, D.A.; Pulwarty, R.S. Characteristics of the western United States snowpack from snowpack telemetry (SNOTEL) data. Water Resour. Res. 1999, 35, 2145–2160. [Google Scholar] [CrossRef] [Green Version]
- Tamaddun, K.A.; Kalra, A.; Bernardez, M.; Ahmad, S. Multi-Scale Correlation between the Western U.S. Snow Water Equivalent and ENSO/PDO Using Wavelet Analyses. Water Resour. Manag. 2017, 31, 2745–2759. [Google Scholar] [CrossRef]
- Dierauer, J.R.; Allen, D.M.; Whitfield, P.H. Snow drought risk and susceptibility in the western United States and southwestern Canada. Water Resour. Res. 2019, 55, 3076–3091. [Google Scholar] [CrossRef]
- Lapo, K.E.; Hinkelman, L.M.; Raleigh, M.S.; Lundquist, J.D. Impact of errors in the downwelling irradiances on simulations of snow water equivalent, snow surface temperature, and the snow energy balance. Water Resour. Res. 2015, 51, 1649–1670. [Google Scholar] [CrossRef]
- Gergel, D.R.; Nijssen, B.; Abatzoglou, J.T.; Lettenmaier, D.P.; Stumbaugh, M.R. Effects of climate change on snowpack and fire potential in the western USA. Clim. Chang. 2017, 141, 287–299. [Google Scholar] [CrossRef]
- Kelleners, T.J.; Chandler, D.G.; McNamara, J.P.; Gribb, M.M.; Seyfried, M.S. Modeling runoff generation in a small snow-dominated mountainous catchment. Vadose Zone J. 2010, 9, 517–527. [Google Scholar] [CrossRef] [Green Version]
- Papalexiou, S.M.; Montanari, A. Global and Regional Increase of Precipitation Extremes under Global Warming. Water Resour. Res. 2019, 55, 4901–4914. [Google Scholar] [CrossRef]
- Tague, C.; Grant, G.E. Groundwater dynamics mediate low-flow response to global warming in snow-dominated alpine regions. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Tang, G.; Arnone, J.A., III; Verburg, P.S.J.; Jasoni, R.L.; Sun, L. Trend and climatic sensitivity of vegetation phenology in semiarid and arid ecosystems in the US Great Basin during 1982–2011. Biogeosciences 2009, 12. [Google Scholar] [CrossRef] [Green Version]
- Vincent, L.A.; Zhang, X.; Hogg, W.D. Maximum and minimum temperature trends in Canada for 1895–1995 and 1945–1995. In Proceedings of the 10th Symposium on Global Change Studies, Dallas, TX, USA, 10–15 January 1999; pp. 95–98. [Google Scholar]
- Nayak, A.; Marks, D.; Chandler, D.G.; Seyfried, M. Long-term snow, climate, and streamflow trends at the Reynolds Creek Experimental Watershed, Owyhee Mountains, Idaho, United States. Water Resour. Res. 2010, 46, W06519.1–W06529.15. [Google Scholar] [CrossRef]
- Bonan, G.B. Forests and climate change: Forcings 2010, feedbacks, and the climate benefits of forests. Science 2008, 320, 1444–1449. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hao, L.; Sun, G.; Liu, Y.; Zhou, G.; Wan, J.; Zhang, L.; Niu, J.; Sang, Y.; He, J. Evapotranspiration and soil moisture dynamics in a temperate grassland ecosystem in Inner Mongolia, China. Trans. ASABE 2016, 59, 577–590. [Google Scholar] [CrossRef]
- Sun, G.; Caldwell, P.; Noormets, A.; McNulty, S.G.; Cohen, E.; Moore, M.; Jennifer, D.; Treasure, E.; Mu, Q.; Xiao, J.; et al. Upscaling key ecosystem functions across the conterminous United States by a water-centric ecosystem model. J. Geophys. Res. 2011, 116, G00J05. [Google Scholar] [CrossRef]
- Hewlett, J.D.; Fortson, J.C.; Cunningham, G.B. The effect of rainfall intensity on storm flow and peak discharge from forest land. Water Resour. Res. 1977, 13, 259–266. [Google Scholar] [CrossRef]
- Sun, G.; Hallema, D.; Asbjornsen, H. Ecohydrological processes and ecosystem services in the Anthropocene: A review. Ecol. Process. 2017, 6, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Andréassian, V. Waters and forests: From historical controversy to scientific debate. J. Hydrol. 2004, 291, 1–27. [Google Scholar] [CrossRef]
- Bruijnzeel, L.A. Hydrological functions of tropical forests: Not seeing the soil for the trees? Agric. Ecosyst. Environ. 2004, 104, 185–228. [Google Scholar] [CrossRef]
- Jackson, R.B. Trading water for carbon with biological sequestration. Science 2005, 310, 1944–1947. [Google Scholar] [CrossRef] [Green Version]
- Sun, G.; Riekerk, H.; Kornhak, L.V. Ground-water-table rise after forest harvesting on cypress-pine flatwoods in Florida. Wetlands 2000, 20, 101–112. [Google Scholar] [CrossRef]
- Fu, Z.; Stoy, P.C.; Luo, Y.; Chen, J.; Sun, J.; Montagnani, L.; Wohlfahrt, G.; Rahman, A.F.; Rambal, S.; Bernhofer, C.; et al. Climate controls over the net carbon uptake period and amplitude of net ecosystem production in temperate and boreal ecosystems. Agric. For. Meteorol. 2017, 243, 9–18. [Google Scholar] [CrossRef] [Green Version]
- Hmimina, G.; Yu, R.; Billesbach, D.P.; Huemmrich, K.F.; Gamon, J.A. Changes in Arctic and Boreal Ecosystem Productivity in Response to Changes in Growing Season Length; AGU Fall Meeting Abstracts: New Orleans, LA, USA, 2017. [Google Scholar]
- Dunn, A.L.; Barford, C.C.; Wofsy, S.C.; Goulden, M.L.; Daube, B.C. A long-term record of carbon exchange in a boreal black spruce forest: Means 2017, responses to interannual variability, and decadal trends. Glob. Change Biol. 2007, 13, 577–590. [Google Scholar] [CrossRef] [Green Version]
- Winchell, T.; Molotch, N.P.; Barnard, D.M. Early Snowmelt Decreases Ablation Period Carbon Uptake in a High Elevation, Subalpine Forest; AGU Fall Meeting Abstracts: Niwot Ridge, CO, USA, 2015. [Google Scholar]
- Wohlfahrt, G.; Cremonese, E.; Hammerle, A.; Hortnagl, L.; Galvagno, M.; Gianelle, D.; Marcolla, B.; di Cella, U.M. Trade-offs between global warming and day length on the start of the carbon uptake period in seasonally cold ecosystems. Geophys. Res. Lett. 2013, 40, 6136–6142. [Google Scholar] [CrossRef]
- Saksa, P.C.; Conklin, M.H.; Battles, J.J.; Tague, C.L.; Bales, R.C. Forest thinning impacts on the water balance of Sierra Nevada mixed-conifer headwater basins. Water Resour. Res. 2017, 53, 5364–5381. [Google Scholar] [CrossRef] [Green Version]
- Son, K.; Tague, C. Hydrologic responses to climate warming for a snow-dominated watershed and a transient snow watershed in the California Sierra. Ecohydrology 2019, 12, e2053. [Google Scholar] [CrossRef] [Green Version]
- Bell, C.D.; Tague, C.L.; McMillan, S.K. Modeling Runoff and Nitrogen Loads From a Watershed at Different Levels of Impervious Surface Coverage and Connectivity to Storm Water Control Measures. Water Resour. Res. 2019, 55, 2690–2707. [Google Scholar] [CrossRef]
- Shin, H.; Park, M.; Lee, J.; Lim, H.; Kim, S.J. Evaluation of the effects of climate change on forest watershed hydroecology using the RHESSys model: Seolmacheon catchment. Paddy Water Environ. 2019, 17, 581–595. [Google Scholar] [CrossRef]
- Shields, C.; Tague, C. Ecohydrology in semiarid urban ecosystems: Modeling the relationship between connected impervious area and ecosystem productivity. Water Resour. Res. 2015, 51, 302–319. [Google Scholar] [CrossRef]
- Doten, C.O.; Bowling, L.C.; Lanini, J.S.; Maurer, E.P.; Lettenmaier, D.P. A spatially distributed model for the dynamic prediction of sediment erosion and transport in mountainous forested watersheds. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Tang, G.; Schneiderman, E.M.; Band, L.E.; Hwang, T.; Zion, M.S. Does consideration of water routing affect simulated water and carbon dynamics in terrestrial ecosystems? Hydrol. Earth Syst. Sci. Discuss. 2014, 18, 12537–12571. [Google Scholar] [CrossRef] [Green Version]
- Tang, G.; Carroll Rosemary, W.H.; Lutz, A.; Sun, L. Regulation of precipitation-associated vegetation dynamics on catchment water balance in a semiarid and arid mountainous watershed. Ecohydrology 2016, 9, 1248–1262. [Google Scholar] [CrossRef]
- Tang, G.; Li, S.; Yang, M.; Xu, Z.; Liu, Y.; Gu, H. Streamflow response to snow regime shift associated with climate variability in four mountain watersheds in the US Great Basin. J. Hydrol. 2019, 573, 255–266. [Google Scholar] [CrossRef]
- Tang, G.; Arnone, J.A., III. Trends in surface air temperature and temperature extremes in the Great Basin during the 20th century from ground-based observations. J. Geophys. Res. Atmos. 2013, 118, 3579–3589. [Google Scholar] [CrossRef]
- Menzel, A.; Sparks, T.H.; Estrella, N.; Koch, E.; Aasa, A.; Ahas, R.; Alm-Kübler, K.; Bissolli, P.; Braslavská, O.G.; Briede, A.; et al. European phonological response to climate change matches the warming pattern. Glob. Change Biol. 2006, 12, 1969–1976. [Google Scholar] [CrossRef]
- Prodon, R.; Geniez, P.; Cheylan, M.; Devers, F.; Besnard, A. A reversal of the shift towards earlier spring phenology in several Mediterranean reptiles and amphibians during the 1998–2013 warming slowdown. Glob. Change Biol. 2017, 23. [Google Scholar] [CrossRef]
- Sillett, T.S.; Holmes, R.T.; Sherry, T.W. Impacts of a Global Climate Cycle on Population Dynamics of a Migratory Songbird. Science 2000, 288, 2040–2042. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.; Piao, S.; Delpierre, N.; Hao, F.; Hanninen, H.; Liu, Y.; Sun, W.; Janssens, I.A.; Campioli, M. Larger temperature response of autumn leaf senescence than spring leaf-out phenology. Glob. Change Biol. 2017, 24, 2159–2168. [Google Scholar] [CrossRef] [PubMed]
- Jolly, W.N.; Nemani, R.; Running, S.W. A generalized, bioclimatic index to predict foliarphenology in response to climate. Glob. Change Biol. 2005, 11, 619–632. [Google Scholar] [CrossRef]
- Lieberman, D. Seasonality and phenology in a dry tropical forest in Ghana. J. Ecol. 1982, 70, 791–806. [Google Scholar] [CrossRef]
- Larcher, W.; Bauer, H. Ecological significance of resistance to low temperature. In Physiological Plant Ecology; Springer: Berlin/Heidelberg, Germany, 1981; Volume 12, pp. 403–437. [Google Scholar] [CrossRef]
- Waring, R.H. Forest plants of the eastern Siskiyous: Their environmental and vegetational distribution. Northwest Sci. 1969, 43, 1–17. [Google Scholar]
- Osonubi, O.; Davies, W. The influence of plant water stress on stomatal control of gas exchange at different levels of atmospheric humidity. Oecologia 1980, 46, 1–6. [Google Scholar] [CrossRef]
- Tenhunen, J.D.; Lange, O.L.; Jahner, D. The control by atmospheric factors and water stress of midday stomatal closure in Arbutus unedo growing in a natural macchia. Oecologia 1982, 55, 165–169. [Google Scholar] [CrossRef]
- Borchert, R.; Rivera, G. Photoperiodic control of seasonal development and dormancy in tropical stem-succulent trees. Tree Physiol. 2001, 21, 213–221. [Google Scholar] [CrossRef]
- Xu, B.; Chen, H.; Sun, S.; Gao, C. Large discrepancy between measured and remotely sensed snow water equivalent in the northern Europe and western Siberia during boreal winter. Theor. Appl. Climatol. 2019, 137, 133–140. [Google Scholar] [CrossRef]
- Miranda-Aragón, L. NDVI-rainfall relationship using hyper-temporal satellite data in a portion of North Central Mexico 2000-2010. Afr. J. Agric. Res. 2012, 7, 1023–1033. [Google Scholar] [CrossRef]
- Chuine, I. Why does phenology drive species distribution? Philos. Trans. R. Soc. Lond. B Biol. Sci. 2010, 365, 3149–3160. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hanninen, H. Boreal and Temperate Trees in a Changing Climate; Spirnger: Dordrecht, The Netherlands, 2016; Volume 3. [Google Scholar] [CrossRef]
- Cooke, J.E.; Eriksson, M.E.; Junttila, O. The dynamic nature of bud dormancy in trees: Environmental control and molecular mechanisms. Plant Cell Environ. 2012, 35, 1707–1728. [Google Scholar] [CrossRef] [PubMed]
- Wareing, P. Photoperiodism in woody plants. Annu. Rev. Plant Physiol. 1956, 7, 191–214. [Google Scholar] [CrossRef]
- Jaworski, T.; Hilszczański, J. The effect of temperature and humidity changes on insects development their impact on forest ecosystems in the expected climate change. For. Res. Pap. 2013, 74, 345–355. [Google Scholar] [CrossRef]
- Zeng, H.; Jia, G. Impacts of snow cover on vegetation phenology in the arctic from satellite data. Adv. Atmos. Sci. 2013, 30, 1421–1432. [Google Scholar] [CrossRef]
- Piao, S.; Liu, Q.; Chen, A.; Janssens, I.A.; Fu, Y.; Dai, J.; Liu, L.; Lian, X.; Shen, M.; Zhu, X. Plant phenology and global climate change: Current progresses and challenges. Glob. Change Biol. 2019, 25, 1922–1940. [Google Scholar] [CrossRef]
- Grelle, A.; Lundberg, A.; Lindroth, A.; Moren, A.S.; Cienciala, E. Evaporation components of a boreal forest: Variations during the growing season. J. Hydrol. 1997, 197, 70–87. [Google Scholar] [CrossRef]
- Tapash, D.; Pierce, D.W.; Cayan, R.D.; Vano, J.A.; Lettenmaier, D.P. The importance of warm season warming to western U.S. streamflow changes. Geophys. Res. Lett. 2011, 38, L23403. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Tian, F.; Yang, L.; Hu, H. Exploring the spatial variability of contributions from climate variation and change in catchment properties to streamflow decrease in a mesoscale basin by three different methods. J. Hydrol. 2014, 208, 170–180. [Google Scholar] [CrossRef]
- Yamazaki, T.; Yabuki, H.; Ishii, Y.; Ohata, T. Water and energy exchanges at forests and a grassland in eastern Siberia evaluated using a one-dimensional land surface model. J. Hydrometeorol. 2004, 5, 504–515. [Google Scholar] [CrossRef]
- Schlesinger, W.H.; Jasechko, S. Transpiration in the global water cycle. Agric. For. Meteorol. 2014, 189–190, 115–117. [Google Scholar] [CrossRef]
- Hwang, T.; Martin, K.L.; Vose, J.M.; Wear, D.; Miles, B.; Kim, Y.; Band, L.E. Nonstationary hydrologic behavior in forested watersheds is mediated by climate-induced changes in growing season length and subsequent vegetation growth. Water Resour. Res. 2018, 54, 5359–5375. [Google Scholar] [CrossRef]
- Brooks, J.R.; Barnard, H.R.; Coulombe, R.; McDonnell, J.J. Ecohydrologic separation of water between trees and streams in a Mediterranean climate. Nat. Geosci. 2010, 3, 100–104. [Google Scholar] [CrossRef]
- Wang, H.; Tetzlaff, D.; Buttle, J.; Carey, S.K.; Laudon, H.; McNamara, J.P.; Spence, C.; Soulsby, C. Climate-phenology-hydrology interactions in northern high latitudes: Assessing the value of remote sensing data in catchment ecohydrological studies. Sci. Total Environ. 2019, 656, 19–28. [Google Scholar] [CrossRef] [Green Version]
- Houghton, J.; Ding, Y.H.; Griggs, J.; Noguer, M.; Johnson, C.A. Physical climate processes and feedbacks 2001. In Climate Change 2001: The Scientific Basis; Cambridge University Press: Cambridge, UK, 2001; Chapter 7; pp. 419–470. [Google Scholar]
- Singh, V.P. Effect of spatial and temporal variability in rainfall and watershed characteristics on stream flow hydrograph. Hydrol. Process. 1997, 11, 1649–1669. [Google Scholar] [CrossRef]
- Abramoff, R.Z.; Finzi, A.C. Are above-and below-ground phenology in sync? New Phytol. 2015, 205, 1054–1061. [Google Scholar] [CrossRef] [PubMed]
- Steinaker, D.F.; Wilson, S.D.; Peltzer, D.A. Asynchronicity in root and shoot phenology in grasses and woody plants. Glob. Change Biol. 2010, 16, 2241–2251. [Google Scholar] [CrossRef]
- Kharouba, H.M.; Ehrlén, J.; Gelman, A.; Bolmgren, K.; Allen, J.M.; Travers, S.E.; Wolkovich, E.M. Global shifts in the phenological synchrony of species interactions over recent decades. Proc. Natl. Acad. Sci. USA 2018, 115, 5211–5216. [Google Scholar] [CrossRef] [PubMed] [Green Version]
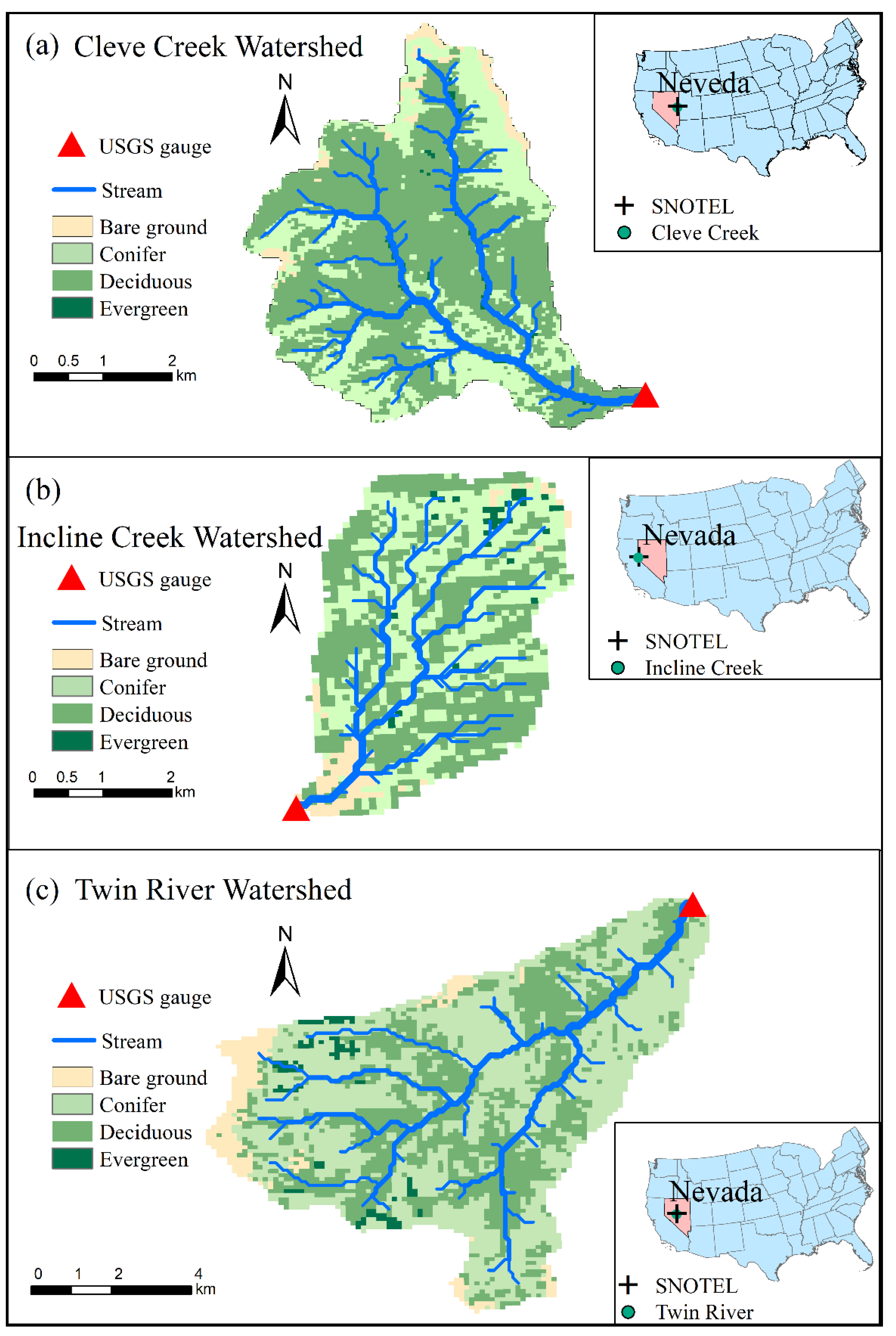
| Watershed | Gauge Station | Weather Station | Local Lapse Rates | ||
|---|---|---|---|---|---|
| Tmax (°C/m) | Tmin (°C/m) | P (mm/m) | |||
| Cleve Creek | 10243700 | 260002 | 0.0073 | 0.0065 | 0.001 |
| Incline Creek | 10336700 | 260024 | 0.0075 | 0.0062 | 0.004 |
| Twin River | 10249300 | 260004 | 0.0076 | 0.0068 | 0.002 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, H.; Zhu, J.; Saydi, M.; Chen, X. Changes of Streamflow Caused by Early Start of Growing Season in Nevada, United States. Water 2021, 13, 1067. https://doi.org/10.3390/w13081067
Fang H, Zhu J, Saydi M, Chen X. Changes of Streamflow Caused by Early Start of Growing Season in Nevada, United States. Water. 2021; 13(8):1067. https://doi.org/10.3390/w13081067
Chicago/Turabian StyleFang, Hong, Jianting Zhu, Muattar Saydi, and Xiaohua Chen. 2021. "Changes of Streamflow Caused by Early Start of Growing Season in Nevada, United States" Water 13, no. 8: 1067. https://doi.org/10.3390/w13081067







