Rainfall Threshold for Flash Flood Warning Based on Model Output of Soil Moisture: Case Study Wernersbach, Germany
Abstract
:1. Introduction
2. Materials and Methods
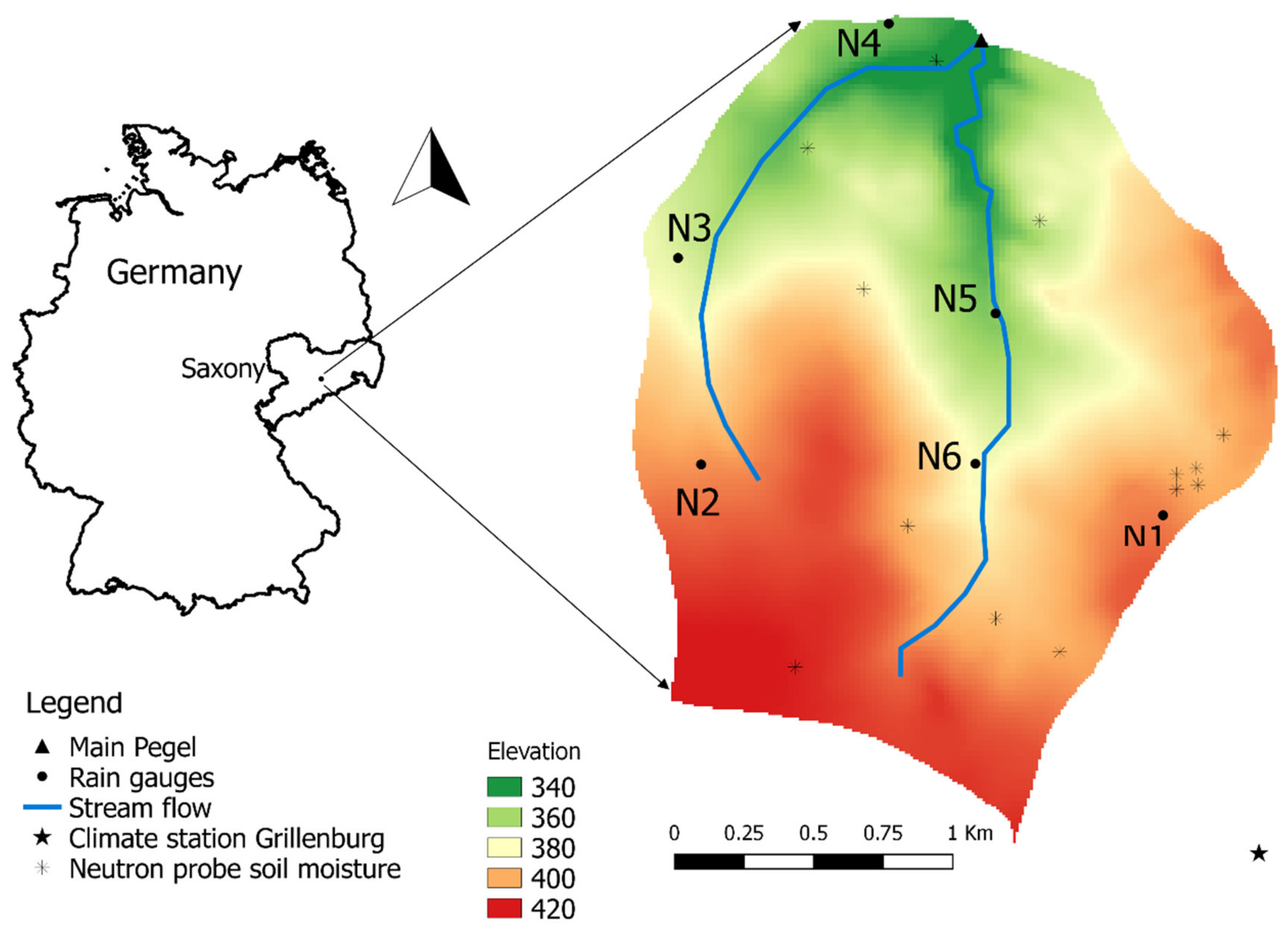
2.1. Catchment Characteristics
2.2. Data Sets and Model
2.2.1. Data Sets
2.2.2. Short Model Description
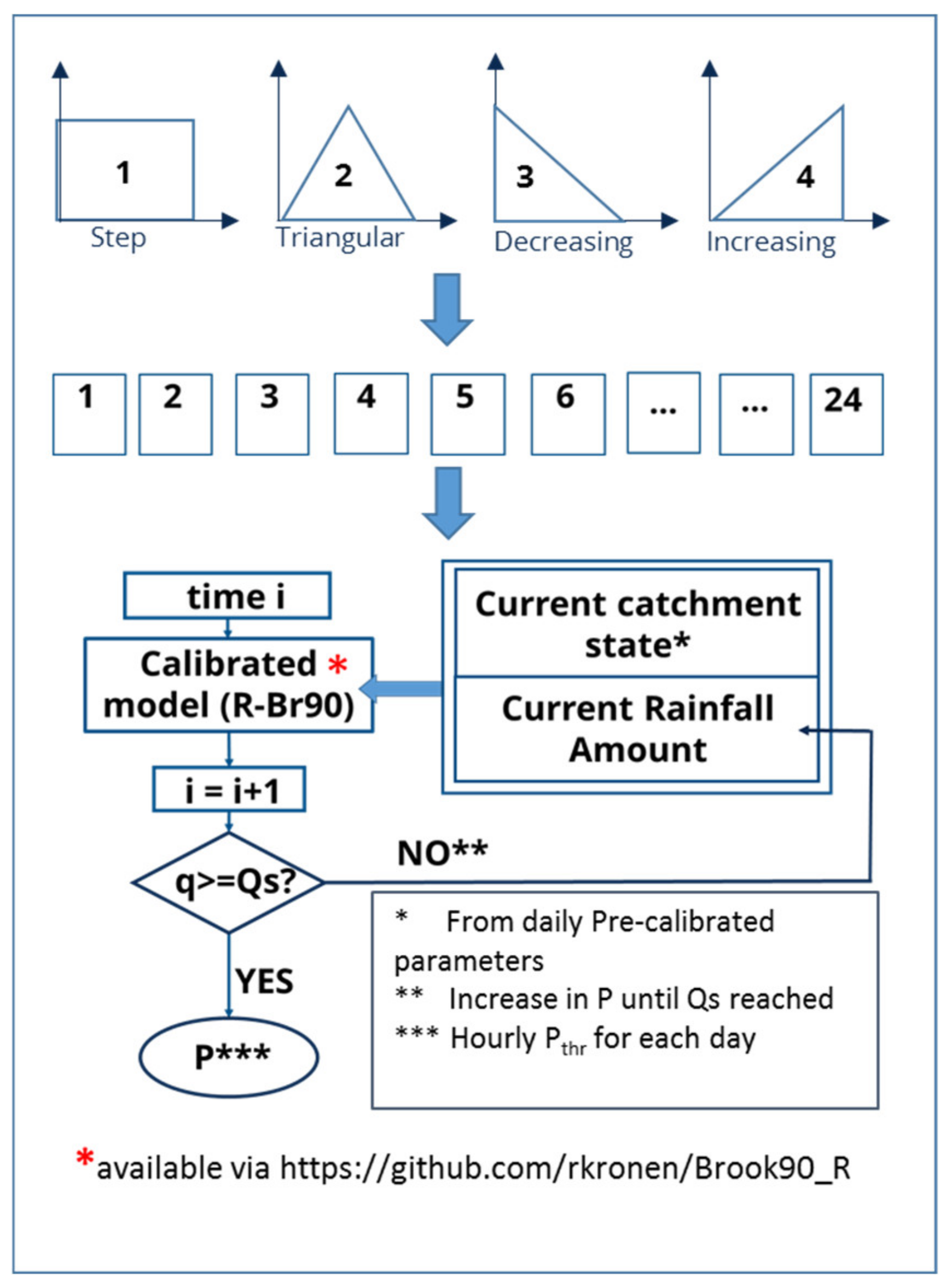
2.3. Flash Flood Guidance Setup
2.4. Validation of the Flash Flood Guidance Approach
2.4.1. Flash Flood Events in the Catchment
2.4.2. Application of Flash Flood Guidance
2.4.3. Validation of FFG
3. Results
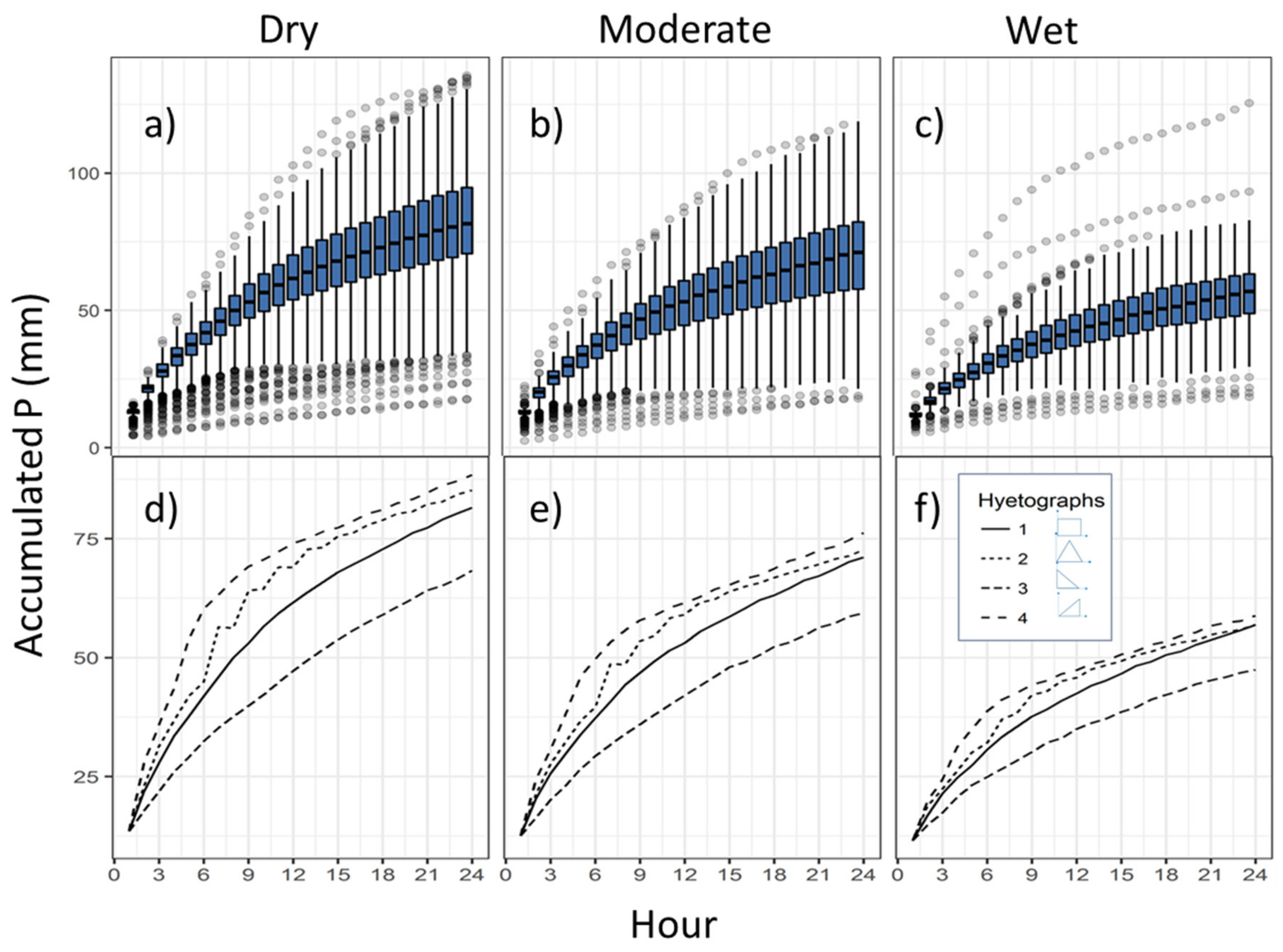
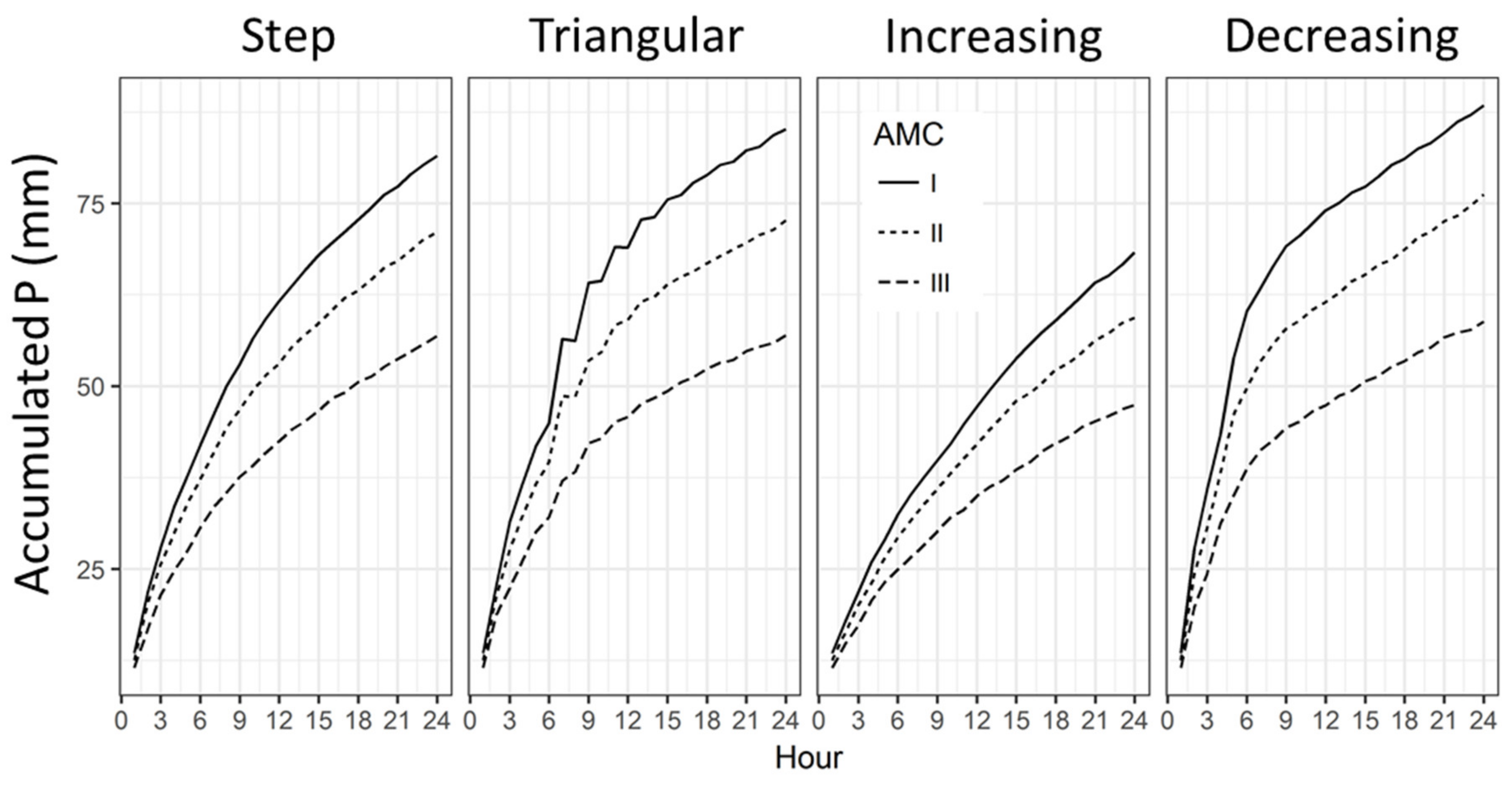
3.1. Rainfall Thresholds
3.2. Performance Evaluation
3.3. Role of Discharge Simulation
4. Conclusions and Outlook
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Borga, M.; Creutin, J.D.; Gaume, E.; Martina, M.; Todini, E.; Thielen, J. Flash flood risk management: Advances in hydrological forecasting and warning. In Flood Risk Management: Research and Practice; CRC Press: Boca Raton, FL, USA, 2009; pp. 1305–1314. [Google Scholar]
- Martina, M.L.V.; Todini, E. Bayesian rainfall thresholds for flash flood guidance. Flood Risk Management: Research and Practice; CRC Press: Boca Raton, FL, USA, 2009; pp. 1399–1408. [Google Scholar]
- Norbiato, D.; Borga, M.; Sangati, M.; Zanon, F. Regional frequency analysis of extreme precipitation in the eastern Italian Alps and the August 29, 2003 flash flood. J. Hydrol. 2007, 345, 149–166. [Google Scholar] [CrossRef]
- Georgakakos, K.P. Analytical results for operational flash flood guidance. J. Hydrol. 2006, 317, 81–103. [Google Scholar] [CrossRef]
- Modrick, T.M.; Georgakakos, K.P. Regional bankfull geometry relationships for southern California mountain streams and hydrologic applications. Geomorphology 2014, 221, 242–260. [Google Scholar] [CrossRef]
- Rusjan, S.; Kobold, M.; Mikoš, M. Characteristics of the extreme rainfall event and consequent flash floods in W Slovenia in September 2007. Nat. Hazards Earth Syst. Sci. 2009, 9, 947–956. [Google Scholar] [CrossRef]
- Gaume, E.; Bain, V.; Bernardara, P.; Newinger, O.; Barbuc, M.; Bateman, A.; Blaškovičová, L.; Blöschl, G.; Borga, M.; Dumitrescu, A.; et al. A compilation of data on European flash floods. J. Hydrol. 2009, 367, 70–78. [Google Scholar] [CrossRef] [Green Version]
- Alpert, P.; Ben-Gai, T.; Baharad, A.; Benjamini, Y.; Yekutieli, D.; Colacino, M.; Diodato, L.; Ramis, C.; Homar, V.; Romero, R.; et al. The paradoxical increase of Mediterranean extreme daily rainfall in spite of decrease in total values. Geophys. Res. Lett. 2002, 29, 29–32. [Google Scholar] [CrossRef] [Green Version]
- Philipp, A.; Kerl, F.; Büttner, U.; Metzkes, C.; Singer, T.; Wagner, M.; Schütze, N. Small-scale (flash) flood early warning in the light of operational requirements: Opportunities and limits with regard to user demands, driving data, and hydrologic modeling techniques. Proc. Int. Assoc. Hydrol. Sci. 2016, 373, 201–208. [Google Scholar] [CrossRef] [Green Version]
- Carpenter, T.M.; Sperfslage, J.A.; Georgakakos, K.P.; Sweeney, T.; Fread, D.L. National threshold runoff estimation utilizing GIS in support of operational flash flood warning systems. J. Hydrol. 1999, 224, 21–44. [Google Scholar] [CrossRef]
- De Luca, D.L.; Versace, P. Diversity of Rainfall Thresholds for early warning of hydro-geological disasters. Adv. Geosci. 2017, 44, 53–60. [Google Scholar] [CrossRef] [Green Version]
- Montesarchio, V.; Napolitano, F.; Rianna, M.; Ridolfi, E.; Russo, F.; Sebastianelli, S. Comparison of methodologies for flood rainfall thresholds estimation. Nat. Hazards 2015, 75, 909–934. [Google Scholar] [CrossRef]
- Rozalis, S.; Morin, E.; Yair, Y.; Price, C. Flash flood prediction using an uncalibrated hydrological model and radar rainfall data in a Mediterranean watershed under changing hydrological conditions. J. Hydrol. 2010, 394, 245–255. [Google Scholar] [CrossRef]
- Tramblay, Y.; Bouvier, C.; Martin, C.; Didon-Lescot, J.F.; Todorovik, D.; Domergue, J.M. Assessment of initial soil moisture conditions for event-based rainfall-runoff modelling. J. Hydrol. 2010, 387, 176–187. [Google Scholar] [CrossRef]
- Borga, M.; Boscolo, P.; Zanon, F.; Sangati, M. Hydrometeorological analysis of the 29 august 2003 flash flood in the Eastern Italian Alps. J. Hydrometeorol. 2007, 8, 1049–1067. [Google Scholar] [CrossRef]
- Norbiato, D.; Borga, M.; Esposti, S.D.; Gaume, E.; Anquetin, S. Flash flood warning based on rainfall thresholds and soil moisture conditions: An assessment for gauged and ungauged basins. J. Hydrol. 2008, 362, 274–290. [Google Scholar] [CrossRef]
- Penna, D.; Tromp-Van Meerveld, H.J.; Gobbi, A.; Borga, M.; Fontana, G.D. The influence of soil moisture on threshold runoff generation processes in an alpine headwater catchment. Hydrol. Earth Syst. Sci. 2011, 15, 689–702. [Google Scholar] [CrossRef] [Green Version]
- Blöschl, G. Rainfall-Runoff Modeling of Ungauged Catchments. Encycl. Hydrol. Sci. 2005. [Google Scholar] [CrossRef]
- Schwärzel, K.; Menzer, A.; Clausnitzer, F.; Spank, U.; Häntzschel, J.; Grünwald, T.; Köstner, B.; Bernhofer, C.; Feger, K.H. Soil water content measurements deliver reliable estimates of water fluxes: A comparative study in a beech and a spruce stand in the Tharandt forest (Saxony, Germany). Agric. For. Meteorol. 2009, 149, 1994–2006. [Google Scholar] [CrossRef]
- IUSS Working Group WRB. World Reference Base for Soil Resources 2006; FAO: Rome, Italy, 2007; ISBN 9251055114. [Google Scholar]
- Spank, U.; Schwärzel, K.; Renner, M.; Moderow, U.; Bernhofer, C. Effects of measurement uncertainties of meteorological data on estimates of site water balance components. J. Hydrol. 2013, 492, 176–189. [Google Scholar] [CrossRef]
- Goldberg, V.; Eichelmann, U.; Prasse, H.; Bernhofer, C. The flash flood event in the catchment of the river Weißeritz (eastern Erzgebirge, Saxony) from 12–14. August 2002 meteorological and hydrological reasons, damage assessment and disaster management. In Proceedings of the EGS-AGU-EUG Joint Assembly, Nice, France, 6–11 April 2003. [Google Scholar]
- Schwärzel, K.; Feger, K.-H.; Häntzschel, J.; Menzer, A.; Spank, U.; Clausnitzer, F.; Köstner, B.; Bernhofer, C. A novel approach in model-based mapping of soil water conditions at forest sites. For. Ecol. Manag. 2009, 258, 2163–2174. [Google Scholar] [CrossRef]
- Luong, T.T.; Kronenberg, R.; Bernhofer, C.; Al Janabi, F.; Schütze, N. Comparative estimation and assessment of initial soil moisture conditions for Flash Flood warning in Saxony. Geophys. Res. Abstr. 2017, 19, 3728. [Google Scholar]
- Grünwald, T.; Bernhofer, C. A decade of carbon, water and energy flux measurements of an old spruce forest at the Anchor Station Tharandt. Tellus Ser. B Chem. Phys. Meteorol. 2007, 59, 387–396. [Google Scholar] [CrossRef] [Green Version]
- Federer, C.A.; Vörösmarty, C.; Fekete, B. Sensitivity of annual evaporation to soil and root properties in two models of contrasting complexity. J. Hydrometeorol. 2003, 4, 1276–1290. [Google Scholar] [CrossRef]
- Clapp, R.B.; Hornberger, G.M. Empirical equations for some soil hydraulic properties. Water Resour. Res. 1978, 14, 601–604. [Google Scholar] [CrossRef] [Green Version]
- Gebrechorkos, S.H.; Bernhofer, C.; Hülsmann, S. Impacts of projected change in climate on water balance in basins of East Africa. Sci. Total Environ. 2019, 682, 160–170. [Google Scholar] [CrossRef] [PubMed]
- Martina, M.L.V.; Todini, E.; Libralon, A. Rainfall thresholds for flood warning systems: A bayesian decision approach. In Hydrological Modelling and the Water Cycle; Springer: Berlin/Heidelberg, Germany, 2009; pp. 203–227. [Google Scholar]
- Montesarchio, V.; Lombardo, F.; Napolitano, F. Rainfall thresholds and flood warning: An operative case study. Nat. Hazards Earth Syst. Sci. 2009, 9, 135–144. [Google Scholar] [CrossRef]
- Doherty, J.; Johnston, J.M. Methodologies for calibration and predictive analysis of a watershed model. J. Am. Water Resour. Assoc. 2003, 39, 251–265. [Google Scholar] [CrossRef]
- Marchi, L.; Borga, M.; Preciso, E.; Gaume, E. Characterisation of selected extreme flash floods in Europe and implications for flood risk management. J. Hydrol. 2010, 394, 118–133. [Google Scholar] [CrossRef]
- Tarolli, P.; Borga, M.; Morin, E.; Delrieu, G. Analysis of flash flood regimes in the North-Western and South-Eastern Mediterranean regions. Nat. Hazards Earth Syst. Sci. 2012, 12, 1255–1265. [Google Scholar] [CrossRef] [Green Version]
- Amponsah, W.; Ayral, P.A.; Boudevillain, B.; Bouvier, C.; Braud, I.; Brunet, P.; Delrieu, G.; DIdon-Lescot, J.F.; Gaume, E.; Lebouc, L.; et al. Integrated high-resolution dataset of high-intensity European and Mediterranean flash floods. Earth Syst. Sci. Data 2018, 10, 1783–1794. [Google Scholar] [CrossRef] [Green Version]
- Amponsah, W.; Marchi, L.; Zoccatelli, D.; Boni, G.; Cavalli, M.; Comiti, F.; Crema, S.; Lucía, A.; Marra, F.; Borga, M. Hydrometeorological characterization of a flash flood associated with major geomorphic effects: Assessment of peak discharge uncertainties and analysis of the runoff response. J. Hydrometeorol. 2016, 17, 3063–3077. [Google Scholar] [CrossRef]
- Schaeffer, J.T. The critical success index as an indicator of warning skill. Weather Forecast. 1990, 5, 570–574. [Google Scholar] [CrossRef] [Green Version]
- Norbiato, D.; Borga, M.; Dinale, R. Flash flood warning in ungauged basins by use of the flash flood guidance and model-based runoff thresholds. Meteorol. Appl. 2009, 16, 65–75. [Google Scholar] [CrossRef]
- Javelle, P.; Fouchier, C.; Arnaud, P.; Lavabre, J. Flash flood warning at ungauged locations using radar rainfall and antecedent soil moisture estimations. J. Hydrol. 2010, 394, 267–274. [Google Scholar] [CrossRef]

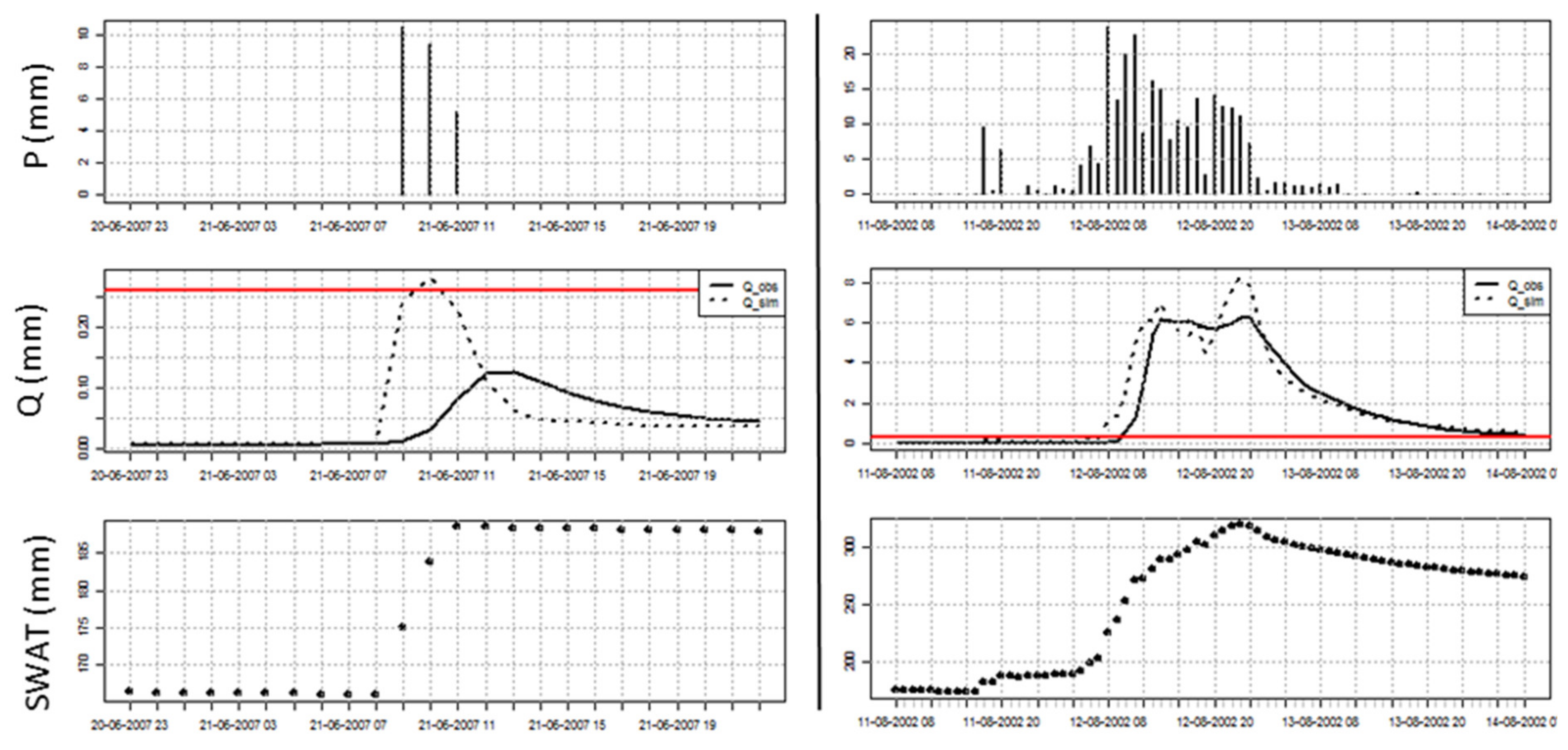
| Date | AMC | Pduration [h] | Psum [mm] | Pmax [mm] | AS [mm] | Intensity [mm/h] |
|---|---|---|---|---|---|---|
| 1997-06-14 | I | 6 | 22 | 11.5 | 163 | 3.7 |
| 1998-06-12 | I | 7 | 24.5 | 10.3 | 148.2 | 3.5 |
| 1998-06-21 | I | 4 | 22.6 | 6.5 | 172.5 | 5.7 |
| 1998-07-27 | II | 3 | 27 | 19.6 | 190.6 | 9 |
| 1998-08-02 | II | 12 | 39.8 | 29.1 | 187.5 | 3.3 |
| 1999-06-18 | I | 32 | 60 | 6.1 | 173.8 | 1.9 |
| 1999-07-06 | III | 19 | 35.6 | 19.8 | 233.4 | 1.9 |
| 1999-07-20 | II | 6 | 21.7 | 12.4 | 217 | 3.6 |
| 1999-09-18 | I | 7 | 21.7 | 21.5 | 153.2 | 3.1 |
| 2001-07-07 | II | 6 | 44.3 | 34.1 | 199.3 | 7.4 |
| 2002-07-16 | I | 5 | 23 | 12.5 | 153.7 | 4.6 |
| 2002-08-08 | II | 2 | 34.7 | 34.5 | 181.6 | 17.4 |
| 2002-08-11 | II | 51 | 272.3 | 23.7 | 181.2 | 5.3 |
| 2002-08-31 | II | 11 | 66 | 40.9 | 192.2 | 6 |
| 2002-09-26 | II | 14 | 22.2 | 5.9 | 214.2 | 1.6 |
| 2003-05-08 | I | 13 | 24 | 9.2 | 160.9 | 1.8 |
| 2004-05-06 | II | 5 | 25.3 | 12.7 | 201.1 | 5.1 |
| 2004-05-10 | II | 14 | 31.8 | 13.3 | 216 | 2.3 |
| 2004-07-22 | II | 8 | 44.4 | 21.7 | 209 | 5.5 |
| 2005-07-05 | I | 14 | 23.2 | 2.9 | 170.8 | 1.7 |
| 2006-06-27 | I | 2 | 46.6 | 38.6 | 150.3 | 23.3 |
| 2006-08-05 | I | 49 | 78.9 | 9 | 136.3 | 1.6 |
| 2007-05-07 | I | 11 | 25.3 | 13.8 | 134.1 | 2.3 |
| 2007-05-14 | I | 5 | 23.1 | 13.8 | 160.4 | 4.6 |
| 2007-05-27 | II | 2 | 20.8 | 20.5 | 182.6 | 10.4 |
| 2007-05-28 | II | 11 | 21.1 | 9.8 | 184.2 | 1.9 |
| 2007-06-15 | I | 1 | 21.7 | 21.7 | 171.5 | 21.7 |
| 2007-06-21 | I | 3 | 25.1 | 10.5 | 174.9 | 8.4 |
| 2007-08-20 | I | 15 | 40.5 | 14.6 | 177.3 | 2.7 |
| 2007-08-31 | II | 9 | 27.1 | 9.2 | 188.4 | 3 |
| 2008-07-03 | I | 1 | 23.6 | 23.6 | 155.8 | 23.6 |
| 2008-08-08 | I | 7 | 31.7 | 31 | 164.3 | 4.5 |
| 2008-08-11 | I | 6 | 20.9 | 10.2 | 170.1 | 3.5 |
| 2009-05-26 | I | 18 | 33.1 | 9.4 | 154.3 | 1.8 |
| 2009-08-02 | I | 16 | 52.6 | 31.1 | 173 | 3.3 |
| 2009-08-26 | I | 6 | 40.6 | 24.9 | 168.3 | 6.8 |
| 2010-06-02 | III | 19 | 49.2 | 16.6 | 242.3 | 2.6 |
| 2010-07-22 | I | 19 | 28.8 | 5.5 | 144.9 | 1.5 |
| 2010-08-03 | II | 16 | 38.8 | 10.6 | 183.3 | 2.4 |
| 2010-08-15 | II | 3 | 27.6 | 16.4 | 219.2 | 9.2 |
| Mean | 11.5 | 39.1 | 17.2 | 191 | 5.8 | |
| S.D. | 11.1 | 40.2 | 9.8 | 25.7 | 5.8 |
| Qobs > Qthreshold | |||
|---|---|---|---|
| Yes | No | ||
| Pobs > Pthreshold | Yes | CORRECT Alarm (CA) | FALSE Alarm (FA) |
| No | MISSING Alarm (MA) | CORRECT Missing Alarm (CMA) | |
| Correct Alarm | Missing Alarm | False Alarm | Correct Missing Alarm | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Hyetotype | H1 | H2 | H3 | H4 | H1 | H2 | H3 | H4 | H1 | H2 | H3 | H4 | H1 | H2 | H3 | H4 |
| AMCI | 1 | 1 | 2 | 1 | 1 | 1 | 0 | 1 | 7 | 7 | 9 | 7 | 13 | 13 | 11 | 13 |
| AMCII | 5 | 4 | 7 | 4 | 3 | 4 | 1 | 4 | 4 | 4 | 5 | 4 | 4 | 4 | 3 | 4 |
| AMCIII | 2 | 2 | 2 | 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| ∑ | 8 | 7 | 11 | 7 | 4 | 5 | 1 | 5 | 11 | 11 | 14 | 11 | 17 | 17 | 14 | 17 |
| H1 | H2 | H3 | H4 | |||||||||||||
| POD (%) | 66.7 | 58.3 | 91.7 | 58.3 | ||||||||||||
| FAR (%) | 57.9 | 61.1 | 56 | 61.1 | ||||||||||||
| CSI (%) | 34.8 | 30.4 | 42.3 | 30.4 | ||||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luong, T.T.; Pöschmann, J.; Kronenberg, R.; Bernhofer, C. Rainfall Threshold for Flash Flood Warning Based on Model Output of Soil Moisture: Case Study Wernersbach, Germany. Water 2021, 13, 1061. https://doi.org/10.3390/w13081061
Luong TT, Pöschmann J, Kronenberg R, Bernhofer C. Rainfall Threshold for Flash Flood Warning Based on Model Output of Soil Moisture: Case Study Wernersbach, Germany. Water. 2021; 13(8):1061. https://doi.org/10.3390/w13081061
Chicago/Turabian StyleLuong, Thanh Thi, Judith Pöschmann, Rico Kronenberg, and Christian Bernhofer. 2021. "Rainfall Threshold for Flash Flood Warning Based on Model Output of Soil Moisture: Case Study Wernersbach, Germany" Water 13, no. 8: 1061. https://doi.org/10.3390/w13081061






