Water Distribution from Artificial Recharge via Infiltration Basin under Constant Head Conditions
Abstract
:1. Introduction
2. Materials and Methods
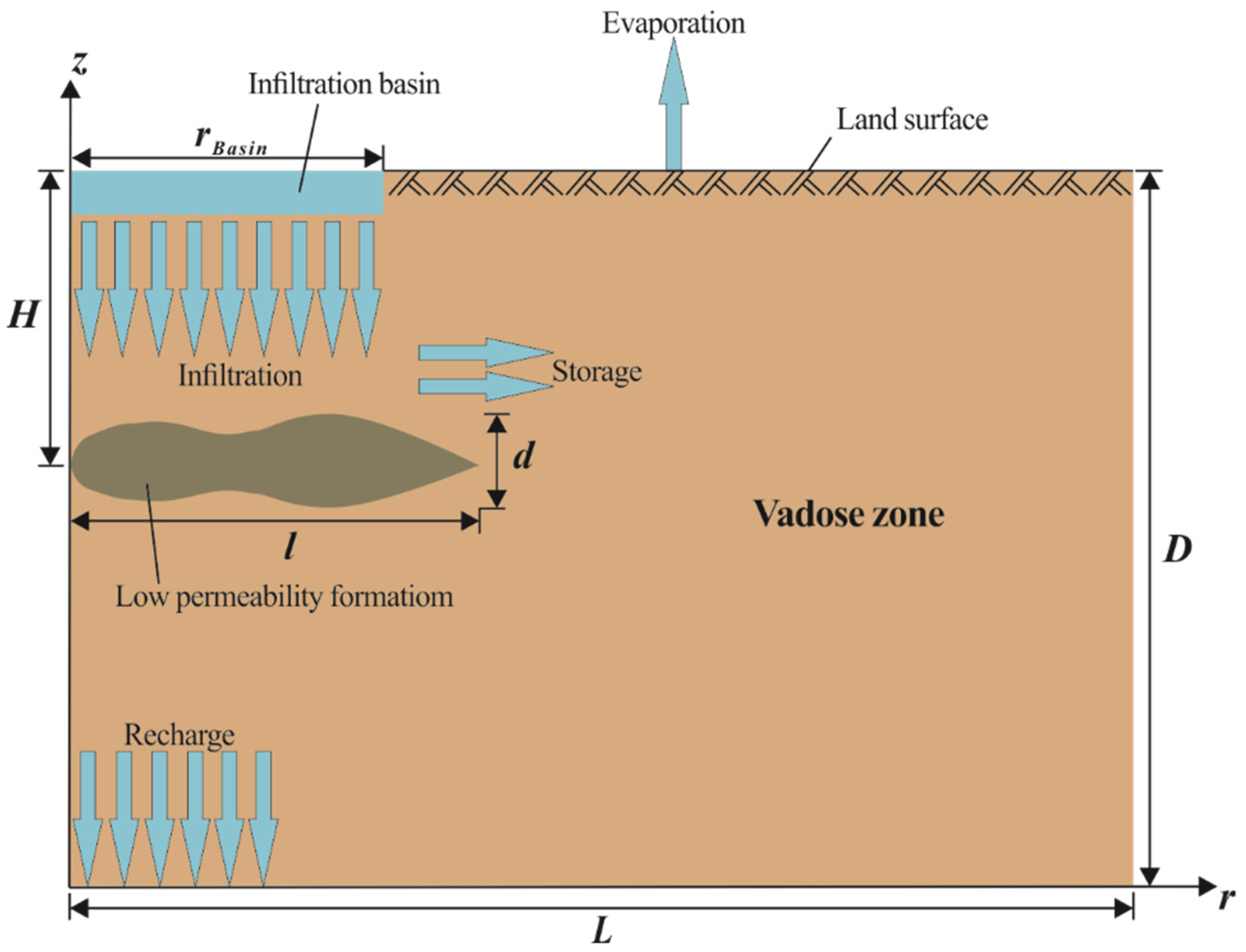
2.1. Conceptual and Mathematical Models
2.2. Numerical Experiments
2.3. Data Analysis
3. Results
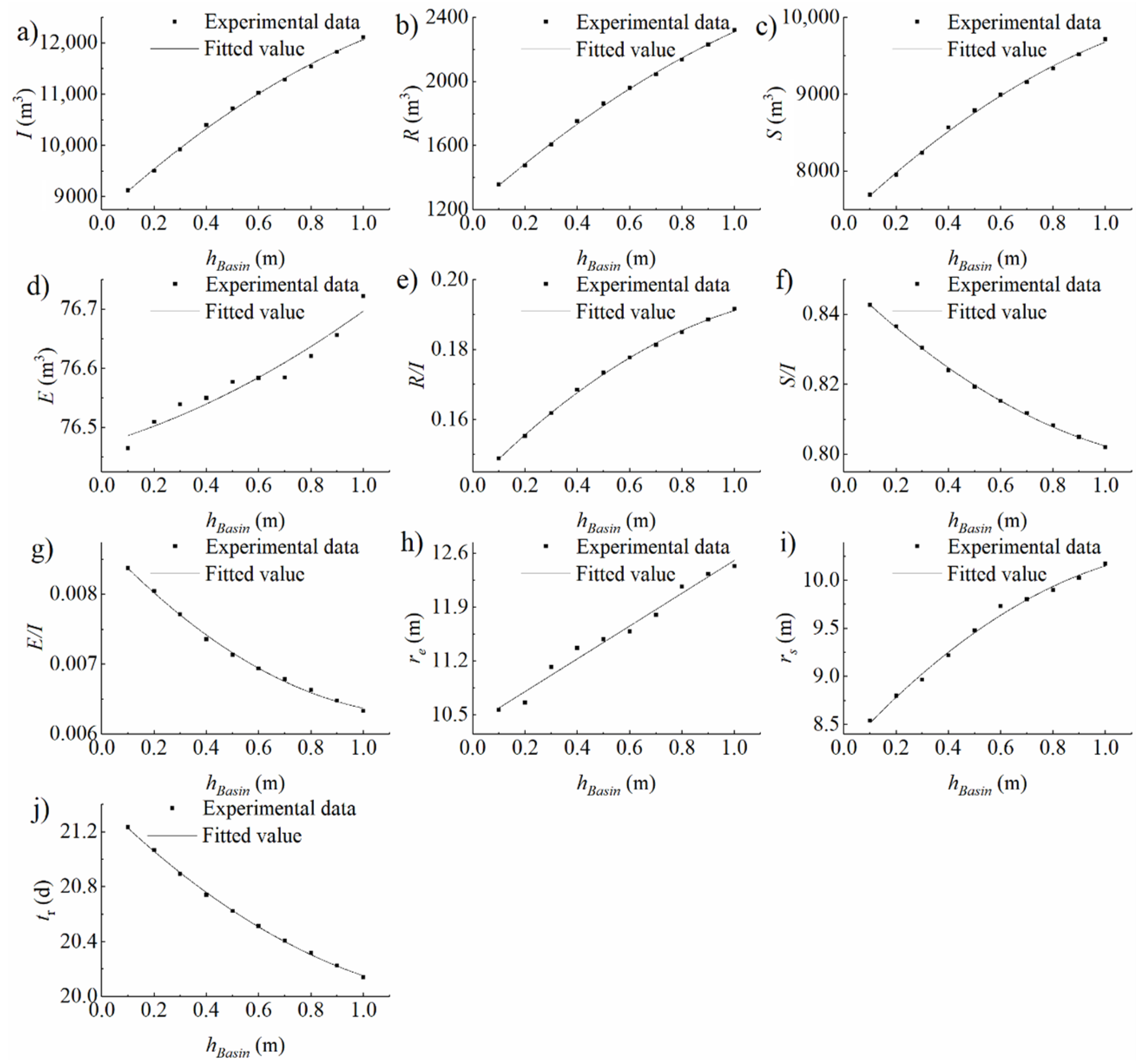
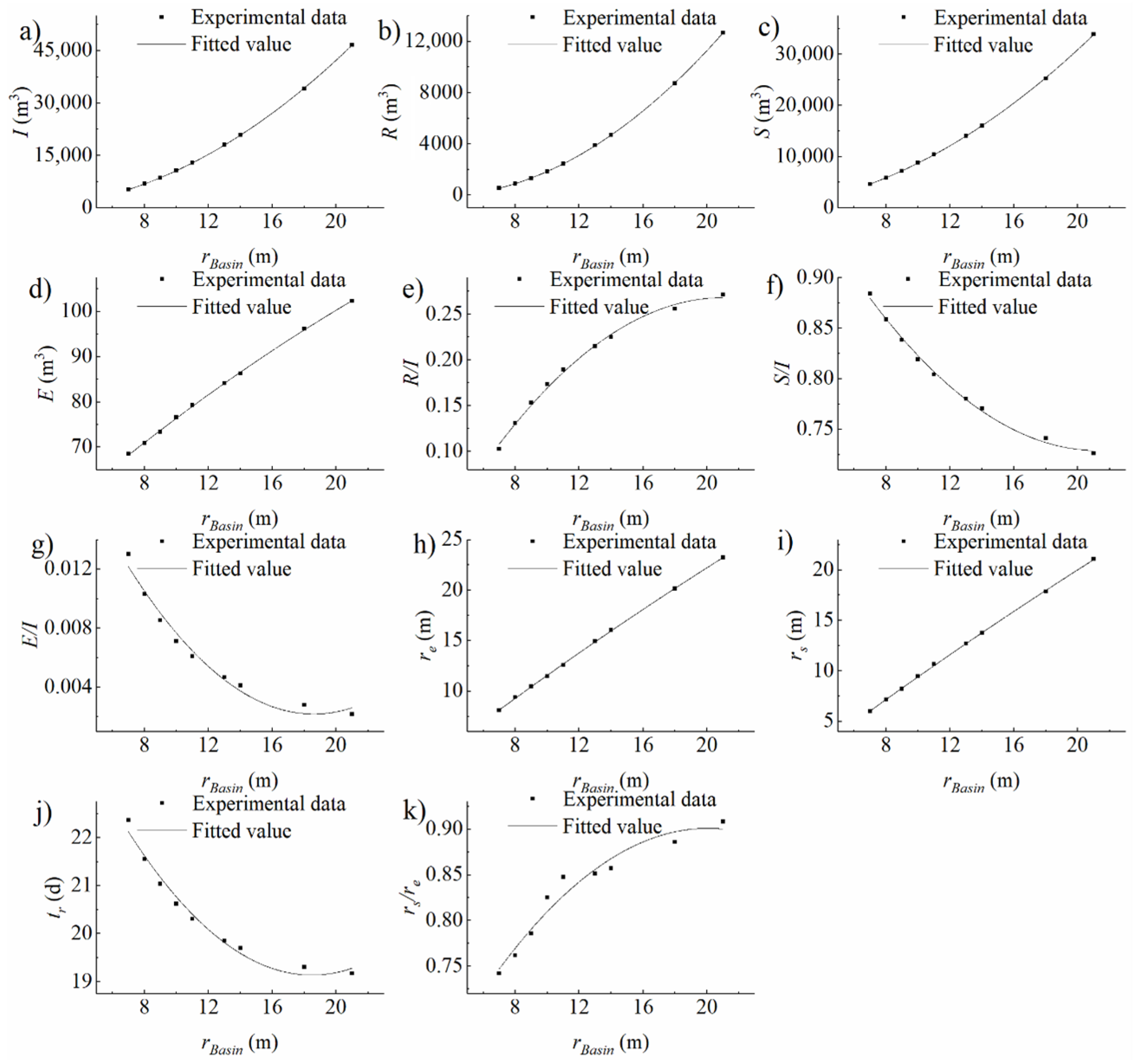
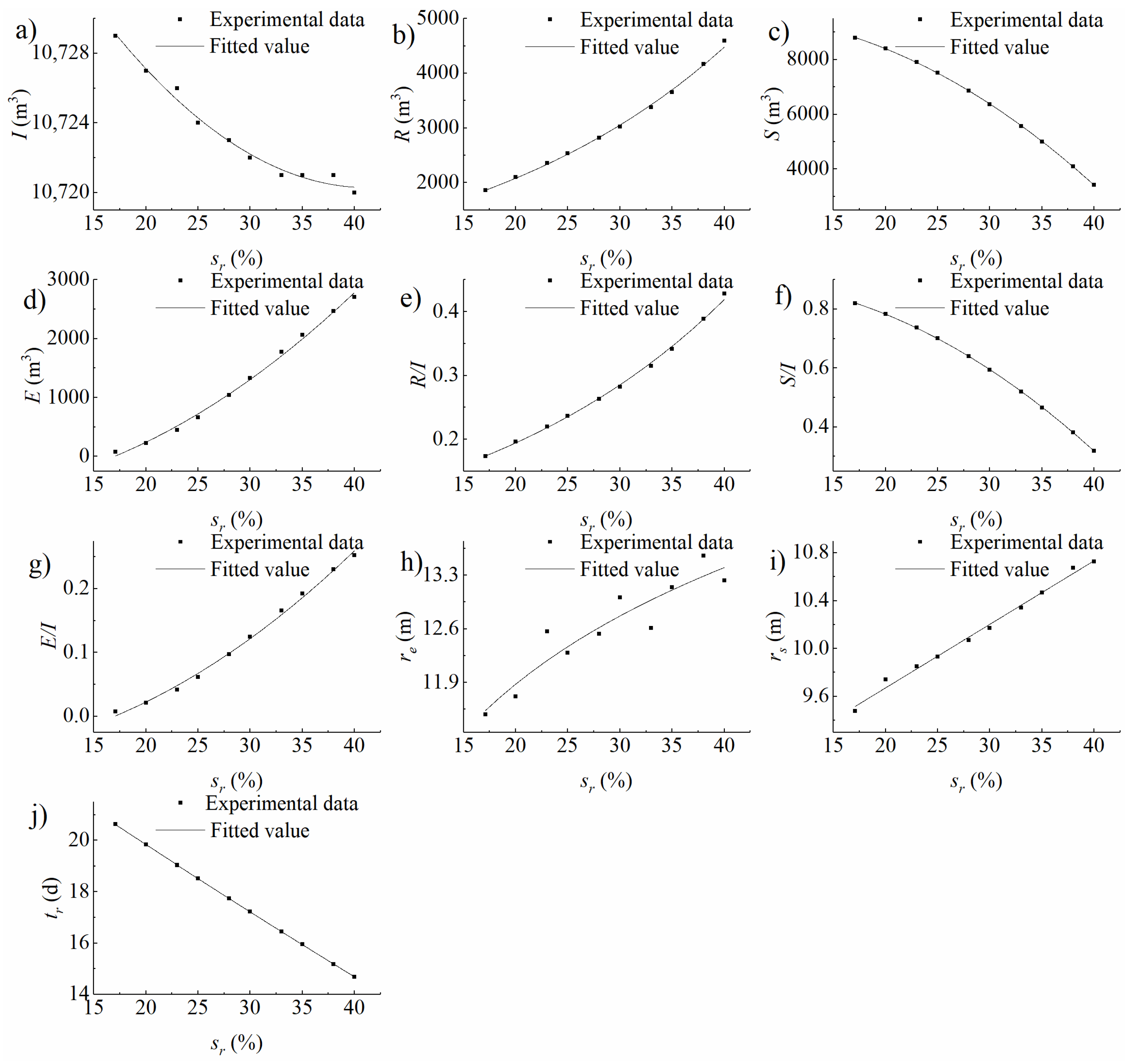
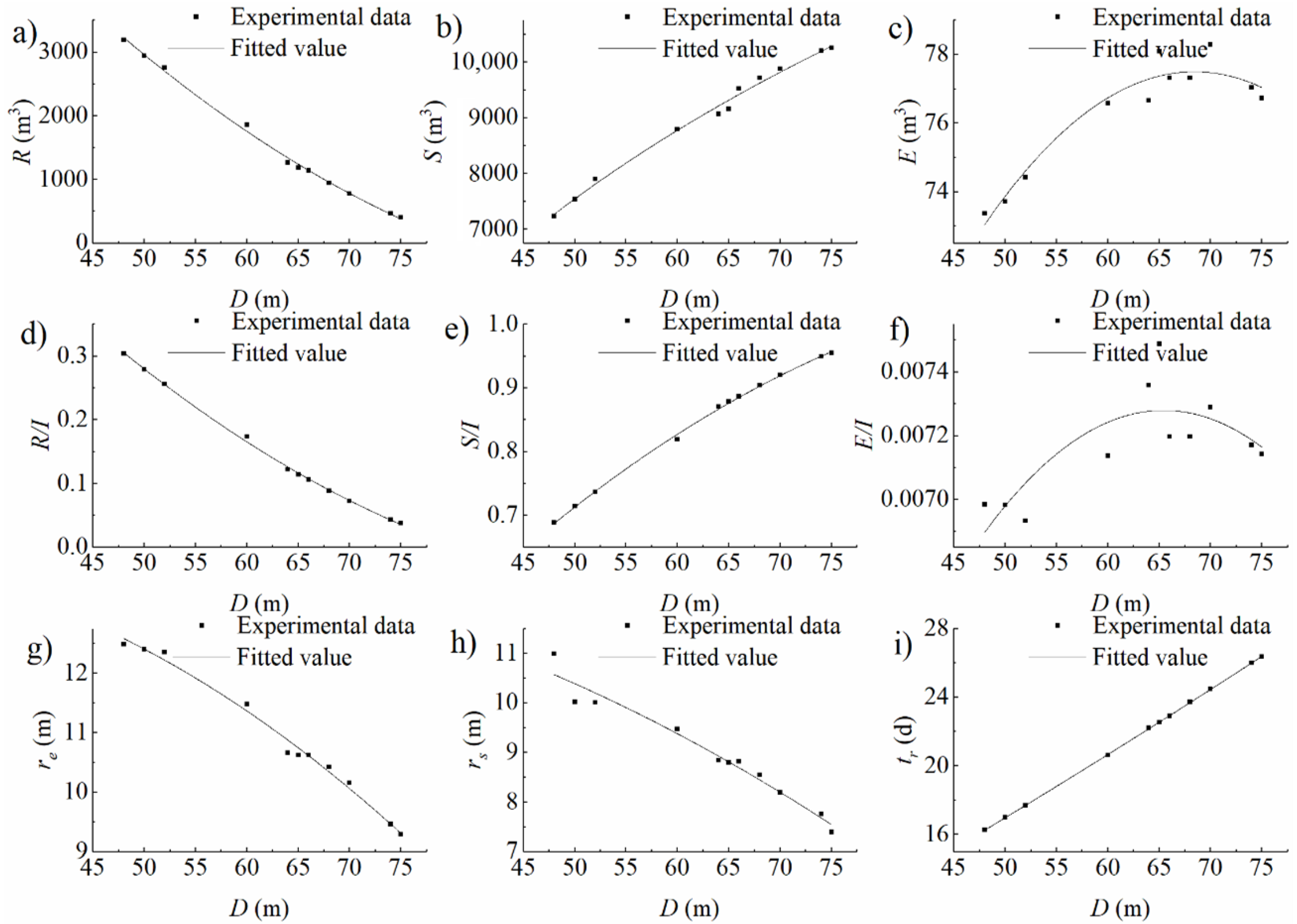
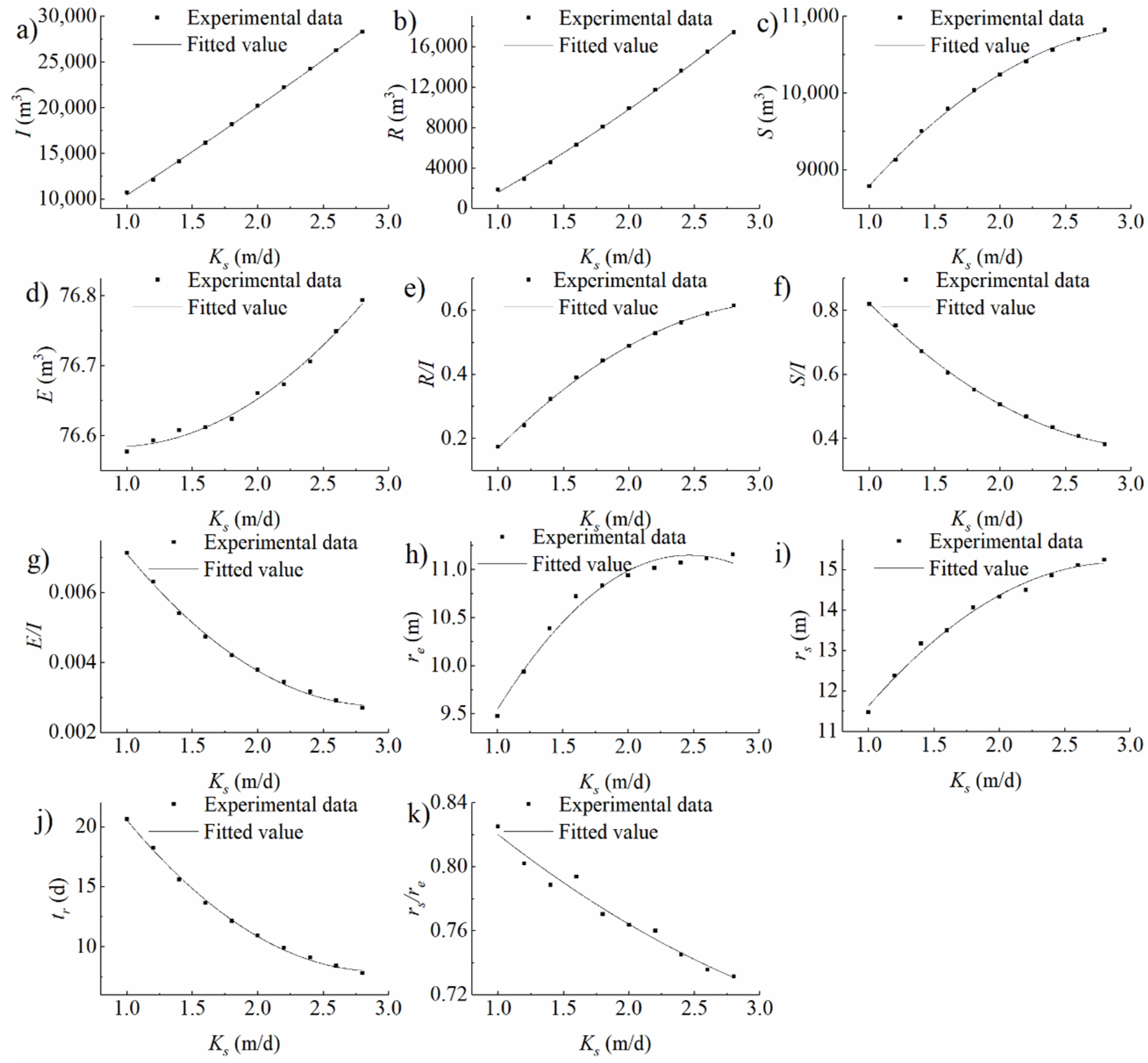
3.1. Homogeneous Domain Experimental Conditions
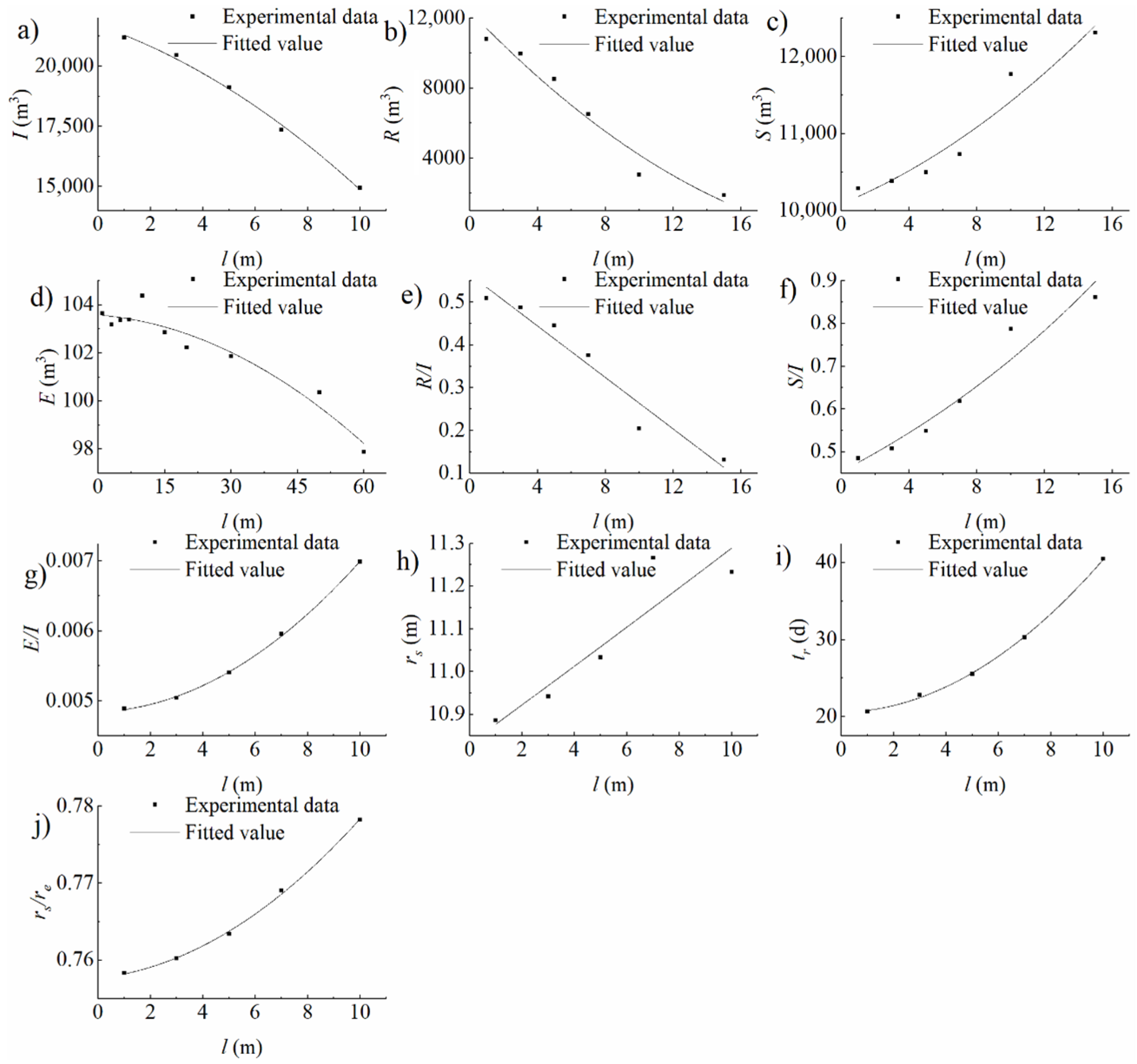
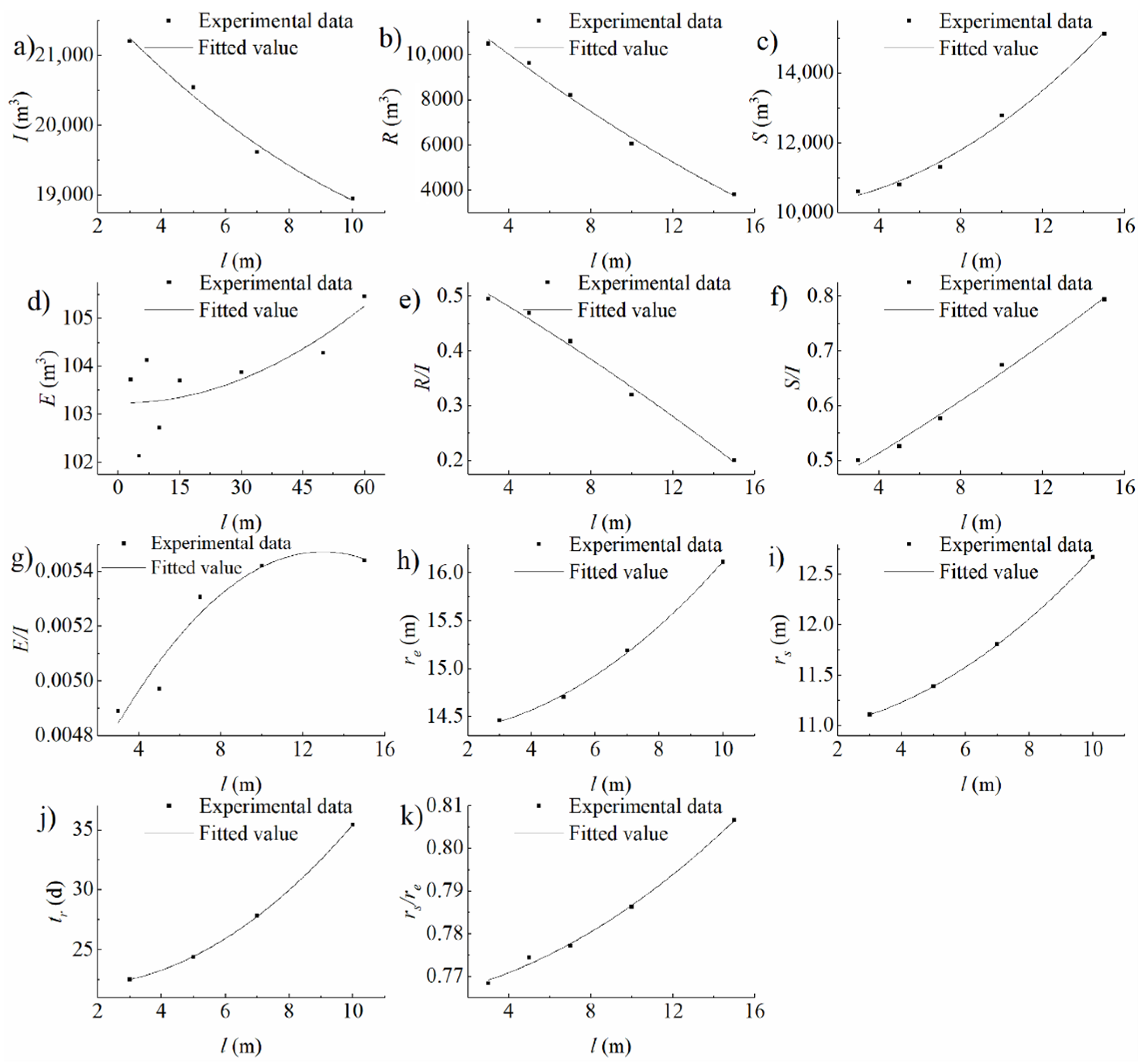
3.2. Heterogeneous Domain Experimental Conditions
4. Discussion
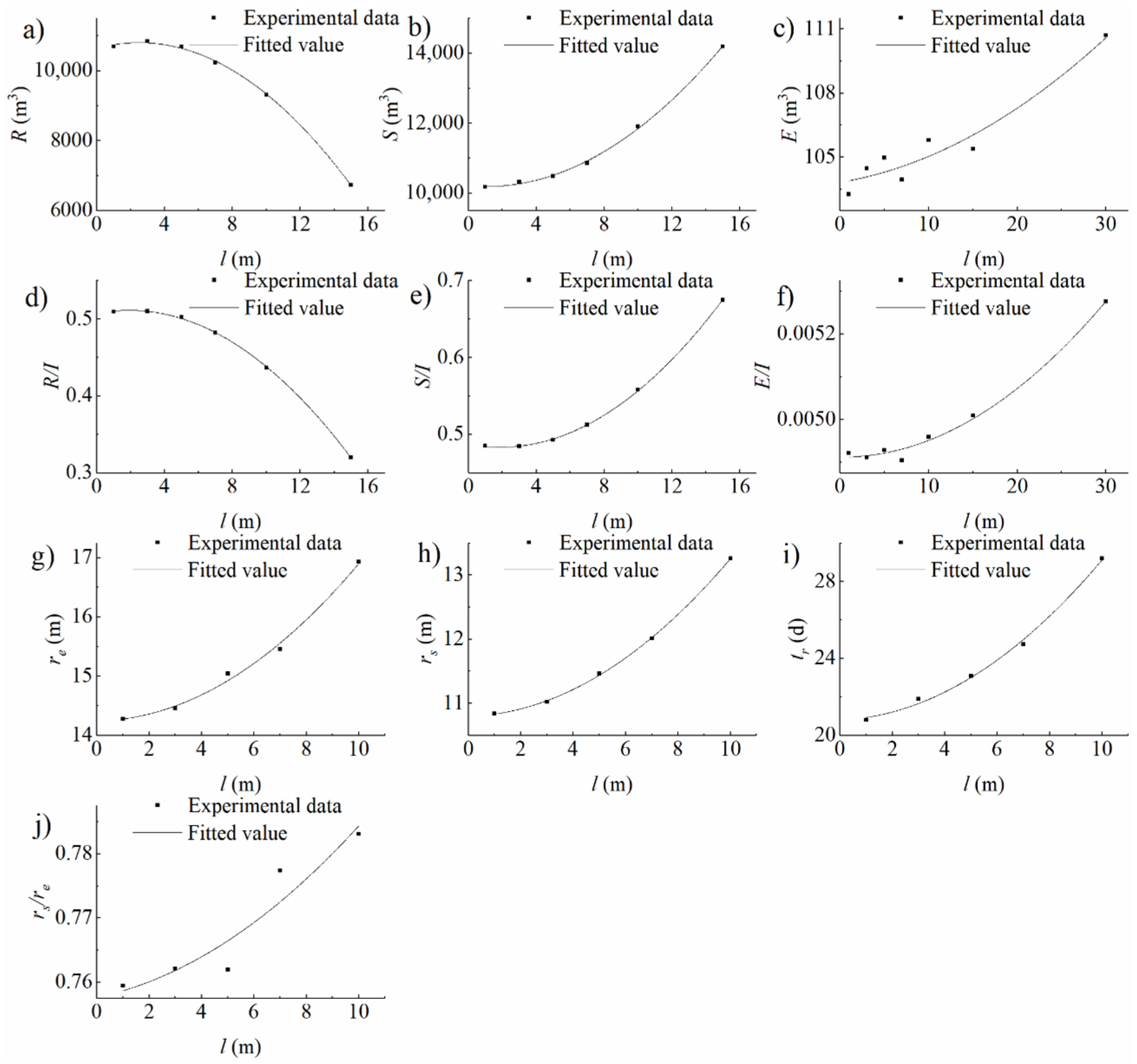
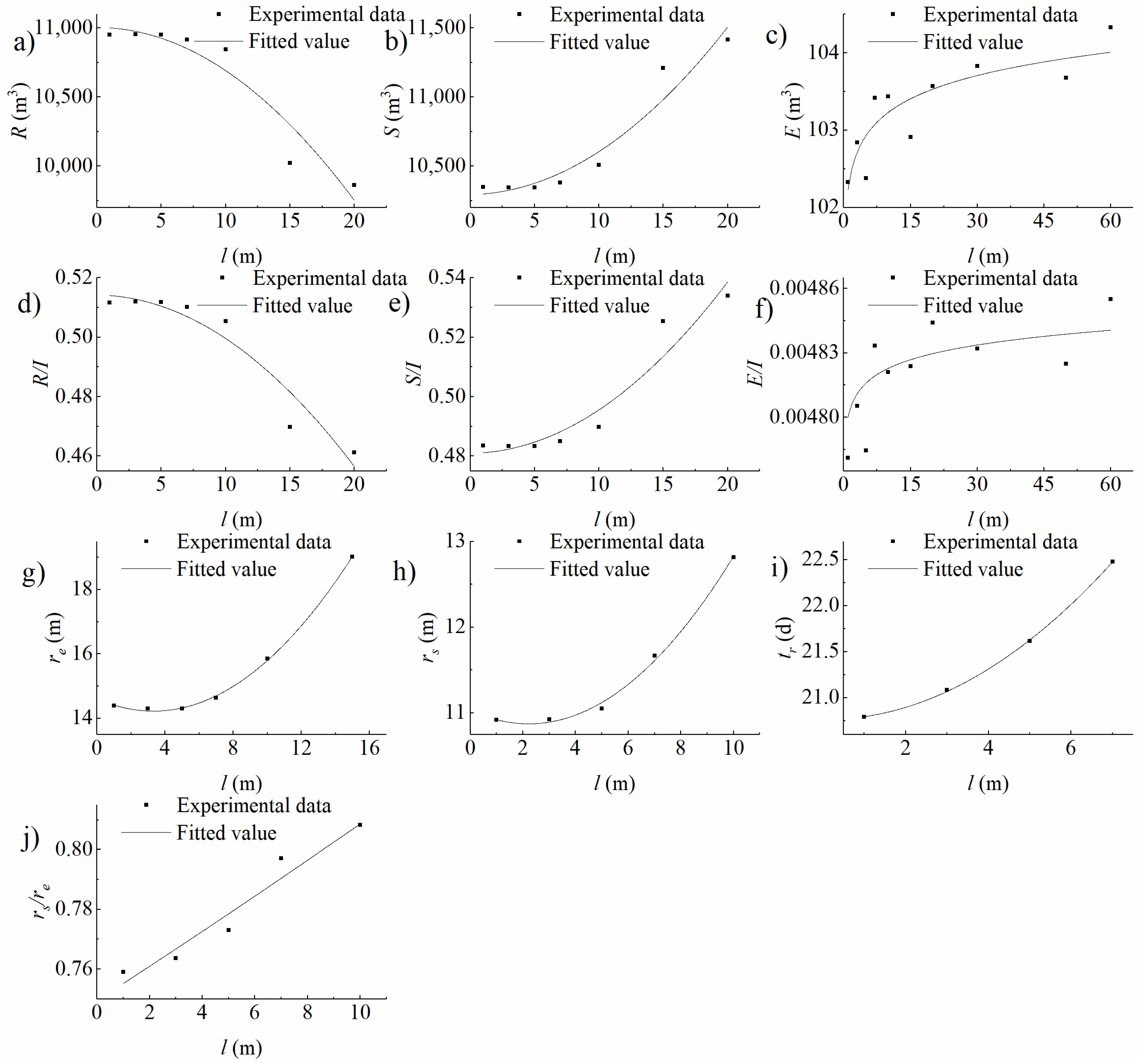
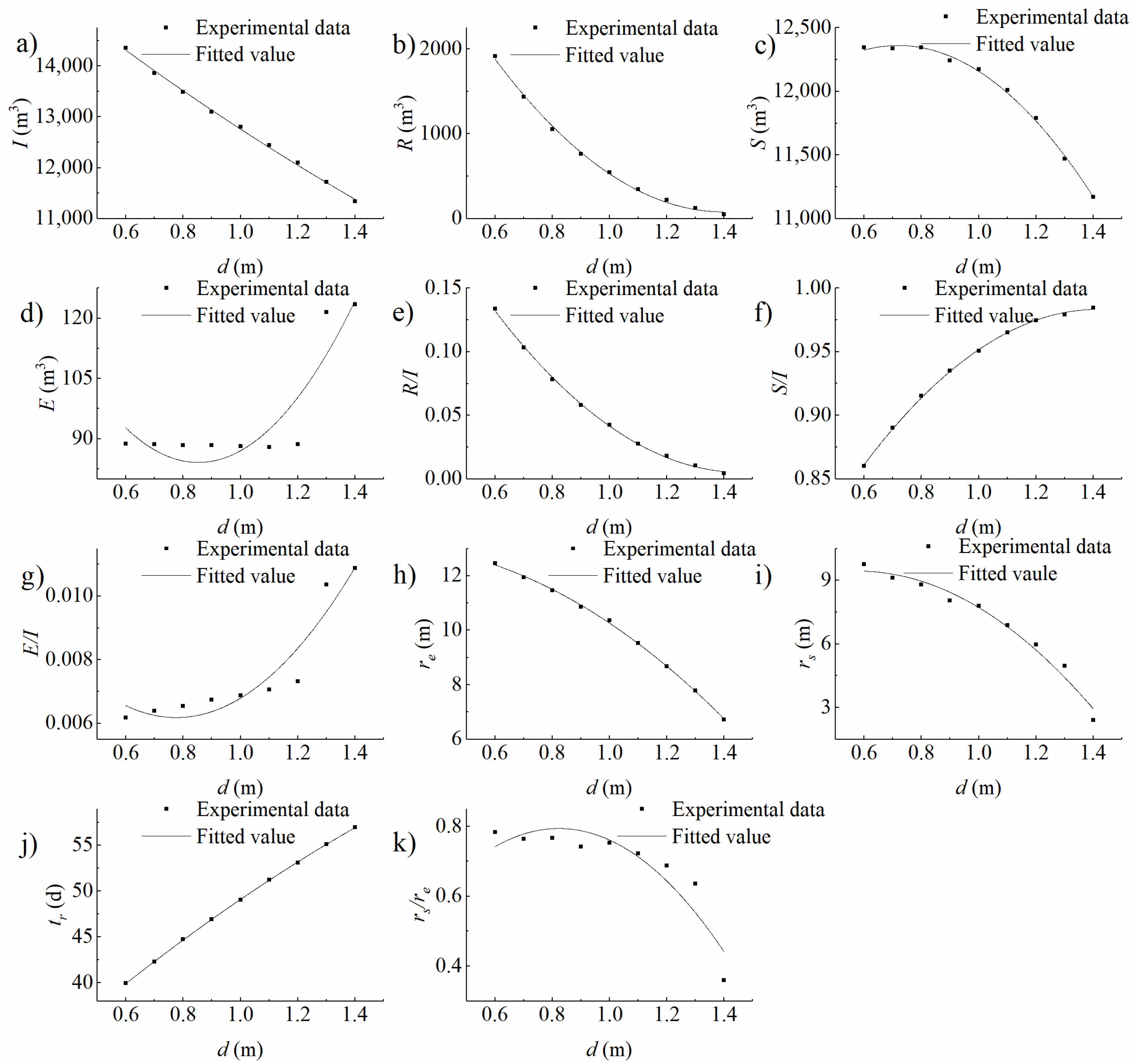
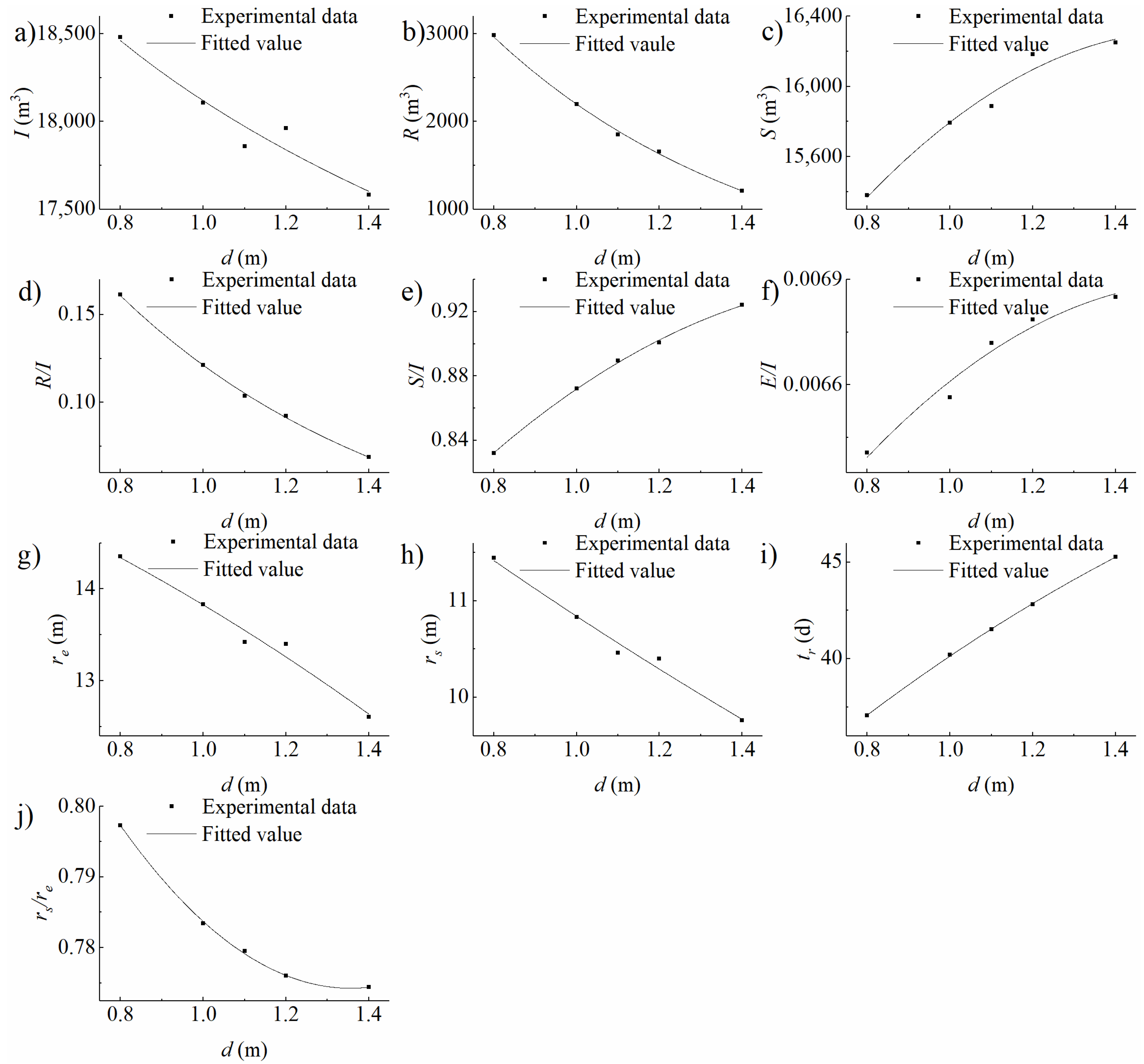
4.1. Analysis on the Impacts of Infiltration Basin Features and Vadose Zone Factors on Water Distribution
4.1.1. Storage in the Vadose Zone
4.1.2. Evaporation to the Air
4.1.3. Recharge into the Aquifer
4.2. Analysis on Consistency, Similarity, and Difference between Infiltration and Recharge Based on Water Distribution
4.2.1. Consistency
4.2.2. Similarity
4.2.3. Differences
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronym | Definition/Notation |
| d | Thickness of the low permeability formation (L) |
| D | Vadose zone thickness (L) |
| e | Potential evaporation rate (L/T) |
| E | Cumulative evaporation to the air (L3) |
| E/I | Ratio of the cumulative evaporation to the cumulative infiltration (-) |
| h | Hydraulic head in the matrix cell (L) |
| H | Depth of the low permeability formation (L) |
| hBasin | Water head in infiltration basin (L) |
| I | Cumulative infiltration from infiltration basin (L3) |
| K | Hydraulic conductivity (L/T) |
| Ks | Saturated hydraulic conductivity (L/T) |
| l | Length of the low permeability formation (L) |
| L | Vadose zone length (L) |
| r | Radius in cylindrical coordinates (L) |
| R | Volume of recharge into the aquifer (L3) |
| rBasin | Infiltration basin radius (L) |
| re | Radius of the flow through the bottom boundary of the vadose zone at the end time of infiltration (L) |
| rs | Radius of the saturated part of the flow through the bottom boundary of the vadose zone at the end time of infiltration (L) |
| rs/re | Ratio of the radius of the saturated part of the flow through the bottom boundary of the vadose zone to the radius of the whole flow at the end time of infiltration (-) |
| R/I | Ratio of the volume of recharge to the cumulative infiltration (-) |
| S | Volume of storage in the vadose zone (L3) |
| Se | Effective water content (-) |
| sr | Antecedent moistures of the vadose zone (-) |
| S/I | Ratio of the volume of storage to the cumulative infiltration (-) |
| t | Time (T) |
| tr | Time when the saturated flow reaches the bottom boundary (T) |
| z | Height in cylindrical coordinates (L) |
| α, n, m, and f | Empirical parameters (L−1), (-), (-), and (-) |
| θ | Volumetric soil water content at soil water matric potential (-) |
| θr | Residual water content (-) |
| θs | Saturated water content (-) |
| φ | Tilt angle in cylindrical coordinates (-) |
References
- Gleeson, T.; Wada, Y.; Bierkens, M.F.P.; Van Beek, L.P.H. Water balance of global aquifers revealed by groundwater footprint. Nature 2012, 488, 197–200. [Google Scholar] [CrossRef]
- Hernandez, E.A.; Uddameri, V. Standardized precipitation evaporation index (SPEI)-based drought assessment in semi-arid south Texas. Environ. Earth Sci. 2014, 71, 2491–2501. [Google Scholar] [CrossRef]
- Dillon, P.; Stuyfzand, P.; Grischek, T.; Lluria, M.; Pyne, R.D.G.; Jain, R.C.; Bear, J.; Schwarz, J.; Wang, W.; Fernandez, E.; et al. Sixty years of global progress in managed aquifer recharge. Hydrogeol. J. 2019, 27, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Beganskas, S.; Fisher, A.T. Coupling distributed stormwater collection and managed aquifer recharge: Field application and implications. J. Environ. Manag. 2017, 200, 366–379. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- García-Menéndez, O.; Ballesteros, B.J.; Renau-Pruñonosa, A.; Morell, I.; Mochales, T.; Ibarra, P.I.; Rubio, F.M. Using electrical resistivity tomography to assess the effectiveness of managed aquifer recharge in a salinized coastal aquifer. Environ. Monit. Assess. 2018, 190. [Google Scholar] [CrossRef]
- Shammas, M.I. The effectiveness of artificial recharge in combating seawater intrusion in Salalah coastal aquifer, Oman. Environ. Geol. 2008, 55, 191–204. [Google Scholar] [CrossRef]
- Shi, X.; Jiang, S.; Xu, H.; Jiang, F.; He, Z.; Wu, J. The effects of artificial recharge of groundwater on controlling land subsidence and its influence on groundwater quality and aquifer energy storage in Shanghai, China. Environ. Earth Sci. 2016, 75, 1–18. [Google Scholar] [CrossRef]
- Elkayam, R.; Sopliniak, A.; Gasser, G.; Pankratov, I.; Lev, O. Oxidizer Demand in the Unsaturated Zone of a Surface-Spreading Soil Aquifer Treatment System. Vadose Zone J. 2015, 14. [Google Scholar] [CrossRef]
- Elkayam, R.; Michail, M.; Mienis, O.; Kraitzer, T.; Tal, N.; Lev, O. Soil Aquifer Treatment as Disinfection Unit. J. Environ. Eng. 2015, 141, 05015001. [Google Scholar] [CrossRef]
- Ganot, Y.; Holtzman, R.; Weisbrod, N.; Nitzan, I.; Katz, Y.; Kurtzman, D. Monitoring and modeling infiltration-recharge dynamics of managed aquifer recharge with desalinated seawater. Hydrol. Earth Syst. Sci. 2017, 21, 4479–4493. [Google Scholar] [CrossRef] [Green Version]
- Ganot, Y.; Holtzman, R.; Weisbrod, N.; Russak, A.; Katz, Y.; Kurtzman, D. Geochemical Processes During Managed Aquifer Recharge with Desalinated Seawater. Water Resour. Res. 2018, 54, 978–994. [Google Scholar] [CrossRef]
- Sharma, S.K.; Kennedy, M.D. Soil aquifer treatment for wastewater treatment and reuse. Int. Biodeterior. Biodegrad. 2017, 119, 671–677. [Google Scholar] [CrossRef]
- Sopilniak, A.; Elkayam, R.; Rossin, A.V.; Lev, O. Emerging organic pollutants in the vadose zone of a soil aquifer treatment system: Pore water extraction using positive displacement. Chemosphere 2018, 190, 383–392. [Google Scholar] [CrossRef] [PubMed]
- Tsangaratos, P.; Kallioras, A.; Pizpikis, T.; Vasileiou, E.; Ilia, I.; Pliakas, F. Multi-criteria Decision Support System (DSS) for optimal locations of Soil Aquifer Treatment (SAT) facilities. Sci. Total Environ. 2017, 603–604, 472–486. [Google Scholar] [CrossRef]
- Kawo, N.S.; Zhou, Y.; Magalso, R.; Salvacion, L. Optimization of an artificial-recharge–pumping system for water supply in the Maghaway Valley, Cebu, Philippines. Hydrogeol. J. 2018, 26, 963–977. [Google Scholar] [CrossRef]
- Stefan, C.; Ansems, N. Web-based global inventory of managed aquifer recharge applications. Sustain. Water Resour. Manag. 2018, 4, 153–162. [Google Scholar] [CrossRef] [Green Version]
- Zakhem, B.A.; Hafez, R. Chemical and isotopic methods for management of artificial recharge in mazraha station (damascus basin, syria). Hydrol. Process. 2012, 26, 3712–3724. [Google Scholar] [CrossRef]
- Abou Zakhem, B. Using principal component analysis (PCA) in the investigation of aquifer storage and recovery (ASR) in Damascus Basin (Syria). Environ. Earth Sci. 2016, 75, 1–15. [Google Scholar] [CrossRef]
- Lopez, O.; Stenchikov, G.; Missimer, T.M. Water management during climate change using aquifer storage and recovery of stormwater in a dunefield in western Saudi Arabia. Environ. Res. Lett. 2014, 9. [Google Scholar] [CrossRef]
- Winde, F.; Stoch, E.J. Threats and opportunities for post-closure development in dolomitic gold-mining areas of the West Rand and Far West Rand (South Africa)—A hydraulic view Part 2: Opportunities. Water SA 2010, 36, 75–82. [Google Scholar] [CrossRef] [Green Version]
- Ringleb, J.; Sallwey, J.; Stefan, C. Assessment of managed aquifer recharge through modeling—A review. Water 2016, 8, 1–31. [Google Scholar] [CrossRef] [Green Version]
- Fatkhutdinov, A.; Stefan, C. Multi-Objective Optimization of Managed Aquifer Recharge. Groundwater 2019, 57, 238–244. [Google Scholar] [CrossRef] [PubMed]
- Rossetto, R.; Barbagli, A.; De Filippis, G.; Marchina, C.; Vienken, T.; Mazzanti, G. Importance of the induced recharge term in riverbank filtration: Hydrodynamics, hydrochemical, and numerical modelling investigations. Hydrology 2020, 7, 96. [Google Scholar] [CrossRef]
- Steinel, A.; Schelkes, K.; Subah, A.; Himmelsbach, T. Analyse spatiale multi-critère pour sélectionner des sites potentiels pour la recharge d’aquifère à partir de collecte et d’infiltration d’eau de ruissellement dans le nord de la Jordanie. Hydrogeol. J. 2016, 24, 1753–1774. [Google Scholar] [CrossRef]
- Lange, J. Dynamics of transmission losses in a large arid stream channel. J. Hydrol. 2005, 306, 112–126. [Google Scholar] [CrossRef]
- Lee, L.J.E.; Lawrence, D.S.L.; Price, M. Analysis of water-level response to rainfall and implications for recharge pathways in the Chalk aquifer, SE England. J. Hydrol. 2006, 330, 604–620. [Google Scholar] [CrossRef]
- Ibn Ali, Z.; Triki, I.; Lajili-Ghezal, L.; Zairi, M. A method to estimate aquifer artificial recharge from a hill dam in Tunisia. J. Arid Land 2017, 9, 244–255. [Google Scholar] [CrossRef] [Green Version]
- Flint, A.L.; Ellett, K.M.; Christensen, A.H.; Martin, P. Modeling a Thick Unsaturated Zone at San Gorgonio Pass, California: Lessons Learned after Five Years of Artificial Recharge. Vadose Zone J. 2012, 11. [Google Scholar] [CrossRef]
- Al-Ismaily, S.S.; Al-Maktoumi, A.K.; Kacimov, A.R.; Al-Saqri, S.M.; Al-Busaidi, H.A.; Al-Haddabi, M.H. Sédimentation préférentielle en blocs et fissures: Structure originale et évolution naturelles. Hydrol. Sci. J. 2013, 58, 1779–1788. [Google Scholar] [CrossRef] [Green Version]
- Villeneuve, S.; Cook, P.G.; Shanafield, M.; Wood, C.; White, N. Groundwater recharge via infiltration through an ephemeral riverbed, central Australia. J. Arid Environ. 2015, 117, 47–58. [Google Scholar] [CrossRef]
- Shanafield, M.; Cook, P.G. Transmission losses, infiltration and groundwater recharge through ephemeral and intermittent streambeds: A review of applied methods. J. Hydrol. 2014, 511, 518–529. [Google Scholar] [CrossRef]
- Bosch, D.D.; Truman, C.C.; Davis, F.M. Vadose Zone Clay Lens Impacts on Groundwater Load Rates. In Proceedings of the Preferential Flow: Water Movement and Chemical Transport in the Environment, Honolulu, HI, USA, 3–5 January 2001; pp. 69–72. [Google Scholar] [CrossRef]
- Lu, X.; Jin, M.; Van Genuchten, M.T.; Wang, B. Groundwater Recharge at Five Representative Sites in the Hebei Plain, China. Ground Water 2011, 49, 286–294. [Google Scholar] [CrossRef]
- Missimer, T.M.; Drewes, J.E.; Amy, G.; Maliva, R.G.; Keller, S. Restoration of Wadi Aquifers by Artificial Recharge with Treated Wastewater. Ground Water 2012, 50, 514–527. [Google Scholar] [CrossRef] [PubMed]
- Jocson, J.M.U.; Jenson, J.W.; Contractor, D.N. Recharge and aquifer response: Northern Guam Lens Aquifer, Guam, Mariana Islands. J. Hydrol. 2002, 260, 231–254. [Google Scholar] [CrossRef]
- Vries, J.J.; Simmers, I. Groundwater recharge: An overview of process and challenges. Hydrogeol. J. 2002, 10, 5–17. [Google Scholar] [CrossRef]
- Azaroual, M.; Pettenati, M.; Ollivier, P.; Besnard, K.; Casanova, J.; Rampnoux, N. Reactive Transfer of Pollutants Through the Unsaturated Soil Zone During an Artificial Aquifer Recharge Process. Procedia Earth Planet. Sci. 2013, 7, 40–43. [Google Scholar] [CrossRef]
- Izbicki, J.A.; Flint, A.L.; Stamos, C.L. Artificial recharge through a thick, heterogeneous unsaturated zone. Ground Water 2008, 46, 475–488. [Google Scholar] [CrossRef]
- Boughanmi, M.; Dridi, L.; Hamdi, M.; Majdoub, R.; Schäfer, G. Impact of floodwaters on vertical water fluxes in the deep vadose zone of an alluvial aquifer in a semi-arid region. Hydrol. Sci. J. 2018, 63, 136–153. [Google Scholar] [CrossRef]
- Alrehaili, A.M.; Hussein, M.T. Use of remote sensing, gis and groundwater monitoring to estimate artificial groundwater recharge in riyadh, saudi arabia. Arab. J. Geosci. 2012, 5, 1367–1377. [Google Scholar] [CrossRef]
- Vandenbohede, A.; Wallis, I.; van Houtte, E.; van Ranst, E. Modélisation du transport hydrogéochimique de l’infiltration d’eaux usées traitées par traitement tertiaire dans une zone de dune, Belgique. Hydrogeol. J. 2013, 21, 1307–1321. [Google Scholar] [CrossRef] [Green Version]
- Beganskas, S.; Gorski, G.; Weathers, T.; Fisher, A.T.; Schmidt, C.; Saltikov, C.; Redford, K.; Stoneburner, B.; Harmon, R.; Weir, W. A horizontal permeable reactive barrier stimulates nitrate removal and shifts microbial ecology during rapid infiltration for managed recharge. Water Res. 2018, 144, 274–284. [Google Scholar] [CrossRef] [Green Version]
- Greskowiak, J.; Prommer, H.; Massmann, G.; Johnston, C.D.; Nützmann, G.; Pekdeger, A. The impact of variably saturated conditions on hydrogeochemical changes during artificial recharge of groundwater. Appl. Geochem. 2005, 20, 1409–1426. [Google Scholar] [CrossRef]
- Wiese, B.; Nützmann, G. Transient leakance and infiltration characteristics during lake bank filtration. Ground Water 2009, 47, 57–68. [Google Scholar] [CrossRef] [Green Version]
- Scanlon, B.R.; Tyler, S.W.; Wierenga, P.J. Hydrologic issues in arid, unsaturated systems and implications for contaminant transport. Rev. Geophys. 1997, 35, 461–490. [Google Scholar] [CrossRef]
- Inoue, K.; Nakazato, H.; Kubota, T.; Takeuchi, M.; Sugimoto, Y.; Kim, H.J.; Furue, K. Three-dimensional inversion of in-line resistivity data for monitoring a groundwater recharge experiment in a pyroclastic plateau. Explor. Geophys. 2017, 48, 332–343. [Google Scholar] [CrossRef] [Green Version]
- Boisson, A.; Baïsset, M.; Alazard, M.; Perrin, J.; Villesseche, D.; Dewandel, B.; Kloppmann, W.; Chandra, S.; Picot-Colbeaux, G.; Sarah, S.; et al. Comparison of surface and groundwater balance approaches in the evaluation of managed aquifer recharge structures: Case of a percolation tank in a crystalline aquifer in India. J. Hydrol. 2014, 519, 1620–1633. [Google Scholar] [CrossRef]
- Zammouri, M.; Feki, H. Managing releases from small upland reservoirs for downstream recharge in semi-arid basins (Northeast of Tunisia). J. Hydrol. 2005, 314, 125–138. [Google Scholar] [CrossRef]
- Allison, G.B.; Gee, G.W.; Tyler, S.W. Vadose-Zone Techniques for Estimating Groundwater Recharge in Arid and Semiarid Regions. Soil Sci. Soc. Am. J. 1994, 58, 6–14. [Google Scholar] [CrossRef]
- Sasidharan, S.; Bradford, S.A.; Šimůnek, J.; Kraemer, S.R. Groundwater recharge from drywells under constant head conditions. J. Hydrol. 2020, 583. [Google Scholar] [CrossRef]


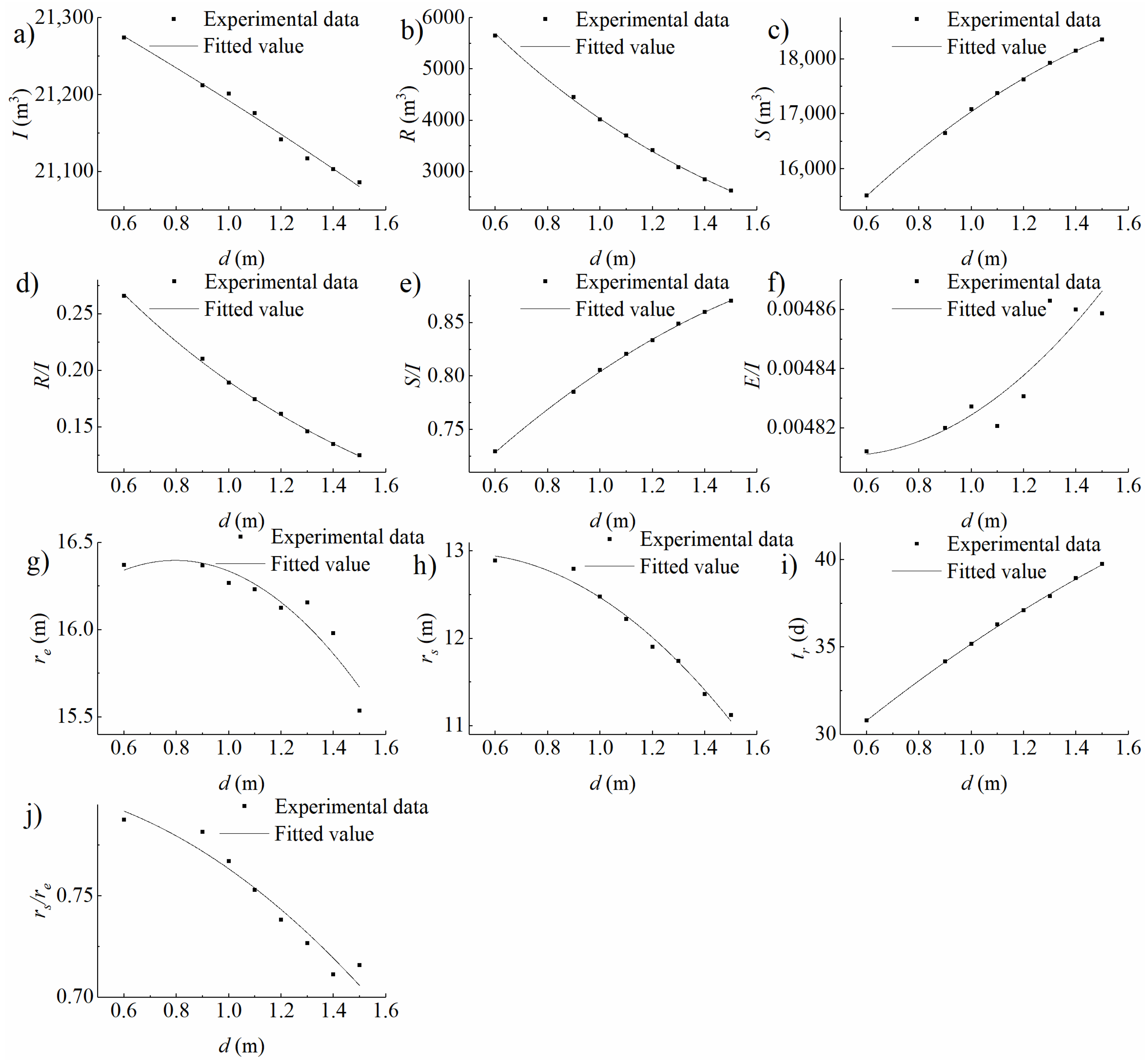
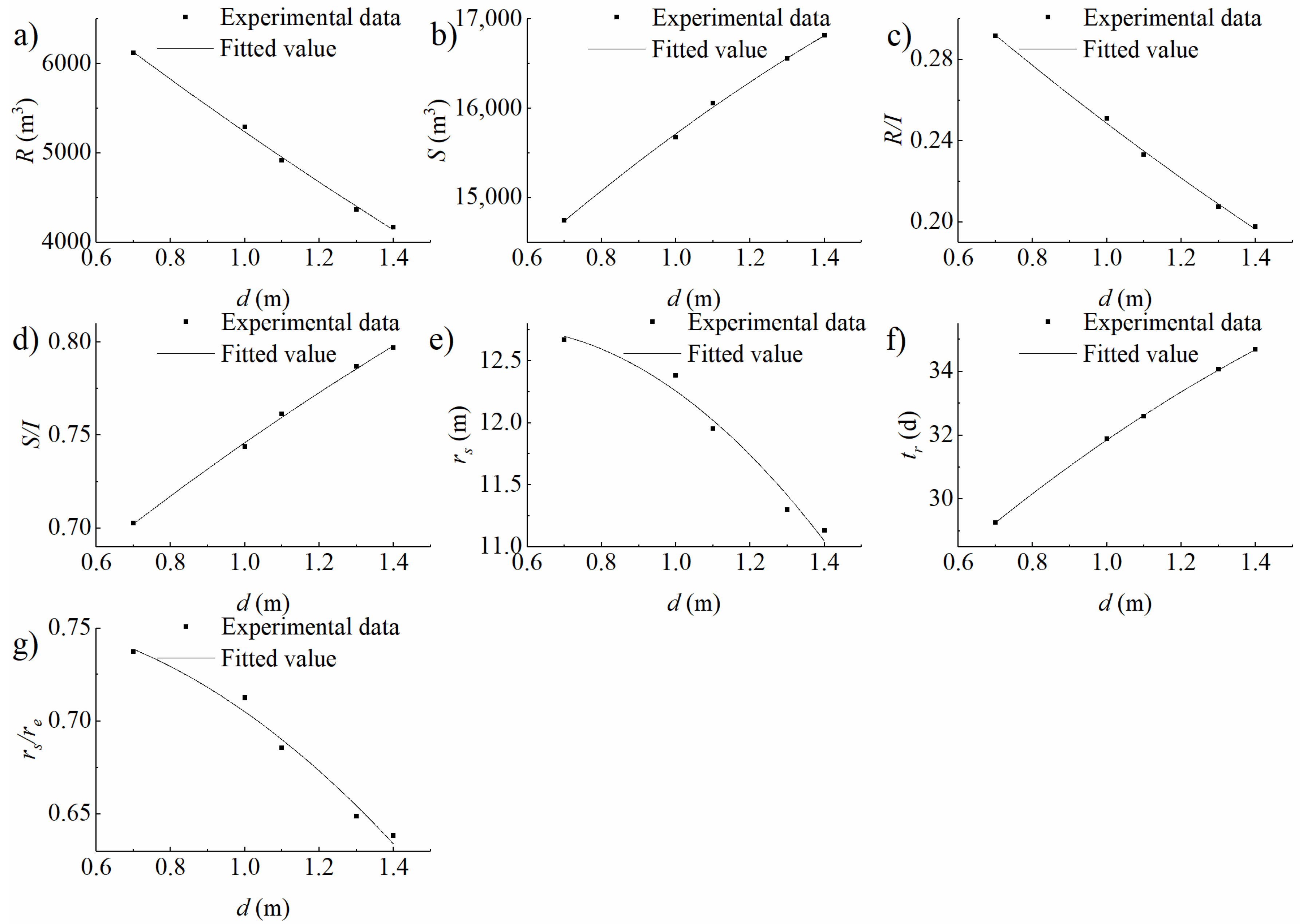
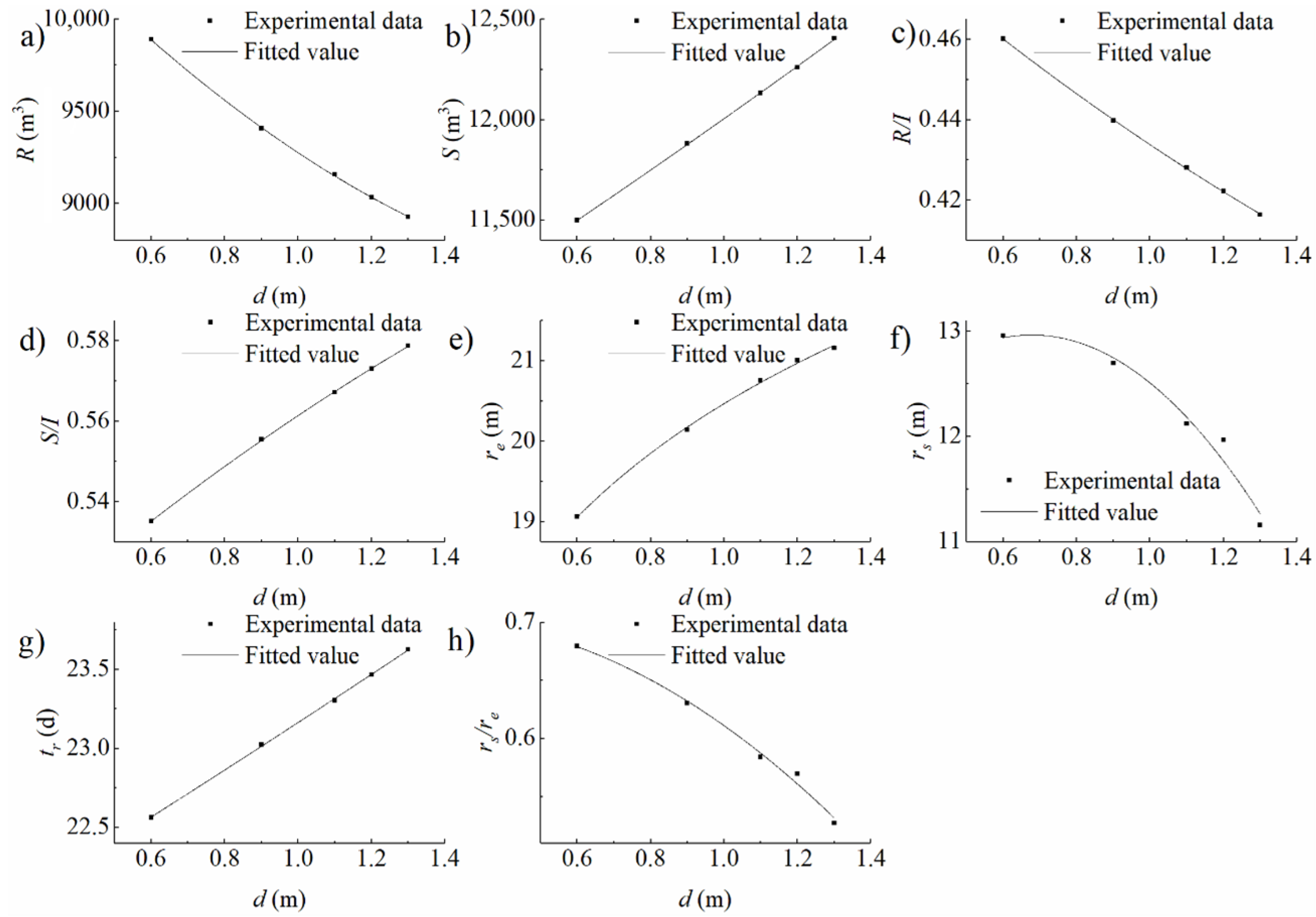
| Experimental Condition Type | Variable of Experiments | Number of Experiments | Variable Range |
|---|---|---|---|
| Water head in infiltration basin | Water head | 10 | 0.1 to 1 m |
| Radius of infiltration basin | Infiltration basin radius | 9 | 7 to 21 m |
| Evaporation intensity | Potential evaporation rate | 12 | 4 to 22 mm/d |
| Antecedent moisture of the vadose zone | Moisture saturation | 10 | 17.1 to 40% |
| Thickness of the vadose zone | Vadose zone thickness | 11 | 48 to 75 m |
| Hydraulic conductivity of the vadose zone | Saturated hydraulic conductivity | 10 | 1 to 2.8 m/d |
| Experimental Condition Type | Variable of Experiments | Number of Experiments | Variable Range (m) |
|---|---|---|---|
| The depth is 5 m, and the thickness is 0.6 m | Length of low permeability formation | 10 | 1 to 60 |
| The depth is 10 m, and the thickness is 0.6 m | 8 | 3 to 60 | |
| The depth is 20 m, and the thickness is 0.6 m | 9 | 1 to 60 | |
| The depth is 30 m, and the thickness is 0.6 m | 7 | 1 to 30 | |
| The depth is 55 m, and the thickness is 0.6 m | 10 | 1 to 60 | |
| The depth is 5 m, and the length is 100 m | Thickness of low permeability formation | 9 | 0.6 to 1.4 |
| The depth is 10 m, and the length is 100 m | 5 | 0.8 to 1.4 | |
| The depth is 20 m, and the length is 100 m | 8 | 0.6 to 1.5 | |
| The depth is 30 m, and the length is 100 m | 5 | 0.7 to 1.4 | |
| The depth is 55 m, and the length is 100 m | 5 | 0.6 to 1.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, T.; Shu, L.; Li, H.; Wang, X.; Men, Y.; Opoku, P.A. Water Distribution from Artificial Recharge via Infiltration Basin under Constant Head Conditions. Water 2021, 13, 1052. https://doi.org/10.3390/w13081052
Qi T, Shu L, Li H, Wang X, Men Y, Opoku PA. Water Distribution from Artificial Recharge via Infiltration Basin under Constant Head Conditions. Water. 2021; 13(8):1052. https://doi.org/10.3390/w13081052
Chicago/Turabian StyleQi, Tiansong, Longcang Shu, Hu Li, Xiaobo Wang, Yanqing Men, and Portia Annabelle Opoku. 2021. "Water Distribution from Artificial Recharge via Infiltration Basin under Constant Head Conditions" Water 13, no. 8: 1052. https://doi.org/10.3390/w13081052





