PISCO_HyM_GR2M: A Model of Monthly Water Balance in Peru (1981–2020)
Abstract
:1. Introduction
2. Study Area
3. Data and Methods
3.1. Hydrometeorological Data
3.1.1. The PISCO Dataset
3.1.2. Discharge Data
3.2. Semi-Distributed GR2M Model
3.3. Sensitivity Analysis
3.4. Calibration Regions and Sub-Regions
3.5. GR2M Calibration and Validation Strategy
3.6. Discharge Simulation at a National Level
4. Results
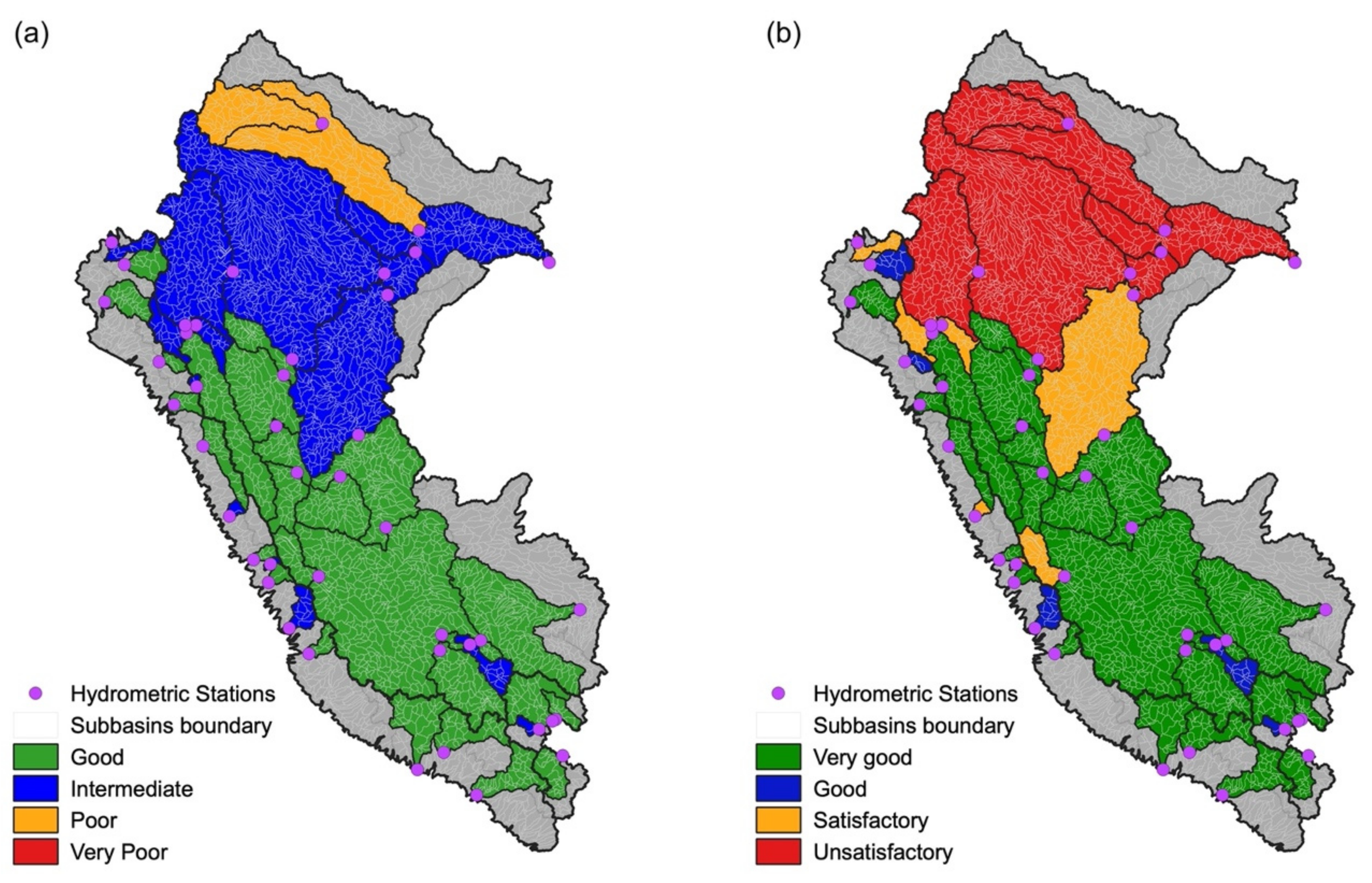
4.1. Sensitivity Analysis and Calibration Regions
4.2. Model Performance Assessment
4.3. Product of Simulated Monthly Discharges at a National Level
5. Discussion
5.1. Sensitivity Analysis and Calibration Regions
5.2. Model Simulations at a National Level
6. Conclusions
- (a)
- The hydrological performance of the GR2M model in Peru performed well in sub-basins of the Pacific slope and the Andes–Amazon transition (part of the Titicaca and the Atlantic slopes). The model adequately represents the seasonality and interannual variability of the streamflows, except for the Amazon lowlands, where only high flows are well-represented.
- (b)
- Through the monthly meteorological PISCO sub-products, it is possible to simulate the runoff volume over most of Peru adequately. However, the uncertainties associated with these sub-products are more significant towards the north of the country where there are not enough meteorological stations, so this error propagates towards the hydrological model outputs for the Amazon lowlands.
- (c)
- The proposed methodology to define the calibration regions based on the spatial patterns of two hydroclimatic indices’ relative sensitivities proved to be an appropriate technique for calibrating and validating the GR2M model and estimating monthly discharge in ungauged sub-basins.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ANA. Plan Nacional de Recursos Hídricos del Perú; Autoridad Nacional del Agua: Lima, Perú, 2013; ISBN 9786124655241.
- Biswas, A.K. Integrated water resources management: A reassessment: A water forum contribution. Water Int. 2004, 29, 248–256. [Google Scholar] [CrossRef]
- Eda, L.E.H.; Chen, W. Integrated Water Resources Management in Peru. Procedia Environ. Sci. 2010, 2, 340–348. [Google Scholar] [CrossRef] [Green Version]
- Budds, J.; Hinojosa, L. Restructuring and Rescaling Water Governance in Mining Contexts: The Co-Production of Waterscapes in Peru. Water Altern. 2012, 5, 119. [Google Scholar]
- Paturel, J.E.; Ouedraogo, M.; Mahe, G.; Servat, E.; Dezetter, A.; Ardoin, S. The influence of distributed input data on the hydrological modelling of monthly river flow regimes in West Africa. Hydrol. Sci. J. 2003, 48, 881–890. [Google Scholar] [CrossRef]
- Louvet, S.; Paturel, J.E.; Mahé, G.; Rouché, N.; Koité, M. Comparison of the spatiotemporal variability of rainfall from four different interpolation methods and impact on the result of GR2M hydrological modeling—case of Bani River in Mali, West Africa. Theor. Appl. Climatol. 2016, 123, 303–319. [Google Scholar] [CrossRef]
- Turan, M.E.; Yurdusev, M.A. Fuzzy Conceptual Hydrological Model for Water Flow Prediction. Water Resour. Manag. 2016, 30, 653–667. [Google Scholar] [CrossRef]
- Mazrooei, A.; Sankarasubramanian, A. Improving monthly streamflow forecasts through assimilation of observed streamflow for rainfall-dominated basins across the CONUS. J. Hydrol. 2019, 575, 704–715. [Google Scholar] [CrossRef]
- Adane, G.B.; Hirpa, B.A.; Gebru, B.M.; Song, C.; Lee, W.-K. Integrating Satellite Rainfall Estimates with Hydrological Water Balance Model: Rainfall-Runoff Modeling in Awash River Basin, Ethiopia. Water 2021, 13, 800. [Google Scholar] [CrossRef]
- Llauca, H.; Lavado-Casimiro, W.; León, K.; Jimenez, J.; Traverso, K.; Rau, P. Assessing Near Real-Time Satellite Precipitation Products for Flood Simulations at Sub-Daily Scales in a Sparsely Gauged Watershed in Peruvian Andes. Remote Sens. 2021, 13, 826. [Google Scholar] [CrossRef]
- Aybar, C.; Fernández, C.; Huerta, A.; Lavado, W.; Vega, F.; Felipe-Obando, O. Construction of a high-resolution gridded rainfall dataset for Peru from 1981 to the present day. Hydrol. Sci. J. 2020, 65, 770–785. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Shalev, G.; Klambauer, G.; Hochreiter, S.; Nearing, G. Towards Learning Universal, Regional, and Local Hydrological Behaviors via Machine-Learning Applied to Large-Sample Datasets. Hydrol. Earth Syst. Sci. 2019, 23, 5089–5110. [Google Scholar] [CrossRef] [Green Version]
- Abou Rafee, S.A.; Uvo, C.B.; Martins, J.A.; Domingues, L.M.; Rudke, A.P.; Fujita, T.; Freitas, E.D. Large-Scale Hydrological Modelling of the Upper Paraná River Basin. Water 2019, 11, 882. [Google Scholar] [CrossRef] [Green Version]
- Lane, R.A.; Coxon, G.; Freer, J.E.; Wagener, T.; Johnes, P.J.; Bloomfield, J.P.; Greene, S.; Macleod, C.J.A.; Reaney, S.M. Benchmarking the predictive capability of hydrological models for river flow and flood peak predictions across over 1000 catchments in Great Britain. Hydrol. Earth Syst. Sci. 2019, 23, 4011–4032. [Google Scholar] [CrossRef] [Green Version]
- Pagliero, L.; Bouraoui, F.; Diels, J.; Willems, P.; McIntyre, N. Investigating regionalization techniques for large-scale hydrological modelling. J. Hydrol. 2019, 570, 220–235. [Google Scholar] [CrossRef]
- Drogue, G.; Ben Khediri, W. Catchment model regionalization approach based on spatial proximity: Does a neighbor catchment-based rainfall input strengthen the method? J. Hydrol. Reg. Stud. 2016, 8, 26–42. [Google Scholar] [CrossRef] [Green Version]
- Wagener, T.; Sivapalan, M.; Troch, P.; Woods, R. Catchment Classification and Hydrologic Similarity. Geogr. Compass 2007, 1, 901–931. [Google Scholar] [CrossRef]
- Rau, P.; Bourrel, L.; Labat, D.; Ruelland, D.; Frappart, F.; Lavado, W.; Dewitte, B.; Felipe, O. Assessing multidecadal runoff (1970–2010) using regional hydrological modelling under data and water scarcity conditions in Peruvian Pacific catchments. Hydrol. Process. 2019, 33, 20–35. [Google Scholar] [CrossRef] [Green Version]
- Beck, H.E.; van Dijk, A.I.J.M.; de Roo, A.; Miralles, D.G.; McVicar, T.R.; Schellekens, J.; Bruijnzeel, L.A. Global-scale regionalization of hydrologic model parameters. Water Resour. Res. 2016, 52, 3599–3622. [Google Scholar] [CrossRef] [Green Version]
- Narbondo, S.; Gorgoglione, A.; Crisci, M.; Chreties, C. Enhancing Physical Similarity Approach to Predict Runoff in Ungauged Watersheds in Sub-Tropical Regions. Water 2020, 12, 528. [Google Scholar] [CrossRef] [Green Version]
- Bock, A.R.; Hay, L.E.; McCabe, G.J.; Markstrom, S.L.; Atkinson, R.D. Parameter regionalization of a monthly water balance model for the conterminous United States. Hydrol. Earth Syst. Sci. 2016, 20, 2861–2876. [Google Scholar] [CrossRef] [Green Version]
- Pagliero, L.; Bouraoui, F.; Willems, P.; Diels, J. Large-scale hydrological simulations using the soil water assessment tool, protocol development, and application in the danube basin. J. Environ. Qual. 2014, 43, 145–154. [Google Scholar] [CrossRef] [PubMed]
- Zamoum, S.; Souag-Gamane, D. Monthly streamflow estimation in ungauged catchments of northern Algeria using regionalization of conceptual model parameters. Arab. J. Geosci. 2019, 12, 342. [Google Scholar] [CrossRef]
- Abdollahi, K.; Bashir, I.; Verbeiren, B.; Harouna, M.R.; Van Griensven, A.; Huysmans, M.; Batelaan, O. A distributed monthly water balance model: Formulation and application on Black Volta Basin. Environ. Earth Sci. 2017, 76, 198. [Google Scholar] [CrossRef]
- Xie, Z.; Yuan, F.; Duan, Q.; Zheng, J.; Liang, M.; Chen, F. Regional Parameter Estimation of the VIC Land Surface Model: Methodology and Application to River Basins in China. J. Hydrometeorol. 2007, 8, 447–468. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Gupta, H.V. Uncertainty in hydrologic modeling: Toward an integrated data assimilation framework. Water Resour. Res. 2007, 43, 160. [Google Scholar] [CrossRef]
- Beven, K. Prophecy, reality and uncertainty in distributed hydrological modelling. Adv. Water Resour. 1993, 16, 41–51. [Google Scholar] [CrossRef]
- Beven, K. Changing ideas in hydrology—The case of physically-based models. J. Hydrol. 1989, 105, 157–172. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Does a large number of parameters enhance model performance? Comparative assessment of common catchment model structures on 429 catchments. J. Hydrol. 2001, 242, 275–301. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Mouelhi, S.; Michel, C.; Perrin, C.; Andréassian, V. Stepwise development of a two-parameter monthly water balance model. J. Hydrol. 2006, 318, 200–214. [Google Scholar] [CrossRef]
- Pumo, D.; Viola, F.; Noto, L.V. Generation of Natural Runoff Monthly Series at Ungauged Sites Using a Regional Regressive Model. Water 2016, 8, 209. [Google Scholar] [CrossRef] [Green Version]
- Pérez-Sánchez, J.; Senent-Aparicio, J.; Segura-Méndez, F.; Pulido-Velazquez, D.; Srinivasan, R. Evaluating Hydrological Models for Deriving Water Resources in Peninsular Spain. Sustain. Sci. Pract. Policy 2019, 11, 2872. [Google Scholar] [CrossRef] [Green Version]
- Bai, P.; Liu, X.; Liang, K.; Liu, C. Comparison of performance of twelve monthly water balance models in different climatic catchments of China. J. Hydrol. 2015, 529, 1030–1040. [Google Scholar] [CrossRef]
- Okkan, U.; Fistikoglu, O. Evaluating climate change effects on runoff by statistical downscaling and hydrological model GR2M. Theor. Appl. Climatol. 2014, 117, 343–361. [Google Scholar] [CrossRef]
- Ouhamdouch, S.; Bahir, M.; Ouazar, D.; Goumih, A.; Zouari, K. Assessment the climate change impact on the future evapotranspiration and flows from a semi-arid environment. Arab. J. Geosci. 2020, 13, 82. [Google Scholar] [CrossRef]
- Topalović, Ž.; Todorović, A.; Plavšić, J. Evaluating the transferability of monthly water balance models under changing climate conditions. Hydrol. Sci. J. 2020, 65, 928–950. [Google Scholar] [CrossRef]
- Rwasoka, D.T.; Madamombe, C.E.; Gumindoga, W.; Kabobah, A.T. Calibration, validation, parameter indentifiability and uncertainty analysis of a 2—Parameter parsimonious monthly rainfall-runoff model in two catchments in Zimbabwe. Phys. Chem. Earth Parts A/B/C 2014, 67–69, 36–46. [Google Scholar] [CrossRef]
- Huard, D.; Mailhot, A. Calibration of hydrological model GR2M using Bayesian uncertainty analysis. Water Resour. Res. 2008, 44, 206. [Google Scholar] [CrossRef] [Green Version]
- Lavado Casimiro, W.S.; Labat, D.; Guyot, J.L.; Ardoin-Bardin, S. Assessment of climate change impacts on the hydrology of the Peruvian Amazon—Andes basin. Hydrol. Process. 2011, 25, 3721–3734. [Google Scholar] [CrossRef]
- O’Connor, P.; Murphy, C.; Matthews, T.; Wilby, R.L. Reconstructed monthly river flows for Irish catchments 1766–2016. Geosci. Data J. 2020. [Google Scholar] [CrossRef]
- Duan, Q.; Schaake, J.; Andréassian, V.; Franks, S.; Goteti, G.; Gupta, H.V.; Gusev, Y.M.; Habets, F.; Hall, A.; Hay, L.; et al. Model Parameter Estimation Experiment (MOPEX): An overview of science strategy and major results from the second and third workshops. J. Hydrol. 2006, 320, 3–17. [Google Scholar] [CrossRef] [Green Version]
- Addor, N.; Newman, A.J.; Mizukami, N.; Clark, M.P. The CAMELS data set:Catchment attributes and meteorology for large-sample studies. Hydrol. Earth Syst. Sci. 2017, 21, 21. [Google Scholar] [CrossRef] [Green Version]
- Jehn, F.U.; Bestian, K.; Breuer, L.; Kraft, P.; Houska, T. Clustering CAMELS using hydrological signatures with high spatial predictability. Hydrol. Earth Syst. Sci. Discuss. 2019, 1–21. [Google Scholar] [CrossRef]
- Ren, K.; Fang, W.; Qu, J.; Zhang, X.; Shi, X. Comparison of eight filter-based feature selection methods for monthly streamflow forecasting—Three case studies on CAMELS data sets. J. Hydrol. 2020, 586, 124897. [Google Scholar] [CrossRef]
- Coxon, G.; Addor, N.; Bloomfield, J.P.; Freer, J.; Fry, M.; Hannaford, J.; Howden, N.J.K.; Lane, R.; Lewis, M.; Robinson, E.L.; et al. CAMELS-GB: Hydrometeorological time series and landscape attributes for 671 catchments in Great Britain. Earth Syst. Sci. Data 2020, 12, 2459–2483. [Google Scholar] [CrossRef]
- Chagas, V.B.P.; Chaffe, P.L.B.; Addor, N.; Fan, F.M.; Fleischmann, A.S.; Paiva, R.C.D.; Siqueira, V.A. CAMELS-BR: Hydrometeorological time series and landscape attributes for 897 catchments in Brazil. Earth Syst. Sci. Data 2020, 12, 2075–2096. [Google Scholar] [CrossRef]
- Alvarez-Garreton, C.; Mendoza, P.A.; Boisier, J.P.; Addor, N.; Galleguillos, M.; Zambrano-Bigiarini, M.; Lara, A.; Cortes, G.; Garreaud, R.; McPhee, J.; et al. The CAMELS-CL dataset: Catchment attributes and meteorology for large sample studies-Chile dataset. Hydrol. Earth Syst. Sci. 2018, 22, 5817–5846. [Google Scholar] [CrossRef] [Green Version]
- Zubieta, R.; Getirana, A.; Espinoza, J.C.; Lavado-Casimiro, W.; Aragon, L. Hydrological modeling of the Peruvian—Ecuadorian Amazon Basin using GPM-IMERG satellite-based precipitation dataset. Hydrol. Earth Syst. Sci. 2017, 21, 3543–3555. [Google Scholar] [CrossRef] [Green Version]
- Hargreaves, G.H.; Samani, Z.A. Reference crop evapotranspiration from ambient air temperature. In Proceedings of the American Society of Agricultural Engineers Meeting, Chicago, IL, USA, 17 December 1985; pp. 85–2517. [Google Scholar]
- Lehner, B.; Verdin, K.; Jarvis, A. HydroSHEDS Technical Documentation, Version 1.0; World Wildlife Fund US: Washington, DC, USA, 2006; pp. 1–27. [Google Scholar]
- Coron, L.; Thirel, G.; Delaigue, O.; Perrin, C.; Andréassian, V. The suite of lumped GR hydrological models in an R package. Environ. Model. Softw. 2017, 94, 166–171. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Sankarasubramanian, A.; Vogel, R.M. Hydroclimatology of the continental United States: U.S. HYDROCLIMATOLOGY. Geophys. Res. Lett. 2003, 30, 140. [Google Scholar] [CrossRef]
- Reusser, D.E.; Buytaert, W.; Zehe, E. Temporal dynamics of model parameter sensitivity for computationally expensive models with the Fourier amplitude sensitivity test. Water Resour. Res. 2011, 47, 703. [Google Scholar] [CrossRef] [Green Version]
- Reusser, D. Implementation of the Fourier Amplitude Sensitivity Test (FAST); R Package 0.51. 2008. Available online: http://www2.uaem.mx/r-mirror/web/packages/fast/fast.pdf (accessed on 5 February 2021).
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis: An Approach Based on L-Moments; Cambridge University Press: Cambridge, UK, 2005; ISBN 9780521019408. [Google Scholar]
- Hassan, B.G.H.; Ping, F. Regional rainfall frequency analysis for the luanhe basin—By using L-moments and cluster techniques. APCBEE Procedia 2012, 1, 126–135. [Google Scholar] [CrossRef] [Green Version]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Duan, Q.Y.; Gupta, V.K.; Sorooshian, S. Effective and Efficient Global Minimization. J. Optim. Theory Appl. 1993, 76. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Chiew, F.H.S.; Stewardson, M.J.; McMahon, T.A. Comparison of six rainfall-runoff modelling approaches. J. Hydrol. 1993, 147, 1–36. [Google Scholar] [CrossRef]
- Thiemig, V.; Rojas, R.; Zambrano-Bigiarini, M.; De Roo, A. Hydrological evaluation of satellite-based rainfall estimates over the Volta and Baro-Akobo Basin. J. Hydrol. 2013, 499, 324–338. [Google Scholar] [CrossRef]
- Mizukami, N.; Rakovec, O.; Newman, A.J.; Clark, M.P.; Wood, A.W.; Gupta, H.V.; Kumar, R. On the choice of calibration metrics for “high-flow” estimation using hydrologic models. Hydrol. Earth Syst. Sci. 2019, 23, 2601–2614. [Google Scholar] [CrossRef] [Green Version]
- Seiller, G.; Hajji, I.; Anctil, F. Improving the temporal transposability of lumped hydrological models on twenty diversified U.S. watersheds. J. Hydrol. Reg. Stud. 2015, 3, 379–399. [Google Scholar] [CrossRef] [Green Version]
- Bock, A.R.; Farmer, W.H.; Hay, L.E. Quantifying uncertainty in simulated streamflow and runoff from a continental-scale monthly water balance model. Adv. Water Resour. 2018, 122, 166–175. [Google Scholar] [CrossRef]
- Strauch, M.; Kumar, R.; Eisner, S.; Mulligan, M.; Reinhardt, J.; Santini, W.; Vetter, T.; Friesen, J. Adjustment of global precipitation data for enhanced hydrologic modeling of tropical Andean watersheds. Clim. Chang. 2017, 141, 547–560. [Google Scholar] [CrossRef] [Green Version]
- Zubieta, R.; Getirana, A.; Espinoza, J.C.; Lavado, W. Impacts of satellite-based precipitation datasets on rainfall–runoff modeling of the Western Amazon basin of Peru and Ecuador. J. Hydrol. 2015, 528, 599–612. [Google Scholar] [CrossRef]
- Wongchuig Correa, S.; de Paiva, R.C.D.; Espinoza, J.C.; Collischonn, W. Multi-decadal Hydrological Retrospective: Case study of Amazon floods and droughts. J. Hydrol. 2017, 549, 667–684. [Google Scholar] [CrossRef] [Green Version]
- Santini, W.; Martinez, J.-M.; Guyot, J.-L.; Espinoza, R.; Vauchel, P.; Lavado, W. Estimation of erosion and sedimentation yield in the Ucayali river basin, a Peruvian tributary of the Amazon River, using ground and satellite methods. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 27 April–2 May 2014; p. 916. [Google Scholar]
- Santini, W.; Martinez, J.-M.; Espinoza-Villar, R.; Cochonneau, G.; Vauchel, P.; Moquet, J.-S.; Baby, P.; Espinoza, J.-C.; Lavado, W.; Carranza, J.; et al. Sediment budget in the Ucayali River basin, an Andean tributary of the Amazon River. Proc. Int. Assoc. Hydrol. Sci. 2015, 367, 320–325. [Google Scholar] [CrossRef] [Green Version]
- David, C.H.; Maidment, D.R.; Niu, G.-Y.; Yang, Z.-L.; Habets, F.; Eijkhout, V. River Network Routing on the NHDPlus Dataset. J. Hydrometeorol. 2011, 12, 913–934. [Google Scholar] [CrossRef] [Green Version]
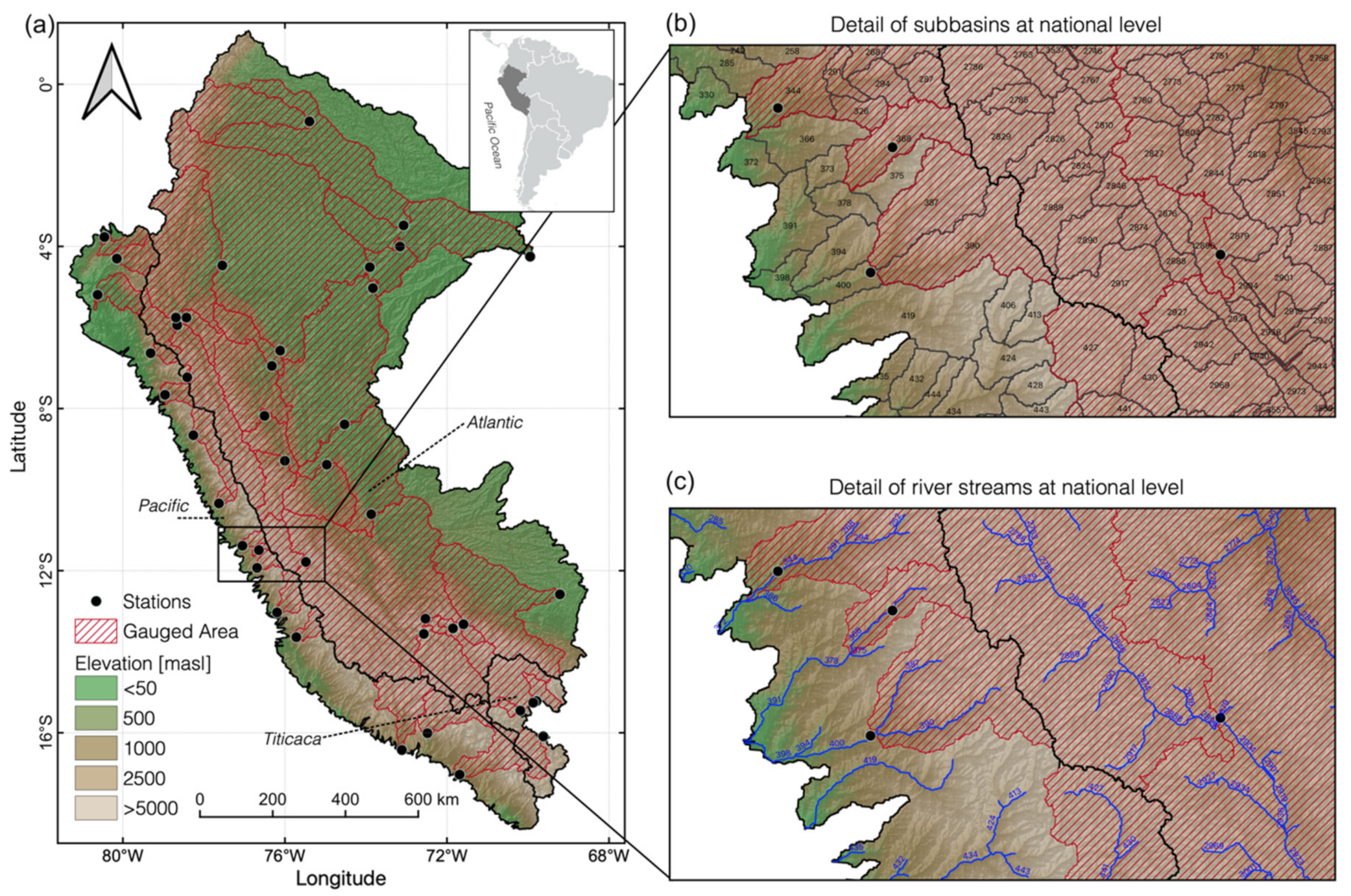


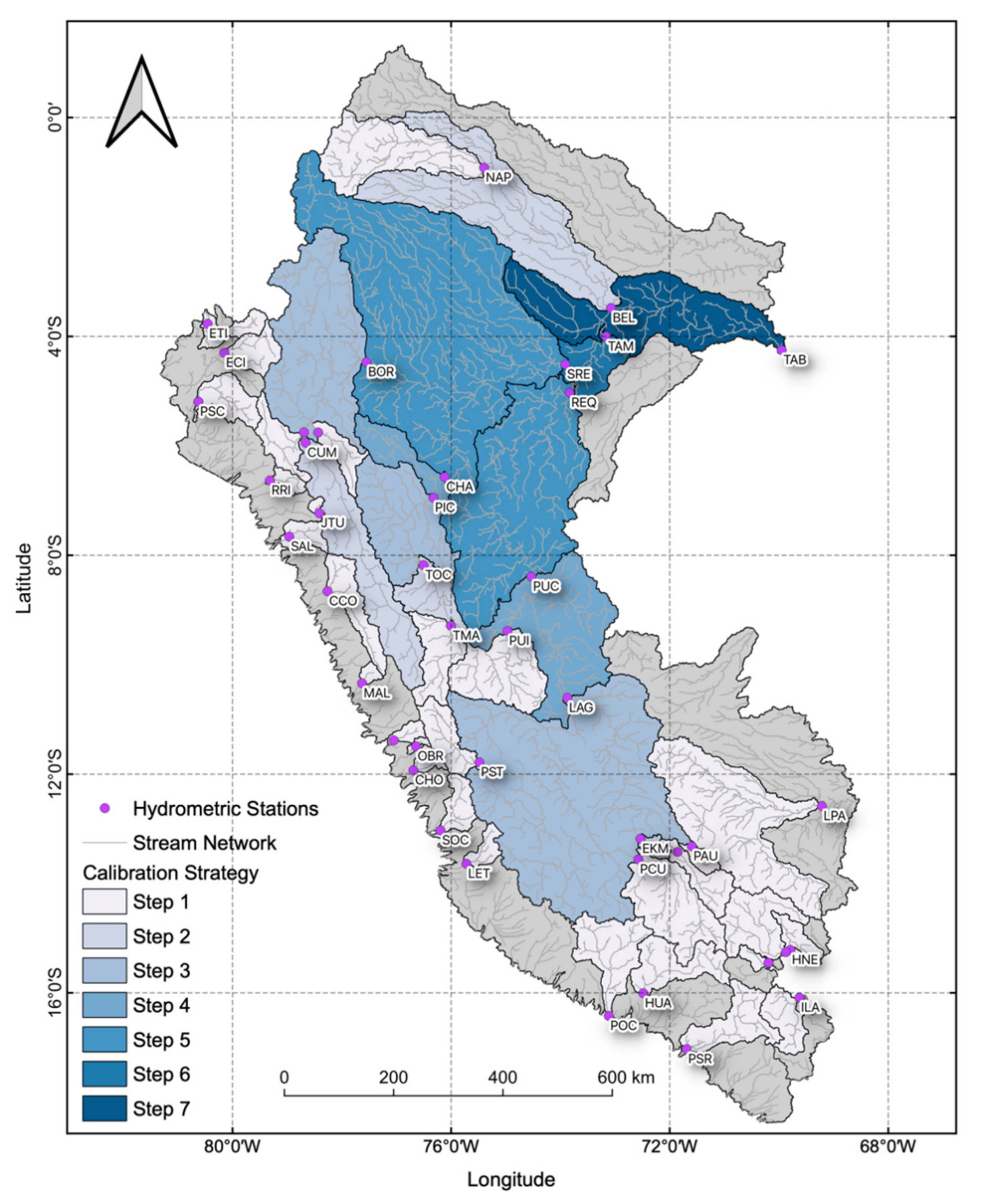

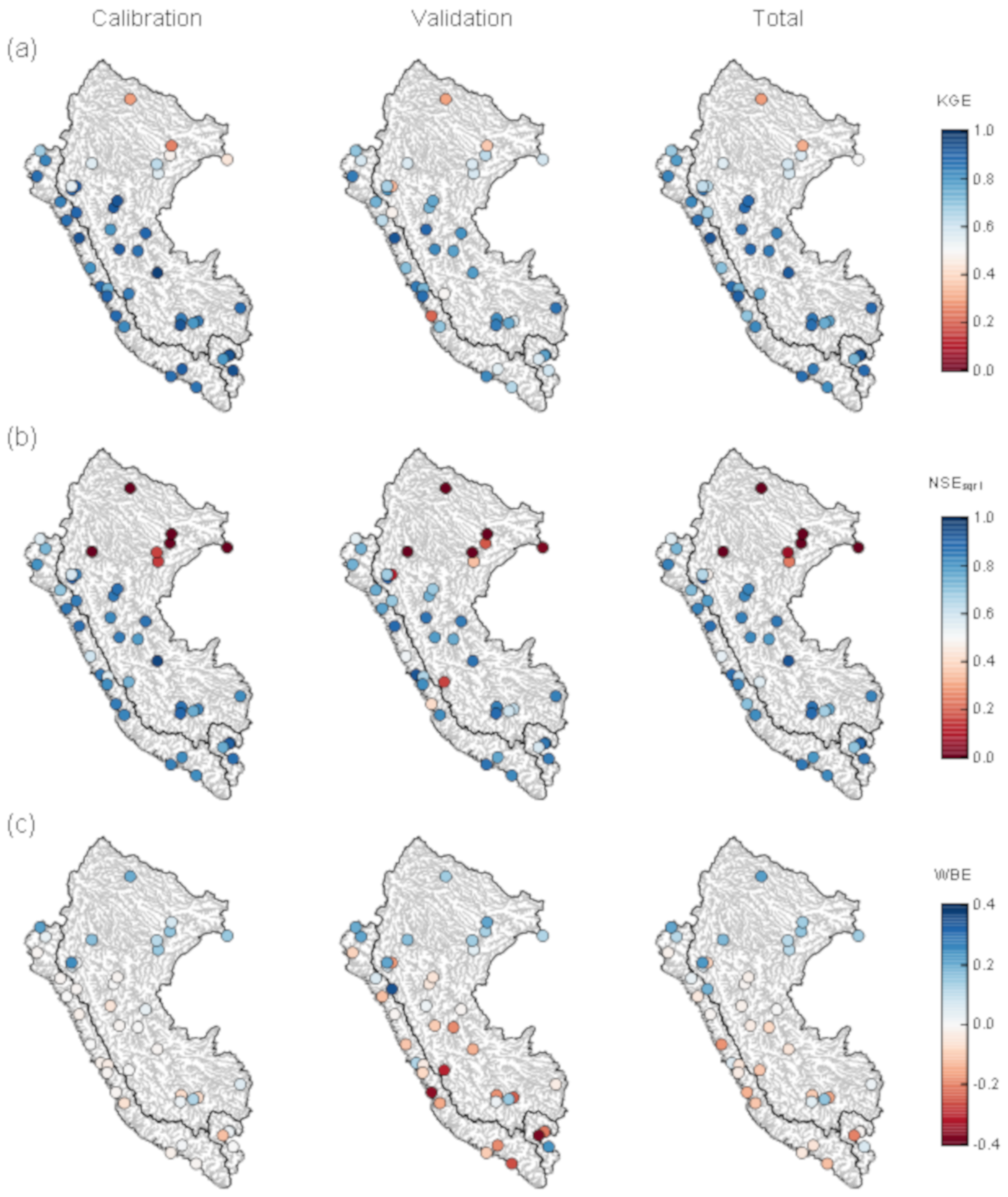

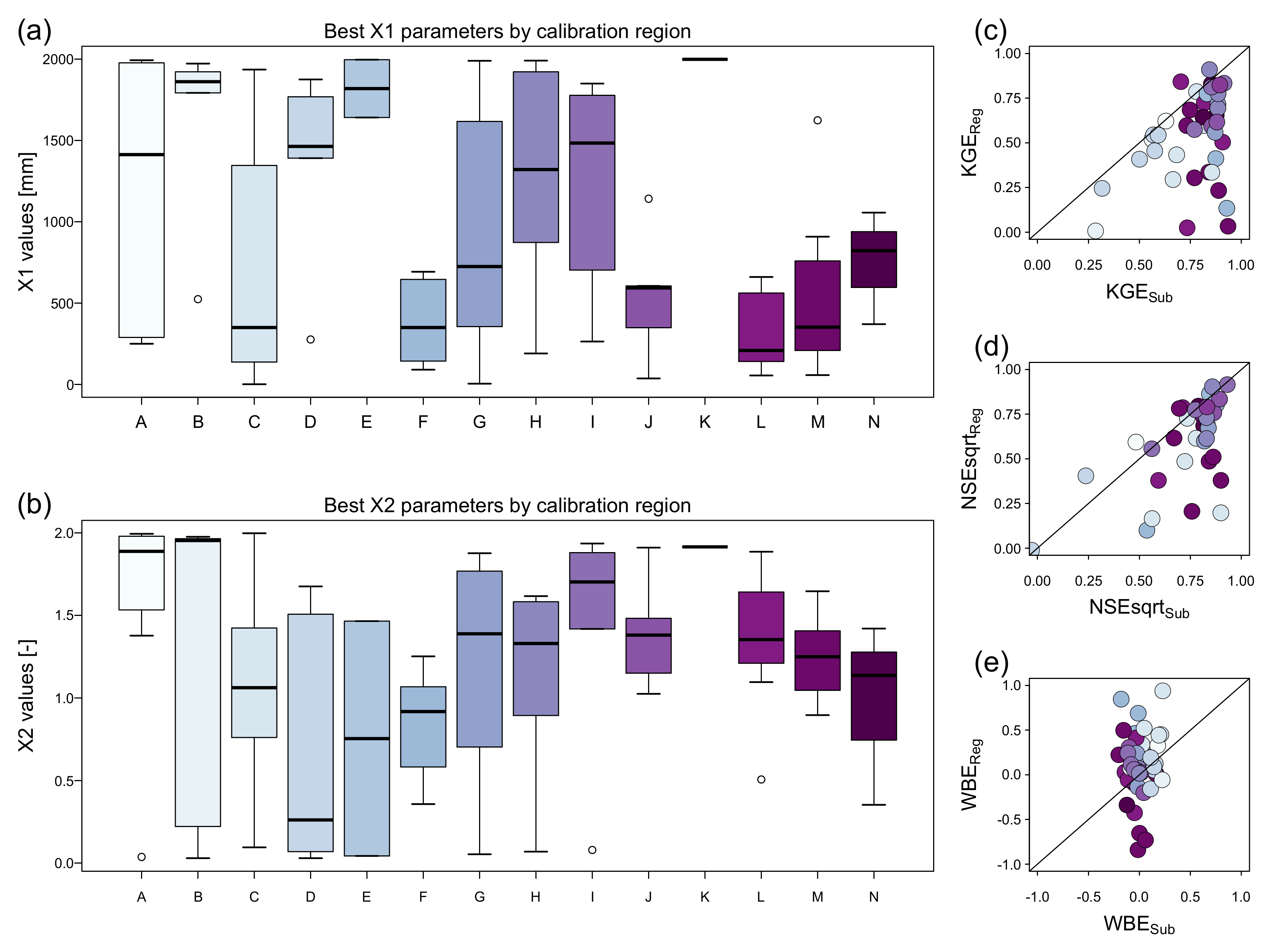
| Slope | Station | Abrev. | Latitude [°S] | Longitude [°W] | Watershed | Source | Coverage [%] |
|---|---|---|---|---|---|---|---|
| Pacific | Huatiapa | HUA | −16.008 | −72.484 | Camaná | SENAMHI | 45.3 |
| Socsi | SOC | −13.029 | −76.195 | Cañete | SENAMHI | 92.9 | |
| Santo Domingo | SDO | −11.384 | −77.050 | Chancay-Huaral | SENAMHI | 66.0 | |
| Racarumi | RRI | −6.633 | −79.317 | Lambayeque | SENAMHI | 99.8 | |
| Salinar | SAL | −7.661 | −78.961 | Chicama | SENAMHI | 92.1 | |
| Obrajillo | OBR | −11.452 | −76.622 | Chillón | SENAMHI | 58.8 | |
| El Ciruelo | ECI | −4.300 | −80.150 | Chira | SENAMHI | 97.6 | |
| Malvados | MAL | −10.340 | −77.630 | Fortaleza | JU FORTALEZA | 31.2 | |
| Pte. Ocoña | POC | −16.422 | −73.115 | Ocoña | SENAMHI | 33.3 | |
| Letrayoc | LET | −13.640 | −75.720 | Pisco | SENAMHI | 89.5 | |
| Pte. Sánchez Cerro | PSC | −5.194 | −80.623 | Piura | PE CHIRA PIURA | 49.1 | |
| Condorcerro | CCO | −8.658 | −78.262 | Santa | PE CHAVIMOCHIC | 98.1 | |
| Pte. Santa Rosa | PSR | −17.030 | −71.690 | Tambo | JU TAMBO | 92.9 | |
| El Tigre | ETI | −3.769 | −80.457 | Tumbes | SENAMHI | 97.4 | |
| Chosica | CHO | −11.930 | −76.690 | Rímac | SENAMHI | 54.7 | |
| Titicaca | Pte. Huancané | HNE | −15.216 | −69.793 | Huancané | SENAMHI | 79.7 |
| Pte. Ramis | RAM | −15.255 | −69.874 | Ramis | SENAMHI | 72.4 | |
| Pte. Unocolla | COA | −15.451 | −70.192 | Coata | SENAMHI | 74.6 | |
| Pte. Ilave | ILA | −16.088 | −69.626 | Ilave | SENAMHI | 72.6 | |
| Atlantic | Egemsa Km105 | EKM | −13.183 | −72.533 | Urubamba | SENAMHI | 86.1 |
| Borja | BOR | −4.470 | −77.548 | Marañón | HYBAM | 86.5 | |
| Jesús Tunel | JTU | −7.221 | −78.404 | Crisnejas | SENAMHI | 97.9 | |
| Cumba | CUM | −5.944 | −78.661 | Marañón | SENAMHI | 13.7 | |
| Los Naranjos | LNA | −5.756 | −78.432 | Marañón | SENAMHI | 17.5 | |
| Puente Tocache | TOC | −8.181 | −76.506 | Huallaga | SENAMHI | 58.3 | |
| Tingo María | TMA | −9.290 | −76.003 | Huallaga | SENAMHI | 51.9 | |
| Picota | PIC | −6.949 | −76.325 | Huallaga | SENAMHI | 42.3 | |
| Chazuta | CHA | −6.570 | −76.119 | Huallaga | HYBAM | 41.7 | |
| Paucartambo | PAU | −13.321 | −71.594 | Urubamba | SENAMHI | 28.8 | |
| Pisac | PIS | −13.422 | −71.855 | Vilcanota | SENAMHI | 66.5 | |
| Pte. Cunyac | PCU | −13.560 | −72.574 | Apurímac | SENAMHI | 26.5 | |
| Pte. Stuart | PST | −11.802 | −75.490 | Mantaro | ELECTROPERU | 68.8 | |
| Puerto Inca | PUI | −9.384 | −74.968 | Pachitea | HYBAM | 43.8 | |
| Tamshiyacu | TAM | −4.003 | −73.162 | Amazonas | HYBAM | 90.6 | |
| Requena | REQ | −5.030 | −73.830 | Ucayali | HYBAM | 58.5 | |
| Lagarto | LAG | −10.607 | −73.871 | Ucayali | HYBAM | 23.1 | |
| Bellavista | BEL | −3.482 | −73.073 | Napo | HYBAM | 71.2 | |
| Pte. Corral Quemado | PCQ | −5.755 | −78.692 | Marañón | SENAMHI | 13.7 | |
| La Pastora | LPA | −12.584 | −69.214 | Madre de Dios | HYBAM | 24.4 | |
| Napo | NAP | −0.917 | −75.396 | Napo | HYBAM | 40.6 | |
| Tabatinga | TAB | −4.250 | −69.950 | Amazonas | HYBAM | 87.6 | |
| Pucallpa | PUC | −8.390 | −74.530 | Ucayali | HYBAM | 43.6 | |
| San Regis | SRE | −4.513 | −73.907 | Marañón | HYBAM | 53.0 |
| Index | Unit | Equation | Description |
|---|---|---|---|
| Runoff Ratio (RR) | - | The ratio of simulated runoff to precipitation | |
| Runoff Variability (RV) | - | The standard deviation of simulated runoff to the standard deviation of precipitation |
| Statistical Metric | Unit | Equation | Optimal Value |
|---|---|---|---|
| Kling–Gupta efficiency (KGE) | - | 1 | |
| Nash–Sutcliffe Squared (NSEsqrt) | - | 1 | |
| Water Balance Error (WBE) | - | 0 |
| Calibration Region | Number of Sub-Regions | Number of Sub-Basins | Number of Hydrometric Stations |
|---|---|---|---|
| A | 8 | 380 | 2 |
| B | 6 | 346 | 1 |
| C | 13 | 239 | 6 |
| D | 6 | 385 | 5 |
| E | 2 | 229 | 1 |
| F | 6 | 158 | 5 |
| G | 10 | 190 | 2 |
| H | 7 | 269 | 2 |
| I | 6 | 316 | 3 |
| J | 6 | 220 | 2 |
| K | 2 | 258 | 1 |
| L | 8 | 159 | 4 |
| M | 12 | 324 | 7 |
| N | 4 | 121 | 2 |
| Total | 96 (100.0%) | 3594 (100.0%) | 43 (100.0%) |
| Gauged area | 84 (87.5%) | 2605 (72.5%) | 43 (100.0%) |
| Ungauged area | 12 (12.5%) | 989 (27.5%) | 0 (0.0%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Llauca, H.; Lavado-Casimiro, W.; Montesinos, C.; Santini, W.; Rau, P. PISCO_HyM_GR2M: A Model of Monthly Water Balance in Peru (1981–2020). Water 2021, 13, 1048. https://doi.org/10.3390/w13081048
Llauca H, Lavado-Casimiro W, Montesinos C, Santini W, Rau P. PISCO_HyM_GR2M: A Model of Monthly Water Balance in Peru (1981–2020). Water. 2021; 13(8):1048. https://doi.org/10.3390/w13081048
Chicago/Turabian StyleLlauca, Harold, Waldo Lavado-Casimiro, Cristian Montesinos, William Santini, and Pedro Rau. 2021. "PISCO_HyM_GR2M: A Model of Monthly Water Balance in Peru (1981–2020)" Water 13, no. 8: 1048. https://doi.org/10.3390/w13081048








