Comparison between the Lagrangian and Eulerian Approach in Simulation of Free Surface Air-Core Vortices
Abstract
:1. Introduction
2. Methods
2.1. The Lagrangian Approach
2.2. The Eulerian Approach
3. The Physical Model
3.1. The Experimental Setup
3.2. Flow Measurement Techniques
3.2.1. Velocity Measurement
3.2.2. Water Surface Measurement
3.3. The Procedure of the Experiments
4. The Numerical Model
5. Results
5.1. The Air Core Vortex
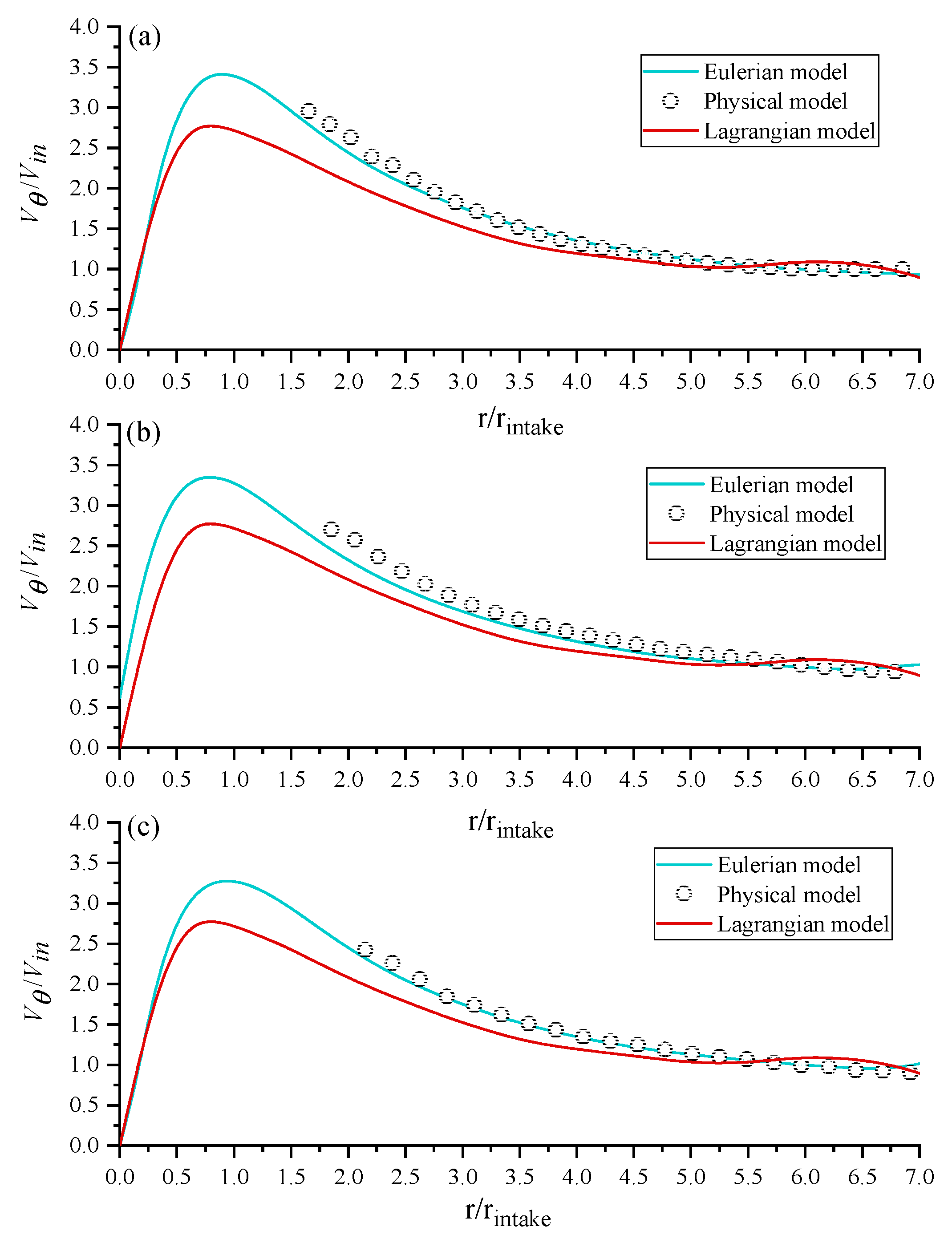
5.2. The Tangential Velocity Distribution
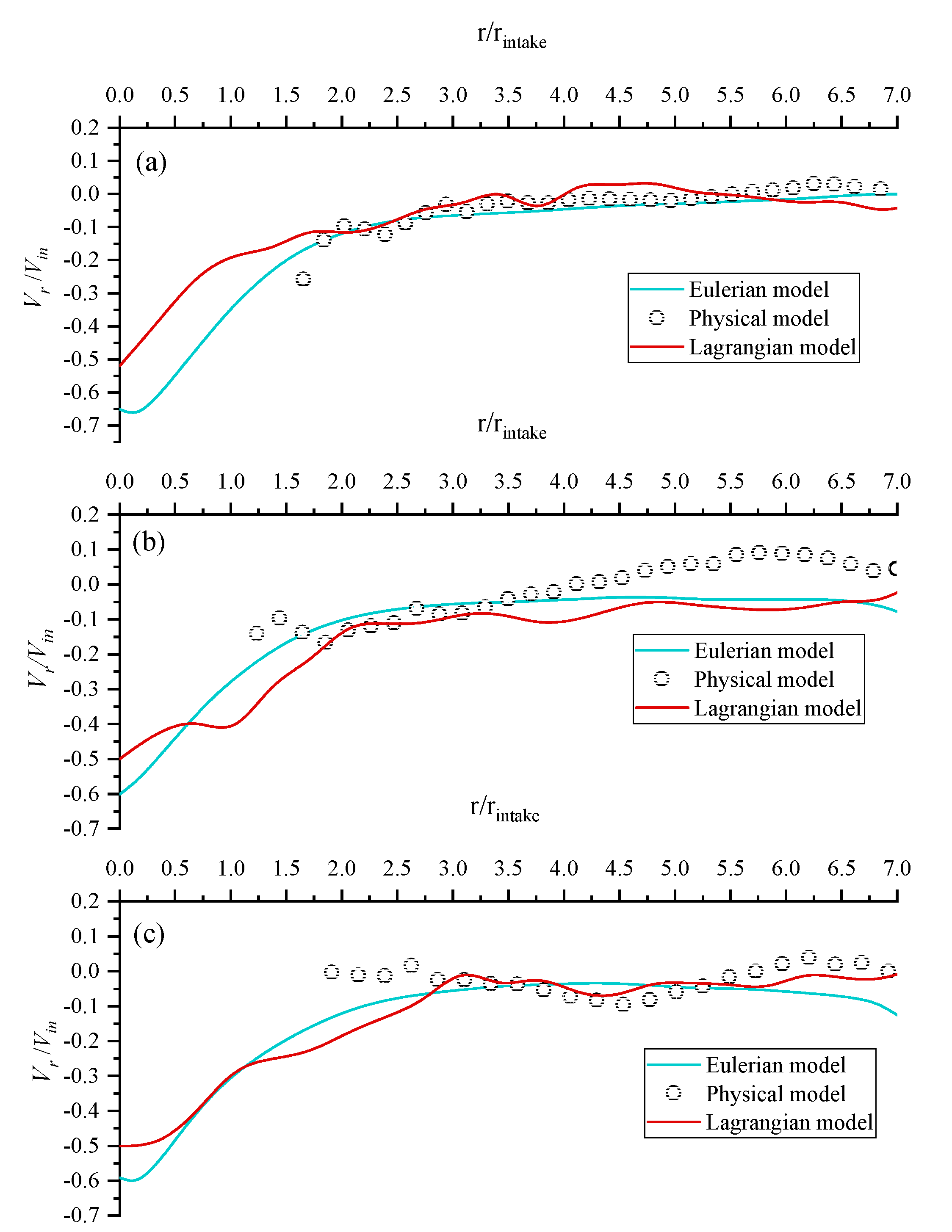
5.3. The Radial Velocity Distribution
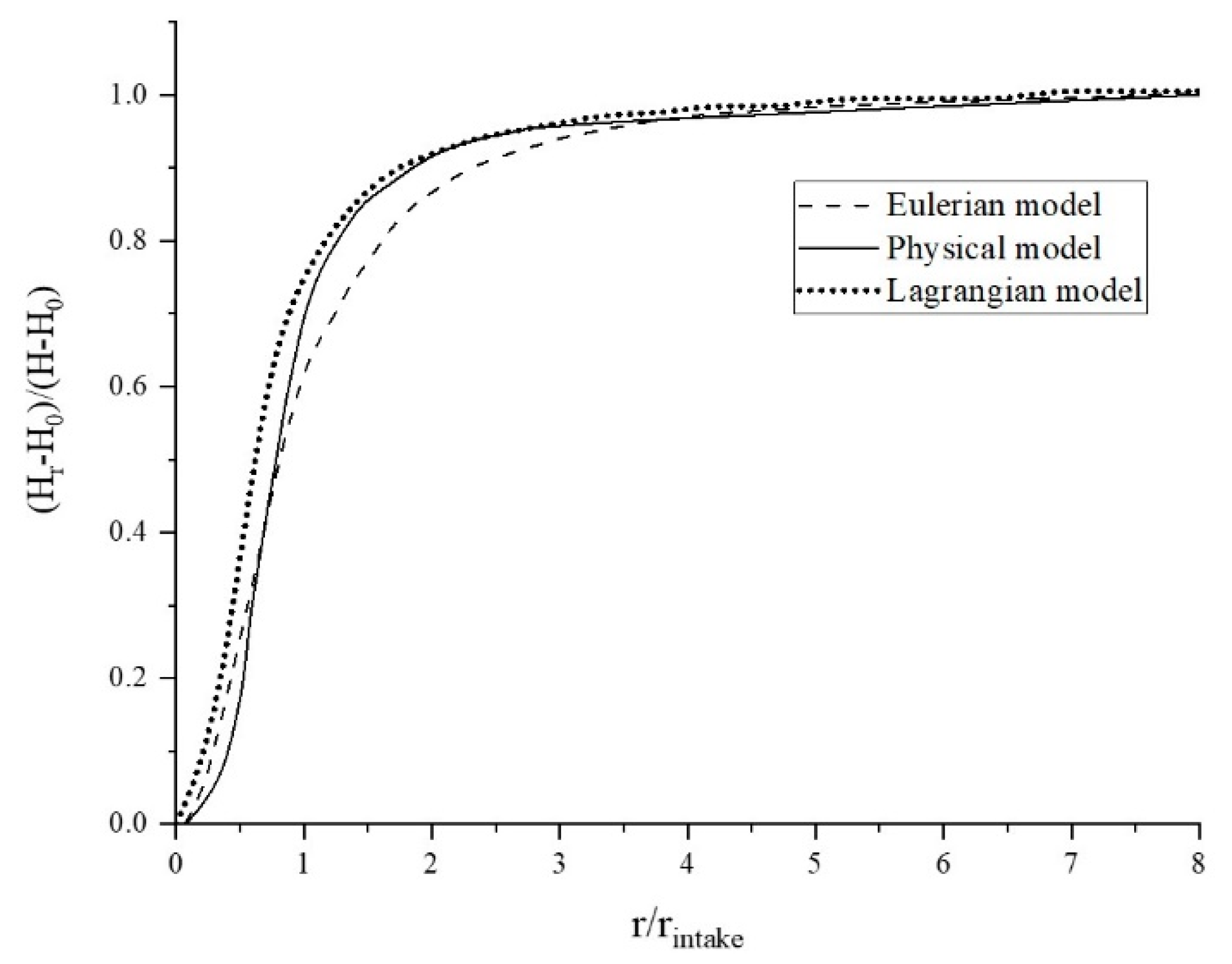
5.4. The Free Surface
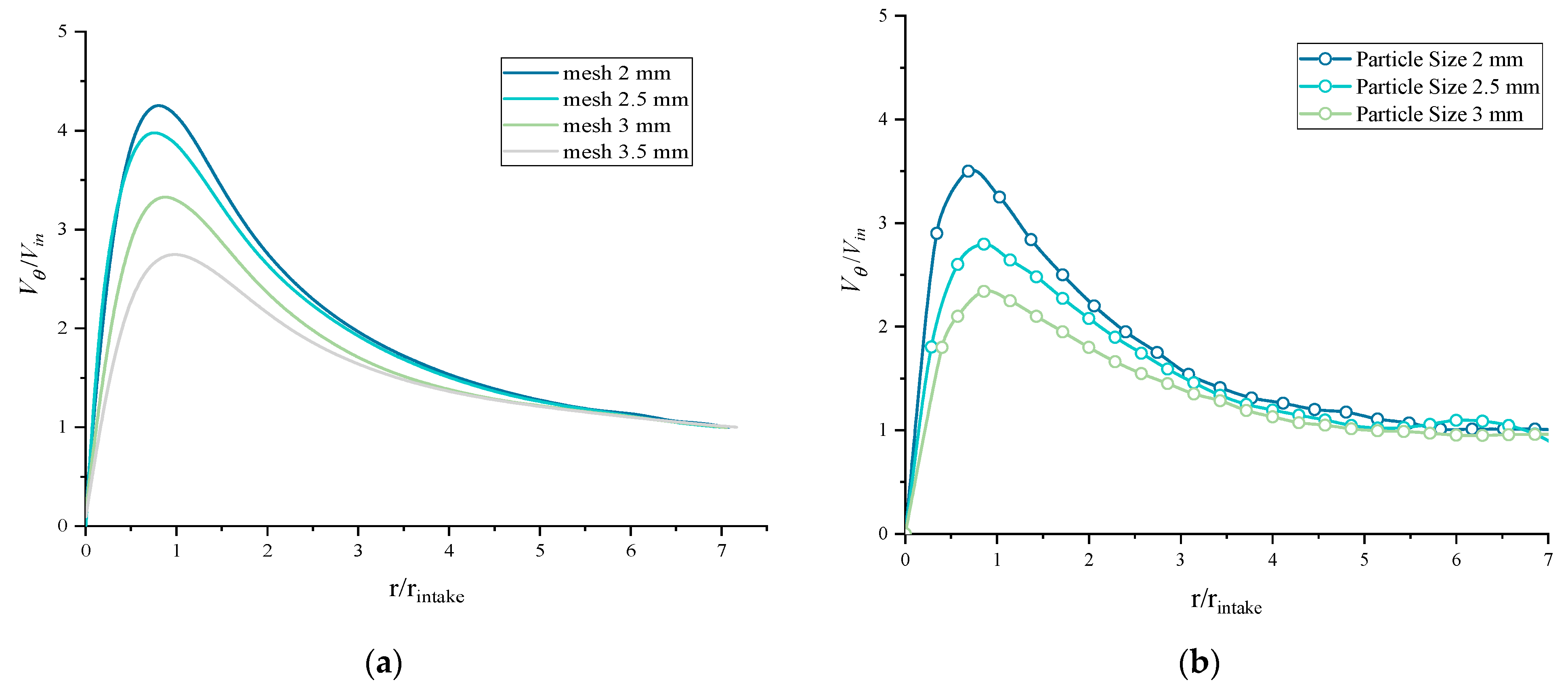
5.5. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hecker, G.A. Fundamentals of Vortex Intake Flow. conclusions. In Proceedings of the Swirling Flow Problems at Intakes; Knauss, J., Ed.; IAHR Hydraulic Structures Design Manual: Balkema, Rotterdam, 1987. [Google Scholar]
- Kocabas, F.; Unal, S. Compared techniques for the critical submergence of an intake in water flow. Adv. Eng. Softw. 2010, 41, 802–809. [Google Scholar] [CrossRef]
- Trivellato, F. Anti-vortex devices: Laser measurements of the flow and functioning. Opt. Lasers Eng. 2010, 48, 589–599. [Google Scholar] [CrossRef]
- Yang, J.; Liu, T.; Bottacin-Busolin, A.; Lin, C. Effects of intake-entrance profiles on free-surface vortices. J. Hydraul. Res. 2014, 52, 523–531. [Google Scholar] [CrossRef]
- Keller, J.; Möller, G.; Boes, R.M. PIV measurements of air-core intake vortices. Flow Meas. Instrum. 2014, 40, 74–81. [Google Scholar] [CrossRef]
- Einstein, H.A.; Li, H. Steady vortex flow in a real fluid. Proc. Heat Transf. Fluid Mech. Institute, Stanford Univ. 1951, 4, 33–43. [Google Scholar]
- Quick, M.C. Scale relationships between geometrically similar free spiral vortices (part I). Civ. Eng. public Work. Rev. 1962, 9, 1135–1138. [Google Scholar]
- Andersen, A.; Bohr, T.; Stenum, B.; Rasmussen, J.J.; Lautrup, B. The bathtub vortex in a rotating container. J. Fluid Mech. 2006, 556, 121–146. [Google Scholar] [CrossRef] [Green Version]
- Anwar, H.O.; Amphlett, M.B. Vortices at vertically inverted intake. J. Hydraul. Res. 1980, 18, 123–134. [Google Scholar] [CrossRef]
- Daggett, L.L.; Keulegan, G.H. Similitude Conditions in Free-Surface Vortex Formations. J. Hydraul. Eng. 1974, 100, 1565–1580. [Google Scholar]
- Jain, A.; Garde, R.; Ranga Raju, K.G. Vortex formation at vertical pipe intakes. J. Hydraul. Div. 1978, 104, 1429–1445. [Google Scholar] [CrossRef]
- Sarkardeh, H.; Zarrati, A.R.; Roshan, R. Effect of intake head wall and trash rack on vortices. J. Hydraul. Res. 2010, 48, 108–112. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Liu, Y. Theoretical and experimental study on the vortex at hydraulic intakes. J. Hydraul. Res. 2015, 53, 787–796. [Google Scholar] [CrossRef]
- Suerich-Gulick, F.; Gaskin, S.J.; Villeneuve, M.; Parkinson, É. Free surface intake vortices: Theoretical model and measurements. J. Hydraul. Res. 2014, 52, 502–512. [Google Scholar] [CrossRef]
- Naderi, V.; Gaskin, S. A 3D study of an intake air-core vortex structure using PIV & flow visualization. Int. Symp. Hydraul. Struct. 2018. [Google Scholar]
- Duinmeijer, A.; Oldenziel, G.; Clemens, F. Experimental study on the 3D-flow field of a free- surface vortex using stereo PIV. J. Hydraul. Res. 2019, 1686. [Google Scholar] [CrossRef]
- Xu, Z.; Han, Z.; Qu, H. Comparison between Lagrangian and Eulerian approaches for prediction of particle deposition in turbulent flows. Powder Technol. 2020, 360, 141–150. [Google Scholar] [CrossRef]
- Rajendran, V.P.; Constantinescu, S.G.; Patel, V.C. Experimental Validation Of Numerical Model Pump-Intake Bays. J. Hydraul. Eng. 1999, 125, 1119–1125. [Google Scholar] [CrossRef]
- Constantinescu, G.S.; Patel, V.C. Role of turbulence model in prediction of pump-bay vortices. J. Hydraul. Eng. 2000, 126, 387–391. [Google Scholar] [CrossRef]
- Suerich-Gulick, F.; Gaskin, S.; Villeneuve, M.; Holder, G.; Parkinson, E. Experimental and numerical analysis of free surface vortices at a hydropower intake. In Proceedings of the The 7th Int. Conf. on Hydroscience and Engineering (ICHE-2006), Philadelphia, PA, USA, 10–13 September 2006; pp. 1–11. [Google Scholar]
- Okamura, T.; Kamemoto, K.; Matsui, J. Cfd Prediction and Model Experiment on Suction Vortices in Pump Sump. In Proceedings of the 9th Asian International Conference on Fluid Machinery, Jeju, Korea, 16–19 October 2007; pp. 1–10. [Google Scholar]
- Li, H.; Chen, H. Experimental and numerical investigation of free surface vortex. J. Hydrodyn. 2008, 20, 485–491. [Google Scholar] [CrossRef]
- Lucino, C.; Gonzalo Dur, S.L. Vortex detection in pump sumps by means of CFD. In Proceedings of the In XXIV Latin American Congress on Hydraulics, Punta Del Este, Uruguay, 21 November 2010; pp. 21–25. [Google Scholar]
- Sarkardeh, H.; Reza Zarrati, A.; Jabbari, E.; Marosi, M. Numerical Simulation and Analysis of Flow In A Reservoir In The Presence of Vortex. Eng. Appl. Comput. Fluid Mech. 2014, 8, 598–608. [Google Scholar] [CrossRef] [Green Version]
- Rabe, B.K.; Najafabadi, S.H.G.; Sarkardeh, H. Numerical simulation of air-core vortex at intake. Curr. Sci. 2017, 113. [Google Scholar] [CrossRef]
- Nakayama, A.; Hisasue, N. Large eddy simulation of vortex flow in intake channel of hydropower facility. J. Hydraul. Res. 2010, 48, 415–427. [Google Scholar] [CrossRef]
- Sungur, A. Numerical investigation of vortex formation at asymmetric horizontal intakes, MIDDLE EAST TECHNICAL UNIVERSITY, Turkey. 2018. Available online: https://open.metu.edu.tr/handle/11511/27424 (accessed on 31 December 2020).
- Zi, D.; Xuan, A.; Wang, F.; Shen, L. Undefined Numerical Study of Mechanisms of Air-core Vortex Evolution in an Intake Flow. Elsevier. 2020. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0142727X1930832X (accessed on 31 December 2020).
- Amicarelli, A.; Kocak, B.; Sibilla, S.; Grabe, J. A 3D smoothed particle hydrodynamics model for erosional dam-break floods. Int. J. Comut. Fluid Dyn. 2017, 31, 413–434. [Google Scholar] [CrossRef]
- Dalrymple, R.A.; Rogers, B.D. Numerical modeling of water waves with the SPH method. Coast. Eng 2006, 53, 147. [Google Scholar] [CrossRef]
- Sun, P.; Le Touzé, D.; Zhang, A. Study of a complex fluid-structure dam-breaking benchmark problem using a multi-phase SPH method with APR. Eng. Anal. Bound. Elem. 2019, 104, 240–258. [Google Scholar] [CrossRef]
- Xu, X. An improved SPH approach for simulating 3D dam-break flows with breaking waves. Comput. Methods Appl. Mech. Eng. 2016, 311. [Google Scholar] [CrossRef]
- Lee, E.S.; Violeau, D.; Issa, R.; Ploix, S. Application of weakly compressible and truly incompressible SPH to 3-D water collapse in waterworks. J. Hydraul. Res. 2010, 48, 50–60. [Google Scholar] [CrossRef]
- Gomez-Gesteira, M.; Benedict, D.; Crespo, A.J.; Dalrymple, R.A.; Narayanaswamy, M.; Dominguez, J.M. SPHysics–development of a free-surface fluid solver–Part 1: Theory and formulations. Comput. Geosci. 2012, 48, 289–299. [Google Scholar] [CrossRef]
- Gómez-Gesteira M, D.R. Using a 3D SPH method for wave impact on a tall structure. J. Waterw Port Coast. Ocean Eng. 2004, 130, 69. [Google Scholar] [CrossRef]
- Liu, G.R.; Liu, M.B. Smoothed Particle Hydrodynamics: A Meshfree Particle Method. 2003. Available online: https://link.springer.com/book/10.1007/978-3-540-71471-2 (accessed on 31 December 2020).
- Crespo, A.C.; Dominguez, J.M.; Barreiro, A.; Gómez-Gesteira, M.; Rogers, B.D. GPUs, a new tool of acceleration in CFD: Efficiency and reliability on smoothed particle hydrodynamics methods. PLoS ONE 2011, 6. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Crespo, A.J.; Valdez-Balderas, D.; Rogers, B.D.; Gómez-Gesteira, M. New multi-GPU implementation for smoothed particle hydrodynamics on heterogeneous clusters. Comput. Phys. Commun. 2013, 184, 1848–1860. [Google Scholar] [CrossRef]
- Domínguez, J.M.; Crespo, A.J.; Gómez-Gesteira, M. Optimization strategies for CPU and GPU implementations of a smoothed particle hydrodynamics method. Comput. Phys. Commun. 2013, 184, 617–627. [Google Scholar] [CrossRef]
- Valdez-Balderas, D.; Domínguez, J.M.; Rogers, B.D.; Crespo, A.J.C. Towards Accelerating Smoothed Particle Hydrodynamics Simulations for Free-Surface Flows on Multi-GPU Clusters. 2012. Available online: https://www.sciencedirect.com/science/article/abs/pii/S0743731512001712 (accessed on 31 December 2020).
- González-Cao, J.; Altomare, C.; Crespo, A.J.C.; Domínguez, J.M.; Gómez-Gesteira, M.; Kisacik, D. On the accuracy of DualSPHysics to assess violent collisions with coastal structures. Comput. Fluids 2019, 179, 604–612. [Google Scholar] [CrossRef]
- Lowe, R.J.; Buckley, M.L.; Altomare, C.; Rijnsdorp, D.P.; Yao, Y.; Suzuki, T.; Bricker, J.D. Numerical simulations of surf zone wave dynamics using Smoothed Particle Hydrodynamics. Ocean Model. 2019, 144, 101481. [Google Scholar] [CrossRef] [Green Version]
- Verbrugghe, T.; Domínguez, J.M.; Altomare, C.; Tafuni, A.; Vacondio, R.; Troch, P.; Kortenhaus, A. Non-linear wave generation and absorption using open boundaries within DualSPHysics. Comput. Phys. Commun. 2019, 240, 46–59. [Google Scholar] [CrossRef]
- Crespo, A.J.C.; Domínguez, J.M.; Rogers, B.D.; Gómez-Gesteira, M.; Longshaw, S.; Canelas, R.; Vacondio, R.; Barreiro, A.; García-Feal, O. DualSPHysics: Open-source parallel CFD solver based on Smoothed Particle Hydrodynamics (SPH). Comput. Phys. Commun. 2015, 187, 204–216. [Google Scholar] [CrossRef]
- Wendland, J.; Vaillancourt, L.J.; Hegner, J.; Lengeler, K.B.; Laddison, K.J.; Specht, C.A.; Raper, C.A.; Kothe, E. The mating-type locus Bα1 of Schizophyllum commune contains a pheromone receptor gene and putative pheromone genes. EMBO J. 1995, 14, 5271–5278. [Google Scholar] [CrossRef]
- Macia, F.; Colagrossi, A.; Antuono, M.; Souto-Iglesias, A. Benefits of Using a Wendland Kernel for Free-surface Flows. 2011, pp. 30–37. Available online: https://www.researchgate.net/profile/Antonio-Souto-Iglesias/publication/303637287_Benefits_of_using_a_Wendland_kernel_for_free-surface_flows/links/5788e72108ae7a588ee851d2/Benefits-of-using-a-Wendland-kernel-for-free-surface-flows.pdf (accessed on 31 December 2020).
- Gomez-Gesteira, M.; Rogers, B.D.; Dalrymple, R.A.; Crespo, A.J.C. State-of-the-art of classical SPH for free-surface flows. J. Hydraul. Res. 2010, 48, 6–27. [Google Scholar] [CrossRef]
- Marrone, S.; Antuono, M.; Colagrossi, A.; Colicchio, G.; Le Touzé, D.; Graziani, G. δ-SPH model for simulating violent impact flows. Comput. Methods Appl. Mech. Eng. 2011, 200, 1526–1542. [Google Scholar] [CrossRef]
- Crespo, A.J.; Gómez-Gesteira, M.; Dalrymple, R.A. Modeling Dam Break Behavior over a Wet Bed by a SPH Technique. J. Waterw. Port, Coastal, Ocean Eng. 2008, 134, 313–320. [Google Scholar] [CrossRef]
- Tafuni, A.; Domínguez, J.M.; Vacondio, R.; Crespo, A.J.C. A versatile algorithm for the treatment of open boundary conditions in Smoothed particle hydrodynamics GPU models. Comput. Methods Appl. Mech. Eng. 2018, 342, 604–624. [Google Scholar] [CrossRef]
- Nichols, B.D.; Hirt, C.W.; Hotchkiss, R.S. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar]
- Carvalho, R.F.; Lemos, C.M.; Ramos, C.M. Numerical computation of the flow in hydraulic jump stilling basins. J. Hydraul. Res. 2008, 46, 739–752. [Google Scholar] [CrossRef]


| Tests | Flow Rate Lit/s | Velocity at the Intake m/s | Intake Froude Number | Elevation of the Velocity Measurement Plane from the Bottom of the Tank (cm) |
|---|---|---|---|---|
| 1 | 0.2 | 0.2 | 0.34 | 5 |
| 2 | 9 | |||
| 3 | 13 |
| Particle/Mesh Size | Eulerian Model | Lagrangian Model | ||
|---|---|---|---|---|
| Computational Cost | Error % | Computational Cost | Error % | |
| 2 mm | 40 h | 2.1 | 168 h | 3.7 |
| 2.5 mm | 19 h | 5.7 | 97 h | 18.1 |
| 3 mm | 12.5 h | 9.2 | 58 h | 29.6 |
| 3.5 mm | 6 h | 14.8 | 29 h | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azarpira, M.; Zarrati, A.R.; Farrokhzad, P. Comparison between the Lagrangian and Eulerian Approach in Simulation of Free Surface Air-Core Vortices. Water 2021, 13, 726. https://doi.org/10.3390/w13050726
Azarpira M, Zarrati AR, Farrokhzad P. Comparison between the Lagrangian and Eulerian Approach in Simulation of Free Surface Air-Core Vortices. Water. 2021; 13(5):726. https://doi.org/10.3390/w13050726
Chicago/Turabian StyleAzarpira, Maryam, Amir Reza Zarrati, and Pouya Farrokhzad. 2021. "Comparison between the Lagrangian and Eulerian Approach in Simulation of Free Surface Air-Core Vortices" Water 13, no. 5: 726. https://doi.org/10.3390/w13050726







