1. Introduction
In recent years, with the development of intensive urbanization, population growth, land use transformation, pollution, and changing climate patterns, fresh water availability has become one of the main issues facing humankind [
1]. In this context, stormwater is being considered in water-stressed cities as an alternative water resource [
2]. Stormwater utilization is also an ecological and sustainable method of water management, resulting in the reduction of urban runoff and flooding [
3].
Despite its potential for augmenting water supplies and reducing runoff flood, urban stormwater contains contaminants that pose risks to human health and aquatic ecosystems. Stormwater is often contaminated by organic matter, nutrients (i.e., phosphorus and nitrogen) and heavy metals [
4,
5] (Some studies suggest it should be replaced with the term potentially toxic elements [
6]). Dissolved nitrogen species include nitrate (NO
3-), nitrite (NO
2-), ammonia and ammonium (NH
3 and NH
4+), and organic N. The distribution between NH
3 versus NH
4+ is pH dependent (pK
a = 9.25), but NH
4+ dominates in stormwater (typical pH values are 6–8) [
7]. The high level of ammonia in water imparts taste and odor problems, can cause symptoms in aquatic organisms such as hypoxia, coma, and decreased immunity, resulting in slow growth and even a large numbers of deaths [
8,
9].
Over the years, various techniques have been used to remove ammonia nitrogen from water, such as biological process [
10], stripping [
11], breakpoint chlorination [
12], chemical precipitation [
13], and adsorption [
14]. As the most commonly used nitrogen removal technology, however, biological processes are critical to the environment. Low temperature or high ammonia concentration may affect the activity of nitrobacteria and reduce the treatment efficiency [
10]. Nitrifying bacteria activity is reduced below 15 °C, and life activities are inhibited below 5 °C [
14]. Therefore, adsorption is considered to be a feasible method to remove ammonia nitrogen from water, since adsorption is a more direct, stable, and low-cost method for contaminants removal from water. Ideally, sorbents for contaminants in stormwater should exhibit high selectivity and rapid sorption kinetics, as well as sufficient sorption capacity [
15]. Activated carbon is a kind of cheap, large specific surface area, easy to obtain, and rich pore structure adsorption material, which is broadly used in the water treatment process [
16], but currently has limited application for other types of contaminated water, including stormwater [
17]. Coal-based granular activated carbon is the most productive of all kinds of activated carbons due to its wide source of raw materials, mature production process, and good adsorption effect, and 70% of it is used for water treatment [
18].
Removal rate is a key parameter in the adsorption process, but it is not available under most operating conditions due to the time and cost of experimental testing. Therefore, it is important to optimize experimental conditions and obtain the maximum removal rate by using modeling and optimization. The adsorption process is a complex process, which is difficult to describe by statistical model due to the complexity of the relationship between input parameters and output. Computational intelligence models are generally more flexible than statistical models in modeling complex data sets that may contain nonlinear or missing data [
19]. In order to reveal the influence of the interaction between variables in the adsorption process on the dependent variables, analyze the relative influence degree of different variables, and obtain the optimal conditions of the adsorption process, more reasonable and accurate methods need to be developed.
Response surface methodology (RSM) is widely used in the optimization of chemical and physical processes. It is an optimization method that integrates mathematical modeling and experimental design [
20]. Through experiments on representative local points, the functional relationship between factors in the global scope and experimental results is fitted by regression, and the optimal value of each factor is obtained. The difference between the response surface method and the traditional orthogonal experimental design method is that the response surface method has high precision of regression equation, short experimental period, and the ability to study the interaction between multiple factors at the same time [
21].
In addition, a number of data analysis tools have evolved into sophisticated modeling techniques, such as fuzzy logic (FL) and artificial intelligence (AI). As one of the main tools of artificial intelligence, artificial neural networks (ANNs) have been widely used due to their general ability to simulate nonlinear changes and process incomplete data. ANN does not require mathematical description of the phenomena in the process, so the simulation of the complicated systems could be performed more efficiently [
22,
23,
24]. Compared with the RSM focusing on the statistical importance of the individual process variables and their interactions via ANOVA, AAN is more reliable in capturing the nonlinear relationship between the removal rate and process variables [
25]. Although, ANN is an effective tool to predict and optimize any complex process parameters, it cannot guarantee the global optimal solution [
26]. Genetic algorithm (GA) can be used to minimize (or maximize) the global search and to obtain feasible solutions with a known fitness function [
19]. GA is a kind of adaptive heuristic optimization search algorithm based on a Darwinian genetic evolution principle, taking “survival of the fittest” as the concept, and using genetic operators such as selection, mutation, and crossover to find the optimal solution of the problem [
27]. Therefore, the combination of artificial neural network and genetic algorithm can generate the optimal operating variables of the process under study.
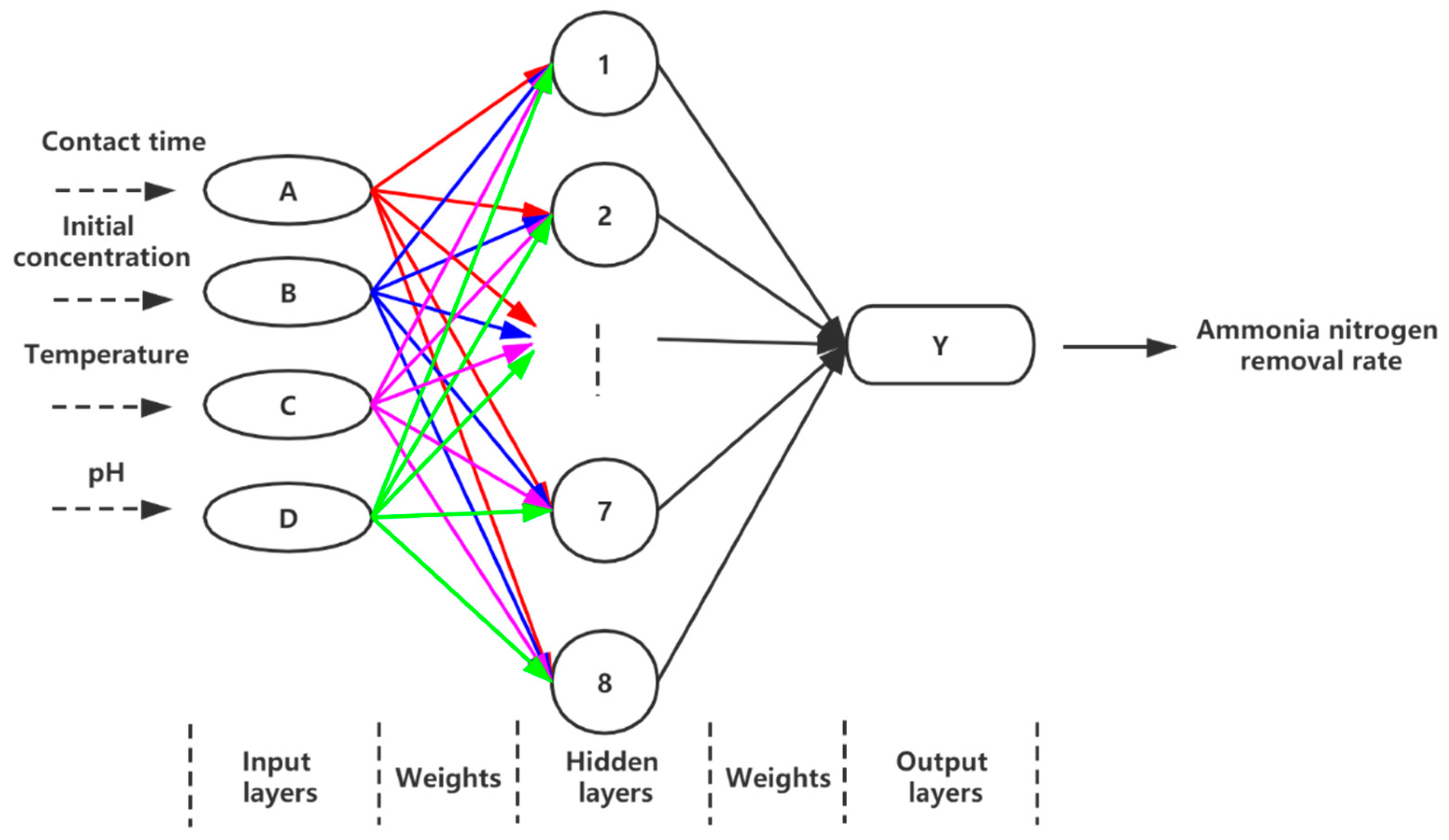
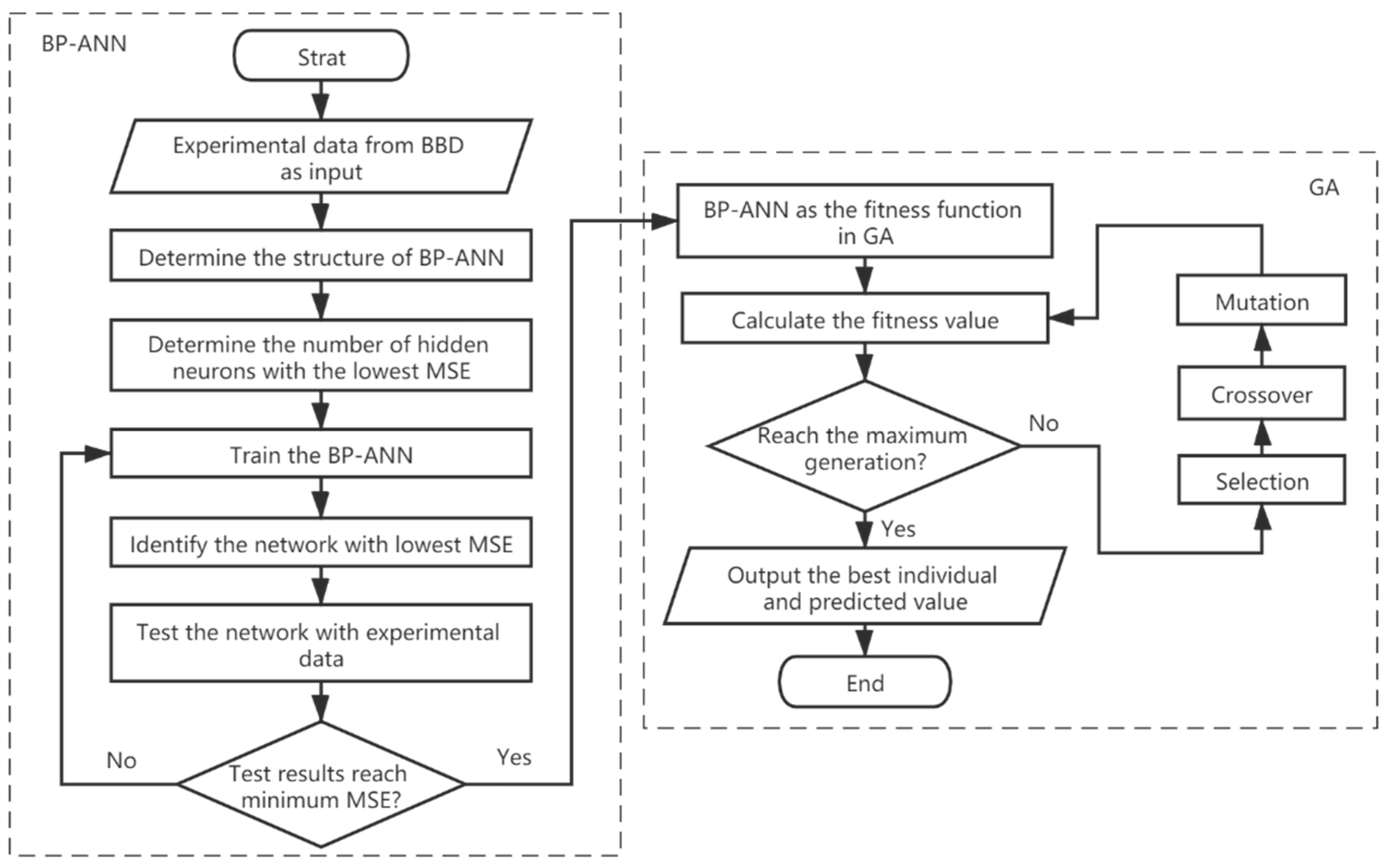
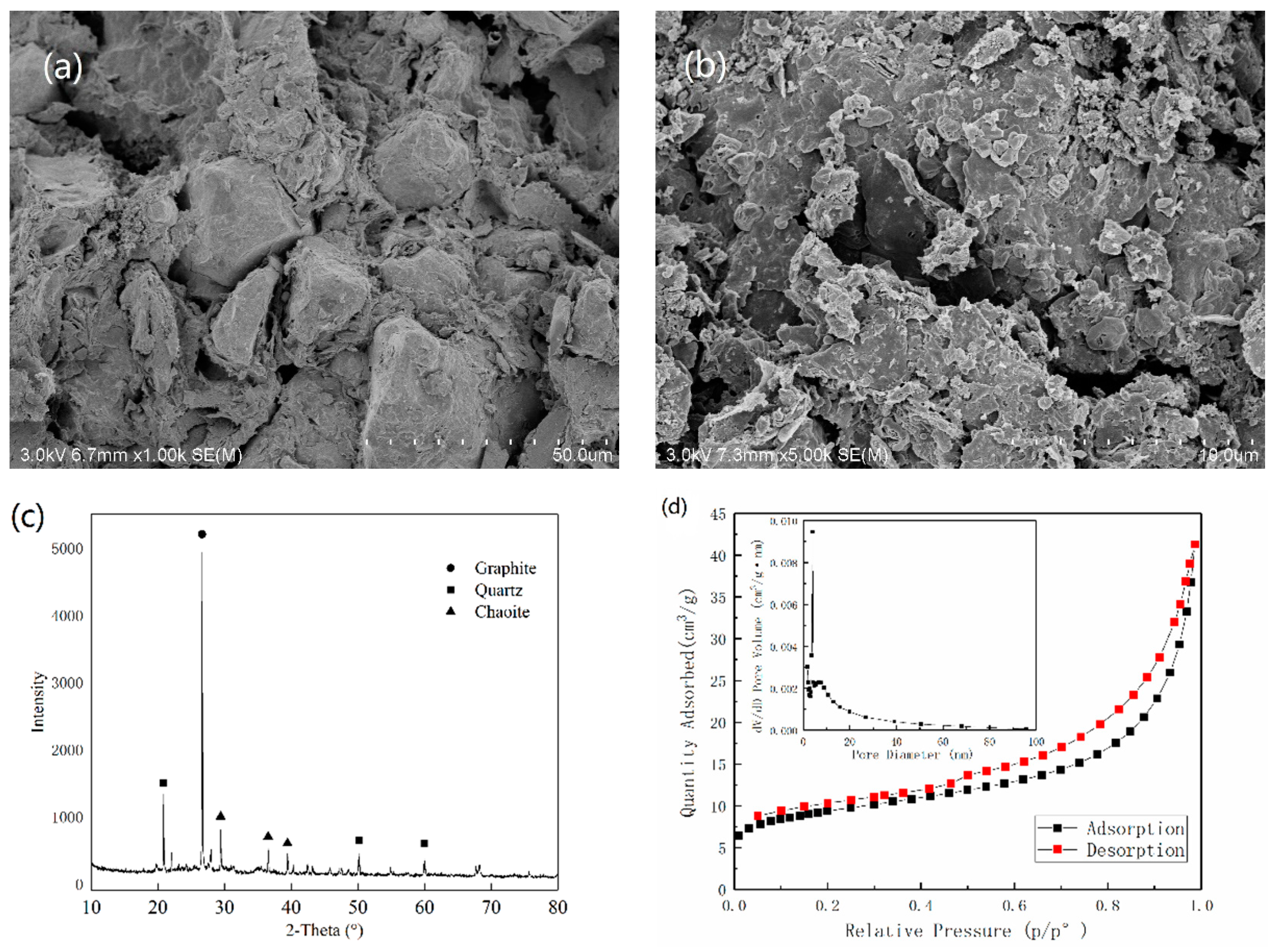
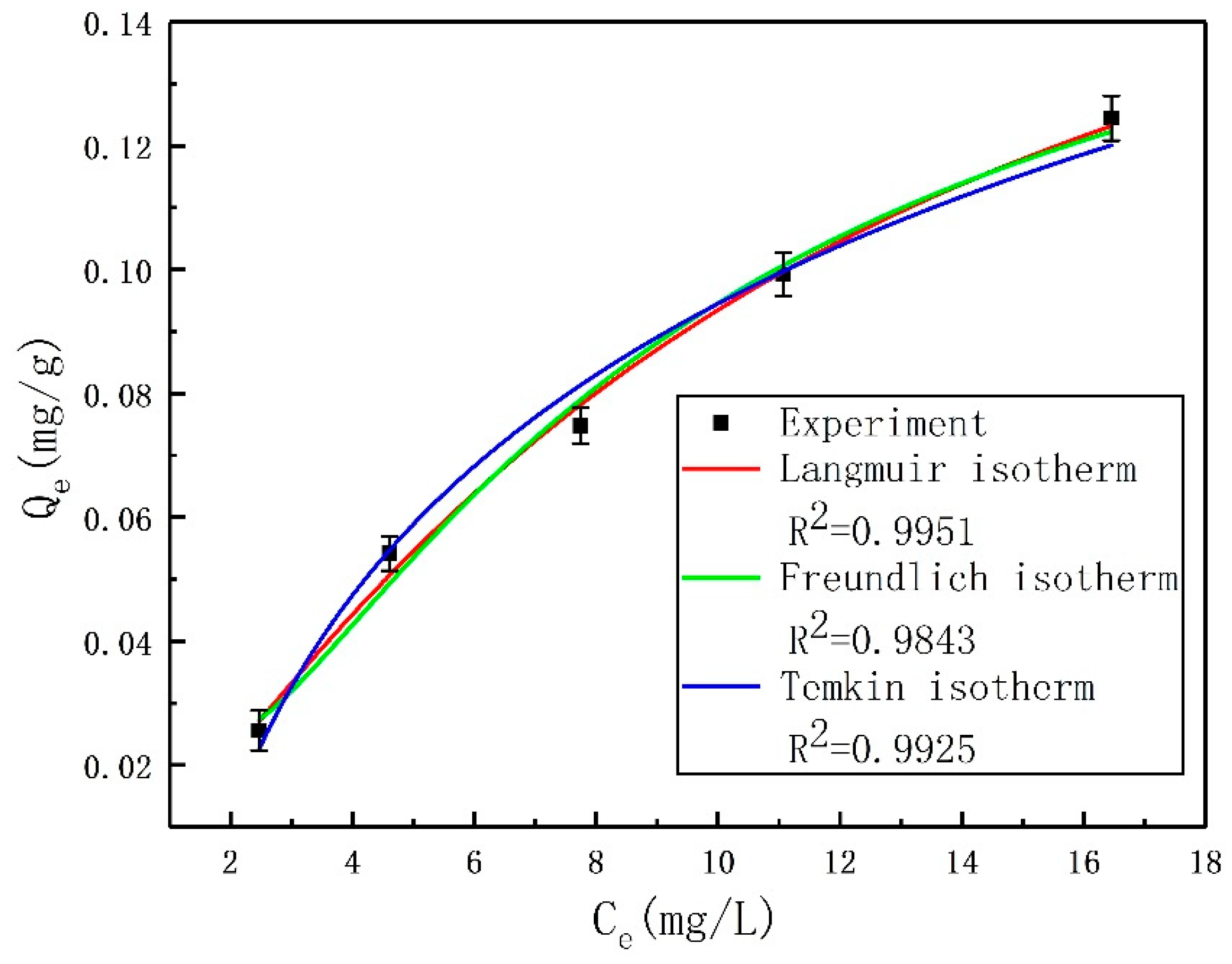
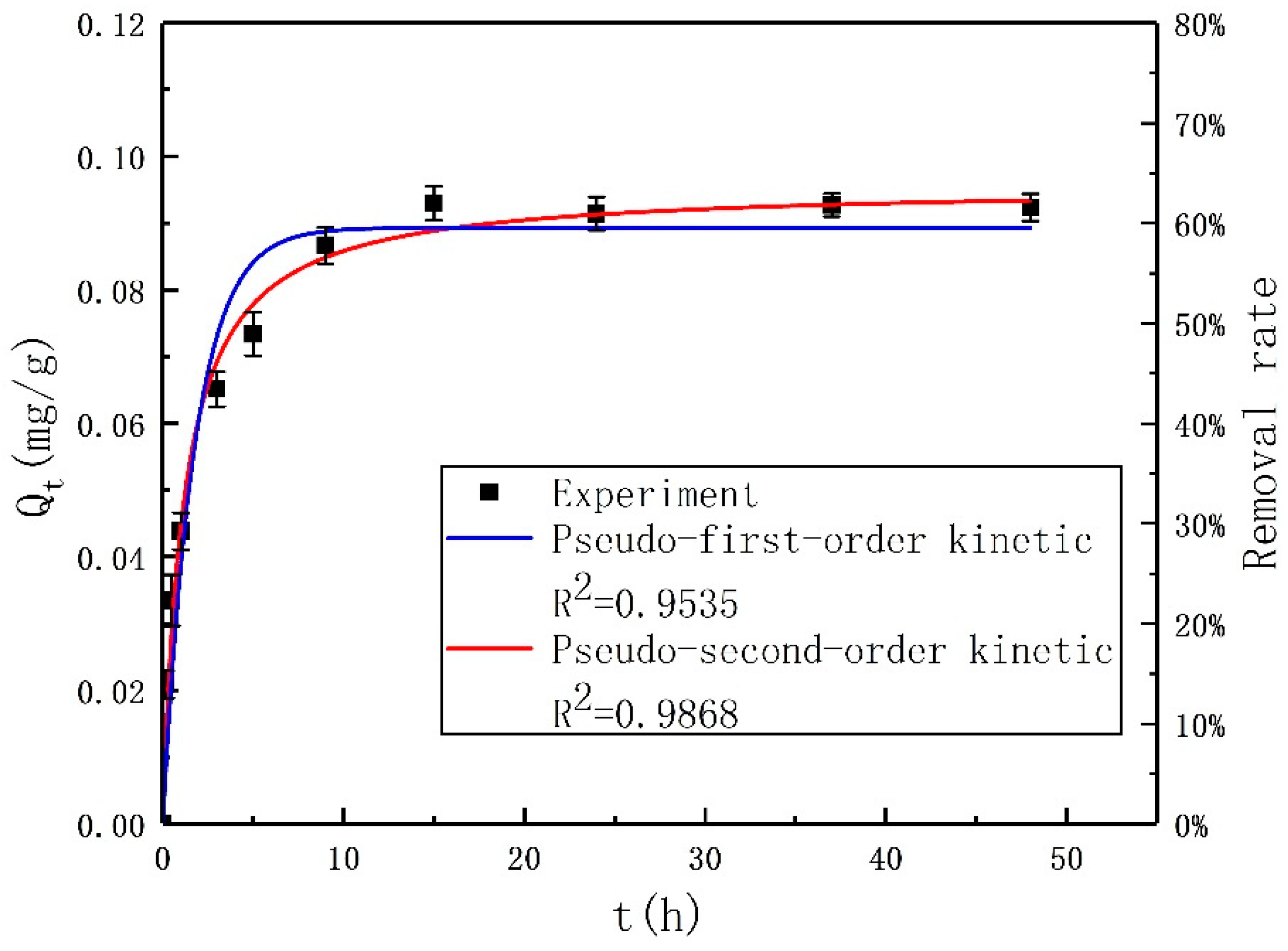
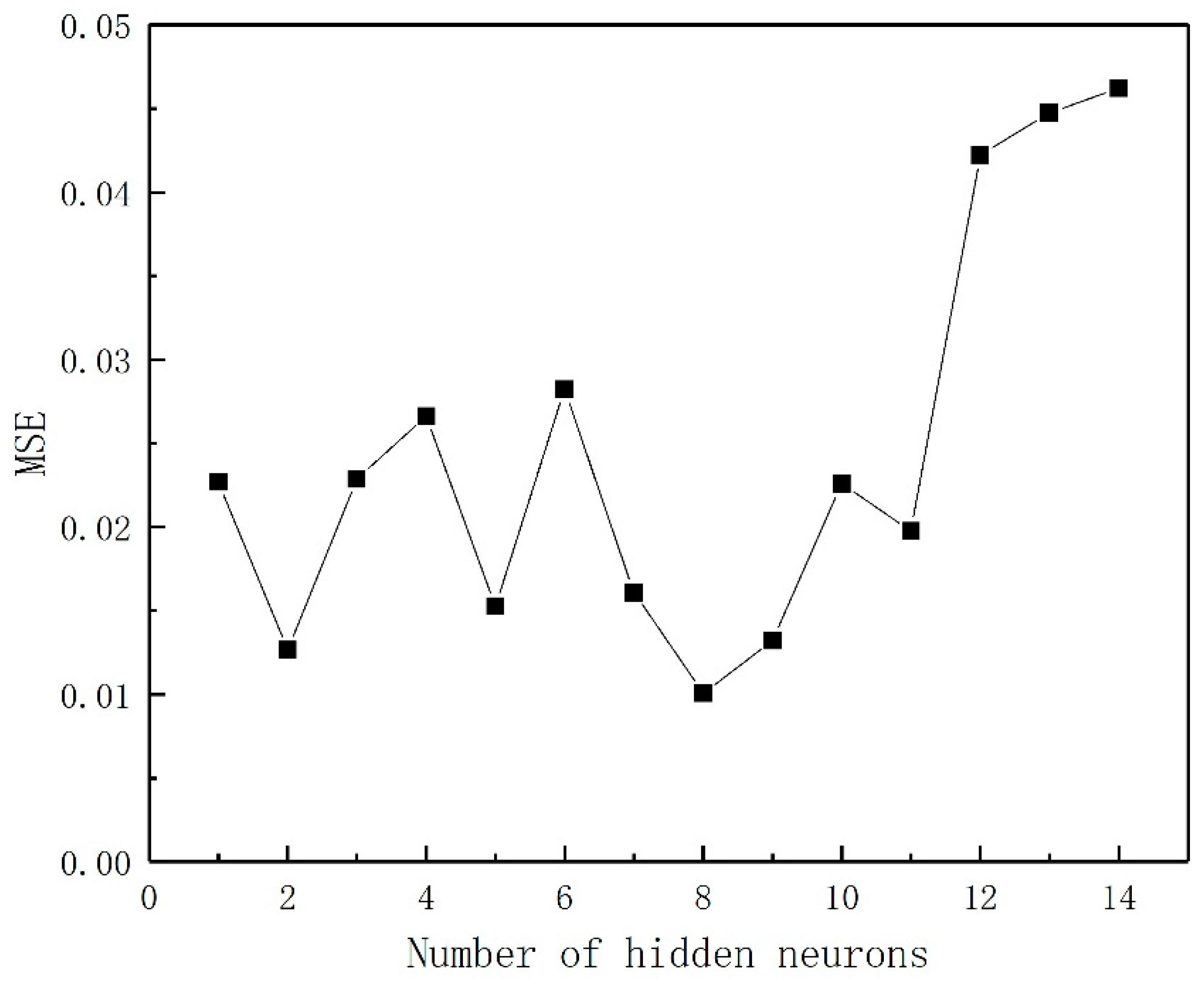
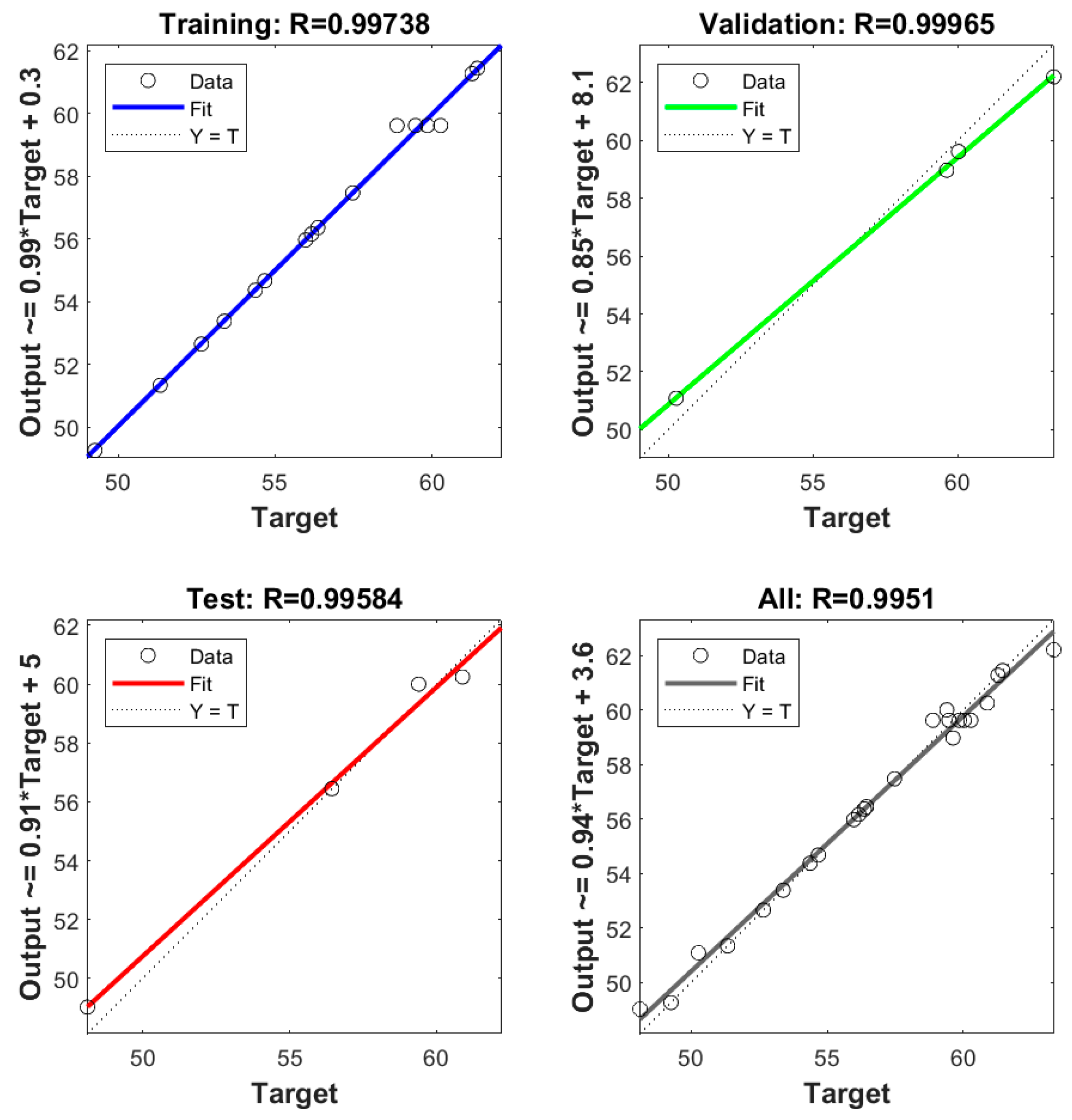
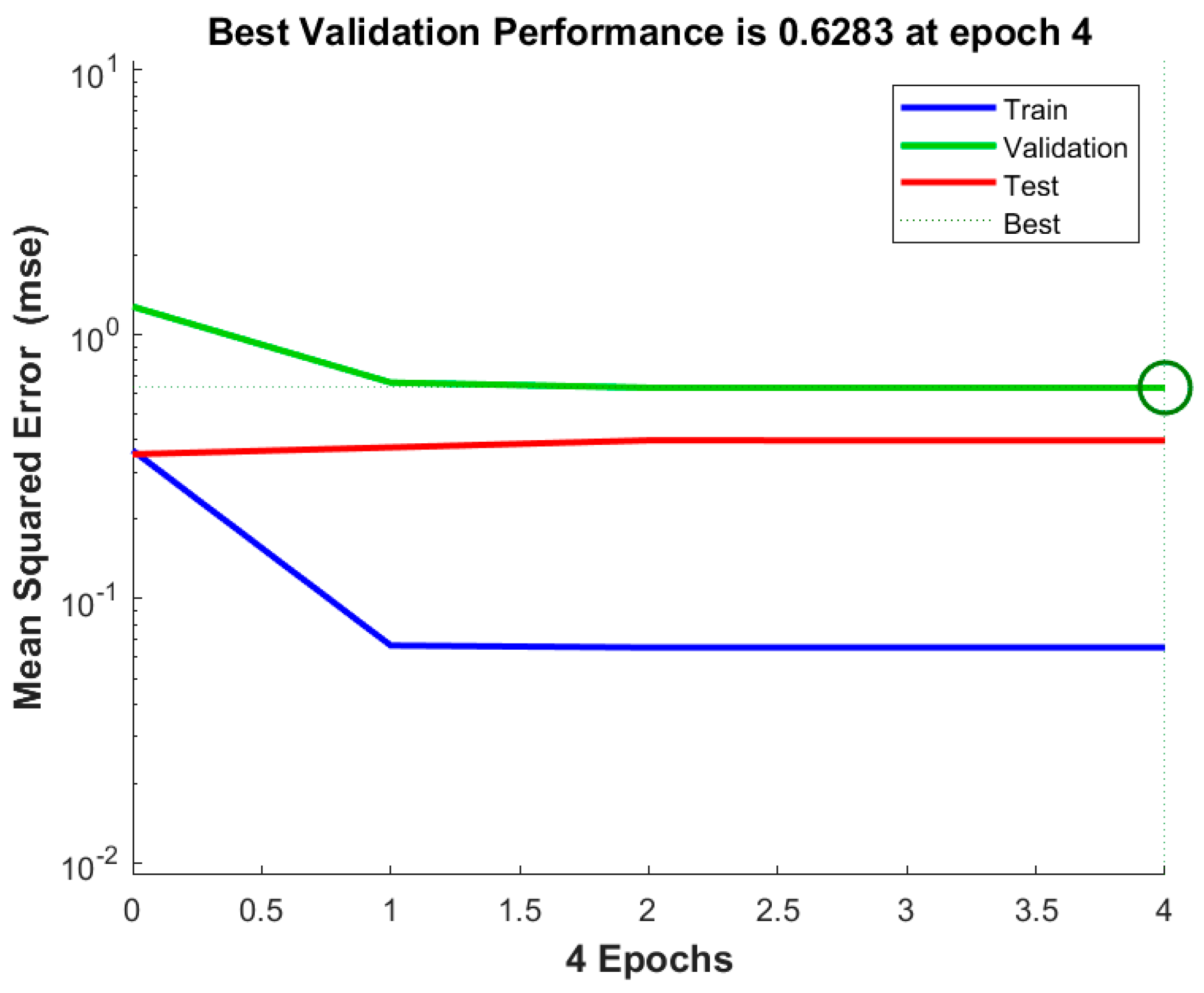
This study was aimed at modeling and optimizing the NH4+ removal process from stormwater by coal-based granular activated carbon (CB-GAC). RSM experimental design was selected to establish the regression model. The model involved four parameters (i.e., contact time, initial concentration, temperature, and pH) as independent variables and NH4+ removal rate as dependent variable. The interaction effect of the independent variables with the response using the response surface plots was illustrated. Meanwhile, the back-propagation artificial neural network BP-ANN model was also developed and the optimal number of hidden neurons was determined by trial and error method. Coupled with GA, the ANN-GA model was used for optimization of the operating conditions to determine the maximum NH4+ removal rate. The predictive capabilities and modelling efficiencies of the two models are compared and verified. Furthermore, the CB-GAC has been characterized by scanning electron microscopy (SEM), X-ray diffraction (XRD), and Brunauer-Emmett-Teller (BET). Finally, adsorption isotherm model (Langmuir, Freundlich, and Temkin) and adsorption kinetics model (pseudo-first-order, pseudo-second-order) had been investigated to explore the mechanisms of the NH4+ removal process.
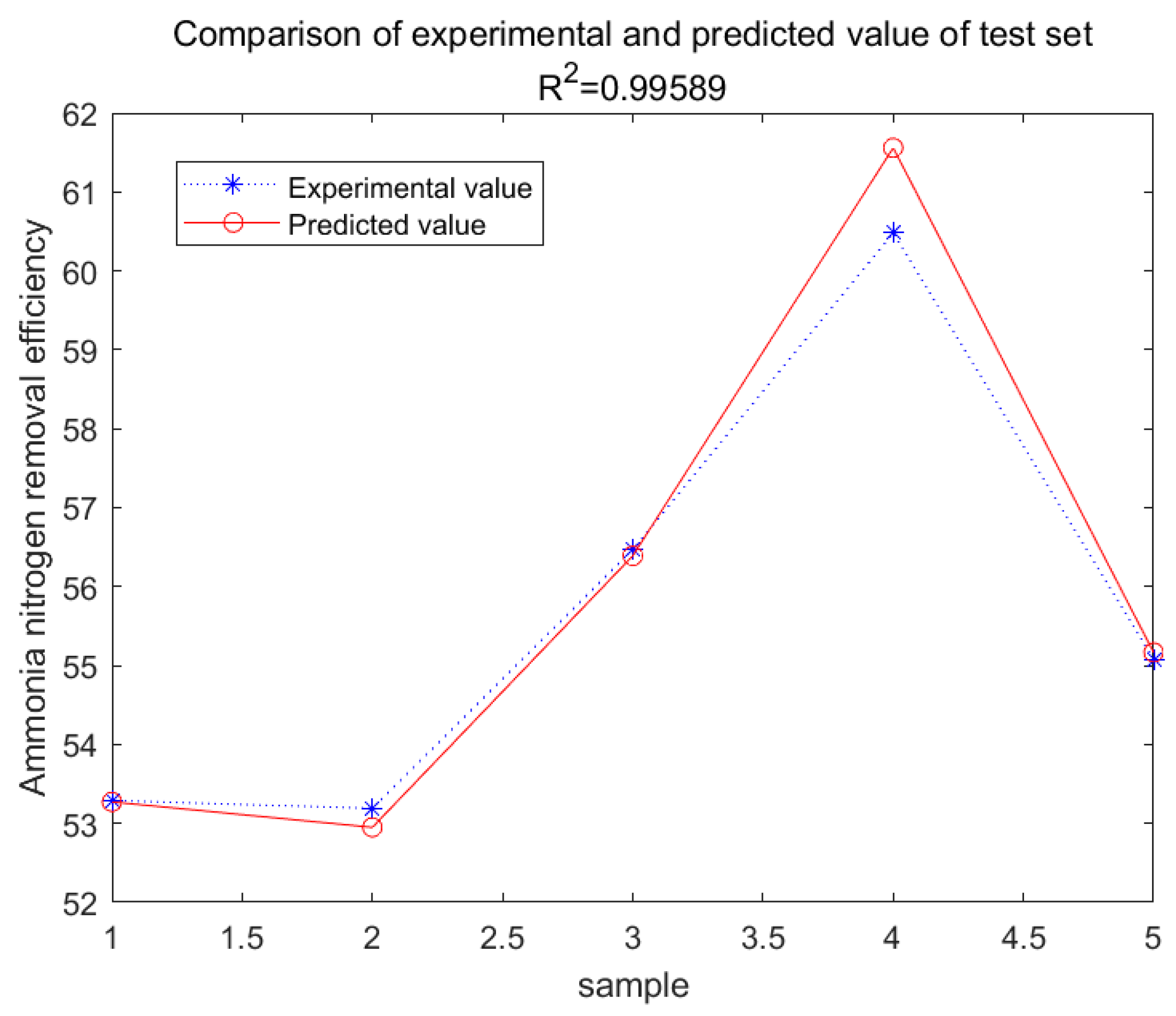
4. Conclusions
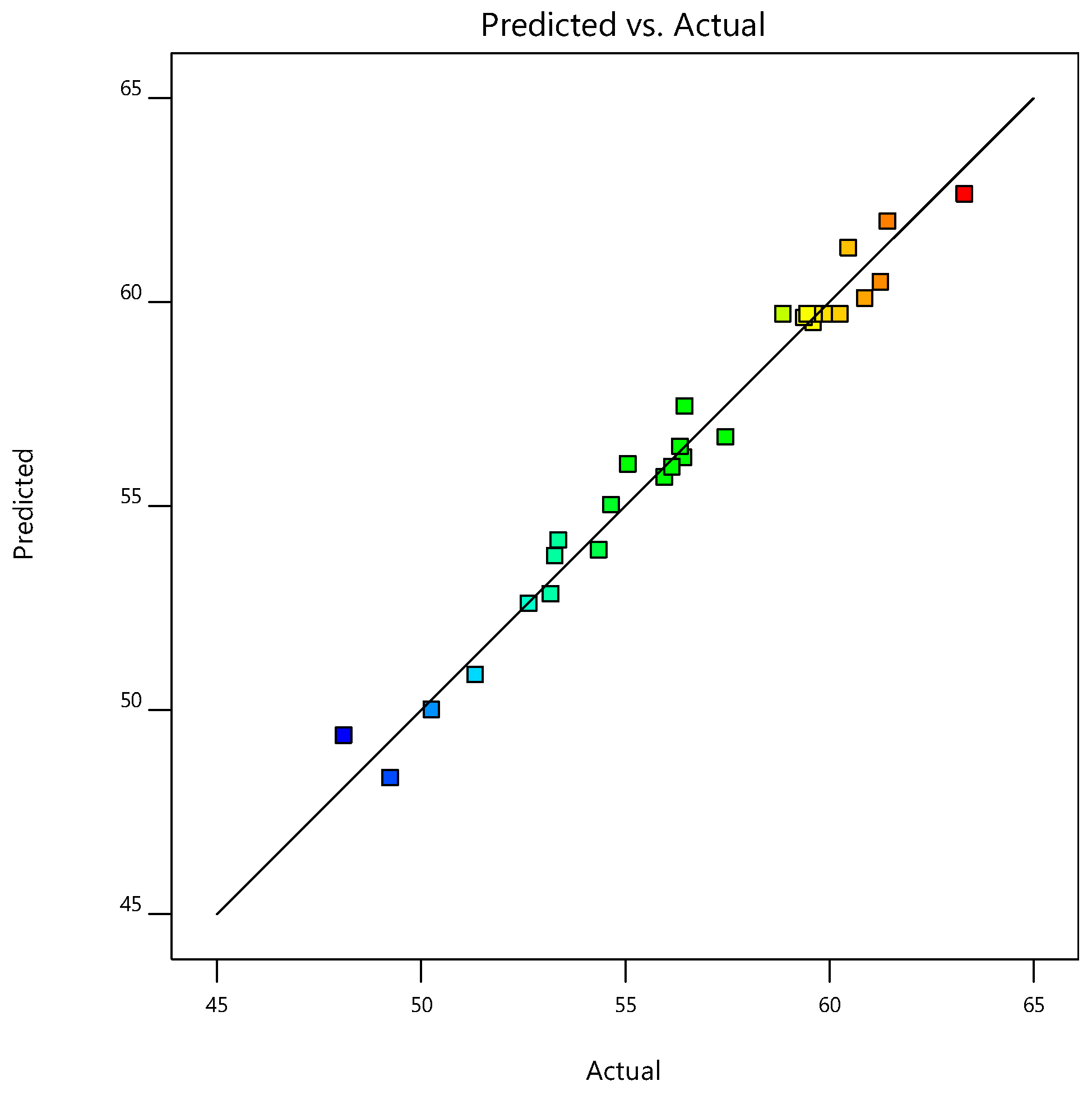
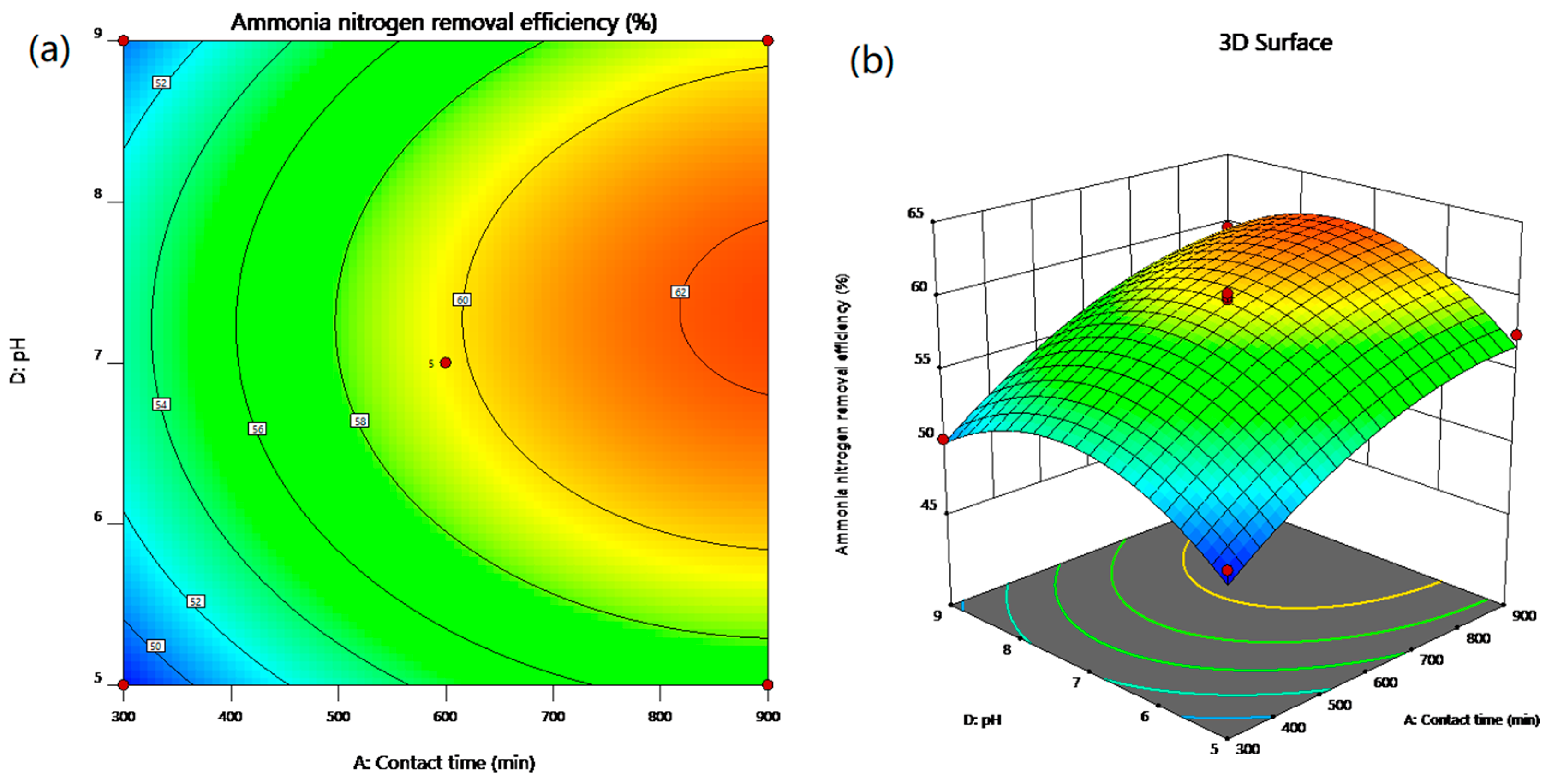
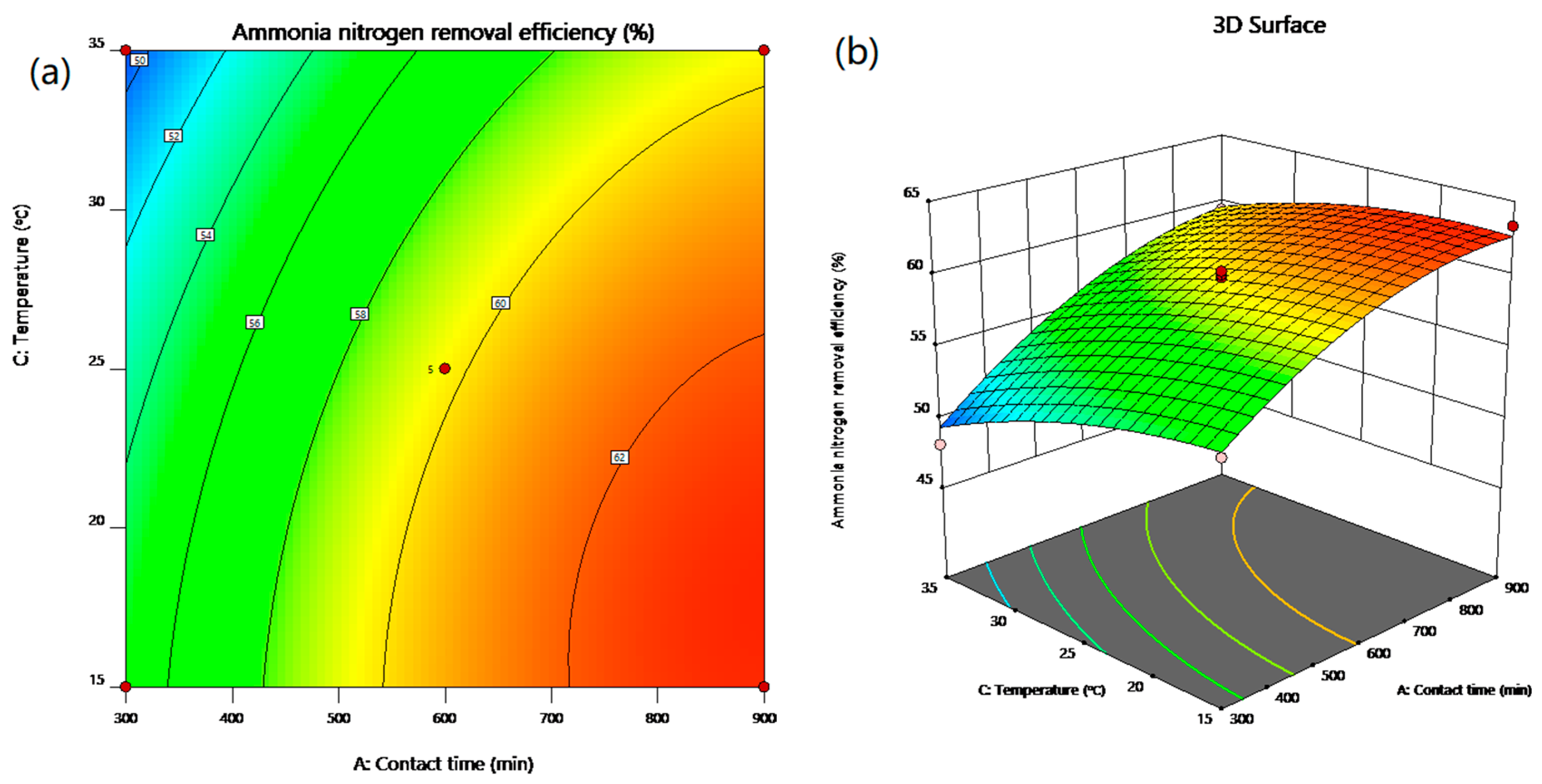
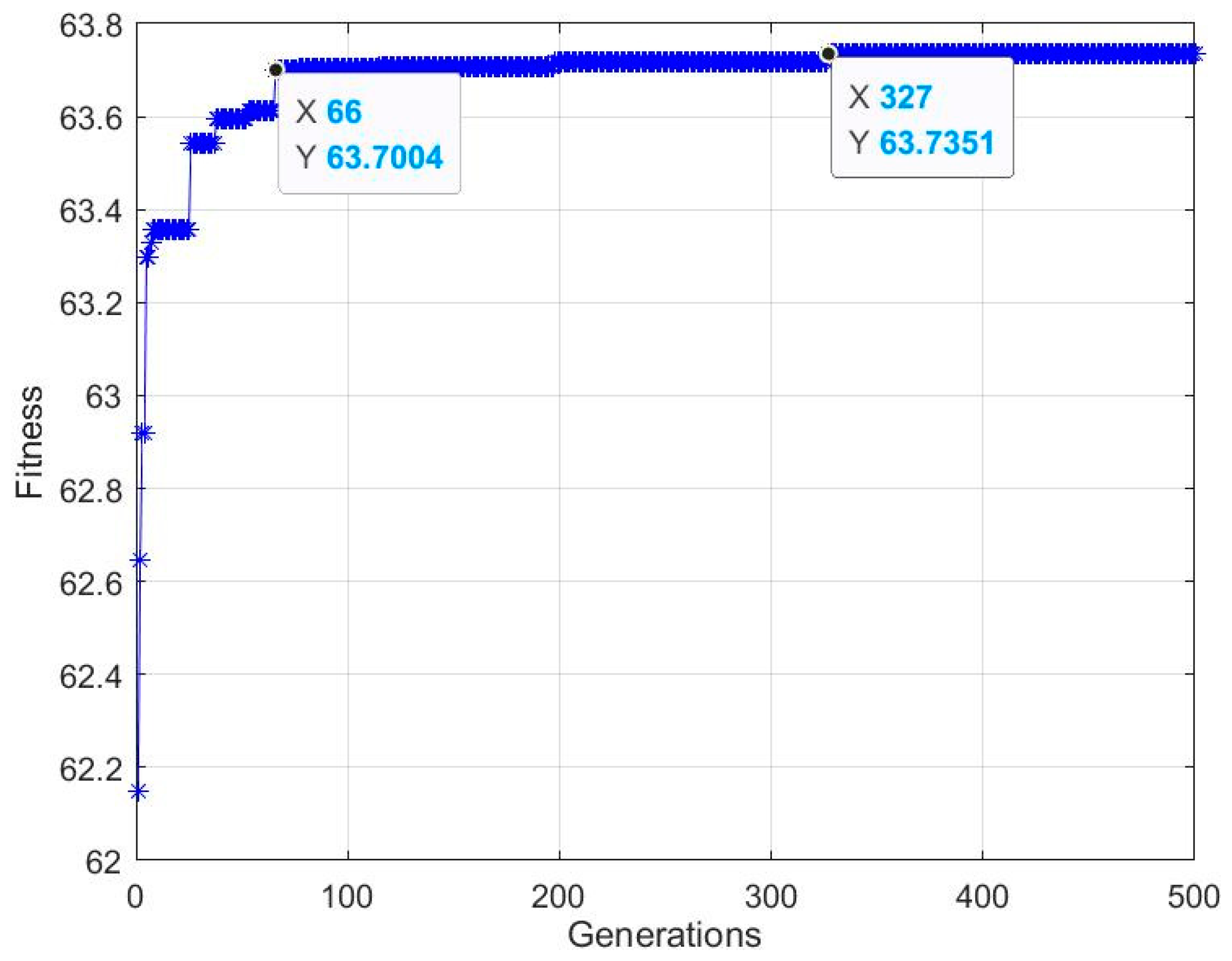
In the present work, the statistical modeling and optimization of process parameters (contact time, initial concentration, temperature, pH) for NH4+ removal from stormwater by CB-GAC was carried out using BBD-RSM and GA-ANN. In terms of prediction, neural network had better prediction accuracy than response surface method, with R2 of 0.9959 and 0.9762, respectively. The ANOVA and response surface plots in RSM confirmed that contact time was the most significant parameter of NH4+ removal, and the relative influence order of the factors according to the coefficients of the code equation is as follows: Contact time > temperature > pH > initial concentration. The best network structure of 4-8-1 was utilized in BP-ANN modeling. The results of sensitivity analysis showed that the factors of NH4+ removal rate were in the order of: Contact time (31.23%) > pH (24.68%) > temperature (22.93%) > initial concentration (21.16%). The process input factors were optimized by GA-ANN and BBD-RSM for the optimum NH4+ removal rate. The predicted results were verified by experiments. According to the results, the predicted values of GA-ANN were in better agreement with the experimental values. The optimum level of contact time, initial concentration, temperature, pH is 899.41 min, 17.35 mg/L, 15 °C, 6.98, respectively, under which condition, the maximum NH4+ removal rate is achieved 63.74%. The proposed method is effective for optimizing the process parameters of NH4+ removal from stormwater by CB-GAC, and is helpful to reduce the time and cost of experiments. In the future research, this method can be applied to the parameter optimization and efficiency prediction of the actual stormwater treatment process.