Water Pipe Replacement Scheduling Based on Life Cycle Cost Assessment and Optimization Algorithm
Abstract
1. Introduction
2. Methodology
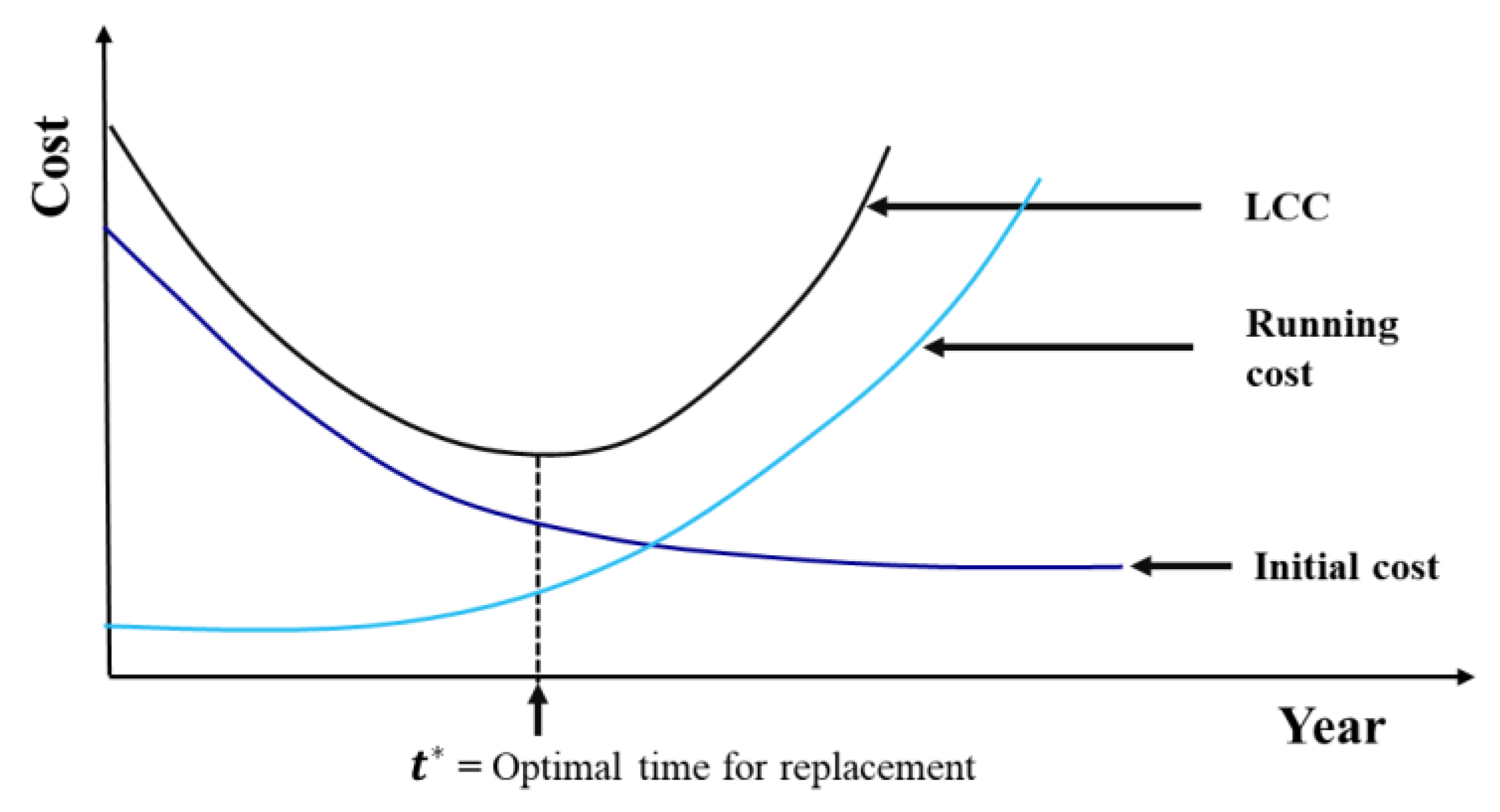
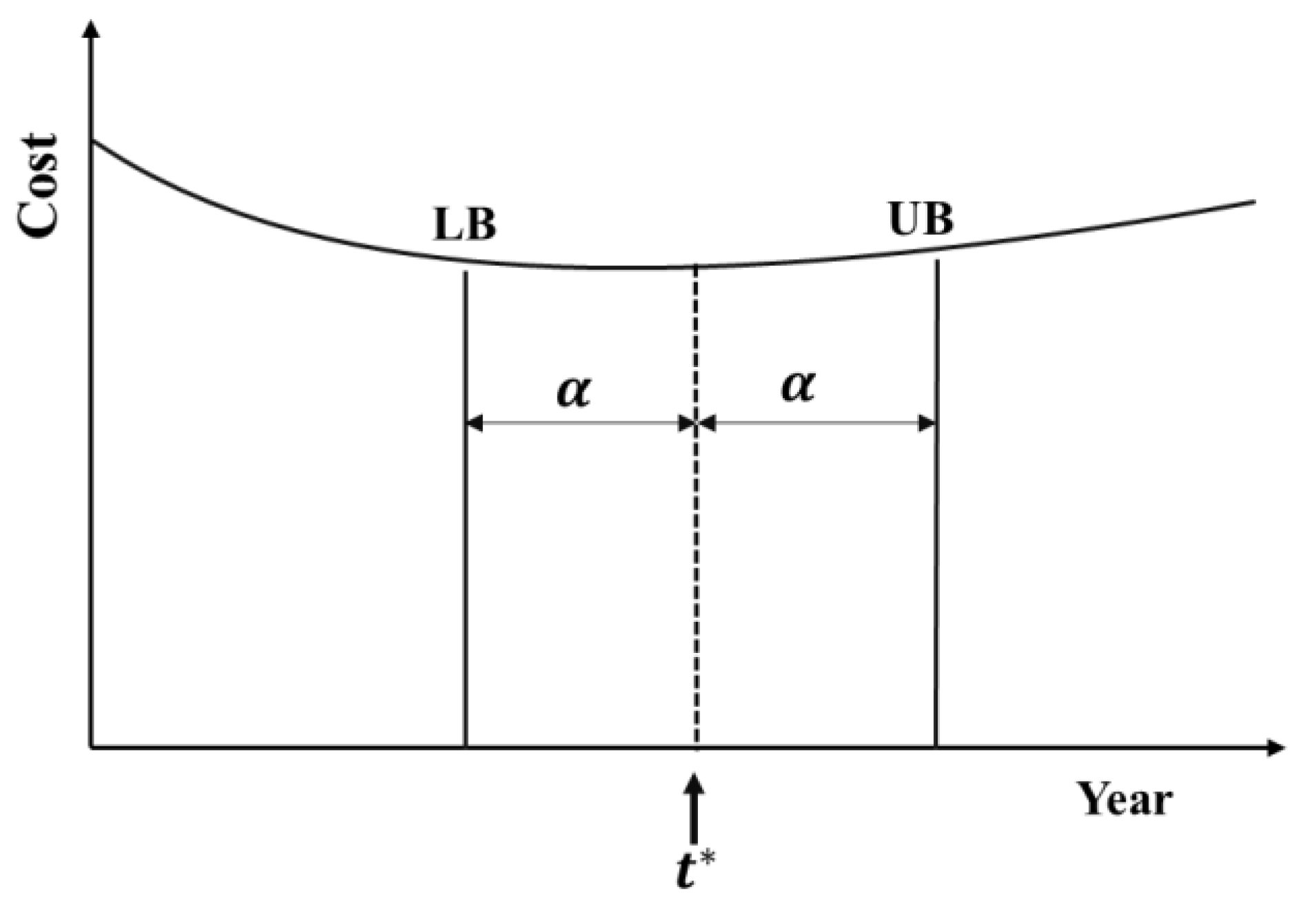
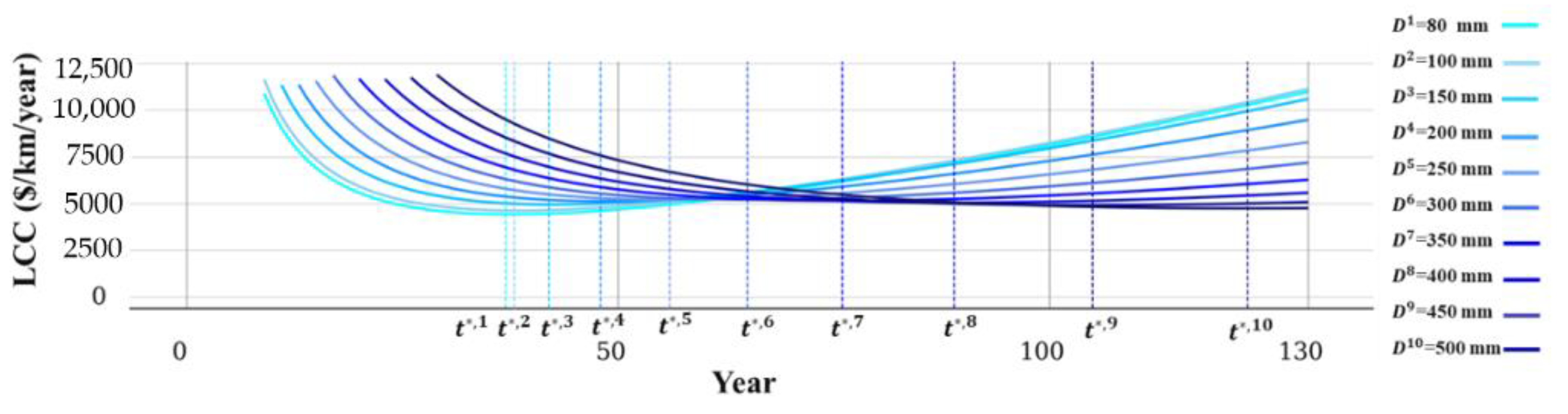
2.1. Optimal Water Pipe Replacement Based on LCC Assessment
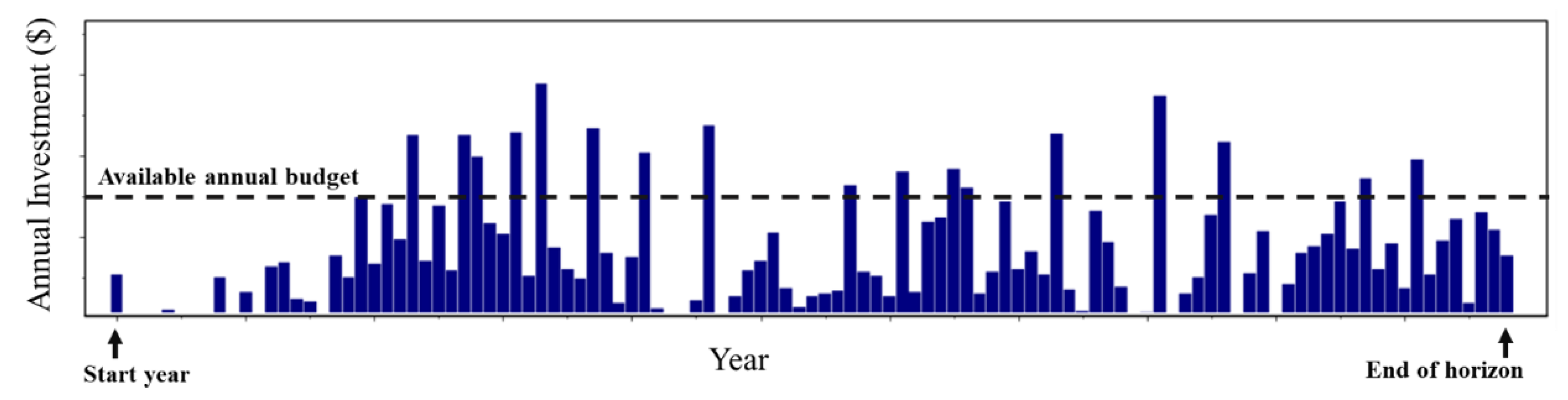
2.2. Smoothing the Investment Time Series
2.3. Pipe Replacement Scheduling Using a Multiobjective Optimization Algorithm
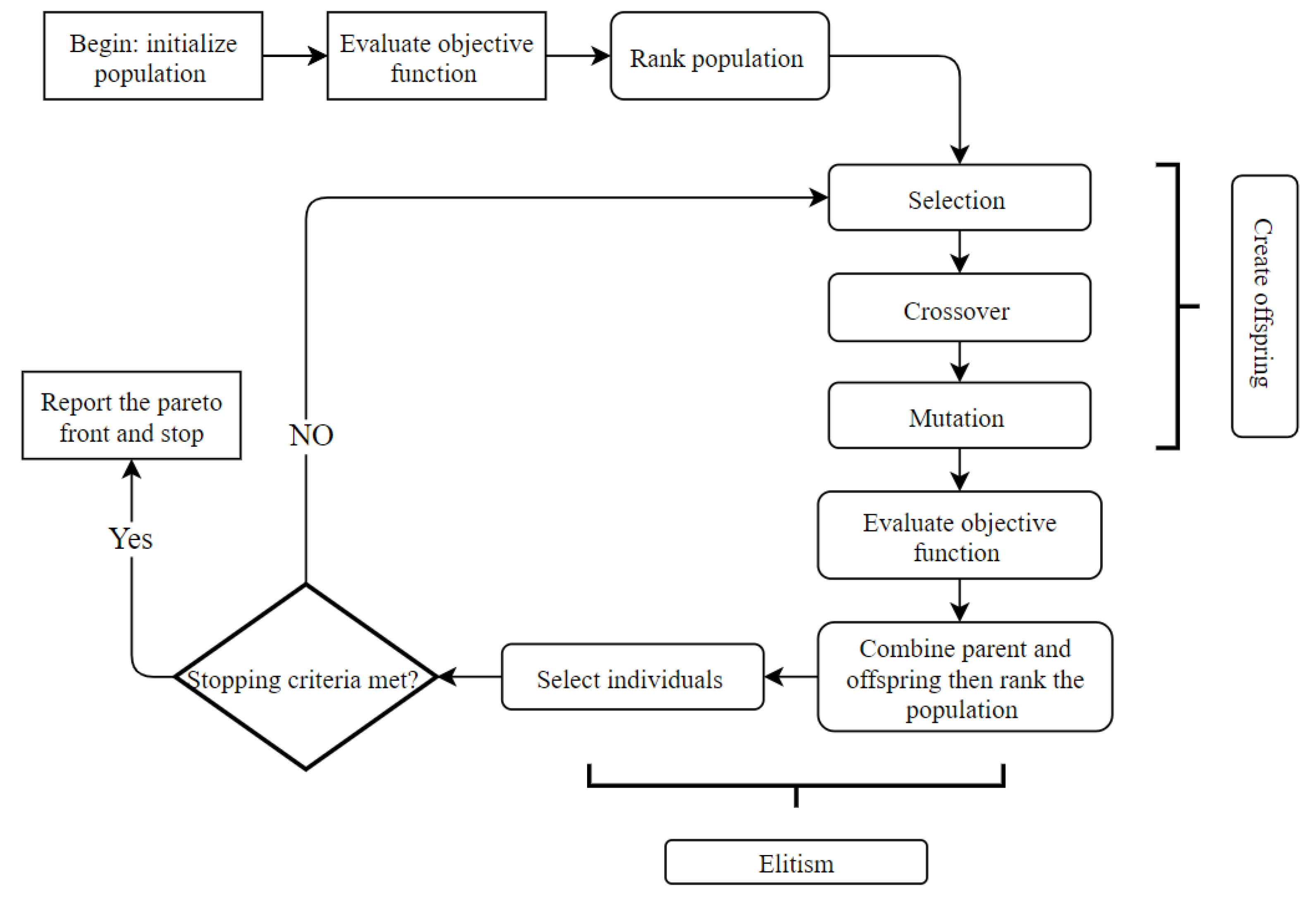
2.3.1. Overview of NSGA-II
- NSGA-II randomly generates an initial population consisting of a number of chromosomes. Each chromosome is the value of the design parameter (i.e., the replacement time of an individual pipe).
- Each individual in the population generated in the previous step is ranked based on an evaluation of the objective function. Then, the individuals are sorted based on their rank by using the crowding distance.
- Parents are randomly selected from a mating pool to create the new generation. The mating pool consists of solutions with a higher crowding distance and rank.
- To produce offspring, parents from the previous step undergo crossover and mutation procedures. In the crossover procedure, two parents breed to produce an offspring that inherits its genes from both parents. In the mutation procedure, some values of the genes in each offspring are changed, thus providing the offspring with the opportunity to have at least one different gene value than their parents.
2.3.2. Construction of Optimization Model
3. Results
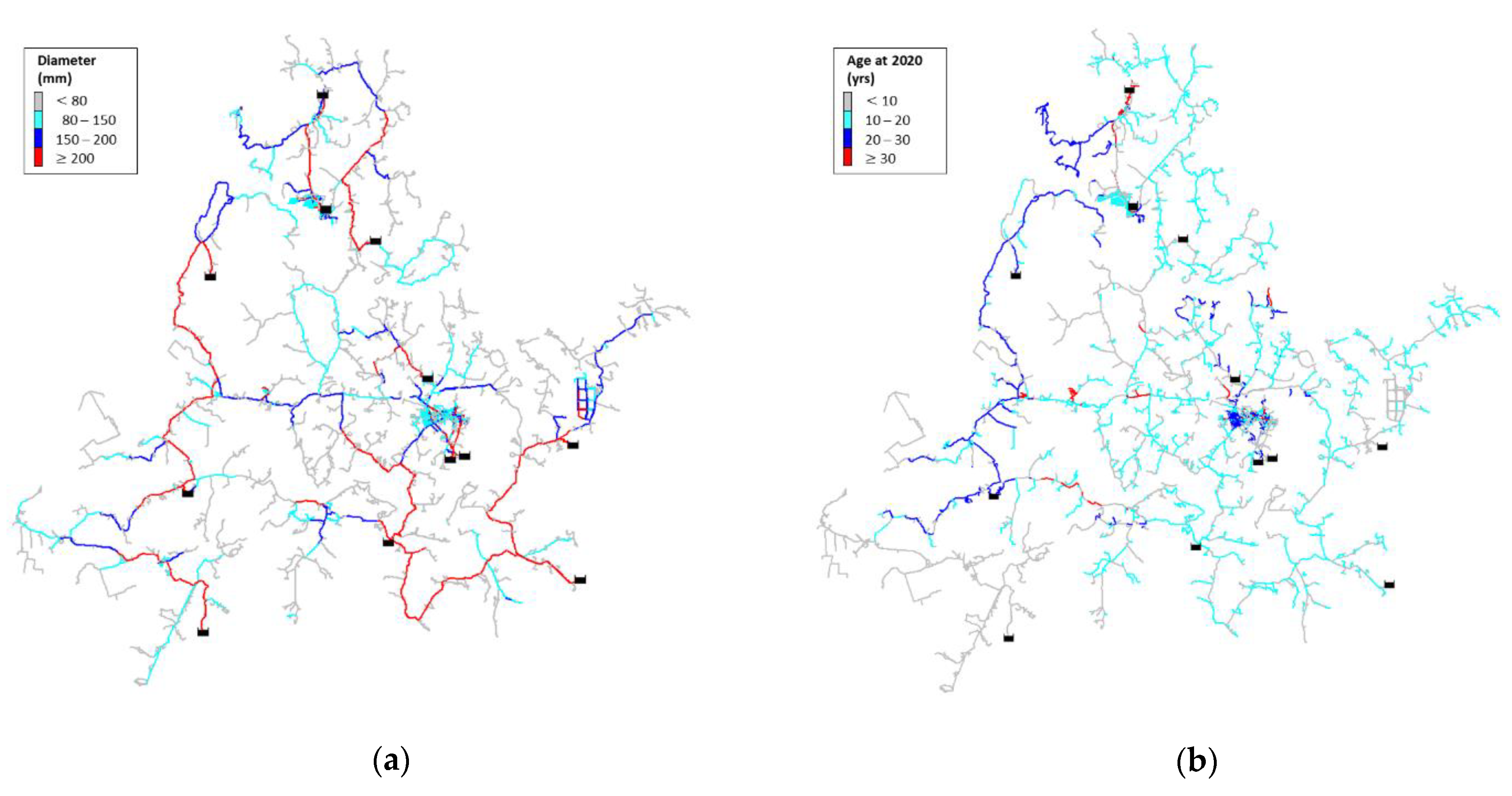
3.1. Case Study and Assumptions
- All pipes need to be replaced at least once in the simulation time horizon in consideration of the diameter and the first installation year of the pipes.
- Pipes that already passed their replacement time () will be replaced on priority in the first year of the scheduling plan.
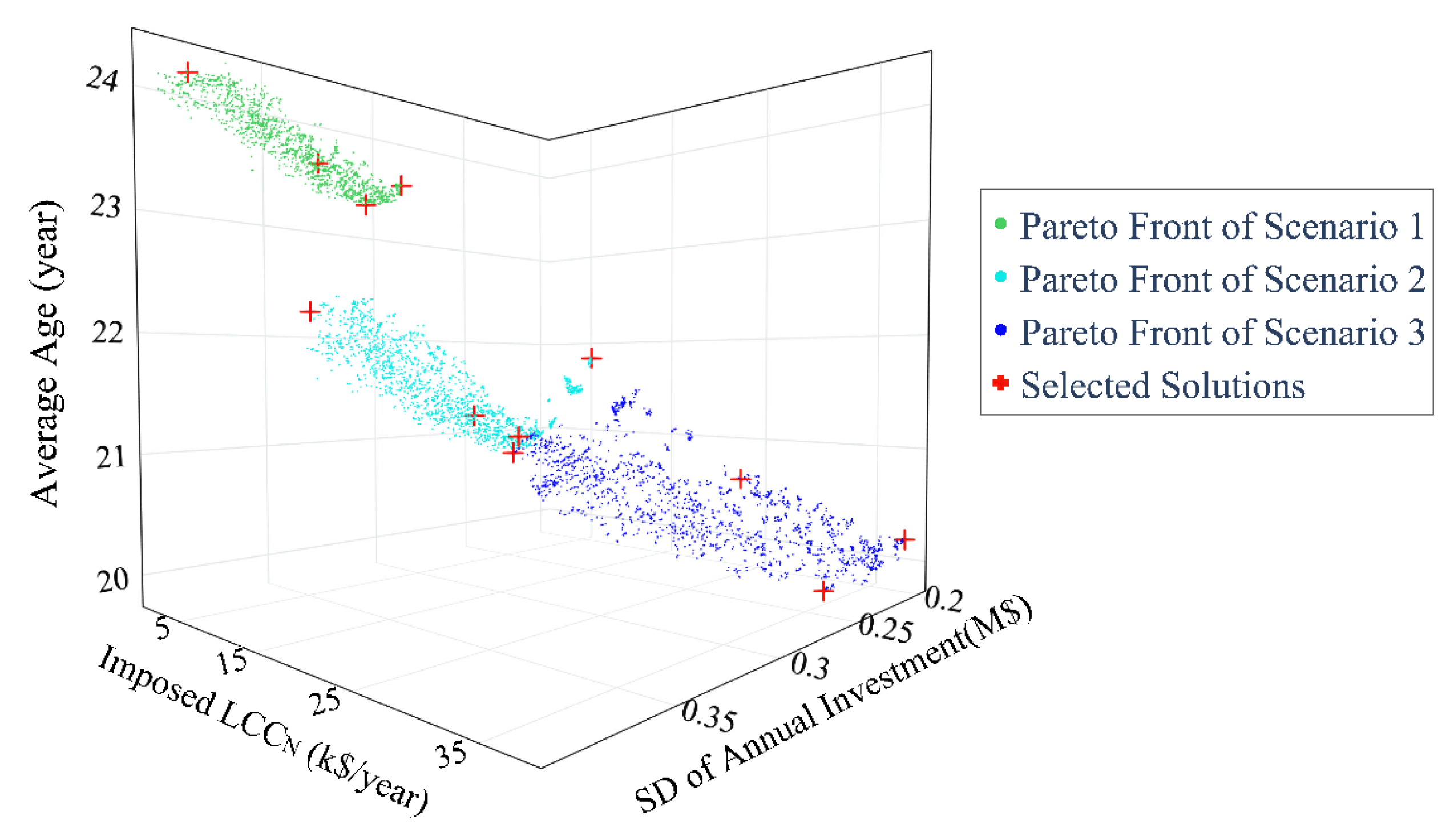
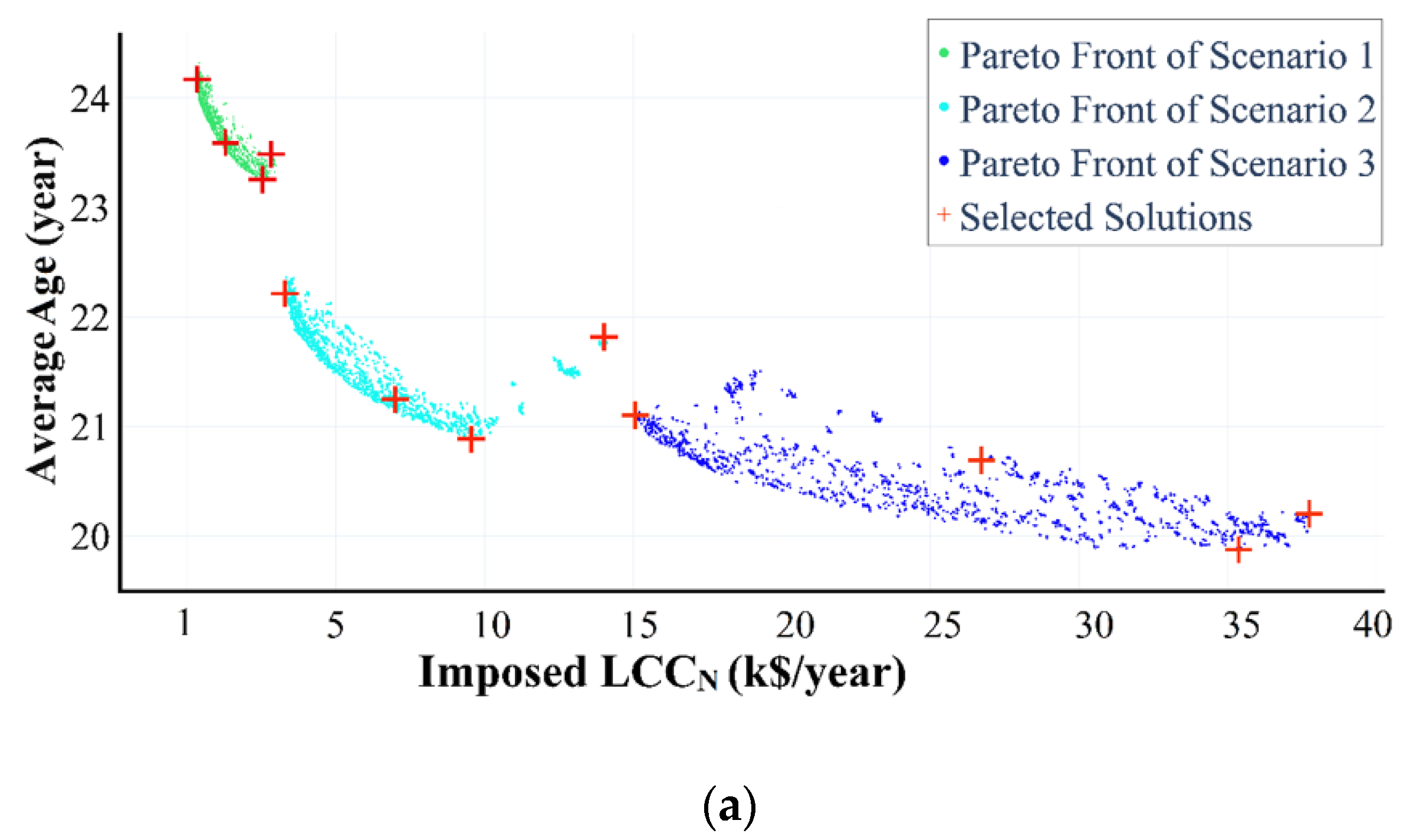
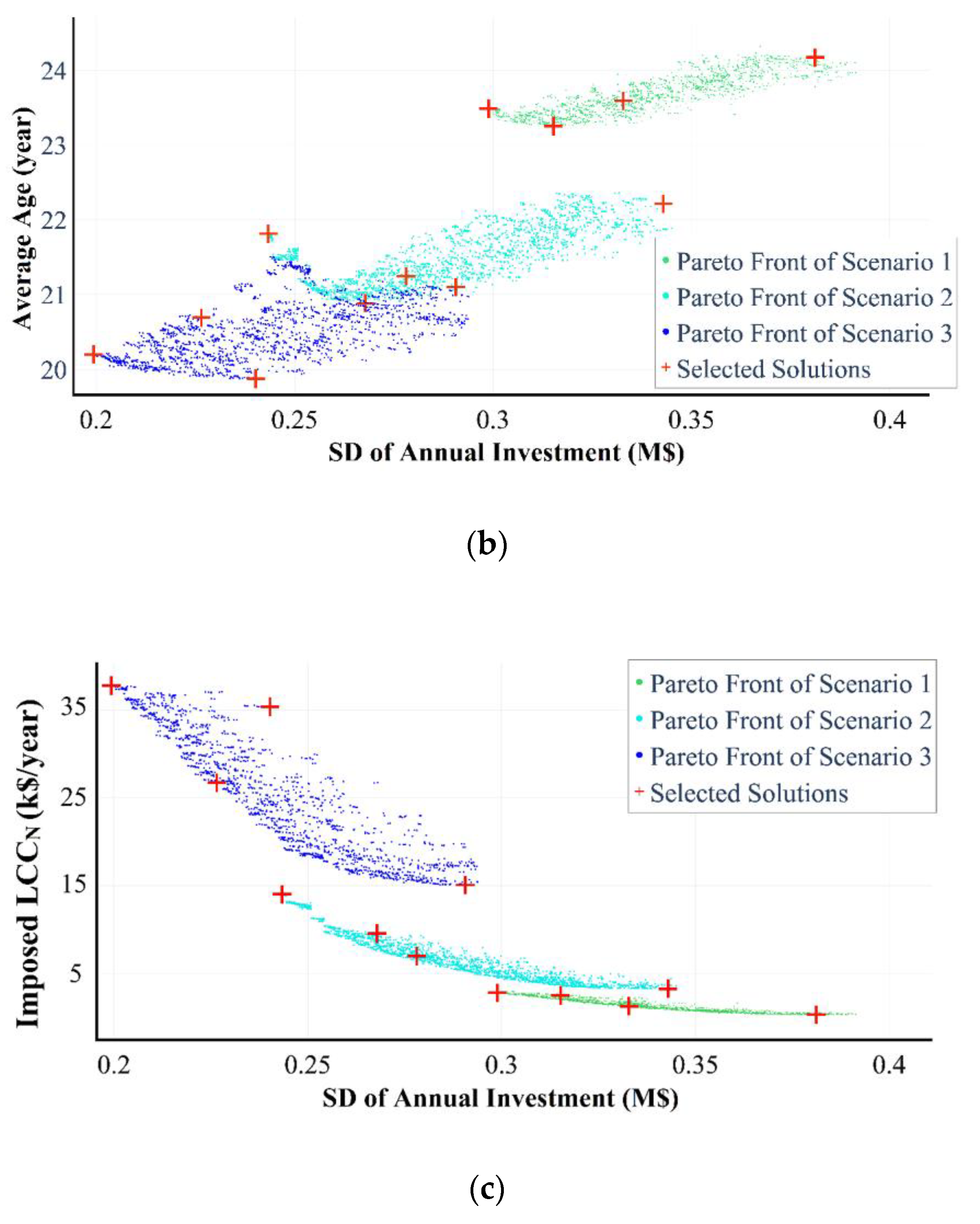
3.2. Pareto Front Obtained by Multiobjective Optimization
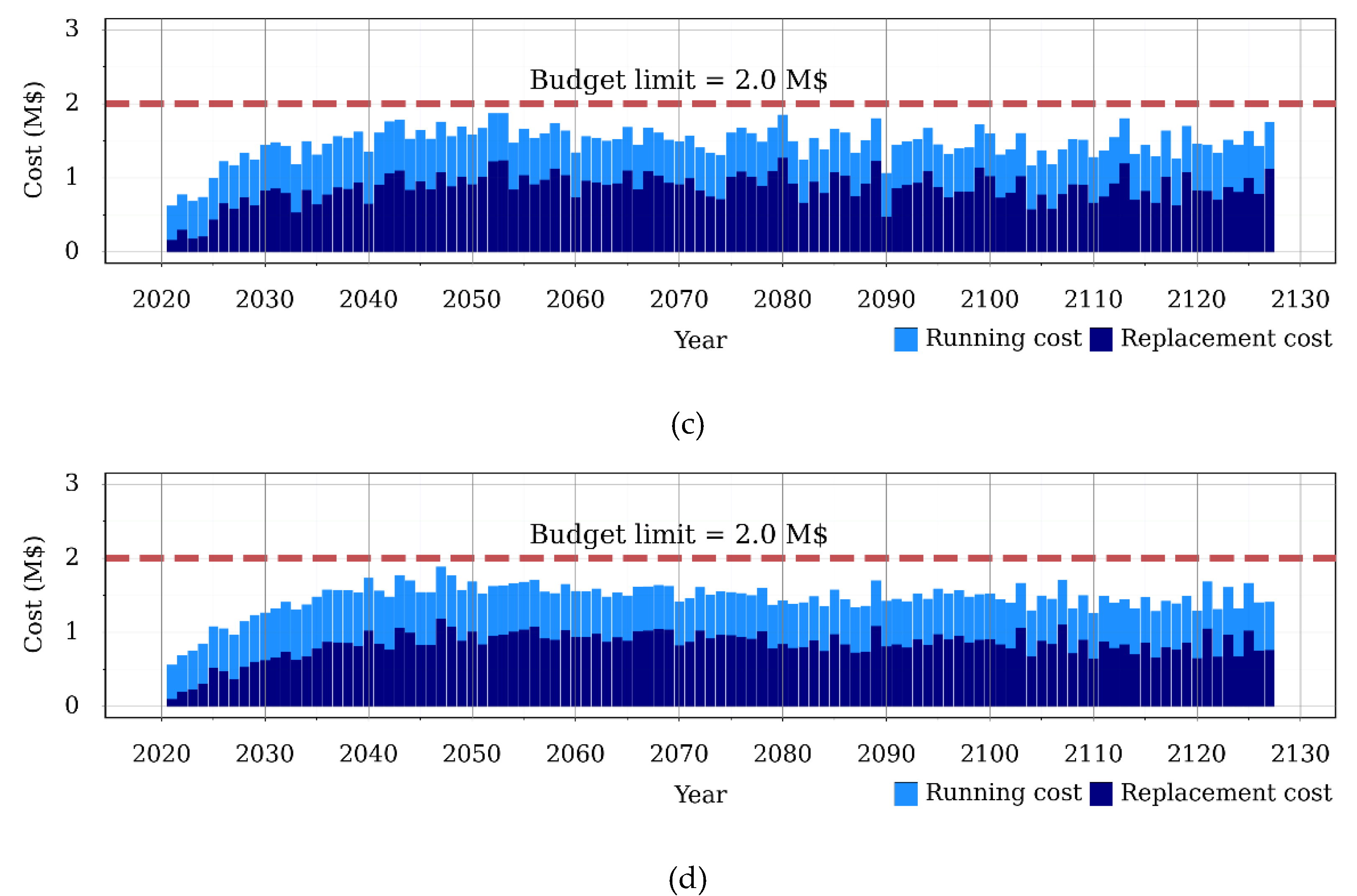
3.3. Comparison of Solutions for WDN Investment
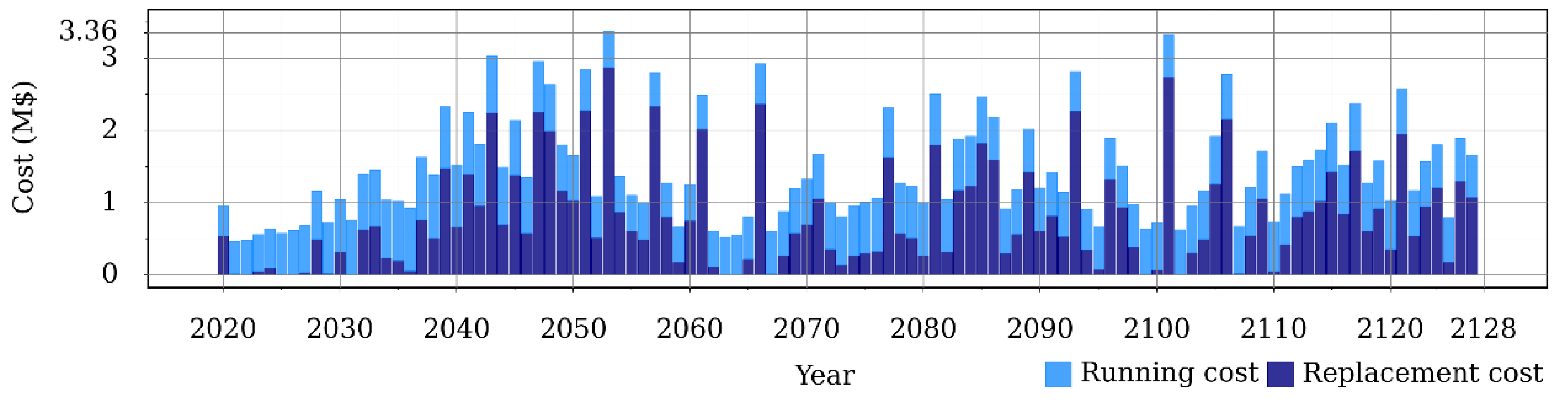
3.3.1. Future Investment Based on LLCCN
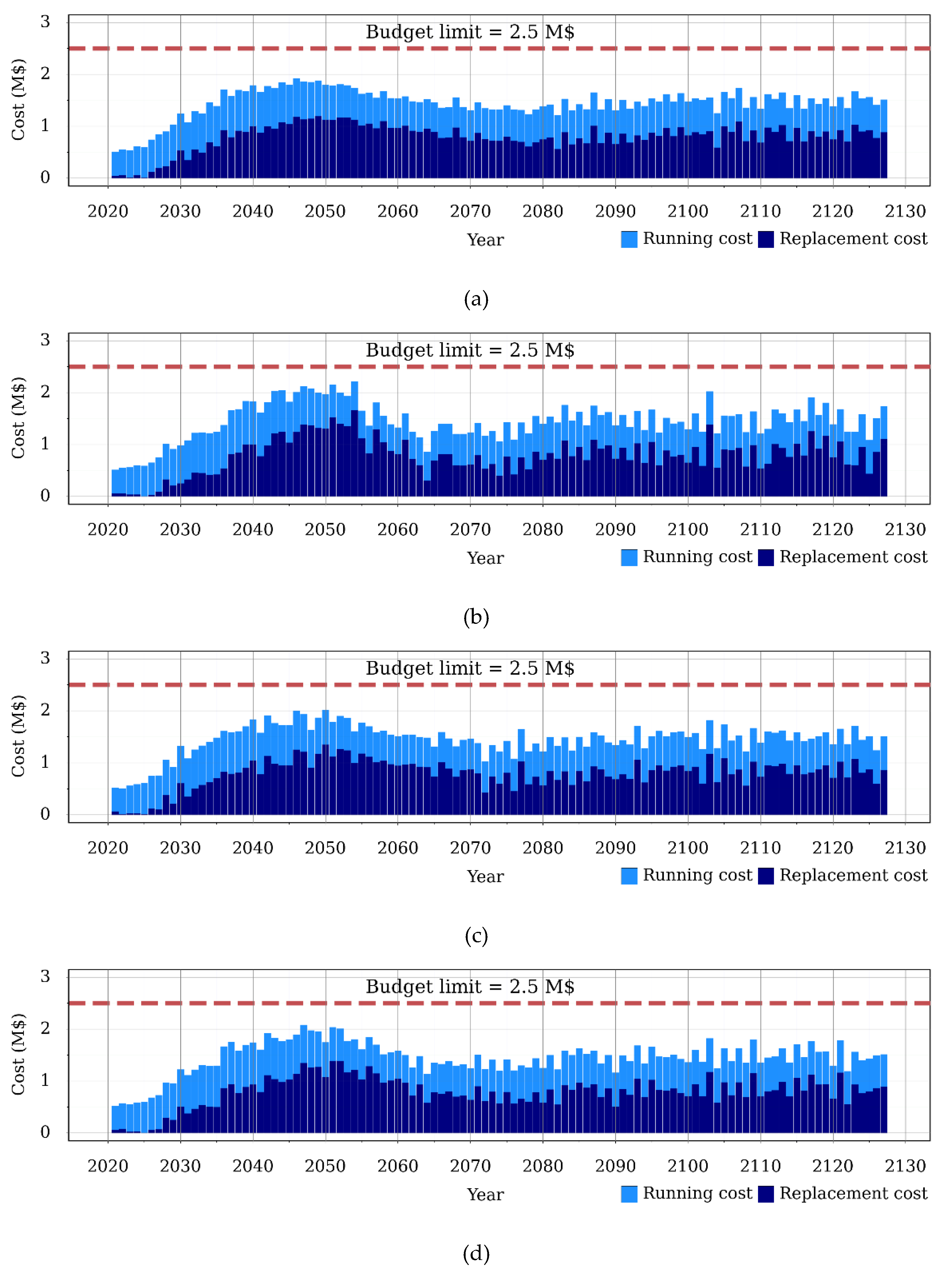
3.3.2. Future Investment Based on Scenario 1
3.3.3. Future Investment Based on Scenario 2
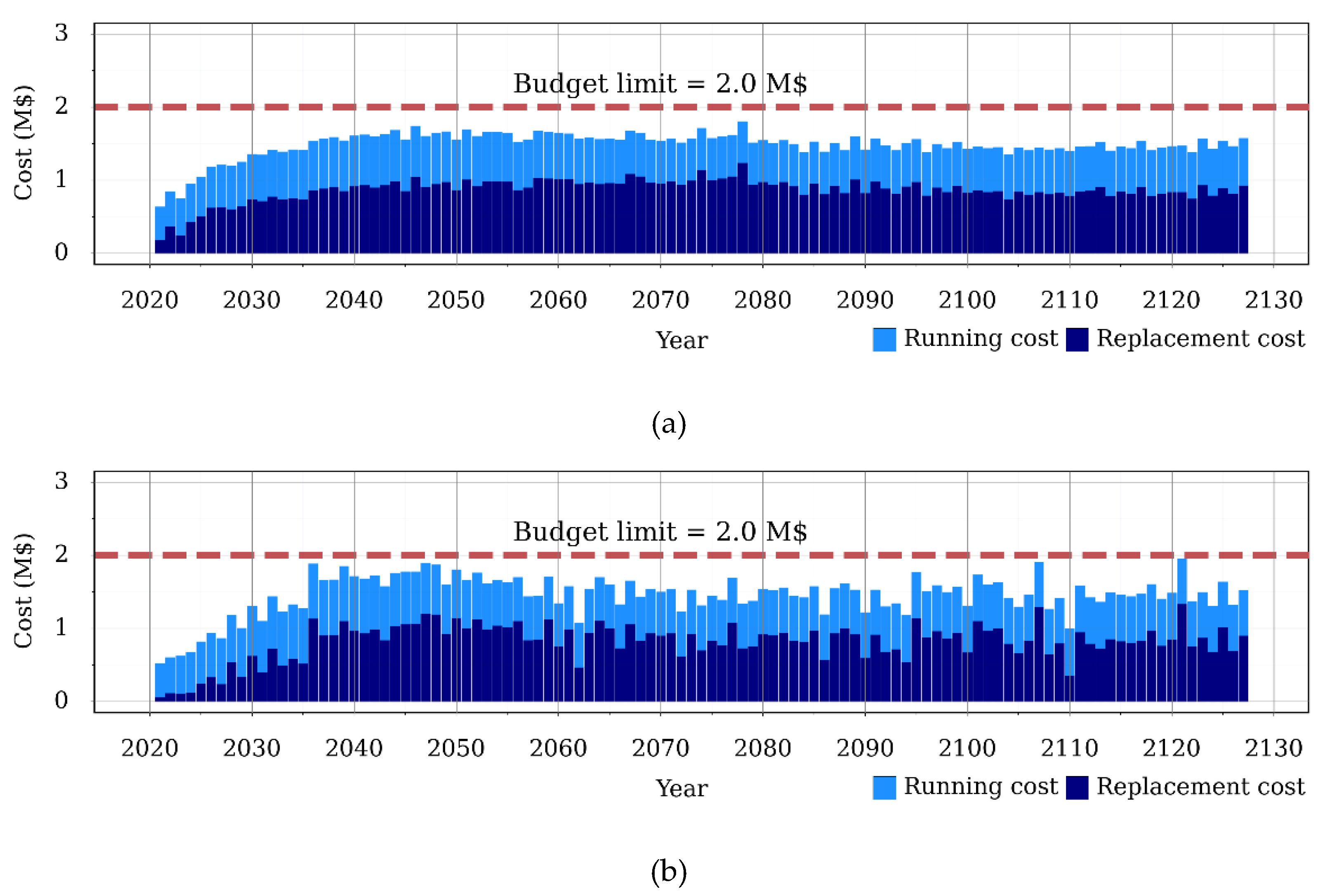
3.3.4. Future Investment Based on Scenario 3
3.3.5. Comparison between Representative Solutions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shahnawaz, K. Design Improvement in Water Distribution Systems: A Life Cycle Thinking Approach. Master’s Thesis, University of British Columbia, Vancouver, BC, Canada, 2019. [Google Scholar]
- Zhou, Y. Deterioration and Optimal Rehabilitation Modelling for Urban Water Distribution Systems; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Selvakumar, A.; Clark, R.M.; Sivaganesan, M. Costs for Water Supply Distribution System Rehabilitation. J. Water Resour. Plan. Manag. 2002, 128, 303–306. [Google Scholar] [CrossRef]
- Shin, H.; Joo, C.; Koo, J. Optimal Rehabilitation Model for Water Pipeline Systems with Genetic Algorithm. Procedia Eng. 2016, 154, 384–390. [Google Scholar] [CrossRef]
- Li, F.; Ma, L.; Sun, Y.; Mathew, J. Optimized Group Replacement Scheduling for Water Pipeline Network. J. Water Resour. Plan. Manag. 2016, 142, 04015035. [Google Scholar] [CrossRef]
- Gill, N.; Shah, J. Which Pipe First? Using Evidence-Based Condition Assessment and Desktop Modeling to Optimize Pipe Replacement. In Pipelines 2019: Condition Assessment, Construction, and Rehabilitation; American Society of Civil Engineers: Reston, VA, USA, 2019; pp. 417–423. [Google Scholar] [CrossRef]
- Olsson, R.J.; Kapelan, Z.; Savić, D.A. Probabilistic building block identification for the optimal design and rehabilitation of water distribution systems. J. Hydroinform. 2009, 11, 89–105. [Google Scholar] [CrossRef]
- Tanyimboh, T.T.; Kalungi, P. Optimal long-term design, rehabilitation and upgrading of water distribution networks. Eng. Optim. 2008, 40, 637–654. [Google Scholar] [CrossRef]
- Marzouk, M.; Osama, A. Fuzzy-Based Methodology for Integrated Infrastructure Asset Management. Int. J. Comput. Intell. Syst. 2017, 10, 745. [Google Scholar] [CrossRef]
- Giustolisi, O.; Laucelli, D.; Savic, D.A. Development of rehabilitation plans for water mains replacement considering risk and cost-benefit assessment. Civ. Eng. Environ. Syst. 2006, 23, 175–190. [Google Scholar] [CrossRef]
- Fu, G.; Kapelan, Z.; Kasprzyk, J.R.; Reed, P. Optimal Design of Water Distribution Systems Using Many-Objective Visual Analytics. J. Water Resour. Plan. Manag. 2013, 139, 624–633. [Google Scholar] [CrossRef]
- Zhou, Y. Optimal Rehabilitation Decision Model. In Deterioration and Optimal Rehabilitation Modelling for Urban Water Distribution Systems; CRC Press: Boca Raton, FL, USA, 2018; pp. 101–161. [Google Scholar]
- Shamir, U.; Howard, C.D. An Analytic Approach to Scheduling Pipe Replacement. J. Am. Water Work. Assoc. 1979, 71, 248–258. [Google Scholar] [CrossRef]
- Walski, T.M.; Pelliccia, A. Economic analysis of water main breaks. J. Am. Water Work. Assoc. 1982, 74, 140–147. [Google Scholar] [CrossRef]
- Kleiner, Y.; Adams, B.J.; Rogers, J.S. Long-term planning methodology for water distribution system rehabilitation. Water Resour. Res. 1998, 34, 2039–2051. [Google Scholar] [CrossRef]
- Dandy, G.C.; Engelhardt, M.O. Optimal Scheduling of Water Pipe Replacement Using Genetic Algorithms. J. Water Resour. Plan. Manag. 2001, 127, 214–223. [Google Scholar] [CrossRef]
- Alvisi, S.; Franchini, M. Multiobjective Optimization of Rehabilitation and Leakage Detection Scheduling in Water Distribution Systems. J. Water Resour. Plan. Manag. 2009, 135, 426–439. [Google Scholar] [CrossRef]
- Tee, K.F.; Khan, L.R.; Chen, H.P.; Alani, A.M. Reliability based life cycle cost optimization for underground pipeline networks. Tunn. Undergr. Space Technol. 2014, 43, 32–40. [Google Scholar] [CrossRef]
- Karamouz, M.; Yaseri, K.; Nazif, S. Reliability-Based Assessment of Lifecycle Cost of Urban Water Distribution Infrastructures. J. Infrastruct. Syst. 2017, 23, 04016030. [Google Scholar] [CrossRef]
- Nafi, A.; Kleiner, Y. Scheduling Renewal of Water Pipes While Considering Adjacency of Infrastructure Works and Economies of Scale. J. Water Resour. Plan. Manag. 2010, 136, 519–530. [Google Scholar] [CrossRef]
- Fuchs-Hanusch, D.; Kornberger, B.; Friedl, F.; Scheucher, R. Whole of life cost calculations for water supply pipes. In Asset Management of Water and Wastewater Infrastructure, including Technical and Socioeconomic Aspects; LESAM 2011 Strategic Asset Management of Water and Wastewater Infrastructure, Mühlheim; International Water Association: London, UK, 27–30 September 2011; Volume 8, pp. 19–24. [Google Scholar]
- Estevan, H.; Schaefer, B. Life Cycle Costing State of the Art Report, ICLEI–Local Governments for Sustainability; European Secretariat: Bonn, Germany, 2017; pp. 4–11. [Google Scholar]
- Gransberg, D. Life Cycle Costing for Engineers. Constr. Manag. Econ. 2010, 28, 1113–1114. [Google Scholar] [CrossRef]
- Lee, H.; Shin, H.; Rasheed, U.; Kong, M. Establishment of an Inventory for the Life Cycle Cost (LCC) Analysis of a Water Supply System. Water 2017, 9, 592. [Google Scholar] [CrossRef]
- Jayaram, N.; Srinivasan, K. Performance-based optimal design and rehabilitation of water distribution networks using life cycle costing. Water Resour. Res. 2008, 44, 1–15. [Google Scholar] [CrossRef]
- Roshani, E.; Filion, Y.R. Event-Based Approach to Optimize the Timing of Water Main Rehabilitation with Asset Management Strategies. J. Water Resour. Plan. Manag. 2014, 140, 04014004. [Google Scholar] [CrossRef]
- Frangopol, D.M.; Soliman, M.S. Life-cycle of structural systems: recent achievements and future directions. Struct. Infrastruct. Eng. 2016, 12, 1–20. [Google Scholar] [CrossRef]
- Godfrey, S.; Hailemichael, G. Life cycle cost analysis of water supply infrastructure affected by low rainfall in Ethiopia. J. Water, Sanit. Hyg. Dev. 2017, 7, 601–610. [Google Scholar] [CrossRef]
- Hasegawa, K.; Arai, Y.; Koizumi, A. Life Cycle Cost-based Pipe Replacement Model and Application in Depopulation Scenario. In Proceedings of the WDSA/CCWI Joint Conference, Kingston, ON, Canada, 23–25 July 2018. [Google Scholar]
- Elsayed, E.A. Life Cycle Costs and Reliability Engineering. In Wiley StatsRef: Statistics Reference Online; Wiley: Hoboken, NJ, USA, 2014; pp. 1–10. [Google Scholar]
- U.S. Army Corps of Engineers. Engineering and Design-Evaluation of Existing Water Distribution Systems; Engineer Technical Letter No. 1110-2-278; U.S. Army Corps of Engineers: Washington, DC, USA, 1983. [Google Scholar]
- Jardine, A.K.S.; Tsang, A.H.C. Maintenance, Replacement, and Reliability Theory and Applications, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2013; ISBN 9789896540821. [Google Scholar]
- Deb, K.; Agrawal, S.; Pratap, A.; Meyarivan, T. A Fast Elitist Non-Dominated Sorting Genetic Algorithm for Multi-Objective Optimization: NSGA-II; Lect. Notes Comput. Sci.; including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics; Springer: Heidelberg/Berlin, Germany, 2000; Volume 1917, pp. 849–858. [Google Scholar] [CrossRef]
- Wang, H.; Chen, X. Optimization of Maintenance Planning for Water Distribution Networks under Random Failures. J. Water Resour. Plan. Manag. 2016, 142, 04015063. [Google Scholar] [CrossRef]
- K-water. Water Facilities Construction Cost Estimation Report; Technical Report; K-water: Daejeon, Korea, 2010. [Google Scholar]
- Blank, J.; Deb, K. Pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]

| Diameter (mm) | Pipe Cost ($/m) | ||
|---|---|---|---|
| Material | Construction | Total | |
| 80 | 15 | 65 | 80 |
| 100 | 28 | 66 | 94 |
| 150 | 41 | 76 | 117 |
| 200 | 59 | 86 | 145 |
| 250 | 81 | 96 | 177 |
| 300 | 103 | 105 | 208 |
| 350 | 125 | 114 | 239 |
| 400 | 149 | 127 | 276 |
| 450 | 156 | 136 | 292 |
| 500 | 182 | 148 | 330 |
| Diameter (mm) | CI ($/km/Year) | CR ($/km/Year) | LLCC ($/km/Year) | |
|---|---|---|---|---|
| 80 | 35 | 2286 | 1725 | 4010 |
| 100 | 37 | 2541 | 1878 | 4418 |
| 150 | 42 | 2786 | 2080 | 4865 |
| 200 | 49 | 2959 | 2223 | 5182 |
| 250 | 57 | 3105 | 2275 | 5380 |
| 300 | 67 | 3104 | 2304 | 5408 |
| 350 | 78 | 3064 | 2264 | 5327 |
| 400 | 91 | 3033 | 2203 | 5236 |
| 450 | 104 | 2808 | 2065 | 4873 |
| 500 | 122 | 2705 | 1991 | 4696 |
| Standard Deviation (M$) | LLCCN (M$/year) | Average Age (Year) | Running Cost (M$) | Initial Cost (M$) | Total Cost (M$) | TAI (M$/Year) | |
|---|---|---|---|---|---|---|---|
| 0.72 | 1.504 | 27.2 | 3.36 | 70.28 | 90.65 | 160.93 | 1.490 |
| Solution Number | Standard Deviation (M$) | Imposed LCC (k$/Year) | Average Age (Year) | MODE (Year) | Running Cost (M$) | Initial Cost (M$) | Total Cost (M$) | TAI (M$/Year) | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.298 | 3.8 | 23.5 | −5 | 1.99 | 69.70 | 90.66 | 160.36 | 1.485 |
| 2 | 0.381 | 1.3 | 24.2 | 0 | 2.22 | 70.53 | 89.48 | 160.00 | 1.481 |
| 3 | 0.315 | 3.5 | 23.2 | −5 | 2.08 | 69.72 | 90.61 | 160.33 | 1.485 |
| 4 | 0.332 | 2.2 | 23.6 | 0 | 2.15 | 70.15 | 90.22 | 160.37 | 1.485 |
| Solution Number | Standard Deviation (M$) | Imposed LCC (k$/Year) | Average Age (Year) | MODE (Year) | Running Cost (M$) | Initial Cost (M$) | Total Cost (M$) | TAI (M$/Year) | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.243 | 15 | 22.4 | −10 | 1.80 | 68.27 | 92.79 | 161.06 | 1.491 |
| 2 | 0.342 | 4 | 22.2 | 0 | 2.18 | 69.83 | 90.56 | 160.39 | 1.485 |
| 3 | 0.268 | 10 | 20.8 | −10 | 2.08 | 68.03 | 92.82 | 160.86 | 1.489 |
| 4 | 0.278 | 8 | 21.2 | −3 | 1.97 | 68.48 | 92.07 | 160.56 | 1.487 |
| Solution Number | Standard Deviation (M$) | Imposed LCC (k$/Year) | Average Age (Year) | MODE (Year) | Running Cost (M$) | Initial Cost (M$) | Total Cost (M$) | TAI (M$/year) | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.193 | 51 | 22.2 | −10 | 1.79 | 66.47 | 98.61 | 165.08 | 1.523 |
| 2 | 0.290 | 16 | 21.1 | 0 | 1.97 | 68.56 | 93.00 | 161.57 | 1.496 |
| 3 | 0.240 | 36 | 19.9 | −12 | 1.90 | 65.82 | 97.85 | 163.67 | 1.515 |
| 4 | 0.226 | 28 | 20.7 | −5 | 1.91 | 67.43 | 94.87 | 162.31 | 1.503 |
| Scenarios | Budget Constraint (M$) | Replacement Time Span [LB,UB] (Year) | Minimum Standard Deviation (M$) | Minimum Imposed LCC (k$/Year) | Minimum Average Age (Year) |
|---|---|---|---|---|---|
| 1 | 2.5 | −5, 5 | 0.298 | 1.3 | 23.2 |
| 2 | 2.2 | −10, 10 | 0.243 | 4.0 | 20.8 |
| 3 | 2.0 | −16, 16 | 0.193 | 16.0 | 19.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghobadi, F.; Jeong, G.; Kang, D. Water Pipe Replacement Scheduling Based on Life Cycle Cost Assessment and Optimization Algorithm. Water 2021, 13, 605. https://doi.org/10.3390/w13050605
Ghobadi F, Jeong G, Kang D. Water Pipe Replacement Scheduling Based on Life Cycle Cost Assessment and Optimization Algorithm. Water. 2021; 13(5):605. https://doi.org/10.3390/w13050605
Chicago/Turabian StyleGhobadi, Fatemeh, Gimoon Jeong, and Doosun Kang. 2021. "Water Pipe Replacement Scheduling Based on Life Cycle Cost Assessment and Optimization Algorithm" Water 13, no. 5: 605. https://doi.org/10.3390/w13050605
APA StyleGhobadi, F., Jeong, G., & Kang, D. (2021). Water Pipe Replacement Scheduling Based on Life Cycle Cost Assessment and Optimization Algorithm. Water, 13(5), 605. https://doi.org/10.3390/w13050605







