Electrically Induced Liquid–Liquid Phase Transition in a Floating Water Bridge Identified by Refractive Index Variations

Abstract

A horizontal electrohydrodynamic (EHD) liquid bridge (also known as a “floating water bridge”) is a phenomenon that forms when high voltage DC (kV·cm⁻¹) is applied to pure water in two separate beakers. The bridge, a free-floating connection between the beakers, acts as a cylindrical lens and refracts light. Using an interferometric set-up with a line pattern placed in the background of the bridge, the light passing through is split into a horizontally and a vertically polarized component which are both projected into the image space in front of the bridge with a small vertical offset (shear). Apart from a 100 Hz waviness due to a resonance effect between the power supply and vortical structures at the onset of the bridge, spikes with an increased refractive index moving through the bridge were observed. These spikes can be explained by an electrically induced liquid–liquid phase transition in which the vibrational modes of the water molecules couple coherently.

1. Introduction

An electrohydrodynamic (EHD) liquid bridge (aka “floating water bridge”) constitutes an intriguing phenomenon that occurs when a high (~kV·cm⁻¹) potential difference is applied between two beakers of pure water. Induced by the field, the water jumps to the edges of the beakers and forms a free hanging string through air connecting the two beakers. The discovery of the bridge dates back to the 19th century [1]. In contrast to similar effects like electrowetting [2] or the Sumoto effect [3] the water bridge was forgotten until its recent rediscovery [4,5]. At the macroscopic level electrohydrodynamics discussions of the Maxwell stress tensor [6] are sufficient to provide an explanation of the gross features of the bridge. Under these scenarios the electric field induces a negative pressure which draws liquid into the bridge and also accelerates suspended liquid elements against gravity, essentially being a form of electrostriction. Formal relationships between the physical fluid parameters, electric field intensity, and experimental configuration have been worked out by Marín and Lohse [7]. Later Morawetz [8,9,10] successfully modelled the bridge as a charged catenary, and his considerations concerning the flow profile match the experimental findings of Wexler et al. [11]. Aerov [12], on the other hand, proposed a model where surface tension is responsible for holding the bridge against the gravity. A reduction of the surface tension was experimentally determined by Teschke et al. [13], and the visco-elastic behavior of the bridge in terms of Young’s modulus was also determined by this group [14]. Woisetschläger et al. [15] presented a macroscopic theory based on the works of Widom et al. [6] and Marín and Lohse [7]. The molecular-scale properties of an aqueous EHD bridge have been studied thoroughly [16,17,18,19]. Molecular dynamics simulations show effects of electric fields on water structure [20,21] or increased dissociation [22,23], but these calculations concern electric fields that are ~1000 times higher than those present in an EHD bridge. So, whereas the average radial distribution function of electrically stressed liquid in an EHD bridge is comparable to that of the bulk [17], ultrafast IR pump/probe spectroscopy [24] and Raman studies [25,26,27,28] showed that the molecular dynamics in the bridge differ considerably from the bulk liquid. The electrochemistry of the system has been thoroughly investigated [29] describing the bridge to be a protonic semi-conductor. In the bridge the protons are more mobile than in the bulk [30] and their transport causes a non-thermic IR emission [31] Details about how to safely build and run an EHD bridge set-up were described by Wexler et al. [32]. Recently, it was shown that the application of an electric field of comparable magnitude to water in an electrolysis-less needle-plate set-up [33] induces a second-order phase transition [34] in the sense of Landau [35]. In the present work we highlight some of the macroscopic features of the bridge that have puzzled many authors over the years—scattering in the outer layer of the bridge which was first attributed to birefringence [36] or nano-bubbles [18], none of which turned out to be true. These scatter centers are reinvestigated here and explained in terms of an electrically induced liquid–liquid phase transition. Summarizing, the EHD related considerations of this work are based upon the work of Widom et al. [6], the electrochemical considerations on the paper of Sammer et al. [29], and the quantum field theory (QFT)-related physics is based on the work of Wexler et al. [32].

2. Materials and Methods

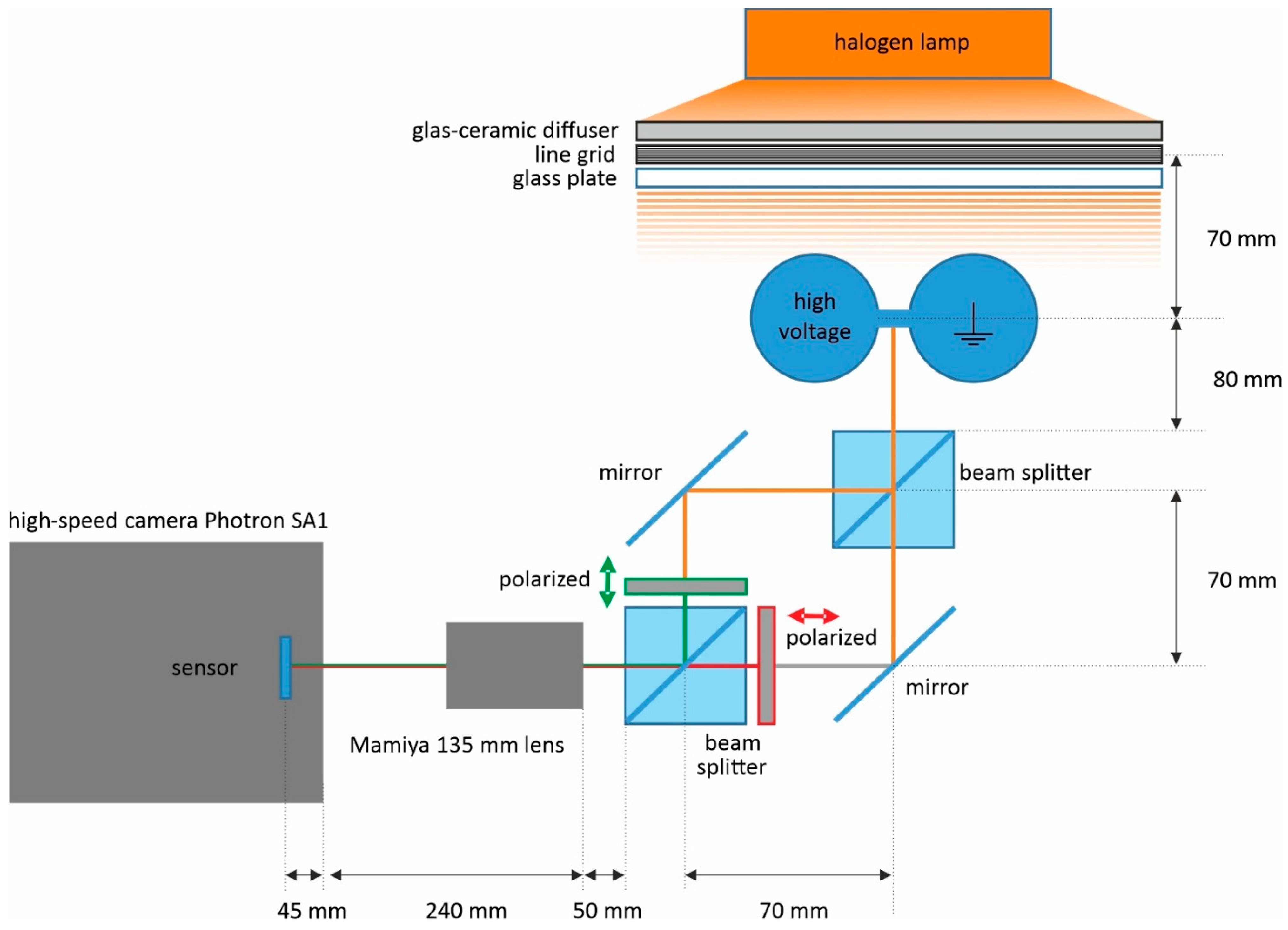
2.1. Experimental

The objective of this experimental investigation was to sample the bridge for refractive index variations and their possible polarization dependence. In order to do that, we made use of the optical properties of the bridge and imaged background fringes through a Mach–Zehnder interferometer (MZI) with each beam polarized differently.

A horizontal EHD bridge acts as a cylindrical lens [5] and refracts light. The refraction through such a cylindrical lens can be discussed by analytical ray-tracing using a system matrix A,

$$A=\left(\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right)=R_2{T}_{21}{R}_1$$

(1)

with T₂₁ being the transmission matrix between the 1st and 2nd refracting surface of the bridge with the geometrical distance d₂₁ and the refractive index n_t in between (for small angles of incidence, $\tan \alpha \approx \alpha$),

$$T_{21}=\left(\begin{array}{cc}1& 0\\ \frac{d_{21}}{n_t}& 1\end{array}\right)$$

(2)

R₁ the refraction matrix for refraction at the 1st interface,

$$R_1=\left(\begin{array}{cc}1& -D_1\\ 0& 1\end{array}\right),$$

(3)

and D the diopter of a single refracting surface,

$$D=\frac{n_t-n_i}{r},$$

(4)

and r the radius of curvature, while n_i and n_t indicate the refractive indices for the incoming and transmitted light rays, respectively. This approach is related to the concept of optical path length OPL, so the geometrical length d and the refractive index n are the characteristic quantities. From the system matrix A one can derive the focal length f of the lens the bridge represents,

$$a_{12}=-\frac{1}{f}.$$

(5)

Here the focal length of the bridge is specified in air with n = 1. Therefore, the bridge projects a fringe pattern placed in the background into the image space in front of itself. Thus a real (upside-down) image of the background pattern will form in front of the bridge approximately half the diameter away from the bridge’s surface. With the above matrix it can be shown that the focal length of an aqueous bridge equals the diameter of the bridge. A purely horizontal line grid was chose in order to focus on the radial refraction only.

A floating water-bridge set-up was built according to Wexler et al. [32]. Two glass beakers (6 cm diameter, 3 cm height, 100 mL, borosilicate) were filled with 66 mL of deionized water (18.2 MΩ, Millipore Corp., Burlington, MA, USA), and two Pt electrodes (1 cm²) were submerged into these beakers connected to the high-voltage output of a DC power supply (HCP 30000-300, FuG Elektronik GmbH, Schechen, Germany). All measurements were performed at 16 kV with bridge lengths of approximately 10 mm and currents of 0.3 to 0.6 mA unless explicitly stated otherwise. The electrodes were placed in the center of the beakers.

An MZI was constructed as diagrammatically shown in Figure 1. As light source a 100 W halogen lamp was placed behind a ceramic glass diffuser onto which a grid was placed (grid spacing 6.4 mm; line thickness 5.5 mm) which was held in place by the glass plate. The resultant image was projected onto a 50 × 50 × 50 mm³ beam splitter cube by the bridge which acted as a cylindrical lens. The two emergent images were linearly polarized (horizontally and vertically, respectively), and then recombined with another 50 × 50 × 50 mm³ beamsplitter cube and projected onto the sensor of a high-speed camera (Photron SA1, Photron, Tokyo, Japan) with a 135 mm Mamiya lens (Mamiya Digital Imaging Co., Ltd., Tokyo, Japan). With the help of the MZI the differently polarized light waves were then sheared against each other (see Figure 2) which made distinction between the two polarization directions possible. The vertical shear was aligned with a needle tip, with no horizontal shear allowed. In the resultant image the two polarization directions showed different intensities, since the vertical polarization was reflected three times, whereas the vertical polarization was reflected only once. Images were collected at 5000 frames per second full frame resolution (1024 × 1024 pixels).

2.2. Electrohydrodynamic Simulation of the Bridge

The flow field in the water bridge was calculated by the laminar flow and the electrostatics module in Comsol 5.5 multiphysics software (Comsol Inc., Palo Alto, CA, USA) using a simple 2D model of the set-up with the Maxwell pressure [15] as volume force in the laminar flow module in combination with the electrostatics module. In detail, the electric field E is defined as the gradient of the electric potential V,

$$E=-\mathbf{\nabla }V,$$

(6)

and the displacement field was simulated using the Gauss law:

$$\mathbf{\nabla }·D=\mathbf{\nabla }\left({\epsilon }_0{\epsilon }_{r}E\right)={\rho }_V$$

(7)

with D being the electric displacement, $\mathbf{\nabla }$ the Nabla operator, ${\epsilon }_0$ the permittivity of the vacuum, ${\epsilon }_r$ the respective permittivity of the medium for a static electric field E, and ${\rho }_V$ the number of free charges per volume unit.

From these values the Maxwell stress tensor $T_{ij}$ was calculated (Equation (8)) and used in connection with the Navier Stokes Equation (9) where the density variation is assumed small and effects of buoyancy have been neglected,

$$T_{ij}={\epsilon }_0{\epsilon }_r{E}_i{E}_j-\frac{1}{2}{\delta }_{ij}{\epsilon }_0{\epsilon }_r{E}_k{E}_k$$

(8)

$$\rho \left(u·\mathbf{\nabla }\right)u=-\mathbf{\nabla }p+\mu {\nabla }^{2}u+\mathbf{\nabla }·T$$

(9)

where ${\delta }_{ij}$ is the Kronecker delta, µ the dynamic viscosity, and p the pressure.

2.3. Topological Changes in Electrically Stressed Water

Previous results from quasi-elastic neutron scattering [30], femtosecond mid-infrared spectroscopy [24], and Raman spectroscopy [33] strongly indicated that neither EHD flow simulation nor molecular dynamic simulations are sufficient to explain some of the macroscopic effects observed in the experiments mentioned. Among these are increased proton mobility and increased molecular vibrational relaxation in the bridge, as well as long-range vibrational coupling among water molecules. Based on experiments performed in an electrostatic experiment in bulk water [34] we developed a framework based on quantum field theory (QFT). While under thermal equilibrium molecular dipole vibrations are randomly oriented. By the influence of an electric field this random orientation is spontaneously broken, leading to an effect known as spontaneous breakdown of symmetry (SBS).

This result from previous work [34] can be interpreted in terms of Landau’s theory of phase transitions [35] which is best known for its application to magnets or superconductors. In this discussion we will use an (albeit limited) analogy to magnetism, a very well understood Landau-like phase transition. So, we will not discuss a structural change in the liquid, but rather a dynamic one between the dipole vibrational states of the water molecules involved.

In a magnet, below a certain critical temperature, T_C, the electron spins will align in either “up” or “down” direction, and the net magnetization becomes non-zero. When starting from a completely randomized situation there is nothing in the underlying physics that will decide in which direction the resultant magnetization will point, which is why this effect we wish to discuss is called spontaneous breaking of symmetry (SBS). Whereas a rotation of 180° of said magnet on an axis perpendicular to the magnetic field lines was a valid symmetry operation before the SBS with respect to the net magnetization, it is no longer the case after the SBS, since now such a rotation will change the sign of the net magnetization. So the new phase is missing a symmetry element, the symmetry is broken. Landau described this phase transition using the free energy of the system F,

$$F=U-TS$$

(10)

where U is the internal energy, T the temperature, and S the entropy of the system. F is a function of an order parameter, in this case the magnetization M. Landau defined F(M) simply as a power series,

$$F=F_0+a{M}^2+b{M}^4+\cdots$$

(11)

A thermodynamic equilibrium is reached when F is at a minimum, which relies on both maximizing the entropy S and minimizing the internal energy U. It is straightforward from Equation (11) that for a negative parameter, a, F(M) will have two equivalent minima, representing the “up” (M = +M₀) and “down” states (M = −M₀) of the spins (also known as “Lifshitz’s buttocks”), whereas the previous ground state M = 0 is now at a position of a metastable equilibrium. Since in quantum field theory every particle in a system can be considered an excitation of the vacuum, the occurrence of an SBS creates a new vacuum which can give rise to the emergence of new particles that did not exist before the SBS. Such particles are massless and are referred to as Goldstone bosons [35,37]. The Goldstone bosons condense in the (new) vacuum state, and the phase transition is complete.

In order to understand how this mechanism is at work in the water bridge, we have to consider the fact that water in its liquid state is not a ferroelectric crystal when undergoing a SBS. But, similar to the spins coupling in a magnet, in the water bridge the asymmetric stretch vibrations of water molecules can couple through the electromagnetic field of these dipole oscillations. Without an external static electric field applied to the water sample, there is no net polarization density, and the system of dipole oscillations is spherically symmetric concerning rotations. If, however, an external electric field is applied and penetrates the system, vibrational coupling occurs. The symmetry is reduced from spherical SO(3) (actually for the Lagrangian describing our system the isomorph special unitary group SU(2) is used) to cylindrical (actually to U(1)), and an SBS takes place. As explained above, this SBS gives rise to a new ground state, and of course, a new class of excitations of this ground state. During this SBS, and through combination with the gauge field (here the electromagnetic field from the oscillating dipoles), the Goldstone bosons condense in the ground state and the gauge field becomes massive, an effect which is referred to as the Higgs mechanism [35,37,38].

Such states present topologically non-trivial structures referred to as topological objects. The simplest topological objects are kinks, solitons, and vortices, depending on the dimensions involved [35]. They may be thought of as lumps of energy, and we will show that they are highly relevant for understanding the experimental observations described in the present paper. In the case of the water bridge, we observe these objects as ring-like vortices, formed at the onset of the bridge, then stretched and deformed while moving through it. In order to explain how and why these objects can be experimentally detected and why they form where they do, let us go back to the molecular view of the system. After the phase transition the liquid contains a large number of coupled vibrations (quanta) in the same (new) ground state. These Goldstone bosons can be described by a state designated as coherent by Roy Glauber [39], which by definition is an eigenstate of the annihilation operator. Examples for such states include the laser, where a large number of photons in a cavity obtain the same wave vector (in-phase correlation). In the water bridge the number density of bosons is large and their phase is no longer arbitrary but becomes well-defined. Thus the resultant topological phase not only contains a new ground state, we now also know that it is coherent in the sense that the emergent phase of the coupled asymmetric stretch vibrations is defined over macroscopic distances, and identifies as transverse optically active phonon-like sidebands to the asymmetric stretch mode observed in Raman spectroscopy [34]. This correlation implies a different interaction between the molecules when an external static electric field is applied to the water sample compared to the non-coherent state; in other words the polarizability and thus also the related refractive index are different compared to a non-coherent phase. This electrically induced liquid–liquid phase transition has been described before in detail [34], and for mathematical details the reader is kindly referred to that work and the papers cited therein for a deeper insight into SBS, the Anderson–Higgs–Kibble mechanism and the Nambu–Goldstone boson condensation [40].

In contrast to the mentioned electrostatic experiment in bulk water [34], in the water bridge we also have to consider variations of the macroscopic wave-function Ψ of this coherent state. These variations occur during the phase transition process and are caused by fluctuations in the external E field due to EHD instabilities. The Ginzburg–Landau approach brings us back to the free energy functional F of the system [41,42,43,44]. Calculating the extrema with respect to Ψ yields the stationary, non-linear Ginzburg–Landau equation,

$$\frac{\partial F}{\partial {\Psi }^{*}}=\left[\frac{1}{2m}{\left(-i\hslash \nabla -qA\right)}^2+{\mu }^2+\lambda {\left|\Psi \right|}^2\right]\Psi =0$$

(12)

The first term in the right-hand side is the kinetic energy and contains the mass of the state m, its charge q, and the electromagnetic vector potential A. ${\mu }^2$ and λ act as mass term and coupling constant, respectively. The Haken interpretation for the lasering process provides a vivid picture of the phase transition by identifying ${\mu }^2$ as pump parameter starting the coherent laser process (in our case, the transition to the coherent phase regime).

In the non-stationary phase transition regime, the derivative $\partial F/\partial {\Psi }^{*}$ is no more equal to zero, in contrast to the stationary case of Equation (12). It is indeed non-vanishing while approaching the free energy minimum. As a result, the so-called time-dependent Ginzburg–Landau (TDGL) [41,42,43,44] equation is obtained

$$i\hslash \frac{\partial \Psi }{\partial t}=\widehat{H}\Psi -\frac{i}{\gamma }\frac{\partial F}{\partial {\Psi }^{*}},$$

(13)

with $\widehat{H}$ the Hamiltonian of the coherent state. The second term on the right-hand side describes the dissipative contribution and includes the relaxation parameter γ. This second term vanishes when the stationary regime is reached. A more detailed discussion of Equation (13) is given elsewhere [41,42,43,44], and reveals how the phase transition begins with an abrupt, adiabatic event, often called the null spike due to its extreme spatiotemporal localization. This singularity constitutes the core whence a vortex starts to form with the new phase emerging around the singularity. As can be seen from Equation (12), the boson condensation in water requires a permanent energy input from the forcing electric field, while the process of reaching the new state involves a rearrangement of the internal energy density content, resulting in the non-thermal equilibrium of the new coherent state [34]. Thus, any instabilities in the external electric field E will trigger a new ground state configuration. Due to the non-linearity of Equation (13) strong local variations in condensate density will result. The vortex equation is indeed obtained from the TDGL Equation (13) (for the detailed derivation cf., e.g., [42,43]).

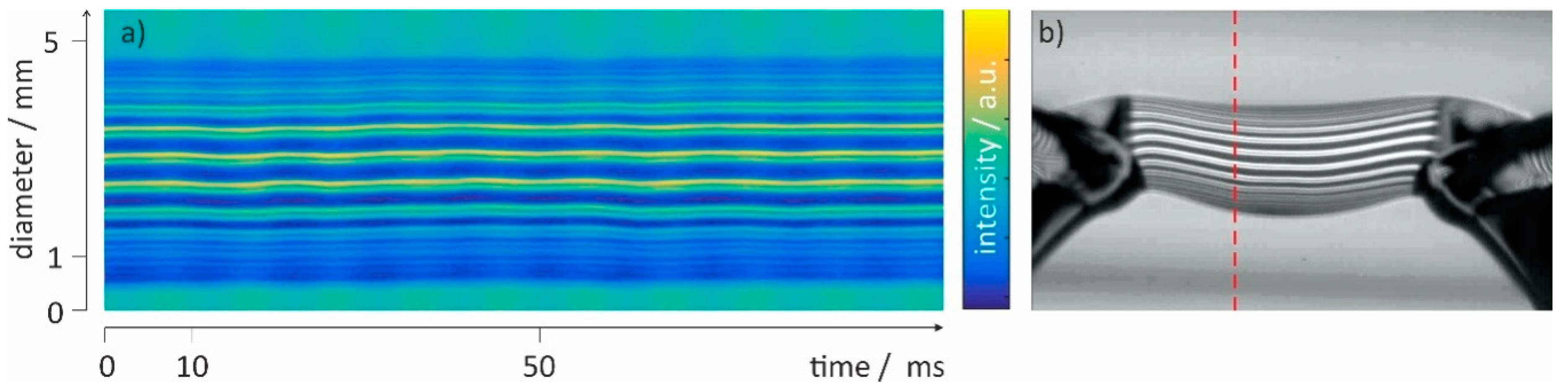
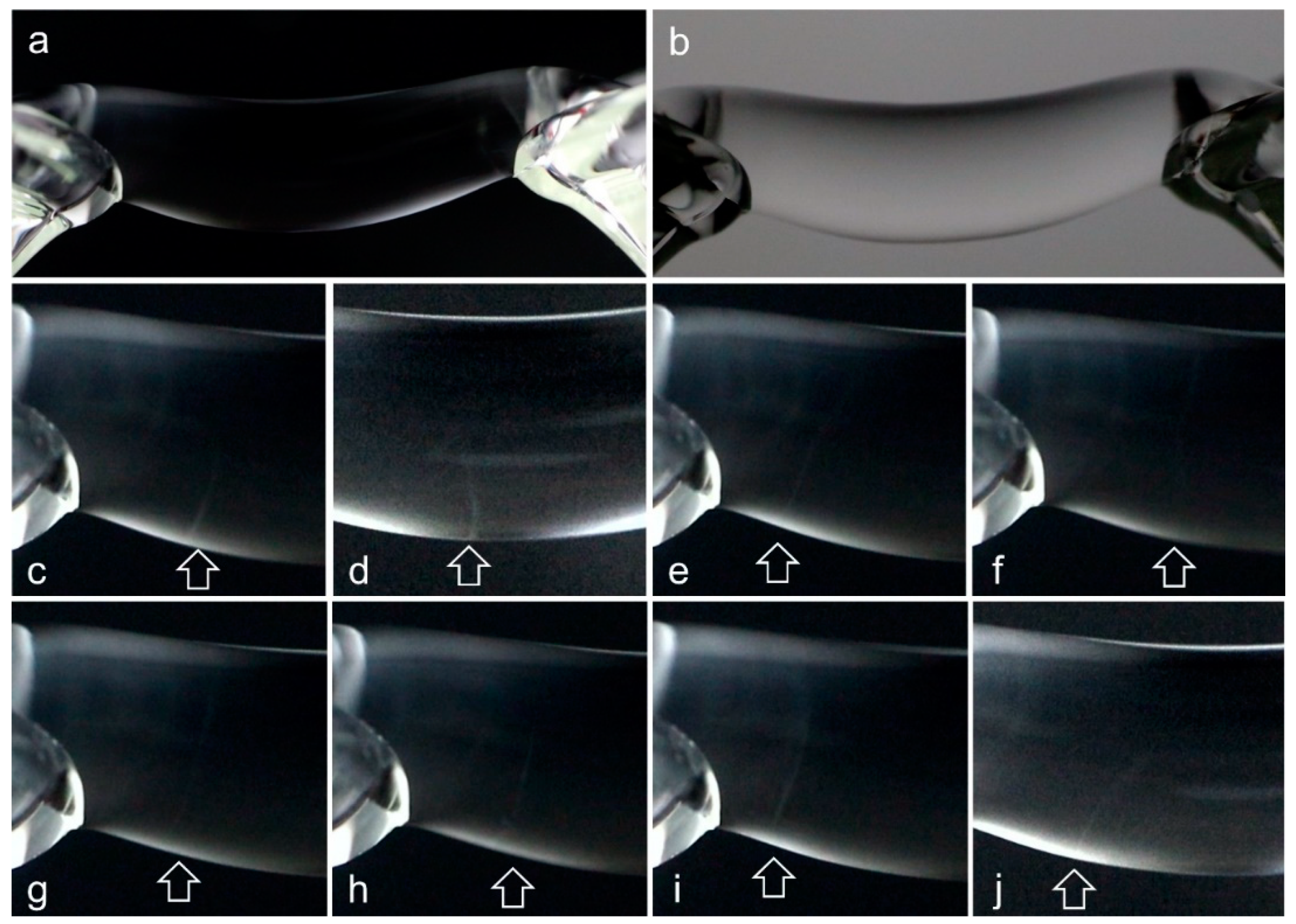
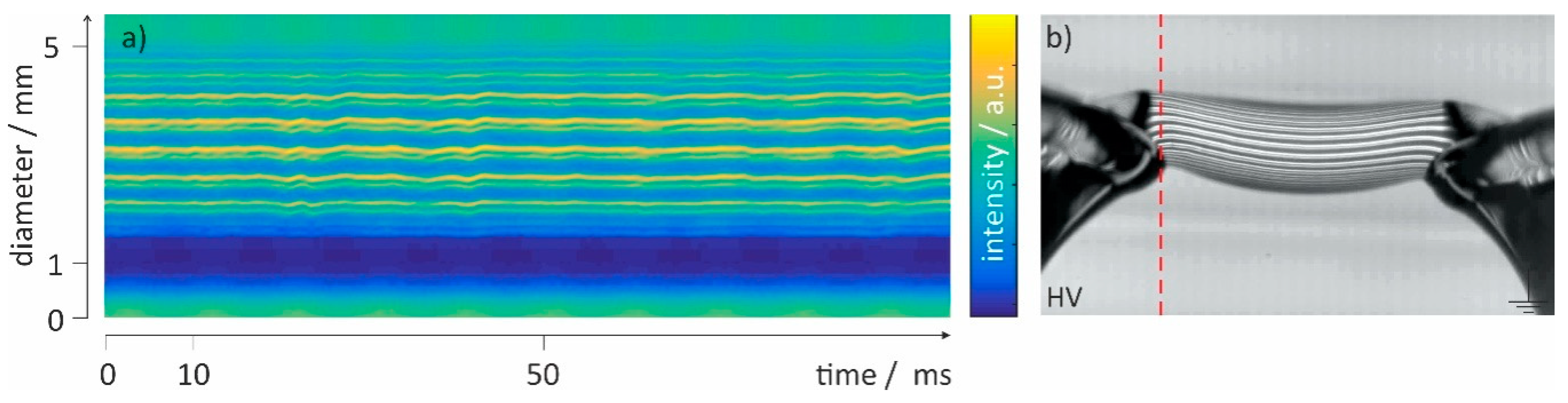
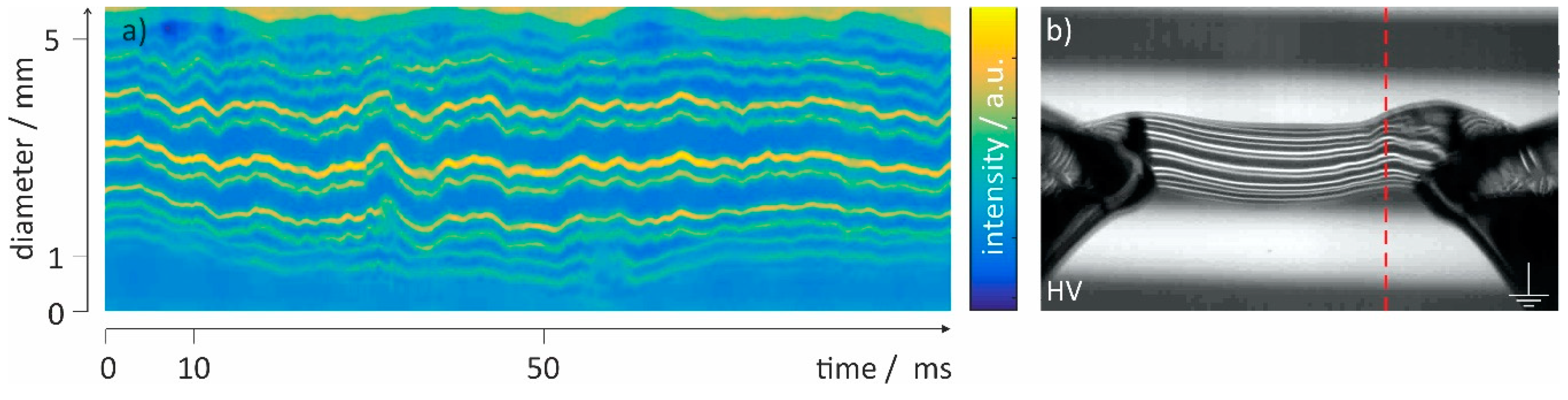
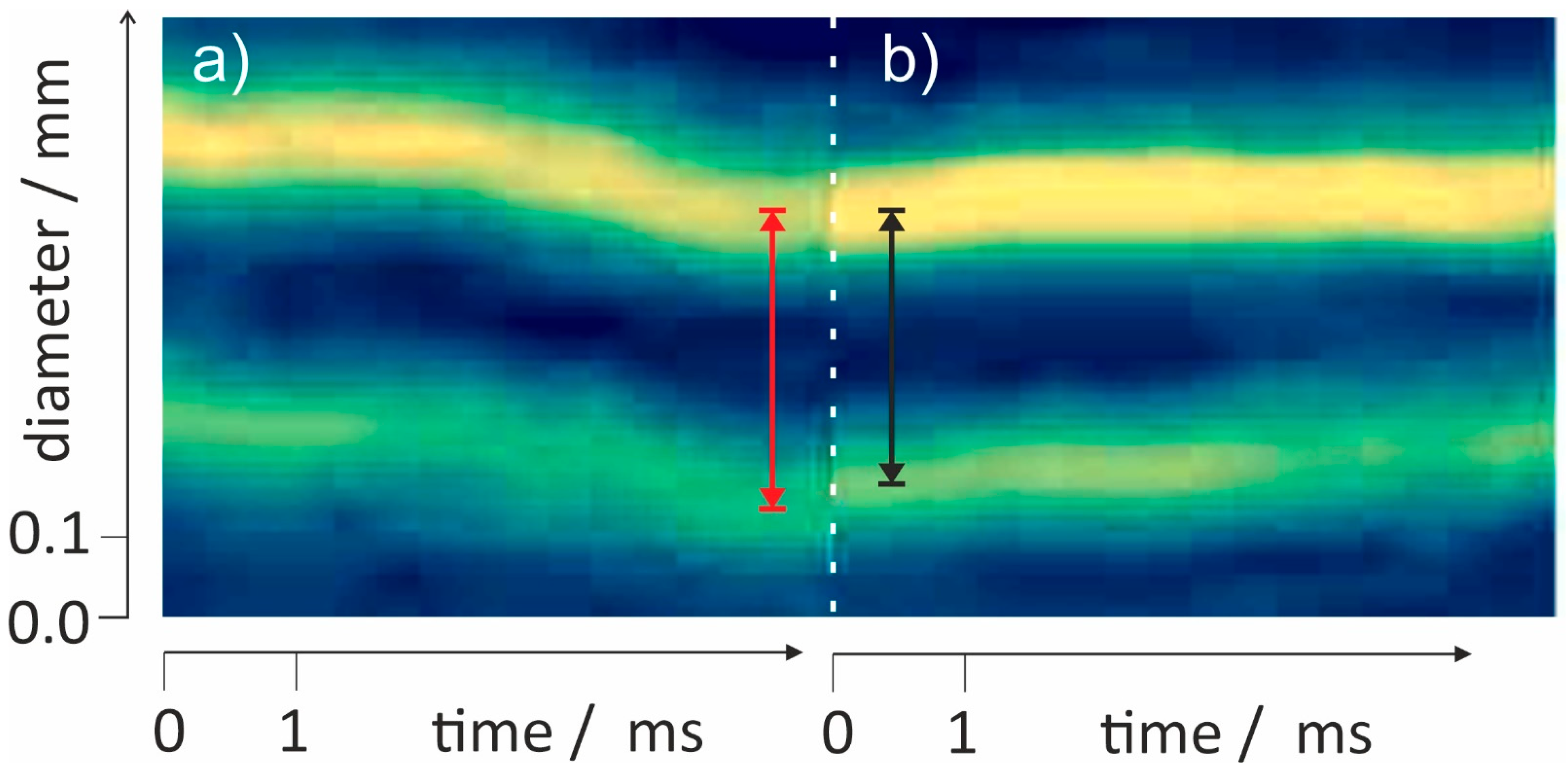
3. Results and Discussion

It has been shown experimentally [45] that EHD fluctuations at the transition points between bridge and bulk produce oscillations of about 100 Hz that travel through the bridge at flow speed. These shear layer oscillations between incoming charged flow and outgoing discharged flow are triggered by the minimal 50 Hz waviness still being present in the output of the high-voltage DC power supply. We have simulated this situation for a 19 kV bridge using the waviness given by the specifications of the manufacturer of the power supply, ±0.05% or, in this case, ±9.5 V, resulting in velocity variations up to 0.6 mm/s. This amount is too small to destabilize the bridge, but sufficient to trigger resonance effects in the shear layer. Moreover, since a change of diameter has a direct impact on the electrical current, the ripple causes a feed-back loop with the power supply amplifying the effect. In order to elucidate this situation we calculated the flow field for a 19 kV ±1% bridge as shown in Figure 3. In Figure 3b a vortex is clearly visible, as also found experimentally [45]. For the visualization of the flow field changes due to voltage variations we chose to depict the vorticity $\mathsf{\omega }$, a pseudo-vector field that describes the local spinning motion of a continuum or its tendency to rotate, and it is defined as

$$\mathsf{\omega }\equiv \mathbf{\nabla }\times u,$$

(14)

where $u$ is the flow velocity vector and $\mathbf{\nabla }$, the Nabla operator.

When the waviness of the power supply causes a back-and-forth movement of these local vorticity as shown in Figure 3c, small 100 Hz (squared amplitude of 50 Hz) pumping oscillations propagating through the bridge are the result. This effect has been reported before [45], and using the MZI visualization method described, this waviness was also observed in the present work as can be seen from the time–space plot created for radial sections defined by the column number in the frames as shown in Figure 4. Because a halogen lamp was used as light source, the 100 Hz intensity fluctuation caused by the lamp operated at 230 V/50 Hz can serve as reference for these pumping oscillations changing the bridge diameter (“ripples”) and thus the OPL and refraction R. These variations in R cause a periodical shift in the vertical position of the fringe pattern imaged (see Figure 4).

Next to these very regular oscillations, highly irregular ones can also be observed, as shown in Figure 5. In this figure, the bridge is imaged between two crossed polarizers (Figure 5a) and with normal illumination (Figure 5b). It is easy to recognize regions where light is reflected by the bridge or the beakers since these regions appear bright between polarizers (Figure 5a) and dark under normal illumination (Figure 5b).

However, there are very fine vertical lines in the bridge in the above images that have no dark correspondence in the images without the crossed polarizers (Figure 5c–j). Their scattering signal was weak, which is why we could only see them using single photographs with a Canon 250D DLR camera, whose sensor is much more sensitive than the one of the SA-1 high speed camera. These lines are due to scatter centers moving from anode to cathode. They appear more often in bridges operated at higher potentials (~19 kV) and low conductivity (freshly deionized water ≥ 18 MΩ) in addition to the aforementioned waves. In long time exposures these structures add up and appear foggy, first attributed to nano-bubbles [18,19], which turned out not to be true [46].

In the projected fringe patterns, these highly irregular structures appear as spikes in the otherwise horizontal fringes. They are visible all over the length of the bridge but are most pronounced close the spout of the beaker at high potential. In contrast to the 100 Hz waves discussed before, the spikes have no equivalent oscillations in diameter, which would be otherwise seen along the surface. With the diameter being unchanged it is only the refractive index which can vary to produce these spikes. This phenomenon is shown in Figure 6.

As can be seen from Figure 6, the spikes can change the refraction so strongly that the image of the line pattern gets fuzzy at the position of the spikes. This issue is due to the fact that with strong variations in refractive index, the focal length of the bridge varies locally and the projected image moves out of focus of the camera. The problem can be somewhat mitigated by optimizing the focus of the camera lens, but it cannot be avoided completely.

It is known [15,19] that too high a current heats up the water in the bridge and can destabilize it in the process. Such an unstable, hotter bridge is visualized in Figure 7.

This figure shows that the spikes can occur at a higher frequency than the surface oscillations in unstable bridges with unstable vortices forming. Moreover, sometimes we observed that the differently polarized line patterns do not move in parallel which could indicate a local occurrence of birefringence. This is highlighted in Figure 8 where the line distance from a region within a spike (left) is compared to the line distance where there is no spike (right), taken from Figure 7. Compared to Figure 7, in this figure the contrast was enhanced in order to improve visibility. It should be noted that the displacement is very small and was only observed in unstable bridges with pronounced spike events. However, the onset of birefringence—the directional dependence of the relative permittivity, here due to effects involving the electronic polarizability [47]—was observed in previous experiments only very close to a needle charged with 20 kV. So another explanation for this variations in fringe displacement could be a very small horizontal misalignment which would show the greatest effect in steep gradients of the spikes.

While the regular surface wave observed at 100 Hz frequency can be discussed in terms of EHD, these irregular spikes deserve a closer look.

In order to locate and describe this phase transition in the water bridge experiment, we first need to point out both similarities and differences between the aforementioned experiment using a needle-plate set-up [34] and the water bridge. There are two important differences:

(1)

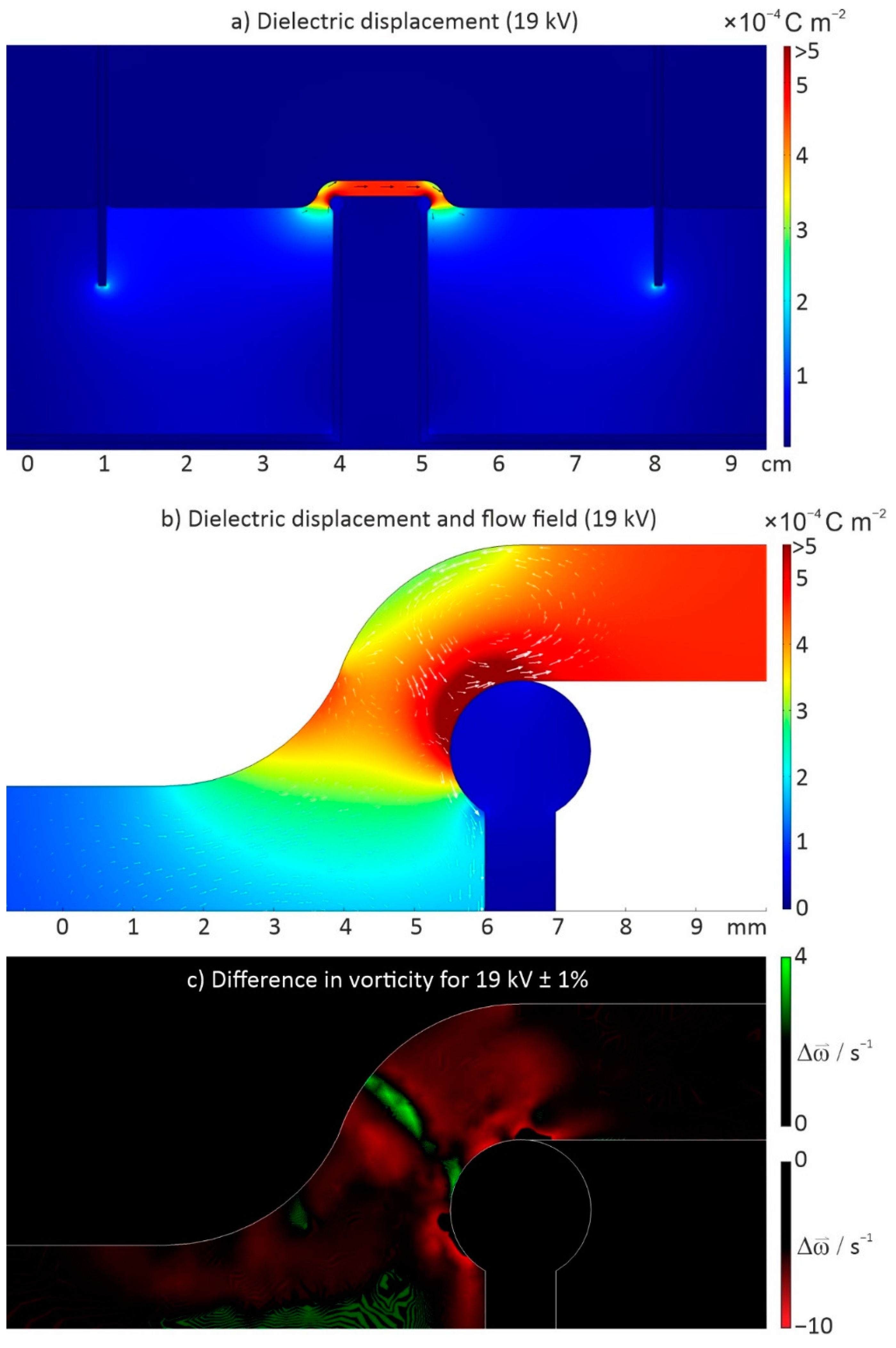
In the needle-plate set-up the water stands still, whereas in the water-bridge set-up there is a continuous electrohydrodynamic flow. Since the hydrodynamic flow and the electric field are intrinsically coupled, small variations in the flow create variations in the field and vice versa. As can be seen from Figure 3, the electric field density is highest in the bridge. Whereas the potential barely changes within the beakers, it drops drastically across the bridge where the dielectric displacement is maximized. The phase transition thus occurs when water enters or leaves the bridge, since at these points the gradients are highest.

(2)

In the water-bridge setup the EHD flow also carries charge whereas in the needle-plate set-up the external field induces a phase transition without internal disturbances. In the water bridge, the boson condensate is locally distorted by hydrated, electrolytic protons flowing through the bridge from anode to cathode. Such distortions can, in principle, be separated into three distinct situations:

(a).

Suppose the influence of the disturbing charges is weaker than the Goldstone correlation strength among dipoles in the ground state. In this case, according to the low energy theorem [48], the correlation cannot be disturbed.

(b).

Suppose the disturbing field from local charges to be much stronger than the dipole correlation field. In that case any correlation is immediately destroyed, and a phase transition cannot be induced. This situation has been observed experimentally as EHD instabilities in the water bridge due to the addition of ions, which result in the destruction of the liquid bridge [49].

(c).

The disturbing charge field is locally restricted and dampens the SBS locally. This is most likely the case in the water-bridge set-up. Here, the electrically induced phase correlation between the molecular vibrations forms periodically, or stochastically, due to variations in the charge density caused by the changes in vorticity shown in Figure 3c. As a result a flow of phase transitions according to the nonlinear time-dependent Ginzburg–Landau Equation (13) is observed.

From previous experiments [33,34] it is known that spike-like refractive index changes similar to the ones observed in the present experiment (see Figure 4, Figure 5 and Figure 6) occur in a needle-plate set-up when the high voltage is switched on or off, so during the electrically induced phase transition. These spikes are the kinks, solitons or vortices discussed earlier, and partly consist of both phases. They are indicative of the process of the phase transition, not the electrically induced phase itself. Since these spikes can be seen correlated all over the diameter, the underlying structure must be disk- or ring-like, but rather ring-like due to the local topological singularity defined at zero radius along the bridge axis [34].

Whereas, in the needle-plate set-up this transition only happens when the high voltage is turned on (or off) [33], in the water bridge it happens continuously to the water passing the points of highest field gradients, the location of which is at either end of the bridge nearest the rim of each beaker from which the bridge is suspended. Within the beakers themselves the electric field is almost uniform, as has been both measured [45] and simulated before in two [15] and three dimensions [50,51]. Thus, it is reasonable to expect that the topological structures are created at these points. They will be stretched and blurred while moving through the bridge, but as explained earlier, they decay slowly, which is why they are still detectable inside of the bridge, but more clearly close to the onset of the bridge as we have indeed observed experimentally. The more unstable the bridge, the more spikes will be observed due the EHD fluctuations in E, which is the driving pump for the transition.

In the experiment discussed we sample refractive index variations by an incident light-wave. As light passes through the bridge the incident electromagnetic wave induces an oscillating dipole moment in the molecules. In water the relation between the refractive index n, the number density N, and the (electronic) polarizability α is given by

$$n^2=1+\frac{N\alpha }{1-\left(\frac{N\alpha }{3}\right)}.$$

(15)

Since $\alpha$ is a frequency-dependent complex number, the polarization is phase-shifted compared to the incident wave, resulting in a new wavefront with an apparent lower speed due to this interaction. The refractive index signifies the ratio between the speed of light in vacuum and this wavefront speed. When light interacts with a single water molecule, the induced polarization of the nearest neighbors must be considered as well, increasing the cross-section of interaction by an additional expression in the denominator. Equation (15) is the well-known Clausius–Mossotti relationship [52]. It is important to note that $\alpha$ used in this equation characterizes the forced electronic dipole oscillations by the forcing alternating electric field from the light-wave, with frequencies in the THz range. For water, such an interaction results in a refractive index around 1.33.

Let us now examine the strong variations in refractive index as indicated by the spikes in Figure 6, Figure 7 and Figure 8. When the molecules are electrically pre-stressed by a static electric field of sufficient strength, the polarization of the ensemble becomes directional and birefringence occurs (Kerr effect). However, in the present experiments the electric field is too low in magnitude to orient the permanent water dipoles against thermal motion [21,22] or pre-stress the electronic orbitals enough to show a directional dependence of the (electronic) dipole oscillations enforced by the sampling light-wave. This is why no significant birefringence is observed (as shown in Figure 8).

Another possible explanation for gradients in refractive index are temperature fluctuations and their accompanying density variations. However, in none of the many thermographic recordings from previous research, ring-like structures in temperature had been observed [19]. On the contrary, the IR emission can be well described by more or less uniform ohmic heating and non-ohmic emission from proton conduction [31], the water flow through the bridge shows a clearly visible turbulent motion in all thermographic recordings. On the other hand, gradients in local density influencing the refractive index so severely would cause structural changes which have never been reported from experiments (see for example the X-ray studies reported elsewhere [46]).

These observations leave us with an important question: Where does the significant fluctuation in refractive index in the ring-like spikes, which cannot be explained classically, come from? A possible answer is the strong local variations in the emergent phase of coupled molecular stretch vibrations, identified as transverse optically-active phonon-like states [34]. Together with Equations (12) and (13) these variations in the condensate density are likely to be triggered by instabilities in the electrostatic field E applied to the water in the bridge. Due to the non-linearity involved in the time-dependent Ginzburg–Landau regime, such instabilities in pumping must [33] trigger strong spike-like variations in the emergent phase. Since in-phase coherent correlation of dipole oscillations consequent to SBS is also responsible for a change in material properties (as shown in previous experiments [18,24,30,33,34]), in-phase collective mode will certainly increase the cross-section for the interaction with light-waves at the frequencies used in this experiment. This suggests that the topologically non-trivial boson condensate regions may contribute to the optical detection with an effective polarizability term, say ${\alpha }_{SBS},$ to the refractive index.

4. Conclusions and Outlook

A floating water bridge represents a simple, straightforward example of a dynamic second-order phase transition. We have shown that water undergoes this phase transition when entering (and leaving) the bridge due to the action of an external electric field gradient, resulting in a breakdown of rotational symmetry of the water dipole oscillations. Variations in phase transition are identified by the appearance of strong distortions of the refractive index (spikes) generated at its suspension points. Previous experiments show that the new, electrically induced phase differs both macroscopically (e.g., visco-elastic behavior [14,19]) and microscopically (enhanced proton mobility [30] and in its hydrogen bond strength [24]) from bulk water. As demonstrated before in a simpler system [34] the massive electromagnetic field and phonon conserved polarization currents generate enhanced collective behavior among water molecules over macroscopic length scales. These elementary excitations manifest as a new, electrically induced phase of liquid water. With the present findings we show that it is possible to not only establish long-range dynamic order in liquid matter, but that this order manifests itself as a macroscopic, dynamic object of defined topology