Using Long Term Simulations to Understand Heat Transfer Processes during Steady Flow Conditions in Combined Sewers
Abstract
1. Introduction
1.1. The Need for Modeling Heat Transfer in Sewers
1.2. Complexity of Modeling Heat Transfer in Sewer Pipes
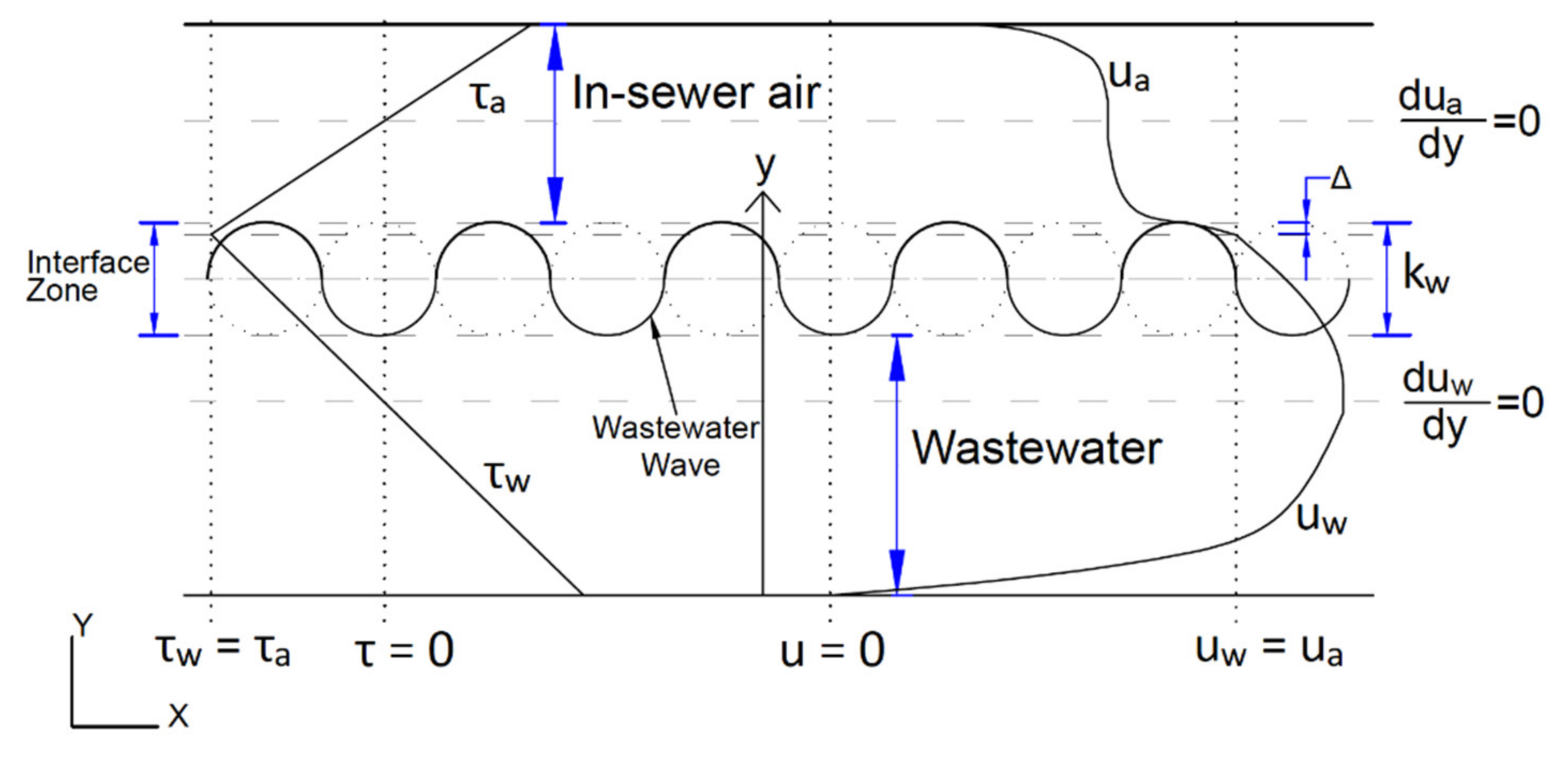
1.3. Challenges Associated with Modeling In-Sewer Air Velocity
1.4. Introducing a New Parameterisation for the Heat Exchange between Wastewater and In-Sewer Air
1.5. Taylor Diagram
1.6. Novelty, Aim and Objectives
- Analyse the fluid dynamics at the interface between wastewater and in-sewer air to develop a dimensionless heat transfer parameter;
- Utilise long-term measured seasonal datasets for calibrating the new parameterisation for the heat transfer coefficient;
- Compare the accuracy of the new model developed in this paper and existing models by employing advanced analysis techniques, e.g., the Taylor diagram.
2. Methodology
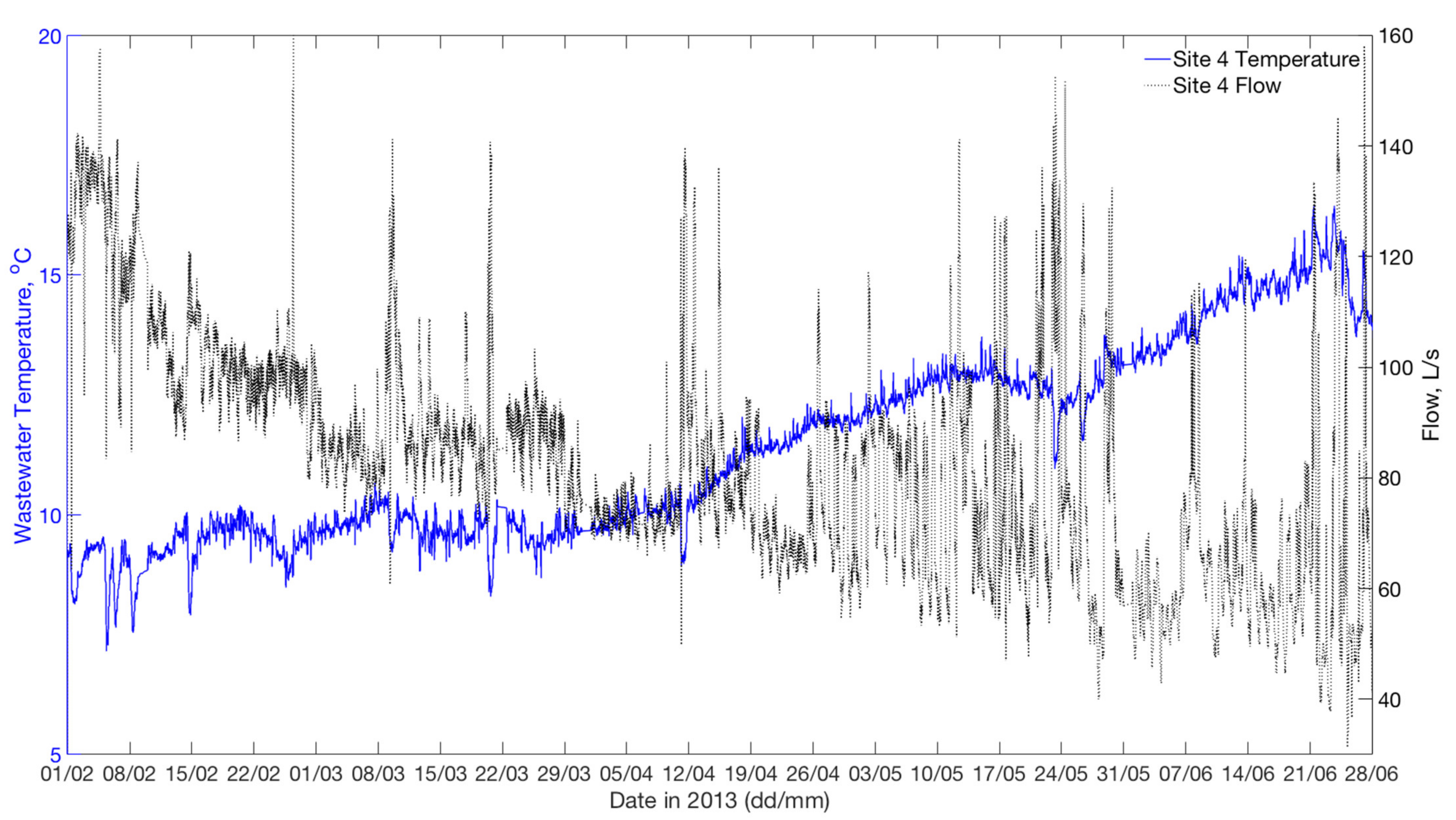
2.1. Data Collection
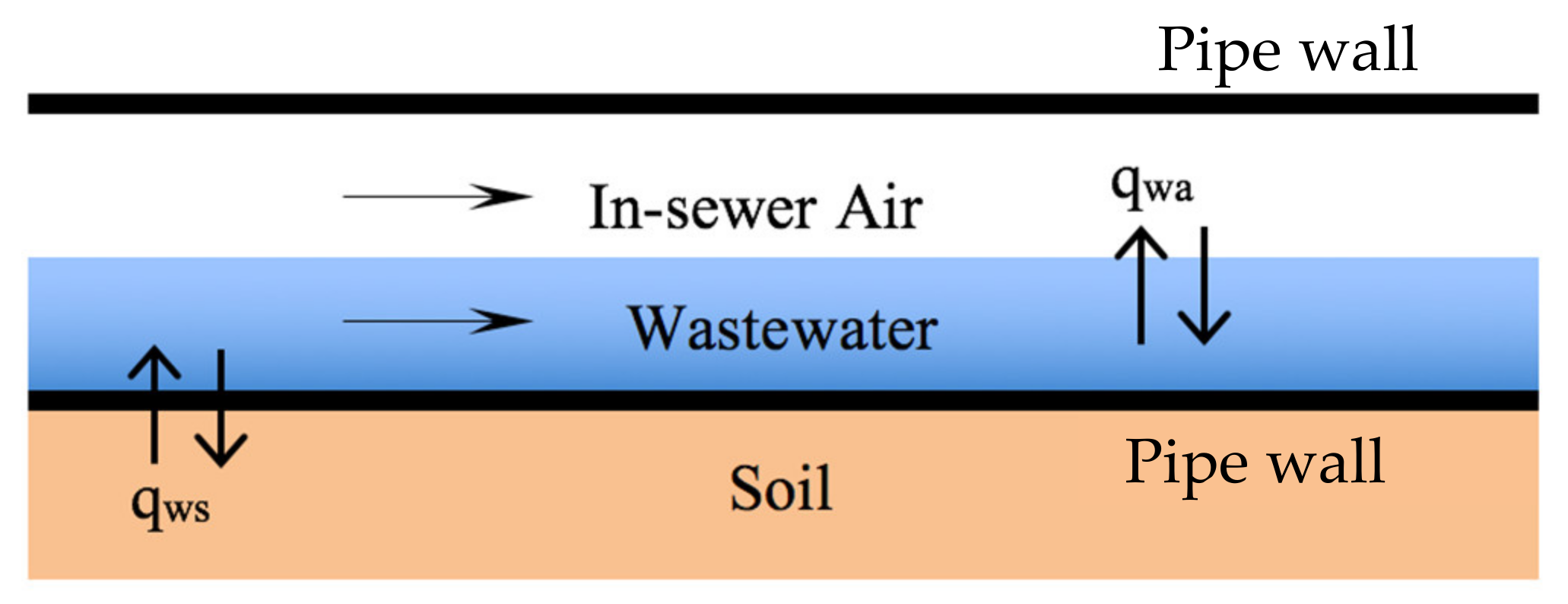
2.2. Existing Technique of Modeling Heat Exchange between Wastewater and In-Sewer Air
2.3. New Parameterisation for the Heat Exchange between Wastewater and In-Sewer Air
2.4. Modelling
2.5. Comparison with Existing Sewer Pipe Models
2.6. Calibration
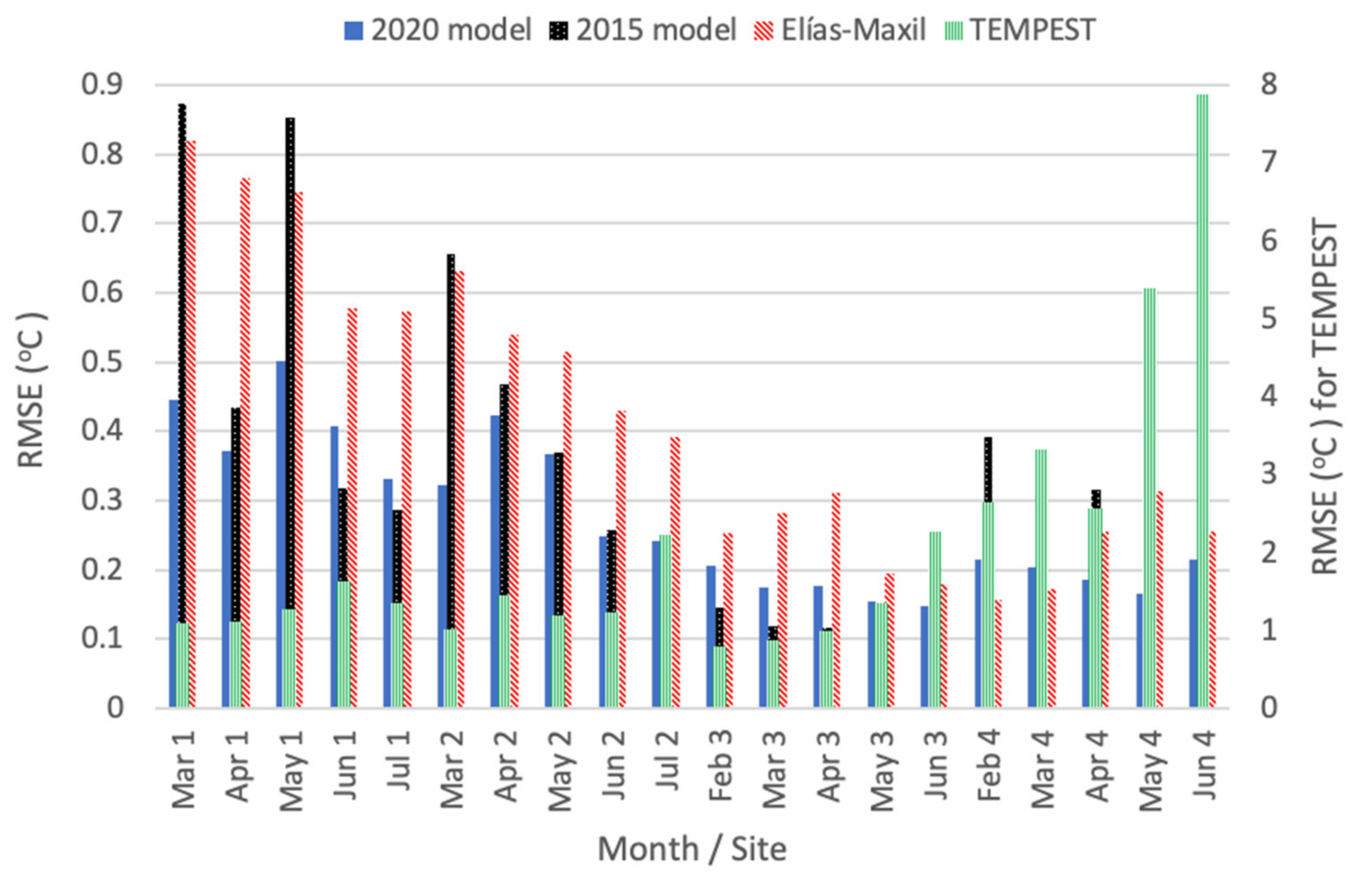
2.7. Summarising the Models’ Performance
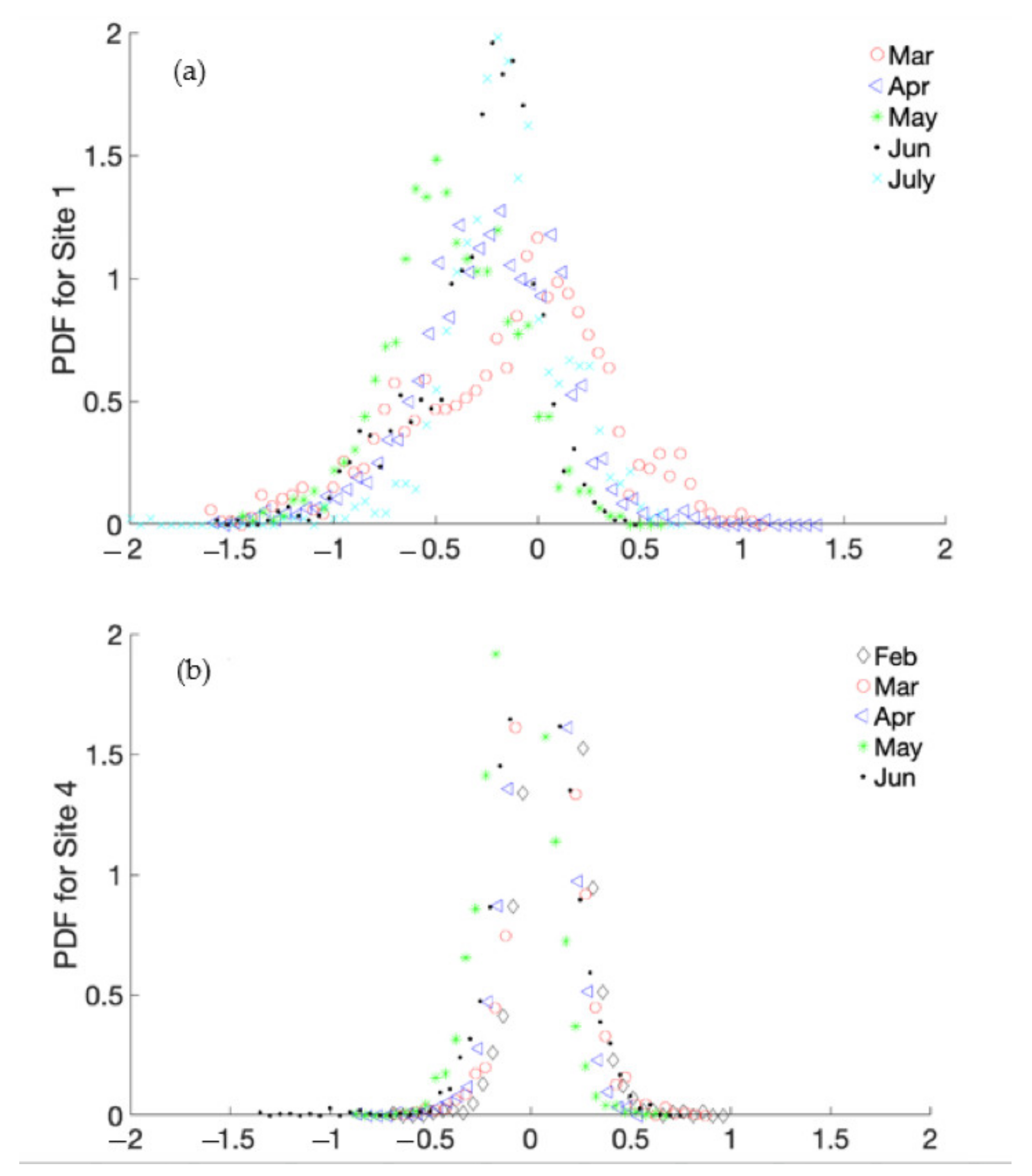
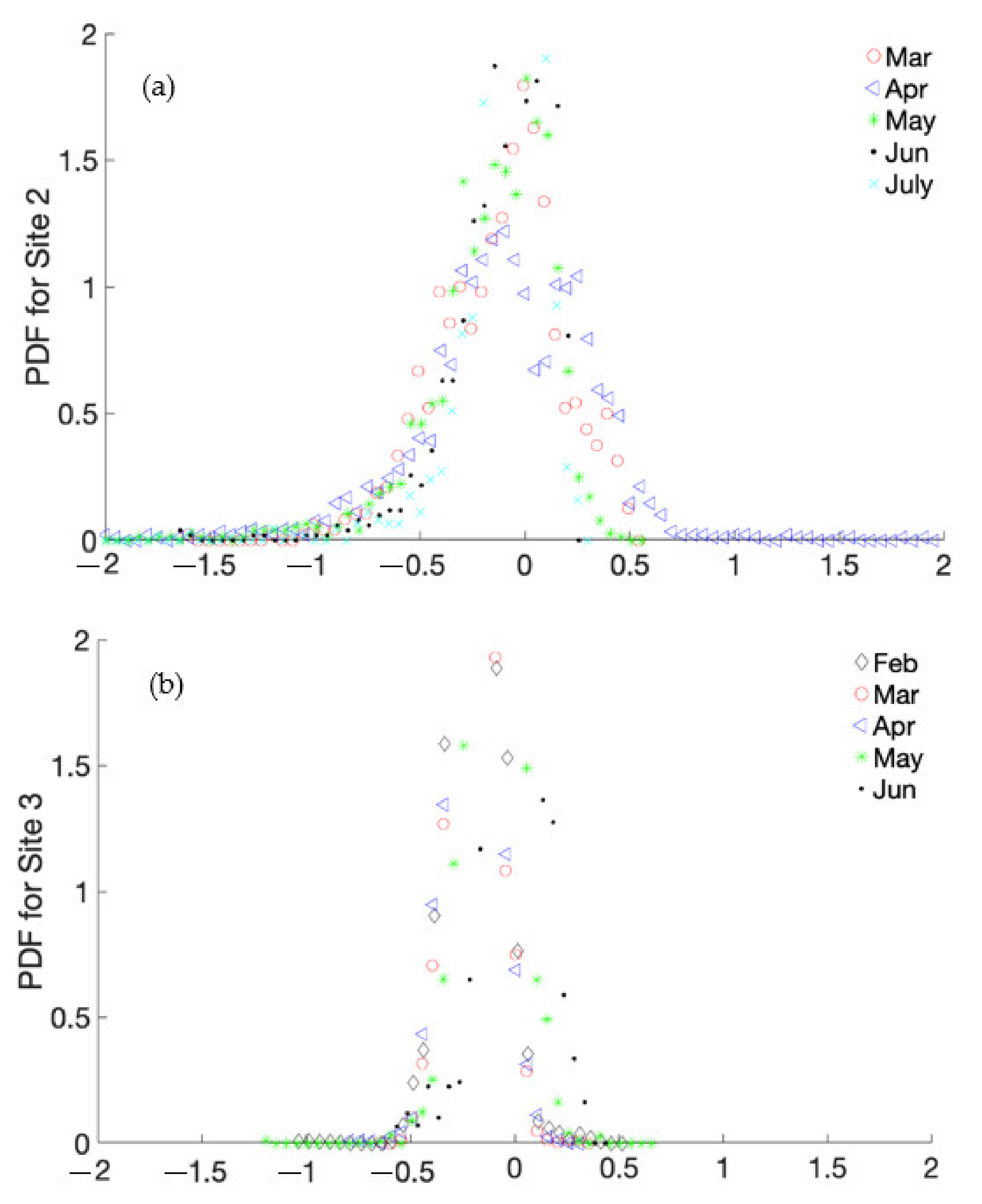
2.7.1. Probability Density Function (PDF)
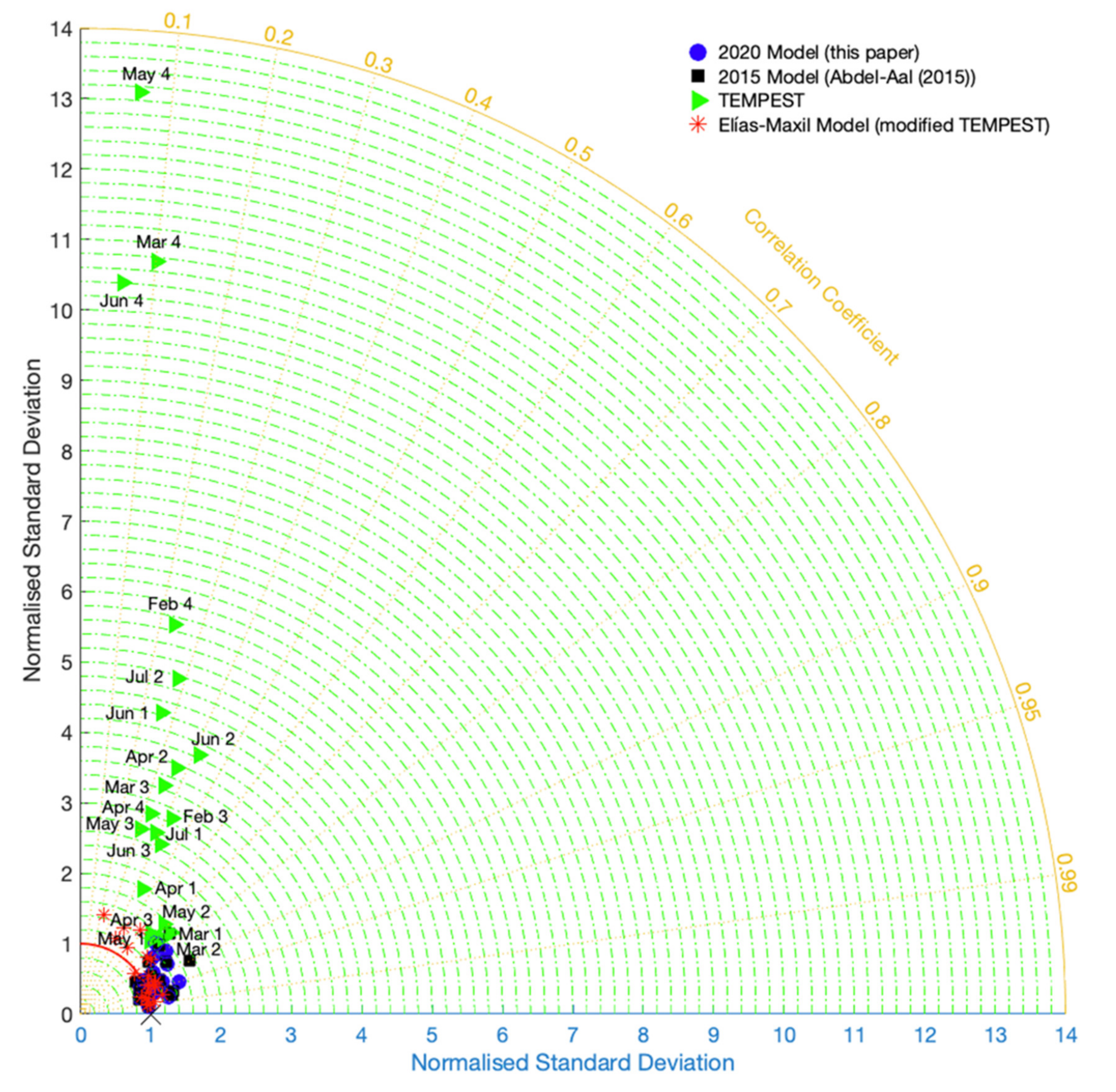
2.7.2. Taylor Diagrams
2.8. Estimating the Significance of the 2020 Model on a Sewer Network
3. Results
3.1. Calibration Results
3.2. Validation Results
3.3. Assessing Model Performance through the Taylor Diagram
3.4. The Significance of the 2020 Model in Estimating Potential Heat Recovery
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hao, X.; Li, J.; Van Loosdrecht, M.C.; Jiang, H.; Liu, R. Energy recovery from wastewater: Heat over organics. Water Res. 2019, 161, 74–77. [Google Scholar] [CrossRef] [PubMed]
- Bulteau, G.; Hoffman, J.; Fairhurst, R.; Orman, N. Energy from Sewers; 19/SW/03/1; UK Water Industry Research (UKWIR): London, UK, 2019. [Google Scholar]
- Schilperoort, R.P.S.; Clemens, F.H.L.R. Fibre-optic distributed temperature sensing in combined sewer systems. Water Sci. Technol. 2009, 60, 1127–1134. [Google Scholar] [CrossRef] [PubMed]
- Cipolla, S.; Maglionico, M. Heat recovery from urban wastewater: Analysis of the variability of flow rate and temperature. Energy Build. 2014, 69, 122–130. [Google Scholar] [CrossRef]
- Abdel-Aal, M.; Schellart, A.; Kroll, S.; Mohamed, M.; Tait, S. Modelling the potential for multi-location in-sewer heat recovery at a city scale under different seasonal scenarios. Water Res. 2018, 145, 618–630. [Google Scholar] [CrossRef] [PubMed]
- Durrenmatt, D.J. Berechnung des Verlaufs der Abwassertemperatur im Kanalisationsrohr (Calculation of wastewater temperature profiles in sewers). Master’s Thesis, Swiss Federal Institute of Technology (ETH), Zurich, Switzerland, 2006. [Google Scholar] [CrossRef]
- Dürrenmatt, D.J.; Wanner, O. Simulation of the wastewater temperature in sewers with TEMPEST. Water Sci. Technol. 2008, 57, 1809–1815. [Google Scholar] [CrossRef] [PubMed]
- Durrenmatt, D.J.; Wanner, O. A mathematical model to predict the effect of heat recovery on the wastewater temperature in sewers. Water Res. 2014, 48, 548–558. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Aal, M. Modelling the Viability of Heat Recovery from Underground Pipes- Deterministic modelling of wastewater temperatures in a 3048 sewer pipes network. Ph.D. Thesis, University of Bradford, Bradford, UK, 2015. Available online: goo.gl/bk3F66 (accessed on 2 November 2020).
- Elías-Maxil, J.A.; Hofman, J.; Wols, B.; Clemens, F.; Van Der Hoek, J.P.; Rietveld, L. Development and performance of a parsimonious model to estimate temperature in sewer networks. Urban Water J. 2017, 14, 829–838. [Google Scholar] [CrossRef]
- Pescod, M.; Price, A. Major Factors in Sewer Ventilation. J. Water Pollut. Control Fed. 1982, 54, 385–397. [Google Scholar]
- Edwini-Bonsu, S.; Steffler, P.M. Modeling ventilation phenomenon in sanitary sewer systems: A system theoretic approach. J. Hydraul. Eng. 2006, 132, 778–790. [Google Scholar] [CrossRef]
- Qian, Y.; Zhu, D.Z.; Edwini-Bonsu, S. Air Flow Modeling in a Prototype Sanitary Sewer System. J. Environ. Eng. 2018, 144, 04018008. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Space Phys. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Abdel-Aal, M.; Mohamed, M.; Smits, R.; Abdel-Aal, R.E.; De Gussem, K.; Schellart, A.; Tait, S. Predicting wastewater temperatures in sewer pipes using abductive network models. Water Sci. Technol. 2014, 71, 89–96. [Google Scholar] [CrossRef] [PubMed]
- Abdel-Aal, M.; Smits, R.; Mohamed, M.; De Gussem, K.; Schellart, A.; Tait, S. Modelling the viability of heat recovery from combined sewers. Water Sci. Technol. 2014, 70, 297–306. [Google Scholar] [CrossRef] [PubMed]
- Flinspach, D. Wärmelastplan neckar plochingen bis mannheim stand; Ministerium für Ernährun: Stuttgart, Germany, 1973.
- Schlichting, H.; Gersten, K. Boundary Layer Theory; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2003. [Google Scholar]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; J. Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Einstein, H.A.; El-Samni, E.-S.A. Hydrodynamic forces on a rough wall. Rev. Mod. Phys. 1949, 21, 520. [Google Scholar] [CrossRef]
- Romanova, A. Acoustic Monitoring of Hydraulic Resistance in Partially Filled Pipes. Ph.D. Thesis, University of Bradford, Bradford, UK, 2013. [Google Scholar]
- Mitchell, J.K.; Soga, K. Fundamentals of Soil Behavior; John Wiley & Sons, Inc.: New York, NY, USA, 1993. [Google Scholar]
- MATLAB 2020 (software). Find Minimum of Constrained Nonlinear Multivariable Function; The MathWorks Inc.: Natick, MA, USA, 2020. [Google Scholar]
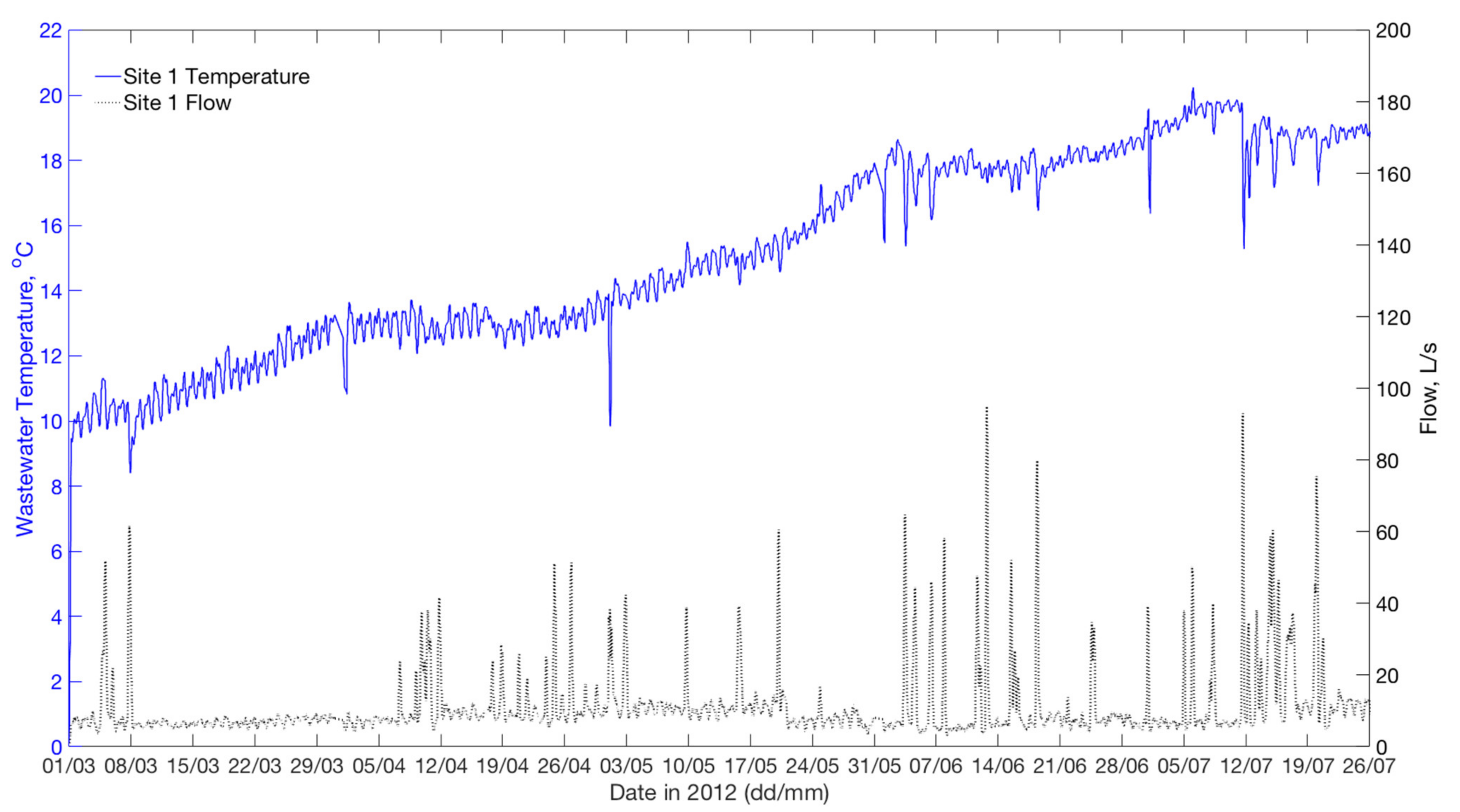
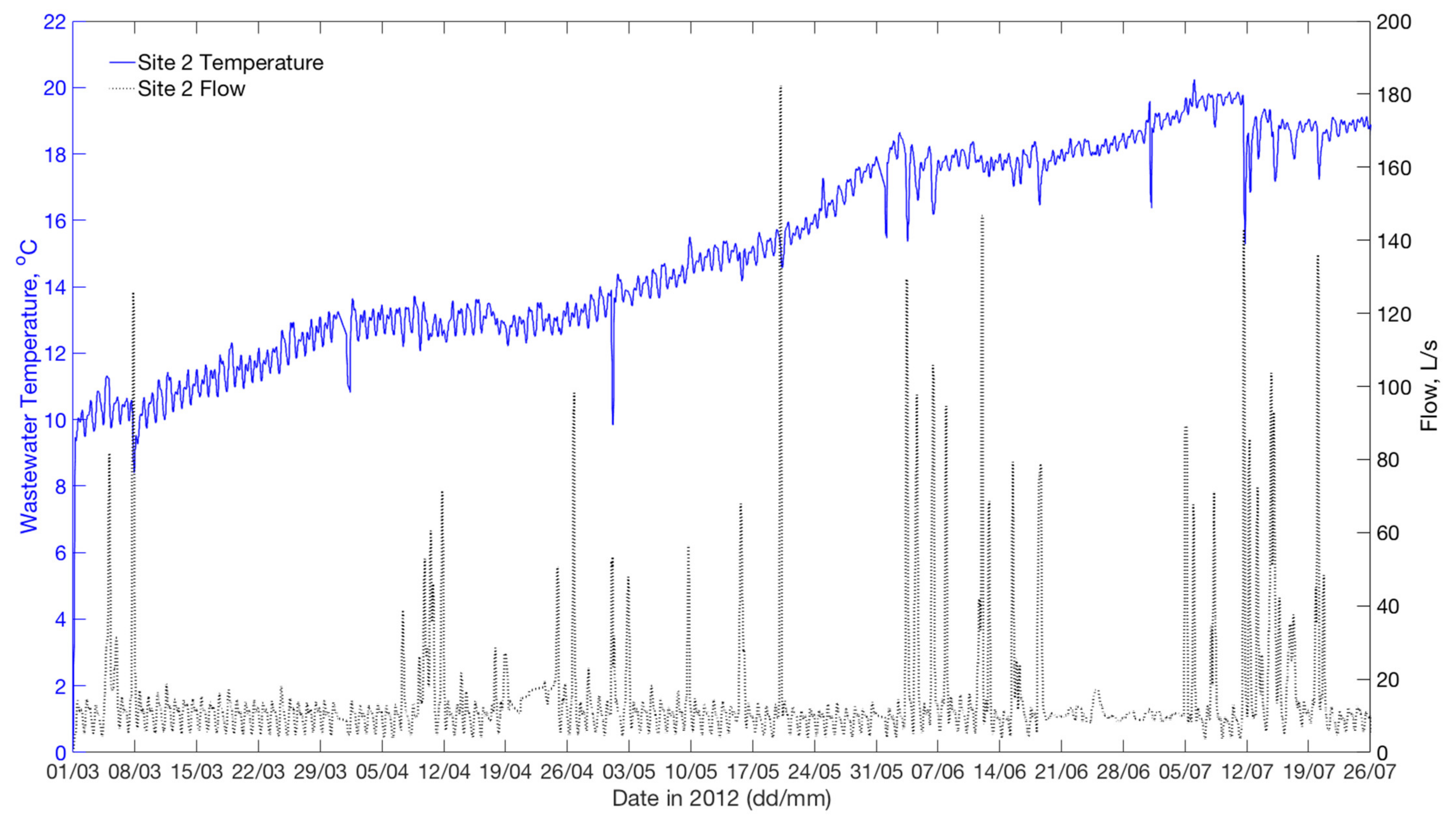
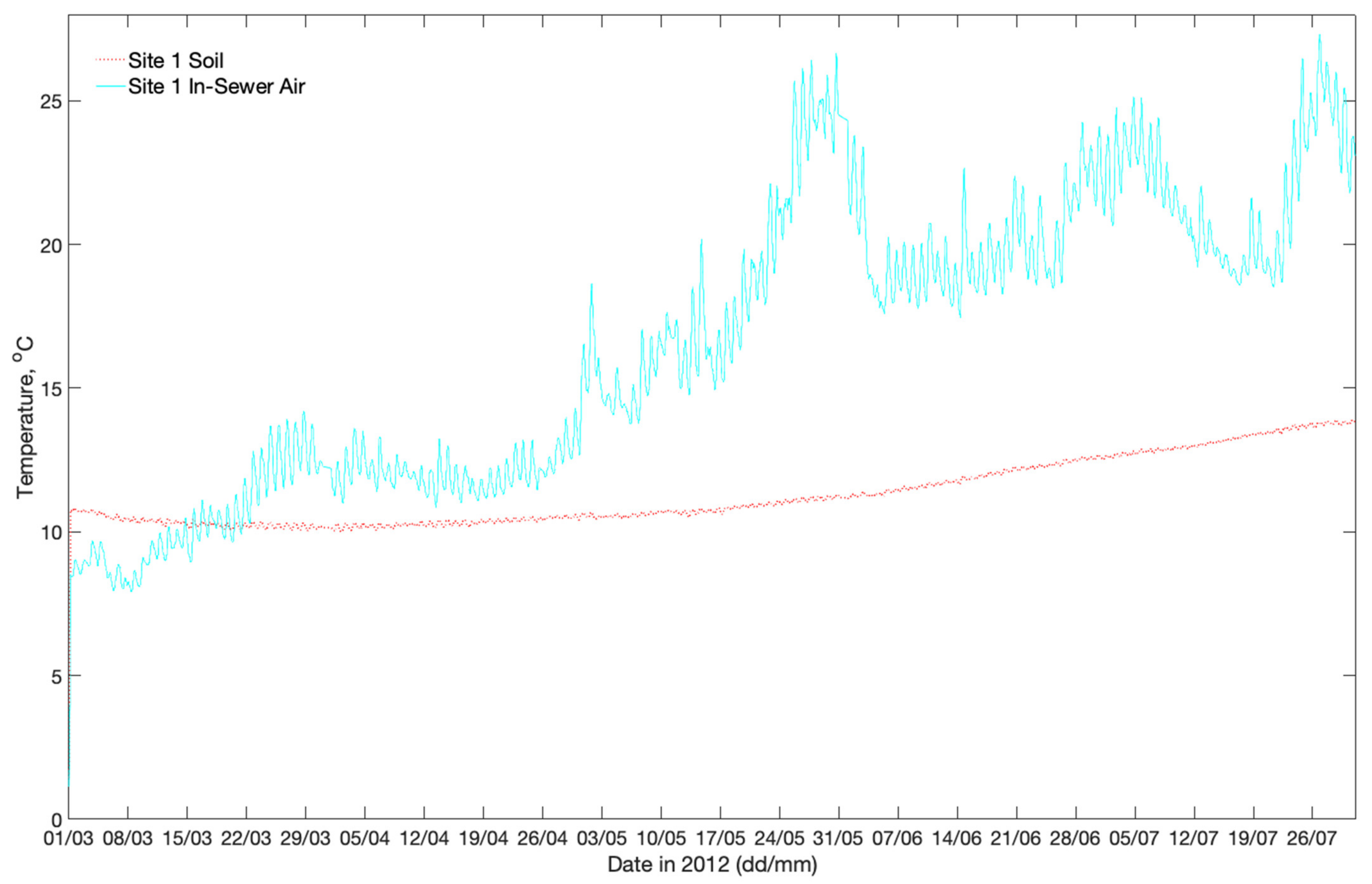
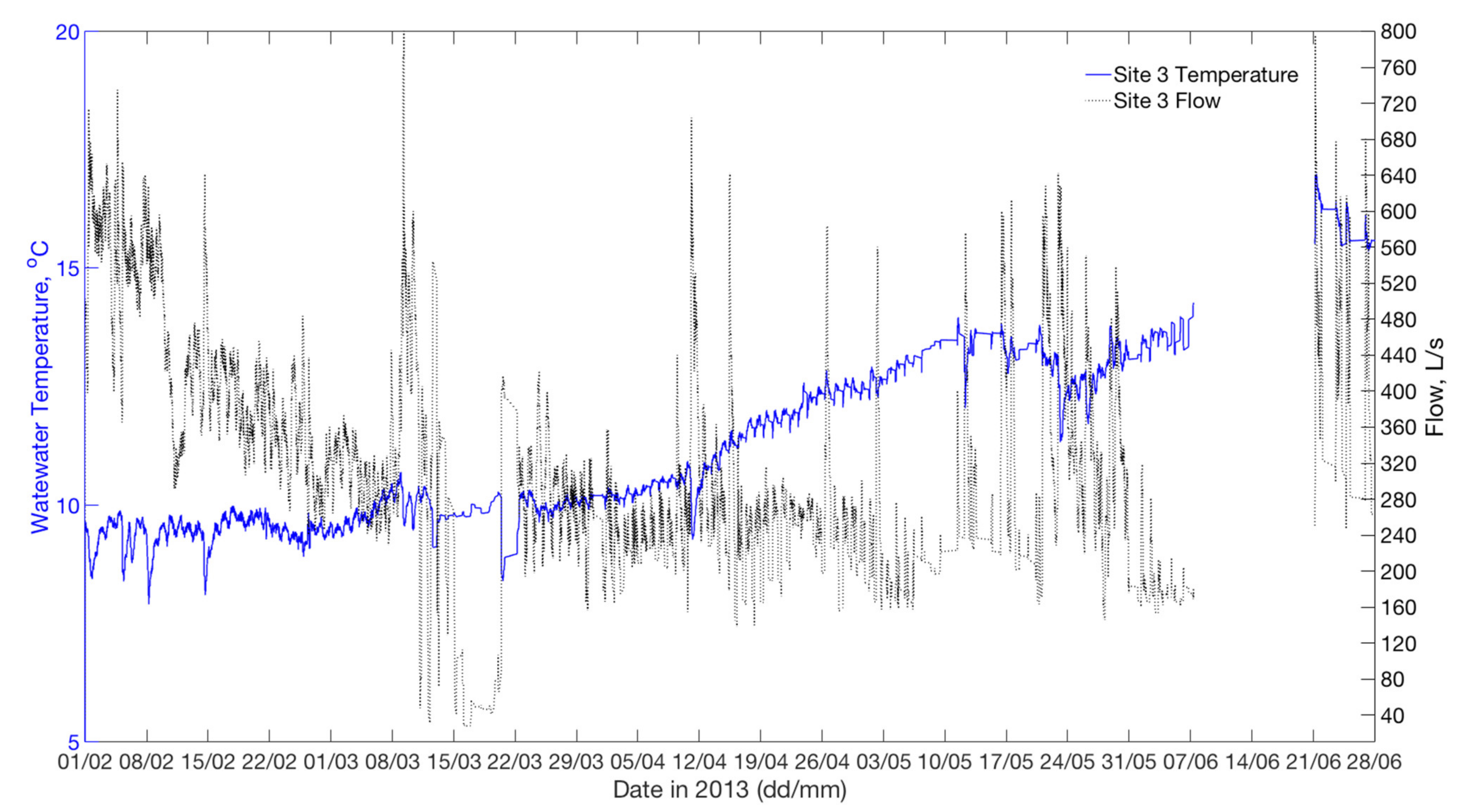
| Site | Average DWF | Pipe Length | Pipe Depth | Pipe Outer Diameter | Slope | Material | Shape | Type | |
|---|---|---|---|---|---|---|---|---|---|
| US | DS | m | |||||||
| L/s | m | m | m | ||||||
| 1 | 10 | 464 | 2.4 | 3 | 1.34 | 0.13% | Concrete | Circular | Residential |
| 2 | 13 | 232 | 3 | 4 | 1.34 | 0.56% | Concrete | Circular | Residential |
| 3 | 350 | 1031 | 3.5 | 3 | 1.34 | 0.1% | Concrete | Circular | Collector |
| 4 | 100 | 749 | 3 | 2.8 | 0.78 | 0.13% | Concrete | Circular | Collector |
| Month | ks/ds (W/m2·K) | fc (W/m2·K) | hFr (W/m2·K) | Rwa (m·K/W) | Rws (m·K/W) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Residential | Collector | Residential | Collector | Residential | Collector | Residential | Collector | Residential | Collector | |
| February | No data | 100 | No data | 236 | No data | 66 | No data | 0.02 | No data | 0.07 |
| March | 67 | 100 | 44 | 225 | 32 | 58 | 0.07 | 0.02 | 0.32 | 0.08 |
| April | 62 | 100 | 58 | 218 | 43 | 52 | 0.05 | 0.03 | 0.30 | 0.08 |
| May | 63 | 100 | 9 | 209 | 7 | 50 | 0.28 | 0.03 | 0.31 | 0.08 |
| June | 7 | 33 | 8 | 163 | 6 | 49 | 0.37 | 0.02 | 0.60 | 0.11 |
| July | 4 | No data | 7 | No data | 5 | No data | 0.40 | No data | 0.83 | No data |
| Month | Heat Recovery (GWh/Year) | |
|---|---|---|
| 2015 Model | 2020 Model | |
| January | 50.81 | 63.51 |
| March | 50.81 | 63.51 |
| May | 71.83 | 81.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdel-Aal, M.; Tait, S.; Mohamed, M.; Schellart, A. Using Long Term Simulations to Understand Heat Transfer Processes during Steady Flow Conditions in Combined Sewers. Water 2021, 13, 570. https://doi.org/10.3390/w13040570
Abdel-Aal M, Tait S, Mohamed M, Schellart A. Using Long Term Simulations to Understand Heat Transfer Processes during Steady Flow Conditions in Combined Sewers. Water. 2021; 13(4):570. https://doi.org/10.3390/w13040570
Chicago/Turabian StyleAbdel-Aal, Mohamad, Simon Tait, Mostafa Mohamed, and Alma Schellart. 2021. "Using Long Term Simulations to Understand Heat Transfer Processes during Steady Flow Conditions in Combined Sewers" Water 13, no. 4: 570. https://doi.org/10.3390/w13040570
APA StyleAbdel-Aal, M., Tait, S., Mohamed, M., & Schellart, A. (2021). Using Long Term Simulations to Understand Heat Transfer Processes during Steady Flow Conditions in Combined Sewers. Water, 13(4), 570. https://doi.org/10.3390/w13040570






