Reliable Evapotranspiration Predictions with a Probabilistic Machine Learning Framework
Abstract
1. Introduction
- Background
- Scientific challenge
- Research questions, motivations, and objectives
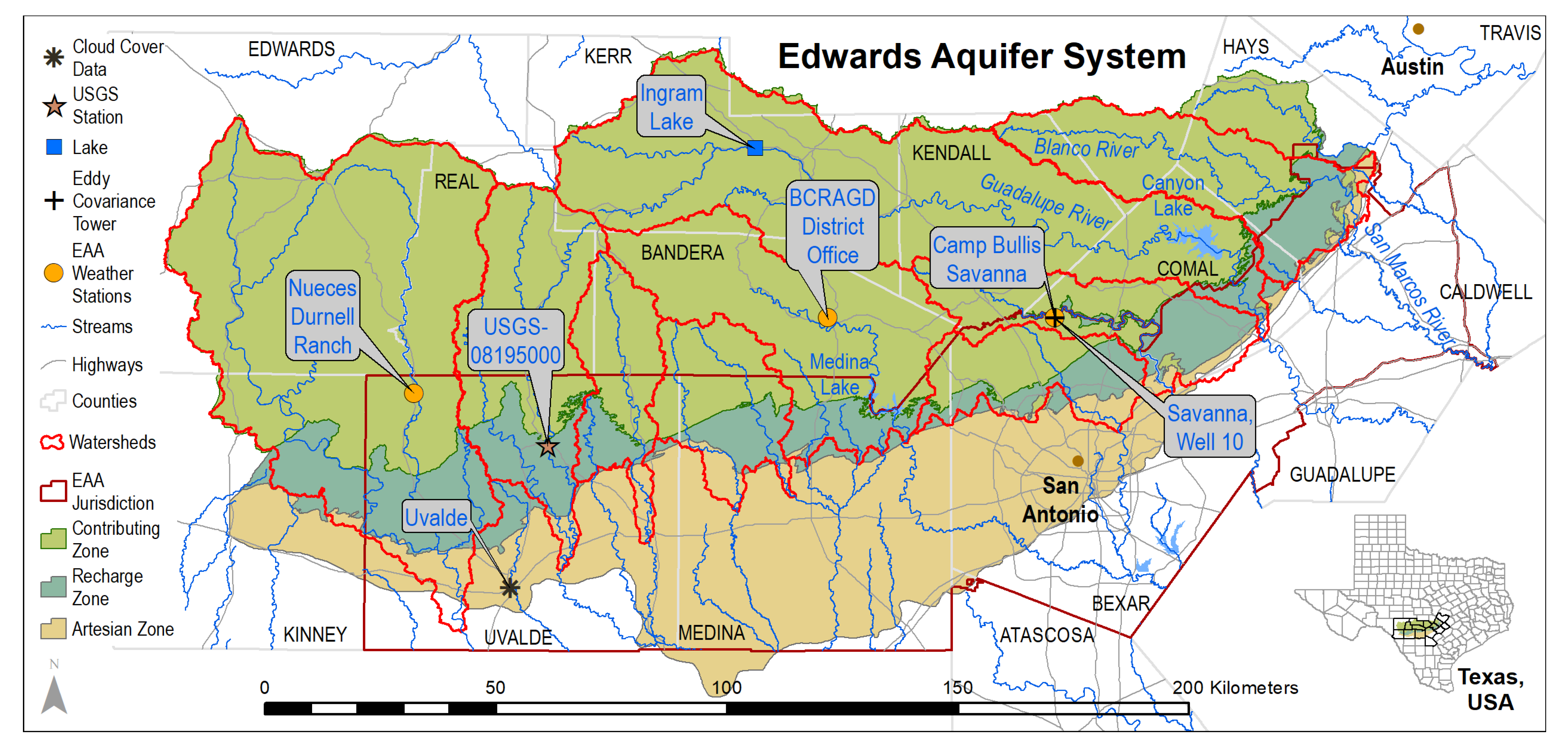
2. Study Area & Data Availability
3. Methods
3.1. FAO56 Penman-Monteith Equation (FAO56 PME)
3.2. Meyer’s Formula (MF)
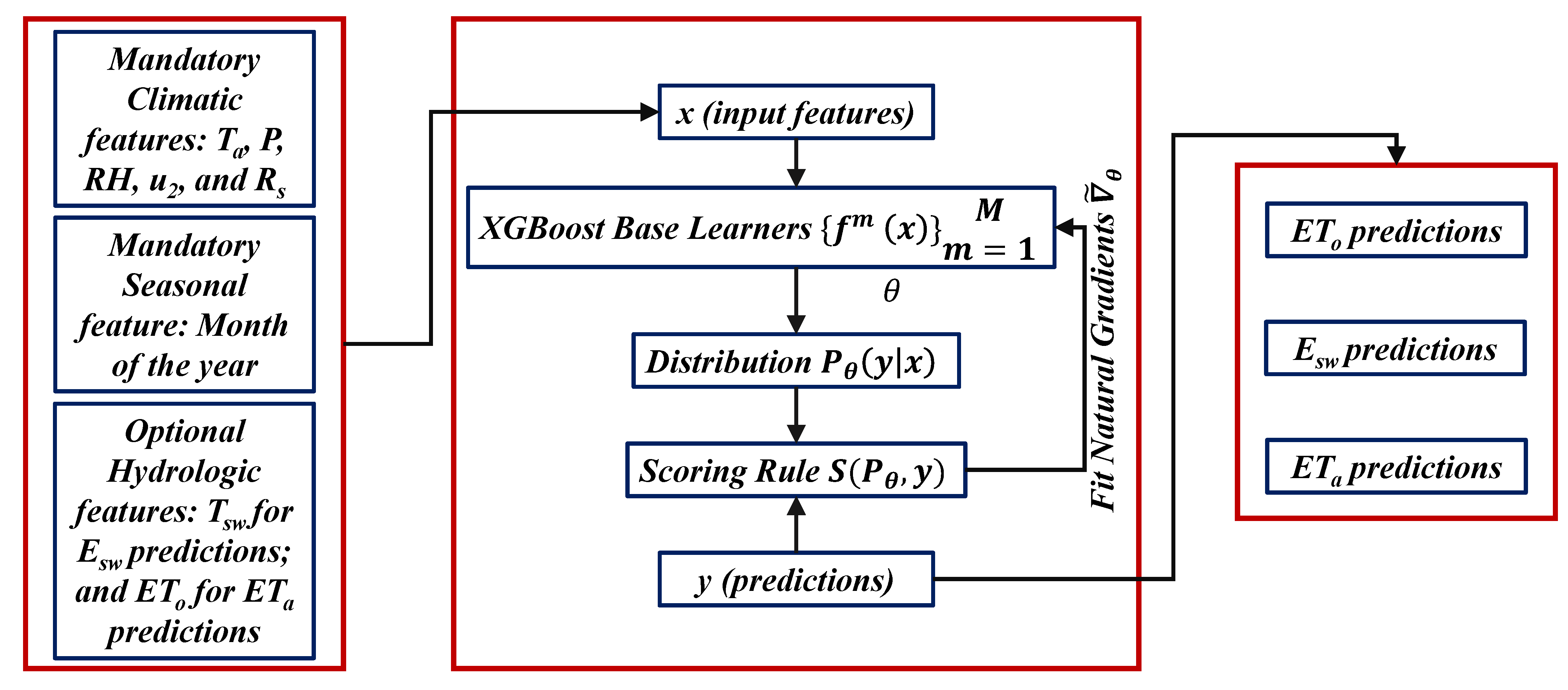
3.3. Probabilistic Machine Learning Models
4. Results
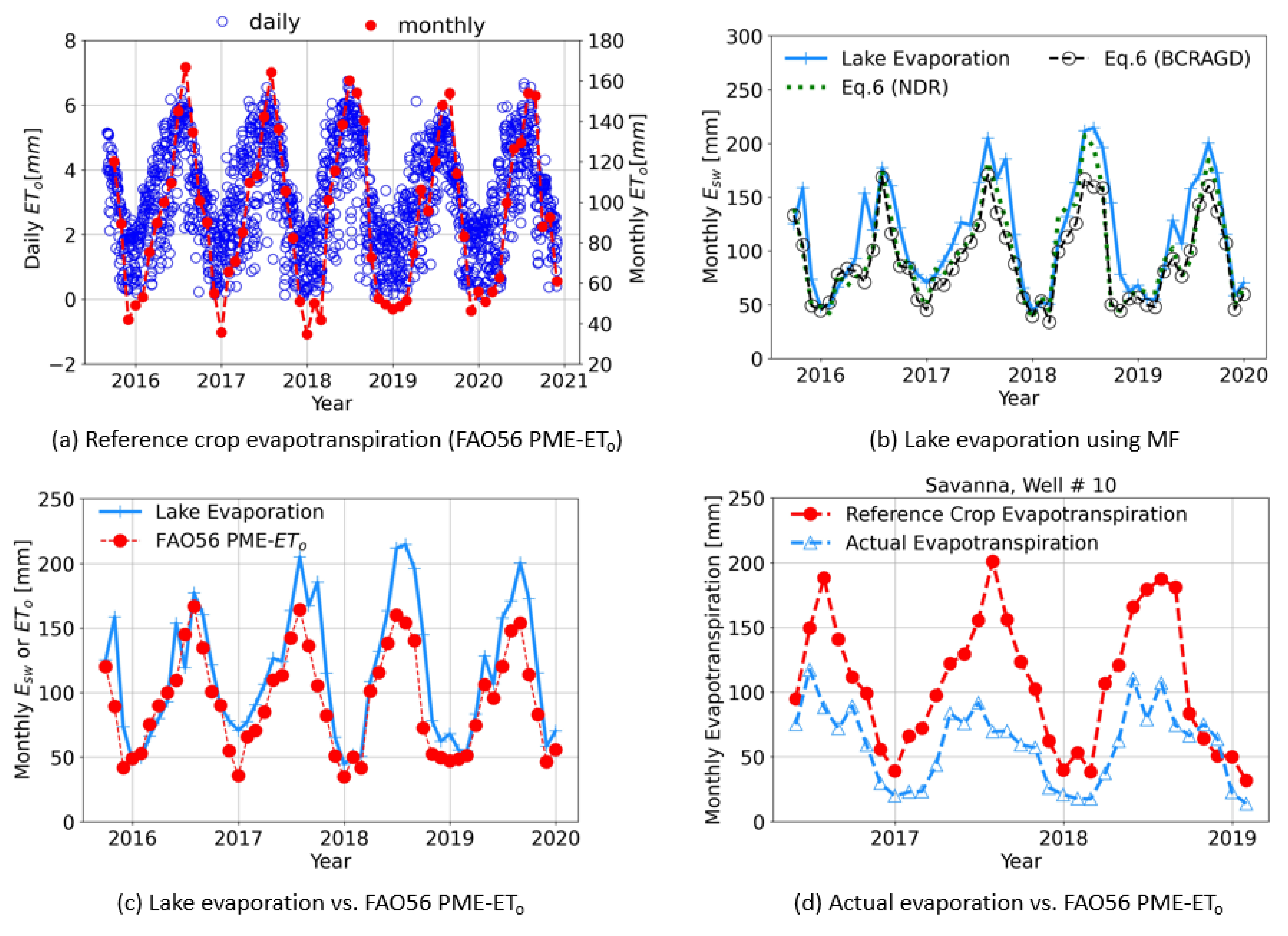
4.1. Predictions Using FAO56 PME and MF
4.2. Predictions Using Probabilistic ML Models
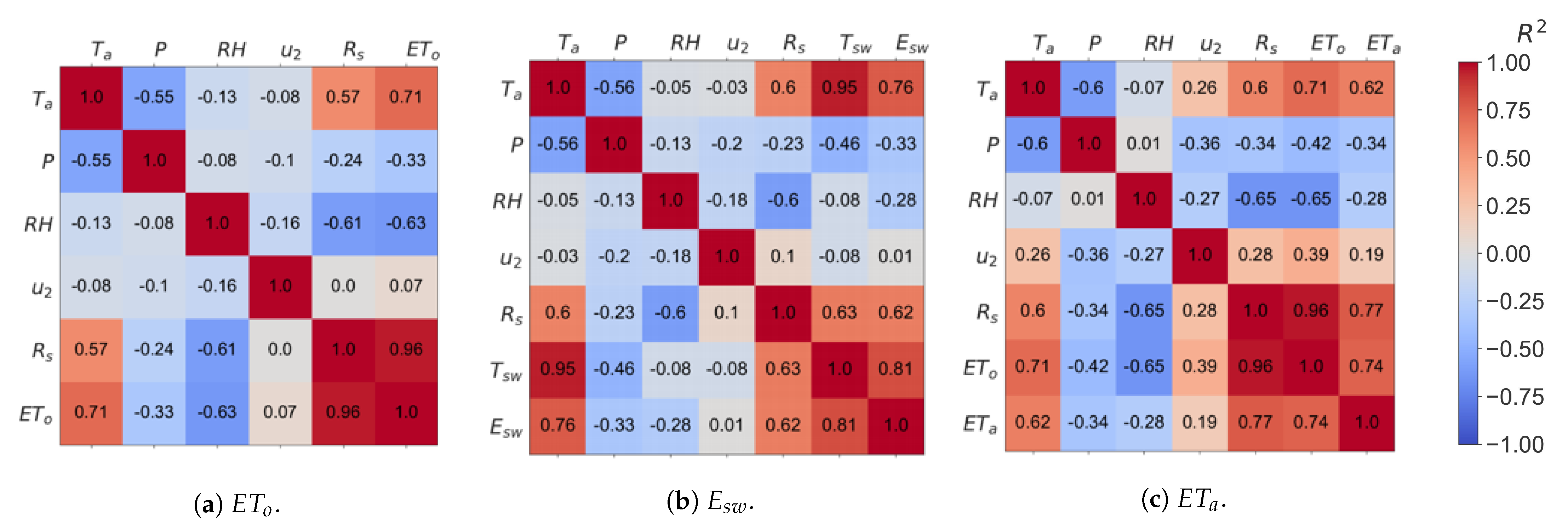
4.3. Feature Importance in , , and Predictive ML Models Using a Game Theory Approach
5. Discussion
5.1. What the Hybrid NGBoost-XGBoost Model Accomplished?
5.2. How Shapley Analysis Results Compare to Findings in the Current Literature?
5.3. What Are the New Insights from the NGBoost-XGBoost That Can Not Be Obtained from Other ML Models?
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Pan evaporation | |
| Evapotranspiration | |
| Reference crop evapotranspiration | |
| Actual evapotranspiration | |
| Potential evapotranspiration | |
| Surface Water Evaporation | |
| P | Atmospheric pressure |
| Shortwave solar radiation | |
| Relative humidity | |
| Air temperature | |
| Surface water temperature | |
| wind speed at 2 m above the ground surface | |
| BCRAGD | Bandera County River Authority and Groundwater District’s office |
| CBS | Camp Bullis, Savanna |
| EC | Eddy covariance |
| ML | Machine learning |
| MF | Meyer’s formula |
| MSE | Mean square error |
| NDR | Nueces Durnell Ranch |
| PME | Penman-Montheith equation |
| RMSE | Root mean square error |
Appendix A. Hydroclimotogical Data
Appendix A.1. Nueces Durnell Ranch (NDR) Weather Station
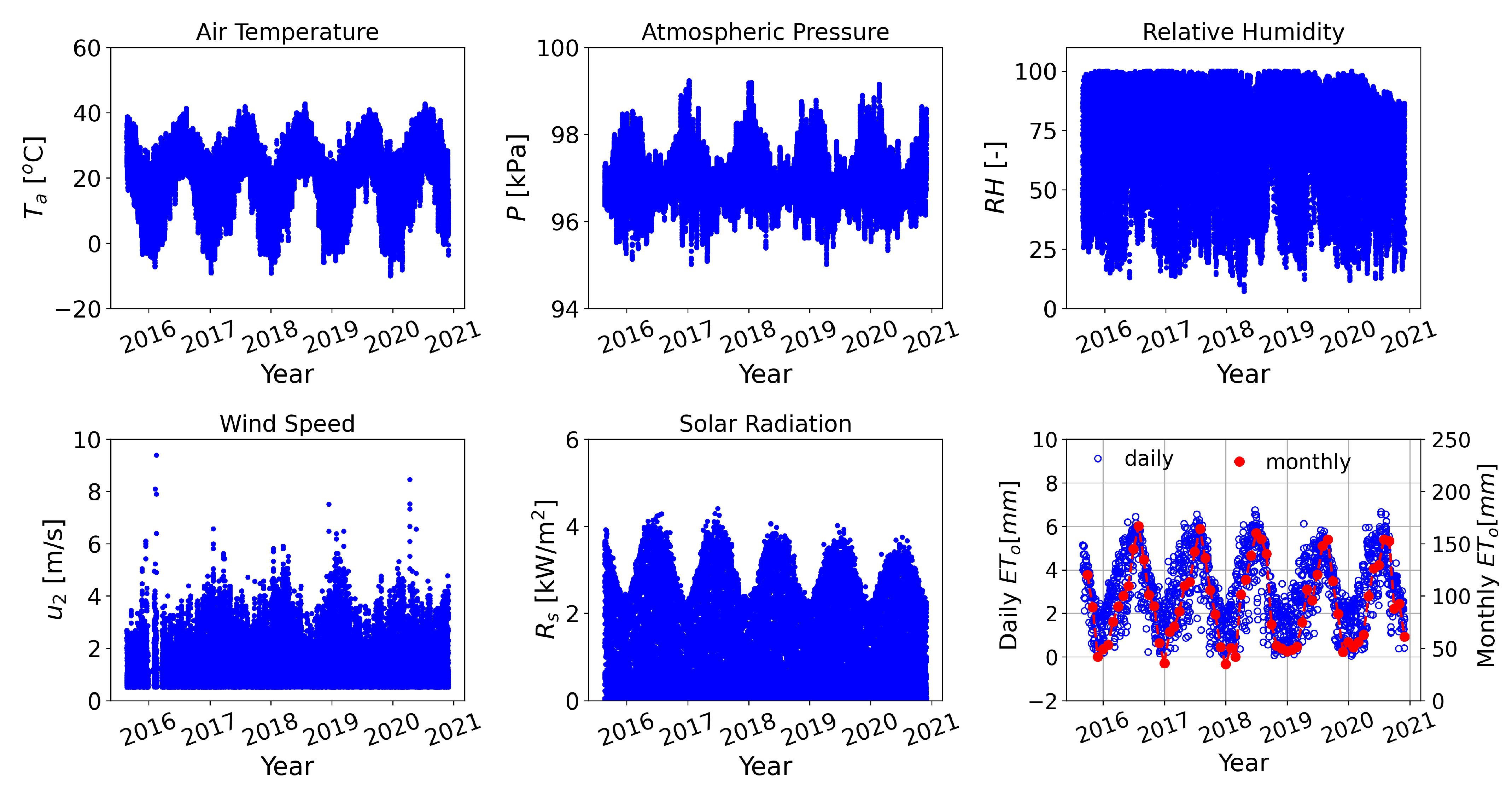
Appendix A.2. Bandera County River Authority and Groundwater District’s office (BCRAGD) Weather Station
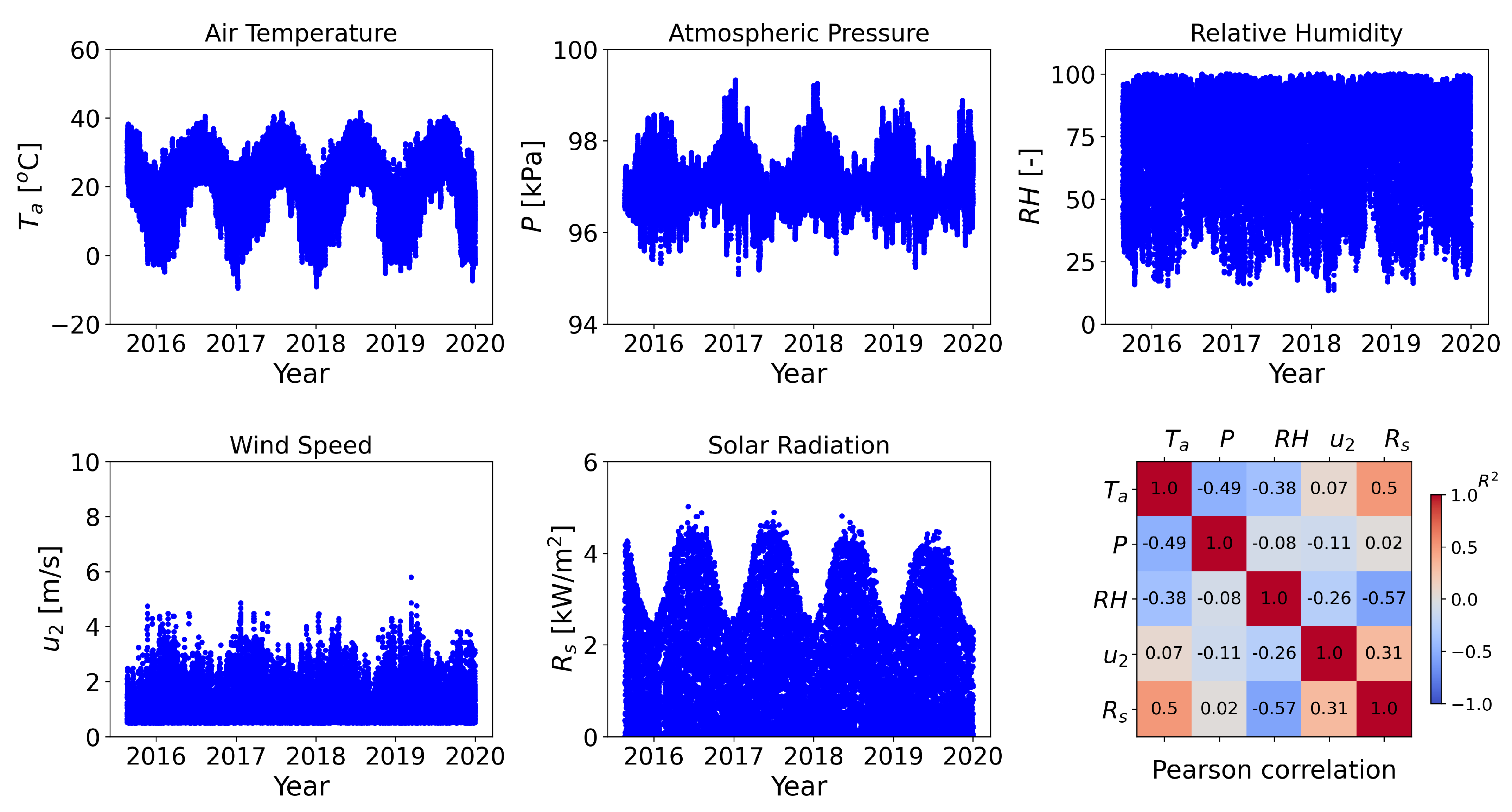
Appendix A.3. Camp Bullis Site (CBS) Weather Station
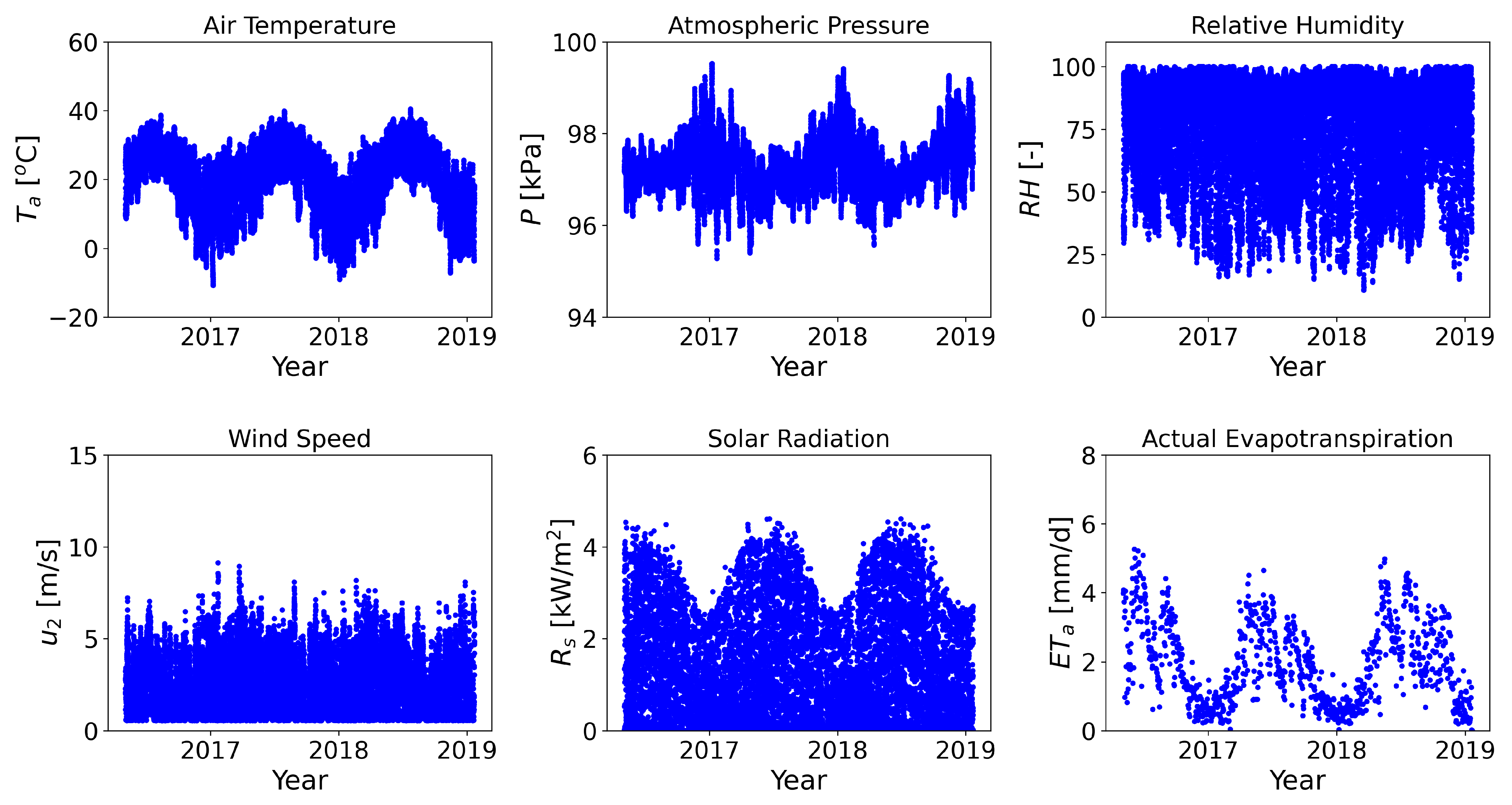
Appendix A.4. Surface Water Data
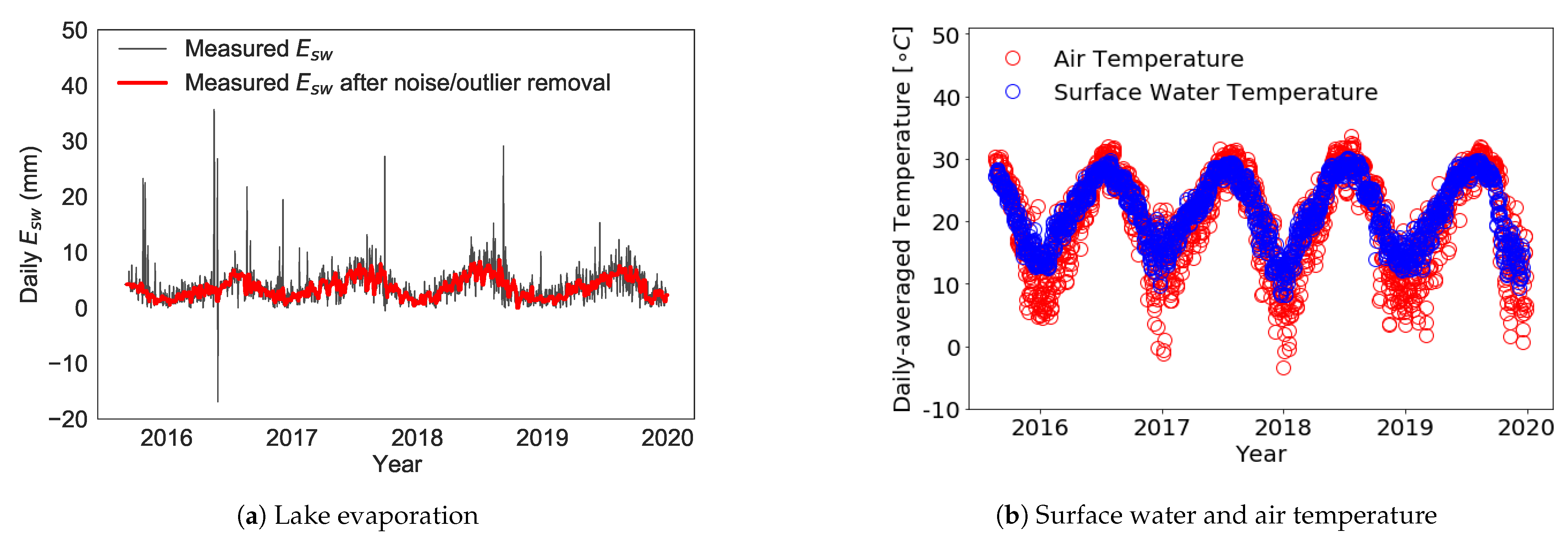
Appendix B. NGBoost and XGBoost Models
Appendix B.1. Natural Gradient Boosting (NGBoost)

Appendix B.2. eXtreme Gradient Boosting (XGBoost)
Appendix C. Statistical Correlations among Daily Variables
References
- Heilman, J.L.; McInnes, K.J.; Kjelgaard, J.F.; Owens, M.K.; Schwinning, S. Energy balance and water use in a subtropical karst woodland on the Edwards Plateau, Texas. J. Hydrol. 2009, 373, 426–435. [Google Scholar] [CrossRef]
- Gokmen, M.; Vekerdy, Z.; Lubczynski, M.W.; Timmermans, J.; Batelaan, O.; Verhoef, W. Assessing groundwater storage changes using remote sensing–based evapotranspiration and precipitation at a large semiarid basin scale. J. Hydrometeorol. 2013, 14, 1733–1753. [Google Scholar] [CrossRef]
- Glenn, E.P.; Scott, R.L.; Nguyen, U.; Nagler, P.L. Wide-area ratios of evapotranspiration to precipitation in monsoon dependent semiarid vegetation communities. J. Arid Environ. 2015, 117, 84–95. [Google Scholar] [CrossRef]
- Wu, W.Y.; Lo, M.H.; Wada, Y.; Famiglietti, J.S.; Reager, J.T.; Yeh, P.J.F.; Ducharne, A.; Yang, Z.L. Divergent effects of climate change on future groundwater availability in key mid-latitude aquifers. Nat. Commun. 2020, 11, 3710. [Google Scholar] [CrossRef]
- Hauwert, N.; Sharp, J.M. Measuring autogenic recharge over a karst aquifer utilizing Eddy covariance evapotranspiration. J. Water Resour. Prot. 2014, 6, 869–879. [Google Scholar] [CrossRef]
- Xie, Y.; Crosbie, R.; Yang, J.; Wu, J.; Wang, W. Usefulness of soil moisture and actual evapotranspiration data for constraining potential groundwater recharge in semiarid regions. Water Resour. Res. 2018, 54, 4929–4945. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration–Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998; ISBN 92-5-104219-5. [Google Scholar]
- Stöckle, C.O.; Kjelgaard, J.; Bellocchi, G. Evaluation of estimated weather data for calculating Penman-Monteith reference crop evapotranspiration. Irrig. Sci. 2004, 23, 39–46. [Google Scholar] [CrossRef]
- Scheff, J.; Frierson, D.M.W. Scaling potential evapotranspiration with greenhouse warming. J. Clim. 2014, 27, 1539–1558. [Google Scholar] [CrossRef]
- Chiarelli, D.D.; Passera, C.; Rosa, L.R.; Davis, K.F.; D’Odorico, P.; Rulli, M. The green and blue crop water requirement WATNEEDS model and its global gridded outputs. Sci. Data 2020, 7, 273. [Google Scholar] [CrossRef]
- Ndiaye, P.; Bodian, A.; Diop, L.; Deme, A.; Dezetter, A.; Djaman, K.; Ogilvie, A. Trend and sensitivity analysis of reference evapotranspiration in the Senegal river basin using NASA meteorological data. Water 2020, 12, 1957. [Google Scholar] [CrossRef]
- Irmak, S.; Irmak, A.; W, J.J.; Howell, T.A.; Jacobs, J.M.; Allen, R.G. Predicting daily net radiation using minimum climatological data. J. Irrig. Drain. Eng. 2003, 129, 256–269. [Google Scholar] [CrossRef]
- Peng, L.; Feng, H. The best alternative for estimating reference crop evapotranspiration in different sub-regions of mainland China. Sci. Rep. 2017, 7, 5458. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Yue, W.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluation of SVM, ELM and four tree-based ensemble models for predicting daily reference evapotranspiration using limited meteorological data in different climates of China. Agric. For. Meteorol. 2018, 263, 225–241. [Google Scholar] [CrossRef]
- Celestin, S.; Qi, F.; Li, R.; Yu, T.; Cheng, W. Evaluation of 32 simple equations against the Penman–Monteith method to estimate the reference evapotranspiration in the Hexi corridor, Northwest China. Water 2020, 12, 2772. [Google Scholar] [CrossRef]
- Berti, A.; Tardivo, G.; Chiaudani, A.; Rech, F.; Borin, M. Assessing reference evapotranspiration by the Hargreaves method in north-eastern Italy. Agric. Water Manag. 2017, 140, 20–25. [Google Scholar] [CrossRef]
- Hartmann, A.; Gleesonc, T.; Wadae, Y.; Wagener, T. Enhanced groundwater recharge rates and altered recharge sensitivity to climate variability through subsurface heterogeneity. Proc. Natl. Acad. Sci. USA 2017, 114, 2842–2847. [Google Scholar] [CrossRef]
- Dewes, C.F.; Rangwala, I.; Barsugli, J.J.; Hobbins, M.T.; Kumar, S. Drought risk assessment under climate change is sensitive to methodological choices for the estimation of evaporative demand. PLoS ONE 2017, 12, e0174045. [Google Scholar] [CrossRef]
- Naumann, G.; Alfieri, L.; Wyser, K.; Mentaschi, L.; Betts, R.; Carrao, H.; Spinoni, J.; Vogt, J.; Feyen, L. Global changes in drought conditions under different levels of warming. Geophys. Res. Lett. 2018, 45, 3285–3296. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Cook, B.I.; Smerdon, J.E.; Seager, R.; Coats, S. Global warming and 21st century drying. Clim. Dyn. 2014, 43, 2607–2627. [Google Scholar] [CrossRef]
- Greve, P.; Ukkola, A.M.; Roderick, M.L.; Wada, A.M. The aridity Index under global warming. Environ. Res. Lett. 2019, 14, 124006. [Google Scholar] [CrossRef]
- Paltineanu, C.; Mihailescu, I.; Seceleanu, I.; Dragota, C.; Vasenciuc, F. Using aridity indices to describe some climate and soil features in Eastern Europe: A Romanian case study. Theor. Appl. Climatol. 2007, 90, 263–274. [Google Scholar] [CrossRef]
- Park, C.; Jeong, S.; Joshi, M.; Osborn, T.J.; Ho, C.H.; Piao, S.; Chen, D.; Liu, J.; Yang, H.; Park, H.; et al. Keeping global warming within 1.5 °C constrains emergence of aridification. Nat. Clim. Chang. 2018, 8, 70–74. [Google Scholar] [CrossRef]
- Nouri, M.; Bannayan, M. Spatiotemporal changes in aridity index and reference evapotranspiration over semi-arid and humid regions of Iran: Trend, cause, and sensitivity analyses. Theor. Appl. Climatol. 2019, 136, 1073–1084. [Google Scholar] [CrossRef]
- Pereira, L.S.; Allen, R.G.; Smith, M.; Raes, D. Crop evapotranspiration estimation with FAO56: Past and future. Agric. Water Manag. 2015, 147, 4–20. [Google Scholar] [CrossRef]
- Corbari, C.; Ravazzani, G.; Galvagno, M.; Cremonese, E.; Mancini, M. Assessing crop coefficients for natural vegetated areas using satellite data and Eddy covariance stations. Sensors 2017, 17, 2664. [Google Scholar] [CrossRef]
- Zanotelli, D.; Montagnani, L.; Andreotti, C.; Tagliavini, M. Evapotranspiration and crop coefficient patterns of an apple orchard in a sub-humid environment. Agric. Water Manag. 2019, 226, 105756. [Google Scholar] [CrossRef]
- van der Kamp, G.; Keir, D.; Evans, M. Long-term water level changes in closed-basin lakes of the Canadian prairies. Can. Water Resour. J. 2008, 33, 23–38. [Google Scholar] [CrossRef]
- Wang, W.; Lee, X.; Xiao, W.; Liu, S.; Schultz, N.; Wang, Y.; Zhang, M.; Zhao, L. Global lake evaporation accelerated by changes in surface energy allocation in a warmer climate. Nat. Geosci 2018, 11, 410–414. [Google Scholar] [CrossRef]
- Vercauteren, N.; Bou-Zeid, E.; Huwald, H.; Parlange, M.B.; Brutsaert, W. Estimation of wet surface evaporation from sensible heat flux measurements. Water Resour. Res. 2009, 45, 735–742. [Google Scholar] [CrossRef]
- Roderick, M.L.; Hobbins, M.T.; Farquhar, G. Pan evaporation trends and the terrestrial water balance. II. Energy balance and interpretation. Geogr. Compass. 2009, 3, 761–780. [Google Scholar] [CrossRef]
- Boughton, W. The Australian water balance model. Environ. Modell. Softw. 2004, 19, 943–956. [Google Scholar] [CrossRef]
- Xu, C.Y.; Sing, V.P. Cross comparison of empirical equations for calculating potential evapotranspiration with data from Switzerland. Water Resour. Manag. 2002, 16, 197–219. [Google Scholar] [CrossRef]
- Burn, D.H.; Hesch, N.M. A comparison of trends in potential and pan evaporation for the Canadian Ppairies. Can. Water Resour. J. 2006, 31, 173–184. [Google Scholar] [CrossRef]
- Tanny, J.; Cohen, S.; Berger, D.; Teltch, B.; Mekhmandarov, Y.; Bahar, M.; Katul, G.; Assouline, S. Evaporation from a reservoir with fluctuating water level: Correcting for limited fetch. J. Hydrol. 2011, 404, 146–156. [Google Scholar] [CrossRef]
- Xiao, K.; Griffis, T.J.; Baker, J.M.; Bolstad, P.V.; Erickson, M.D.; Leed, X.; Wood, J.D.; Hu, C.; Nieberg, J.L. Evaporation from a temperate closed-basin lake and its impact on present, past, and future water level. J. Hydrol. 2018, 561, 59–75. [Google Scholar] [CrossRef]
- Fu, G.; Liu, C.; Chen, S.; Hong, J. Investigating the conversion coefficients for free water surface evaporation of different evaporation pans. J. Hydrol. 2004, 18, 2247–2262. [Google Scholar] [CrossRef]
- Tanny, J.; Cohen, S.; Assouline, S.; Lange, F.; Grava, A.; Berger, D.; Teltch, B.; Parlange, M. Evaporation from a small water reservoir: Direct measurements and estimates. J. Hydrol. 2008, 351, 218–229. [Google Scholar] [CrossRef]
- Zhang, Y.; Peña-Arañcibia, J.L.; McVicar, T.R.; Chiew, F.H.S.; Vaze, J.; Liu, C.; Lu, X.; Zheng, H.; Wang, Y.; Liu, Y.Y.; et al. Multi-decadal trends in global terrestrial evapotranspiration and its components. Sci. Rep. 2016, 6, 19124. [Google Scholar] [CrossRef]
- Burba, G. Eddy Covariance Method for Scientific, Industrial, Agricultural and Regulatory Applications: A Field Book on Measuring Ecosystem Gas Exchange and Areal Emission Rates; Li-Cor Biosciences: Lincoln, NE, USA, 2013. [Google Scholar]
- Vesala, T.; Huotari, J.; Rannik, U.; Suni, T.; Smolander, S.; Sogachev, A.; Launiainen, S.; Ojala, A. Eddy covariance measurements of carbon exchange and latent and sensible heat fluxes over a boreal lake for a full open-water period. J. Geophys. Res. 2006, 111, D11101. [Google Scholar] [CrossRef]
- Wang, S.; Pan, M.; Mu, Q.; Shi, X.; Mao, J.; Brummer, C.; Jassal, R.S.; Praveena, K.; Li, J.; Black, T.A. Comparing evapotranspiration from Eddy covariance measurements, water budgets, remote sensing, and land surface models over Canada. J. Hydrometeorol. 2015, 16, 1540–1560. [Google Scholar] [CrossRef]
- Wilson, K.; Hanson, P.J.; Mulholland, P.J.; Baldocchi, D.D.; Wullschleger, S.D. A comparison of methods for determining forest evapotranspiration and its components: Sap-flow, soil water budget, Eddy covariance and catchment water balance. Agric. Forest Meteorol. 2001, 106, 153–168. [Google Scholar] [CrossRef]
- Zitouna-Chebbi, R.; Prévot, L.; Chakhar, A.; Marniche-Ben Abdallah, M.; Jacob, F. Observing actual evapotranspiration from flux tower Eddy covariance measurements within a Hilly watershed: Case Study of the Kamech site, Cap Bon Peninsula, Tunisia. Atmosphere 2018, 9, 68. [Google Scholar] [CrossRef]
- Lascano, R.J.; van Bavel, C.H.M. Explicit and recursive calculation of potential and actual evapotranspirations. Agron. J. 2007, 99, 585–590. [Google Scholar] [CrossRef]
- Li, S.; Kang, S.; Zhang, L.; Zhang, J.; Du, T.; Tong, L.; Ding, R. Evaluation of six potential evapotranspiration models for estimating crop potential and actual evapotranspiration in arid regions. J. Hydrol. 2016, 543, 450–461. [Google Scholar] [CrossRef]
- Wang, T.; Zlotnik, V.A. A complementary relationship between actual and potential evapotranspiration and soil effects. J. Hydrol. 2012, 456–457, 146–150. [Google Scholar] [CrossRef]
- Morton, F.I. Potential evaporation and river basin evaporation. J. Hydraul. Div. Am. Soc. Civ. Eng. 1965, 102, 275–291. [Google Scholar] [CrossRef]
- Milly, P.C.D.; Dunne, K.A. Potential evapotranspiration and continental drying. Nat. Clim. Chang. 2016, 6, 946–951. [Google Scholar] [CrossRef]
- Liu, Y.; Hao, L.; Zhou, D.; Pan, C.; Liu, P.; Xiong, Z.; Sun, G. Identifying a transition climate zone in an arid river basin using the evaporative stress index. Nat. Hazards Earth Syst. Sci. 2019, 19, 2281–2294. [Google Scholar] [CrossRef]
- Choi, M.; Jacobs, J.M.; Anderson, M.C.; Bosch, D.D. Evaluation of drought indices via remotely sensed data with hydrological variables. J. Hydrol. 2013, 476, 265–273. [Google Scholar] [CrossRef]
- Yao, A.Y.M. Agricultural potential estimated from the ratio of actual to potential evapotranspiration. Agric. Meteorol. 1974, 13, 405–417. [Google Scholar] [CrossRef]
- Anderson, M.C.; Zolin, C.A.; Sentelhas, P.C.; Hain, C.R.; Semmens, K.; Yilmaz, M.T.; Gao, F.; Otkin, J.A.; Tetrault, R. The Evaporative Stress Index as an indicator of agricultural drought in Brazil: An assessment based on crop yield impacts. Remote Sens. Environ. 2016, 174, 82–99. [Google Scholar] [CrossRef]
- Lingling, Z.; Jun, X.; Chong-yu, X.; Zhonggen, W.; Leszek, S.; Cangrui, L. Evapotranspiration estimation methods in hydrological models. J. Geogr. Sci. 2013, 23, 359–369. [Google Scholar] [CrossRef]
- Wu, L.; Fan, J. Comparison of neuron-based, kernel-based, tree-based and curve based machine learning models for predicting daily reference evapotranspiration. PLoS ONE 2019, 14, e0217520. [Google Scholar] [CrossRef]
- Lifeng, W.; Youwen, P.; Junliang, F.; Wang, Y. Machine learning models for the estimation of monthly mean daily reference evapotranspiration based on cross-station and synthetic data. Hydrol. Process. 2019, 50, 1730–1750. [Google Scholar] [CrossRef]
- Sattari, M.; Apaydin, H.; Shamshirband, S. Performance evaluation of deep learning-based gated recurrent units (GRUs) and tree-based models for estimating ETo by using limited meteorological variables. Mathematics 2020, 8, 972. [Google Scholar] [CrossRef]
- Chakraborty, D.; Başağaoğlu, H.; Winterle, J. Interpretable vs. noninterpretable machine learning models for data-driven hydro-climatological process modeling. Expert Syst. Appl. 2021, 170, 114498. [Google Scholar] [CrossRef]
- Goyal, M.K.; Bharti, B.; Quilty, J.; Adamowski, J.; Pandey, A. Modeling of daily pan evaporation in sub tropical climates using ANN, LS-SVR, Fuzzy Logic, and ANFIS. Expert Syst. Appl. 2014, 41, 5267–5276. [Google Scholar] [CrossRef]
- Lua, X.; Jua, Y.; Wu, L.; Fan, J.; Zhang, F.; Li, Z. Daily pan evaporation modeling from local and cross-station data using three tree-based machine learning models. J. Hydrol. 2018, 566, 668–684. [Google Scholar] [CrossRef]
- Alsumaiei, A. Utility of artificial neural networks in modeling pan evaporation in hyper-arid climates. Water 2020, 12, 1508. [Google Scholar] [CrossRef]
- Filgueiras, R.; Almeida, T.S.; Mantovani, E.C.; Dias, S.H.B.; InácioFernandes-Filho, E.; Cunha, F.F.; Venancio, L.P. Soil water content and actual evapotranspiration predictions using regression algorithms and remote sensing data. Agric. Water Manag. 2020, 241, 106346. [Google Scholar] [CrossRef]
- Nema, M.K.; Khare, D.; Chandniha, S.K. Application of artificial intelligence to estimate the reference evapotranspiration in sub-humid Doon valley. App. Water Sci. 2017, 7, 3903–3910. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Gong, D.; Zhang, Q.; Zhao, L. Evaluation of random forests and generalized regression neural networks for daily reference evapotranspiration modelling. Agric. Water Manag. 2017, 193, 163–173. [Google Scholar] [CrossRef]
- Jovic, S.; Nedeljkovic, B.; Golubovic, Z.; Kostic, N. Evolutionary algorithm for reference evapotranspiration analysis. Comput. Electron. Agric. 2018, 150, 1–4. [Google Scholar] [CrossRef]
- Dou, X.; Yang, Y. Evapotranspiration estimation using four different machine learning approaches in different terrestrial ecosystems. Comput. Electron. Agric. 2018, 148, 95–106. [Google Scholar] [CrossRef]
- Mehdizadeh, S. Estimation of daily reference evapotranspiration (ETo) using artificial intelligence methods: Offering a new approach for lagged ETo data-based modeling. J. Hydrol. 2018, 559, 794–812. [Google Scholar] [CrossRef]
- Kisi, O.; Alizamir, M. Modelling reference evapotranspiration using a new wavelet conjunction heuristic method: Wavelet extreme learning machine vs wavelet neural networks. Agric. Forest Meteorol. 2018, 263, 41–48. [Google Scholar] [CrossRef]
- Tao, H.; Diop, L.; Bodian, A.; Djaman, K.; Ndiaye, P.M.; Yaseen, Z.M. Reference evapotranspiration prediction using hybridized fuzzy model with firefly algorithm: Regional case study in Burkina Faso. Agric. Water Manag. 2018, 208, 140–151. [Google Scholar] [CrossRef]
- Sanikhani, H.; Kisi, O.; Maroufpoor, E.; Yaseen, Z.M. Temperature-based modeling of reference evapotranspiration using several artificial intelligence models: Application of different modeling scenarios. Theor. Appl. Clim. 2019, 135, 449–462. [Google Scholar] [CrossRef]
- Saggi, M.K.; Jain, S. Reference evapotranspiration estimation and modeling of the Punjab northern India using deep learning. Comput. Electron. Agric. 2019, 156, 387–398. [Google Scholar] [CrossRef]
- Chia, M.; Huang, Y.; Koo, C.; Fung, K. Recent advances in evapotranspiration estimation using artificial intelligence approaches with a focus on hybridization techniques—A review. Agronomy 2020, 10, 101. [Google Scholar] [CrossRef]
- Li, X.; Liu, S.; Li, H.; Ma, Y.; Wang, J.; Zhang, Y.; Xu, Z.; Xu, T.; Song, L.; Yang, X.; et al. Intercomparison of six upscaling evapotranspiration methods: From site to the satellite pixel. J. Geophys. Res. Atmos. 2018, 123, 6777–6803. [Google Scholar] [CrossRef]
- Xu, T.; Guo, Z.; Liu, S.; He, X.; Meng, Y.; Xu, Z.; Xia, Y.; Xiao, J.; Zhang, Y.; Ma, Y.; et al. Evaluating Different Machine Learning Methods for Upscaling Evapotranspiration from Flux Towers to the Regional Scale. J. Geophys. Res. Atmos. 2018, 123, 8674–8690. [Google Scholar] [CrossRef]
- Tang, D.; Feng, Y.; Gong, D.; Hao, W.; Cui, N. Evaluation of artificial intelligence models for actual crop evapotranspiration modeling in mulched and non-mulched maize croplands. Comp. Electron Agric. 2018, 152, 375–384. [Google Scholar] [CrossRef]
- Duan, T.; Avati, A.; Ding, D.Y.; Basu, S.; Ng, A.Y.; Schuler, A. NGBoost: Natural Gradient Boosting for Probabilistic Prediction. arXiv 2019, arXiv:1910.03225. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 2522–5839. [Google Scholar] [CrossRef]
- Devitt, T.J.; Wright, A.M.; Canntella, D.C.; Hillis, D.M. Species delimitation on endangered groundwater salamanders: Implications for aquifer management for biodiversity conservation. Proc. Natl. Acad. Sci. USA 2019, 116, 2624–2633. [Google Scholar] [CrossRef] [PubMed]
- Dugas, W.A.; Hicks, R.A.; Wright, P. Effect of removal of Juniperus ashei on evapotranspiration and runoff in the Seco creek Yatershed. Water Resour. Res. 1998, 34, 1499–1506. [Google Scholar] [CrossRef]
- Deng, K.; Ting, M.; Yang, S.; Tan, Y. Increased frequency of summer extreme heat waves over Texas area tied to the amplification of Pacific zonal SST gradient. J. Clim. 2018, 31, 5629–5647. [Google Scholar] [CrossRef]
- Hoerling, M.; Kumar, A.; Dole, R.; Nielsen-Gammon, J.; Eischeid, J.; Perlwitz, J.; Quan, X.-W.; Perlwitz, J.; Quan, X.W.; Zhang, T.; et al. Anatomy of an extreme event. J. Clim. 2013, 26, 2811–2832. [Google Scholar] [CrossRef]
- Rupp, D.E.; Li, S.; Massey, N.; Sparrow, S.N.; Mote, P.W.; Allen, M. Anthropogenic influence on the changing likelihood of an exceptionally warm summer in Texas, 2011. Geophys. Res. Lett. 2015, 42, 2392–2400. [Google Scholar] [CrossRef]
- Mahler, B.; Bourgeais, R. Dissolved oxygen fluctuations in karst spring flow and implications for endemic species: Barton springs, Edwards aquifer, Texas, USA. J. Hydrol. 2013, 505, 291–298. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Chiew, F.H.S.; Zhang, L.; Leuning, R.; Cleugh, H.A. Estimating catchment evaporation and runoff using MODIS leaf area index and the Penman-Monteith equation. Water Resour. Res. 2008, 44, W10420. [Google Scholar] [CrossRef]
- Raza, D.S.M.H.; Mahmood, S.A. Estimation of net rice production through improved CASA model by addition of soil suitability constant (hα). Sustainability 2018, 10, 1788. [Google Scholar] [CrossRef]
- Meyer, A.F. Computing Runoff from Rainfall and Other Physical Data. Trans. Am. Soc. Civ. Eng. 1915, 79, 1055–1155. [Google Scholar]
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Pedreschi, D.; Giannotti, F. A Survey of Methods for Explaining Black Box Models. ACM Comput. Surv. 2018, 51, 93. [Google Scholar] [CrossRef]
- Hargreaves, G.; Samani, Z. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Yoo, B.H.; Kim, J.; Byun-Woo, L.; Hoogenboom, G.; Kim, K.S. A surrogate weighted mean ensemble method to reduce the uncertainty at a regional scale for the calculation of potential evapotranspiration. Sci. Rep. 2020, 10, 870. [Google Scholar] [CrossRef] [PubMed]
- Gong, L.; Xu, C.Y.; Chen, D.; Halldin, S.; Chen, Y.D. Sensitivity of the Penman–Monteith reference evapotranspiration to key climatic variables in the Changjiang (Yangtze River) basin. J. Hydrol. 2006, 329, 620–629. [Google Scholar] [CrossRef]
- Yan, H.; Shugart, H.H. An air relative-humidity-based evapotranspiration model from Eddy covariance data. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Wobus, C.; Zarakas, C.; Malek, P.; Sanderson, B.; Crimmins, A.; Kolian, M.; Sarofim, M.; Weaver, C. Reframing Future Risks of Extreme Heat in the United States. Earths Future 2018, 6, 1323–1335. [Google Scholar] [CrossRef] [PubMed]
- Thompson, S.A. Water Use, Management, and Planning In the United States; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
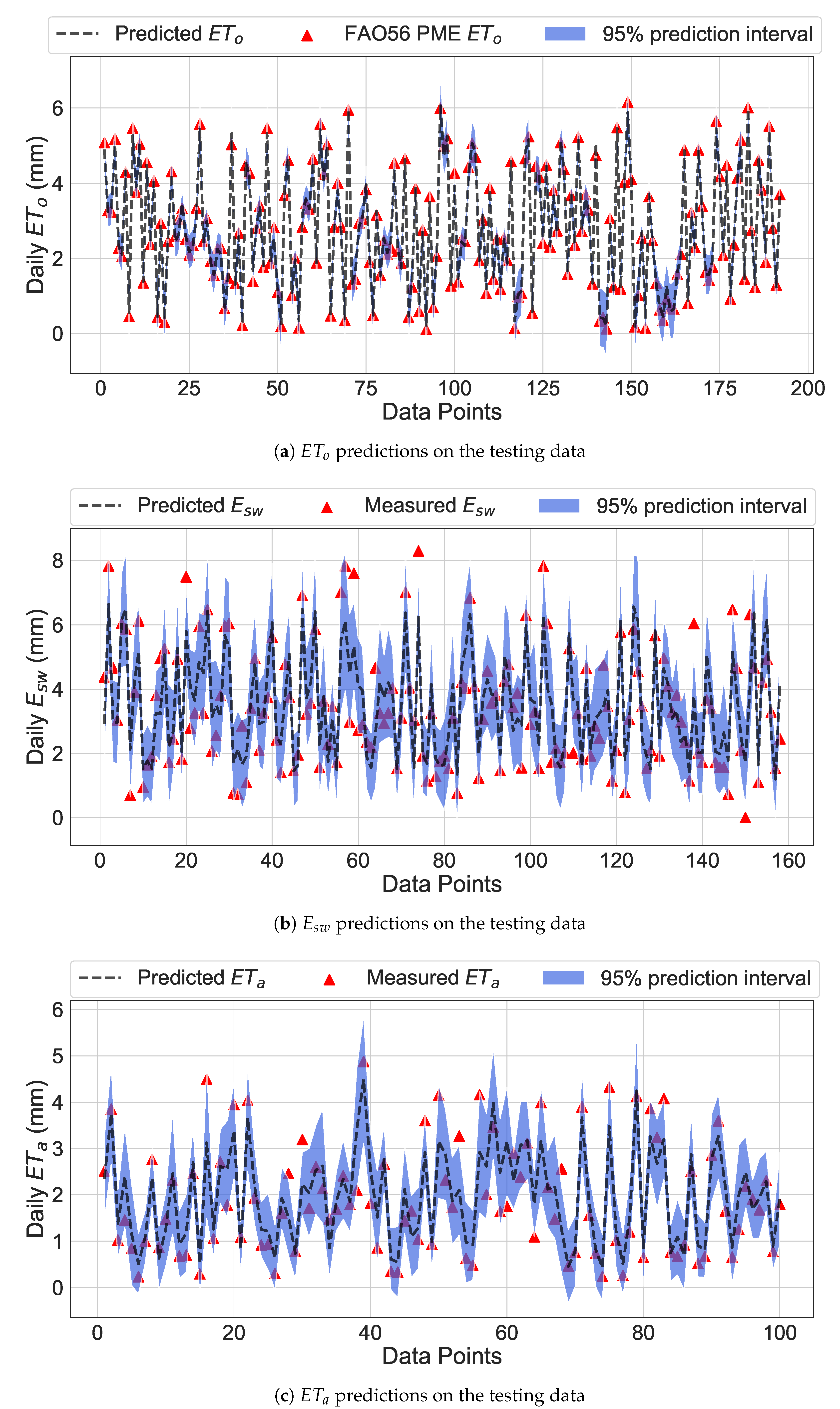
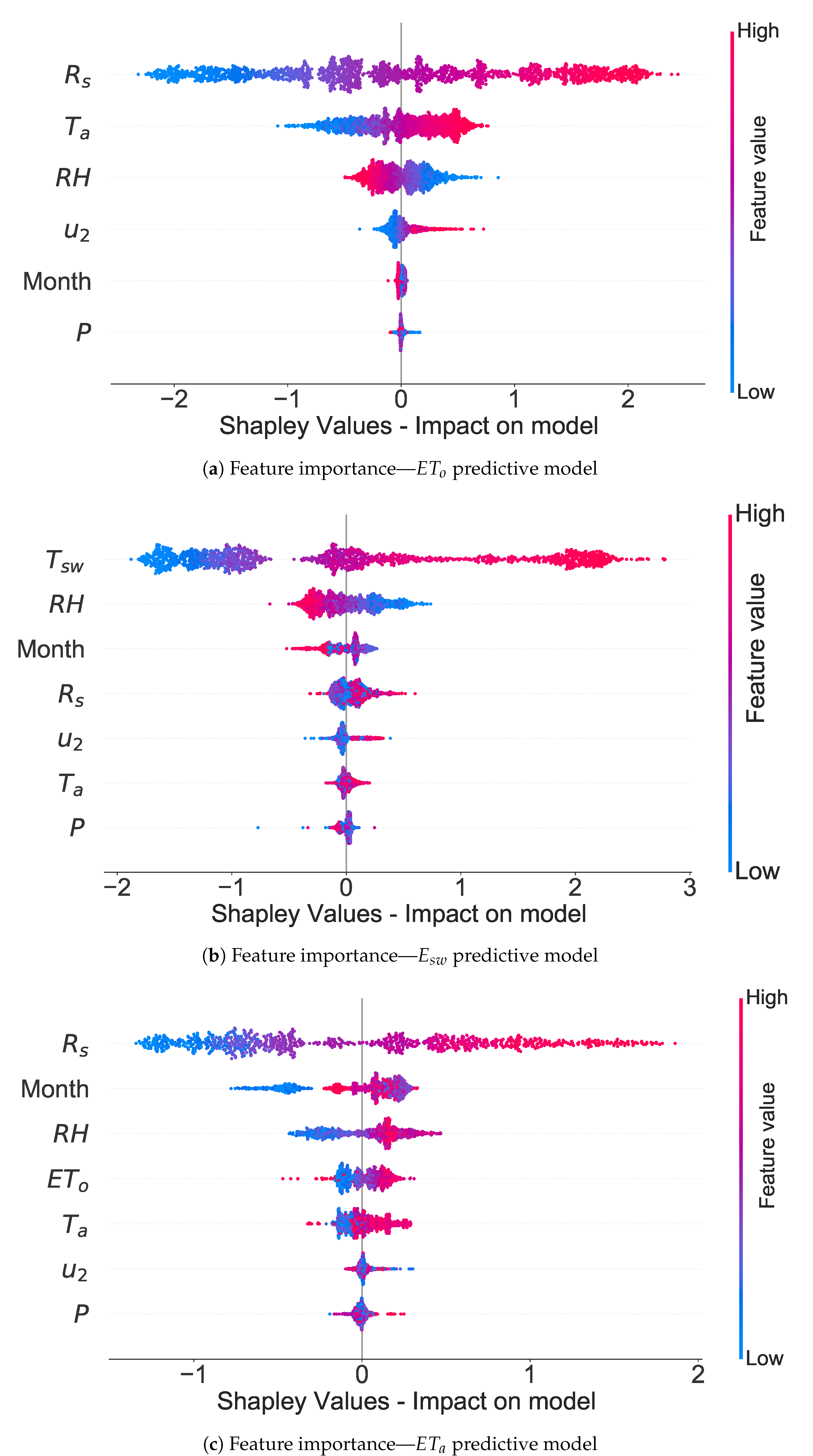
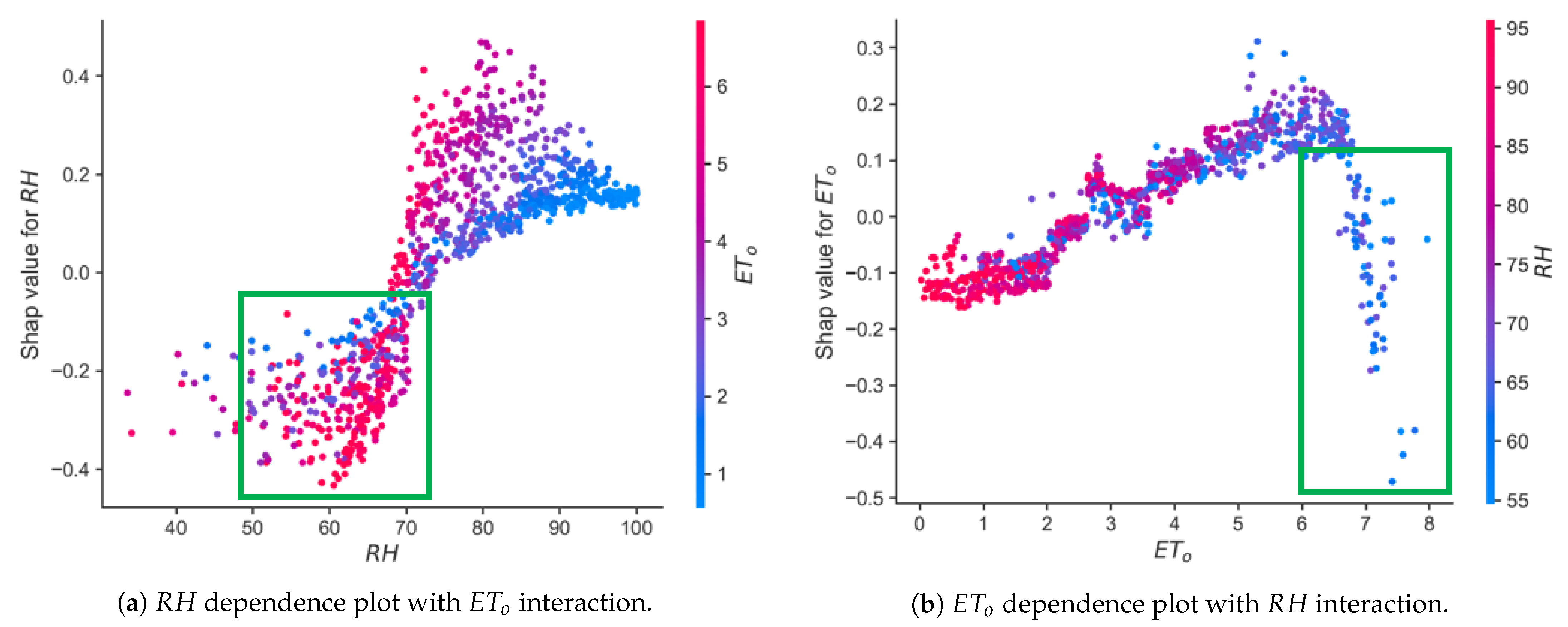
| Model | Data | RMSE * (mm) | MAE (mm) | (%) | ||
|---|---|---|---|---|---|---|
| Random Forest | Training data only | 0.064 | 1.345 | 0.998 | - | |
| Testing data only | 0.163 | 1.360 | 0.990 | - | ||
| NGBoost-XGBoost | Training data only | 0.098 | 0.074 | 0.996 | 100 | |
| Testing data only | 0.124 | 0.092 | 0.994 | 100 | ||
| Random Forest | Training data only | 0.324 | 1.493 | 0.967 | - | |
| Testing data only | 0.870 | 1.504 | 0.776 | - | ||
| NGBoost-XGBoost | Training data only | 0.703 | 0.545 | 0.843 | 99.1 | |
| Testing data only | 0.918 | 0.736 | 0.750 | 89.9 | ||
| Random Forest | Training data only | 0.192 | 1.003 | 0.973 | - | |
| Testing data only | 0.580 | 1.005 | 0.767 | - | ||
| NGBoost-XGBoost | Training data only | 0.414 | 0.311 | 0.876 | 99.4 | |
| Testing data only | 0.537 | 0.418 | 0.801 | 93 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Başağaoğlu, H.; Chakraborty, D.; Winterle, J. Reliable Evapotranspiration Predictions with a Probabilistic Machine Learning Framework. Water 2021, 13, 557. https://doi.org/10.3390/w13040557
Başağaoğlu H, Chakraborty D, Winterle J. Reliable Evapotranspiration Predictions with a Probabilistic Machine Learning Framework. Water. 2021; 13(4):557. https://doi.org/10.3390/w13040557
Chicago/Turabian StyleBaşağaoğlu, Hakan, Debaditya Chakraborty, and James Winterle. 2021. "Reliable Evapotranspiration Predictions with a Probabilistic Machine Learning Framework" Water 13, no. 4: 557. https://doi.org/10.3390/w13040557
APA StyleBaşağaoğlu, H., Chakraborty, D., & Winterle, J. (2021). Reliable Evapotranspiration Predictions with a Probabilistic Machine Learning Framework. Water, 13(4), 557. https://doi.org/10.3390/w13040557







