Deep Learning Method Based on Physics Informed Neural Network with Resnet Block for Solving Fluid Flow Problems
Abstract
:1. Introduction
2. Methodology
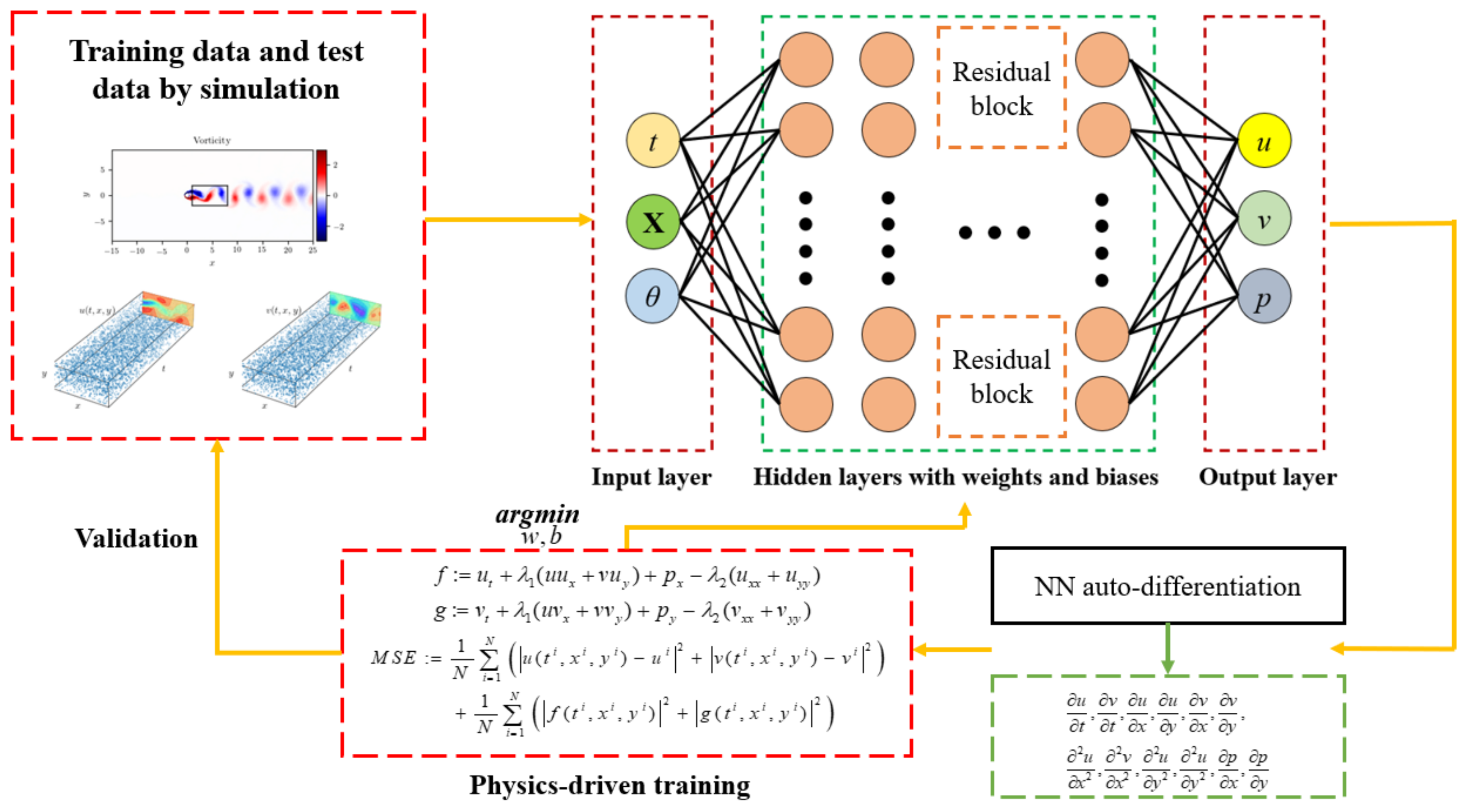
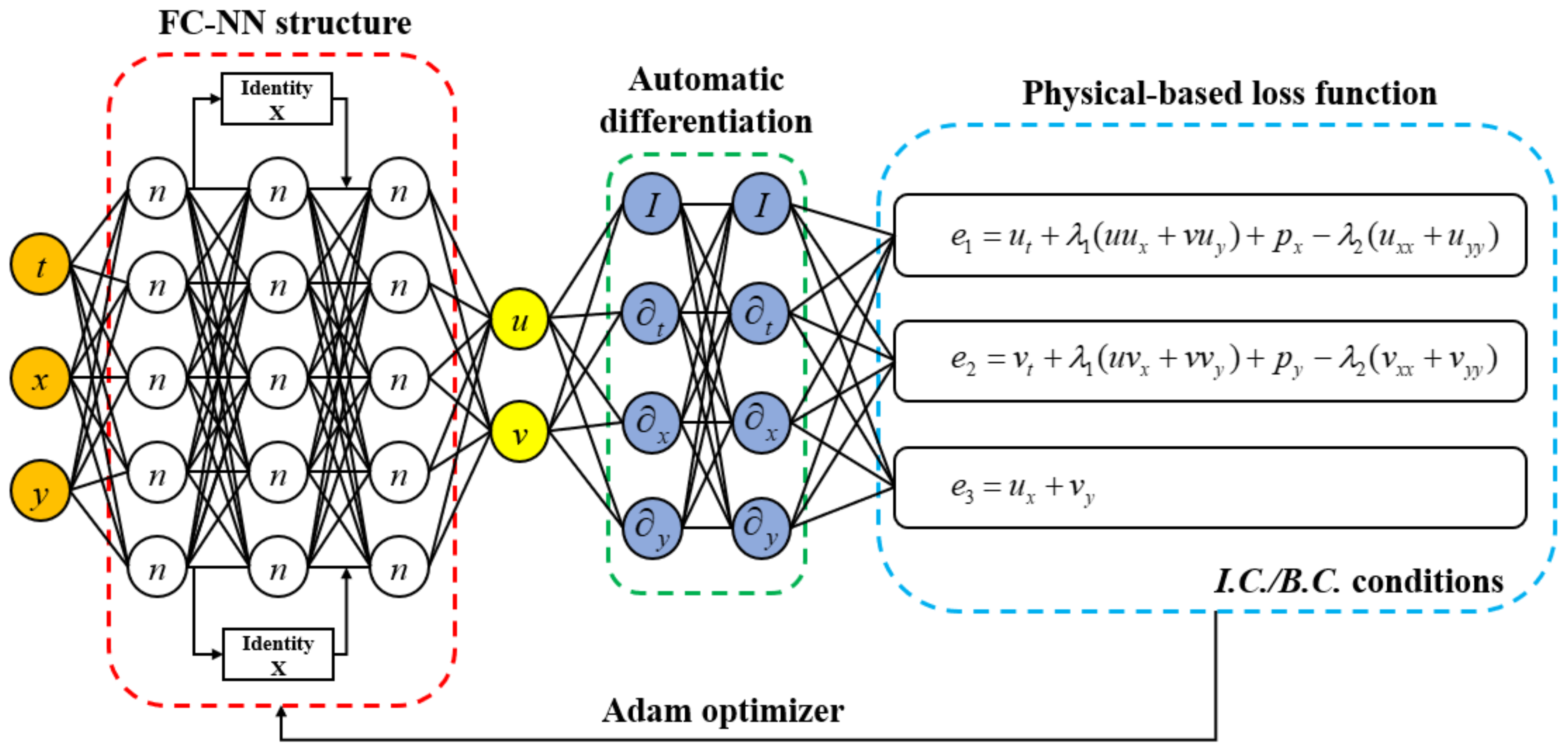
2.1. Overview
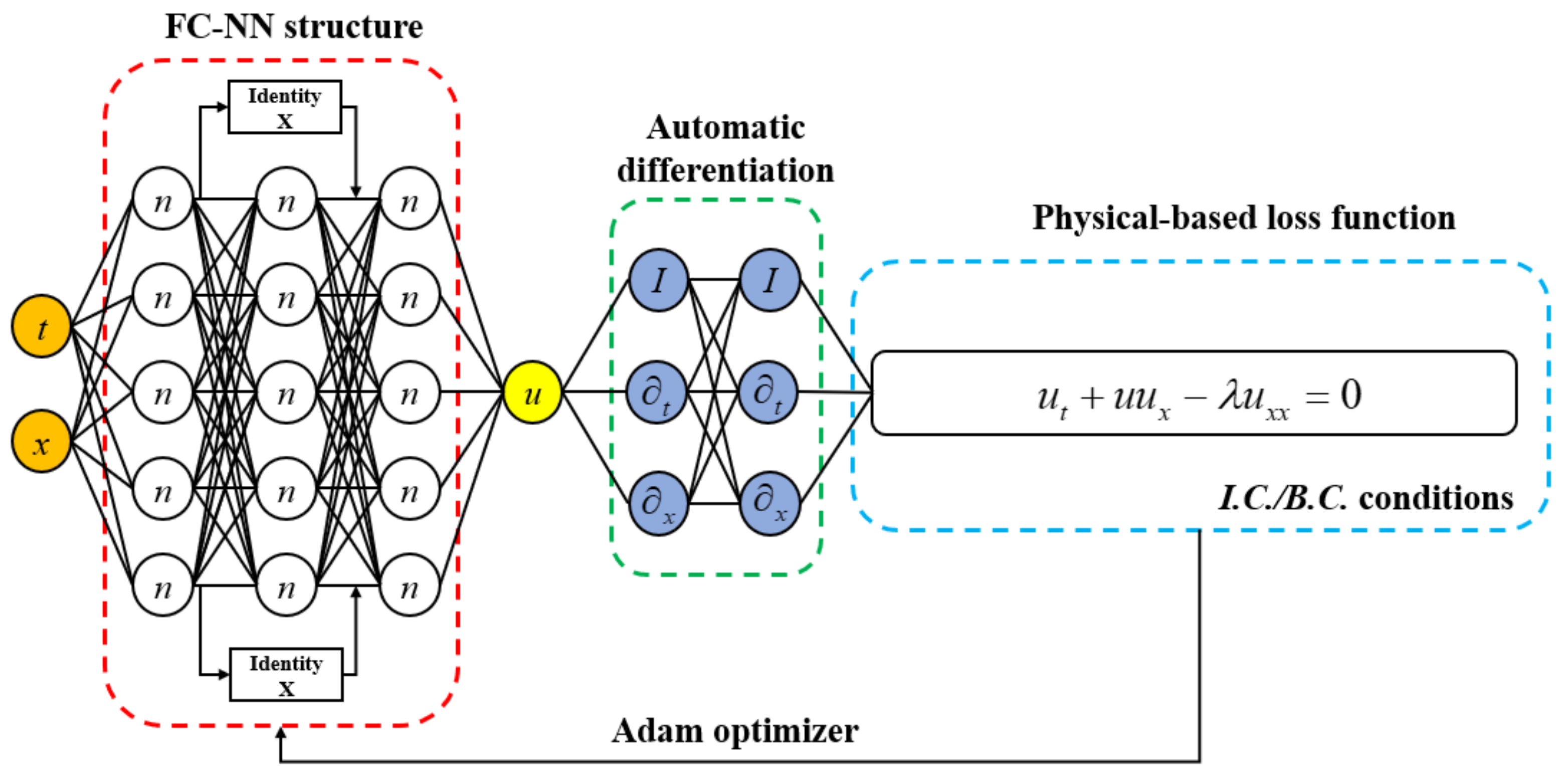
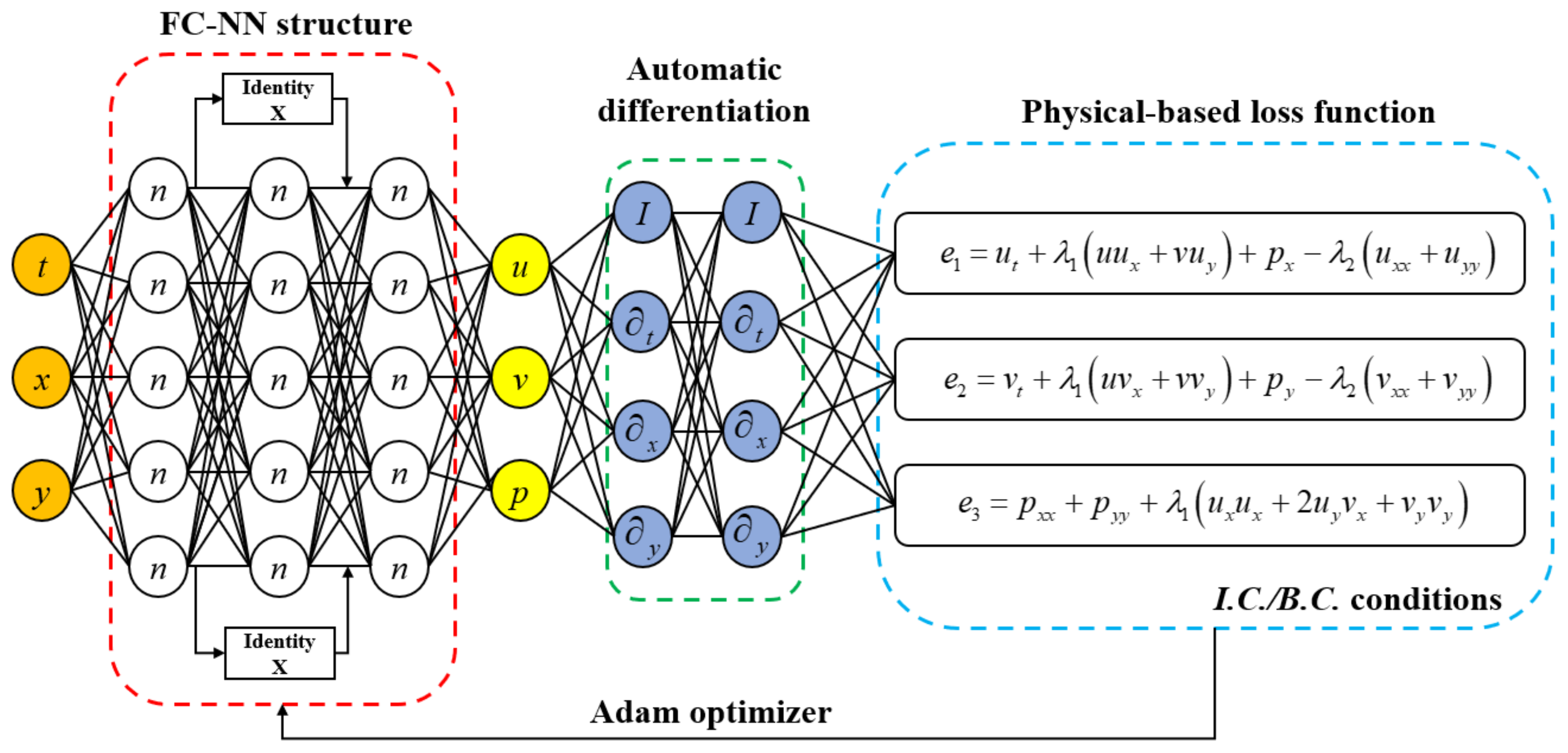
2.2. Deep Neural Network and Physical Informed Neural Network
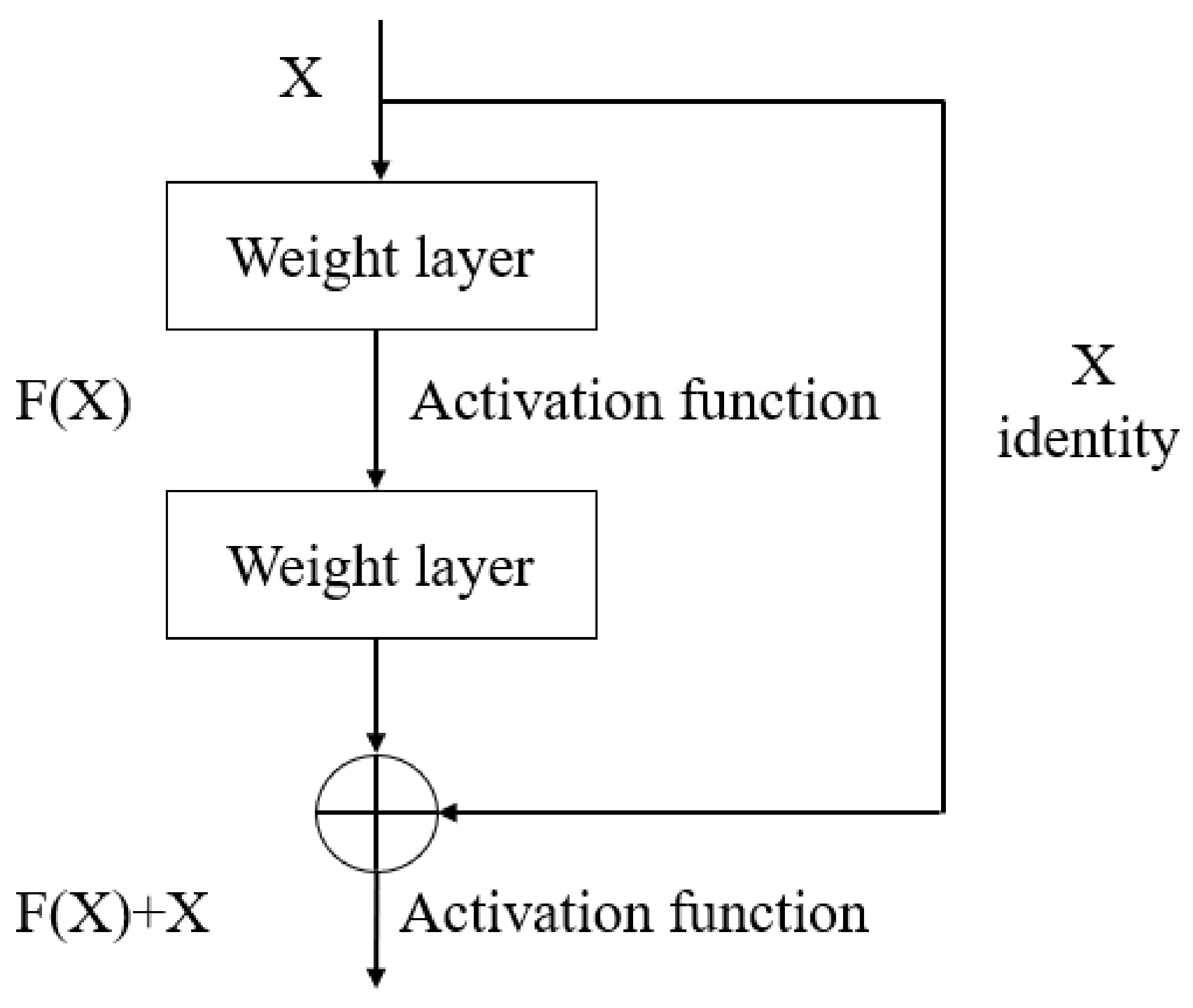
2.3. Residual Neural Network (Resnet)
3. Structural Optimization
3.1. Model Parameter Initialization Method
3.2. Adam Optimization
- Step 1: compute gradients of parameters at time step w.r.t stochastic objective functions;
- Step 2: compute first moment estimate, to help avoid disordered moving, and to prevent settling into local optima;
- Step 3: estimate second moment estimate, to guarantee an upper bound of step size;
- Step 4: compute unbiased estimate of first moment estimate and second moment estimate;
- Step 5: update parameters.
4. Discussion
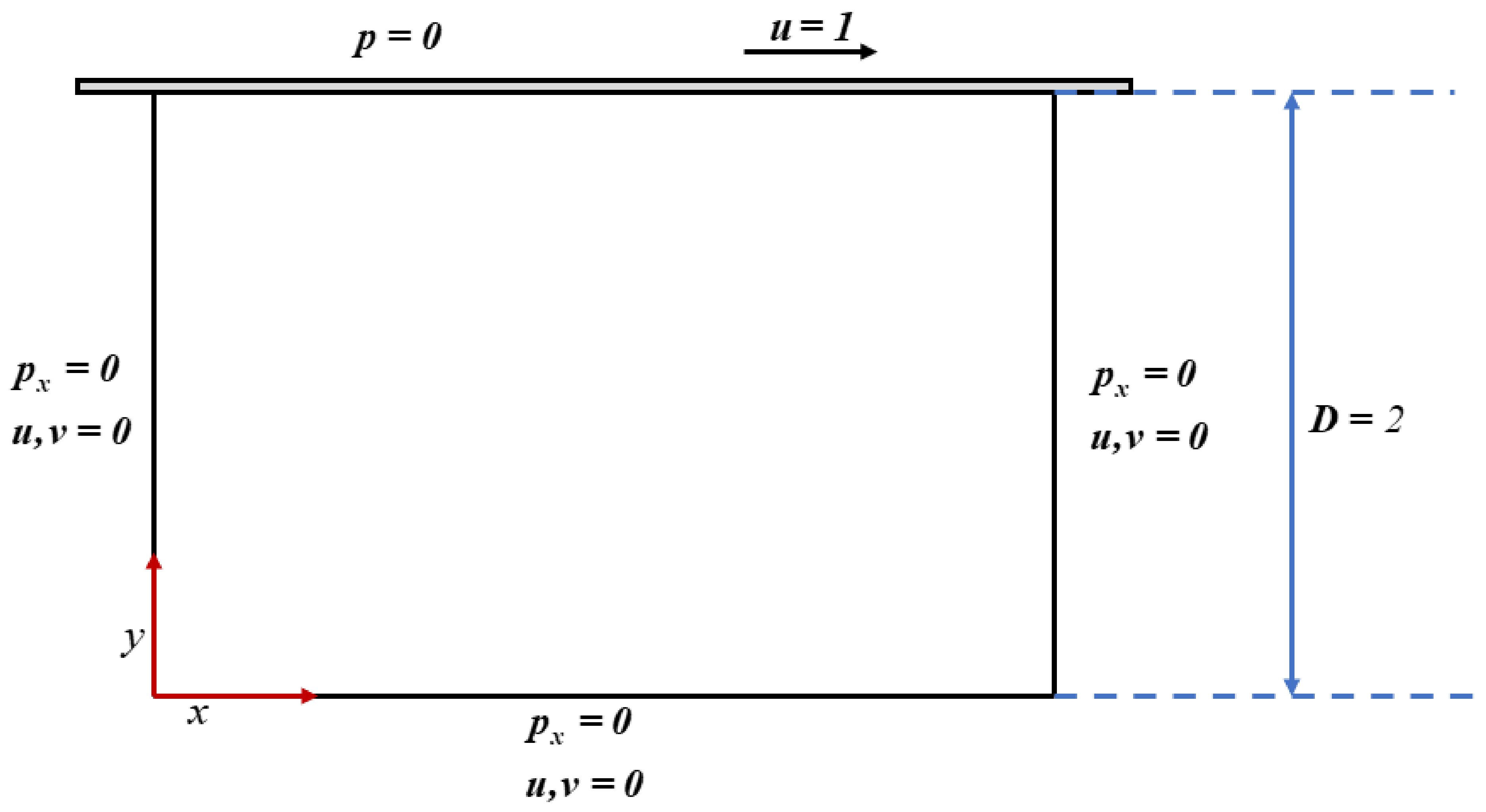
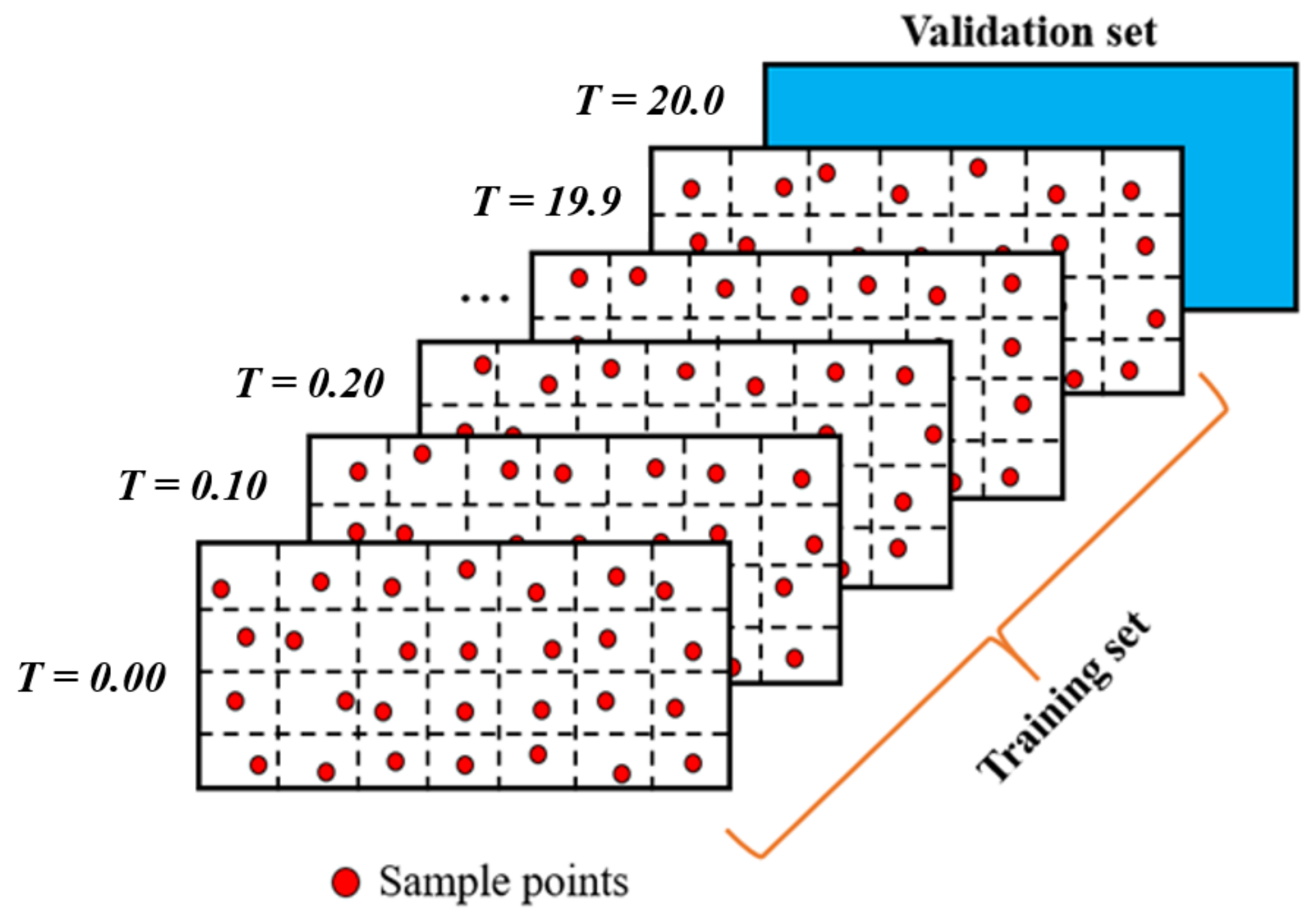
4.1. Problem Setup
4.2. PINN Method for Burger’s Equation with Discontinuous Solution
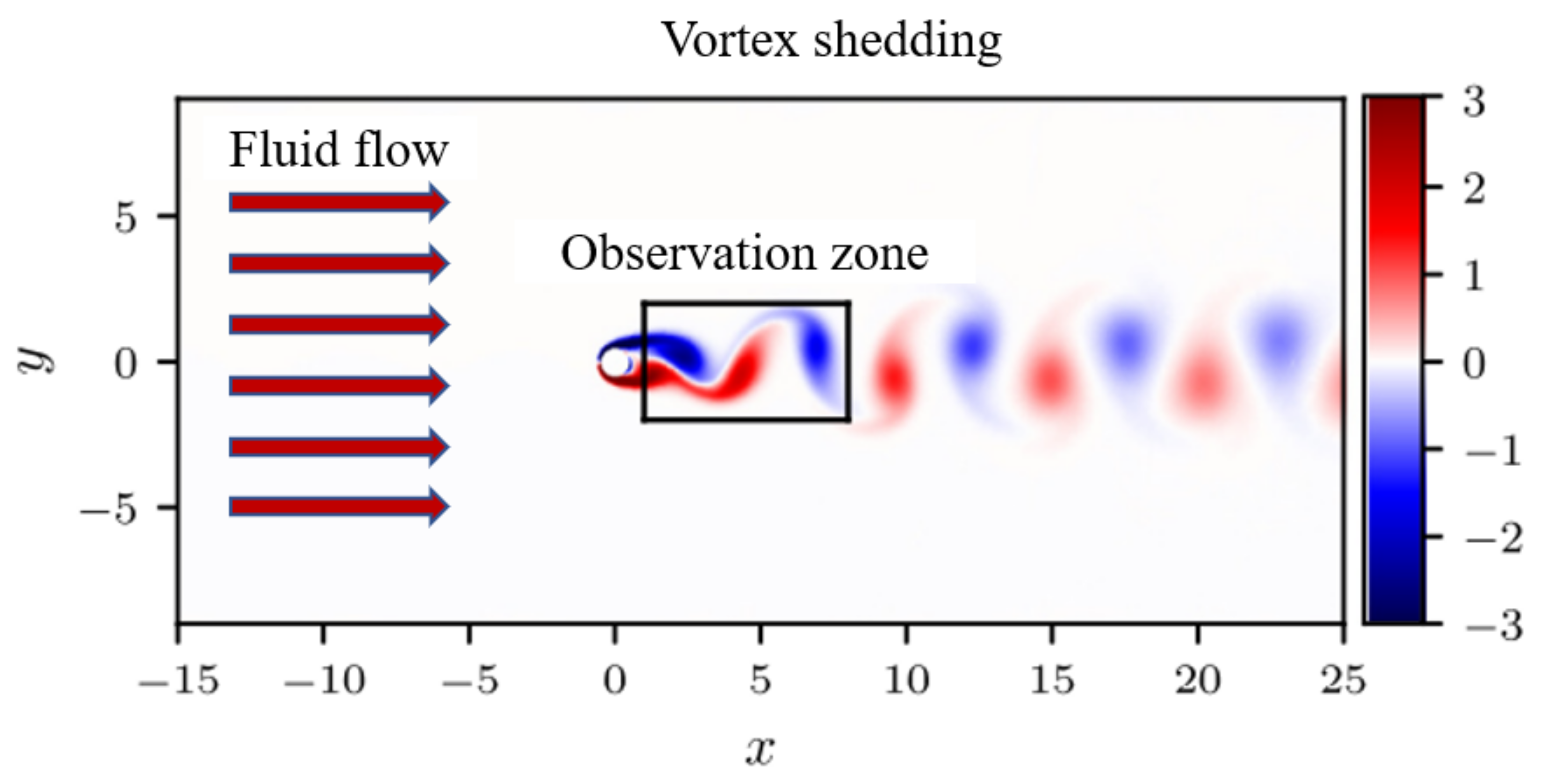
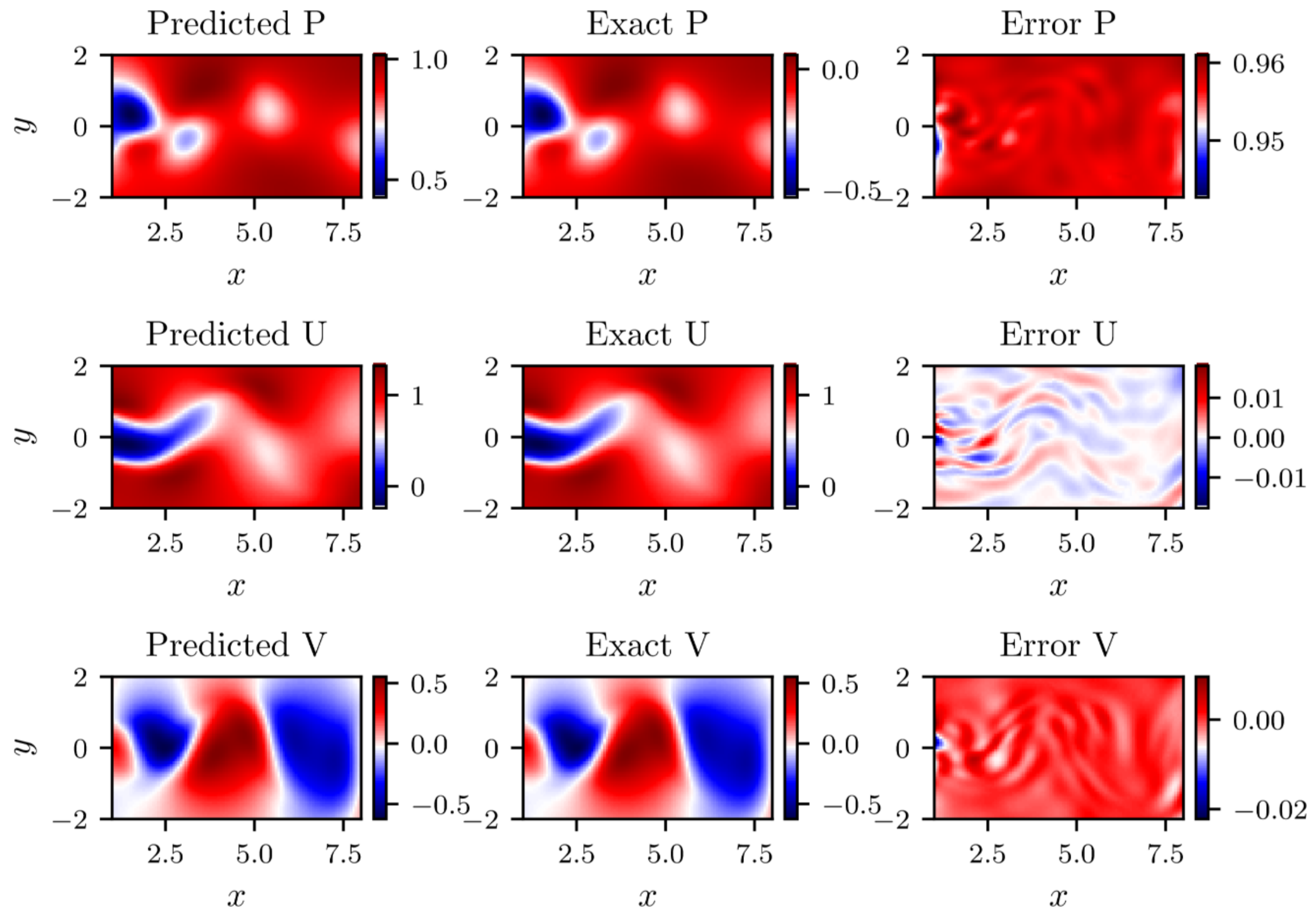
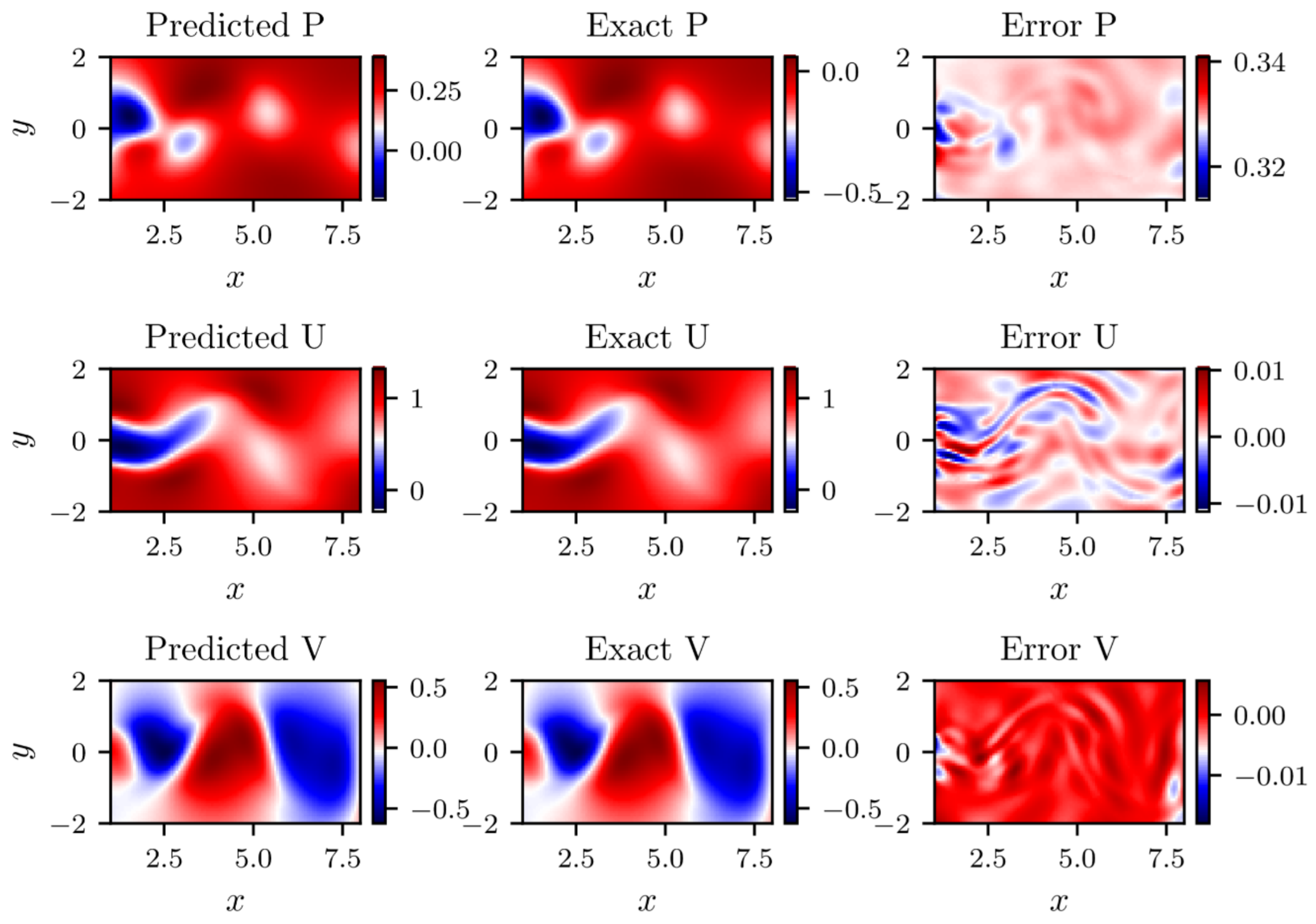
4.3. Res-PINN Method for N-S Equation with Continuous Solution
5. Conclusions
- (1)
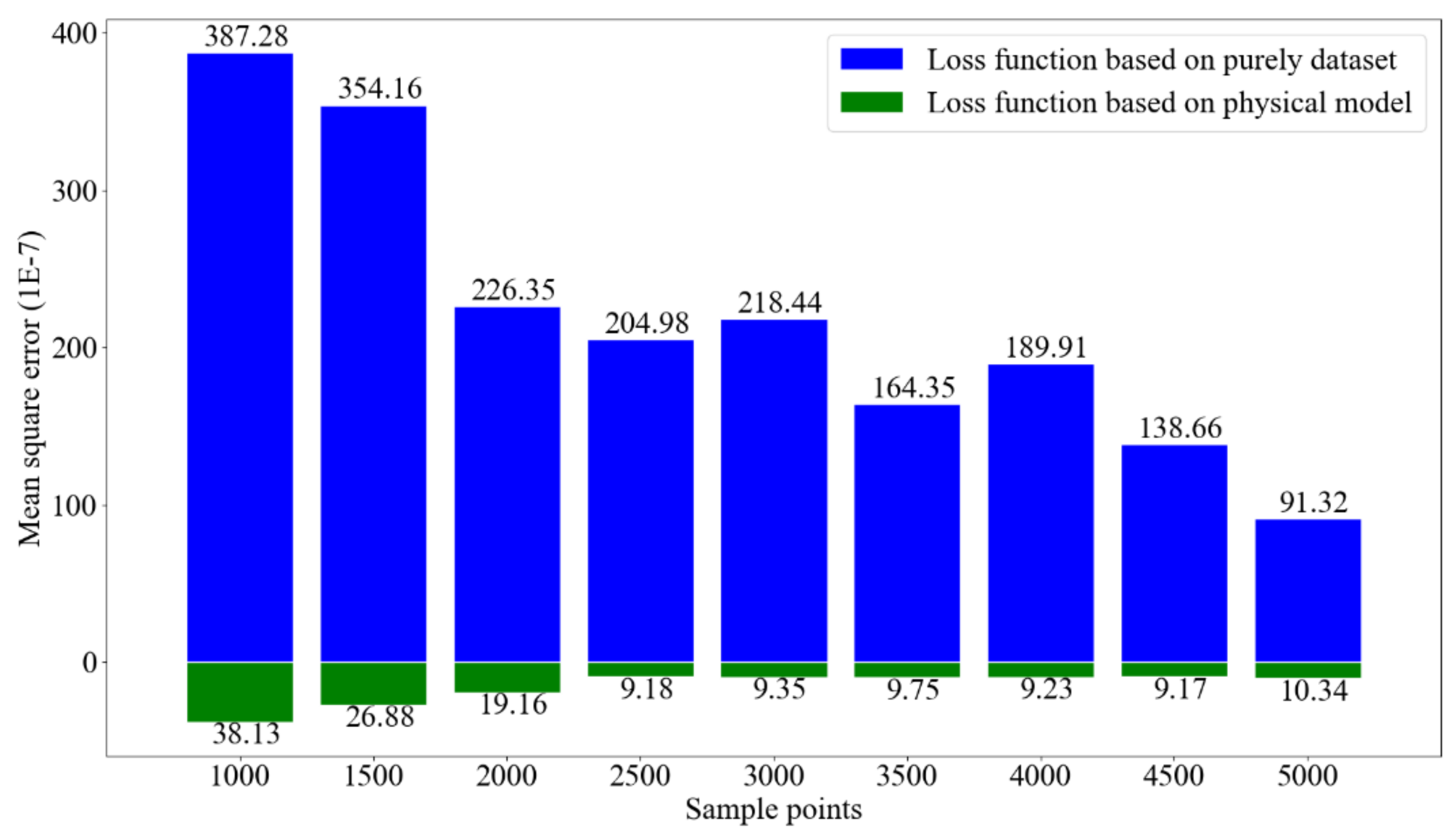
- The Burger’s equation predicted by the Res-PINN and that predicted by the traditional deep learning are compared and the results show that the Res-PINN has better performance in calculating and predicting the flow fields. The Res-PINN can well predict the results under only 1000 samples.
- (2)
- The Navier-Stokes equations predicted by PINN and that predicted by Res-PINN are contrasted and the results demonstrate that the Res-PINN can ensure the better at accuracy. The magnitude of mean square errors of problems reach to 10−5.
- (3)
- the Res-PINN can well calculate the inverse parameters in partial differential equations. The errors of the inverse parameters are 0.98% and 3.1% in clean data while 0.99% and 3.1% in noisy data, it demonstrates that can well solve the inverse problem even in the noisy data.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ding, H.; Shu, C.; Yeo, K.S.; Xu, D. Simulation of incompressible vis-cous flows past a circular cylinder by hybrid FD scheme and meshless least square-based finite difference method. Comput. Methods Appl. Mech. Eng. 2004, 193, 727–744. [Google Scholar] [CrossRef]
- Liu, F.; Zheng, X.Q. A Strongly Coupled Time-Marching Method for Solving the Navier–Stokes and k-ω Turbulence Model Equations with Multigrid. J. Comput. Phys. 1996, 128, 289–300. [Google Scholar] [CrossRef] [Green Version]
- Lucia, D.J.; Beran, P.S.; Silva, W.A. Reduced-order modeling: New approached for computational physics. Prog. Aerosp. Sci. 2004, 40, 51–117. [Google Scholar] [CrossRef] [Green Version]
- Henshawa, M.J.; Badcock, K.J.; Vio, G.A. Non-linear aeroelastic prediction for aircraft applications. Prog. Aerosp. Sci. 2007, 43, 65–137. [Google Scholar] [CrossRef]
- Jovanovie, M.R.; Schmid, P.J.; Nichols, J.W. Sparsity-promoting dynamic mode decomposition. Phys. Fluids 2014, 26, 024103. [Google Scholar] [CrossRef]
- Hemati, M.S.; Williams, M.O.; Rowley, C.W. Dynamic mode decomposition for large and streaming datasets. Phys. Fluids 2014, 26, 111701. [Google Scholar] [CrossRef] [Green Version]
- Chen, G.; Li, D.; Zhou, Q. Efficient aeroelastic prediction for aircraft applications. Prog. Aerosp. Sci. 2018, 40, 51–117. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Sainath, T.N.; Mohamed, A.; Kingsbury, B.; Ramabhadran, B. Deep convolutional neural networks for LVCSR. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, 26–31 May 2013; IEEE: New York, NY, USA, 2013; pp. 8614–8618. [Google Scholar]
- Xiong, H.Y.; Alipanahi, B.; Lee, L.J.; Bretschneider, H.; Merico, D.; Yuen, R.K.; Hua, Y.; Gueroussov, S.; Najafabadi, H.S.; Hughes, T.R. The human splicing code reveals new insights into the genetic determinants of disease. Science 2015, 347, 1254806. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ma, M.; Lu, J.; Tryggvason, G. Using statistical learning to close two-fluid multiphase flow equations for a simple bubbly system. Phys. Fluids 2015, 27, 092101. [Google Scholar] [CrossRef]
- Roshko, A. Perspectives on bluff body aerodynamics. J. Wind Eng. Ind. Aerodyn. 1993, 49, 79–100. [Google Scholar] [CrossRef]
- Ling, J.; Kurzawski, A.; Templeton, J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid Mech. 2016, 807, 155–166. [Google Scholar] [CrossRef]
- Wu, J.; Xiao, H.; Paterson, E. Physics-informed machine learning approach for augmenting turbulence models: A comprehensive framework. Phys. Rev. Fluids 2018, 3, 074602. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Li, H.; Chen, X.; Chen, Y. Deep learning-based model reduction for distributed parameter systems. IEEE Trans. Syst. Man Cybern. Syst. 2016, 46, 1664–1674. [Google Scholar] [CrossRef]
- Maulik, R.; San, O.; Rasheed, A.; Vedula, P. Data-driven deconvolution for large eddy simulation of Kraichnan turbulence. Phys. Fluids 2018, 30, 125109. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.; Parsian, A.; Khodadadi, H.; Akbari, M.; Ghani, K.; Goodarzi, M.; Bach, Q.-V. Develop optimal network topology of artificial neural network (AONN) to predict the hybrid nanofluids thermal conductivity according to the empirical data of Al203-Cu nanoparticles dispersed in ethylene glycol. Phys. A Stat. Mech. Appl. 2020, 549, 124015. [Google Scholar] [CrossRef]
- Omataa, N.; Shirayama, S. A novel method of low-dimensional representation for temporal behavior of flow fields using deep autoencoder. AIP Adv. 2019, 9, 015006. [Google Scholar] [CrossRef]
- Fukami, K.; Fukagata, K.; Taira, K. Super-resolution reconstruction of turbulent flows with machine learning. J. Fluid Mech. 2019, 870, 106–120. [Google Scholar] [CrossRef] [Green Version]
- Jin, X.; Cheng, P.; Chen, W.; Li, H. Prediction model of velocity field around circular cylinder over various Reynolds numbers by fusion convolutional neural networks based on pressure on the cylinder. Phys. Fluids 2018, 30, 047105. [Google Scholar] [CrossRef]
- Sekar, V.; Jiang, Q.; Shu, C.; Khoo, B. Fast flow field prediction over airfoils using deep learning approach. Phys. Fluids 2019, 31, 057103. [Google Scholar] [CrossRef]
- Han, R.G.; Wang, Y.X.; Zhang, Y.; Chen, G. A novel spatial-temporal prediction method for unsteady wake flows based on hybrid deep neural network. Phys. Fluids 2019, 31, 127101. [Google Scholar]
- Farimani, A.B.; Gomes, J.; Pande, V.S. Deep learning the physics of transport phenomena. arXiv 2017, arXiv:1709.02432. [Google Scholar]
- Xie, Y.; Franz, E.; Chu, M.; Thuerey, N. tempoGAN: A temporally coherent, volumetric GAN for super-resolution fluid flow. ACM Trans. Graph. 2018, 37, 95. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Piscopo, M.L.; Spannowsky, M.; Waite, P. Solving differential equations with neural networks: Application to the calculation of cosmological phase transitions. arXiv 2019, arXiv:1902.05563. [Google Scholar] [CrossRef] [Green Version]
- Sun, L.; Gao, H.; Pan, S.; Wang, J.-X. Surrogate modeling for fluid flows based on physics-constrained deep learning without simulation data. Comput. Methods Appl. Mech. Eng. 2020, 361, 112732. [Google Scholar] [CrossRef] [Green Version]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. arXiv 2015, arXiv:1502.05767. [Google Scholar]
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. J. Mach. Learn. 2010, 9, 249–256. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics Informed Deep Learning (Part I): Data-driven Solutions of Nonlinear Partial Differential Equations. arXiv 2017, arXiv:1711.10671. [Google Scholar]



| Neurons | 10 | 20 | 30 | 40 | |
|---|---|---|---|---|---|
| Layers | |||||
| 2 (without Restnet) | |||||
| 4 | |||||
| 6 | |||||
| 8 | |||||
| 10 | |||||
| Mean Square Error (Training Set) | Mean Square Error (Validation Set) | |
|---|---|---|
| Correct N-S eqaution | |
| Identified N-S equation with clean data (PINN) | |
| Identified N-S equation with clean data (Res-PINN) | |
| Identified N-S equation with noise data (PINN) | |
| Identified N-S equation with noise data (Res-PINN) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, C.; Zhang, G.-T. Deep Learning Method Based on Physics Informed Neural Network with Resnet Block for Solving Fluid Flow Problems. Water 2021, 13, 423. https://doi.org/10.3390/w13040423
Cheng C, Zhang G-T. Deep Learning Method Based on Physics Informed Neural Network with Resnet Block for Solving Fluid Flow Problems. Water. 2021; 13(4):423. https://doi.org/10.3390/w13040423
Chicago/Turabian StyleCheng, Chen, and Guang-Tao Zhang. 2021. "Deep Learning Method Based on Physics Informed Neural Network with Resnet Block for Solving Fluid Flow Problems" Water 13, no. 4: 423. https://doi.org/10.3390/w13040423





