2.1. The Tilted V benchmark Problem
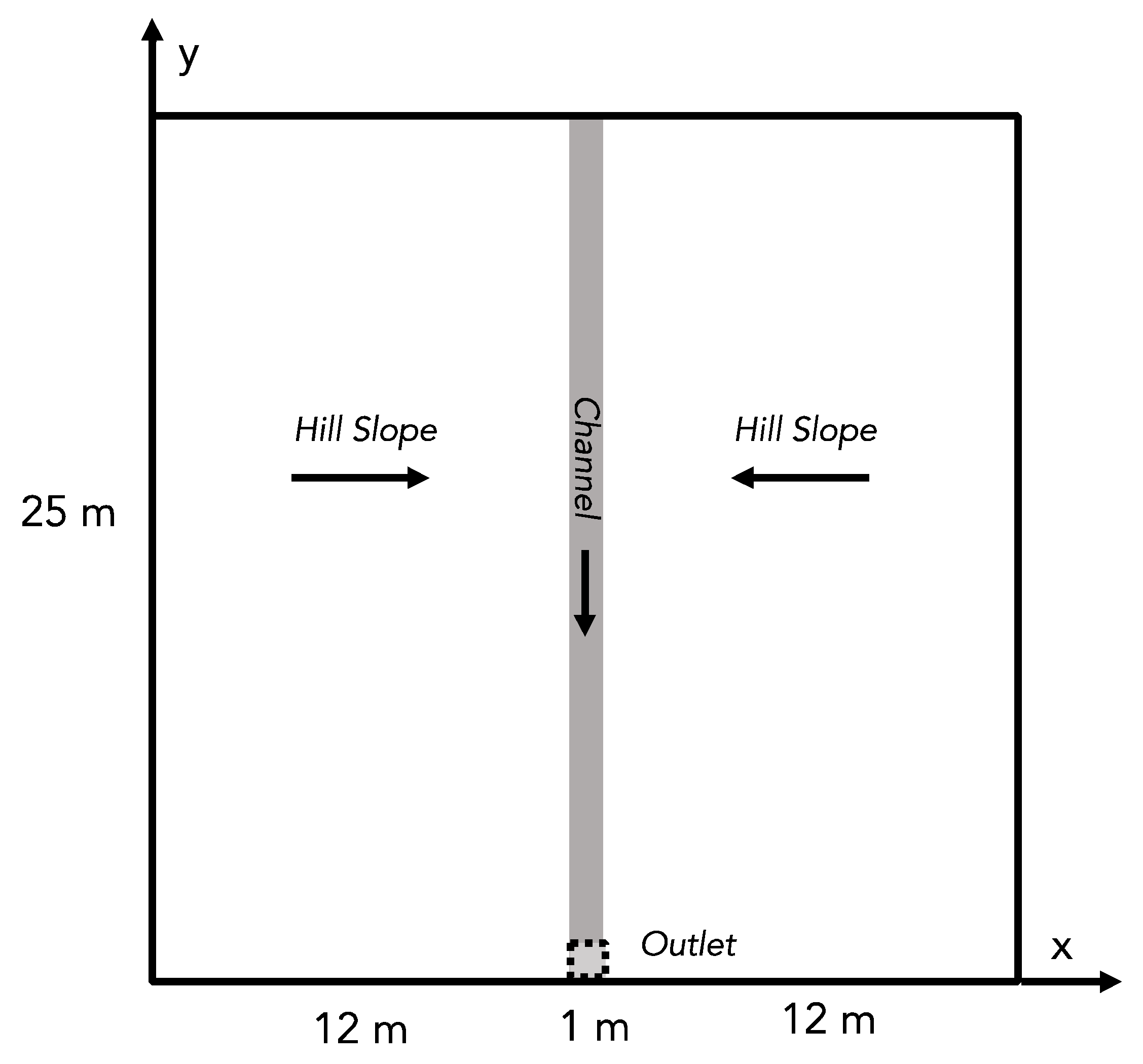
The Tilted V test problem [
23,
24,
25,
26] is an established benchmark used to test hydrologic models [
27]. This test problem is shown in
Figure 1 and is one of the simplest representations of a watershed shape. The problem domain is square and contains two hillslopes that drain inward to a central channel. The entire domain is then sloped along the channel (the y-direction in
Figure 1), usually with a shallower channel slope than the hillslopes. Though there are different variations, generally, the domain is initialized dry and rained on for a given duration after which there is a period of recession. The total flow for the domain is usually calculated at the outlet of the channel, shown in
Figure 1. This test problem is solved with the surface water equations.
The surface water equations [
27] combine the continuity equation and the Manning’s depth-discharge relationship in two spatial dimensions as follows:
where
h is the pressure head (m),
qrain is the rainfall flux (mh
−1),
t is time (h), and
v is the velocity given by the depth-discharge relationship:
Sx,y are the topographic slopes in the
x and
y directions (-), and
n is the Manning’s roughness coefficient (m
1/3h
−1). There are many approaches to solving for surface water flow; however, no analytical solutions exist for the Tilted V test problem. In this work, the integrated hydrologic model ParFlow [
26,
28,
29] was used to solve these equations.
2.2. Numerical Solution of the Tilted V and General Training Approach
The integrated hydrologic model ParFlow [
30] was used to solve the 2D overland flow equations for the Tilted V benchmark problem. Model input parameters were systematically varied across a range of values to generate a suite of ensemble simulations (
Table 1). Three sets of simulations were conducted with ParFlow: a 1024-member ensemble used to train the ML models and two test ensembles with 243 and 32 ensemble members, respectively. One of the two test datasets was constructed to have same parameter ranges as the training dataset (
In Range), while the other was constructed to have parameters outside the range used for training (
Full Range).
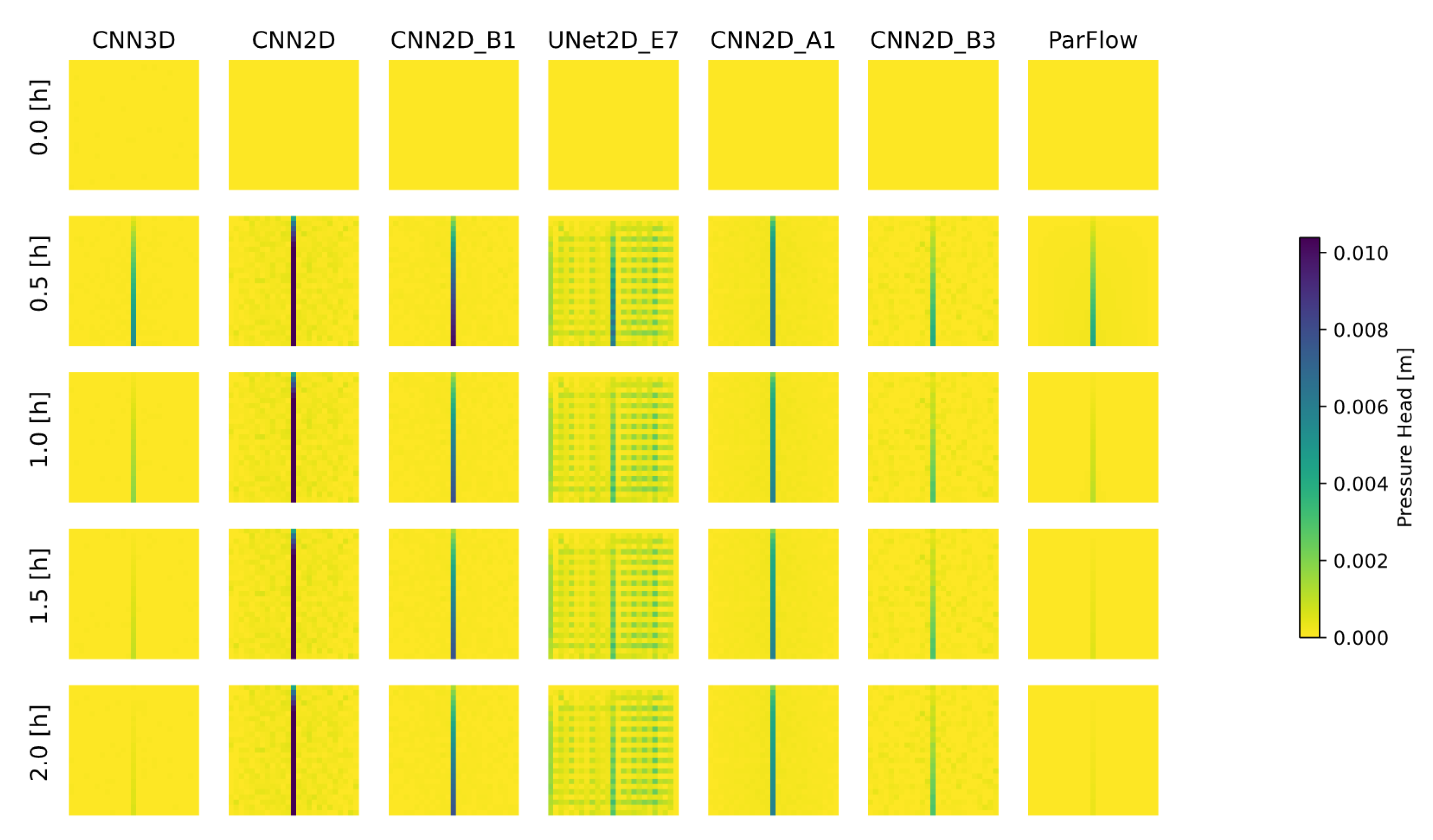
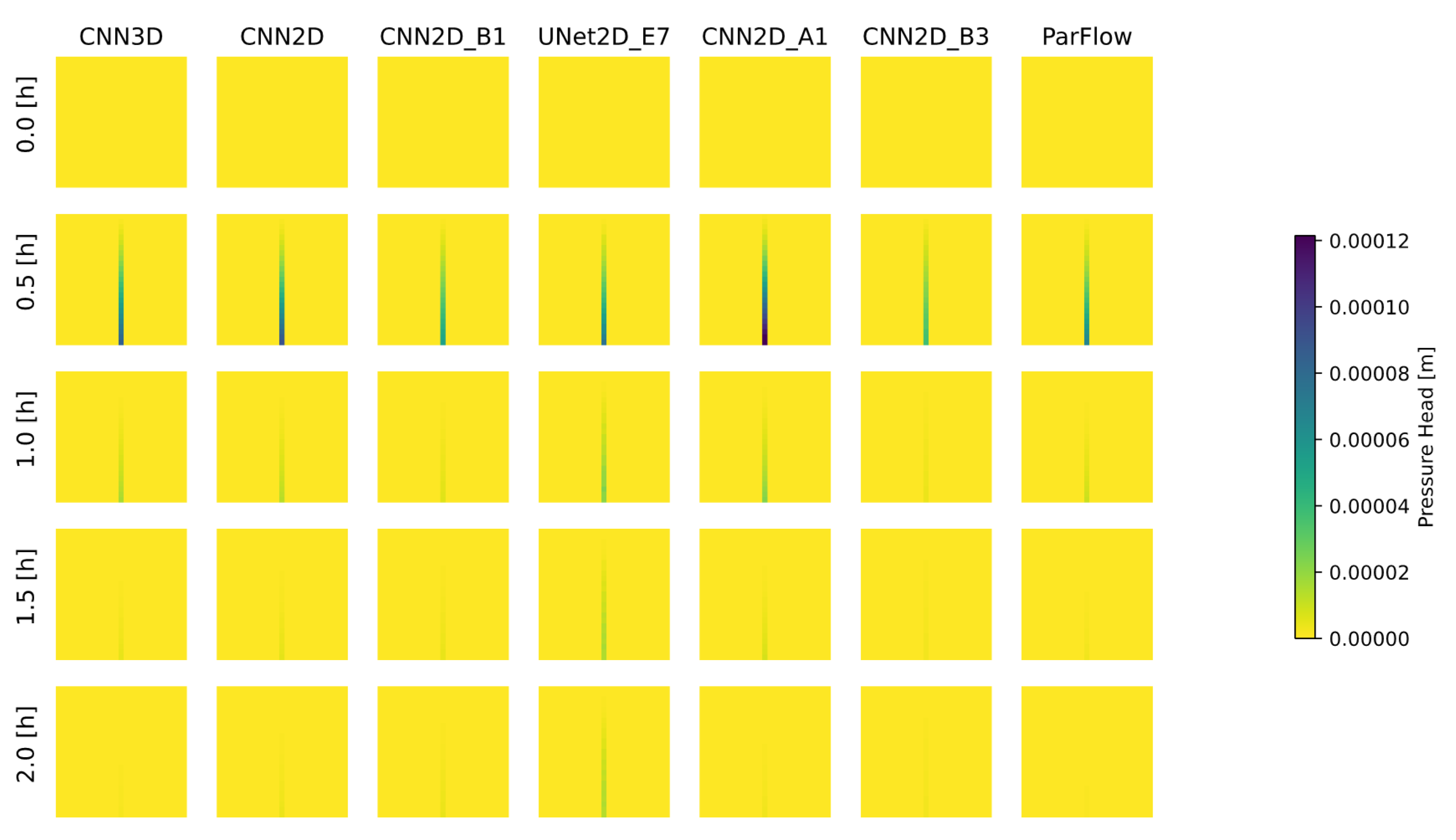
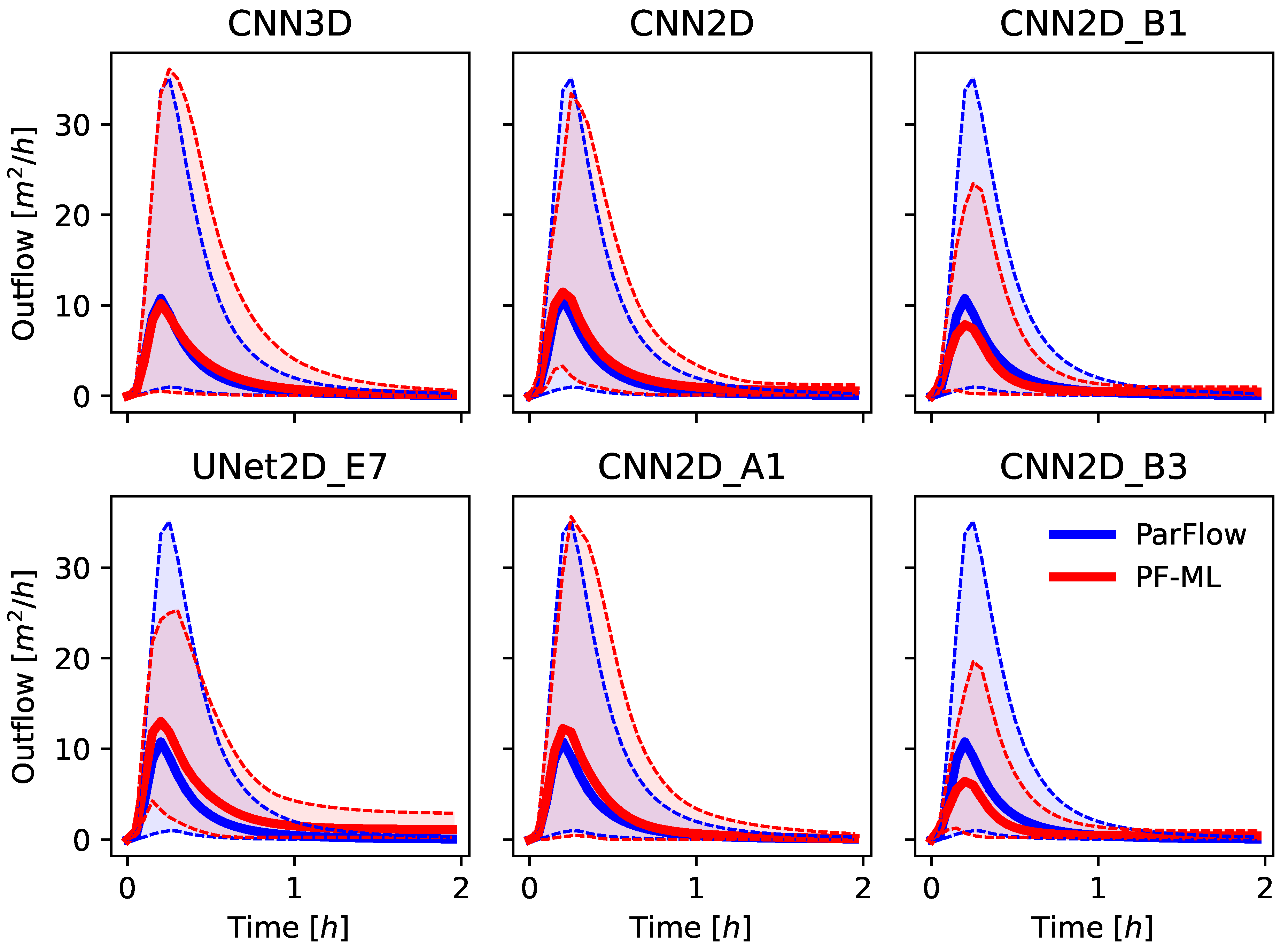
The solution for both ParFlow and the ML-emulator models results in a 2D time-dependent map of pressure-head over the domain, which represents the height of ponded water above the ground surface. Most solutions to the Tilted V then calculate the hydrograph at the outlet (discussed above) using Manning’s Equation (Equation (2)) with the surface pressure at the outlet cell as input. This same approach was used for the ML-emulator models as well. Specifically, only the surface pressure was used in the loss function during training, not the outflow hydrograph from the ParFlow simulations. This is in contrast to prior ML approaches that might focus on learning the hydrograph directly [
3,
5]. This approach is more general and allows for the ML model to produce other hydrologic quantities that could be of interest for, e.g., flooding or water management; however, the hydrographs produced are very sensitive to the convergence of the surface pressure.
2.3. ML Model Architectures
We chose several machine learning architectures from which to construct emulator model of the Titled V problem. Six ML models were chosen to be described in the experiments presented here from a trial-and-error process that involved over 30 different emulators. Because the focus here is on reproducing the change in a 2D grid of values over time, we developed models based upon the Convolution Neural Net (CNN) architectures [
31,
32] commonly used in video reconstruction and extrapolation [
33]. We also applied U-Net approaches, which are better suited for maintaining spatial information [
34]. The ML models used in this study were chosen to represent three main architectures (2D CNN, 3D CNN, and U-Net) with a varying degree of depth, as indicated by the total number of parameters. The 3D model was designed to be trained on temporal behavior of the system explicitly and simulates the entire timeseries at once, while the 2D models are designed to simulate only one timestep at a time. Complete details of the models developed for this study are provided in
Appendix A, and the models are summarized as follows:
CNN3D, a deep 3D convolution (third dimension is time) detailed in
Table A1;
CNN2D, a deep 2D convolution detailed in
Table A2;
CNN2D_B1, a moderately deep 2D convolution detailed in
Table A3;
UNet2D_E7, a three-level U-Net detailed in
Table A4;
CNN2D_A1, a deep 2D convolution with no pooling detailed in
Table A5; and
CNN2D_B3, a very shallow 2D convolution detailed in
Table A6.
The CNN3D model had the most parameters (>240M), while the CNN2D_B3 model had the least (83K). The CNN2D model is quite similar in architecture and size to the CNN3D but, as noted above, is not explicitly trained on the time series of the simulation results. The CNN2D and CNN2D_A1 models are similar in size and architecture except that the CNN2D_A1 model has no pooling steps, only convolutions. The models were all implemented using the Pytorch Python library [
35]. Numerical experiments and training details are provided in the following section.
2.4. ML Model Training
As shown in
Table 1, the channel and hill slopes were varied (see
Figure 1) to construct 2D slope inputs (in
x and
y); the Manning’s roughness value was uniform over the domain and varied across the values as given. The given rain rate, start, and length were used to create a time series of rainfall inputs. A training dataset and two independent test datasets were developed as indicated.
Table 1.
Tilted V test case, training, and test parameters.
Table 1.
Tilted V test case, training, and test parameters.
| | Training | | Test In Range | | Test Full Range |
|---|
| Variable | Units | Lower | Mid1 | Mid2 | Upper | Lower | Mid | Upper | Lower | Upper |
| channel slope | (-) | 0.001 | 0.004 | 0.007 | 0.01 | 0.0015 | 0.0055 | 0.0095 | 0.01 | 0.02 |
| hill slopes | (-) | 0.05 | 0.083 | 0.117 | 0.15 | 0.055 | 0.0775 | 0.1 | 0.01 | 0.2 |
| Manning’s n | (m1/3h−1) | 8.3 × 10−6 | 8.8 × 10−6 | 9.3 × 10−6 | 9.7 × 10−6 | 8.5 × 10−6 | 8.8 × 10−6 | 9.0 × 10−6 | 5.0 × 10−6 | 2.1 × 10−5 |
| rain rate | (mh−1) | −0.005 | −0.01 | −0.015 | −0.02 | −0.007 | −0.011 | −0.015 | −0.004 | −0.02 |
| rain start | (h) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| rain length | (h) | 0.1 | 0.15 | 0.2 | 0.25 | 0.1 | 0.15 | 0.25 | 0.1 | 0.3 |
These were all fed into the ML models as static (Sx, Sy, n) or time-dependent (rainfall) two-dimensional fields that corresponded to the grid. That is, instead of using a single-channel slope or rainfall value as input, a full 2D map was constructed, even for variables like the Manning’s n, which were constant in space. This was done to allow the framework to accommodate heterogeneity in parameter values in future studies. All models had the same domain configuration, where nx = ny = 25 with ∆x = ∆y = 1 [m]. All models were also run for a total time of two hours with forty uniform timesteps, ∆t = 0.05 [h].
All six of the ML models were trained on the training ensemble (detailed below) using a Nvidia 2080 Super Max-Q GPU. The learning rate was set to 10
−4 using the Adam optimizer [
36], with 2500 epochs of training for each case. A Smooth L1 loss function was calculated between the ML-predicted pressure field and the field produced by the ParFlow simulation at each snapshot in time. Only two hyperparameters (learning rate and number of epochs) were chosen through experimentation on the training data. Note that other hyperparameters in the models themselves (e.g., number of output channels, size of the linear layer) were not tuned but vary between model simulations in the experiments presented here. The final loss values for all models was below 10
−4, with some being below 10
−5. Training times were not rigorously tracked but ranged from approximately 2 min for the 2DCNN_B3 model to about an hour for the U-Net.
The base case simulations used all 1024 training realizations for training, while some models were also trained with a reduced set of training realizations chosen at random (512, 256, 128, 64, and 32) to test the sensitivity of the trained model to size of the input data. This process is similar in principle to an Ablation Study [
37] except that here, the number of realizations systematically removed some of the training input rather than systematically removing components of the ML model. This resulted in 27 total model simulations, as shown in
Table 2. Hereafter, these models will be referred to by the model name and the number of realizations; e.g., CNN3D.1024 would be the three-dimensional CNN trained on all 1024 of the ParFlow Tilted V simulations.
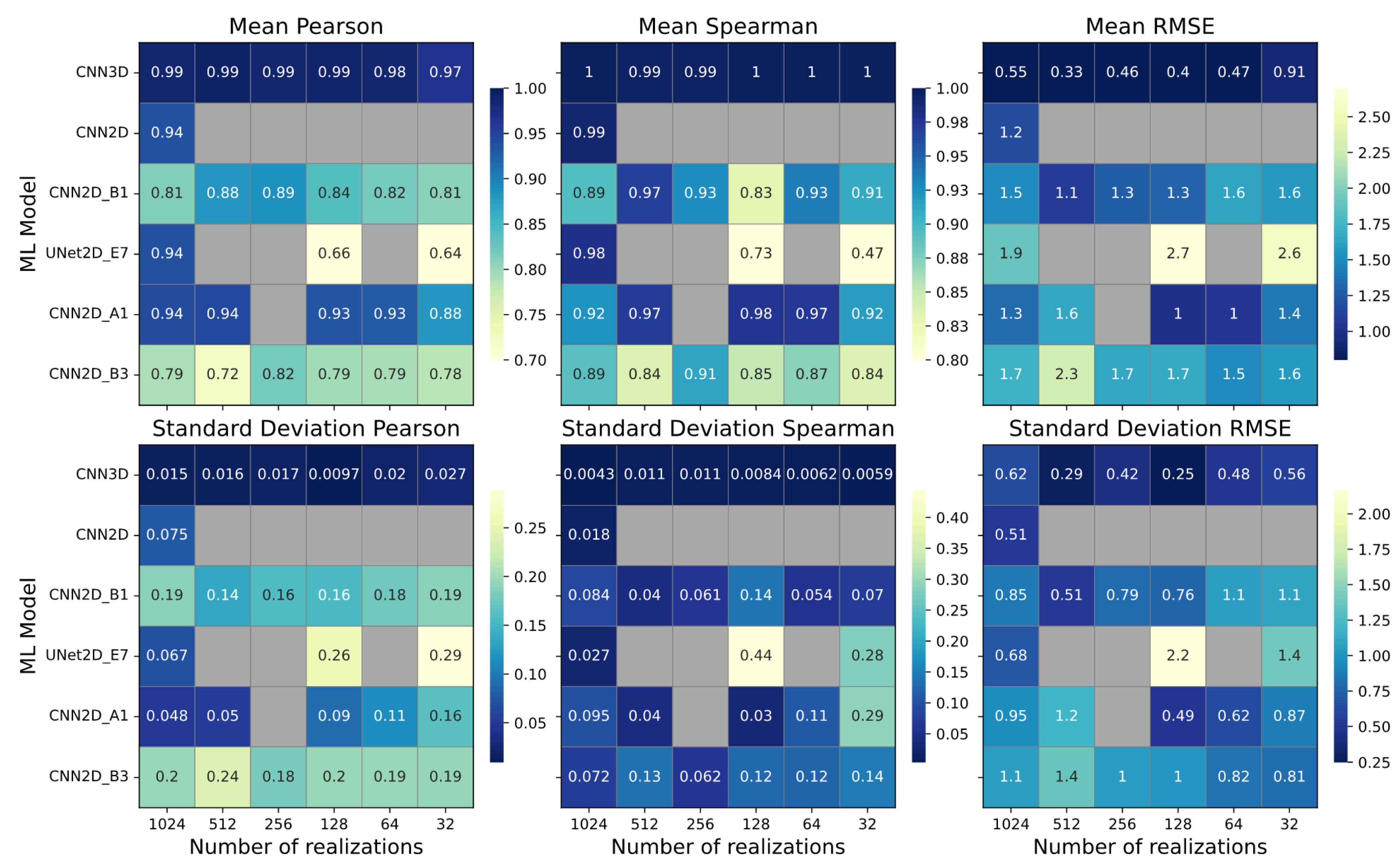
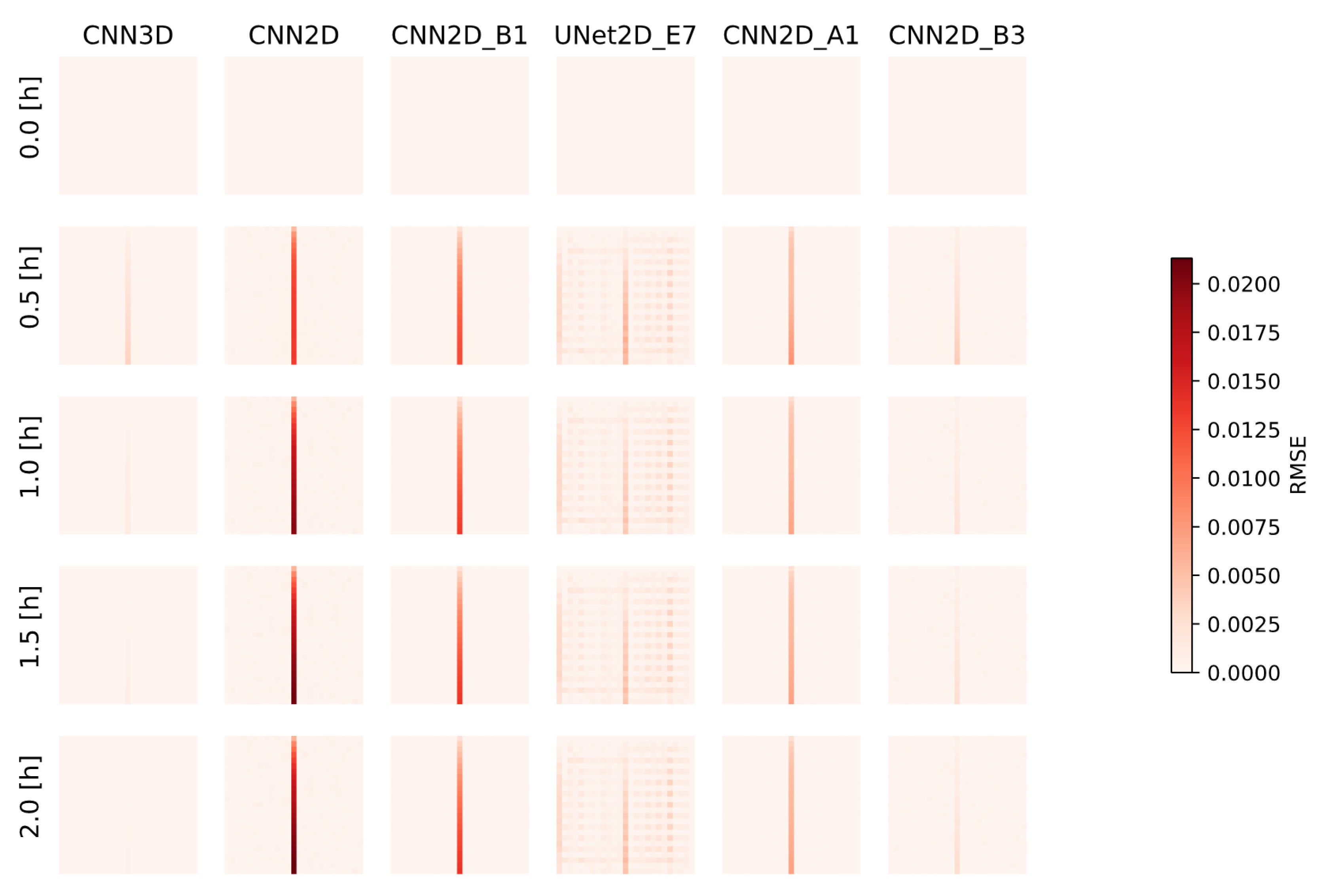
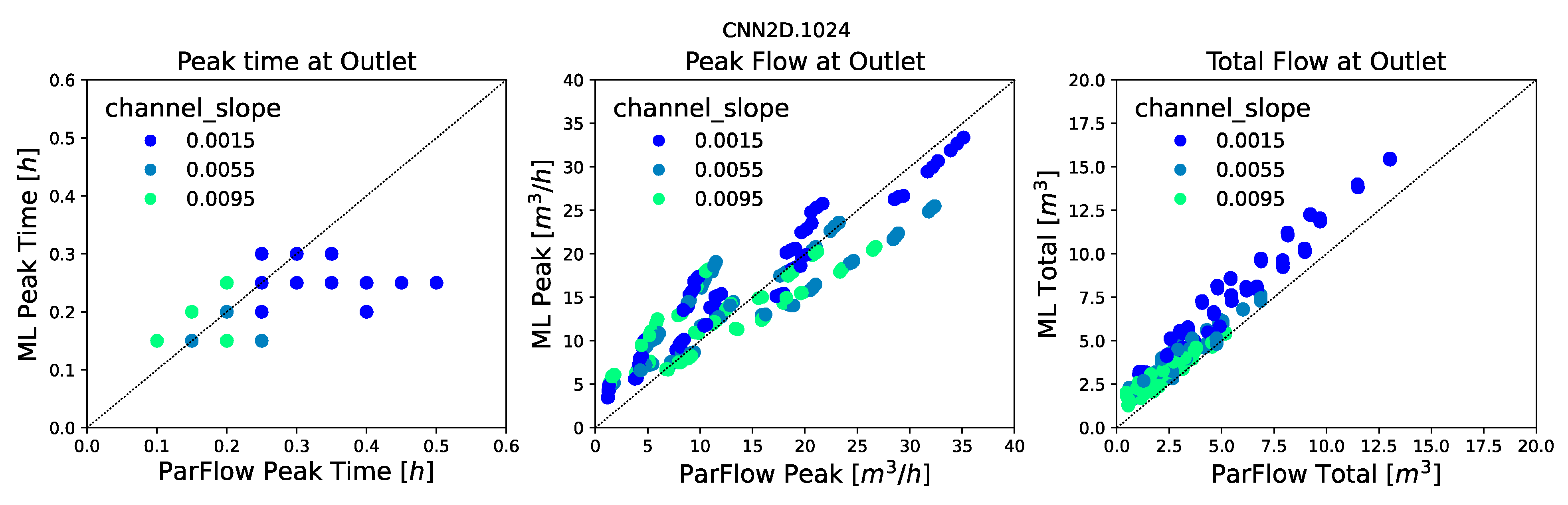
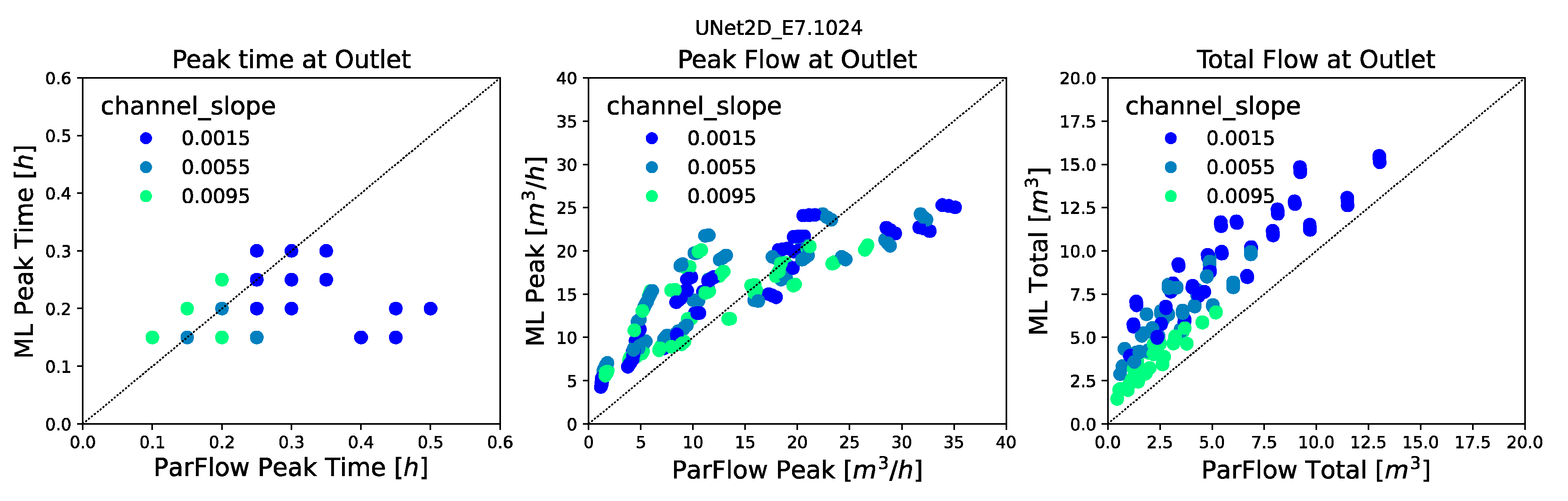
Several model evaluation metrics were used in this study to assess ML model performance both for the spatially distributed outputs and the calculated hydrographs. These include the Root Mean Squared Error (RMSE) of the pressure fields and of the calculated hydrographs, the Pearson’s Correlation Coefficient (commonly the R2 statistic), and Spearman’s Rank Correlation Coefficient (commonly the Spearman’s Rho) of the ML predicted and ParFlow simulated hydrographs. These metrics were calculated for each realization in the ensemble, and the mean and variance were reported across the test ensembles.
2.5. Parameter Evaluation
Finally, we evaluated whether the ML simulations can match the parameters of the model ParFlow in addition to the outputs (i.e., if our ML models get the right answer for the right reasons). Model calibration or parameter estimation is widely used in the hydrologic sciences (e.g., [
38]). Simulation Based Inference (SBI, see, e.g., Cranmer et al. [
39]) is somewhat different than traditional calibration. Briefly, SBI compares the simulation outputs to observations to infer the likelihood of a particular parameter set given some observations. Simulations are used to define the relationship between parameters and target variables in cases where a conventional likelihood evaluation is either theoretically or practically infeasible.
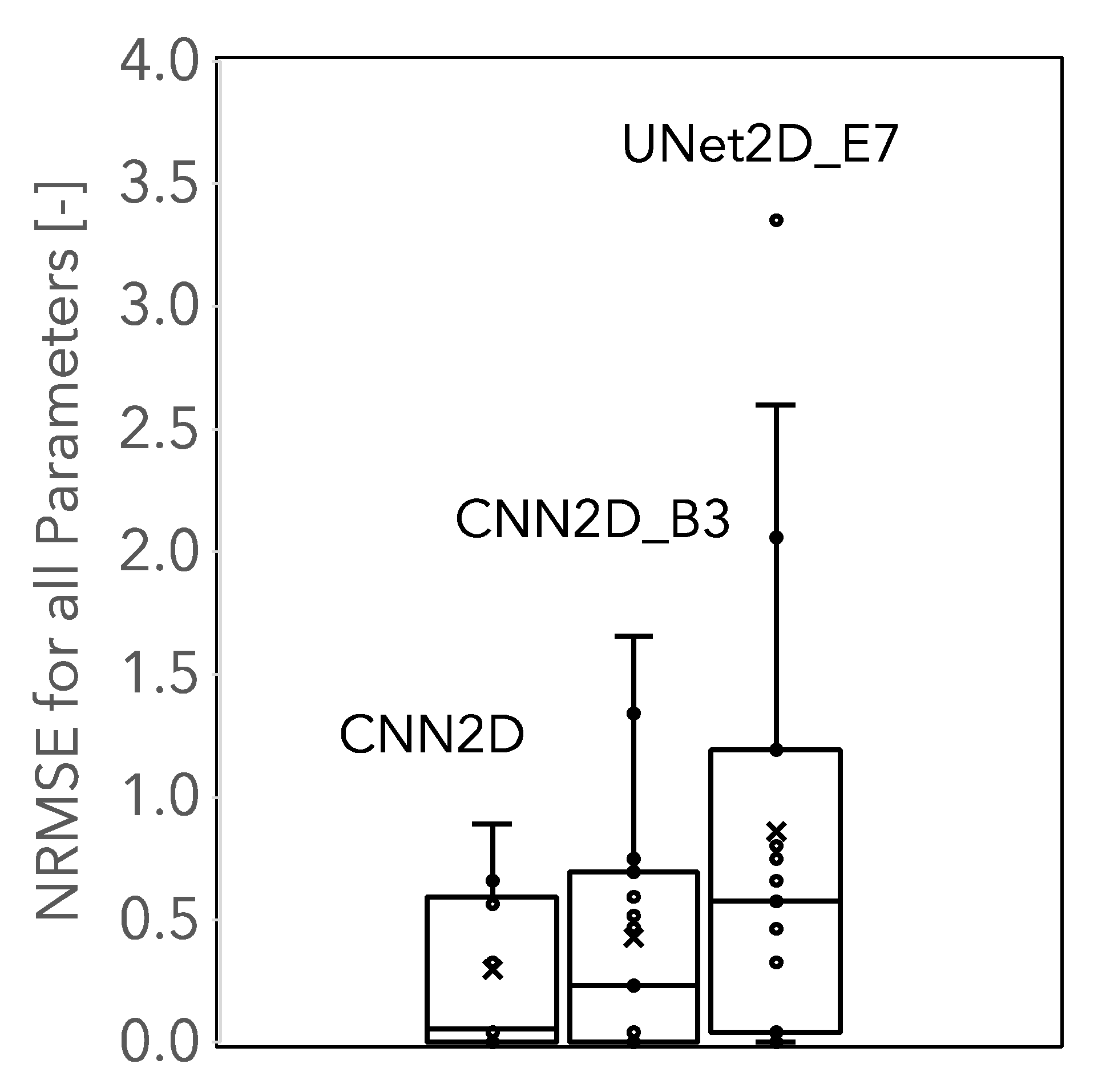
Here, we do not apply full SBI; rather, we tested whether our trained emulator models are able to match the parameters of the underlying simulations and not just their outputs. For this test, we used three of the trained emulator models (CNN2D.1024, UNet2D.1024, and CNN2D_B3.1024) using the following a procedure that resembles Approximate Bayesian Computation (ABC, [
40]):
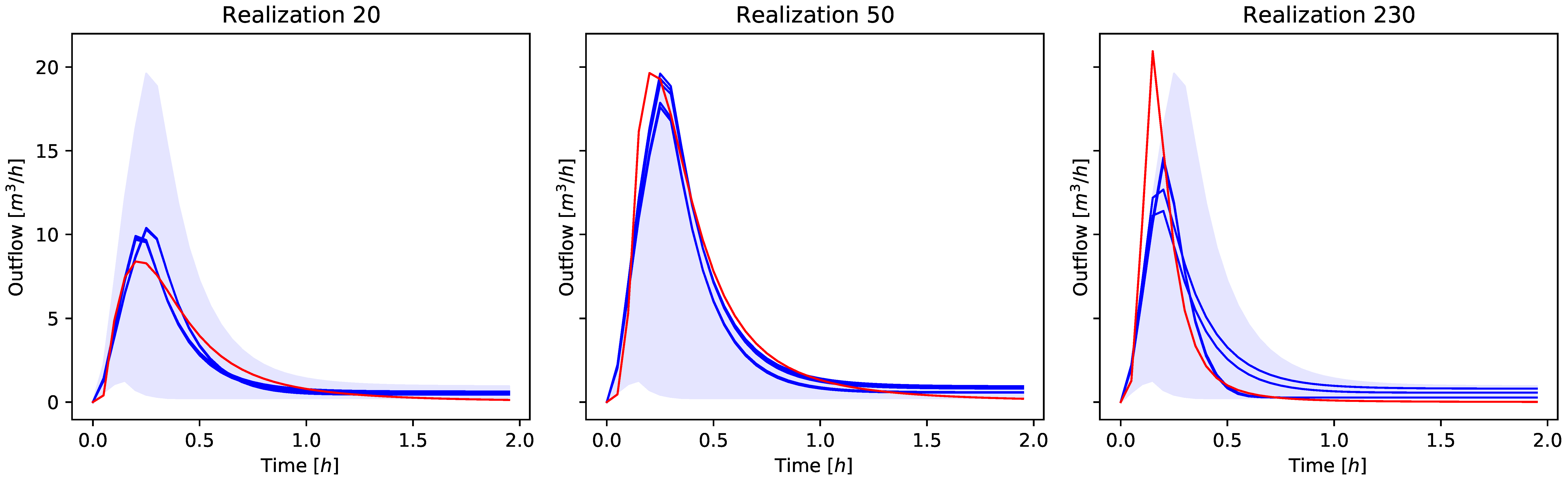
Three ParFlow simulations were selected at random from the In Range ensemble and their hydrographs calculated, and these are defined as our target ParFlow “truth” simulations;
A full suite of simulations were conducted with the three ML models varying parameters shown in
Table 1 across the complete set of
In Range ensemble values;
Hydrographs were calculated from the entire suite of the ML models, and the RMSE was calculated for every realization compared to each of the ParFlow “truth” simulations;
The five realizations with the lowest RMSE values were selected as the best performing ML realizations;
The parameters for the best-matching ML realizations were compared to the parameters from the ParFlow “truth” simulations to evaluate whether the emulators would preserve the behavior of the ParFlow parameters.
This analysis is not intended to be a formal SBI or model calibration; rather, the purpose is to further explore the validity of our emulators. This approach is much more simple than other calibration approaches that might employ an evolution search algorithm [
41], gradient-based method to adjust parameters in a series of more limited model simulations [
42] or even use ML approaches to replace the calibration routine [
43]. Given this proof of concept, future work should include more complex frameworks, including those that loop parameters back to the original physical model simulation or use a more formalized Bayesian framework [
44].