Modelling Snowmelt Runoff from Tropical Andean Glaciers under Climate Change Scenarios in the Santa River Sub-Basin (Peru)
Abstract
:1. Introduction
2. Materials and Methods
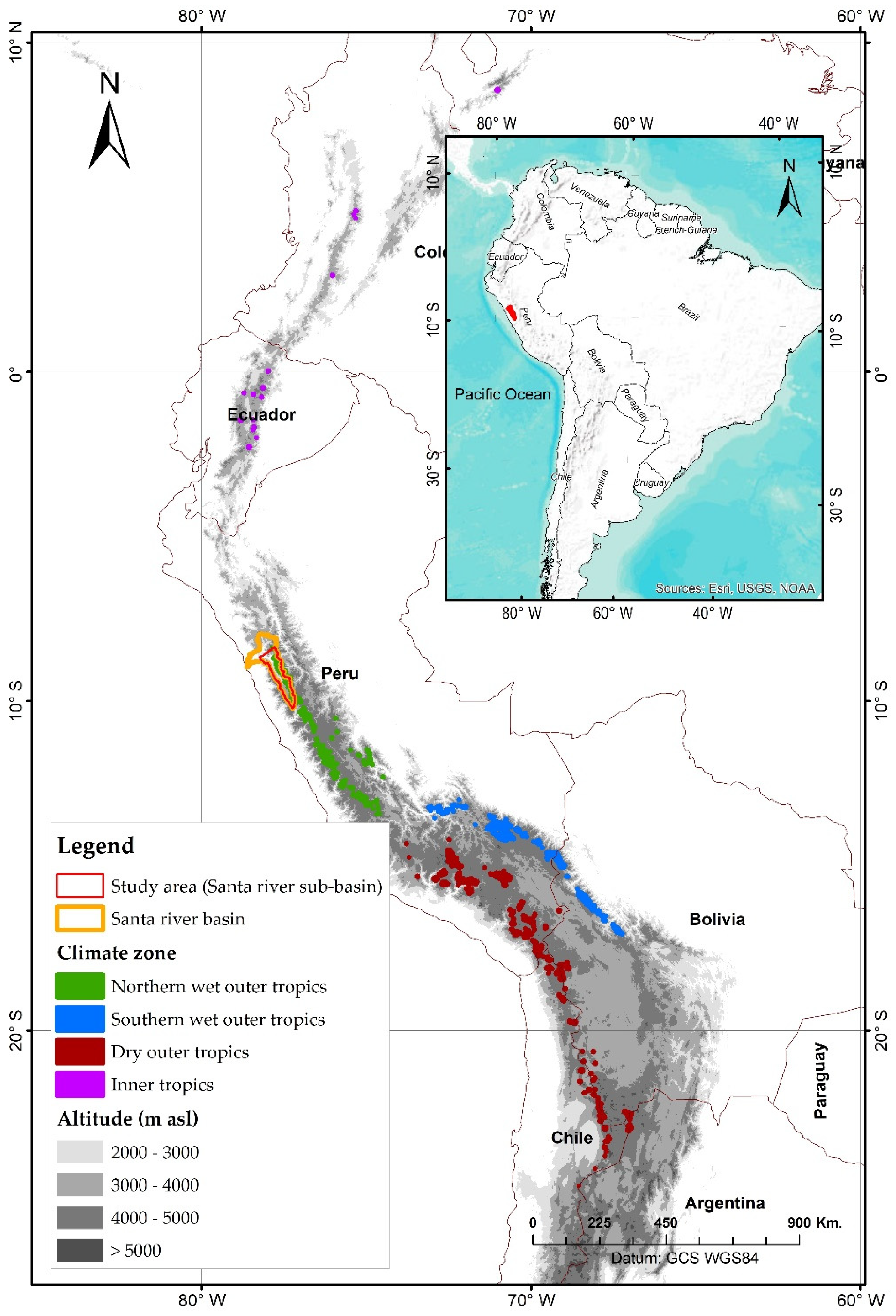
2.1. Study Area
2.2. Data Processing
2.3. Historical Climate and Discharge Data
2.4. Estimation of Snow Covered Area (SCA)
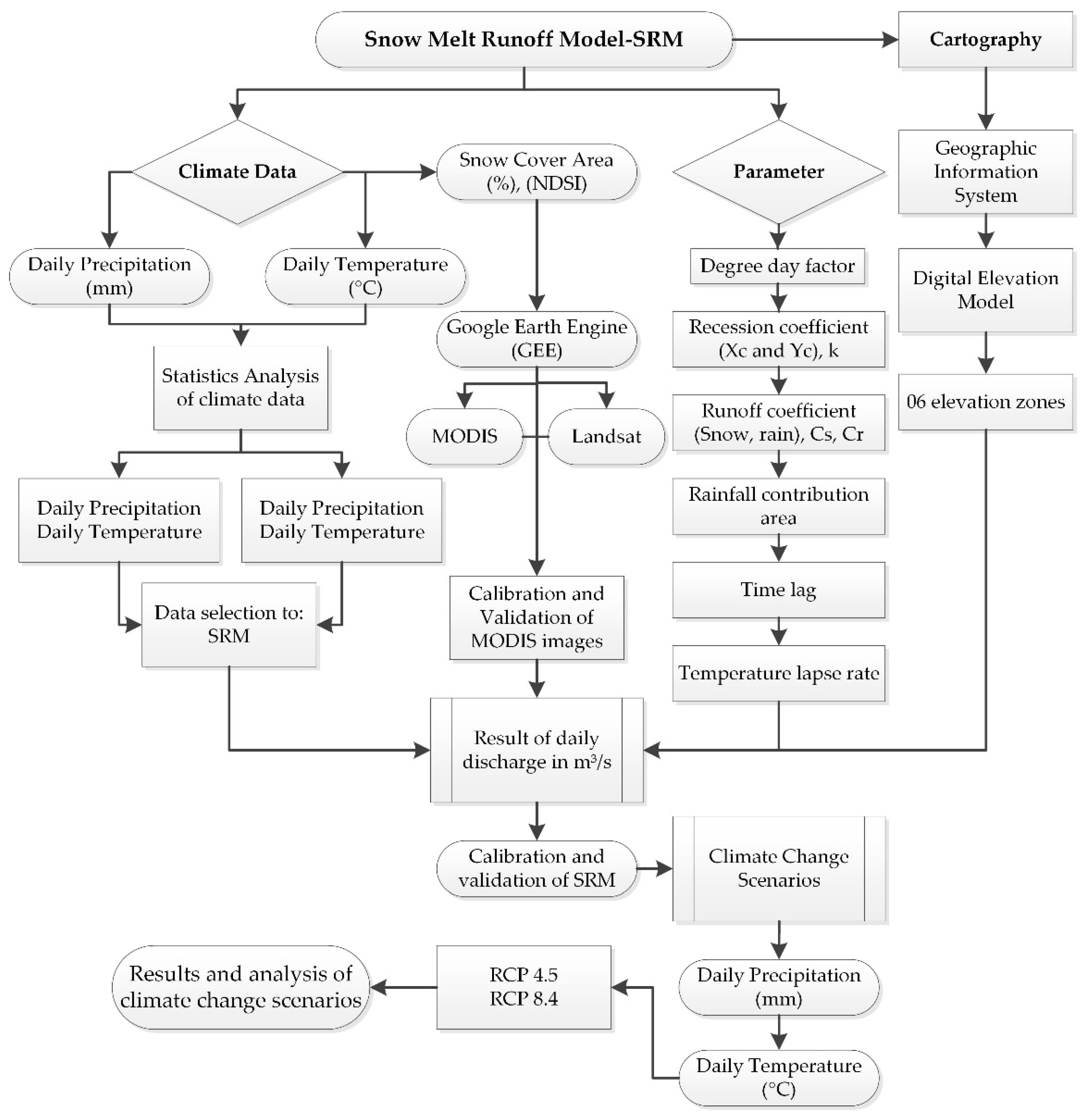
2.5. Snowmelt Runoff Model (SRM)
2.6. SRM Model Calibration
2.7. Data of Future Climate
3. Results
3.1. Snow Coverage Validation
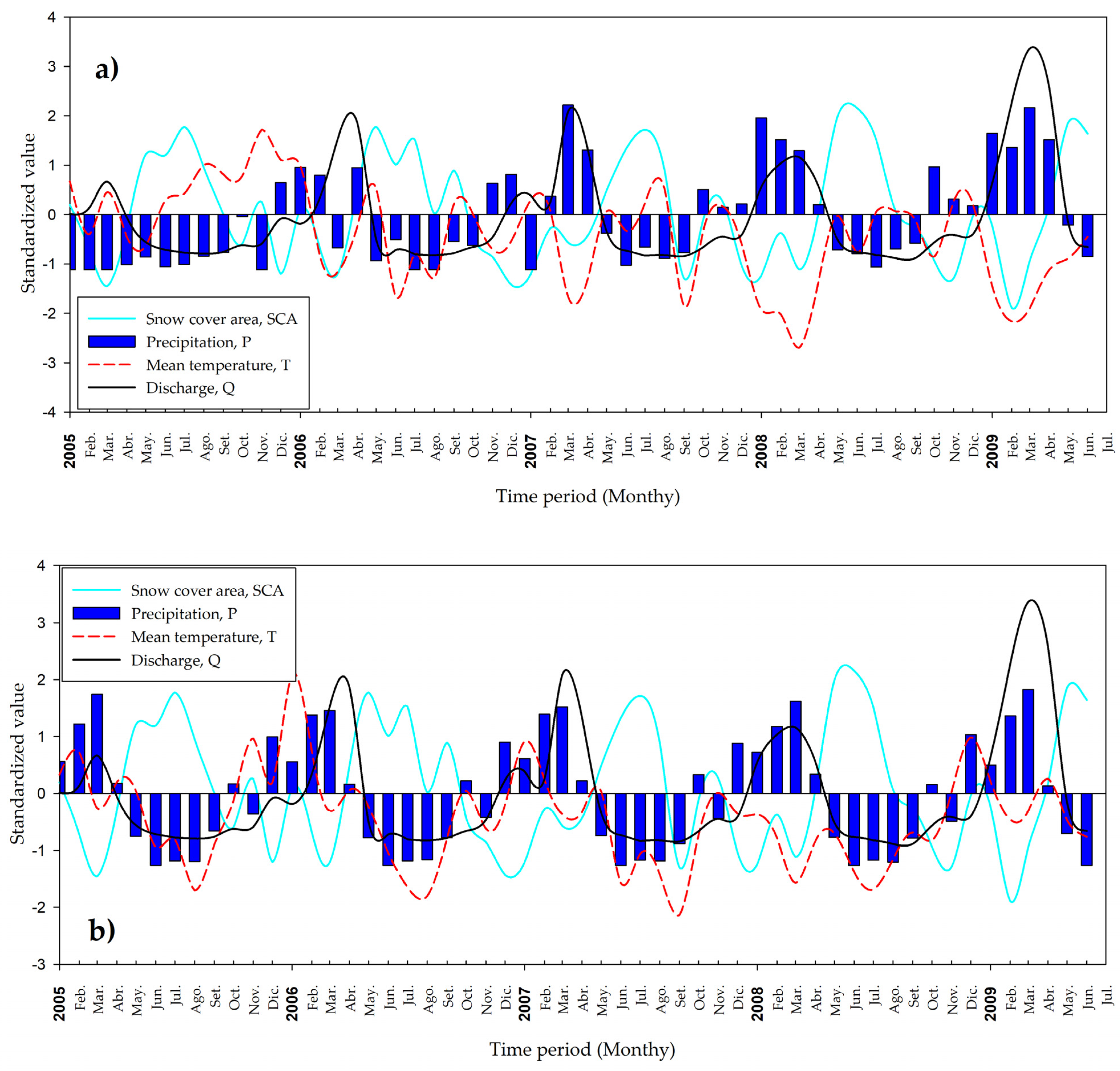
3.2. Standardised Correlation Analysis of Precipitation, Temperature, SCA and Discharge
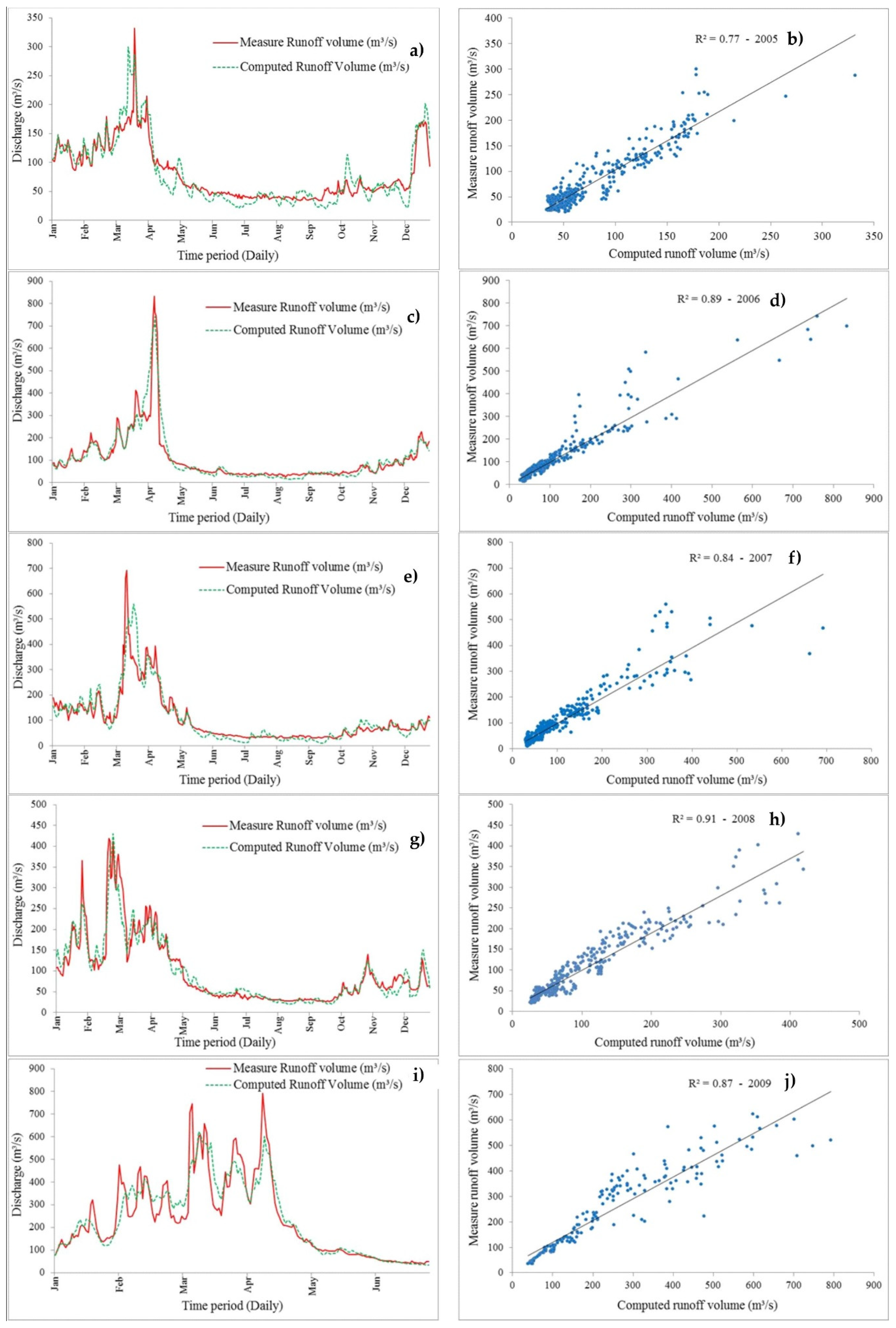
3.3. Simulation, Calibration and Validation of the SRM
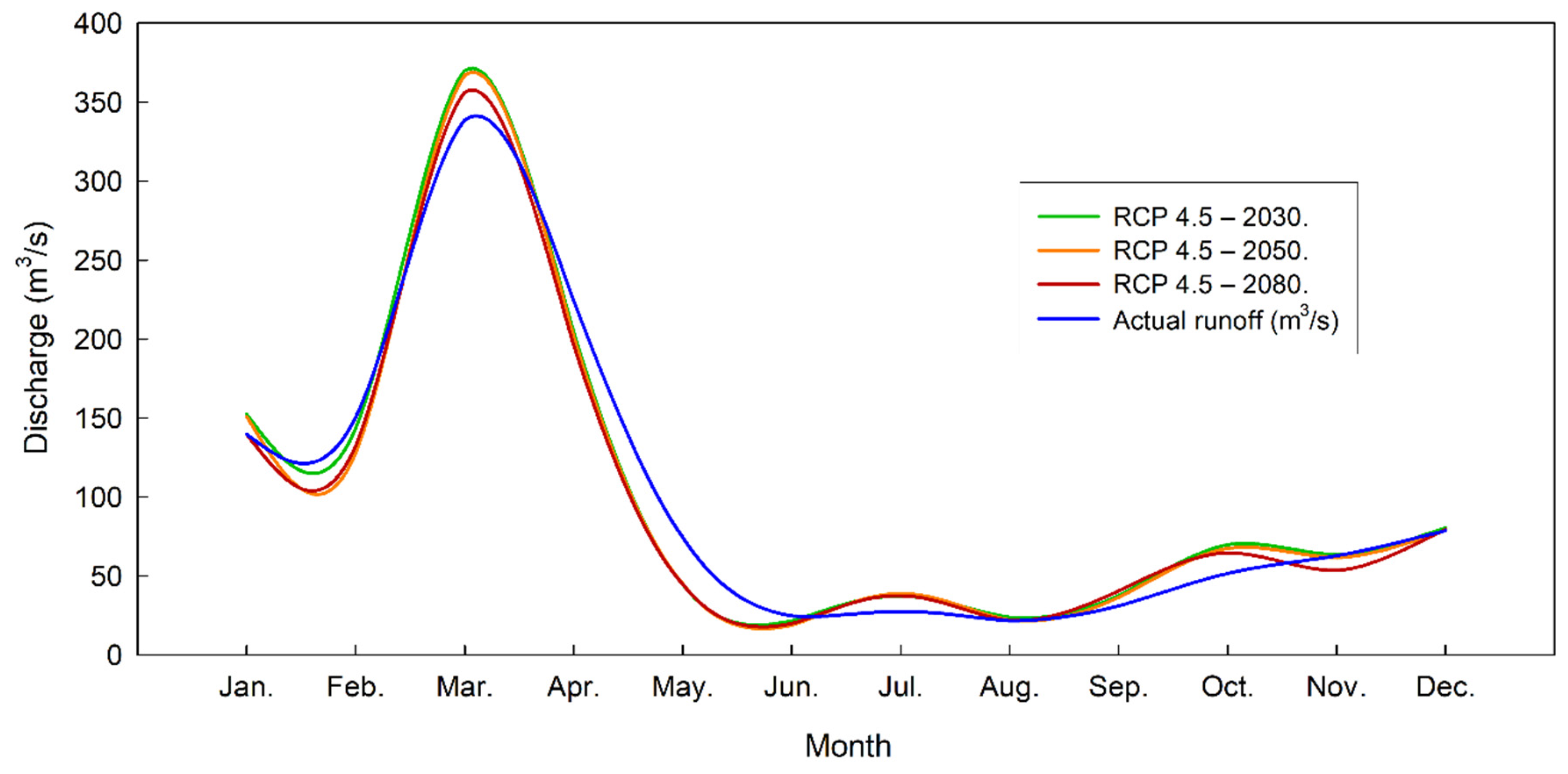
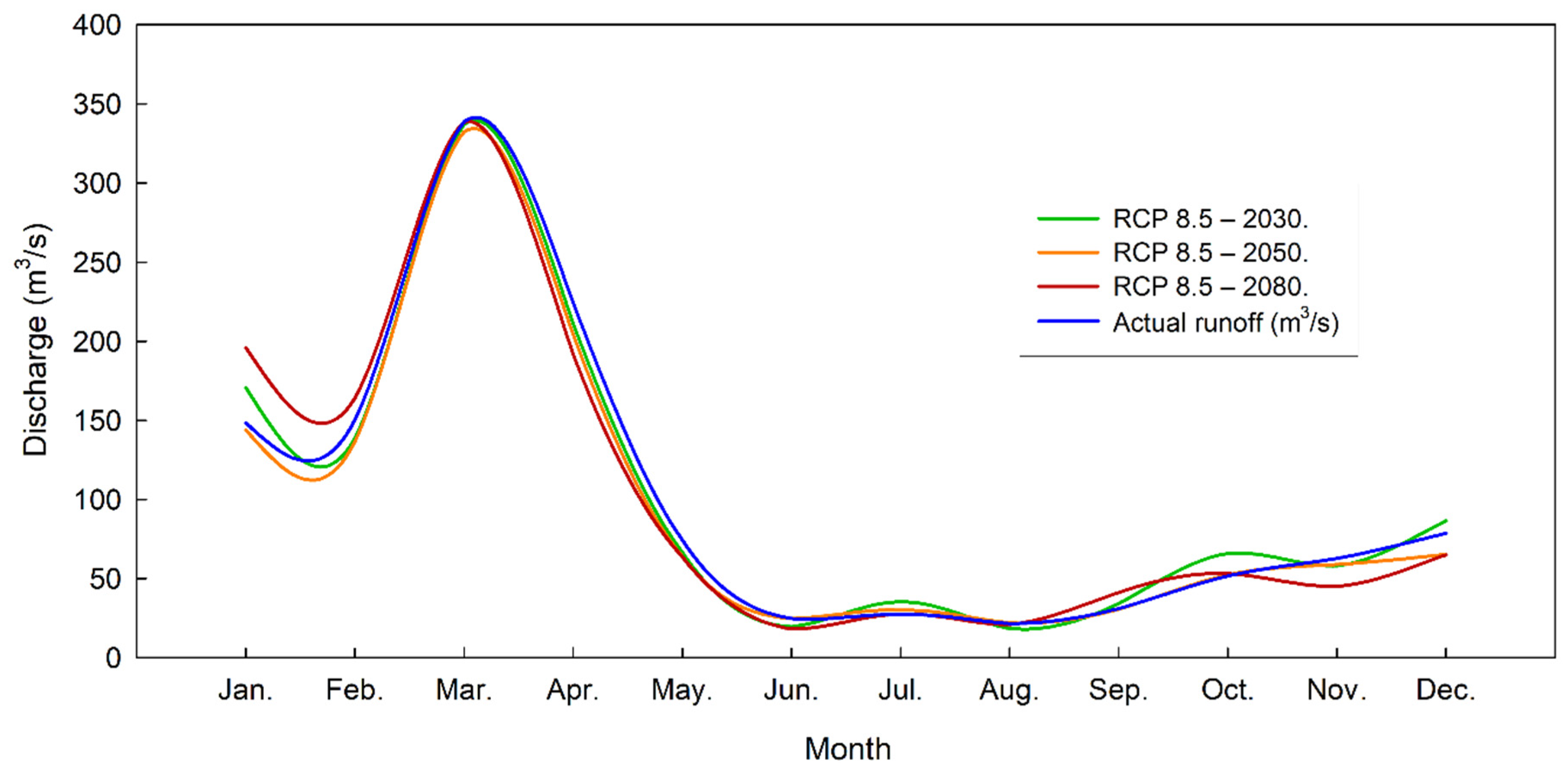
3.4. Climate Change Scenario RCP 4.5 and RCP 8.5
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Banerjee, C.; Sharma, A. Decline in terrestrial water recharge with increasing global temperatures. Sci. Total Environ. 2021, 764, 142913. [Google Scholar] [CrossRef] [PubMed]
- Blöschl, G.; Hall, J.; Parajka, J.; Perdigão, R.A.P.; Merz, B.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; Bonacci, O.; Borga, M.; et al. Changing climate shifts timing of European floods. Science 2017, 357, 588–590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rosenzweig, C.; Karoly, D.; Vicarelli, M.; Neofotis, P.; Wu, Q.; Casassa, G.; Menzel, A.; Root, T.L.; Estrella, N.; Seguin, B.; et al. Attributing physical and biological impacts to anthropogenic climate change. Nat. Cell Biol. 2008, 453, 353–357. [Google Scholar] [CrossRef] [PubMed]
- Kaser, G. A review of the modern fluctuations of tropical glaciers. Glob. Planet. Chang. 1999, 22, 93–103. [Google Scholar] [CrossRef]
- Migliavacca, F.; Confortola, G.; Soncini, A.; Senese, A.; Diolaiuti, G.A.; Smiraglia, C.; Barcaza, G.; Bocchiola, D. Hydrology and potential climate changes in the Rio Maipo (Chile). Geogr. Fis. Din. Quat. 2015, 38, 155–168. [Google Scholar]
- Zhang, H.; Li, Z.; Zhou, P.; Zhu, X.; Wang, L. Mass-balance observations and reconstruction for Haxilegen Glacier No. 51, eastern Tien Shan, from 1999 to 2015. J. Glaciol. 2018, 64, 689–699. [Google Scholar] [CrossRef] [Green Version]
- Hagg, W.; Mayer, C.; Lambrecht, A.; Kriegel, D.; Azizov, E. Glacier changes in the Big Naryn basin, Central Tian Shan. Glob. Planet. Chang. 2013, 110, 40–50. [Google Scholar] [CrossRef]
- Pellicciotti, F.; Ragettli, S.; Carenzo, M.; McPhee, J. Changes of glaciers in the Andes of Chile and priorities for future work. Sci. Total Environ. 2014, 493, 1197–1210. [Google Scholar] [CrossRef]
- Abudu, S.; Sheng, Z.-P.; Cui, C.-L.; Saydi, M.; Sabzi, H.-Z.; King, J.P. Integration of aspect and slope in snowmelt runoff modeling in a mountain watershed. Water Sci. Eng. 2016, 9, 265–273. [Google Scholar] [CrossRef]
- Steele, C.; Dialesandro, J.; James, D.; Elias, E.; Rango, A.; Bleiweiss, M. Evaluating MODIS snow products for modelling snowmelt runoff: Case study of the Rio Grande headwaters. Int. J. Appl. Earth Obs. Geoinf. 2017, 63, 234–243. [Google Scholar] [CrossRef]
- Leavesley, G.H. Problems of snowmelt runoff modelling for a variety of physiographic and climatic conditions. Hydrol. Sci. J. 1989, 34, 617–634. [Google Scholar] [CrossRef] [Green Version]
- Hock, R. Glacier melt: A review of processes and their modelling. Prog. Phys. Geogr. Earth Environ. 2005, 29, 362–391. [Google Scholar] [CrossRef]
- Siemens, K.; Dibike, Y.; Shrestha, R.; Prowse, T. Runoff projection from an alpine watershed in Western Canada: Application of a snowmelt runoff model. Water 2021, 13, 1199. [Google Scholar] [CrossRef]
- Hock, R. Temperature index melt modelling in mountain areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Condom, T.; Escobar, M.; Purkey, D.; Pouget, J.C.; Suarez, W.; Ramos, C.; Apaéstegui, J.; Tacsi, A.; Gomez, J. Simulating the implications of glaciers’ retreat for water management: A case study in the Rio Santa basin, Peru. Water Int. 2012, 37, 442–459. [Google Scholar] [CrossRef]
- Shirsat, T.S.; Kulkarni, A.V.; Momblanch, A.; Randhawa, S.; Holman, I.P. Towards climate-adaptive development of small hydropower projects in Himalaya: A multi-model assessment in upper Beas basin. J. Hydrol. Reg. Stud. 2021, 34, 100797. [Google Scholar] [CrossRef]
- Han, P.; Long, D.; Han, Z.; Du, M.; Dai, L.; Hao, X. Improved understanding of snowmelt runoff from the headwaters of China’s Yangtze River using remotely sensed snow products and hydrological modeling. Remote Sens. Environ. 2019, 224, 44–59. [Google Scholar] [CrossRef]
- Long, D.; Shen, Y.; Sun, A.; Hong, Y.; Longuevergne, L.; Yang, Y.; Li, B.; Chen, L. Drought and flood monitoring for a large karst plateau in Southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Kult, J.; Choi, W.; Choi, J. Sensitivity of the snowmelt runoff model to snow covered area and temperature inputs. Appl. Geogr. 2014, 55, 30–38. [Google Scholar] [CrossRef]
- Martinec, J.; Rango, A.; Major, E. Snowmelt-Runoff Model (SRM) User’s Manual; NASA: Washington, DC, USA, 2008.
- Di Marco, N.; Avesani, D.; Righetti, M.; Zaramella, M.; Majone, B.; Borga, M. Reducing hydrological modelling uncertainty by using MODIS snow cover data and a topography-based distribution function snowmelt model. J. Hydrol. 2021, 599, 126020. [Google Scholar] [CrossRef]
- Gascoin, S.; Hagolle, O.; Huc, M.; Jarlan, L.; Dejoux, J.-F.; Szczypta, C.; Marti, R.; Sánchez, R. A snow cover climatology for the Pyrenees from MODIS snow products. Hydrol. Earth Syst. Sci. 2015, 19, 2337–2351. [Google Scholar] [CrossRef] [Green Version]
- Engel, M.; Notarnicola, C.; Endrizzi, S.; Bertoldi, G. Snow model sensitivity analysis to understand spatial and temporal snow dynamics in a high-elevation catchment. Hydrol. Process. 2017, 31, 4151–4168. [Google Scholar] [CrossRef]
- Parajka, J.; Holko, L.; Kostka, Z.; Blöschl, G. MODIS snow cover mapping accuracy in a small mountain catchment–comparison between open and forest sites. Hydrol. Earth Syst. Sci. 2012, 16, 2365–2377. [Google Scholar] [CrossRef] [Green Version]
- Di Marco, N.; Righetti, M.; Avesani, D.; Zaramella, M.; Notarnicola, C.; Borga, M. Comparison of MODIS and model-derived snow-covered areas: Impact of land use and solar illumination conditions. Geosciences 2020, 10, 134. [Google Scholar] [CrossRef] [Green Version]
- Klein, A.G.; Barnett, A.C. Validation of daily MODIS snow cover maps of the upper rio grande river basin for the 2000–2001 snow year. Remote Sens. Environ. 2003, 86, 162–176. [Google Scholar] [CrossRef]
- Valderrama, P.; Vilca, O. Dinamica e implicancias del aluvión de la laguna 513, Cordillera Blanca, Ancash Perú. Rev. Asoc. Geol. Argent. 2012, 69, 400–406. [Google Scholar]
- Zapata, M.; Arnaud, Y.; Gallaire, R. Inventario de glaciares de la cordillera blanca. In Proceedings of the 13th IWRA World Water Congress, Montpellier, France, 1–4 September 2008; pp. 1–4. [Google Scholar]
- Schauwecker, S.; Rohrer, M.; Acuña, D.; Cochachin, A.; Dávila, L.; Frey, H.; Giráldez, C.; Gómez, J.; Huggel, C.; Jacques-Coper, M.; et al. Climate trends and glacier retreat in the Cordillera Blanca, Peru, revisited. Glob. Planet. Chang. 2014, 119, 85–97. [Google Scholar] [CrossRef]
- Kaser, G.; Juen, I.; Georges, C.; Gómez, J.; Tamayo, W. The impact of glaciers on the runoff and the reconstruction of mass balance history from hydrological data in the tropical Cordillera Bianca, Perú. J. Hydrol. 2003, 282, 130–144. [Google Scholar] [CrossRef]
- Hänchen, L.; Klein, C.; Maussion, F.; Gurgiser, W.; Wohlfahrt, G. Vegetation indices as a proxy for spatio-temporal variations in water availability in the semi-arid Rio Santa valley (Callejón de Huaylas, Peru). In Proceedings of the EGU General Assembly 2021 (EGU21-8330), Online, 19–30 April 2021. [Google Scholar] [CrossRef]
- Lynch, B.D. Vulnerabilities, competition and rights in a context of climate change toward equitable water governance in Peru’s Rio Santa Valley. Glob. Environ. Chang. 2012, 22, 364–373. [Google Scholar] [CrossRef]
- ANA. Inventario de Glaciares Coordillera Blanca; ANA: Lima, Peru, 2010; Available online: https://repositorio.ana.gob.pe/bitstream/handle/20.500.12543/490/ANA0000276.pdf?sequence=1&isAllowed=y (accessed on 1 October 2017).
- Vuille, M.; Kaser, G.; Juen, I. Glacier mass balance variability in the Cordillera Blanca, Peru and its relationship with climate and the large-scale circulation. Glob. Planet. Chang. 2008, 62, 14–28. [Google Scholar] [CrossRef] [Green Version]
- Vuille, M.; Francou, B.; Wagnon, P.; Juen, I.; Kaser, G.; Mark, B.G.; Bradley, R.S. Earth-science reviews climate change and tropical andean glaciers: Past, present and future. Earth-Sci. Rev. 2008, 89, 79–96. [Google Scholar] [CrossRef] [Green Version]
- INEI Perú. Estimaciones y Proyecciones de Población por Departamento, Provincia y Distrito, 2018–2020; INEI Perú: Lima, Peru, 2020. Available online: https://www.inei.gob.pe/media/MenuRecursivo/publicaciones_digitales/Est/Lib1715/libro.pdf (accessed on 1 October 2017).
- Chevallier, P.; Pouyaud, B.; Suarez, W.; Condom, T. Climate change threats to environment in the tropical Andes: Glaciers and water resources. Reg. Environ. Chang. 2011, 11, 179–187. [Google Scholar] [CrossRef]
- Bury, J.; Mark, B.G.; Carey, M.; Young, K.R.; McKenzie, J.M.; Baraer, M.; French, A.; Polk, M.H. New geographies of water and climate change in Peru: Coupled natural and social transformations in the Santa River watershed. Ann. Assoc. Am. Geogr. 2013, 103, 363–374. [Google Scholar] [CrossRef] [Green Version]
- Tadono, T.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Precise global DEM generation by ALOS PRISM. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 71–76. [Google Scholar] [CrossRef] [Green Version]
- Riggs, G.A.; Hall, D.; Román, M.O. MODIS snow products: Collection 6 user guide. Earth Sci. 2016, 6, 1–80. [Google Scholar]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V.; DiGirolamo, N.E.; Bayr, K.J. MODIS snow-cover products. Remote Sens. Environ. 2002, 83, 181–194. [Google Scholar] [CrossRef] [Green Version]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google earth engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Riggs, G.A.; Hall, D.K.; Salomonson, V.V. MODIS Snow Products User Guide to Collection 5. Available online: https://modis-snow-ice.gsfc.nasa.gov/uploads/sug_c5.pdf (accessed on 1 September 2017).
- Dozier, J. Spectral signature of alpine snow cover from the Landsat thematic mapper. Remote Sens. Environ. 1989, 28, 9–22. [Google Scholar] [CrossRef]
- Adnan, M.; Nabi, G.; Poomee, M.S.; Ashraf, A. Snowmelt runoff prediction under changing climate in the Himalayan cryosphere: A case of Gilgit River Basin. Geosci. Front. 2017, 8, 941–949. [Google Scholar] [CrossRef] [Green Version]
- Tahir, A.A.; Chevallier, P.; Arnaud, Y.; Neppel, L.; Ahmad, B. Modeling snowmelt-runoff under climate scenarios in the Hunza River basin, Karakoram Range, Northern Pakistan. J. Hydrol. 2011, 409, 104–117. [Google Scholar] [CrossRef]
- Zhang, G.; Xie, H.; Yao, T.; Li, H.; Duan, S. Quantitative water resources assessment of Qinghai Lake basin using snowmelt runoff model (SRM). J. Hydrol. 2014, 519, 976–987. [Google Scholar] [CrossRef]
- Hoar, T.; Doug, N. Statistical Downscaling of the Community Climate System Model (CCSM) Monthly Temperature and Precipitation Projections; Institute for Mathematics Applied to Geosciences/National Center for Atmospheric Research: Boulder, CO, USA, 2008.
- Escanilla-Minchel, R.; Alcayaga, H.; Soto-Alvarez, M.; Kinnard, C.; Urrutia, R. Evaluation of the impact of climate change on runoff generation in an andean glacier watershed. Water 2020, 12, 3547. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Hussainzada, W.; Lee, H.S.; Vinayak, B.; Khpalwak, G.F. Sensitivity of snowmelt runoff modelling to the level of cloud coverage for snow cover extent from daily MODIS product collection 6. J. Hydrol. Reg. Stud. 2021, 36, 100835. [Google Scholar] [CrossRef]
- Saleem, J.; Butt, A.; Shafiq, A.; Ahmad, S.S.; Supervisor, A.S. Cryosphere dynamic study of Hunza Basin using remote sensing, GIS and runoff modeling. J. King Saud Univ.-Sci. 2020, 32, 2462–2467. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Foster, J.L.; Kumar, S.V. Development and evaluation of a cloud-gap-filled MODIS daily snow-cover product. Remote Sens. Environ. 2010, 114, 496–503. [Google Scholar] [CrossRef] [Green Version]
- Khan, A.; Naz, B.; Bowling, L. Separating snow, clean and debris covered ice in the Upper Indus Basin, Hindukush-Karakoram-Himalayas, using landsat images between 1998 and 2002. J. Hydrol. 2015, 521, 46–64. [Google Scholar] [CrossRef] [Green Version]
- Archer, D. Contrasting hydrological regimes in the upper Indus Basin. J. Hydrol. 2003, 274, 198–210. [Google Scholar] [CrossRef]
- Archer, D.R.; Forsythe, N.; Fowler, H.J.; Shah, S.M. Sustainability of water resources management in the Indus Basin under changing climatic and socio economic conditions. Hydrol. Earth Syst. Sci. 2010, 14, 1669–1680. [Google Scholar] [CrossRef] [Green Version]
- Baraer, M.; Mark, B.G.; McKenzie, J.M.; Condom, T.; Bury, J.; Huh, K.-I.; Portocarrero, C.; Gómez, J.; Rathay, S. Glacier recession and water resources in Peru’s Cordillera Blanca. J. Glaciol. 2012, 58, 134–150. [Google Scholar] [CrossRef] [Green Version]
- Bury, J.T.; Mark, B.; McKenzie, J.M.; French, A.; Baraer, M.; Huh, K.I.; Luyo, M.A.Z.; López, R.J.G. Glacier recession and human vulnerability in the Yanamarey watershed of the Cordillera Blanca, Peru. Clim. Chang. 2010, 105, 179–206. [Google Scholar] [CrossRef] [Green Version]

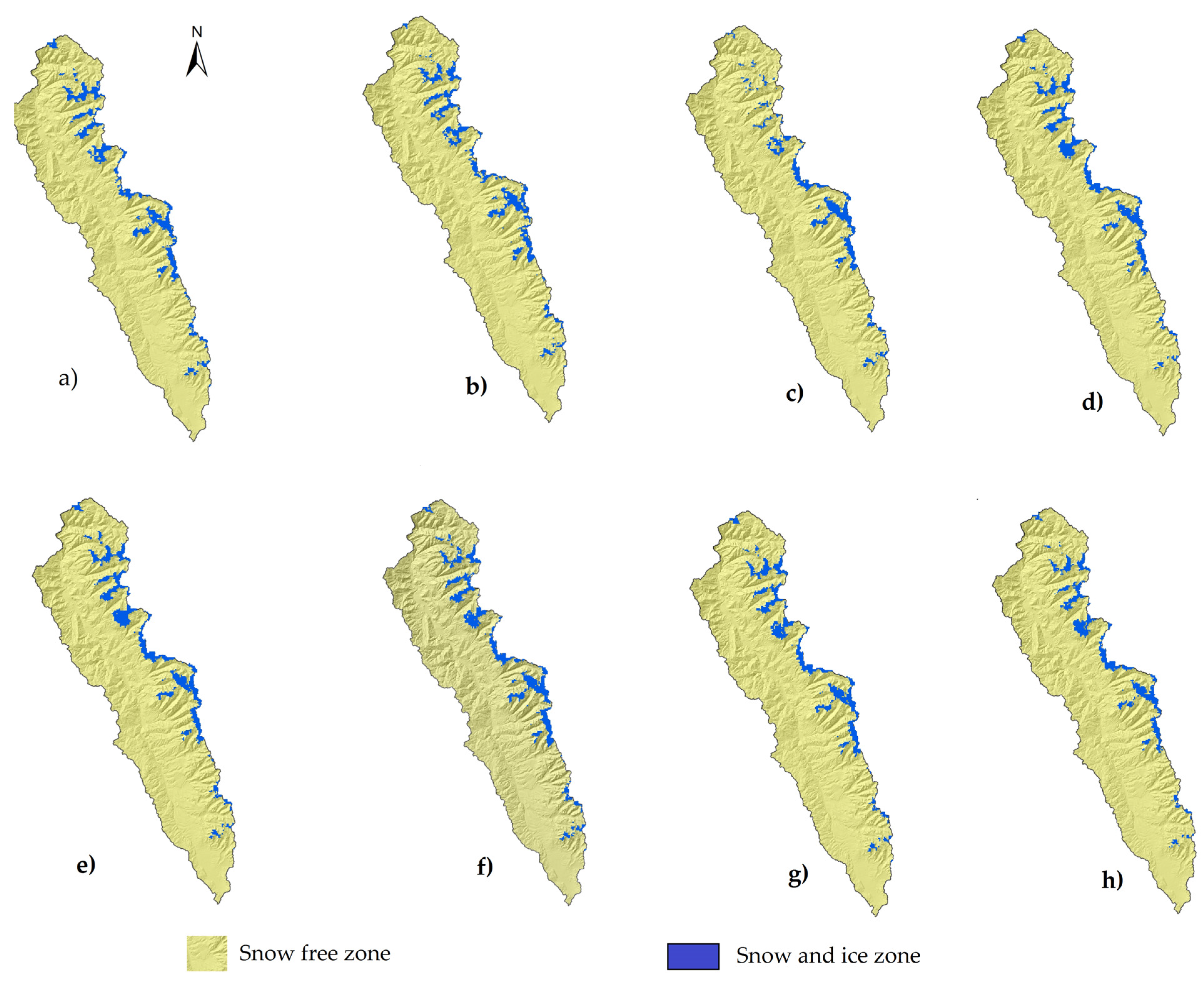
| Date of Images | Snow Cover Area (%) | |
|---|---|---|
| MODIS (500 m) | Landsat (30 m) | |
| 18 October 2003 | 6.1 | 6.5 |
| 13 May 2004 | 6.8 | 6.2 |
| 6 July 2006 | 6.0 | 6.1 |
| 7 August 2006 | 5.8 | 5.9 |
| 9 June 2008 | 6.3 | 6.5 |
| 15 August 2009 | 6.9 | 6.4 |
| 18 August 2010 | 5.4 | 5.7 |
| 5 August 2011 | 6.0 | 5.6 |
| 12 July 2014 | 6.7 | 6.2 |
| 17 September 2015 | 5.7 | 5.1 |
| 23 January 2016 | 4.8 | 5.6 |
| 22 November 2016 | 4.6 | 5.2 |
| Statistical Parameter | 2005 | 2006 | 2007 | 2008 | 2009 |
|---|---|---|---|---|---|
| Measure Runoff Volume (106 m3) | 253,704.00 | 3310.98 | 3306.03 | 3082.62 | 3082.62 |
| Average Measured Runoff (m3/s) | 80.45 | 104.99 | 104.83 | 97.48 | 97.48 |
| Computed Runoff Volume (106 m3) | 2436.69 | 3308.71 | 3284.96 | 3076.93 | 3076.93 |
| Average Computed Runoff (m3/s) | 77.27 | 104.92 | 104.17 | 97.30 | 97.30 |
| Coefficient of Determination R2 Nash-Sutcliffe | 0.80 | 0.89 | 0.84 | 0.91 | 0.87 |
| Coefficient of Determ. R2 Log (Nash-Sutcliffe) | 0.67 | 0.83 | 0.76 | 0.92 | 0.94 |
| Volume Difference (%) | 3.95 | 0.07 | 0.64 | 0.18 | 0.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calizaya, E.; Mejía, A.; Barboza, E.; Calizaya, F.; Corroto, F.; Salas, R.; Vásquez, H.; Turpo, E. Modelling Snowmelt Runoff from Tropical Andean Glaciers under Climate Change Scenarios in the Santa River Sub-Basin (Peru). Water 2021, 13, 3535. https://doi.org/10.3390/w13243535
Calizaya E, Mejía A, Barboza E, Calizaya F, Corroto F, Salas R, Vásquez H, Turpo E. Modelling Snowmelt Runoff from Tropical Andean Glaciers under Climate Change Scenarios in the Santa River Sub-Basin (Peru). Water. 2021; 13(24):3535. https://doi.org/10.3390/w13243535
Chicago/Turabian StyleCalizaya, Elmer, Abel Mejía, Elgar Barboza, Fredy Calizaya, Fernando Corroto, Rolando Salas, Héctor Vásquez, and Efrain Turpo. 2021. "Modelling Snowmelt Runoff from Tropical Andean Glaciers under Climate Change Scenarios in the Santa River Sub-Basin (Peru)" Water 13, no. 24: 3535. https://doi.org/10.3390/w13243535
APA StyleCalizaya, E., Mejía, A., Barboza, E., Calizaya, F., Corroto, F., Salas, R., Vásquez, H., & Turpo, E. (2021). Modelling Snowmelt Runoff from Tropical Andean Glaciers under Climate Change Scenarios in the Santa River Sub-Basin (Peru). Water, 13(24), 3535. https://doi.org/10.3390/w13243535








