A Polynomial Method Approximating S-Curve with Limited Availability of Reliable Rainfall Data
Abstract
1. Introduction
2. The Proposed Method
2.1. Procedure of the Proposed Method
2.2. Derivation of CFR Polynomial
2.3. Inverse Transformation of S-Curve into Time Domain
2.4. Model Performance Indices
3. Results
4. Discussion
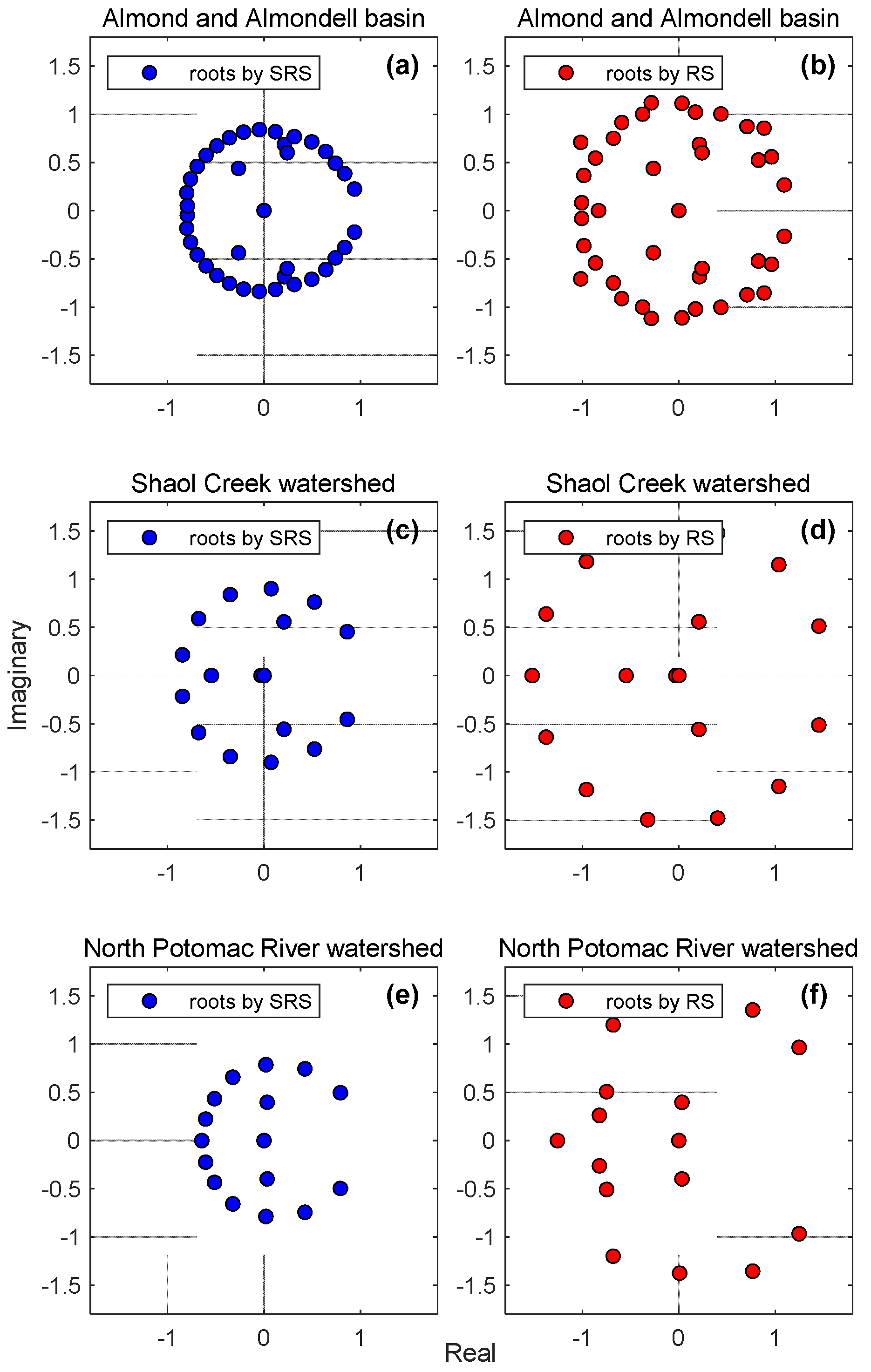
4.1. Comparison of Argand Diagrams
4.2. Examples for Different River Basins
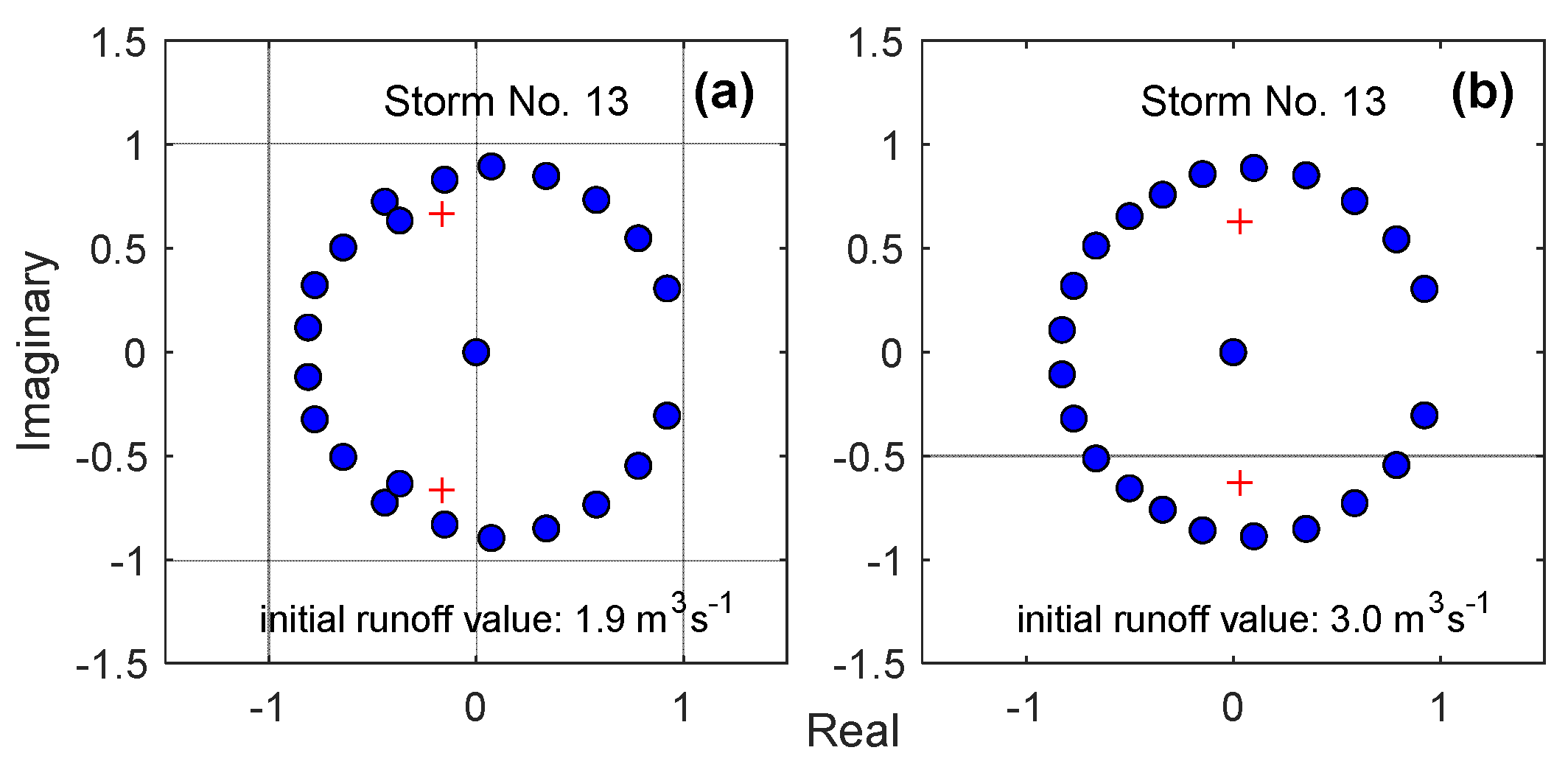
4.3. Consideration of Stability Using Argand Diagram
5. Conclusions
- (1)
- The proposed method provided a clear and effective tool identifying the S-curve solely from the effective runoff of given storm data.
- (2)
- The roots of the S-curve polynomial described a clearer circular pattern that allowed root separation for the polynomial without any additional efforts.
- (3)
- The proposed method did not affect the root pattern of rainfall provided by the root selection method
- (4)
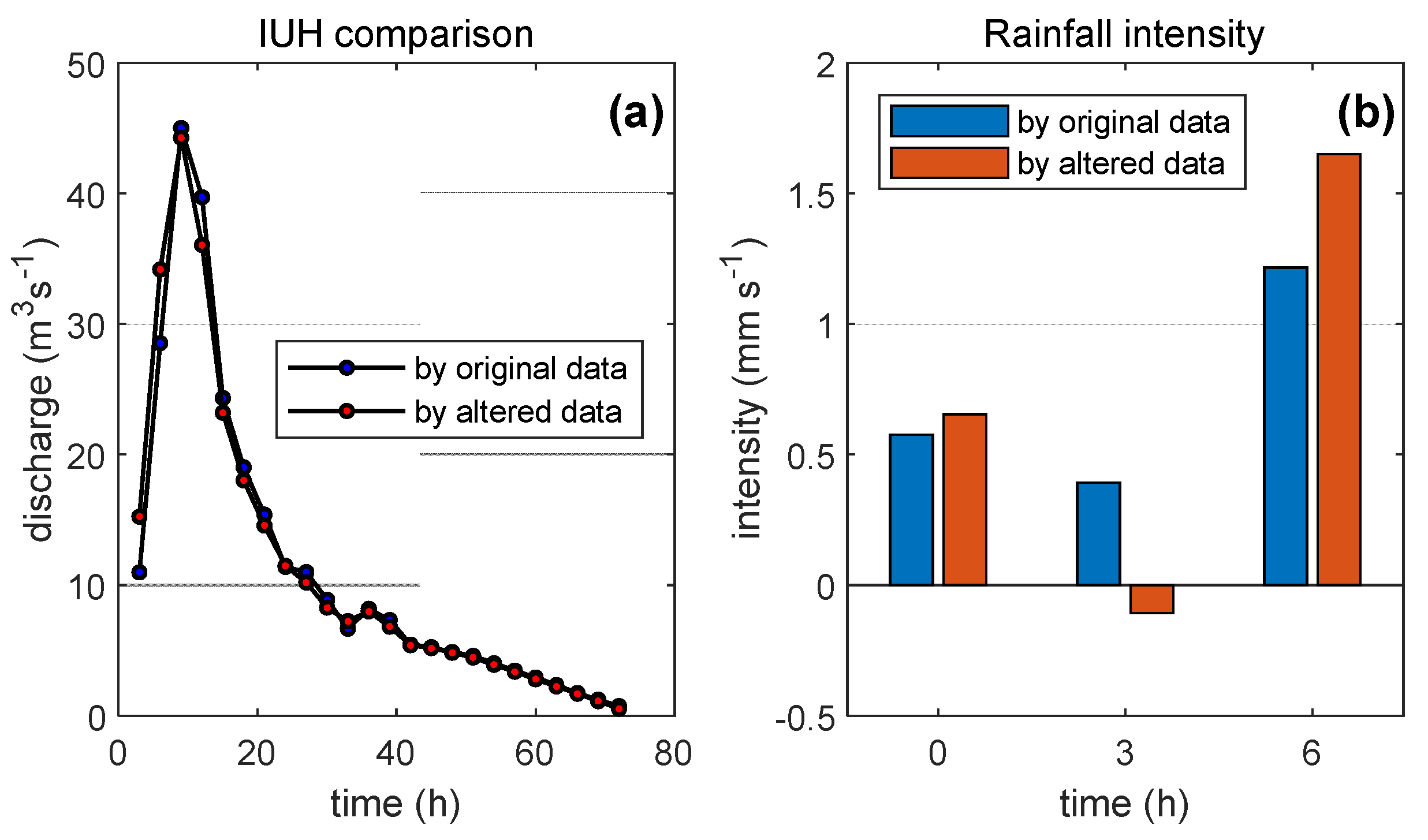
- The estimates of IUHs were in general agreement with those of previous studies.
- (5)
- The ordinates of the reproduced direct runoff were in good agreement with those of previous studies.
- (6)
- Hydrologic stability evaluation could be performed by comparing the roots of observed rainfall and abnormal roots on the Argand diagram.
- (7)
- The sensitivity of roots for rainfall was relatively larger than that of the S-curve polynomial with respect to a small variation of initial runoff ordinate.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Seong, K.-W.; Sung, J. Derivation of S-Curve from Oscillatory Hydrograph Using Digital Filter. Water 2021, 13, 1456. [Google Scholar] [CrossRef]
- Patil, P.R.; Mishra, S.K. Analytical Approach for Derivation of Oscillation-Free Altered Duration Unit Hydrographs. J. Hydrol. Eng. 2016, 21, 06016010. [Google Scholar] [CrossRef]
- Hunt, B. The meaning of oscillations in unit hydrograph S-curves. Hydrol. Sci. J. 1985, 30, 331–342. [Google Scholar] [CrossRef]
- Parmentier, B.; Dooge, J.; Bruen, M. Root selection methods in flood analysis. Hydrol. Earth Syst. Sci. 2003, 7, 151–161. [Google Scholar] [CrossRef][Green Version]
- Prasad, T.D.; Gupta, R.; Prakash, S. Determination of Optimal Loss Rate Parameters and Unit Hydrograph. J. Hydrol. Eng. 1999, 4, 83–87. [Google Scholar] [CrossRef]
- Turner, J.; Dooge, J.; Bree, T. Deriving the unit hydrograph by root selection. J. Hydrol. 1989, 110, 137–152. [Google Scholar] [CrossRef]
- Al-Dabbagh, A.R. Mathematical Model To Simulate The Surface Runoff For Ubaiyidh Valley In The Western Desert. Eng. J. Univ. Quatar 1998, 11, 153–167. [Google Scholar]
- Seong, K.-W.; Lee, Y.-H. A practical estimation of Clark IUH parameters using root selection and linear programming. Hydrol. Process. 2011, 25, 3676–3687. [Google Scholar] [CrossRef]
- Rai, R.K.; Jain, M.K.; Mishra, S.K.; Ojha, C.S.P.; Singh, V.P. Another Look at Z-transform Technique for Deriving Unit Impulse Response Function. Water Resour. Manag. 2007, 21, 1829–1848. [Google Scholar] [CrossRef]
- Bree, T. The stability of parameter estimation in the general linear model. J. Hydrol. 1978, 37, 47–66. [Google Scholar] [CrossRef]
- Mohan, S.; Vijayalakshmi, D.P. Estimation of Nash’s IUH parameters using stochastic search algorithms. Hydrol. Process. 2008, 22, 3507–3522. [Google Scholar] [CrossRef]
- James, G.; Burley, D.; Clements, D.; Dyke, P.; Searl, J. Modern Engineering Mathematics; Pearson Education: Essex, UK, 2008. [Google Scholar]
- Sharma, T. Response functions applied to a drainage system. J. Hydrol. 1980, 45, 279–287. [Google Scholar] [CrossRef]
- Bhunya, P.K.; Ghosh, N.C.; Mishra, S.K.; Ojha, C.S.; Berndtsson, R. Hybrid Model for Derivation of Synthetic Unit Hydrograph. J. Hydrol. Eng. 2005, 10, 458–467. [Google Scholar] [CrossRef]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Reddy, J.M.; Babu, A.S.; Mallikarjuna, C. Rainfall—Runoff Modeling: Comparison and Combination of Simple Time-Series, Linear Autoregressive and Artificial Neural Network Models. WSEAS Trans. Fluid Mech. 2008, 3, 126–136. [Google Scholar]
- Cleveland, T.G.; He, X.; Asquith, W.H.; Fang, X.; Thompson, D.B. Instantaneous Unit Hydrograph Evaluation for Rainfall-Runoff Modeling of Small Watersheds in North and South Central Texas. J. Irrig. Drain. Eng. 2006, 132, 479–485. [Google Scholar] [CrossRef]
- Zhao, B.; Tung, Y.-K.; Yang, J.-C. Estimation of Unit Hydrograph by Ridge Least-Squares Method. J. Irrig. Drain. Eng. 1995, 121, 253–259. [Google Scholar] [CrossRef]
- Bhattacharjya, R.K. Optimal design of unit hydrographs using probability distribution and genetic algorithms. Sadhana 2004, 29, 499–508. [Google Scholar] [CrossRef]
- Lattermann, A. System-Theoretical Modelling in Surface Water Hydrology; Springer Series in Physical Environment; Springer: Berlin/Heidelberg, Germany, 1991; Volume 6, ISBN 978-3-642-83821-7. [Google Scholar]
- Turner, J.E.; Dooge, J.C.I.; Bree, T. Comment on Single Storm Runoff Analysis Using Z-Transform. J. Hydrol. Eng. 2001, 6, 173–174. [Google Scholar] [CrossRef]
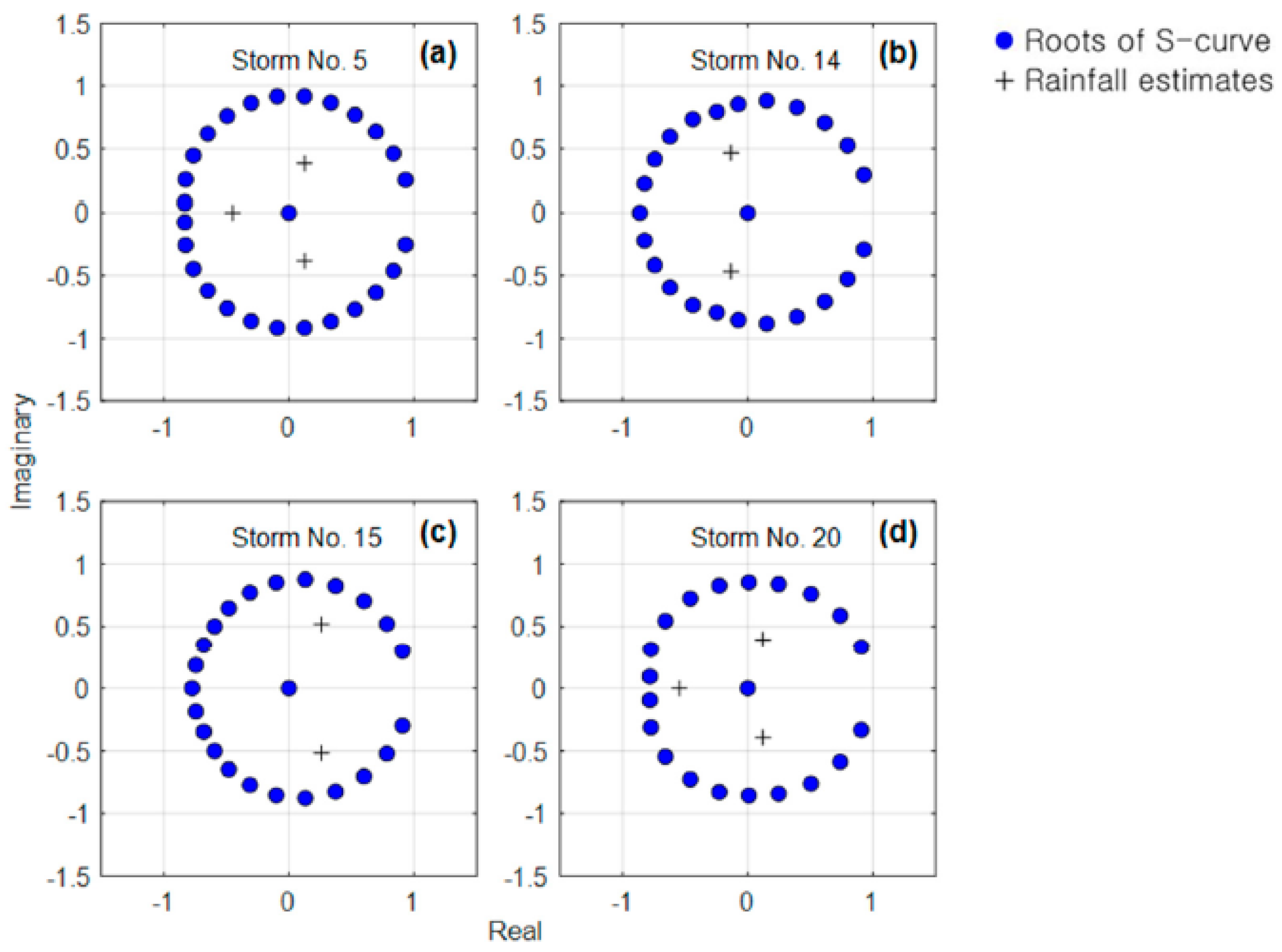
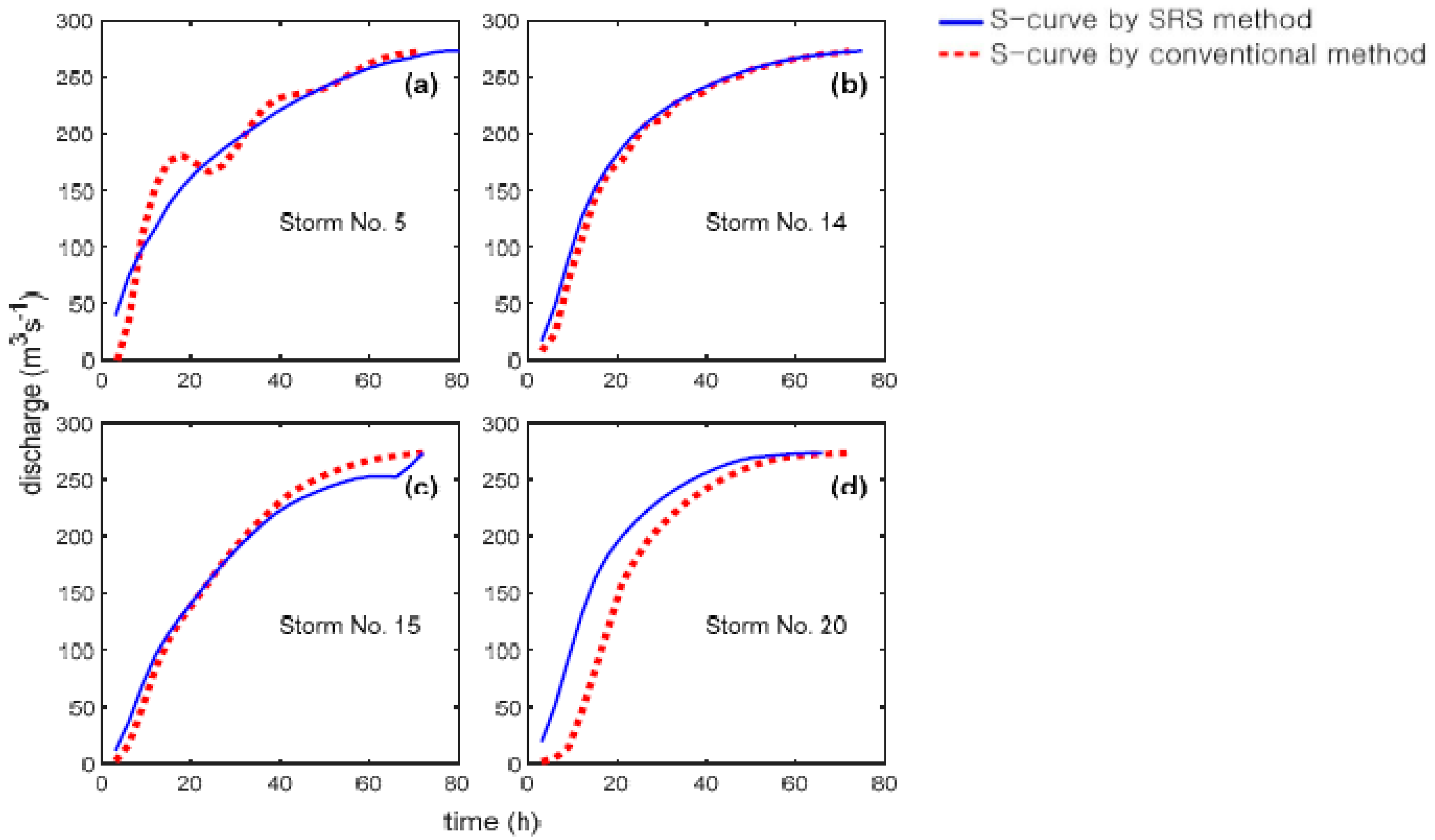
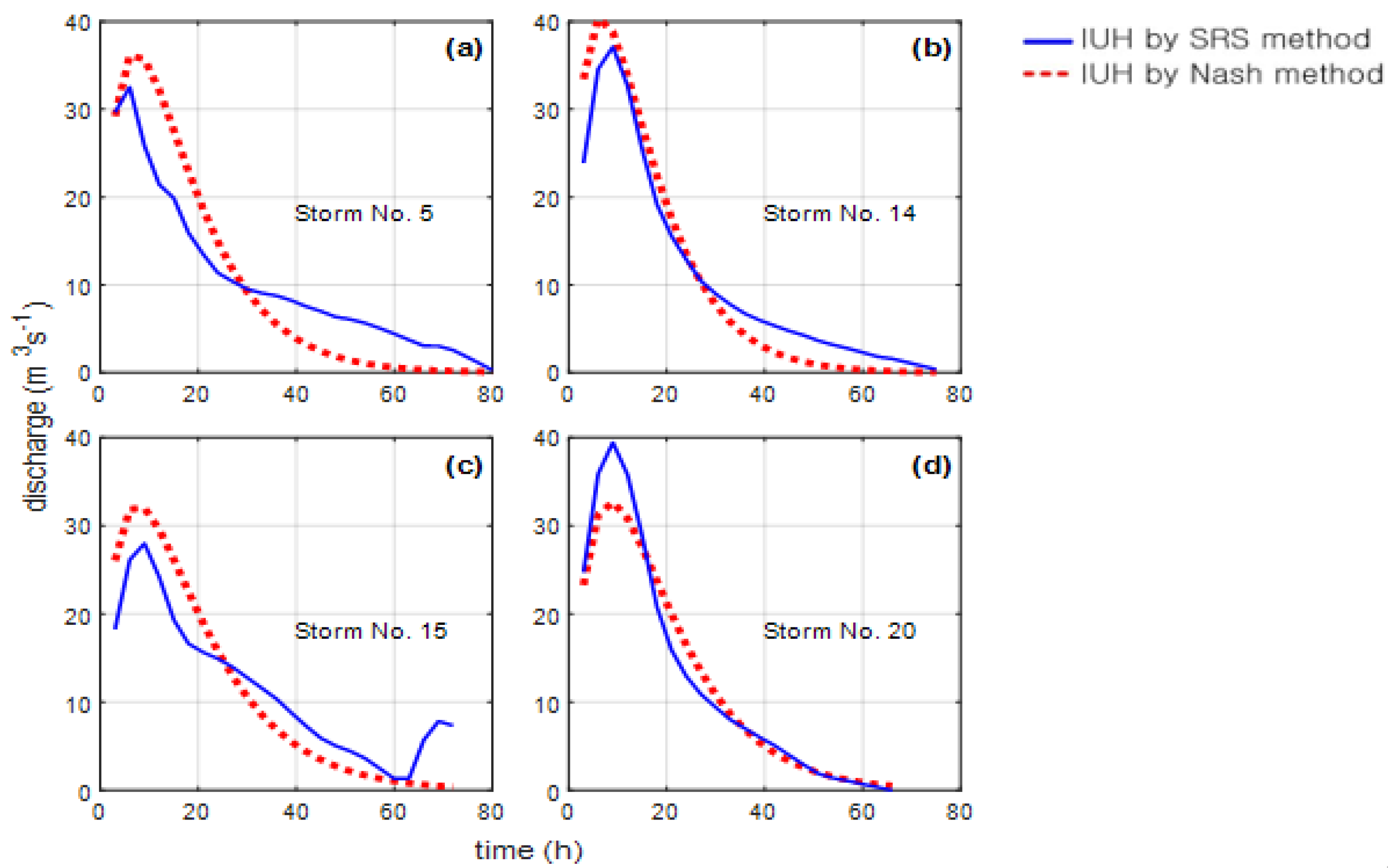
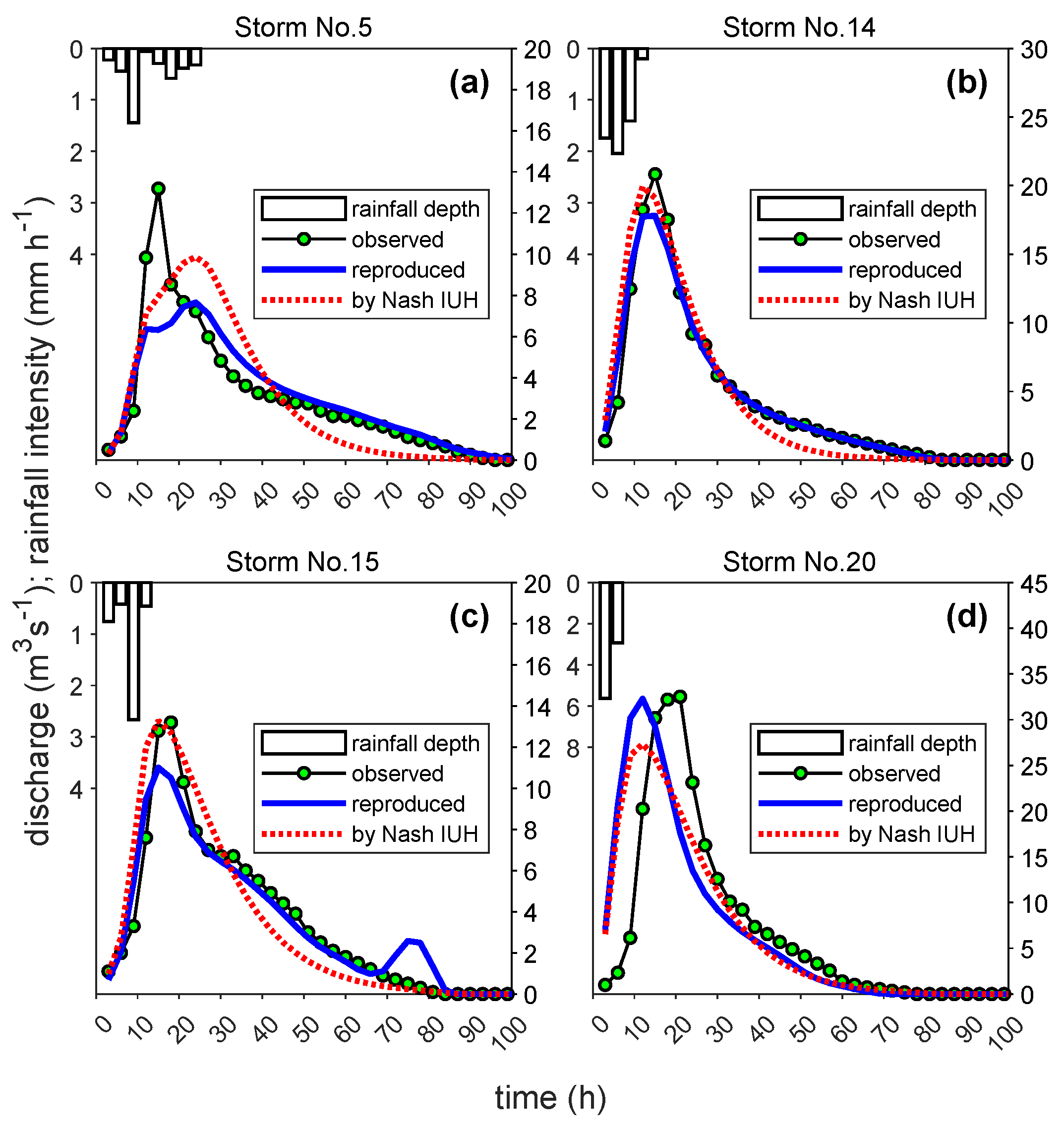

| Event Number | Time to Peak (h) | Peak Flow Rate (m3s−1) | Base Time (h) |
|---|---|---|---|
| 5 | 15 | 13.19 | 93 |
| 13 | 15 | 25.32 | 78 |
| 14 | 15 | 20.84 | 81 |
| 15 | 18 | 13.20 | 81 |
| 20 | 21 | 23.52 | 75 |
| Average | 16.80 | 19.21 | 81.6 |
| Event Number | n | K | STDER (%) | E | QB | ||
|---|---|---|---|---|---|---|---|
| Nash Model (%) | SRS Method (%) | Nash Model | SRS Method | ||||
| 5 | 1.779 | 3.050 | 5.67 | 67.1 | 77.6 | 0.252 | 0.420 |
| 14 | 1.808 | 2.0705 | 3.79 | 91.0 | 97.1 | 0.044 | 0.145 |
| 15 | 1.692 | 3.605 | 4.62 | 83.3 | 90.8 | −0.006 | 0.167 |
| 20 | 1.867 | 3.259 | 3.23 | 60.5 | 40.2 | 0.159 | 0.007 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seong, K.-W.; Sung, J.H. A Polynomial Method Approximating S-Curve with Limited Availability of Reliable Rainfall Data. Water 2021, 13, 3447. https://doi.org/10.3390/w13233447
Seong K-W, Sung JH. A Polynomial Method Approximating S-Curve with Limited Availability of Reliable Rainfall Data. Water. 2021; 13(23):3447. https://doi.org/10.3390/w13233447
Chicago/Turabian StyleSeong, Kee-Won, and Jang Hyun Sung. 2021. "A Polynomial Method Approximating S-Curve with Limited Availability of Reliable Rainfall Data" Water 13, no. 23: 3447. https://doi.org/10.3390/w13233447
APA StyleSeong, K.-W., & Sung, J. H. (2021). A Polynomial Method Approximating S-Curve with Limited Availability of Reliable Rainfall Data. Water, 13(23), 3447. https://doi.org/10.3390/w13233447






