GIS-Based Three-Dimensional SPH Simulation for the 11 April 2018 Yabakei Landslide at Oita Nakatsu, Japan

Abstract

Landslides are usually triggered by strong earthquakes, heavy rainfalls, or intensive human activities in common wisdom. However, an unexpected landslide occurred in the Yabakei area, Nakatsu, Oita, Japan, at the pre-dawn hour 3:50 a.m. on 11 April 2018, without any accompanying rainfall and earthquake records during the event. This catastrophic landslide was 200 m in width, 110 m in height, and 60,000 m³ in mass volume, damaging four residential buildings with fatalities of six residents at the landslide toe. Field investigation was conducted immediately to identify geological setting, hydrological condition, and landslide geomorphological characteristics. Key findings speculate that infiltration of groundwater stored in the internal fractures led to the swelling and breaking of illite and askanite in the weathered sediment rocks, resulting in the failure of the Yabakei landslide. To reproduce and explore the dynamic process of this landslide event, based on spatial GIS data, we applied the proposed three-dimensional, Herschel-Bulkley-Papanastasiou rheology model-based smooth particle hydrodynamics (HBP-SPH) method to simulate the landslide dynamic process. Buildings in the landslide area are covered by a set of surfaced cells (SC) to analyze the mass impact on the residential buildings. Results showed good accordance between observation and simulation by the proposed SC-HBP-SPH method. The landslide impact force to the residential buildings could be up to 4224.89 kN, as indicated by the simulation.

1. Introduction

Landslides are important landscape forming process in mountainous regions [1], posing serious risks to humans and the local society [2,3,4,5]. As reported by [6], a total of 2620 catastrophic landslides were recorded worldwide during a 7 year period, causing 32,322 fatalities in total. Japan, for instance, has only 0.1% of Earth’s land area, but over 10% of all active volcanoes and is where 10% of the world’s seismic energy emissions are concentrated, as well as having a doubled annual precipitation compared with the global average [7]. As such, it suffers from many landslide disasters every year.

Landslide hazards are the result of the coupling of endogenic and exogenic geological processes [8]. Previous studies have summarized common causes of landslides, including earthquakes [9], rainfalls [10,11,12], freeze-thaw [13], vegetation reduction [14], and human activities [15]. The triggering mechanism of a landslide frequently comprises a complex interaction between hydrological and geotechnical processes, which in turn depends on irregular topography, hydro-geotechnical properties, boundary conditions such as permeability, and the initial state of the slope [16]. Usually, landslides are associated with heavy rainfalls in the minds of most people. In general, when rainfalls occur in the mountains, the slope mass becomes saturated with rainfall infiltration [17], which increases its mass and the sliding force, thereby decreasing the landslide stability [18].

Rainfall infiltration also affects the groundwater table in the slope. The groundwater table is usually low but can rise quickly to the ground surface during heavy rainfall [19]. Groundwater is a key factor in the formation, occurrence, and development of landslides. The arisen groundwater table significantly reduces the shearing strength of the weathered material, leading to slope failure. In fact, previous studies have substantiated that more than 90% of the rocky slopes damage in reservoir bank were caused by the groundwater flow [20]. Recent studies also link the geology properties and rainfall conditions to the landslides, and suggest that meta-sediments, including greywacke, argillite, and sandstone can be extremely susceptible to landslides during heavy rainfalls [11,21,22,23] because these meta-sediments are prone to weathering and often contain groundwater in the fissure. Yet, huge and numerous landslides have been triggered due to a variation of groundwater level, and prediction and rational prevention of this kind of landslide are still scientific challenges owing to the complex groundwater transportation.

Except for the triggering mechanism, effective analysis of the landslide dynamic process is fundamental to landslide hazard mitigation [24]. Extensive runout of the landslide materials and their impact on the movement path leads to massive destruction [25]. In previous studies, landslide dynamics have been commonly explored by empirical-based methods, physics-based methods, and numerical methods, where the numerical methods compute the time-elapsed results of landslide process and provide better solutions. These kinds of methods can be majorly divided into continuous models, e.g., the finite element method (FEM) and finite volume method (FVM), and discrete models, e.g., discontinuous deformation analysis (DDA) and smoothed particle hydrodynamics (SPH). Recent studies (e.g., [26,27]) indicate that the continuous models are sometimes limited in landslide dynamic process simulation due to their requirement to track the violent free-surface using additional techniques.

Recently, the SPH methods have been applied for problems with computational fluid dynamics for free surface flow and large deformation. The method has been proved to have robustness and reliability in solving integral equations or partial deviation equations [28,29,30]. One growing concern of the SPH method in landslide dynamics simulation is with respect to the rheology model, that the commonly used Bingham model should be suitable for the fluid-kind materials. In this aspect, many previous studies attempted to incorporate different rheology models, e.g., the general Cross model [31,32], the Herschel-Bulkley model (HB) [33,34], and the Herschel-Bulkley-Papanastasiou (HBP) [35,36] to describe the rheological behavior of landslide mass. Another key issue of the SPH method is regarding to the representation of the landslide dynamic. Landslide mass in the SPH scheme consists of a large amount of particles with complex velocity vectors and dispersed locations in three-dimensional coordinate system. Therefore, a rational representation of the landslide dynamic is necessary. To address this issue, we proposed a novel surface cell-based model, i.e., the so-called SC-HBP-SPH model [37], in which the space is meshed, over which the SPH particles belonging to a certain cell at each time step are identified to represent the dynamics such as velocities and mass depths. This method also benefits the analysis of the time-elapsed variation of landslide mass impact. Consequently, in the past years, SPH was used in landslide modeling [30,38,39,40]. The results indicate that the SPH is robust and reliable in modeling the fundamental dynamic behavior of mass flows. Therefore, HBP-SPH was adapted in this work to investigate the influence of landslide mass on the impact pressure in building.

GIS is a system used to process the corresponding attribute information related to spatial location and consists of data collection, storage, description, retrieval, analysis, and application functions [41]. GIS is widely applied in slope information management, correlation analysis of landslides, dynamic environmental factors, and landslide stability evaluation based on its spatial analysis capabilities in geotechnical engineering [42,43]. The SPH-terrain model based on the GIS spatial data of the landslide will significantly improve the efficiency of the dynamic analysis and research of the landslide simulation.

To reproduce and explore the dynamic process of this landslide event, based on spatial GIS data, we applied the proposed three-dimensional, Herschel-Bulkley-Papanastasiou rheology model-based smooth particle hydrodynamics (HBP-SPH) method to simulate the landslide dynamic process. Buildings in the landslide area are covered by a set of surfaced cells (SC) to analyze the mass impact on the residential buildings. In Section 2, we report a recent massive landslide event that occurred in the mountainous area of Yabakei, Nakatsu, Oita Prefecture in southwestern Japan. In Section 3, we introduce the triggering factors of the landslide event. Based on information regarding geomorphology, hydrology, and geological setting condition, in Section 4, preliminary speculation with respect to the triggering mechanisms of this landslide event is presented. In Section 5, based on spatial GIS data, we apply the established SC-HBP-SPH model to reproduce and explore the dynamic process of this landslide event. Section 6 is the discussion of this paper. Generally, this case provides a good example of landslides to illustrate the key role of weathered meta-sediment and groundwater transportation for triggering a landslide, as well as its dynamic for landslide mitigation.

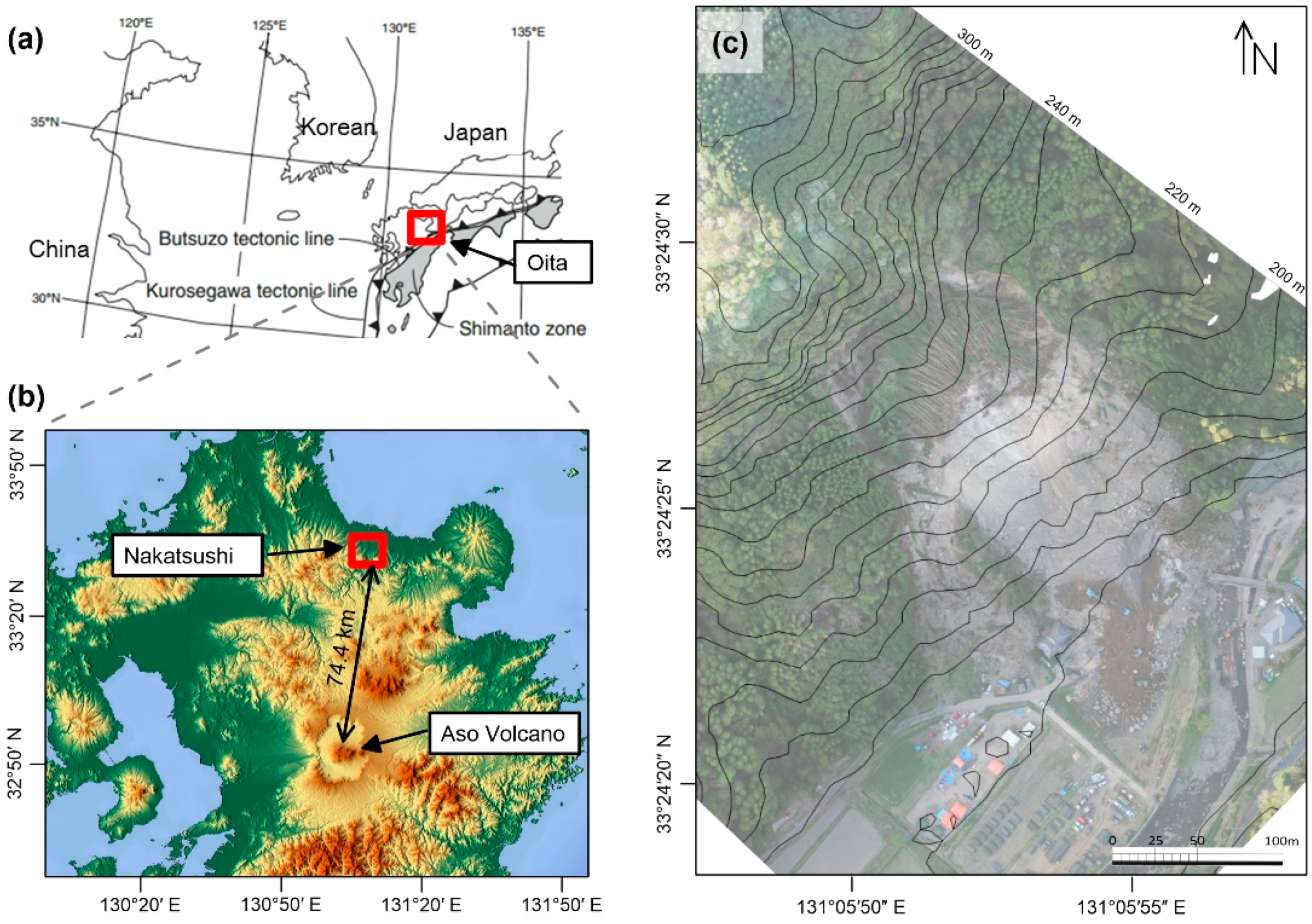
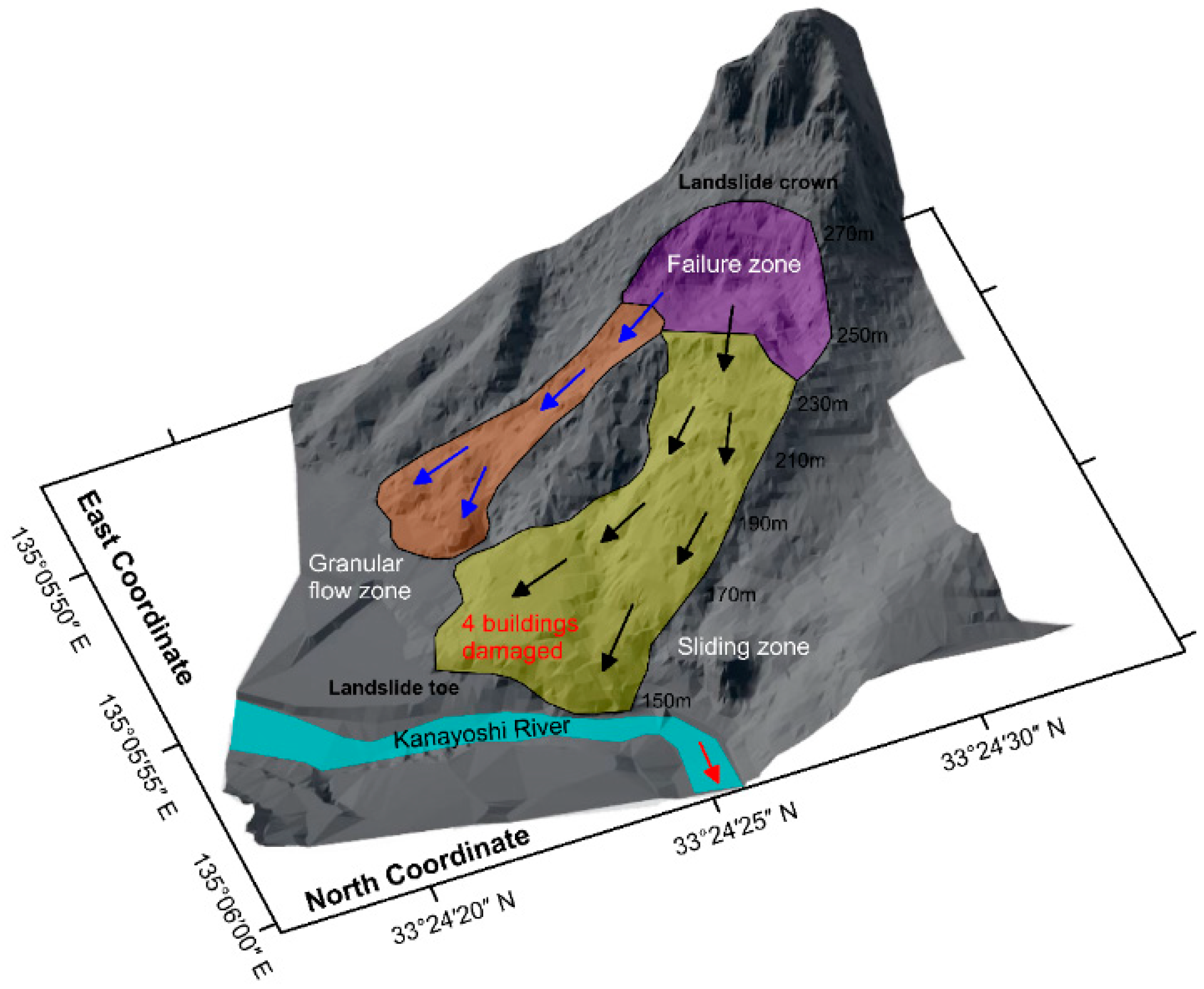
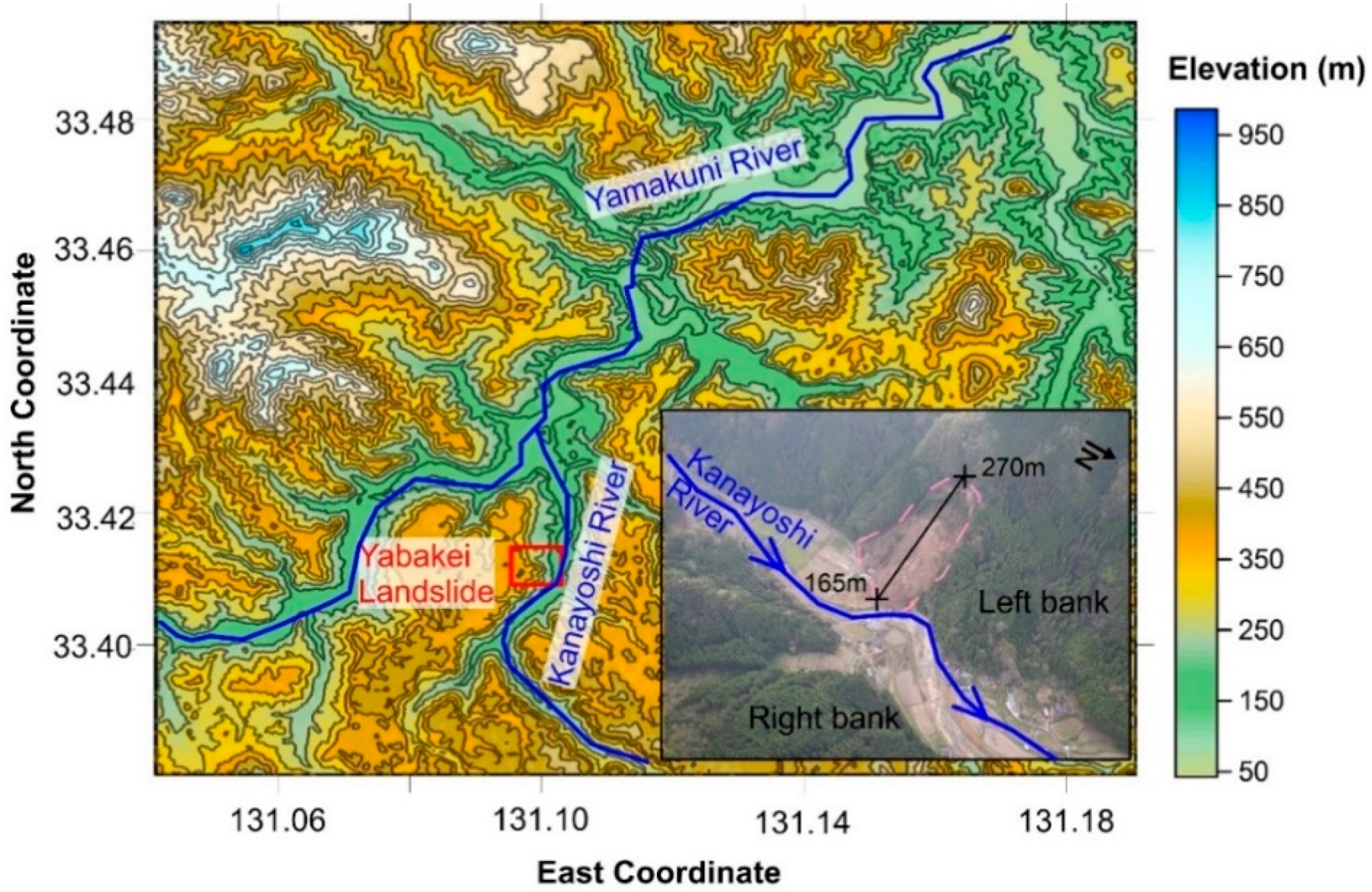
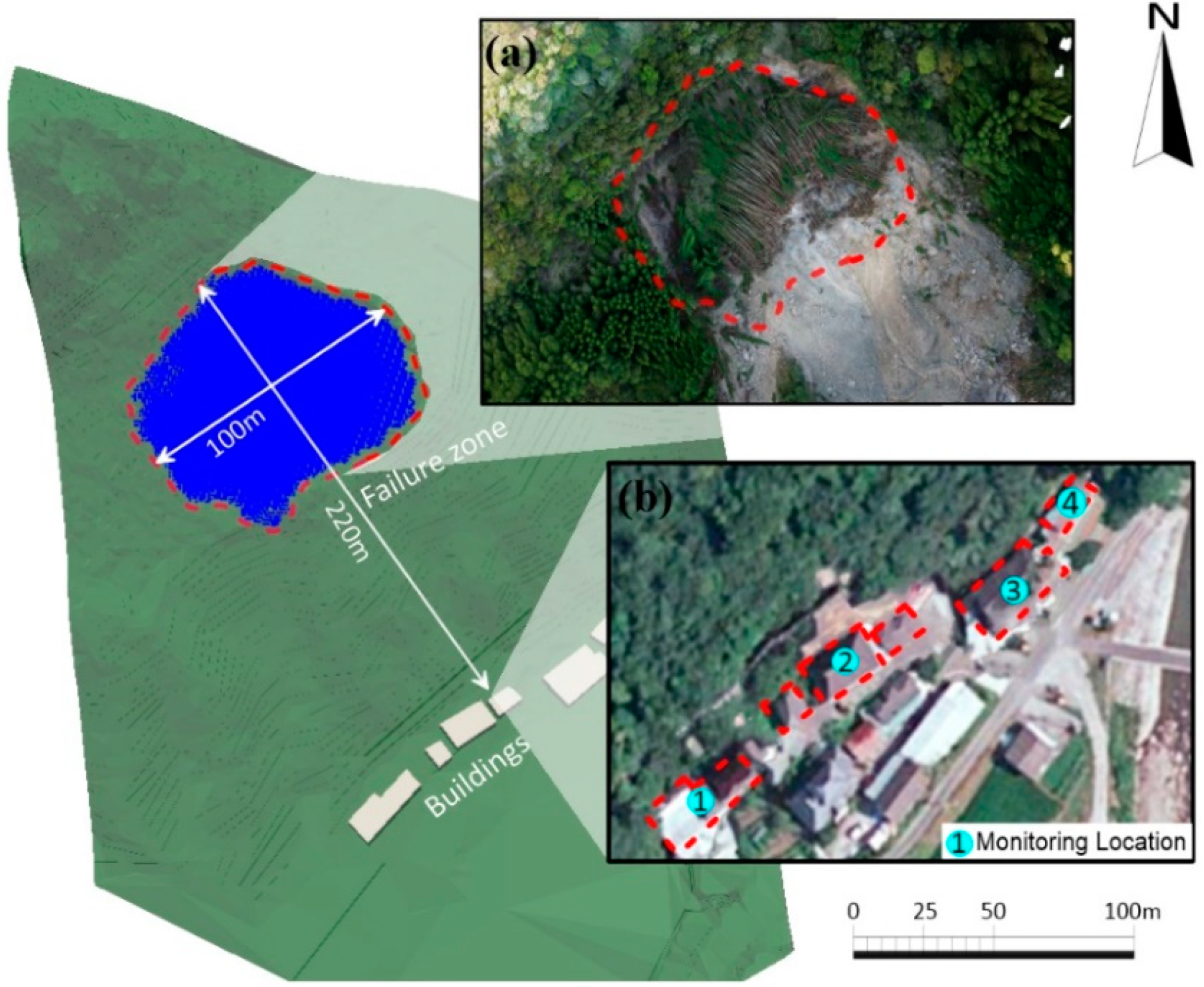
2. Characteristics of the Landslide Event

The Yabakei landslide was located in the mountainous region at Nakatsu, Oita Prefecture of southwestern Japan (Figure 1a,b). At the pre-dawn hour 3:50 a.m. of 11 April 2018, the landslide occurred with a collapsed slope of 200 m in width and 110 m in height (Figure 1c). Unfortunately, no emergency alarm was issued because there was no significant rainfall or earthquake in this region over the past few days. The sliding deposit with a mass volume of approximately 60,000 m³, therefore, damaged four local resident buildings at the landslide toe, leading to a total of six fatalities in the event. Landform change before and after the event is shown in Figure 2.

After the event, an immediate in-situ survey was organized by the local government. Figure 1c is the topographic map of the landslide site. A digital terrain model (DTM) with 2.0 m in resolution was obtained by the unmanned aerial vehicle (UAV) after the landslide. Comparison between the pre-and post-landslide DTM demonstrates that the landslide zone can be roughly divided into three sub-zones, i.e., the failure zone at the crown, the sliding zone, and the granular flow zone at the landslide toe, as shown in Figure 3. The resolution of the pre-event DTM is 5.0 m.

Different processes dominated each sub-zone. The deformation zone presents a significant deformation during the slope failure process. The deformation on the landslide crown forms a platform and a scarp approximately 30 m high. The sandstone bedding can be found at the crown, with obvious cracks and joints. It suggested that the failure plane was located near the boundary between the relatively hard bed rocks and weathered material. It was supposed that the weathered material on the platform slid immediately after the slope failure and entrained the superficial deposit on the slope body. The entrainment process developed and a scarp approximately 10 m in depth formed along the slide path. The sliding mass was finally deposited at the alluvial of the river, with a total run-out distance of approximately 80 m.

3. Triggering Factors of the Landslide Event

In order to explore the triggering mechanism of this landslide event, key triggering factors have been identified, including geomorphological characteristics, geological settings, and hydrological conditions.

3.1. Geomorphology of the Area

The area is located at the left bank of Kanayoshi River, 2.7 km away from the junction of the first level tributary, Yamakuni River. The hilly mountain has an elevation ranging 150 m–350 m (as shown in Figure 4). Owing to the alluvial deposit of the right-side bank, the cross-section of Kanayoshi River is compressed, forming an obvious river bend to the left-side bank. The regional geomorphology was significantly affected by the volcanic activities in the Pleistocene, Quaternary.

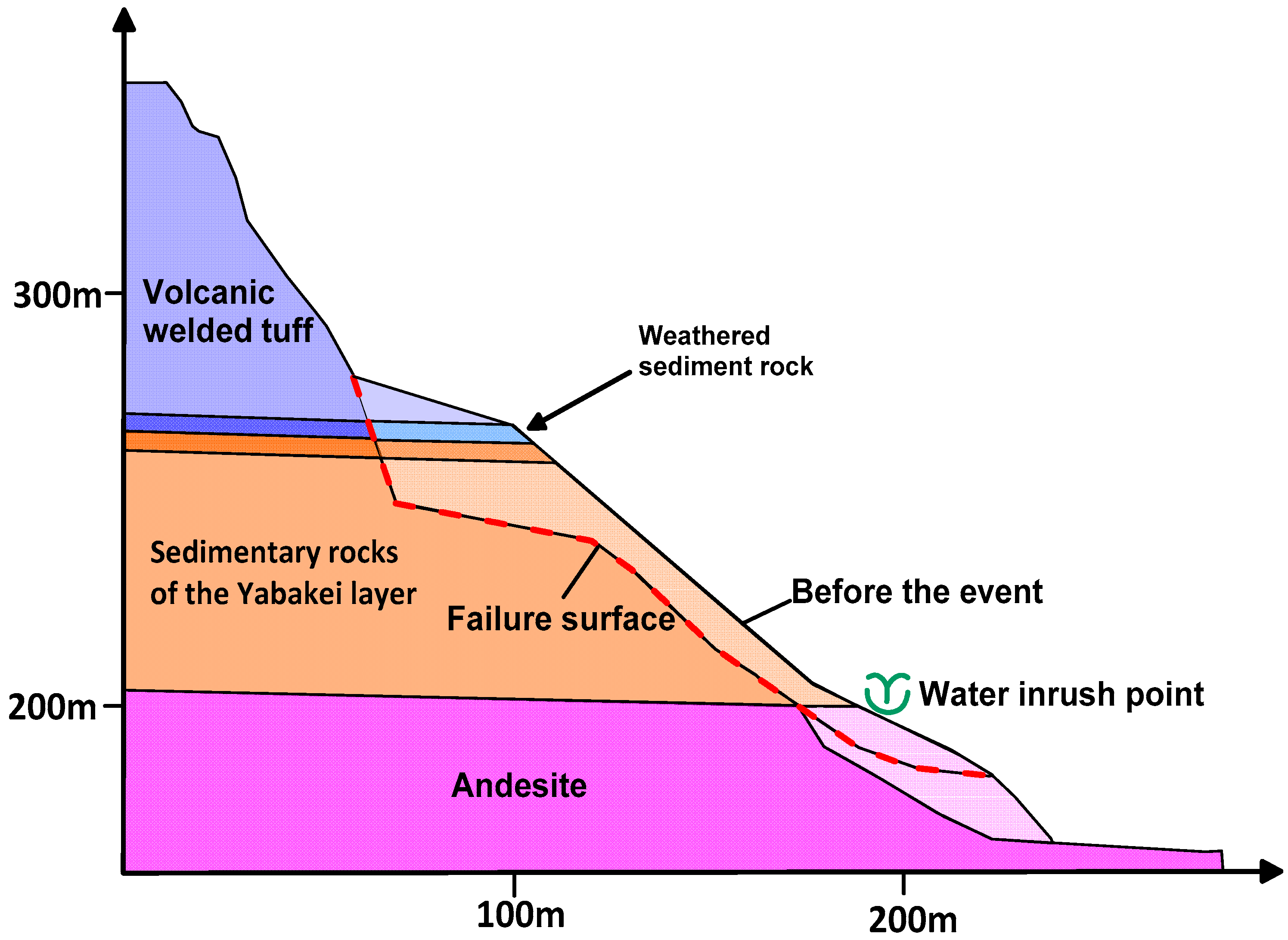
3.2. Geology of the Area

Based on the geological map of Yababei-Nakatsu area in Figure 5 [44], the slope is underlain majorly by pyroclastic-flow deposits and volcanic rocks with lava. The sedimentary rocks are majorly sandstone and mudstone. These sedimentary rocks contain abundant illite and askanite, which are consequently sensitive to weathering and prone to swell and break when contacting with water. The longitudinal geological section of the landslide is shown in Figure 6.

According to the geotechnical testing report [45], permeability test and standard cone penetration test using five samples collected in-situ were conducted to evaluate the strength of landslide material. The density is around 16.6–17.4 kN/cm³, with an averaged permeability of 10⁻⁴~10⁻³ cm/s. Three layers of landslide soil are indicated: superficial deposits with a Nd value less than 5 are 1.4 m in depth, the weathered rocks and soil with a Nd value ranging from 6 to 49 are 2.3–3.4 m in depth, while the unweathered substrate that has a Nd value greater than 50 is underlying.

The investigation report of Yabakei landslide also explored the internal structure of the landslide area. Standard Gamma Ray (SGR) logs were introduced to identify the internal fractures of the slope. Radioactive isotopes of elements continuously decay to more stable forms and emit radiation of several types. Gamma rays have longer penetrations than either alpha or beta rays and can be well-measured. Interpretation results demonstrated that four major fractures are distributed in the landslide area, with fracture widths ranging from 1.6 m to 3.1 m. These fractures in the rock mass of the slope provide possible storage for perched groundwater.

3.3. Hydrology Condition

Rainfall data were recorded by AMeDAS (Automated Meteorological Data Acquisition System) at Yabakei station, which is approximately 5.0 km from the site. According to the historical rainfall data between January 2009 and April 2018, the maximum monthly rainfall intensity 947 mm was reported on July, 2012. The 24-h rainfall strength of the past 30 days before the landslide event is documented in Figure 7. It is illustrated that no rainfall was observed accompanying with the landslide occurrence. The antecedent rainfall was reported 4 days before the event; rainfall intensities of 4.5 mm and 1.5 mm were recorded on 6 April and 7 April respectively.

Despite the absent accompanying rainfall, water outflow was still observed during the post-event survey (pieces of evidence are shown in Figure 8). The water outflow at the main body of the landslide was located at the elevation of 235 m [46]. The measured discharge was approximately 0.3 L/s. It is speculated that the groundwater, maybe perched water, existed in the residual soil and the fissure of the highly fractured rock mass. The field geological testing based on SGR log supports our speculation that one sub-horizontal fracture and three sub-vertical fractures exist across the main body of the landslide, providing possible storage of groundwater. Based on the geological information of this region, the mountain is underlain by volcanic rocks, deposits, and sedimentary rocks. The sedimentary rocks are majorly sandstone and mudstone. These sedimentary rocks contain abundant illite and askanite, and therefore are sensitive to weathering and prone to swelling and breaking when contacting perched water.

4. Triggering Mechanism Analysis

The catastrophic Yabakei landslide collapsed suddenly without any alarm sign. It is a quite typical case in view of that no earthquake or rainfall was recorded accompanying the landslide occurrence. The mechanism of this landslide can be explained in part by the geological settings because four major fractures in the welded tuff were identified in the post-event survey. The antecedent rainfall 4 days before the event resulted in the water infiltration into the fissure of the highly fractured rock mass, causing the long-term effect of soil water on slope destabilization [47]. The perched groundwater was leaking out of the fractures in the weathered meta-sediment rock, accordingly increasing the water content of the surface near the slope failure, as well as the potential possibility of landslide occurrence [48]. Pieces of evidence of the perched groundwater are supported by the measurement of water outflow discharge in the post-event survey (as shown in Figure 8). In this sense, the slope failure of this case had a close relation with perched groundwater in the fissure of the fractured sediment rocks, and the rise of the groundwater table in the slope and the loss of the inbound shear strength of the soils can be explained (Figure 9).

Additionally, the geological setting of this area is mainly composed of volcanic deposits based on the map from Geological Survey of Japan (GSJ) in Figure 5. Volcanic deposits were frequently vulnerable to landslides and several associated sediment-disasters have been reported [49,50]. Numerous landslide types occur in such volcanic deposits, such as rock falls, granular flows, debris flow, flank collapses, slumps, etc., depending on the characteristics of the volcanic deposits. A similar case has been reported in Sounkyo gorge, Hokkaido, Japan, where a landslide occurred on volcanic welded tuff, while accompanying rainfall or earthquakes were not recorded.

Moreover, in this case, rock weathering is remarkable based on the survey. The sedimentary rocks are majorly sandstone and mudstone, which are sensitive to weathering and prone to swelling and breaking when contacting water. Many related sediment-disaster studies have been conducted [51,52]. For instance, [53] demonstrated that the rock weathering is supposed to accelerate owing to the removal of overlying beds, and the alternating beds beneath the sandstone had been influenced by weathering because of the groundwater transportation through the permeable sandstone. In the present case, the competent andesite and weathered rocks were likely to be weakened due to water infiltration through the fissures of the fractured rocks. The filling was made up of wreathing sediment and the sediment deposits enclosed an amount of water after the failure. In view of the above evidence, it is considered that the weakening of the base rock and welded tuff with extremely developed columnar joints inside may have been highly likely to trigger the 2018 Yabakei landslide. Such special depositional patterns in volcanic residuals effect localized weathering of these materials should pay more attention to precursor phenomena such as falling rocks and spring water increase and decrease.

5. Dynamic Process Simulation Using SC-HBP-SPH Model

The above analysis speculates that infiltration of groundwater stored in the internal fractures leds to the swelling and breaking of illite and askanite in the weathered sediment rocks, resulting in the occurrence of the 11 April 2018 Yabakei landslide. In this event, the sliding mass finally deposited at the alluvial of the river, with a total run-out distance of approximately 80 m, damaging four local buildings with fatalities of six residents. Catastrophic landslides can be commonly explained by the mass volume and its dynamics, including the distance of run-out, and the impact force on the structure. In this section, based on the geomorphology of the area, geology of the area, and hydrology condition of the landslide, we back-analyze and simulate the landslide dynamic process using our SC-HBP-SPH model [37,54], and extract the variation of impact force of landslide mass to the buildings.

5.1. The Three-Dimensional HBP-SPH Method

Smooth Particle Hydrodynamics (SPH) is a meshless method under the Lagrangian framework. The calculation domain is generalized by discrete particles, and the inter-particle relationship is described by the kernel function to solve the field variables such as velocity, density, and stress tensor [55]. This kind of method has been recently applied for investigating the mechanism of landslides [29,56,57]. The SPH-based methods provide a means of a mesh-free, particle-based simulation and 3D space description.

In this paper, we used the SPH method that incorporates the Herschel-Bulkley-Papanastasiou (HBP) rheology model to describe landslide propagations [54]. The HBP rheological model has been substantiated as robust when simulating nonlinear rheological bodies, and its expression is as follows:

$${\tau }^{\alpha \beta }=2{\mu }_{eff}{\epsilon }^{\alpha \beta },$$

(1)

$${\epsilon }^{\alpha \beta }=\frac{1}{2}\left[\frac{\partial v^{\alpha }}{\partial x^{\beta }}+\frac{\partial v^{\beta }}{\partial x^{\alpha }}\right],$$

(2)

$${\mu }_{eff}=K{\dot{\gamma }}^{n-1}+\frac{{\tau }_y}{2\dot{\gamma }}\left(1-e^{-m\dot{\gamma }}\right), K=2^{n-1}·\mu ,$$

(3)

where ${\tau }^{\alpha \beta }$ the shear stress tensor,${\mu }_{eff}$ is the effective viscosity, and ${\epsilon }^{\alpha \beta }$ is the local strain rate tensor. $m$ and $n$ are the constants and power law exponents that control the growth of stress at different shear rates, respectively.${\tau }_y$ is the yield stress of the Mohr-Coulomb yield criterion.$P$ is the pressure and $\dot{\gamma }$ is the norm of the strain rate tensor and is defined as

$${\tau }_y=coh+Ptan\phi ,$$

(4)

$$\dot{\gamma }=\sqrt{\frac{1}{2}{\epsilon }^{\alpha \beta }{\epsilon }^{\alpha \beta }},$$

(5)

In the Lagrangian form, the three-dimensional SPH framework combined with the HBP rheological model, the Navier-Stokes equation composed of the momentum conservation equation effectively describes the propagation of the landslide,

$$\frac{d{v}_i^{\alpha }}{dt}=-{\sum }_{j=1}^N{m}_j\left(\frac{P_i}{{\rho }_i^2}+\frac{P_j}{{\rho }_j^2}\right)\frac{\partial W_{ij}}{\partial x_i^{\alpha }}+{\sum }_{j=1}^N{m}_j\left(\frac{2{\mu }_{effi}{\epsilon }_i^{\alpha \beta }}{{\rho }_i^2}+\frac{2{\mu }_{effj}{\epsilon }_j^{\alpha \beta }}{{\rho }_j^2}\right)\frac{\partial W_{ij}}{\partial x_i^{\beta }}+g^{\alpha },$$

(6)

where $W_{ij}$ denotes the kernel function.$v^{\alpha }$ and $g^{\alpha }$ present the particle velocity and gravity, respectively. For a detailed description of the HBP-SPH method, refer to our previous work [32,37,54].

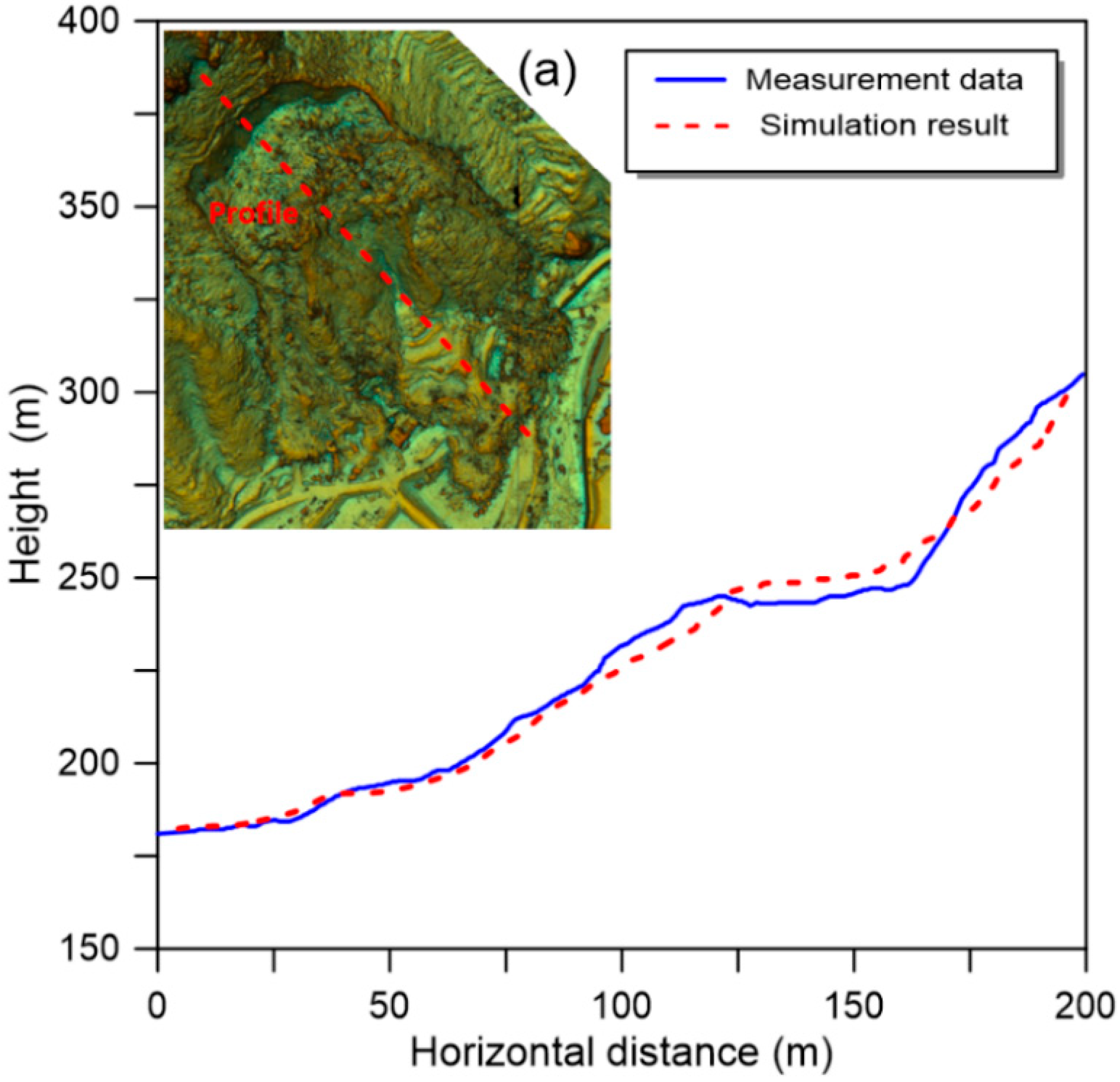
5.2. Configuration of the Numerical Model

As shown in Figure 10, according to the available topography of the landslide, the sliding mass is described by a large number of particles with smoothing length of 1.732 m. The smoothing length in three dimensions can be calculated by [55],

$$l_s=ϵ\sqrt{{\left(d_{px}\right)}^2+{\left(d_{py}\right)}^2+{\left(d_{pz}\right)}^2},$$

(7)

where the coefficient $ϵ$ is determined as 1.0 in this study. $d_{px}$, $d_{py}$, and $d_{pz}$ denote the SPH particle distance in the X, Y, and Z directions, respectively.

The initial particle distance is manipulated as 1.0 m, therefore generating 10,987 boundary particles and 44,974 mass particles. The parameters in the SPH simulation are listed in

Table 1. Influencing parameters and their values in the landslide simulation.

Parameter	Notation	Unit	Value
Density	$\rho$	kg/m3	1730
Apparent dynamic viscosity	$\mu$	Pa·s	0.001
Yield strength 1	$coh$	Pa	0
	$\phi$	°	40
Key coefficients of HBP model	$m$	/	100
	n	/	1.00
Total number of fluid particles	$N_{pf}$	/	44,974
Total number of boundary particles	$N_{pb}$	/	10,987
Particle distance	$d_p$	m	1.0
Smoothing length	$l_s$	m	1.732
Artificial viscosity coefficient	${\alpha }_{\mathrm{II}},{\beta }_{\mathrm{II}}$	/	0.1
EoS constant	$\lambda$	/	7
Initial time interval	$\Delta t$	s	0.0001
CFL coefficient	$CFL$	/	0.2
Simulation duration	t	s	1400

¹ According to [45], yield strength value was estimated by the relevant in-situ test.

. It should be noted that the artificial viscosity term can be calculated by using the formulas proposed by [58]. In our study, the artificial viscosity coefficients ${\alpha }_{\mathrm{II}}$ and ${\beta }_{\mathrm{II}}$ were chosen as 0.1 according to the suggestion in a previous study [59]. The Verlet scheme was used for the time integration in the proposed numerical model, and the variable time step algorithm was adopted. The Courant-Friedrichs-Lewy (CFL) coefficient was chosen as 0.2 as suggested by previous studies [55,60].

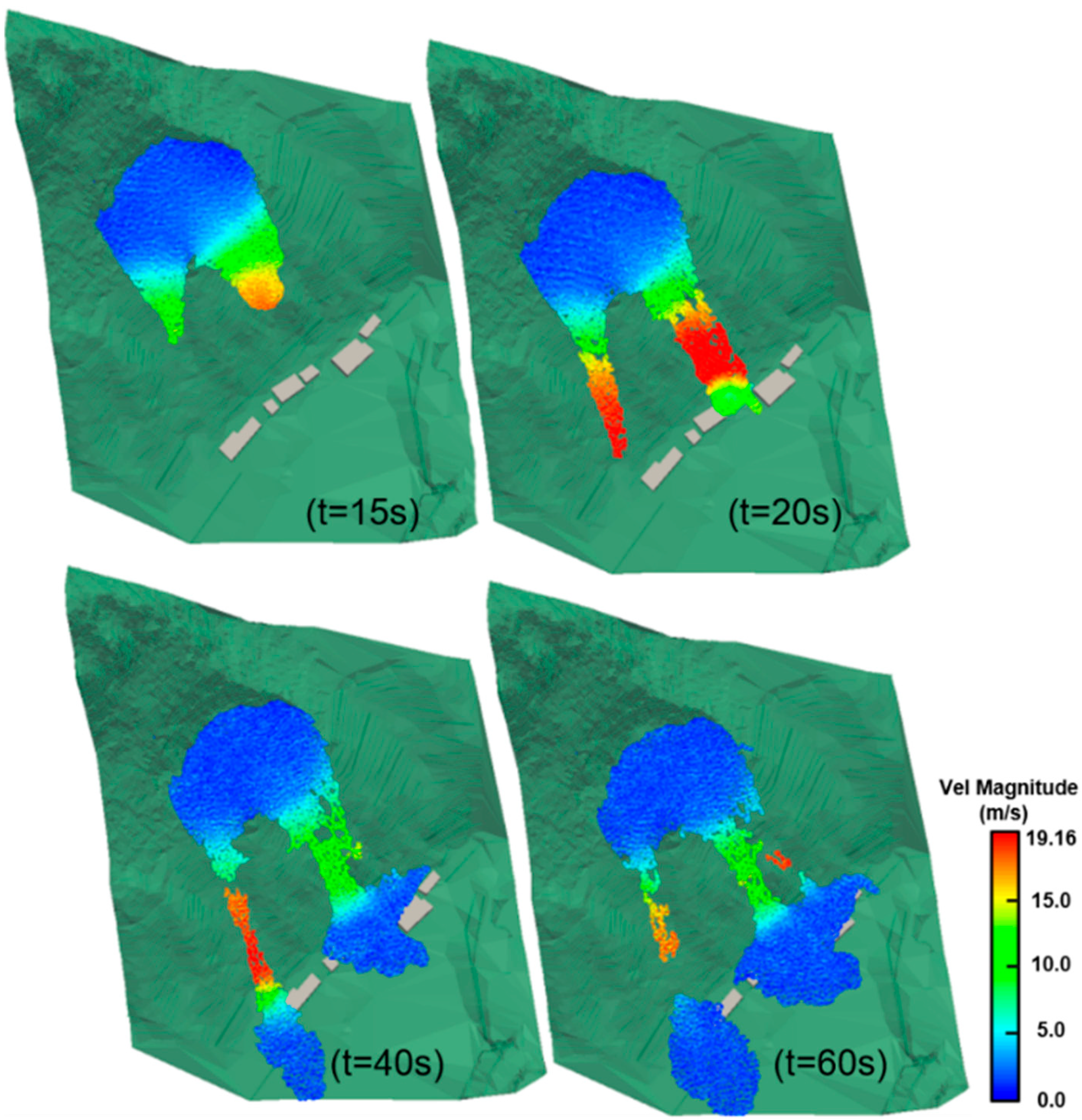
5.3. Analysis of Dynamic Simulation Results

The simulated time-elapsed results of landslide dynamic behavior during the process are shown in Figure 11. Especially the complex destruction process that the landslide mass contact and impact the residential buildings downslope. Figure 12 presents the variation of the main section of the slope after the landslide, showing the comparison between the measurement data and the simulation results. The results demonstrate that the impact range of this landslide was about 75 m in the vertical direction, and about 200 m in the horizontal direction. The dynamic simulation results also demonstrate the dynamics of the landslide at each time step. The failure mass passed through the sliding area and impacted the buildings within 17 s of initiation, with a maximum impact velocity of 19.16 m/s.

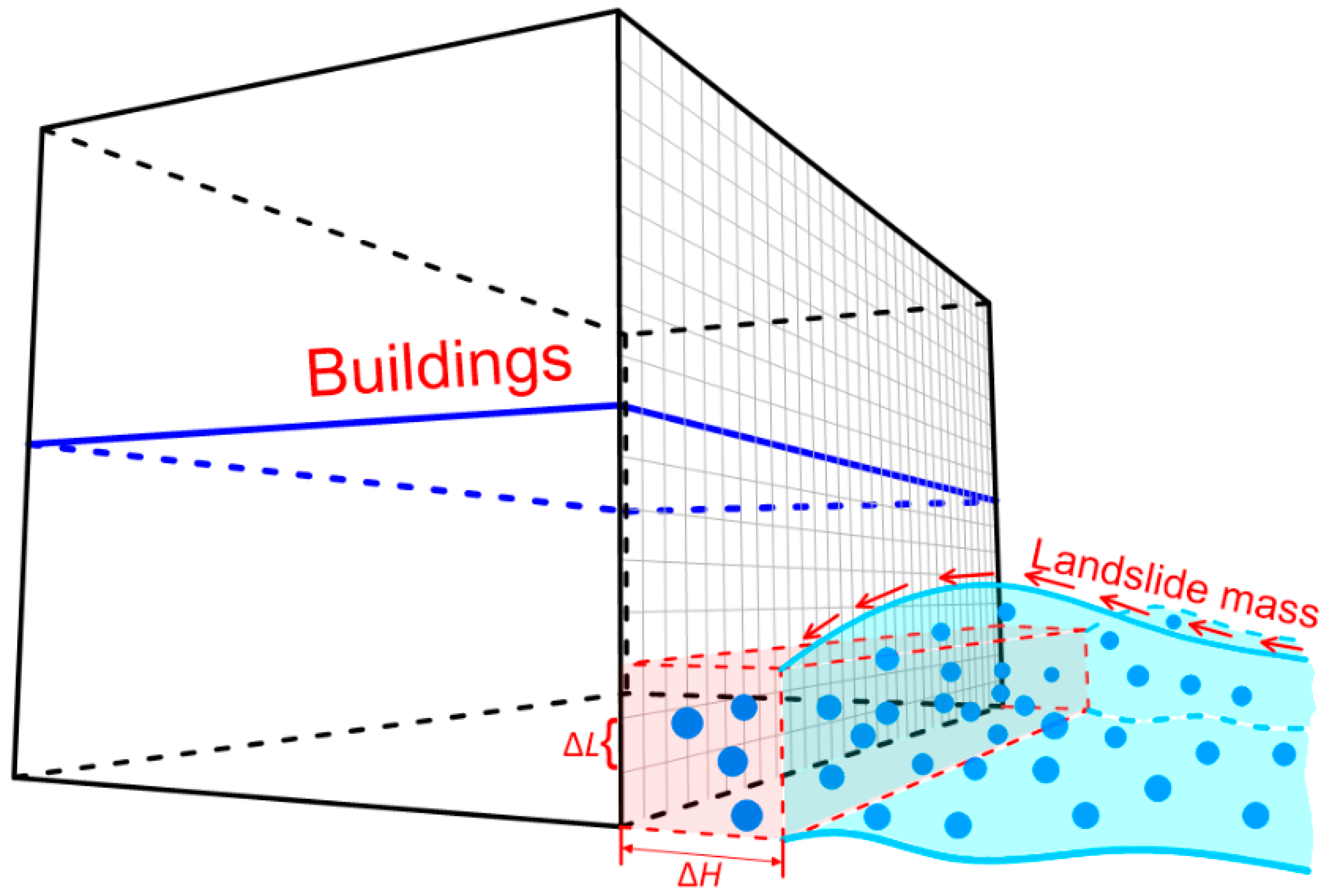
5.4. Extraction of Landslide Impact Force Using SC-Based Method

The simulation results of dynamics of this landslide case by HBP-SPH method were beneficial to analyze the impact force exerting by landslide mass. We used the following empirical-based equation (Equation (8)) to calculate impact force, where impact force is a function of particle velocity and its density. Although Equation (8) is empirical-based, it has been widely applied in many previous studies, e.g., [24,61,62,63].

$${\sigma }_d=\alpha \rho v^2,$$

(8)

In the equation, ${\sigma }_d$denotes the dynamic impact force exerted by landslide mass particles, $\alpha$is an empirical coefficient, and $\rho$ represents the density of the landslide mass,$v$ are the velocity of each individual particle. Equation (8) is also further explained by the fluid momentum balance and Bernoulli equation, which is suitable for calculating the impact pressure of saturated mixtures. Due to the difference in landslide regime and proportions of granular composition, the empirical correction coefficient $\alpha$ needs a trial-and-error adjusting. The suggested value of $\alpha$ ranges from 0 to 5.0 in many previous studies [61,62,63,64]. The impact force on Jiangjia gully in the situ test was observed on 21–25 August 2004. Based on it, the best-fitting $\alpha$ value was subsequently determined to be 3.0, which is acceptable for estimating the impact force in most cases [65].

In order to analyze the impact force on the residential buildings by landslide mass, the surface cell (SC)-based method that was proposed in our previous study [37] was used. The SC-based method sorts the SPH particles according to their spatial location and extracts the general velocity and mass depth. Figure 13 illustrates this concept and presents a schematic depiction of the landslide mass impact on the building. The key parameters for calculating the impact force are listed in

Table 2. Parameters used in the impact force estimation.

Parameters	Notation	Unit	Value
The empirical correction coefficient of impact force formula	$\alpha$	/	3.0
Distance of impact contact surface	$\Delta H$	m	2.0
Size of the SC	$\Delta L$	m	0.5
Landslide duration	$T$	s	1400
Time increment	$\Delta t$	s	0.1

. Based on the reproduction analysis of the 2018 Yabakei landslide events, the maximum impact velocity of particles was 19.16 m/s. To optimize monitor the velocity of particles impacting the surface of buildings, the value of distance of impact contact surface $\Delta H$ was set to 2.0 m when the time increment $\Delta t$ was 0.1 s.

To record the spatial variation of impact forces exerting by landslide mass, we set four monitoring points from 1# to 4# at different locations of the residential buildings (shown in Figure 10b). Each monitoring points record a set of time-elapsed instantaneous impact force at the location. Figure 14 shows temporal and spatial variation of impact forces exerting by landslide mass at different locations. It is shown that the maximum impact forces of 4224.89 kN and 1704.42 kN existed at the 2# and 3# monitoring points respectively, along the main sliding profile. Impact forces also showed a significant decreasing at the building near 1# and 4# monitoring points, where impact forces both reduced to approximately 300 kN. The spatial distribution of impact forces at the 2018 Yabakei landslide area illustrates that the residential buildings near 2# and 3# points suffered from the maximum impact force, and have a high risk for structural damage. This speculation has been also verified by the in-situ survey, i.e., that the two buildings were damaged during the landslide event as shown in Figure 1c and Figure 2b.

6. Discussion

In this paper, we reported on a catastrophic landslide event in the Yabakei area, Japan, 2018, and discussed its triggering mechanism and dynamic process. The proposed SC-HBP-SPH method in our previous study was applied and verified as an alternative solution for analyzing the run-out distance and impact force by landslides in this case.

6.1. Limitations

The novelty-based methodology of this paper is as follows: Taking the surface cells covered by the building as the research object, analyze and count the particles impact force of each cell. Frist, according to the three-dimensional HBP-SPH method, simulate the movement of the landslide. Then, apply the impact model to solve the impact force in each cell. Last, based on the impact force function in each surface cell, calculate and solve the impact force of the entire building. Adopting the above algorithm for each instance can realize the dynamic solution to the landslide mass impact process. The above method can solve the complex process of landslide impact in real-time, effectively and conveniently.

However, the proposed SC-HBP-SPH method theoretically assumes a uniform size of particles, which may underestimate the impact force because, in reality, there are many large boulders in the landslide mass, in particular rocky landslides. This may somehow limit its application in other cases. In this paper, we made a compromise by adopting the semi-empirical impact force equation (Equation (8)) to calculate the impact force. The optimal fitting α value was determined as 3.0, which is acceptable in most cases to simplify the analysis of landslide impact process [65]. Therefore, for analyzing the dynamic process of landslide impact, the coupled DDA-SPH model involving Solid-Fluid Interaction [40], as well as the discretization for the modeling of free-surface flows and rigid body dynamics (SPH-DEM) [66,67] could be beneficial solutions.

6.2. Sensitivity Analysis of Impact Force

In order to extract the general velocity and impact of SPH particles, the surface-based algorithm from our previous method [37] was applied. However, in this case, we noticed that the extracted impact forces were sensitive to some manipulated parameters, in particular, the distance of impact contact surface $\Delta H$ and surface cell size $\Delta L$ as shown in Figure 13. Herein, a one-at-a-time sensitivity analysis was performed to assess the impact of input parameters’ variation on the impact force. The 2# data along the main sliding profile were used. The initial parameters are listed in Table 2. All the initial parameters were kept constant except the one chosen for sensitivity analysis. The given parameters generated the maximum impact force on the main sliding line, being 4224.89 kN. Figure 15 shows the reproduced landslide impact force as a function of the chosen parameters. The figure demonstrates that the distance of impact contact surface $\Delta H$ has good robustness to the maximum impact force on the main sliding profile. Since the impact force of the grid was calculated based on the maximum velocity of particles in the scope of the calculation code, we determined that the variation of the maximum impact force is between −36.47% and 41.97% on the main sliding line when the surface cell size $\Delta L$ varied ±20%. In summary, surface cell size $\Delta L$ is a key parameter in the SC-HBP-SPH method, and a trial-and-error adjustment is required to obtain its best-fitting value.

7. Conclusions

This paper presented the Yabakei landslide event in Nakatsu city, Oita prefecture, Japan, which occurred on 11 April 2018. Different from the common rainfall- or earthquake-induced landslides, the Yabakei landslide occurred suddenly, without any accompanying rainfall or earthquake. The conclusions are as follows.

(1)

To explore the triggering mechanism of the event, information regarding the geo-morphology, geology, and hydrology conditions of this event were obtained. Key findings by Standard Gamma Ray (SGR) log are that four major internal fractures distributed in the slope body were identified, providing possible storages for perched groundwater. Groundwater stored in the internal fractures infiltrated through the permeable sand-stone.

(2)

It is speculated that abundant illite and askanite in the weathered sediment rocks swelled and broke when contacting the infiltrated groundwater, initiating the Yabakei land-slide event. Through the dynamic process analysis of the landslide event, there was a maximum value on the main sliding line. The strategy of landslide prevention also cannot neglect the damage formed during the landslide deposition process.

(3)

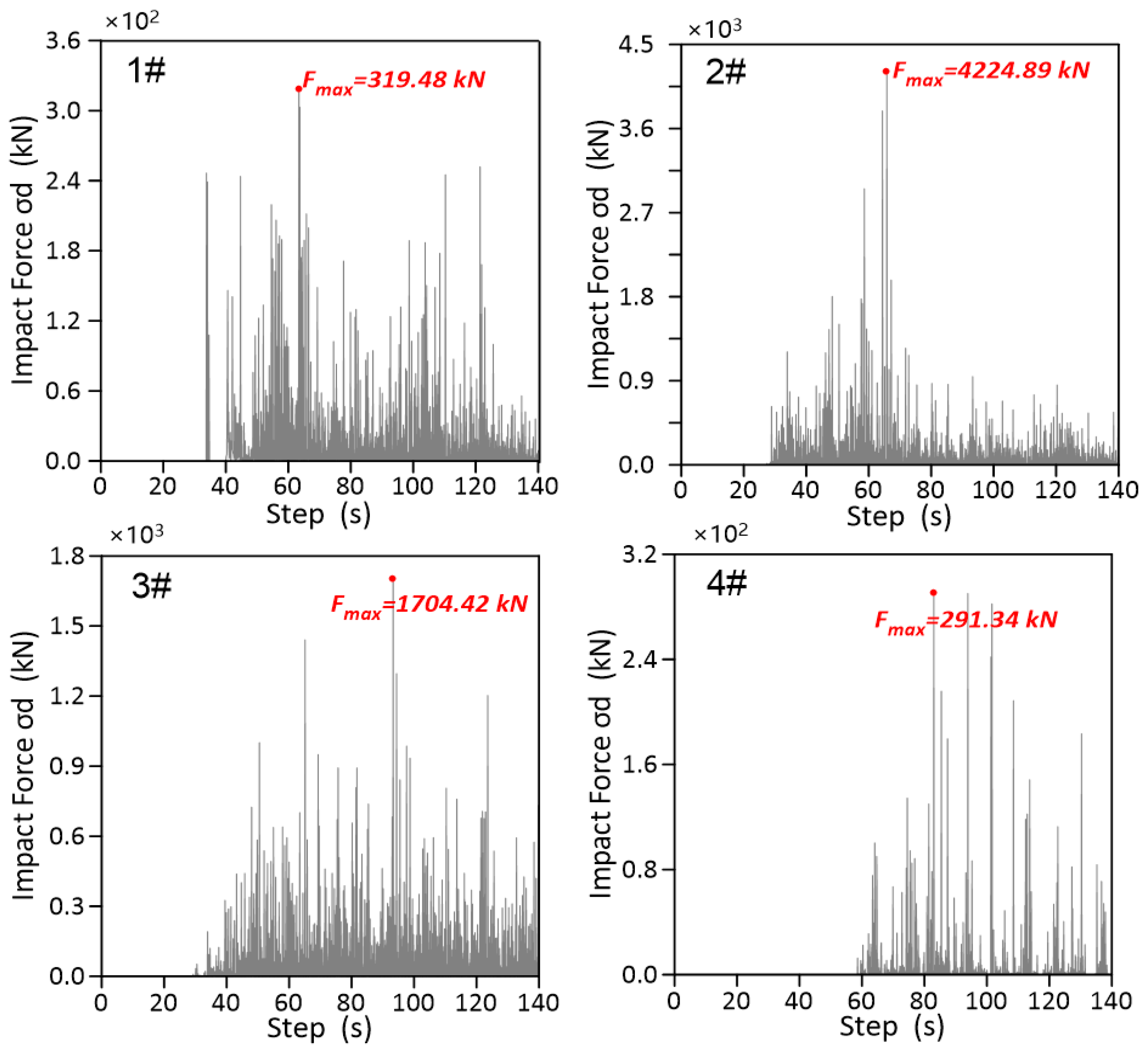
To reproduce the dynamic process of the 2018 Yabakei landslide event, we further applied the proposed three-dimensional, HBP-SPH method to simulate the landslide dynamic process. Buildings in the landslide area are covered by a set of surfaced cells (SC) to analyze the landslide mass impact to the residential buildings. The above method can solve the complex process of landslide impact in real-time, effectively and conveniently. Four monitoring points were set to record the temporal and spatial variation of landslide impact forces.

(4)

Results showed that the landslide impact force to the 2# and 3# residential building could be up towards 4224.89 kN and 1704.42 kN, respectively, indicating that these two buildings have a high risk for structural damage. Through dynamic process simulation of landslide and the solution of impact force, we provided a reference for the prevention and site selection of buildings.

In the future work, we will continue to explore the application of this method to other geological hazards.