1. Introduction
In the water resources field, forecasting, planning, and management technologies have been actively developed based on vast data collected using intelligent technologies and stored in various databases. Hydrological data, such as precipitation and river water levels, are valuable and essential for flood and drought analysis. However, databases affect the reliability of analysis on water resources because they include various types of missing and false-reading data owing to errors in measurement equipment or data processing. To prevent this problem, the accuracy of measurement equipment has been improved, and quality management systems for the collected data have been developed. Data quality control is the process of validating missing data or false-reading data in an abnormal range for a collected dataset and reconstructing them into normal-range data.
As for research on such quality control, early researchers, such as Bedient and Cressman [
1], Shuman [
2], and Haug [
3], have recognized the reliability problems with such data and attempted to manage weather observation data using computer systems. In particular, for research in the field of weather observation data, including temperature, precipitation, water level, and wind speed, the overall data quality control process has been identified through technical reports published by the World Meteorological Organization (WMO) [
4,
5,
6,
7].
As for research on the validation of false-reading data, mathematical theories considering the inconsistency and nonhomogeneity of observation data were first adopted in the 20th century [
8]. Various methods have been proposed, including a method that uses spatial consistency [
9] and a study for establishing standardized rules, such as the high-low range and change limit [
10]. Abbott [
5] and Aguilar et al. [
6] systematically established and shared methodologies and standards for data validation, leading to studies that reflect regional characteristics. In this instance, most data validation algorithms exhibit different levels of applicability depending on spatiotemporal factors; thus, the automation of the data validation field has been actively researched to derive and apply the most suitable validation technique. There exist some representative cases [
11,
12,
13] establishing automation platforms that consider database management structures, such as on/offline and real-time/postanalysis quality control.
For many false-reading data validation methods, expected observation values are predicted first considering the continuity and consistency of data, and these are compared with the actual observed values. In other words, the expected data range is produced along with data validation, which naturally leads to research on the reconstruction of missing and false-reading data. March [
14] first divided the data reconstruction field into two sets, one including data obtained from the same observation station as the error data and one including data obtained from other observation stations, and presented simple interpolation methods. Linacre [
15] and Acock and Pachepsky [
16] presented initial reconstruction methods using statistical values, such as mean and standard deviation, or nonlinear regression. These methods are widely used owing to their ease of application and constitute representative reconstruction techniques for databases obtained from the same observation station. In contrast, Willmott et al. [
17], Xia et al. [
18], and Teegavarapu and Chandramouli [
19] introduced well-known spatial interpolation methods, such as arithmetic averaging and inverse distance weighing method. Subsequently, spatiotemporal interpolation [
20,
21] and machine learning-based reconstruction techniques [
22,
23,
24], such as artificial neural networks (ANNs), have been developed to improve the reliability of reconstructed data.
HYMOS [
25] and AQUARIUS Time Series [
26] are representative software that provides quality control functions for hydrological databases using such data validation and reconstruction techniques. They include functions for determining and reconstructing outliers using statistical comparative analysis of time-series data and homogeneity analysis of spatial data. Despite the efforts mentioned above, however, there are still concerns over validating the false-reading data in the collected dataset and reconstructing them into user-defined values in terms of data reliability. Therefore, in the field of data quality control based on practical systems, decision making by data managers still represents the largest proportion. This indicates that quality control procedures must be developed to support data managers for effective decision making.
However, previous studies on data quality control often revealed the limited practical implementation. Improved validation algorithms such as machine learning techniques have been developed, but the algorithms still include drawbacks and have limited practical implementation due to their complexity and lack of theoretical background. Here, we propose an approach that utilizes and integrates well-known conventional algorithms for easy implementation in the field. The developed process reduces unnecessary data processing by classifying false data into suspected false and confirmed false datasets based on the combined results of the validation methods. In addition, an iterative feedback analysis to further improve the quality control procedure of hydrological databases is proposed.
In this study, for the effective quality control of precipitation and water level data, the observation data were classified into missing, suspected false-reading, confirmed false-reading, and normal data using various validation algorithms (validation process). In this instance, depending on the individual validation method, the data determined to be false-readings were divided into suspected and confirmed false-reading data based on the combination of each validation type to support a more precise identification of false-readings. Next, the developed quality control process suggested reconstructed values through various reconstruction methods to replace missing and false-reading data and support data reconstruction of managers (reconstruction process). Finally, an integrated quality control process was proposed to provide the best data availability through an iterative feedback process considering the influence of repeated data validation and reconstruction. In this case study, the developed quality control process was applied to the hydrological data collected in the Daecheong Dam basin, South Korea, and the suitability of the process for each procedure was analyzed in detail.
The remainder of this paper is organized as follows. In
Section 2.1, the overall structure and procedure of the proposed approaches are introduced. In
Section 2.2, the missing and false-reading data validation methods are summarized. In
Section 2.3, the reconstruction methods of error data are summarized, then the iterative quality control process is summarized in
Section 2.4. The status of precipitation and water level stations in the target basin for the case study is summarized in
Section 3.1. The results of applying the quality control process to the target basin are analyzed in
Section 3.2 and
Section 3.3. In
Section 4 and
Section 5, the discussions and conclusions are presented, respectively.
2. Methodology
2.1. Overview
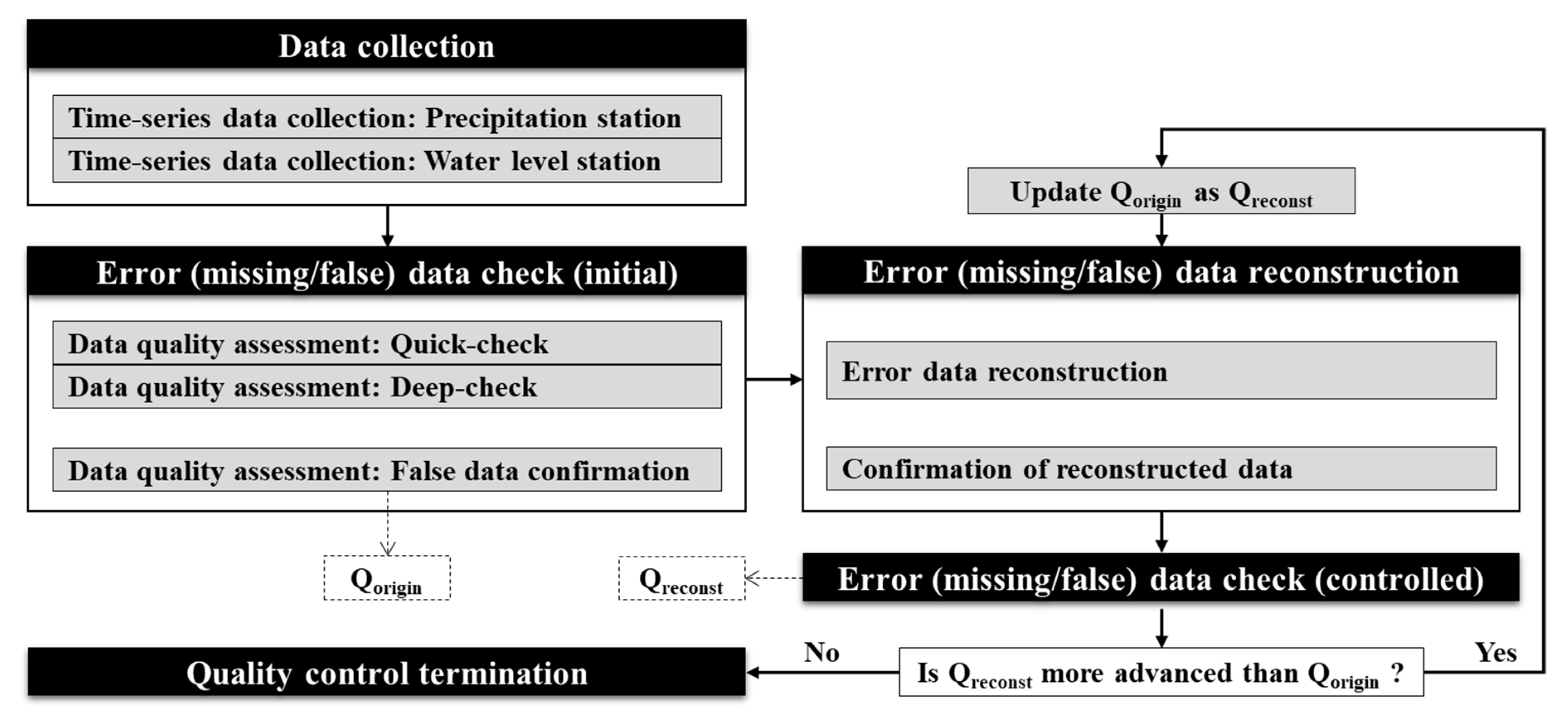
Hydrological data quality control techniques in South Korea, which are the basis of this study, have been presented by major institutions such as the Korea Water Resources Corporation (K-water), Korea Institute of Civil Engineering and Building Technology (KICT), and Korea Meteorological Administration (KMA). They have presented historical or statistical normal observation ranges based on the climate environment of South Korea and validated outliers through temporal or spatial relationships based on a theoretical approach. For data reconstruction, they also use representative practical techniques, such as the mean value reconstruction, linear programming, exponential function method, and reciprocal distance squared (RDS) method, for overall quality control. In the quality control process developed in this study, the above data quality control methods were mainly divided into data validation and reconstruction steps, as shown in
Figure 1.
In the data validation step of this study, the observed data were validated through six types (missing, physical, duration, trend, statistical, and spatial false) of validation algorithms. As for the major characteristics of the developed process, the six algorithms can be divided into quick-check and deep-check algorithms and applied gradually according to the intensity of the data quality control. In the data reconstruction step, the data classified as missing or false-reading data in the previous validation step were reconstructed into normal range through five types (selected-time, linear, spline, autoregressive integrated moving average (ARIMA), and spatial) of reconstruction algorithms. Different reconstructed values are proposed by each algorithm, and the final reconstructed values are determined by the data managers.
During the validation and reconstruction of error data, referring to preceding and subsequent time-series data or data from nearby observation stations is essential, and reliability may decrease if abnormal data is referred to. Therefore, data quality can be further improved if the already modified data are used again for quality control. This study presents an iterative validation and reconstruction process, in which quality control was repeatedly applied until the data quality was no longer improved.
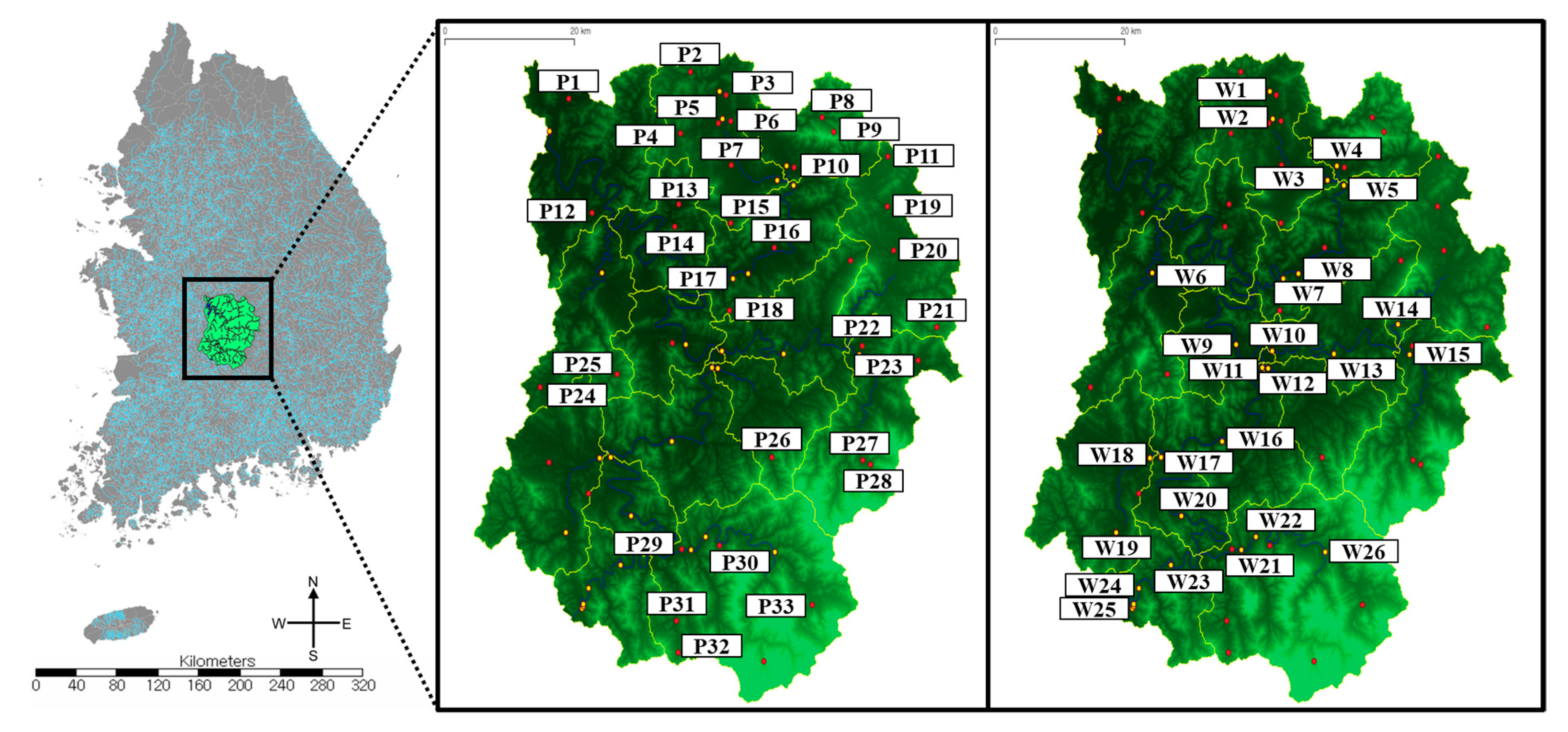
In the case study, the developed integrated quality control process was applied to 32 precipitation stations and 24 water level stations located in the Daecheong Dam basin with a data collection period of more than five years. The databases contained precipitation and water level data with a 10-min interval.
2.2. Missing and False-Reading Data Validation
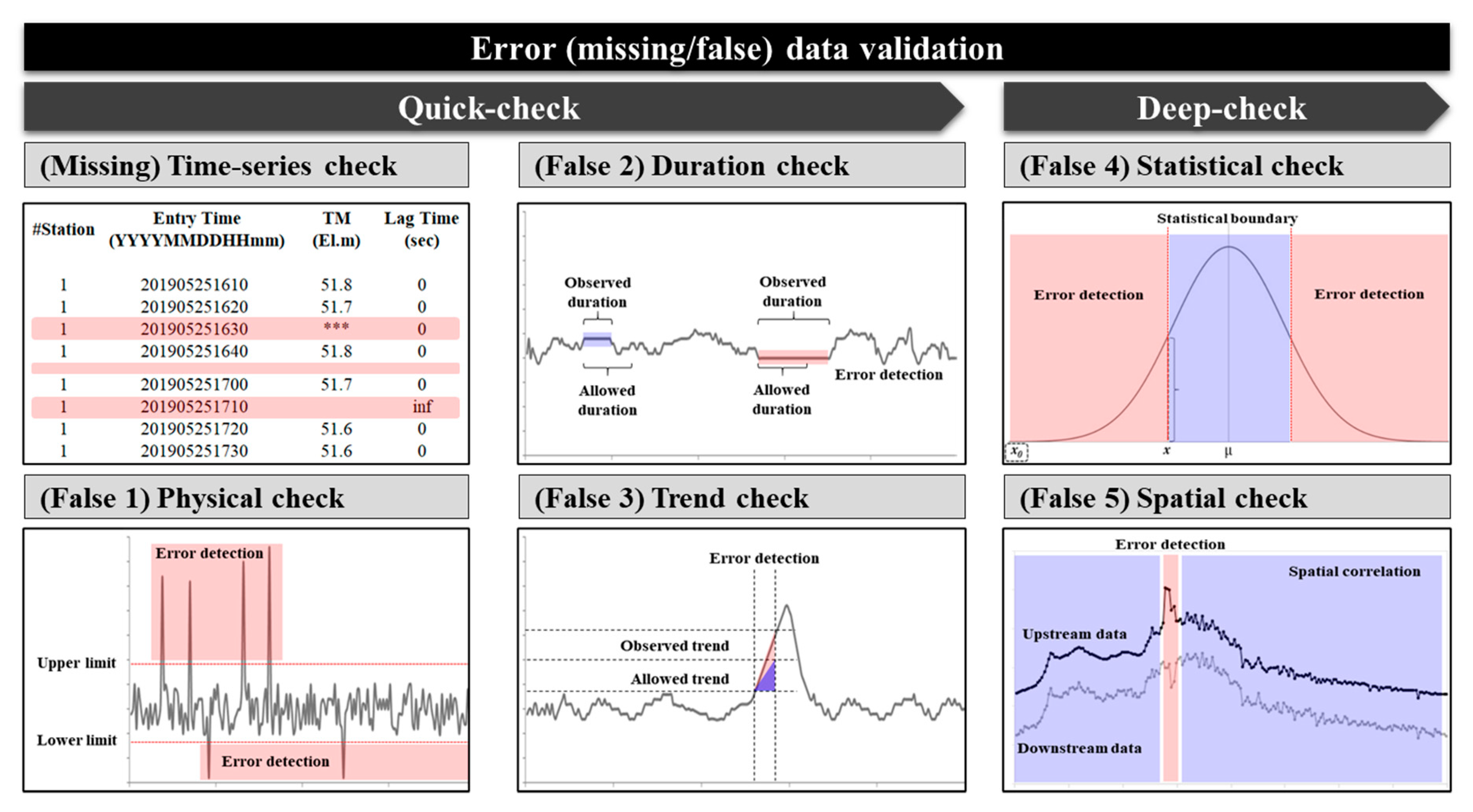
In this study, six (missing, physical, duration, trend, statistical, and spatial) validation methods were applied to validate the quality of observation data. In this instance, relatively simple validation methods may require relatively short-term data, but more rigorous validation methods require long-term data or data from nearby stations. The proposed quality control process comprises quick-check algorithms, which are based on missing, physical, duration, and trend methods, and deep-check algorithms for precise quality control based on statistical and spatial methods.
For the precipitation and water level data used in this study, the overall validation procedure can be applied in the same manner. However, the detailed application process and reference value may vary depending on the characteristics of the data.
Figure 2 shows a conceptual diagram of the applied six validation methods. The details of validation methods are explained in the following sections.
2.2.1. Data Validation Algorithms: Quick-Check
The quick-check algorithms are simple validation methods that can be applied in real-time or at a quasi-real-time because relatively small amount of data is required for validation. The inspection methods of the quick-check items presented here, and the application standards are as follows:
First, missing data represents the data not secured in time-series databases because measuring instruments failed or errors occurred in the data transmission and storage steps. Such missing data can be specifically divided into the following cases in which: (1) the corresponding time series have not been recorded, (2) data of the corresponding time series have been recorded as null, and (3) data of the corresponding time series have been recorded in a non-numeric form. In this study, missing data were validated for the databases constructed in the form of a CSV spread sheet using a time-series check algorithm that identifies cases corresponding to cases 1–3.
Second, false-reading data are data recorded differently from the actual values or data that are corrupted due to errors in the transmission and storage steps, even though numeric data were recorded in the database. Among the validation methods that correspond to the quick-check items, the physical check algorithm is practically difficult to implement considering the climate and locational characteristics of the area where the target station is located. In other words, cases that exceed the upper or lower boundaries of the physical observation range can be classified. In this study, false-reading data were validated, as shown in Equation (1). In this instance, the applied physical boundaries for precipitation and water level data are classified as shown in
Table 1.
where
Xt is
t-th observation data,
BP,min is the minimum physical boundary of the data, and
BP,max is the maximum physical boundary of data.
KMA [
27] presented 100 mm per 10 min and 300 mm per hour as the maximum physical observation limits of precipitation data in Korea. Therefore, in this study, the maximum observation limit of 100 mm per 10 min and minimum of 0 mm per 10 min (nonprecipitation) were applied for the physical check of precipitation data. Meanwhile, KICT [
28] suggested a method of applying the past maximum and minimum observation histories as the maximum and minimum physical observation limits of water level data. Therefore, in this study, the past maximum and minimum observation values of the target stations were collected and applied as observation limits of the station for the physical check of water level data.
Among the validation methods corresponding to the quick-check items, the duration check algorithm inspects whether the same observation value is recorded during an abnormally long time period. Therefore, false-reading data can be validated according to the duration boundaries for precipitation and water level data, as summarized in
Table 2.
Regarding the duration check of precipitation data, there is no specific duration limit for identical observations in Korea. In this study, when the same 10-minute precipitation data were repeated for more than one hour (i.e., more than six consecutive identical data), except for the nonprecipitation period, they were validated as false-reading data. In the case of water level data, the ministry of land, transport, and maritime affairs (MLTM) [
29] in Korea classifies the same water level data repeated for more than 24 h as false-reading data. This guideline was adopted in this study, and 24 h was set as the duration limit of the 10-minute water level data (i.e., more than 144 consecutive identical data).
Among the validation methods that correspond to the quick-check items, the trend check algorithm inspects whether the data within a specific period abnormally fluctuates. The application of the increase and decrease limits may vary depending on the data. In this study, false-readings of precipitation and water level data were validated as shown in Equations (2a) and (2b), and the applied increase and decrease limits for the data are summarized in
Table 3.
where
is the decrease limit of observation data within unit time-step and
is the increase limit of observation data within unit time-step.
Shulski et al. [
30] suggested the fluctuation range of precipitation data within a unit time-step through a statistical approach. In this study, the increase limit of precipitation data was applied using the mean (
) and standard deviation (
) of precipitation variation for the same month of the previous year, as shown in
Table 3. Meanwhile, KICT [
28] suggested the water level fluctuation boundary depending on the slope (
) of the water level change during the last two hours: that is, if water level increased (i.e.,
> 0), a range of −1 to 3 times the slope (
) is applied, while if it decreased (i.e.,
< 0), a range of 3 to −1 times the slope (
) is applied as given in
Table 3. This guideline was adopted in this study, and the increase and decrease limits of water level data were applied for cases in which the average slope over the last two hours was not zero, as shown in
Table 3.
2.2.2. Data Validation Algorithms: Deep-Check
Deep-check algorithms for data validation are precision validation methods that can be applied at a non-real-time because they require a relatively large amount of reference data for validation. The inspection methods of the deep-check algorithms and the detailed application standards are as follows:
The statistical check algorithm inspects the data based on the statistical tolerance calculated using historical data, with the data period used to calculate the appropriate observation range being applied differently depending on the characteristics of hydrological data. In this study, data false-readings were validated, as shown in Equation (3) and the applied statistical boundaries for the data are summarized in
Table 4. In the case of statistical inspection, statistical differences depending on the observation season of the data are reflected, and a larger amount of the collected historical data is more favorable for quality control. In this study, it was found that the applicability of the corresponding validation method can be applicable to a data period of at least five years.
where
and
are the minimum and maximum statistical boundary of the data, respectively.
Hubbard et al. [
31] suggested statistical boundaries considering the mean (
) and standard deviation (
) ranges of past precipitation observation data. In this study, nonprecipitation data were excluded, and statistical boundaries were calculated based on the precipitation data for the same month of all available years, as shown in
Table 4. The same method was also applied for the water level data, but statistical boundaries were calculated by dividing the data corresponding to the flood season (June to September) and nonflood season (October to May) of all available years.
The spatial check algorithm inspects false-reading data through spatial boundaries, considering the consistency between the observation data near the target observation station. In this study, data false-readings were validated, as shown in Equation (4) and the applied statistical boundaries for the data are summarized in
Table 5.
where
and
is the minimum and maximum spatial boundary of the data, respectively.
K-water [
32] in South Korea suggested a range corresponding to 0.2–2.8 times the predicted value through the RDS method as the spatial boundary of precipitation data. Here, the RDS method is a reconstruction method based on the concept that the spatial correlation of precipitation is inversely proportional to the physical distance, and the precipitation value reconstructed using the RDS method can be calculated based on data from two or more observation stations located near the target station, as shown in Equation (5).
where
is the precipitation value of the target station (
) at time
reconstructed using the RDS method,
is the observation data of the
-th station near the target station at time
,
is the distance between the target station (
) and the nearby
-th station, and
is the number of nearby stations used for the RDS method.
In the case of water level data, validation methods considering the spatial association between the upstream and downstream stations of a river have been presented through various studies. In this study, the method of Hubbard et al. [
31], which was used as a statistical validation method, was utilized, and spatial boundaries were calculated based on the mean (
) and standard deviation (
) of water level differences between upstream and downstream stations during the past week, as shown in
Table 5.
2.2.3. Distinction between Suspected False-Reading and Confirmed False Data
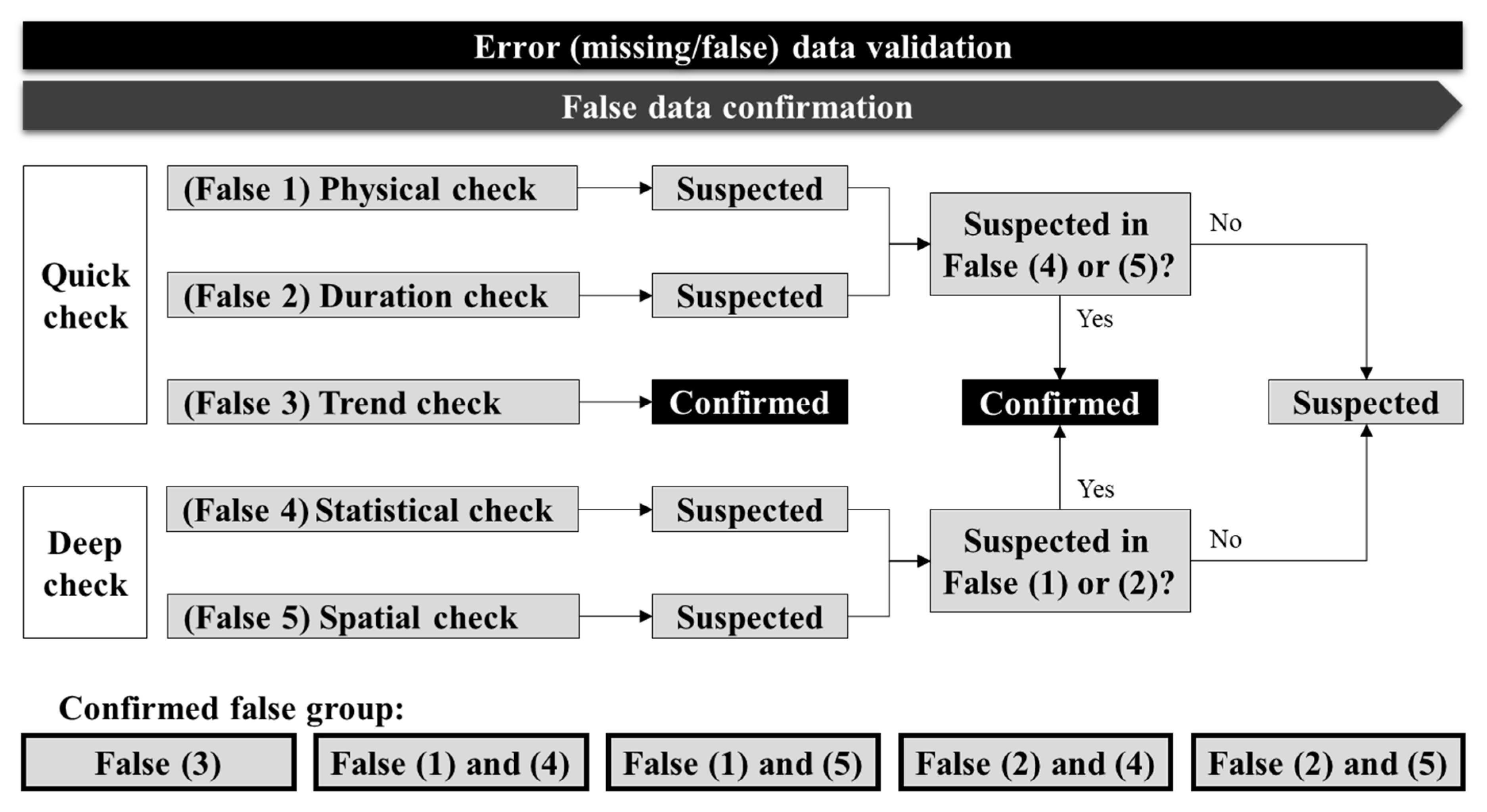
It is likely that a normal data is classified as false data after conducting the aforementioned validation checks. In particular, the false-reading rate of the database increases as more types of validation methods are applied. To improve the reliability of the quality control procedure, efforts to accurately identify false-reading data are required, while various validation methods are applied. In this study, the data determined to be false-readings by each validation method were first classified as suspected false data, then a procedure for determining the data as confirmed false data according to the type of validation method was proposed. In other words, in the proposed quality control procedure, the entire dataset was classified into normal, missing, suspected false, and confirmed false data. Error data, such as missing and confirmed false data, were then reconstructed, and the suspected false data were treated in the same manner as normal data but classified into a separate category.
False data were confirmed by considering the characteristics of each validation method, as shown in
Figure 3. First, continuity, which is the most important observational characteristic of hydrological data, was considered in this study; thus, the data classified as false-reading by trend-check among the quick-check methods were immediately classified as confirmed false data. Next, the data classified as false-reading by physical check and duration check among the quick-check methods were first tagged as suspected false data and were further determined as confirmed false data depending on the deep-check results. In other words, among the data classified as suspected false data by quick-check algorithms, those that were also determined to be suspected false data by the deep-check algorithms were finally classified as confirmed false data.
2.3. Missing and False-Reading Data Reconstruction
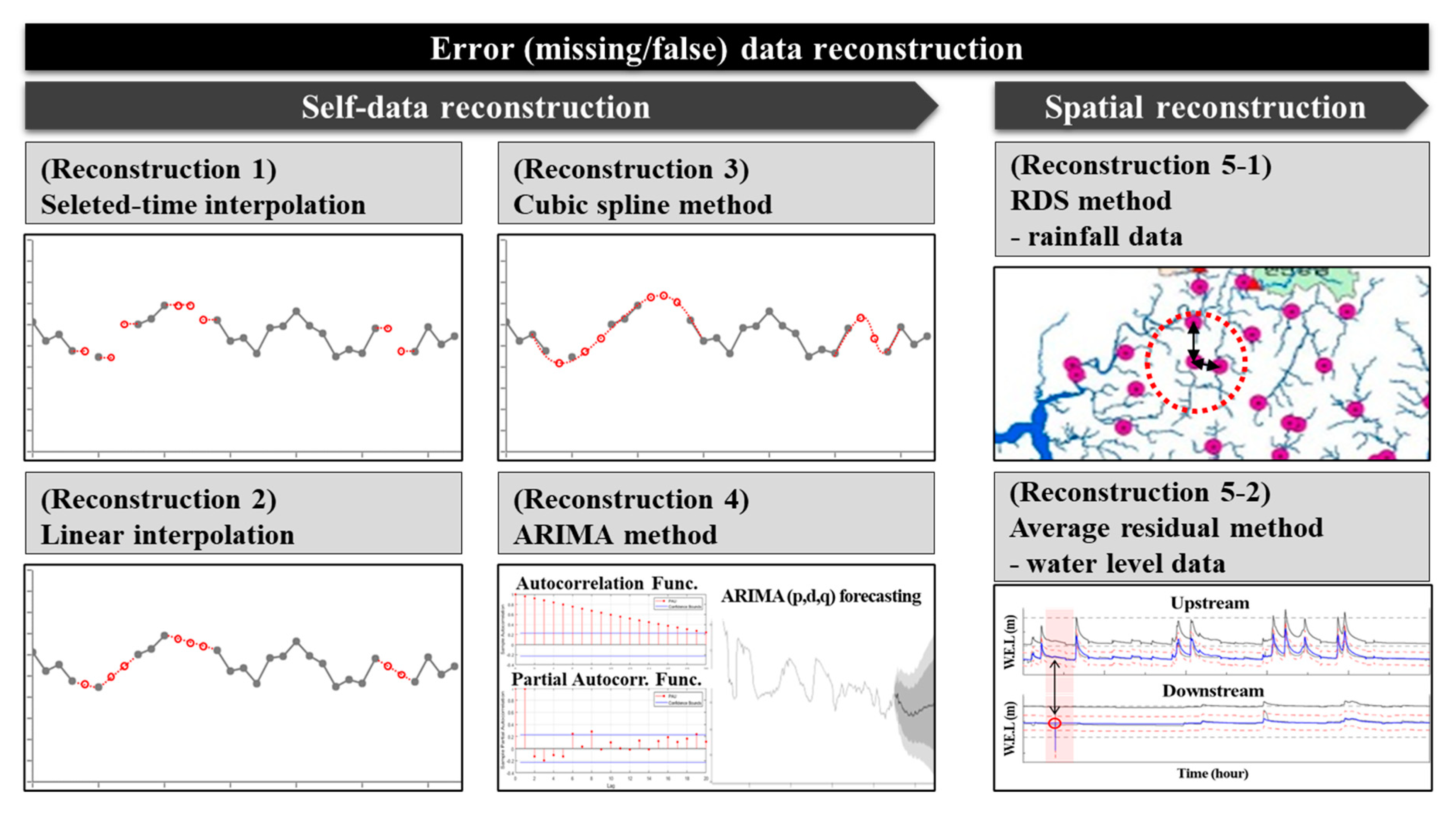
The proposed quality control process includes a procedure for reconstructing the data classified as missing or confirmed false-reading using five types (selected-time, linear, spline, ARIMA, and spatial) of reconstruction methods. In this instance, all the reconstruction methods, except for the spatial reconstruction method, use only data from the target station, and can be applied regardless of the data type (precipitation and water level) in the same manner. In case of the spatial reconstruction method, however, completely different methods are applied depending on the data type. In other words, the reconstruction methods used in this study can be summarized as six methods in five types, as shown in
Figure 4, and the details of each reconstruction method are summarized as follows.
The selected-time interpolation, which is the simplest method, replaces the error data with preceding or subsequent data directly. In general, alternative data for selected-time interpolation can be manually selected by the data manager. However, in this study, the nearest data, which are classified as normal, from the issued error data were selected for automated data reconstruction.
The linear interpolation method reconstructs data at a specific time under the assumption that data linearly increases or decreases, as shown in Equation (6). This method is easy to apply and can reflect the continuity of data in a relatively short time window. That is, the corresponding error data are reconstructed by linearly connecting the data before and after the error data. When missing or false-reading data occurred continuously during a certain period, continuous reconstruction was performed based on the preceding and subsequent data of the corresponding period so that the entire target period could have a linear relationship.
where
t is the observation time point for the missing and false-reading data to be reconstructed;
t0 and
t1 are the time points immediately before and after the error observation, respectively; and
Xt0 and
Xt1 are the observed values at time
t0 and
t1, respectively.
The spline method, similar to the linear interpolation, is a reconstruction method based on the assumption that the observed tendency of the data follows a mathematical pattern. Although only instantaneous continuity with preceding and subsequent single data was considered in the linear interpolation method, a longer continuity pattern was considered in the spline method by referring to the data obtained one day before and after the error observation. When the error data were observed continuously, the spline method could reconstruct the entire period simultaneously.
The ARIMA reconstruction method predicts and reconstructs the data of the target time series. The ARIMA model considers cointegration in addition to the ARMA model, which combines the AR (autoregressive) model that uses the past data pattern and the MA (moving-average) model that utilizes the average of the past data. This can be expressed as an ARIMA (p, d, q) model, where p, d, and q denote the order of the AR model, degree of differencing for securing data stationarity, and order of the MA model, respectively. In this study, the reconstructed values were predicted by referring to the data obtained one week before the error observation. Here, the ARIMA parameters can be directly input by the user or derived by the ARIMA module for a specific observation period.
Finally, in the spatial reconstruction, different methods were applied to the precipitation and water level data. For the precipitation data reconstruction, the calculated RDS value obtained from Equation (5) was applied. For the water level reconstruction, the error data were reconstructed by adding the average difference in water levels between the target and nearby stations estimated from the data obtained during the previous week, as shown in Equation (7).
where
is the reconstructed water level of the target station (
) at time
,
is the observed water level of the nearby station (
) at time
,
is the observed value of the target station (
) at time
,
is the observed value of the nearby station (
) at time
, and
is the maximum period of the past data referenced for data reconstruction (here, one week).
2.4. Iterative Quality Control Feedback Process
Most validation and reconstruction methods require the process of referring to the data of the preceding and subsequent periods from the error observation. Thus, the data validation and reconstruction results may vary as the overall data pool is improved owing to the quality control process. For example, identification of the false-reading data may vary as reconstruction data is newly included, and the proposed reconstructed value may still fall within the range of the false value. In this study, such data dependency of quality control was considered, and an iterative feedback process was proposed. In the proposed feedback process, quality control was applied iteratively until the error rate is no longer improved by comparing the data availabilities before and after the quality control process as shown in
Figure 5. In specific, the error data were identified and reconstructed by data validation and reconstruction methods (Step 1 and 2, respectively). As the data manager obtained five sets of reconstructed values, determination of the reconstruction method was required. Here, an iterative quality control process is used to apply data validation methods to reconstructed datasets and reevaluate their quality (Step 3). Based on this, the data manager could compare and determine the best reconstruction method for each iteration of quality control (Step 4). However, the reconstructed database can be further improved owing to the improved data pool. The iterative quality control process compares the data quality before and after reconstruction, and then repeats Steps 2–4 until no more improvement is identified.
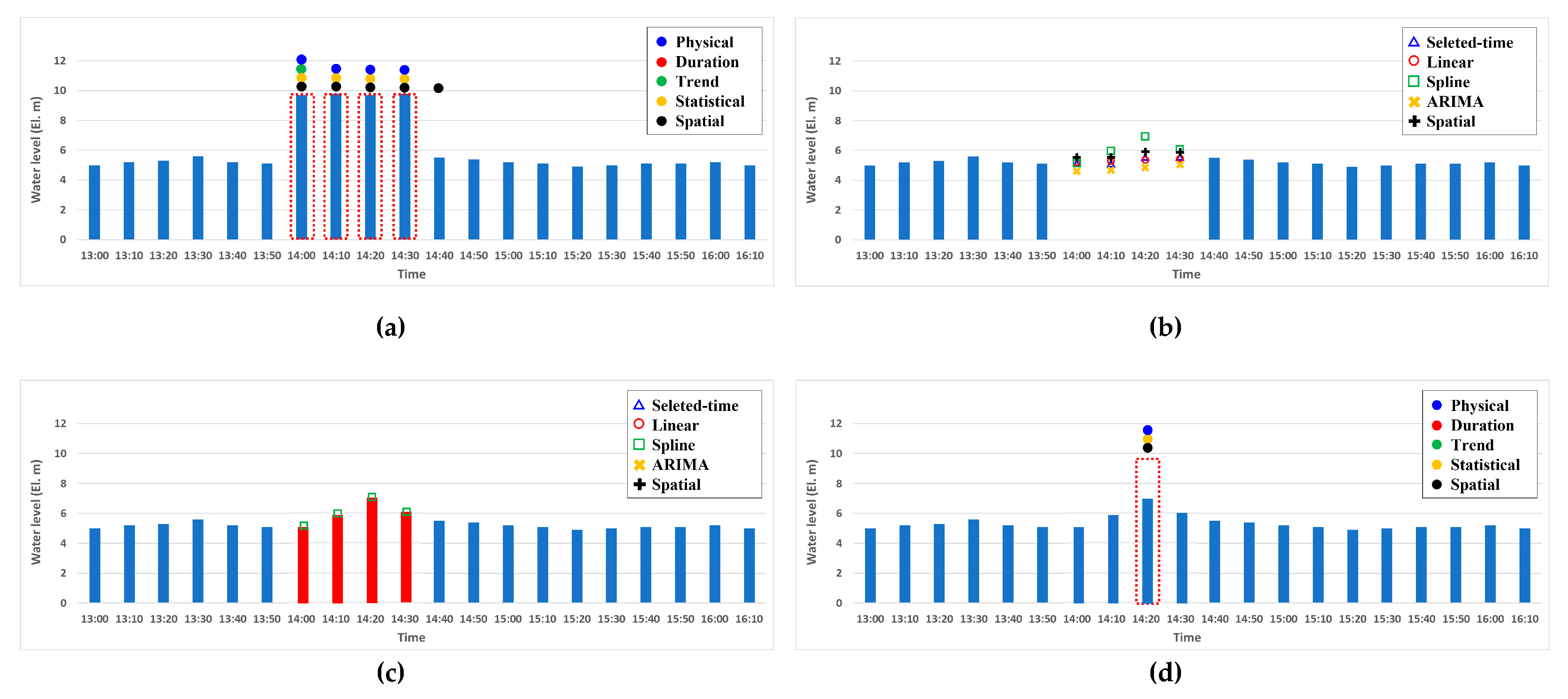
For illustration of the proposed iterative quality control process,
Figure 6a shows the time series, including the false-reading data in the validation step, and
Figure 6b shows the proposed reconstructed values by each reconstruction method. In this step, the data manager can choose the most suitable values among the suggested reconstructed data, as shown in
Figure 6c. After fixing the error data, as shown in
Figure 6d, the reconstructed data were validated again to examine whether the reconstructed data falls within the acceptable range. As seen in the figure, one value is still identified as an error data, then one more iteration of data reconstruction and validation is conducted. The proposed iterative feedback process enhances the data availability by repeating quality control process until the validated error rate is no longer improved.
5. Conclusions
In this study, an integrated quality control process capable of validating and reconstructing the missing and false-reading precipitation and water level data were developed. The validation procedure was composed of a time-series check algorithm for validating missing data and five types of algorithms for validating false-reading data, which was composed of physical, duration, trend, statistical, and spatial checks, which were categorized into the quick-check and deep-check algorithms. For error data reconstruction, five reconstruction methods such as selected-time method, linear interpolation, cubic spline, ARIMA, and spatial interpolation were applied. The developed validation and reconstruction process was applied to 32 precipitation stations and 24 water level stations in the Daecheong Dam basin, South Korea. The application results were obtained by securing observation data at a 10-minute interval for at least five years and applying the developed quality control process to the data for one year in 2016. The analysis results are summarized as follows:
- (1)
The precipitation data validation results revealed that the 32 stations in the target basin had an average of 0.68% error data (missing and confirmed false-reading data combined).
- (2)
When precipitation data were reconstructed, it was found that the error rates of the 32 stations was improved through the five reconstruction methods, and the linear interpolation method exhibited the largest overall error rate improvement.
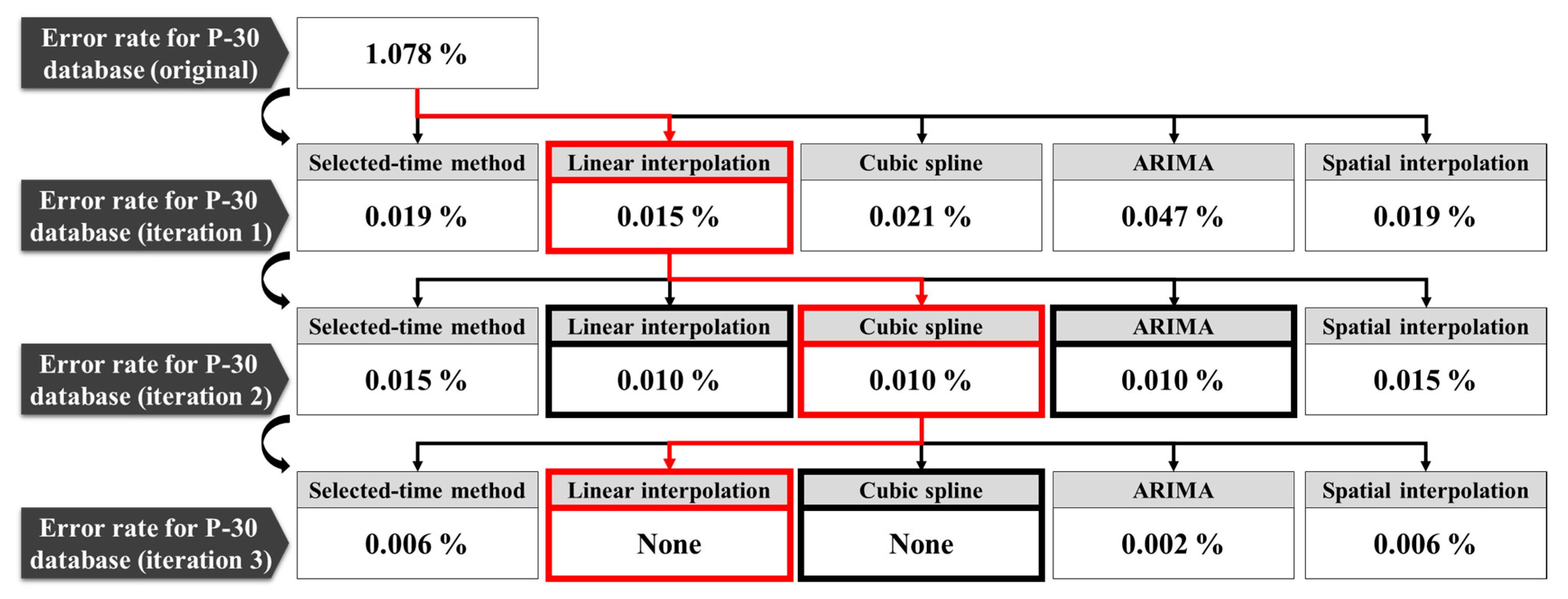
- (3)
For demonstration purposes, the precipitation database from the P-30 station was continuously reconstructed through the feedback procedure. The most effective reconstruction method was selected by evaluating the error reduction rate and user’s selection, and all missing and false-reading data were completely reconstructed after three iterations.
- (4)
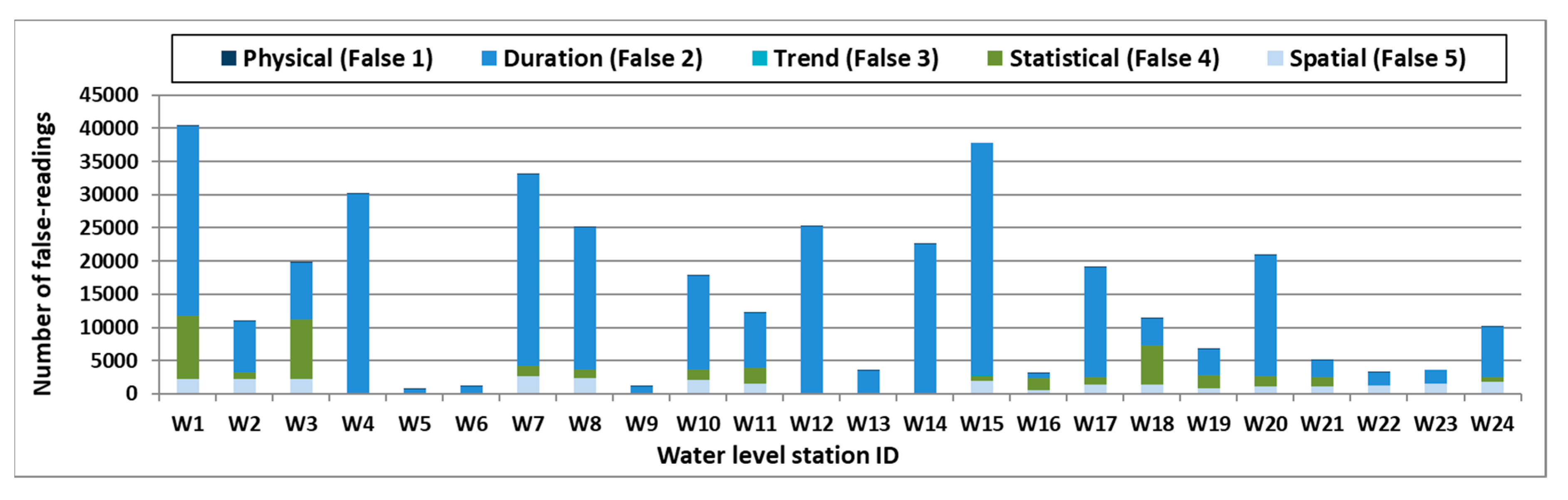
The water level data validation results showed that the 24 stations in the target basin had an average of 1.66% error data (missing and confirmed false-reading data combined).
- (5)
When the water level data were reconstructed, the ARIMA method exhibited the largest error rate improvement owing to the hydrological characteristics of water level with high autocorrelation.
- (6)
When the water level database of the W-10 station was continuously reconstructed through the feedback procedure for demonstration, all missing and false-reading data were completely reconstructed after three iterations.
This study proposed an approach that utilizes and integrates the well-known conventional algorithms for easy implementation in the field. The developed process reduces unnecessary data processing by classifying false data into suspected false and confirmed false datasets based on the combined results of validation methods. In addition, an iterative feedback analysis is proposed to further improve and finally correct the error data.
Most reconstruction methods showed a promising performance, and it is expected that the proposed multiple reconstructed values and iterative feedback process will present a more reasonable basis for developing a data quality control tool to aid data managers. As for related research, real-time automatic validation and reconstruction techniques could be applied to develop a practical quality control model. This will make a wide contribution from basic database management to data-driven diverse research in the field of water resources engineering.