Numerical Study of Fluctuating Pressure on Stilling Basin Slab with Sudden Lateral Enlargement and Bottom Drop
Abstract
1. Introduction
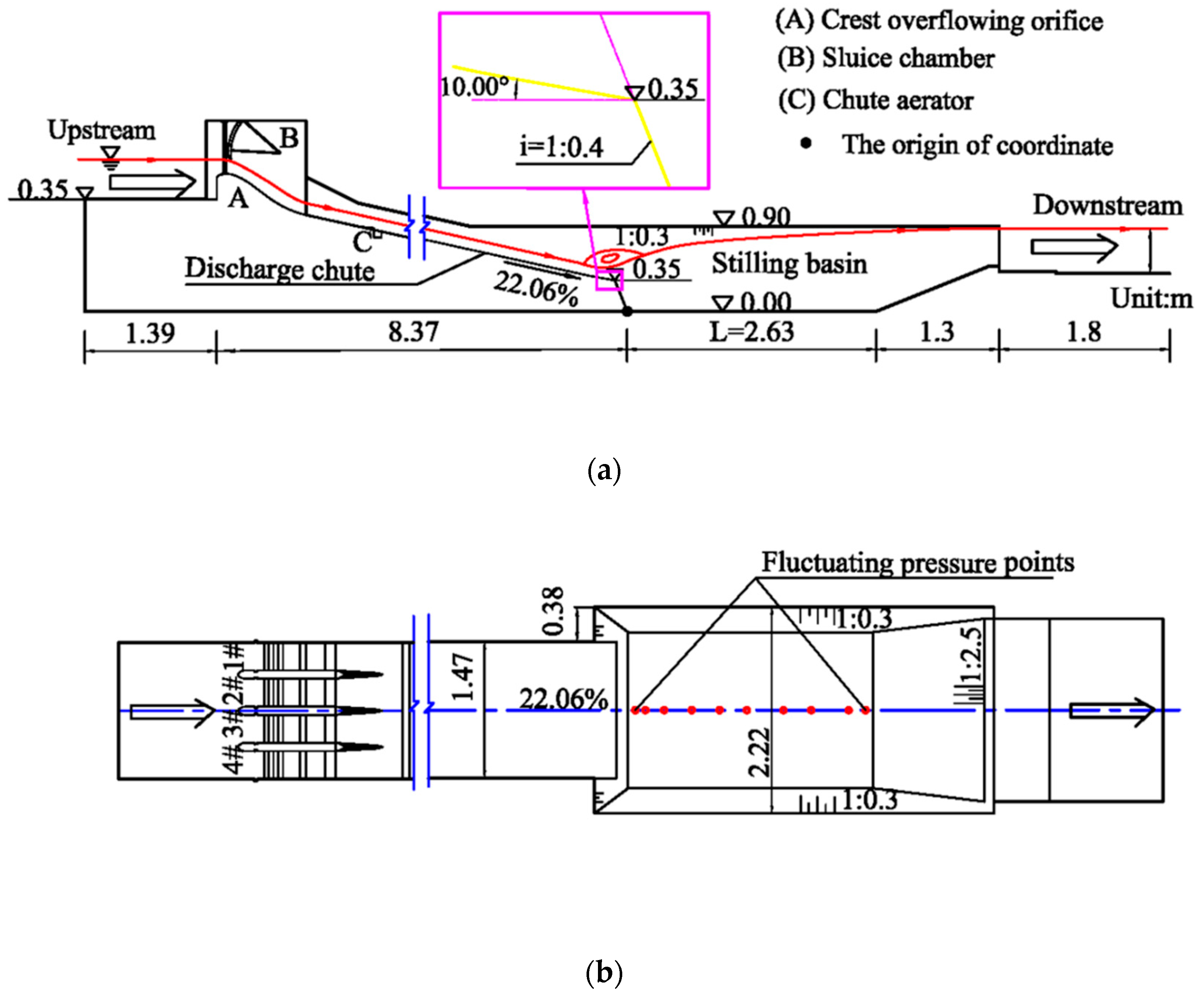
2. Physical Model and Problem Description
2.1. Experimental Setup
2.2. Large Eddy Simulation (LES) Model
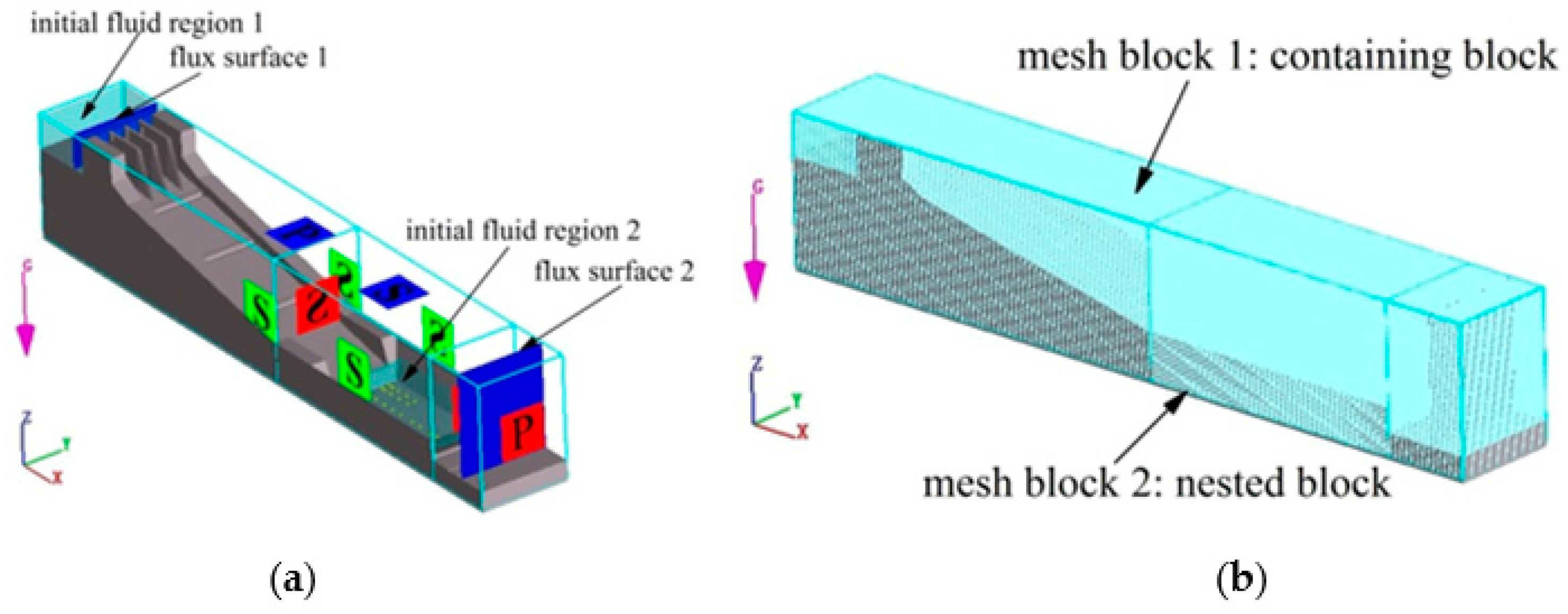
2.3. Computational Domain and Boundary Conditions
3. Numerical Methodology and Model Validation
3.1. Grid Sensitivity Analysis
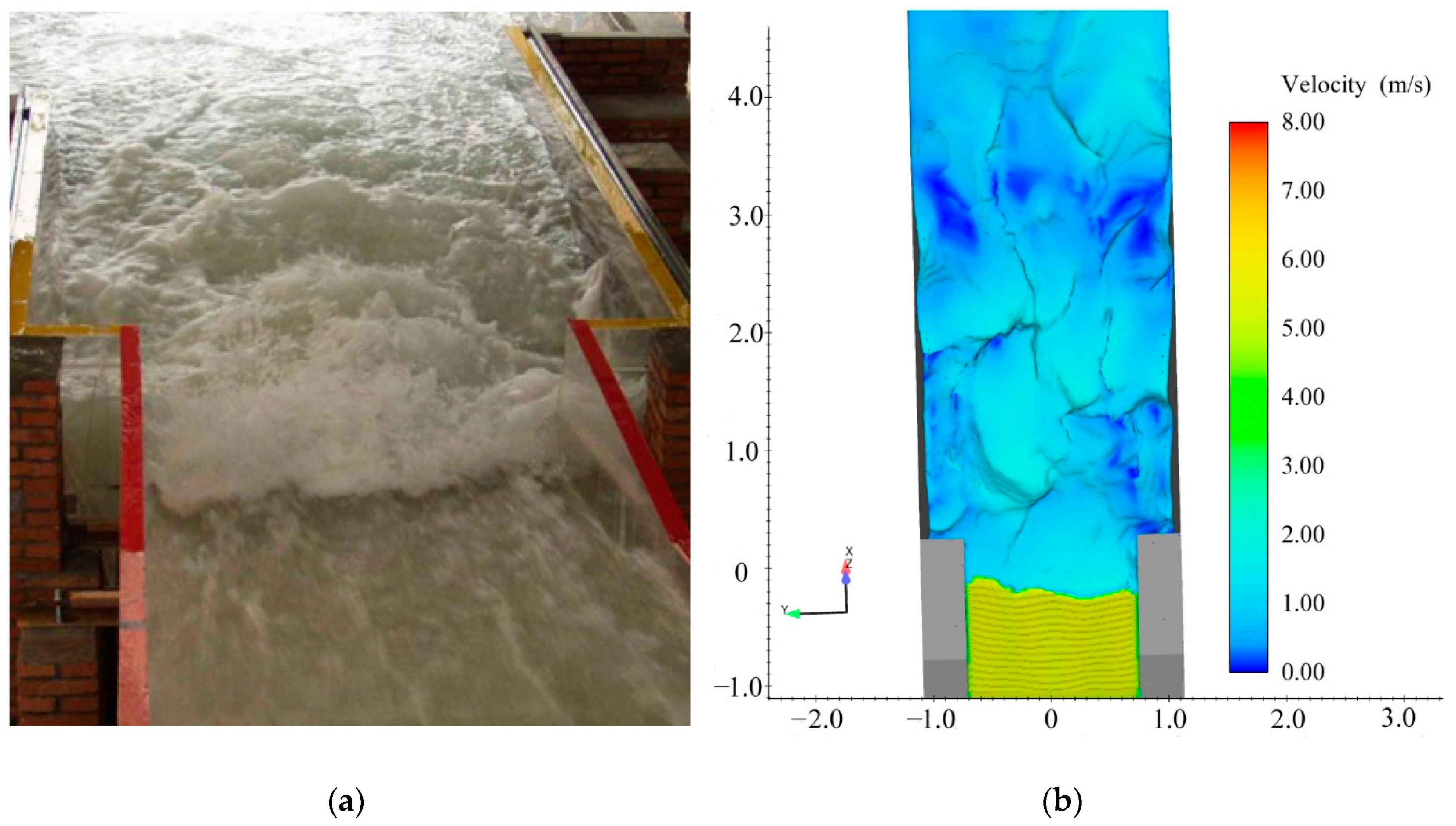
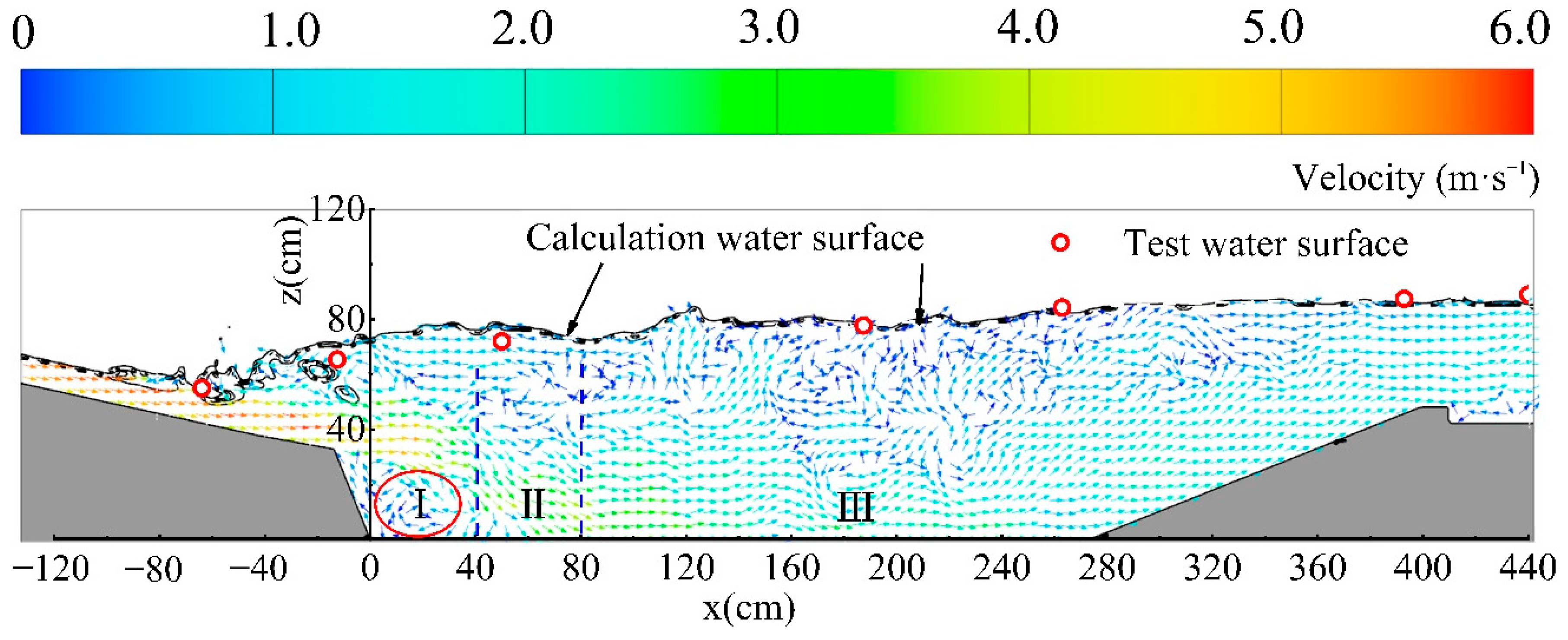
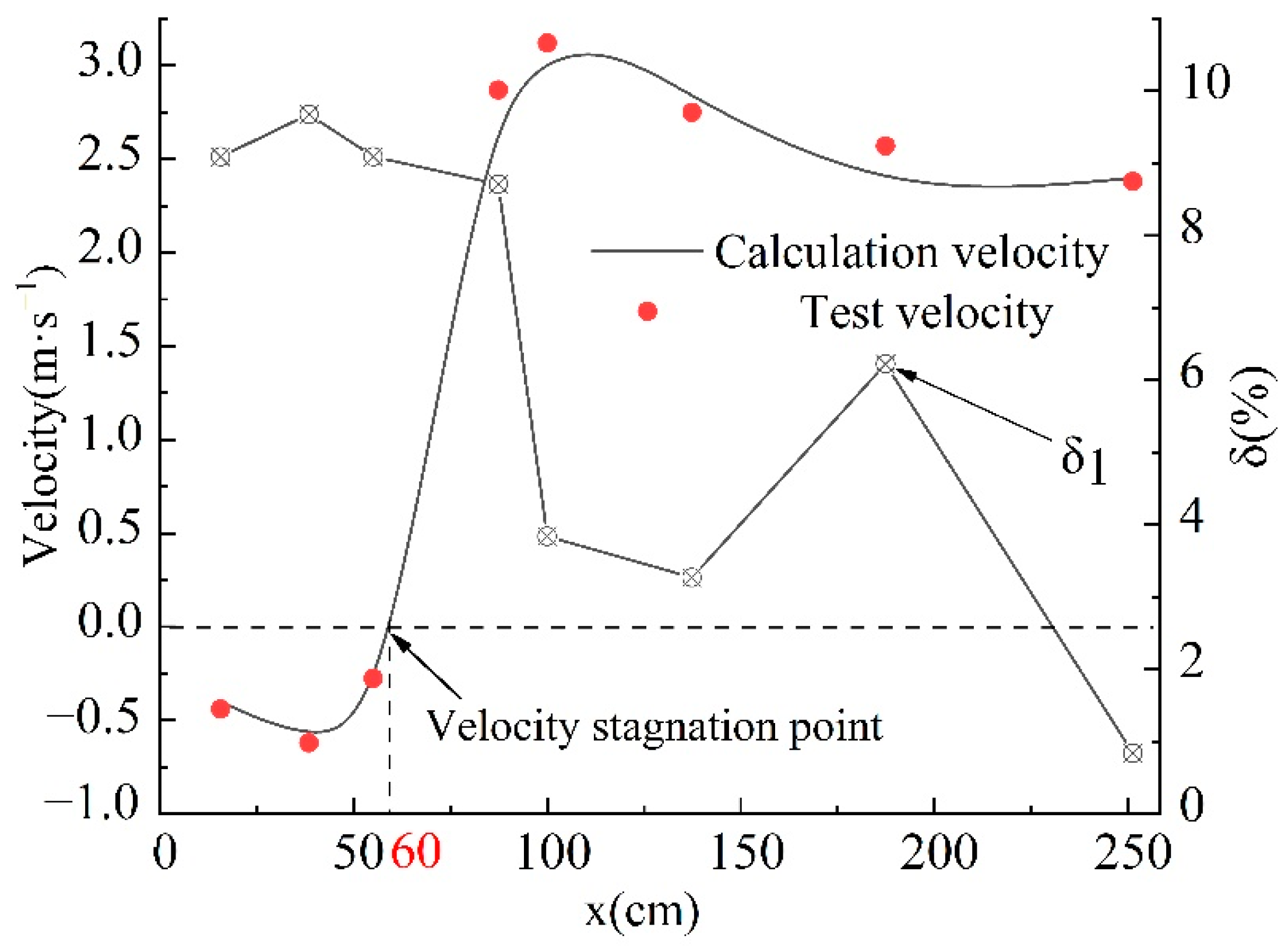
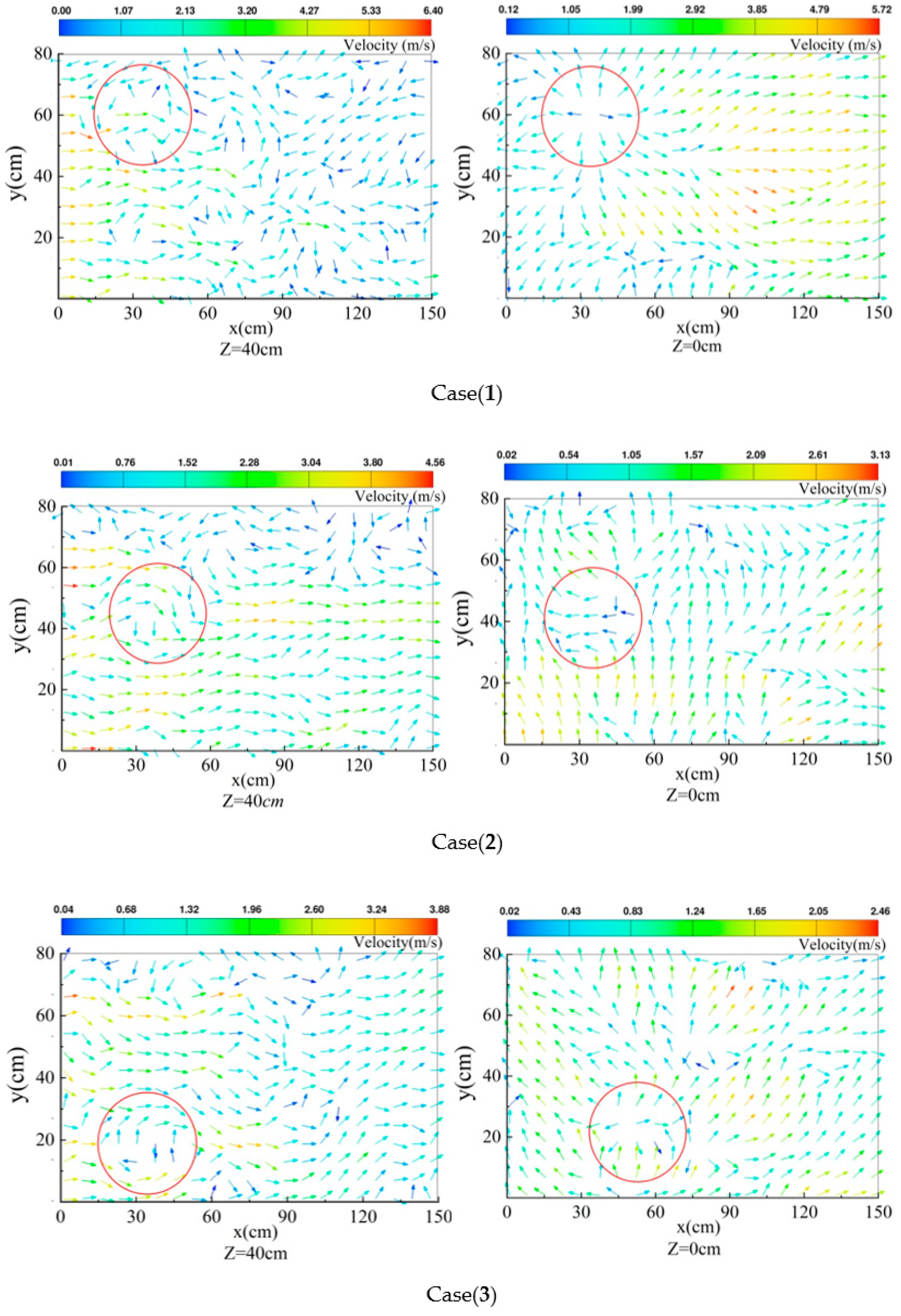
3.2. Comparison of Flow Pattern, Water Surface Profile, and Velocity
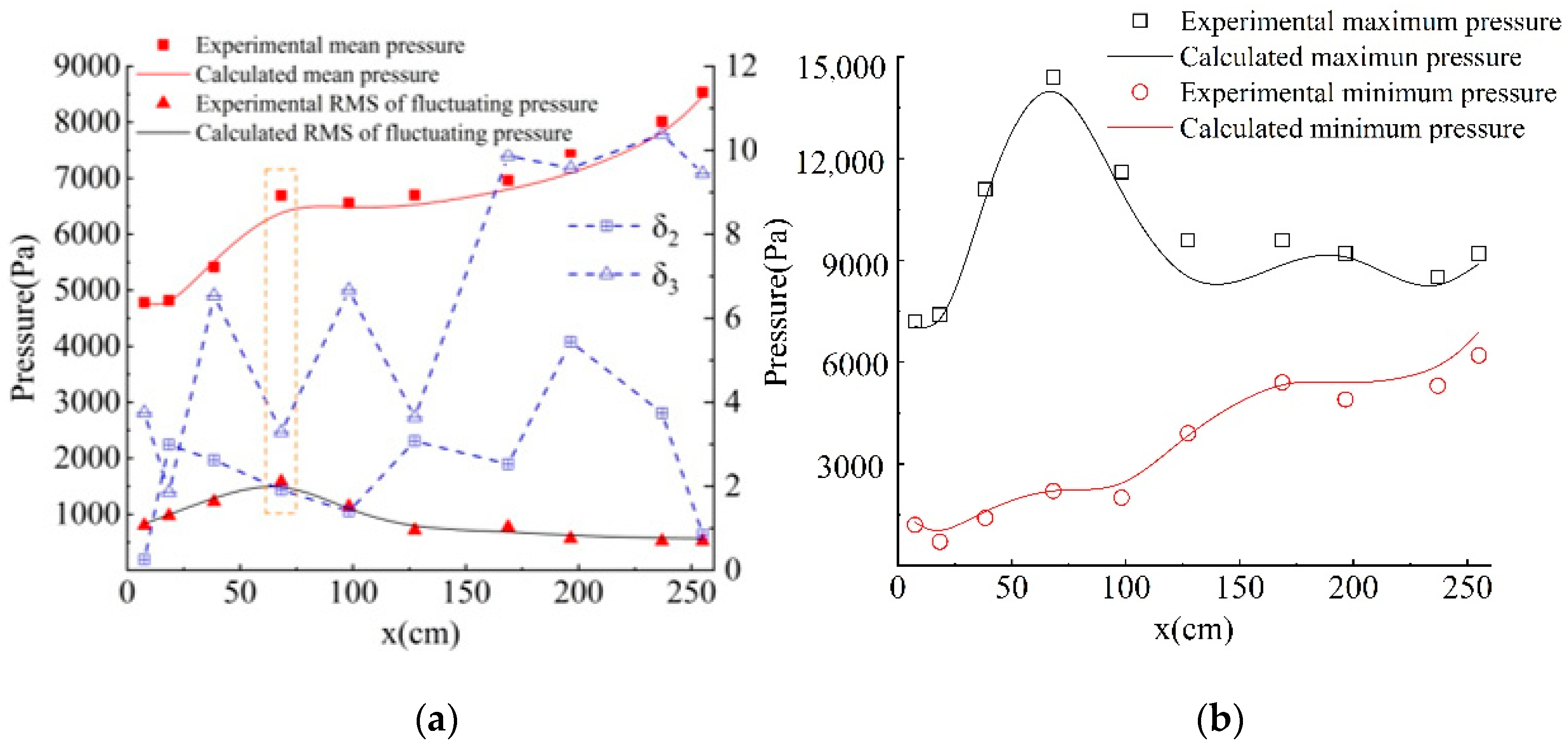
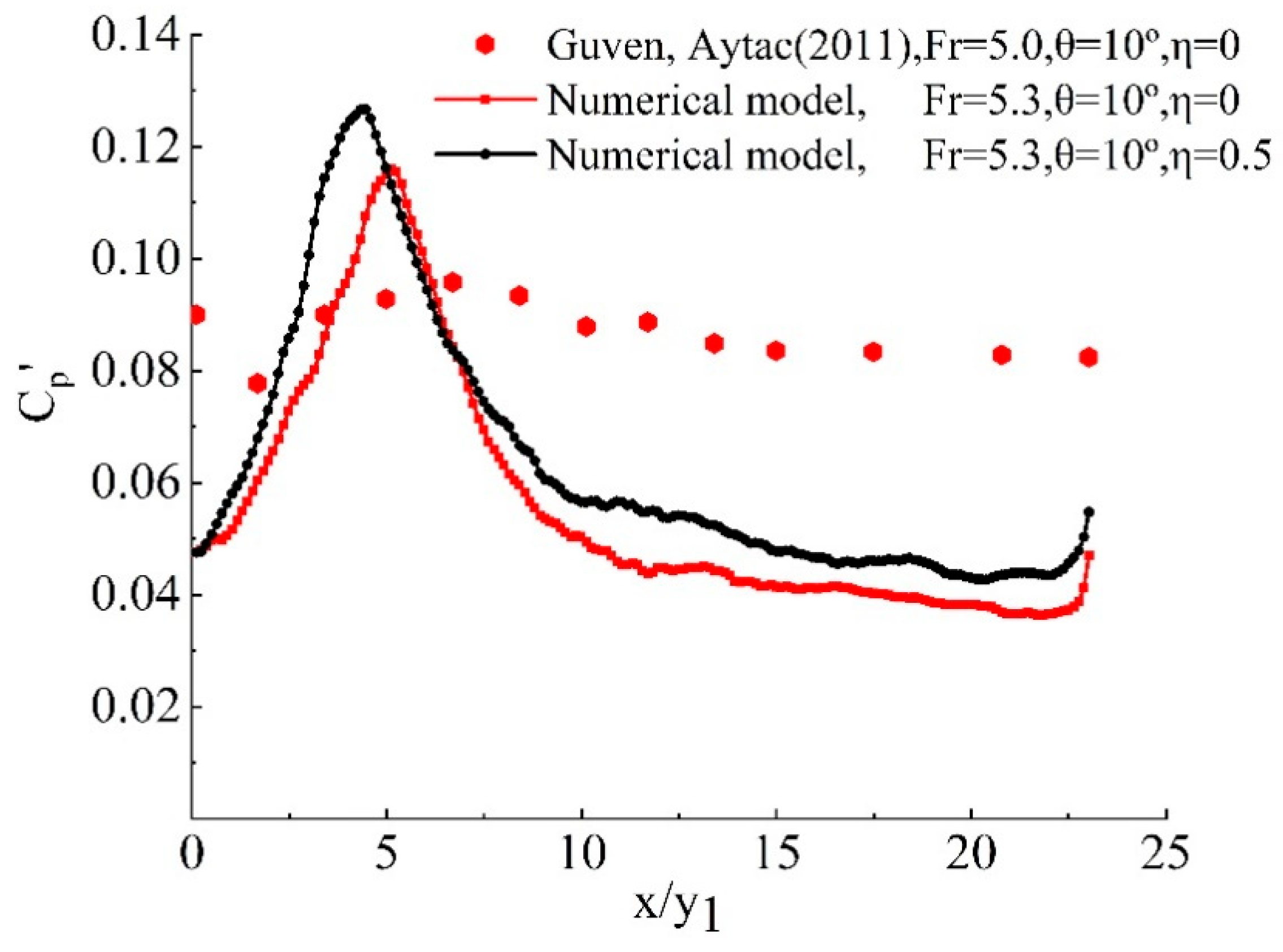
3.3. Verification of Pressure
4. Results and Discussion
4.1. Qualitative Analysis of RMS of Fluctuating Pressure
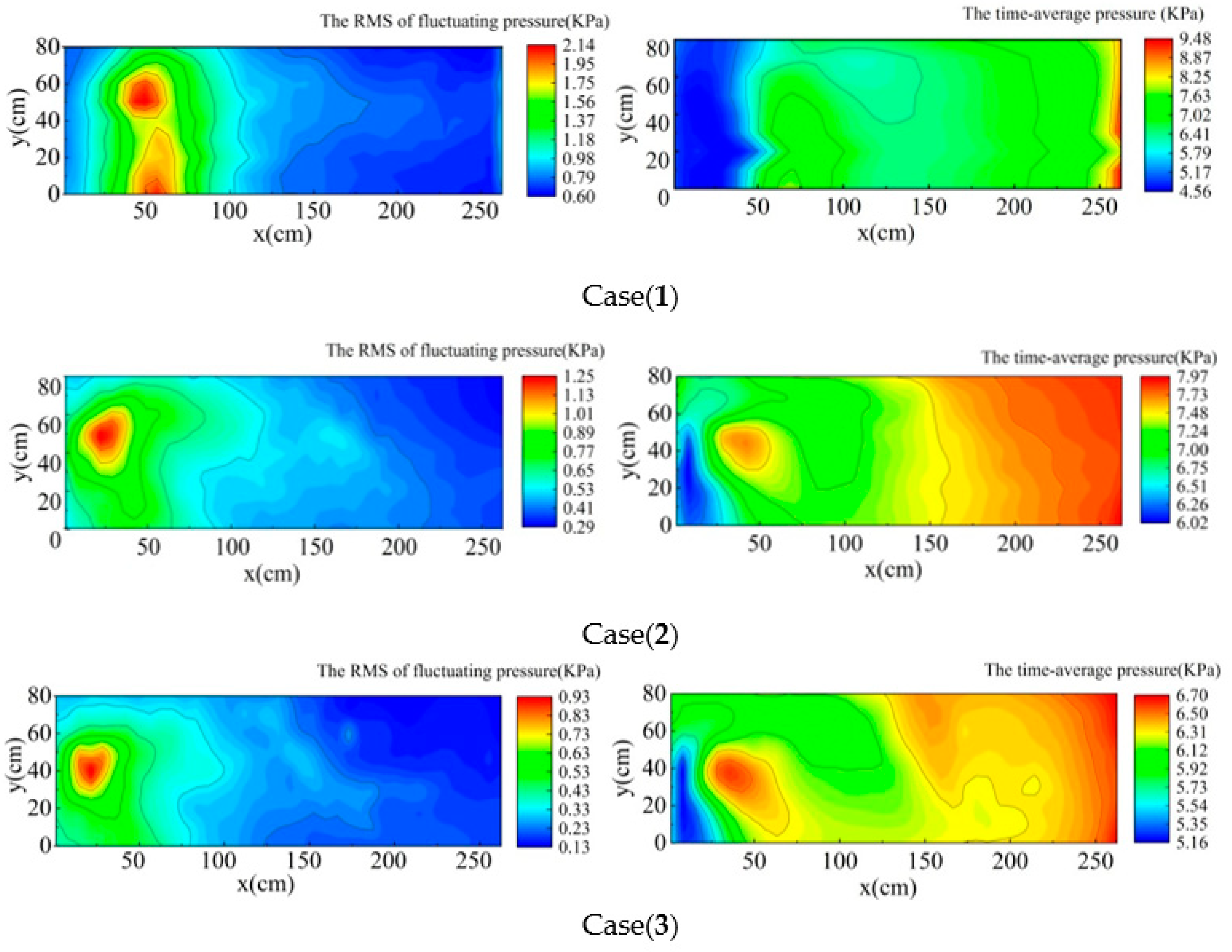
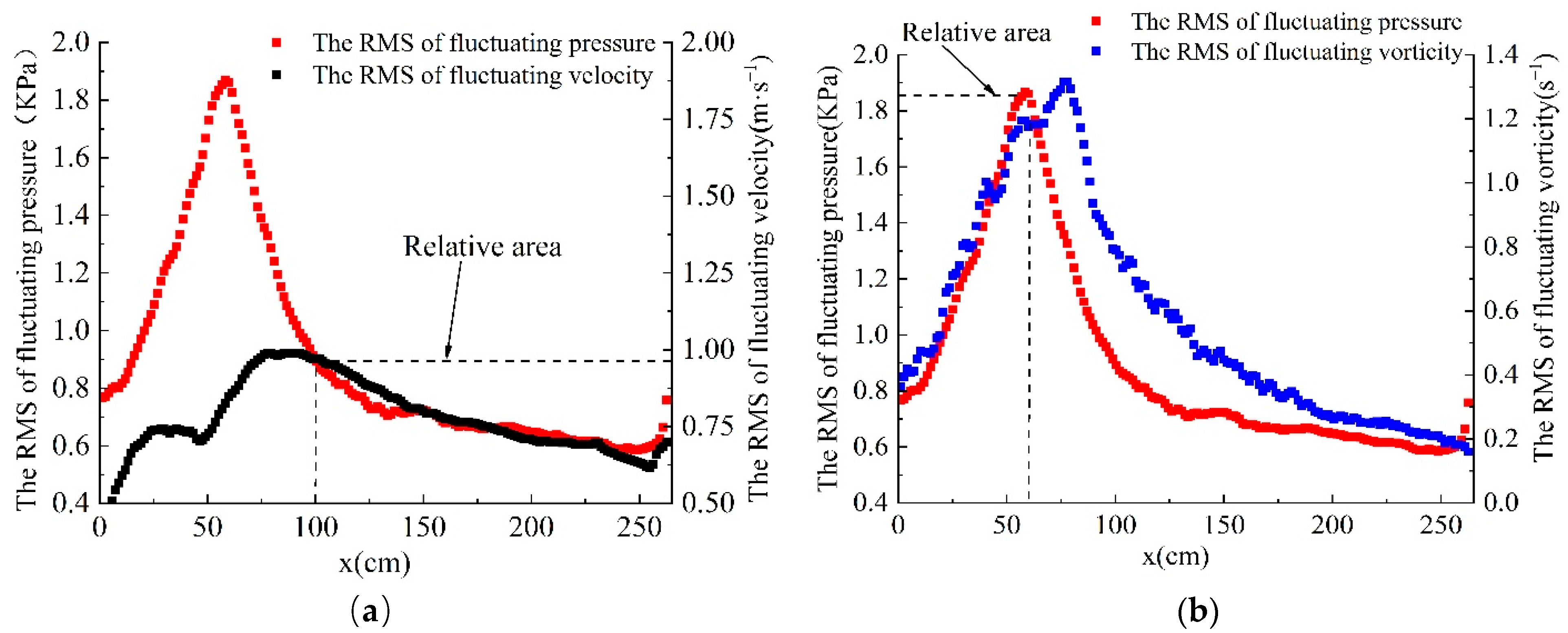
4.1.1. Qualitative Analysis of Longitudinal Distribution
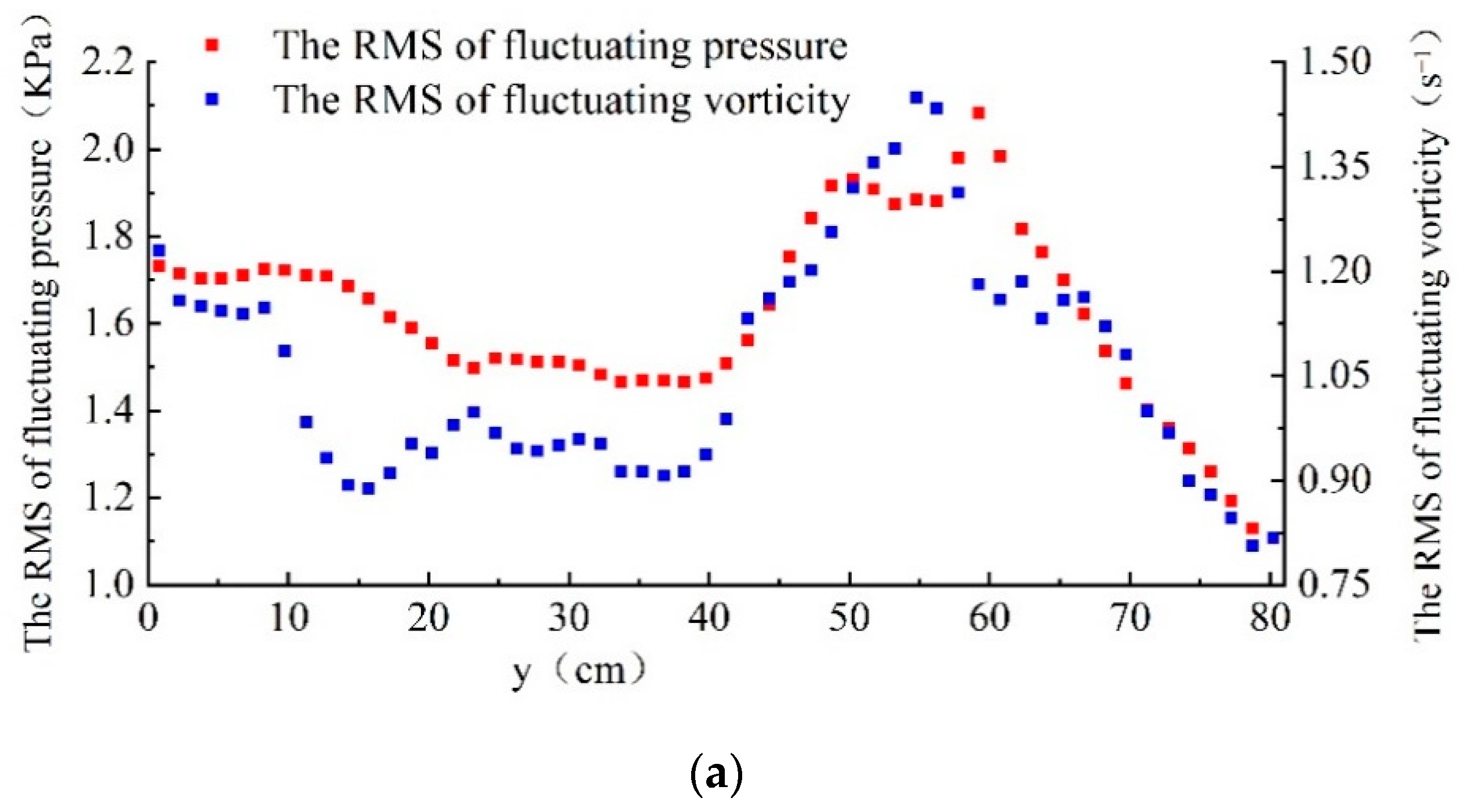
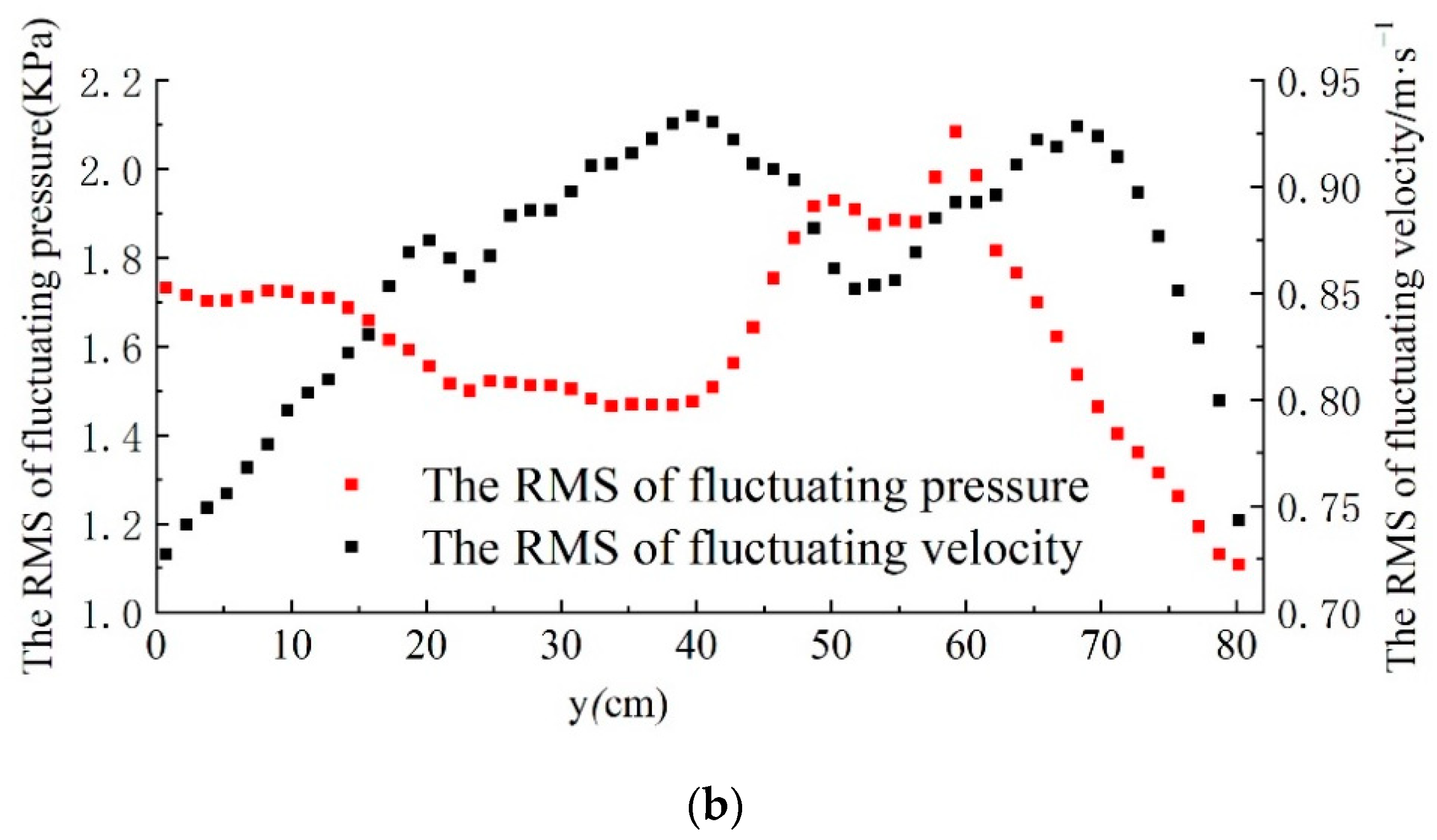
4.1.2. Qualitative Analysis of Horizontal Distribution
4.1.3. RMS of Fluctuating Pressure Distribution at Different Flow Rates
4.2. Quantitative Analysis of Fluctuating Pressure
4.2.1. Mathematical Model
4.2.2. Quantitative Analysis of Longitudinal Distribution
4.2.3. Cross-Sectional Distribution Quantitative Analysis
4.3. Discussion
5. Conclusions
- The flow pattern, velocity distribution, time-average pressure, root mean square (RMS) of fluctuating pressure, maximum and minimum pressure of a stilling basin slab of the water flow obtained by numerical simulation are in good agreement with the experimental results, indicating that it is advisable to use large eddy simulation to study the fluctuating pressure of stilling basin slab.
- Due to the superposition of the horizontal and vertical vortex, the turbulence and mixing of water in the front of the stilling basin and the extension of the side wall of the vent are severe, resulting in a large RMS of fluctuating pressure in this area, which requires attention. With the increase of per-unit width discharge, the peak point of σ deviates from the center line of the stilling basin and approaches the side wall line. Both sudden lateral enlargement and bottom drop will result in the difference distributions of spatial hydraulic jumps compared with those of equivalent classical hydraulic jumps.
- The RMS of fluctuating pressure longitudinally changes along the center line of the stilling basin, first increasing, then decreasing, and finally increasing slightly. The submerged jet zone is mainly affected by the vortex body, and the impinging zone is affected by the fluctuating velocity and the vortex body. The wall-attached jet zone is mainly caused by the fluctuating velocity. The horizontal direction from the front of the stilling basin along the center to the side wall shows a trend of first decreasing, increasing, and then decreasing, which is highly correlated with the vorticity distribution, but has little correlation with the fluctuating velocity distribution.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liu, P.Q.; Dong, J.R.; Yu, C. Experimental investigation of fluctuation uplift on rock blocks at the bottom of the scour pool downstream of Three-Gorges spillway. J. Hydraul. Res. 1998, 36, 55–68. [Google Scholar] [CrossRef]
- Liu, P.Q.; Li, A.H. Model discussion of pressure fluctuations propagation within lining slab joints in stilling basins. J. Hydraul. Eng. 2007, 133, 618–624. [Google Scholar] [CrossRef]
- Mousavi, S.N.; Júnior, R.S.; Teixeira, E.D.; Bocchiola, D.; Nabipour, N.; Mosavi, A.; Shamshirband, S. Predictive Modeling the Free Hydraulic Jumps Pressure through Advanced Statistical Methods. Mathematics 2020, 8, 323. [Google Scholar] [CrossRef]
- Sun, S.-K.; Liu, H.-T.; Xia, Q.-F.; Wang, X.-S. Study on stilling basin with step down floor for energy dissipation of hydraulic jump in high dams. J. Hydraul. Eng. 2005, 36, 1188–1193. (In Chinese) [Google Scholar]
- Li, Q.; Li, L.; Liao, H. Study on the Best Depth of Stilling Basin with Shallow-Water Cushion. Water 2018, 10, 1801. [Google Scholar] [CrossRef]
- Luo, Y.-Q.; He, D.-M.; Zhang, S.-C.; Bai, S. Experimental Study on Stilling Basin with Step-down for Floor Slab Stability Characteristics. J. Basic Sci. Eng. 2012, 20, 228–236. (In Chinese) [Google Scholar]
- Zhang, J.; Zhang, Q.; Wang, T.; Li, S.; Diao, Y.; Cheng, M.; Baruch, J. Experimental Study on the Effect of an Expanding Conjunction Between a Spilling Basin and the Downstream Channel on the Height After Jump. Arab. J. Sci. Eng. 2017, 42, 4069–4078. [Google Scholar] [CrossRef]
- Ram, K.V.S.; Prasad, R. Spatial B-jump at sudden channel enlargements with abrupt drop. J. Hydraul. Eng. -Asce 1998, 124, 643–646. [Google Scholar] [CrossRef]
- Hassanpour, N.; Hosseinzadeh Dalir, A.; Farsadizadeh, D.; Gualtieri, C. An Experimental Study of Hydraulic Jump in a Gradually Expanding Rectangular Stilling Basin with Roughened Bed. Water 2017, 9, 945. [Google Scholar] [CrossRef]
- Siuta, T. The impact of deepening the stilling basin on the characteristics of hydraulic jump. Czas. Tech. 2018. [Google Scholar] [CrossRef]
- Babaali, H.; Shamsai, A.; Vosoughifar, H. Computational Modeling of the Hydraulic Jump in the Stilling Basin with Convergence Walls Using CFD Codes. Arab. J. Sci. Eng. 2014, 40, 381–395. [Google Scholar] [CrossRef]
- Dehdar-behbahani, S.; Parsaie, A. Numerical modeling of flow pattern in dam spillway’s guide wall. Case study: Balaroud dam, Iran. Alex. Eng. J. 2016, 55, 467–473. [Google Scholar] [CrossRef]
- Macián-Pérez, J.F.; García-Bartual, R.; Huber, B.; Bayon, A.; Vallés-Morán, F.J. Analysis of the Flow in a Typified USBR II Stilling Basin through a Numerical and Physical Modeling Approach. Water 2020, 12, 227. [Google Scholar] [CrossRef]
- Tajabadi, F.; Jabbari, E.; Sarkardeh, H. Effect of the end sill angle on the hydrodynamic parameters of a stilling basin. Eur. Phys. J. Plus 2018, 133. [Google Scholar] [CrossRef]
- Valero, D.; Bung, D.B.; Crookston, B.M. Energy Dissipation of a Type III Basin under Design and Adverse Conditions for Stepped and Smooth Spillways. J. Hydraul. Eng. 2018, 144. [Google Scholar] [CrossRef]
- Liu, D.; Fei, W.; Wang, X.; Chen, H.; Qi, L. Establishment and application of three-dimensional realistic river terrain in the numerical modeling of flow over spillways. Water Supply 2018, 18, 119–129. [Google Scholar] [CrossRef]
- Epely-Chauvin, G.; De Cesare, G.; Schwindt, S. Numerical Modelling of Plunge Pool Scour Evolution In Non-Cohesive Sediments. Eng. Appl. Comput. Fluid Mech. 2015, 8, 477–487. [Google Scholar] [CrossRef][Green Version]
- Zhang, J.-M.; Chen, J.-G.; Xu, W.-L.; Peng, Y. Characteristics of vortex structure in multi-horizontal submerged jets stilling basin. Proc. Inst. Civ. Eng. Water Manag. 2014, 167, 322–333. [Google Scholar] [CrossRef]
- Li, L.-X.; Liao, H.-S.; Liu, D.; Jiang, S.-Y. Experimental investigation of the optimization of stilling basin with shallow-water cushion used for low Froude number energy dissipation. J. Hydrodyn. 2015, 27, 522–529. [Google Scholar] [CrossRef]
- Ferreri, G.B.; Nasello, C. Hydraulic jumps at drop and abrupt enlargement in rectangular channel. J. Hydraul. Res. 2010, 40, 491–505. [Google Scholar] [CrossRef]
- Naseri, F.; Sarkardeh, H.; Jabbari, E. Effect of inlet flow condition on hydrodynamic parameters of stilling basins. Acta Mech. 2017, 229, 1415–1428. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, J.-X. Numerical Modeling of 3D Flow Field among a Compound Stilling Basin. Math. Probl. Eng. 2019, 5934274. [Google Scholar] [CrossRef]
- Qian, Z.; Hu, X.; Huai, W.; Amador, A. Numerical simulation and analysis of water flow over stepped spillways. Sci. China Ser. E Technol. Sci. 2009, 52, 1958–1965. [Google Scholar] [CrossRef]
- Liu, F. Study on Characteristics of Fluctuating Wall-Pressure and Its Similarity Law. Ph.D. Thesis, Tianjin University, Tianjin, China, May 2007. (In Chinese). [Google Scholar]
- Yan, Z.-M.; Zhou, C.-T.; Lu, S.-Q. Pressure fluctuations beneath spatial hydraulic jumps. J. Hydrodyn. 2006, 18, 723–726. [Google Scholar] [CrossRef]
- Moin, P.; Kim, J. Numerical investigation of turbulent channel flow. J. Fluid Mech. 2006, 118. [Google Scholar] [CrossRef]
- Rezaeiravesh, S.; Liefvendahl, M. Effect of grid resolution on large eddy simulation of wall-bounded turbulence. Phys. Fluids 2018, 30. [Google Scholar] [CrossRef]
- Stamou, A.I.; Chapsas, D.G.; Christodoulou, G.C. 3-D numerical modeling of supercritical flow in gradual expansions. J. Hydraul. Res. 2010, 46, 402–409. [Google Scholar] [CrossRef]
- Savage, B.M.; Crookston, B.M.; Paxson, G.S. Physical and Numerical Modeling of Large Headwater Ratios for a 15 degrees Labyrinth Spillway. J. Hydraul. Eng. 2016, 142. [Google Scholar] [CrossRef]
- Aydin, M.C.; Ozturk, M. Verification and validation of a computational fluid dynamics (CFD) model for air entrainment at spillway aerators. Can. J. Civ. Eng. 2009, 36, 826–836. [Google Scholar] [CrossRef]
- Ma, B.; Liang, S.; Liang, C.; Li, Y. Experimental Research on an Improved Slope Protection Structure in the Plunge Pool of a High Dam. Water 2017, 9, 671. [Google Scholar] [CrossRef]
- Bai, L.; Zhou, L.; Han, C.; Zhu, Y.; Shi, W.D. Numerical Study of Pressure Fluctuation and Unsteady Flow in a Centrifugal Pump. Processes 2019, 7, 354. [Google Scholar] [CrossRef]
- Guven, A. A predictive model for pressure fluctuations on sloping channels using support vector machine. Int. J. Numer. Methods Fluids 2011, 66, 1371–1382. [Google Scholar] [CrossRef]

| Condition | Flow Discharge (m3/s) | Inflow Froude Number | Inflow Velocity (m/s) | Inflow Water Depth (m) |
|---|---|---|---|---|
| 1 | 0.942 | 5.295 | 5.611 | 0.114 |
| 2 | 0.643 | 4.545 | 4.489 | 0.097 |
| 3 | 0.232 | 4.227 | 3.018 | 0.052 |
| Grid | Containing Block Cell Size (m) | Nested Block Cell Size (m) | Discharge (m3/s) | Relative Error (%) |
|---|---|---|---|---|
| 1 | 0.050 | 0.025 | 0.990 | 5.10 |
| 2 | 0.040 | 0.020 | 0.969 | 2.70 |
| 3 | 0.030 | 0.015 | 0.956 | 1.49 |
| 4 | 0.020 | 0.010 | 0.952 | 1.06 |
| Condition | σmax (Pa) | σmax Point Coordinates (cm) |
|---|---|---|
| 1 | 2139 | (50,60) |
| 2 | 1253 | (35,55) |
| 3 | 932 | (30,35) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Yin, J.; Yang, Z.; Wei, K.; Liu, Z. Numerical Study of Fluctuating Pressure on Stilling Basin Slab with Sudden Lateral Enlargement and Bottom Drop. Water 2021, 13, 238. https://doi.org/10.3390/w13020238
Lu Y, Yin J, Yang Z, Wei K, Liu Z. Numerical Study of Fluctuating Pressure on Stilling Basin Slab with Sudden Lateral Enlargement and Bottom Drop. Water. 2021; 13(2):238. https://doi.org/10.3390/w13020238
Chicago/Turabian StyleLu, Yangliang, Jinbu Yin, Zhou Yang, Kebang Wei, and Zhiming Liu. 2021. "Numerical Study of Fluctuating Pressure on Stilling Basin Slab with Sudden Lateral Enlargement and Bottom Drop" Water 13, no. 2: 238. https://doi.org/10.3390/w13020238
APA StyleLu, Y., Yin, J., Yang, Z., Wei, K., & Liu, Z. (2021). Numerical Study of Fluctuating Pressure on Stilling Basin Slab with Sudden Lateral Enlargement and Bottom Drop. Water, 13(2), 238. https://doi.org/10.3390/w13020238





