Vertical Electrical Sounding (VES) for Estimation of Hydraulic Parameters in the Porous Aquifer
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Sets
2.3. VES Interpretation
2.4. Geoelectric Aquifer Parameters Selection
2.5. Relationship between Hydraulic and Geoelectric Aquifer Parameters
3. Results and Discussion
3.1. Identification and Characterization of the Porous Aquifer
3.2. Relationship between the Geoelectric and Hydraulic Parameters of the Aquifer
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall: Englewood Cliffs, NJ, USA, 1979. [Google Scholar]
- Akhter, G.; Hasan, M. Determination of aquifer parameters using geoelectrical sounding and pumping test data in Khanewal District, Pakistan. Open Geosci. 2016, 8, 630–638. [Google Scholar] [CrossRef]
- Fetter, C.W. Applied Hydrogeology, 3rd ed.; Macmillan College Publishing Company: New York, NY, USA, 1994. [Google Scholar]
- Jones, P.H.; Buford, T.B. Electric Logging Applied to Ground-Water Exploration. Geophysics 1951, 16, 115–139. [Google Scholar] [CrossRef]
- Butler, J.J. Hydrogeological Methods for Estimation of Spatial Variations in Hydraulic Conductivity. In Hydrogeophysic; Springer: Berlin/Heidelberg, Germany, 2005; pp. 23–58. [Google Scholar] [CrossRef]
- Khalil, M.A.; Monterio Santos, F.A. Influence of Degree of Saturation in the Electric Resistivity-Hydraulic Conductivity Relationship. Surv. Geophys. 2009, 30, 601–615. [Google Scholar] [CrossRef]
- Brassington, R. Field Hydrogeology, 4th ed.; Wiley-Blackwell: Oxford, UK, 2017. [Google Scholar]
- Niwas, S.; Singhal, D.C. Estimation of aquifer transmissivity from Dar-Zarrouk parameters in Porous Media. J. Hydrol. 1981, 50, 393–399. [Google Scholar] [CrossRef]
- Worthington, P.F.; Barker, R.D. Methods for the calculation of true formation factors in the Bunter Sandstone of Northwest England. Eng. Geol. 1972, 6, 213–228. [Google Scholar] [CrossRef]
- Archie, G.E. The electrical resistivity log as an aid in determining some reservoir characteristics. Pet. Trans. AIME 1942, 55, 9–16. [Google Scholar] [CrossRef]
- Maillet, R. The fundamental equations of electrical prospectiong. Geophysics 1947, 12, 529–556. [Google Scholar] [CrossRef]
- Oguama, B.E.; Ibuot, J.C.; Obiora, D.N. Geohydraulic study of aquifer characteristics in parts of Enugu North Local Government area of enugu state using electrical resistivity soundings. Appl. Water Sci. 2020, 10, 1–10. [Google Scholar] [CrossRef]
- Wan Bakar, W.Z.; Mohd Saaid, I.; Ahmad, M.R.; Amir, Z.; Mahat, S.Q.A. Derivation of formation factor in shaly sandstone with geometry and clay conductivity effects. J. Pet. Sci. Eng. 2019, 182, 7. [Google Scholar] [CrossRef]
- Tizro, A.T.; Voudouris, K.S.; Salehzade, M.; Mashayekhi, H. Hydrogeological framework and estimation of aquifer hydraulic parameters using geoelectrical data: A case study from West Iran. Hydrogeol. J. 2010, 18, 917–929. [Google Scholar] [CrossRef]
- Mlangi, T.M.; Mulibo, G.D. Delineation of Shallow Stratigraphy and Aquifer Formation at Kahe Basin, Tanzania: Implication for Potential Aquiferous Formation. J. Geosci. Environ. Prot. 2018, 6, 78–98. [Google Scholar] [CrossRef]
- Lech, M.; Skutnik, Z.; Bajda, M.; Markowska-Lech, K. Applications of Electrical Resistivity Surveys in Solving Selected Geotechnical and Environmental Problems. Appl. Sci. 2020, 10, 2263. [Google Scholar] [CrossRef]
- Ammar, A.I.; Kamal, K.A. Effect of structure and lithological heterogeneity on the correlation coefficient between the electric–hydraulic parameters of the Aquifer, Eastern Desert, Egypt. Appl. Water Sci. 2019, 9, 1–21. [Google Scholar] [CrossRef]
- Virupaksha, H.S.; Lokesh, K.N. Electrical resistivity, remote sensing and geographic information system approach for mapping groundwater Potential Zones in Coastal Aquifers of Gurpur Watershed. Geocarto Int. 2019, 1–15. [Google Scholar] [CrossRef]
- Zhu, L.; Gong, H.; Chen, Y.; Li, X.; Chang, X.; Cui, Y. Improved estimation of hydraulic conductivity by combining stochastically simulated hydrofacies with geophysical data. Sci. Rep. 2016, 6, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Choo, H.; Kim, J.; Lee, W.; Lee, C. Relationship between Hydraulic Conductivity and Formation Factor of Coarse-Grained Soils as a Function of Particle Size. J. Appl. Geophys. 2016, 127, 91–101. [Google Scholar] [CrossRef]
- Moreira, C.A.; Cavalheiro, M.L.D.; Pereira, A.M.; Caron, F. Relações entre condutividade hidráulica, transmissividade, condutância longitudinal e sólidos totais dissolvidos para o aquífero livre de caçapava Do Sul (RS), Brasil. Eng. Sanit. Ambient. 2012, 17, 193–202. [Google Scholar] [CrossRef]
- Rosa, F.T.; Moreira, C.A.; Carrara, A.; Dos Santos, S.F. Análise das relações entre resistividade elétrica, condutividade hidráulica e parâmetros físico-químicos para o aquífero livre da região de corumbataí (SP). Águas Subterrâneas 2017, 31, 384–392. [Google Scholar] [CrossRef][Green Version]
- Díaz-Curiel, J.; Biosca, B.; Miguel, M.J. Geophysical estimation of permeability in sedimentary media with porosities from 0 to 50%. Oil Gas. Sci. Technol. 2015, 71. [Google Scholar] [CrossRef]
- Heigold, P.C.; Gilkeson, R.H.; Cartwright, K.; Reed, P.C. Aquifer transmissivity from surficial electrical methods. Groundwater 1979, 338–345. [Google Scholar] [CrossRef]
- Kwami, I.A.; Ishaku, J.M.; Mukkafa, S.; Haruna, A.I.; Ankidawa, B.A. Delineation of aquifer potential zones using hydraulic parameters in gombe and environs, North-Eastern, Nigeria. Heliyon 2019, 5, e01927. [Google Scholar] [CrossRef] [PubMed]
- Ejiogu, B.C.; Opara, A.I.; Nwosu, E.I.; Nwofor, O.K.; Onyema, J.C.; Chinaka, J.C. Estimates of aquifer geo-hydraulic and vulnerability characteristics of imo state and environs, southeastern nigeria, using electrical conductivity data. Environ. Monit. Assess. 2019, 191, 1–19. [Google Scholar] [CrossRef] [PubMed]
- Anosike, S.; Ibuot, J.C.; Obiora, D.N.; Ugbor, D.O. Geophysical and physicochemical investigation of groundwater repositories in Njaba LGA of Imo State, Eastern Nigeria. Int. J. Environ. Sci. Technol. 2019, 16, 8129–8140. [Google Scholar] [CrossRef]
- Urish, D. Electrical resistivity-hydraulic conductivity relationships in glacial Outwash Aquifers. Water Resour. Res. 1981, 17, 3877–3879. [Google Scholar] [CrossRef]
- Mazáč, O.; Kelly, W.E.; Landa, I. A Hydrogeophysical model for relations between electrical and hydraulic properties of aquifers. J. Hydrol. 1985, 79, 1–19. [Google Scholar] [CrossRef]
- George, N.J.; Atat, J.G.; Umoren, E.B.; Etebong, I. Geophysical exploration to estimate the surface conductivity of residual argillaceous bands in the groundwater repositories of coastal sediments of EOLGA, Nigeria. NRIAG J. Astron. Geophys. 2017, 6, 174–183. [Google Scholar] [CrossRef]
- Singh, S.; Singh, V.S. Estimation of hydraulic chracteristics of alluvial aquifers from electrical resistivity data. J. Geol. Soc. India 2016, 88, 77–86. [Google Scholar] [CrossRef]
- Hasan, M.; Shang, Y.; Akhter, G.; Jin, W. Geophysical Assessment of Groundwater Potential: A Case Study from Mian Channu Area, Pakistan. Groundwater 2018, 56, 783–796. [Google Scholar] [CrossRef]
- Ekwe, A.C.; Opara, A.I.; Okeugo, C.G.; Azuoko, G.B.; Nkitnam, E.E.; Abraham, E.M.; Chukwu, C.G.; Mbaeyi, G. Determination of aquifer parameters from geosounding data in parts of Afikpo Sub-Basin, Southeastern Nigeria. Arab. J. Geosci. 2020, 13. [Google Scholar] [CrossRef]
- Okiongbo, K.S.; Mebine, P. Estimation of Aquifer Hydraulic Parameters from Geoelectrical Method—A Case Study of Yenagoa and Environs, Southern Nigeria. Arab. J. Geosci. 2015, 8, 6085–6093. [Google Scholar] [CrossRef]
- Mgbolu, C.C.; Obiadi, I.I.; Obiadi, C.M.; Okolo, C.M.; Irumhe, P.E. Integrated groundwater potentials studies, aquifer hydraulic characterisation and vulnerability investigations of parts of Ndokwa, Niger Delta Basin, Nigeria. Solid Earth Sci. 2019, 4, 102–112. [Google Scholar] [CrossRef]
- Worthington, P.F. The uses and abuses of the archie equations, 1: The formation factor-porosity relationship. J. Appl. Geophys. 1993, 30, 215–228. [Google Scholar] [CrossRef]
- Eiten, G. The cerrado vegetation of Brazil. Bot. Rev. 1972, 38, 201–341. [Google Scholar] [CrossRef]
- Maia, J.M.F.; Baptista, G.M.M. Clima. In Águas Emendadas; Secretaria de Desenvolvimento Urbano e Meio Ambiente (SEDUH): Brasília, Brazil, 2008; pp. 101–110. [Google Scholar]
- Assad, E.D.; Sano, E.E.; Meirelles, M.L.; Silva, F.A.M.; Moreira, L.; Macedo, J.; Resck, D.V.S.; Ker, J.C.; Chagas, C.S.; Carvalho-Junior, V. Caracterização Ambiental Da Microbacia Do Córrego Taquara, DF; EMBRAPA: Planaltina, Brazil, 1992. [Google Scholar]
- Santos, H.G.; Jacomine, P.K.; Anjos, L.H.; Oliveira, V.A.; Lumbreras, J.F.; Coelho, M.R.; Almeida, J.A.; Cunha, T.J.; Oliveira, J.B. Sistema Brasileiro de Classificação de Solos; EMBRAPA: Brasília, Brazil, 2013. [Google Scholar] [CrossRef]
- Gonçalves, T.D.; Lohe, C.; Campos, J.E.G. Hydraulic characterization from porous aquifers of the Brazilian federal district. Brazilian J. Geol. 2015, 45, 259–271. [Google Scholar] [CrossRef][Green Version]
- Freitas-Silva, F.H.; Campos, J.E.G. Geologia Do Distrito Federal. In Inventário Hidrogeológico e dos Recursos Hídricos Superficiais do Distrito Federal; IEMA/SEMATEC/UnB: Brasília, Brazil, 1998; p. 86. [Google Scholar]
- Campos, J.E.G. Hidrogeologia Do Distrito Federal: Bases Para a Gestão Dos Recursos Hídricos Subterrâneos. Rev. Bras. Geociências 2004, 34, 41–48. [Google Scholar] [CrossRef]
- Campos, J.E.G.; Freitas-Silva, F.H. Hidrogeologia Do Distrito Federal. In Inventário Hidrogeológico e dos Recursos Hídricos Superficiais do Distrito Federal; IEMA/SEMATEC/UnB: Brasília, Brazil, 1998. [Google Scholar]
- NRCS; USDA. Keys to Soil Taxonomy; NRCS: USDA: Washington, DC, USA, 2014; Volume 12.
- Oliveira, P.T.S.; Leite, M.B.; Mattos, T.; Nearing, M.A.; Scott, R.L.; de Oliveira Xavier, R.; da Silva Matos, D.M.; Wendland, E. Groundwater recharge decrease with increased vegetation density in the Brazilian Cerrado. Ecohydrology 2017, 10, 1–8. [Google Scholar] [CrossRef]
- SEDHAB. Sicad–Sistema Cartográfico Do Distrito Federal Escala 1:10.000; Secretaria de Habitação, Regularização e Desenvolvimento Urbano: Brasília, Brazil, 2017. [Google Scholar]
- EMBRAPA. Manual de Métodos de Análise de Solo; Centro Nacional de Pesquisa de Solos: Rio de Janeiro, Brazil, 1997. [Google Scholar]
- Cooper, H.H.J.; Bredehoeft, J.D.; Papadopulos, I.S. Response of a Finite-Diameter Well to an Instantaneous Charge Water. Water Resour. Res. 1967, 3, 263–269. [Google Scholar] [CrossRef]
- Bobachev, A.A.; Modin, I.N.; Shevin, V.A. IPI2Win: User’s Guide; State University/Geoscan-M: Moscow, Russia, 2001. [Google Scholar]
- Tofallis, C. A Better Measure of Relative Prediction Accuracy for Model Selection and Model Estimation. J. Oper. Res. Soc. 2015, 66, 1352–1362. [Google Scholar] [CrossRef]
- Garofalo, F.; Sauvin, G.; Socco, L.V.; Lecomte, I. Joint inversion of seismic and electric data applied to 2D media. Geophysics 2015, 80, EN93–EN104. [Google Scholar] [CrossRef]
- Simms, J.E.; Morgan, F.D. Comparison of Four Least-squares Inversion Schemes for Studying Equivalence in One-dimensional Resistivity Interpretation. Geophysics 1992, 57, 1282–1293. [Google Scholar] [CrossRef]
- Attwa, M.; Akca, I.; Basokur, A.T.; Günther, T. Structure-based geoelectrical models derived from genetic algorithms: A case study for hydrogeological investigations along Elbe River Coastal Area, Germany. J. Appl. Geophys. 2014, 103, 57–70. [Google Scholar] [CrossRef]
- Vinegar, H.J.; Waxman, M.H. Induced polarization of shaly sands–The effect of clay counterion type. Geophysics 1984, 49, 1267–1287. [Google Scholar] [CrossRef]
- Pincus, L.N.; Ryan, P.C.; Huertas, F.J.; Alvarado, G.E. The influence of soil age and regional climate on clay mineralogy and cation exchange capacity of moist tropical soils: A case study from late quaternary chronosequences in Costa Rica. Geoderma 2017, 308, 130–148. [Google Scholar] [CrossRef]
- Alekseeva, T.V.; Sokolowska, Z.; Hajnos, M.; Alekseev, A.O.; Kalinin, P.I. Water stability of aggregates in subtropical and tropical soils (georgia and china) and its relationships with the mineralogy and chemical properties. Eurasian Soil Sci. 2009, 42, 415–425. [Google Scholar] [CrossRef]
- Reneau, J.R.B.; Fiskell, J.G.A. Selective dissolution effects on cation-exchange capacity and specific surface of some tropical soil clays. Soil Sci. Soc. Am. J. 1970, 34, 809–812. [Google Scholar] [CrossRef]
- Baty, F.; Ritz, C.; Charles, S.; Brutsche, M.; Flandrois, J.P.; Delignette-Muller, M.L. A toolbox for nonlinear regression in R: The package nlstools. J. Stat. Softw. 2015, 66, 1–21. [Google Scholar] [CrossRef]
- Brandt, S. Data Analysis: Statistical and Computational Methods for Scientists and Engineers, 4th ed.; Springer: Siegen, Germany, 2014. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- De Oliveira Fiori, J.P.; Campos, J.E.G.; Almeida, L. Variabilidade da condutividade hidráulica das principais classes de solos do estado de goiás. Geociencias 2010, 29, 229–235. [Google Scholar]
- Barker, R.D. Depth of investigation of collinear symmetrical four-electrode arrays. Geophysics 1989, 54, 1031–1037. [Google Scholar] [CrossRef]
- Braga, A.C.O. Geofísica Aplicada: Métodos Geoelétricos Em Hidrogeologia; Oficina de Textos: São Paulo, Brazil, 2016. [Google Scholar]
- Nascimento, C.T.C.; Varella, R.F.; Pires, A.C.B.; Santos, R.V. Valores de resistividade elétrica em um latossolo do distrito federal. CISBGF 2001, 7, 289–292. [Google Scholar]
- Martins, É.D.S.; de Carvalho Júnior, O.A.; Mello, G.D.A.; Reatto, A.; de Moraes, R.A.V.; Pires, A.C.B.; Guimarães, R.F. Mapeamento da superfície basal do manto de intemperismo pelo comportamento da resistidade elétrica do distrito federal. Rev. Bras. Geomorfol. 2008, 9, 15–28. [Google Scholar] [CrossRef][Green Version]
- Ker, J.C. Latossolos do Brasil: Uma revisão. Geonomos 1997, 5, 17–40. [Google Scholar] [CrossRef]
- Alvarenga, M.I.N.; Davide, A.C. Características físicas e químicas de um latossolo vermelho-escuro e a sustentabilidade de agroecossistemas. Rev. Bras. Ciência Solo 1999, 23, 933–942. [Google Scholar] [CrossRef]
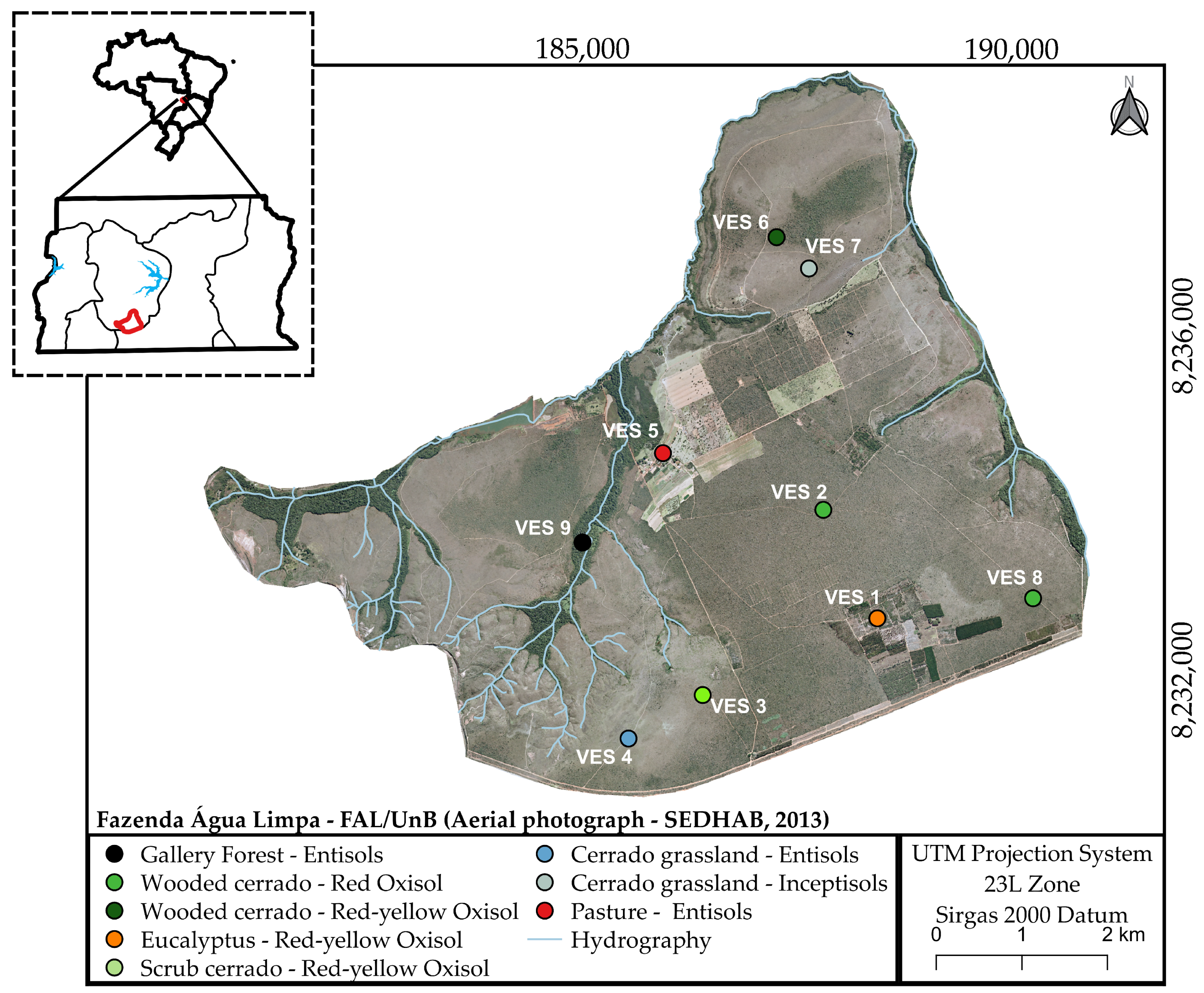
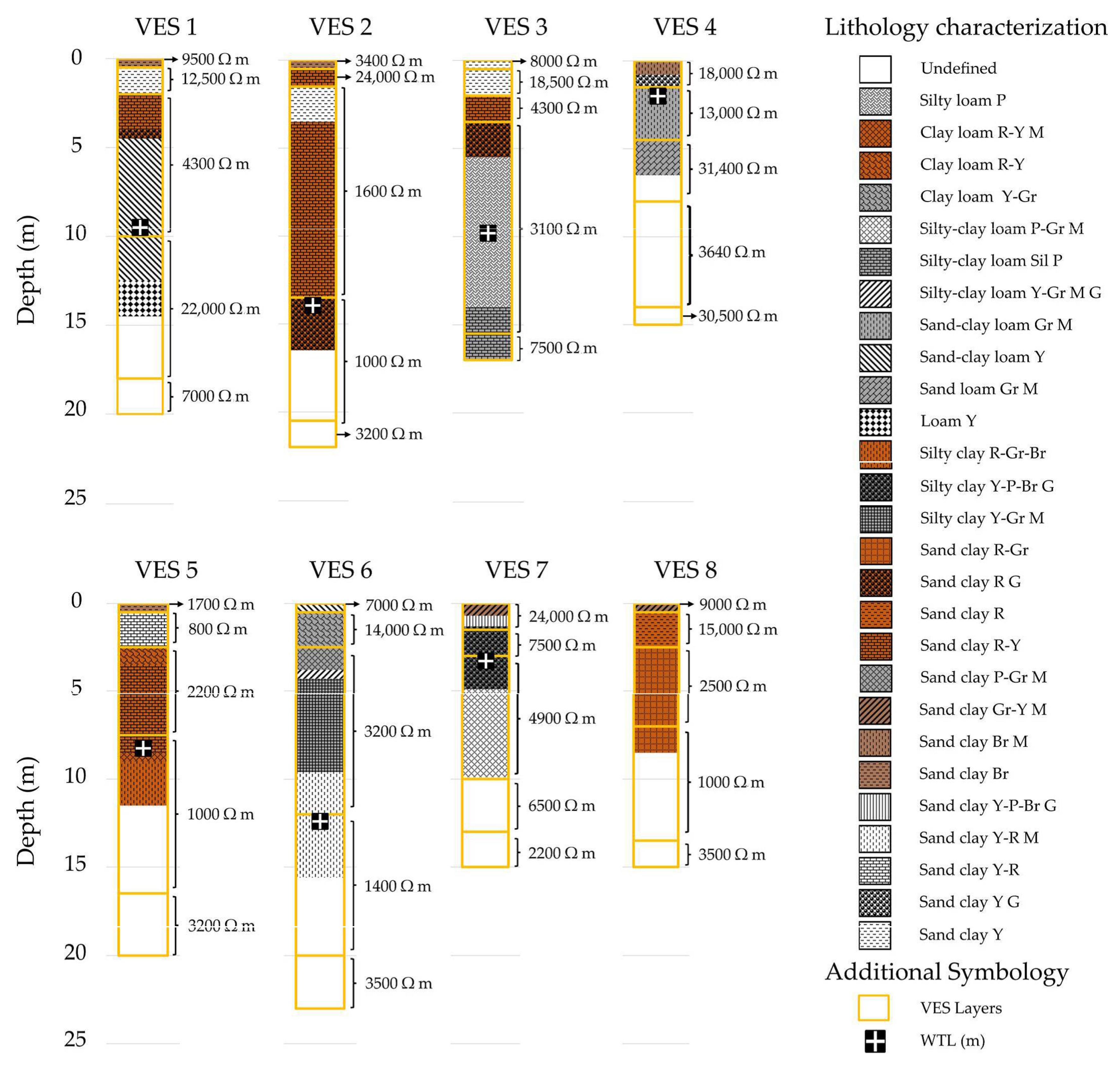
| VES Stations | Latitude (°W) | Longitude (°S) | Electrical Resistivity (Ω m) | Thickness (m) | RMS (%) | WTL (m) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ρ1 | ρ2 | ρ3 | ρ4 | ρ5 | h1 | h2 | h3 | h4 | |||||
| VES 1 | 188,426.06 | 8,232,711.67 | 9500 | 12,500 | 4300 * | 22,000 | 7000 | 0.50 | 1.50 | 8.00 * | 8.00 | 4.50 | 9.50 |
| VES 2 | 187,797.23 | 8,233,971.49 | 3400 | 24,000 | 1600 | 1000 * | 3200 | 0.50 | 1.00 | 12.00 | 7.00 * | 4.80 | 13.95 |
| VES 3 | 186,380.77 | 8,231,821.70 | 8000 | 18,500 | 4300 | 3100 * | 7500 | 0.50 | 1.50 | 1.50 | 12.00 * | 4.85 | 9.80 |
| VES 4 | 185,514.40 | 8,231,319.81 | 18,000 | 13,180 * | 31,400 | 3640 | 30,500 | 1.50 | 3.00* | 3.50 | 6.00 | 5.95 | 2.00 |
| VES 5 | 185,956.75 | 8,234,689.66 | 1700 | 800 | 2200 | 1000 * | 3200 | 0.50 | 2.00 | 5.00 | 9.00 * | 5.10 | 8.25 |
| VES 6 | 187,132.65 | 8,237,119.06 | 7000 | 14,000 | 3200 | 1400 * | 3500 | 0.50 | 2.00 | 9.50 | 8.00 * | 5.95 | 12.40 |
| VES 7 | 187,632.85 | 8,236,764.72 | 24,000 | 7500 | 4900 * | 6500 | 2200 | 1.50 | 1.50 | 7.00 * | 3.00 | 3.65 | 3.30 |
| VES 8 | 190,328.84 | 8,232,909.53 | 9000 | 15,000 | 2500 | 1000 * | 3500 | 0.50 | 2.00 | 4.50 | 6.50 * | 4.20 | - |
| VES 9 | 185,002.99 | 8,233,698.99 | 4500 | 3300 | 1900 * | 5000 | 3800 | 1.00 | 4.00 | 5.00 * | 10.00 | 4.25 | 9.25 |
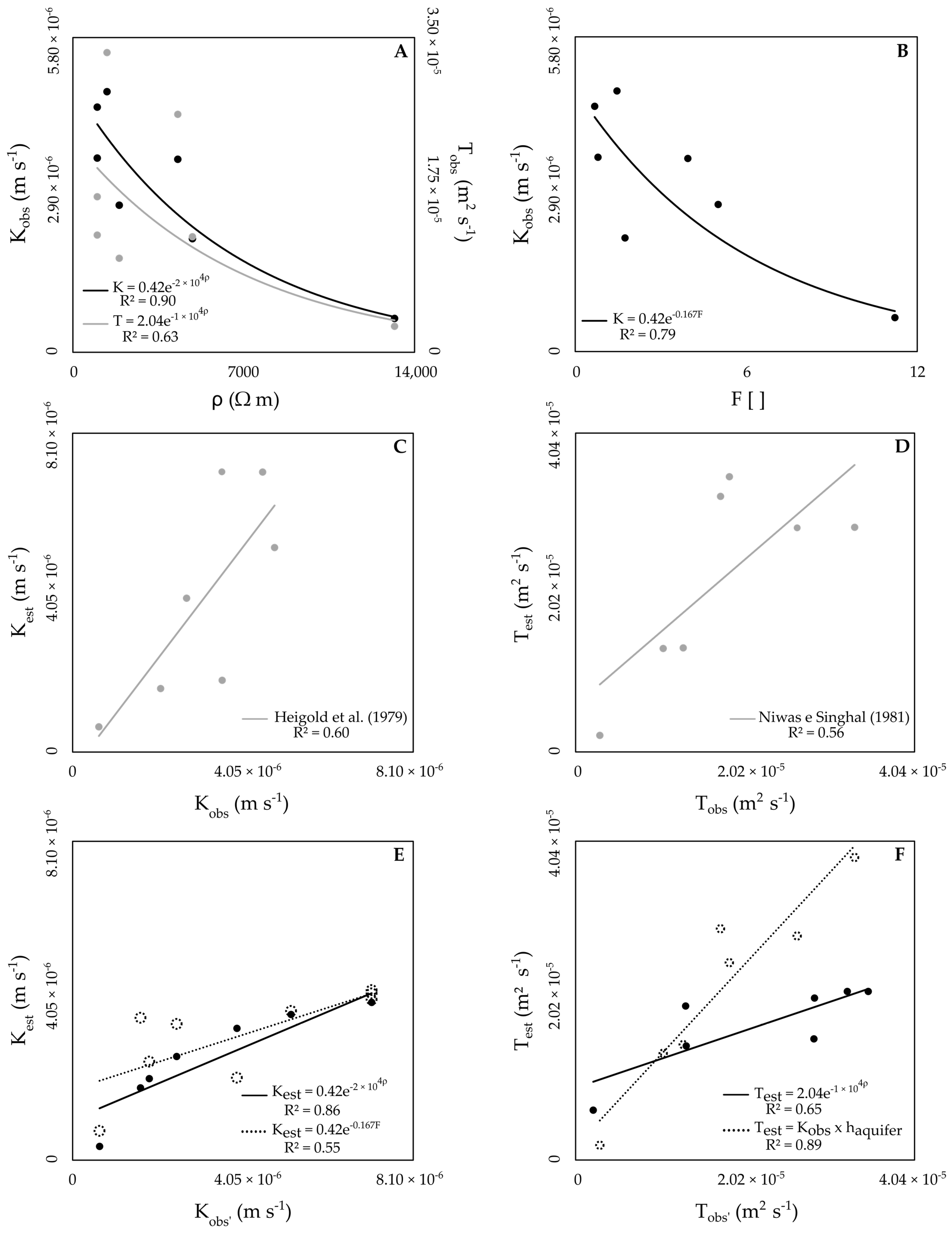
| VES station | Kobs (m s−1) | Tobs (m2 s−1) | ρw (Ω m) | F | Dar Zarrouk Parameters | Kest (m s−1) | Test (m2 s−1) | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C (Siemens) | R (Ω m2) | Model K1 * | Model K2 * | Heigold et al. (1979) | Model T1 * | Model T2 * | Niwas and Singhal (1981) | |||||
| VES 1 | 3.56 × 10−6 | 2.65 × 10−5 | 1088.14 | 3.95 | 1.86 × 10−3 | 34,400 | 2.07 × 10−6 | 2.50 × 10−6 | 1.82 × 10−6 | 1.54 × 10−5 | 2.85 × 10−5 | 2.85 × 10−5 |
| VES 2 | 3.58 × 10−6 | 1.84 × 10−5 | 1250.00 | 0.80 | 7.00 × 10−3 | 7000 | 4.01 × 10−6 | 4.24 × 10−6 | 7.11 × 10−6 | 2.14 × 10−5 | 2.51 × 10−5 | 3.50 × 10−5 |
| VES 3 | NA * | NA | 1540.83 | 2.01 | 3.87 × 10−3 | 37,200 | 2.63 × 10−6 | 3.46 × 10−6 | 2.48 × 10−6 | 1.74 × 10−5 | NA | NA |
| VES 4 | 6.25 × 10−7 | 2.89 × 10−6 | 1175.09 | 11.22 | 2.28 × 10−4 | 39,540 | 3.51 × 10−7 | 7.44 × 10−6 | 6.42 × 10−7 | 6.33 × 10−6 | 1.88 × 10−6 | 2.11 × 10−6 |
| VES 5 | NA | NA | 975.61 | 1.03 | 9.00 × 10−3 | 9000 | 4.01 × 10−6 | 4.08 × 10−6 | 7.11 × 10−6 | 2.14 × 10−5 | NA | NA |
| VES 6 | 4.80 × 10−6 | 3.33 × 10−5 | 954.20 | 1.47 | 5.71 × 10−3 | 11,200 | 3.70 × 10−6 | 3.79 × 10−6 | 5.20 × 10−6 | 2.06 × 10−5 | 3.84 × 10−5 | 2.85 × 10−5 |
| VES 7 | 2.09 × 10−6 | 1.29 × 10−5 | 2801.12 | 1.75 | 1.43 × 10−3 | 34,300 | 1.84 × 10−6 | 3.62 × 10−6 | 1.62 × 10−6 | 1.45 × 10−5 | 1.47 × 10−5 | 1.32 × 10−5 |
| VES 8 | 4.52 × 10−6 | 1.73 × 10−5 | 1464.13 | 0.68 | 6.50 × 10−3 | 6500 | 4.01 × 10−6 | 4.32 × 10−6 | 7.11 × 10−6 | 2.14 × 10−5 | 2.94 × 10−5 | 3.25 × 10−5 |
| VES 9 | 2.71 × 10−6 | 1.05 × 10−5 | 378.79 | 5.02 | 2.63 × 10−3 | 9500 | 3.35 × 10−6 | 2.10 × 10−6 | 3.91 × 10−6 | 1.96 × 10−5 | 1.36 × 10−5 | 1.31 × 10−5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Almeida, A.; Maciel, D.F.; Sousa, K.F.; Nascimento, C.T.C.; Koide, S. Vertical Electrical Sounding (VES) for Estimation of Hydraulic Parameters in the Porous Aquifer. Water 2021, 13, 170. https://doi.org/10.3390/w13020170
de Almeida A, Maciel DF, Sousa KF, Nascimento CTC, Koide S. Vertical Electrical Sounding (VES) for Estimation of Hydraulic Parameters in the Porous Aquifer. Water. 2021; 13(2):170. https://doi.org/10.3390/w13020170
Chicago/Turabian Stylede Almeida, Andreia, Daiane Ferreira Maciel, Karen Félix Sousa, Carlos Tadeu Carvalho Nascimento, and Sérgio Koide. 2021. "Vertical Electrical Sounding (VES) for Estimation of Hydraulic Parameters in the Porous Aquifer" Water 13, no. 2: 170. https://doi.org/10.3390/w13020170
APA Stylede Almeida, A., Maciel, D. F., Sousa, K. F., Nascimento, C. T. C., & Koide, S. (2021). Vertical Electrical Sounding (VES) for Estimation of Hydraulic Parameters in the Porous Aquifer. Water, 13(2), 170. https://doi.org/10.3390/w13020170





