Theoretical Investigation of the Adsorption of Cadmium Iodide from Water Using Polyaniline Polymer Filled with TiO2 and ZnO Nanoparticles
Abstract
:1. Introduction
2. Materials and Methods
2.1. Computational Methods
2.1.1. VdW Interactions between Two Flat Surfaces across Air
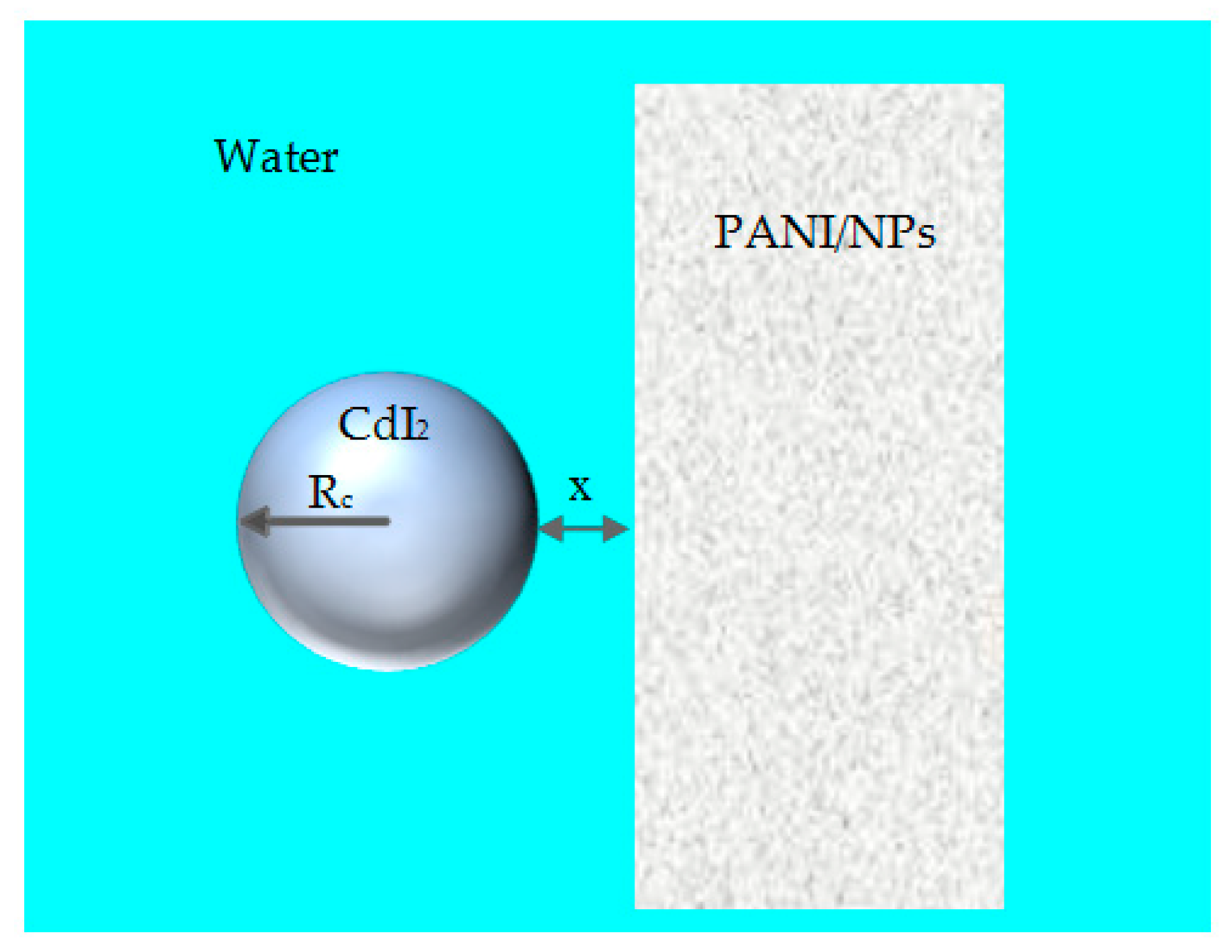
2.1.2. Van der Waals Interactions between Spherical Particle and Flat Surface across Water
2.1.3. Method for Calculation of the Hamaker Constant
2.1.4. Model for Calculation the Dielectric Constant of Nanocomposites
2.1.5. Models for Calculation of the Refractive Index
2.2. Materials
3. Results and Discussion
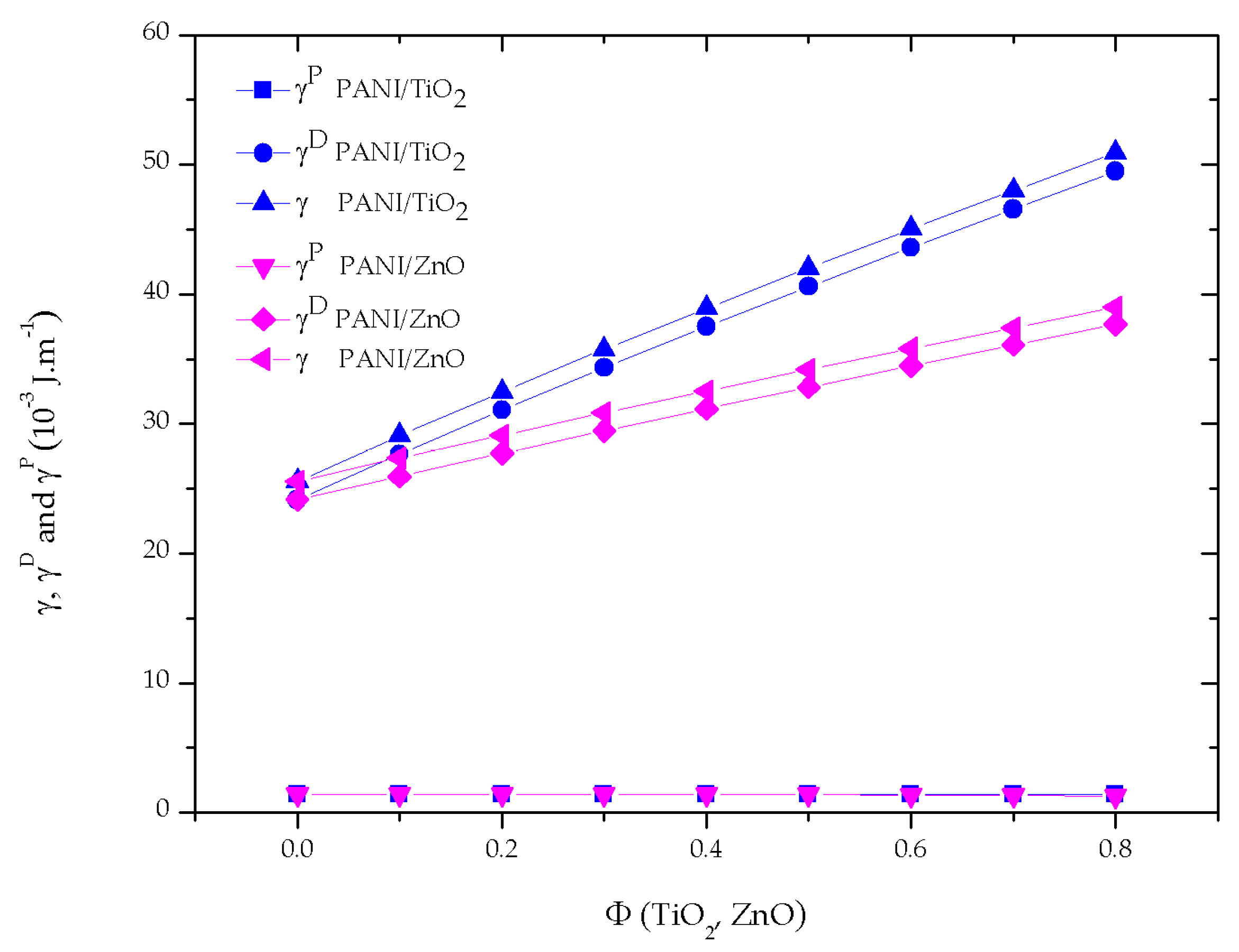
3.1. Dielectric Permittivity and Refractive Index of PANI/NPs: Effect of NPs Type and Rate
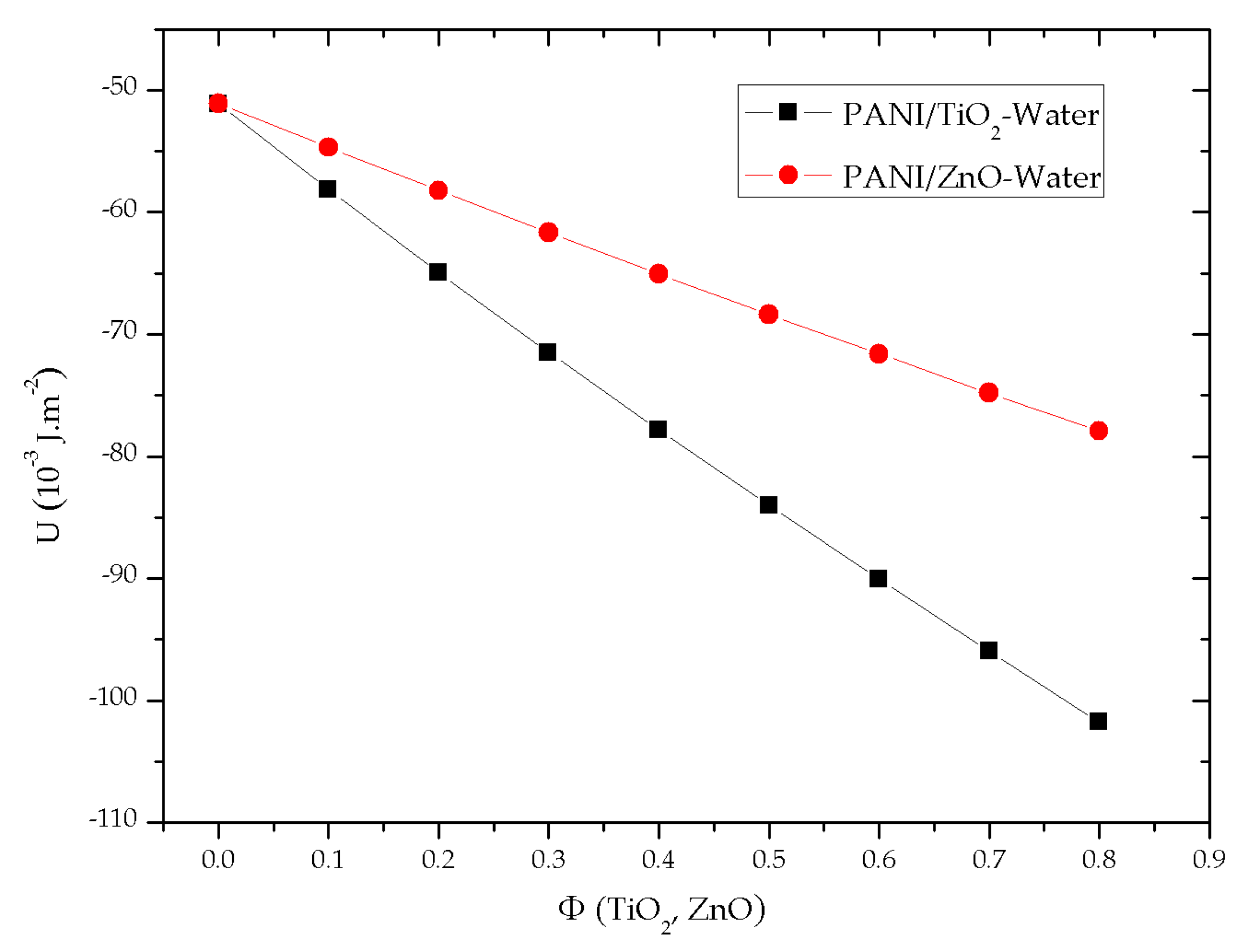
3.2. VdW Interaction between PANI/NPs and Water across Air
3.3. Interaction between Spherical CdI2 Particle Waste and Surface of PANI/NPs across Water
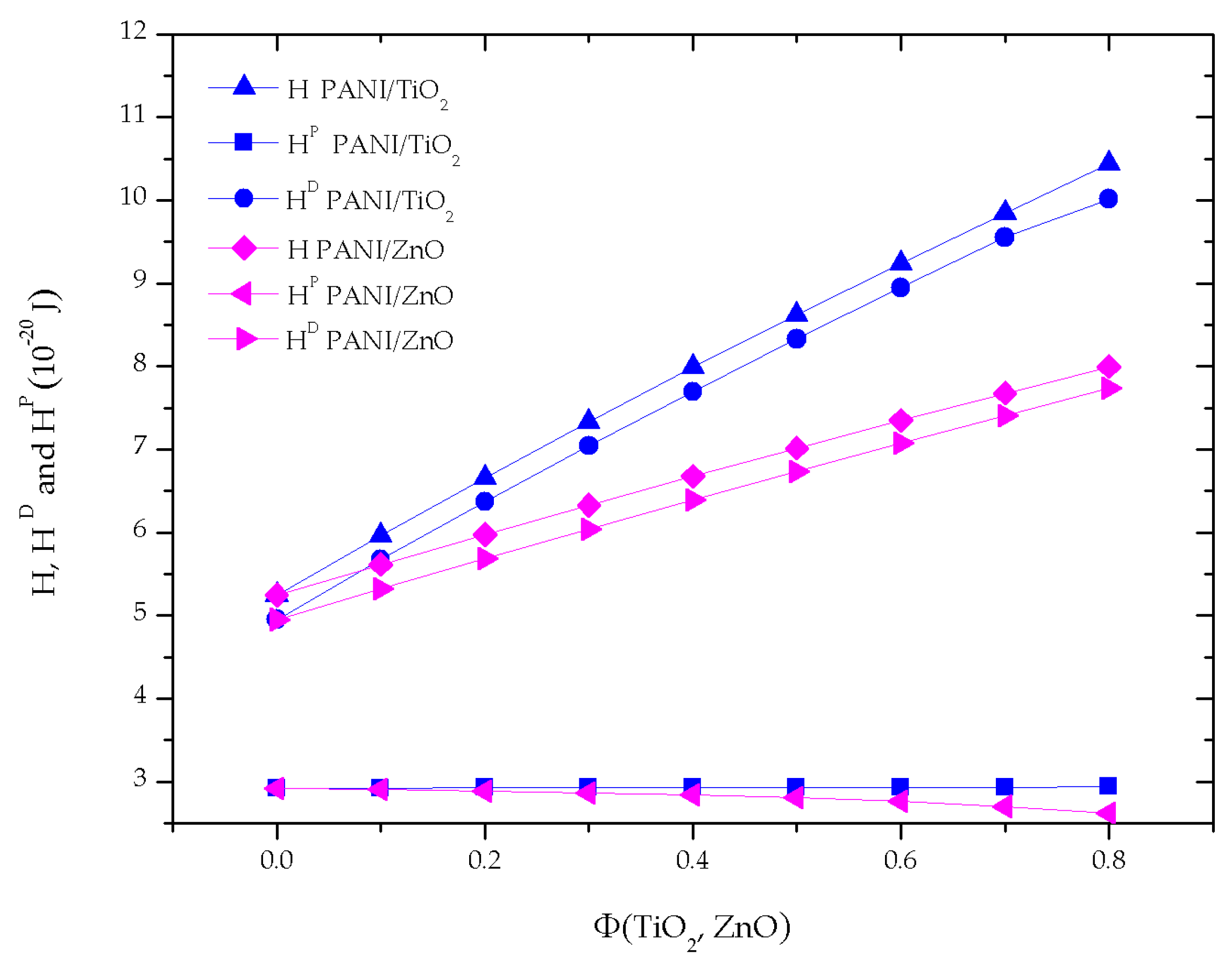
3.3.1. The Nonretarded Hamaker Constants Behavior
3.3.2. VdW Energy
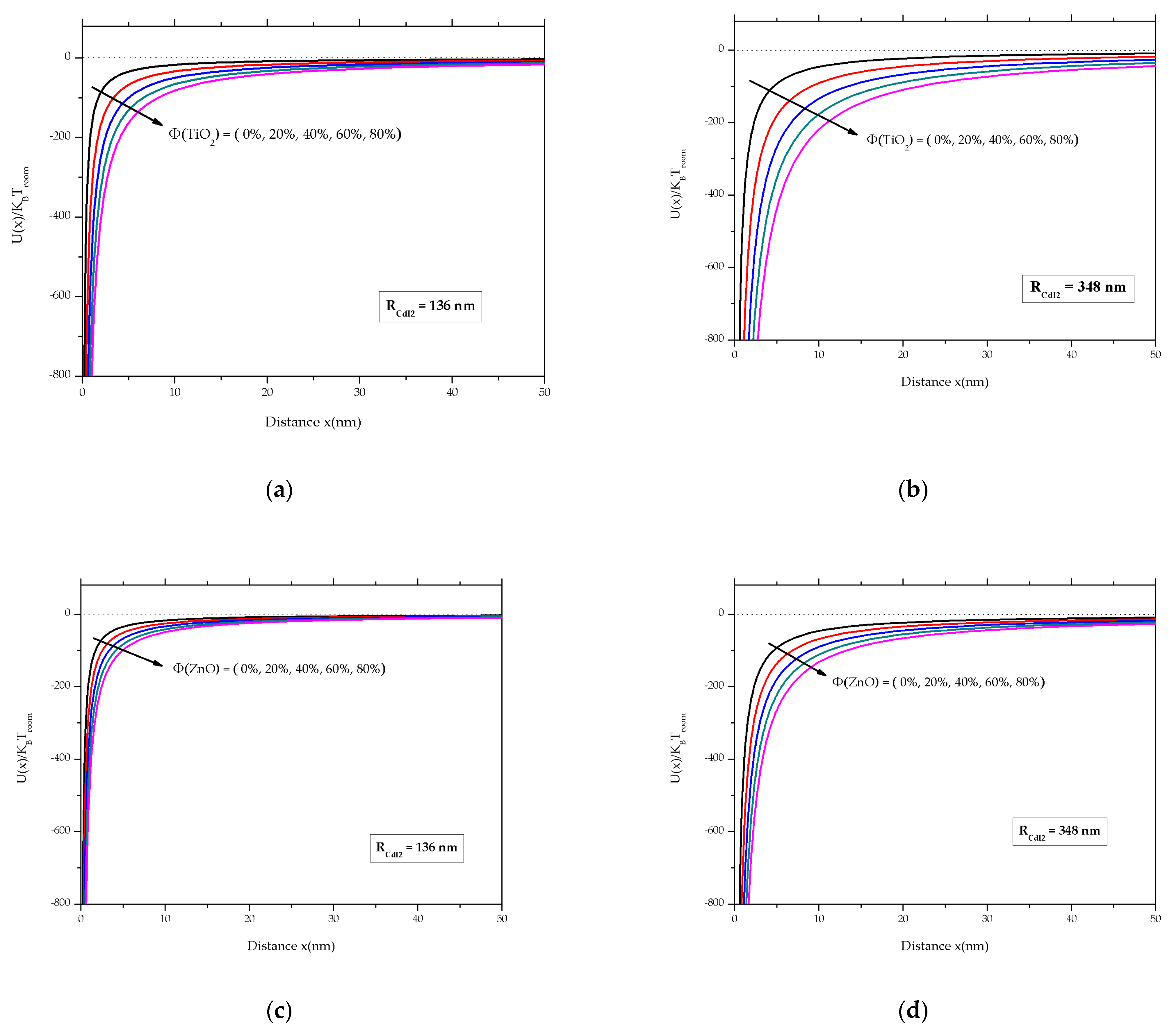
3.3.3. VdW Force–Distance Curves
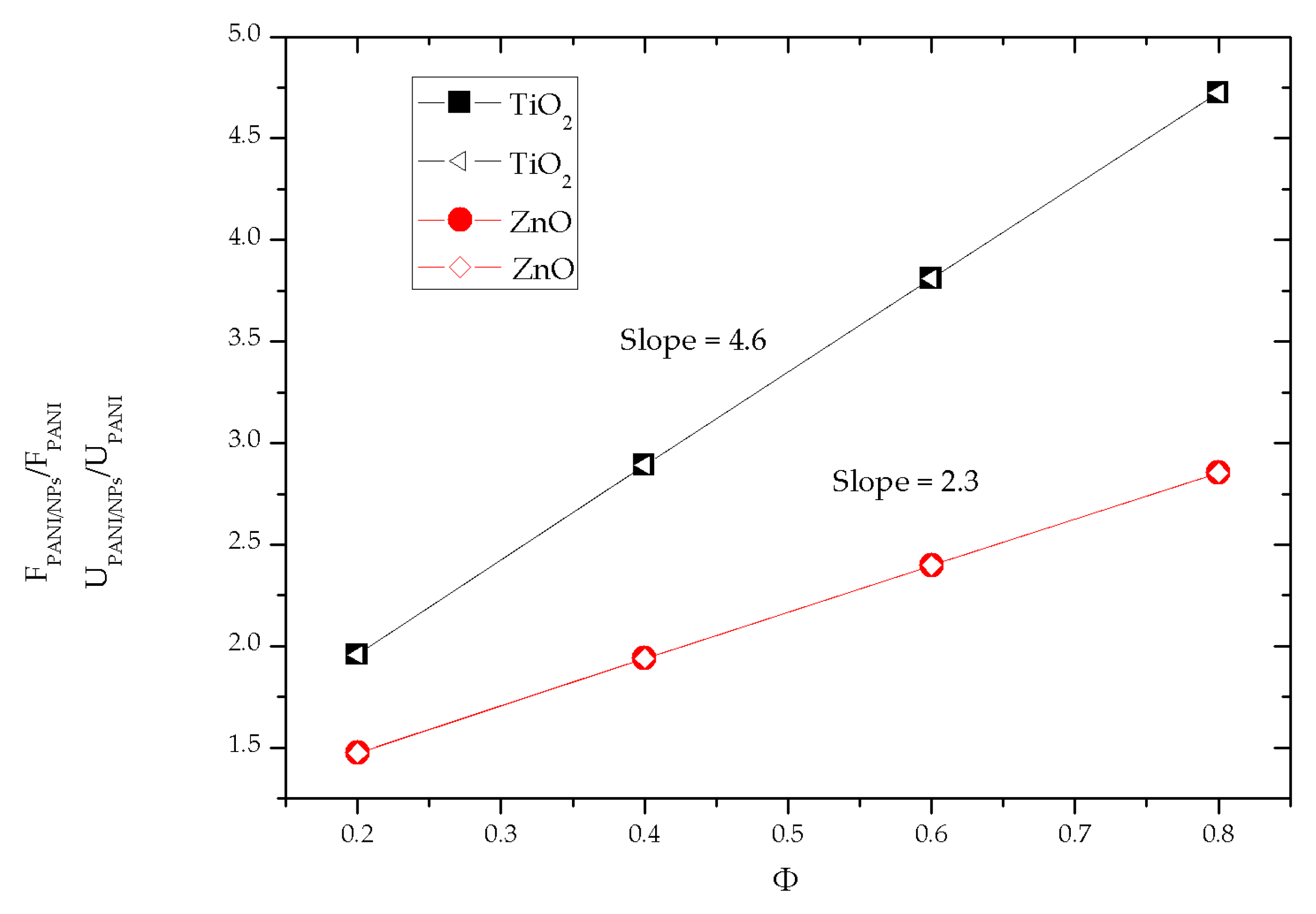
3.3.4. Effect of the Nanoparticle Type
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Galushkin, N.E.; Yazvinskaya, N.N.; Galushkin, D.N. Nickel-cadmium batteries with pocket electrodes as hydrogen energy storage units of high-capacity. J. Energy Storage 2021, 39, 102597. [Google Scholar] [CrossRef]
- Badawi, A.; Al-Gurashi, W.; Al-Baradi, A.M.; Al-Hosiny, N. Alloying cadmium cobalt sulfide quantum dots for solar cells applications. Mater. Sci. Semicond. Process. 2019, 95, 1–6. [Google Scholar] [CrossRef]
- Lohitha, B.; Thanikaikarasan, S.; Marjorie, S.R. Structural and optical properties of electroplated Cadmium Sulphide thin films. Mater. Today Proc. 2020, 33 Pt 7, 3405–3408. [Google Scholar] [CrossRef]
- Shah, D.K.; Devendra, C.K.; Muddassir, M.; Akhtar, M.S.; Kim, C.Y.; Yang, O.B. A simulation approach for investigating the performances of cadmium telluride solar cells using doping concentrations, carrier lifetimes, thickness of layers, and band gaps. Sol. Energy 2021, 216, 259–265. [Google Scholar] [CrossRef]
- Liu, H.; Liu, K.; Fu, H.; Ji, R.; Qu, X. Sunlight mediated cadmium release from colored microplastics containing cadmium pigment in aqueous phase. Environ. Pollut. 2020, 263 Pt A, 114484. [Google Scholar] [CrossRef]
- Gupta, T.; Agarwal, A.K.; Agarwal, R.A.; Labhsetwar, N.K. Environmental Contaminants: Measurement, Modelling and Control; Energy, Environment, and Sustainability Series; Springer: Singapore, 2018; 322p, ISBN 13: 9789811073328. [Google Scholar]
- Han, Y. Advances in Energy and Environmental Materials; Springer Proceedings in Energy Series; Springer: Singapore, 2018; p. 760. [Google Scholar] [CrossRef]
- Asrari, E. Heavy Metal Contamination of Water and Soil: Analysis, Assessment, and Remediation Strategies, 1st ed.; Apple Academic Press: New York, NY, USA, 2014; pp. 1–129. [Google Scholar] [CrossRef]
- Ojo, A.A.; Dharmadasa, I.M. Electroplating of Semiconductor Materials for Applications in Large Area Electronics: A Review. Coatings 2018, 8, 262. [Google Scholar] [CrossRef] [Green Version]
- Chaure, N.; Samantilleke, A.P.; Dharmadasa, I. The effects of inclusion of iodine in CdTe thin films on material properties and solar cell performance. Sol. Energy Mater. Sol. Cells 2003, 77, 303–317. [Google Scholar] [CrossRef]
- Yahia, I.; Shapaan, M.; Ismail, Y.A.; Aboraia, A.; Shaaban, E. Thickness dependence of structural and optical properties of cadmium iodide thin films. J. Alloys Compd. 2015, 636, 317–322. [Google Scholar] [CrossRef]
- Paterson, R.; Anderson, J.; Anderson, S.S.; Lutfullah. Transport in aqueous solutions of group IIB metal salts (298.15 K). Part 3.—Isotopic diffusion coefficients for cadmium-115 ions in aqueous cadmium iodide. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1978, 74, 93–102. [Google Scholar] [CrossRef]
- Paterson, R.; Devine, C. Transport in aqueous solutions of group IIB metal salts. Part 7—Measurement and prediction of isotopic diffusion coefficients for iodide in solutions of cadmium iodide. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1980, 76, 1052–1061. [Google Scholar] [CrossRef]
- Saini, S.; Dhania, G. Cadmium as an Environmental Pollutant: Ecotoxicological Effects, Health Hazards, and Bioremediation Approaches for Its Detoxification from Contaminated Sites. In Bioremediation of Industrial Waste for Environmental Safety; Bharagava, R., Saxena, G., Eds.; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- WHO. Guidelines for Drinking-Water Quality, 4th ed.; Library Cataloguing-in-Publication Data; World Health Organization (WHO): Geneva, Switzerland, 2011; 180p, ISBN 978 92 4 154815 1. [Google Scholar]
- Shrestha, R.; Ban, S.; Devkota, S.; Sharma, S.; Joshi, R.; Tiwari, A.P.; Joshi, M.K. Technological trends in heavy metals removal from industrial wastewater: A review. J. Environ. Chem. Eng. 2021, 9, 105688. [Google Scholar] [CrossRef]
- O’Melia, C.R. Interface Science in Drinking Water Treatment Theory and Application: Chapter 18—Fundamentals of particle Stability. In Interface Science and Technology; Newcombe, G., Dixon, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2006; Volume 10, pp. 317–362. [Google Scholar] [CrossRef]
- Barakat, M.A. New trends in removing heavy metals from industrial wastewater. Arab. J. Chem. 2011, 4, 361–377. [Google Scholar] [CrossRef] [Green Version]
- Nasar, A.; Mashkoor, F. Application of polyaniline-based adsorbents for dye removal from water and wastewater—A review. Environ. Sci. Pollut. Res. 2019, 26, 5333–5356. [Google Scholar] [CrossRef]
- Prabhakar, P.K.; Raj, S.; Anuradha, P.; Sawant, S.N.; Doble, M. Biocompatibility studies on polyaniline and polyaniline–silver nanoparticle coated polyurethane composite. Colloids Surfaces B Biointerfaces 2011, 86, 146–153. [Google Scholar] [CrossRef] [PubMed]
- Prabhu, R.; Jeevananda, T.; Reddy, K.R.; Raghu, A.V. Polyaniline-fly ash nanocomposites synthesized via emulsion polymerization: Physicochemical, thermal and dielectric properties. Mater. Sci. Energy Technol. 2021, 4, 107–112. [Google Scholar] [CrossRef]
- Singh, S.; Perween, S.; Ranjan, A. Dramatic enhancement in adsorption of congo red dye in polymer-nanoparticle composite of polyaniline-zinc titanate. J. Environ. Chem. Eng. 2021, 9, 105149. [Google Scholar] [CrossRef]
- Minisy, I.M.; Salahuddin, N.A.; Ayad, M.M. Adsorption of methylene blue onto chitosan–montmorillonite/polyaniline nanocomposite. Appl. Clay Sci. 2021, 203, 105993. [Google Scholar] [CrossRef]
- Beygisangchin, M.; Abdul Rashid, S.; Shafie, S.; Sadrolhosseini, A.R.; Lim, H.N. Preparations, Properties, and Applications of Polyaniline and Polyaniline Thin Films—A Review. Polymers 2021, 13, 2003. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, M.; Dou, C.; Ma, G.; Wang, Y.; Feng, N.; Wang, W.; Fang, L. Synthesis and biocompatibility assessment of polyaniline nanomaterials. J. Bioact. Compat. Polym. 2019, 34, 16–24. [Google Scholar] [CrossRef]
- Perumal, A.; Kannan, S.; Nallaiyan, R. Silver nanoparticles incorporated polyaniline on TiO2 nanotube arrays: A nanocomposite platform to enhance the biocompatibility and antibiofilm. Surfaces Interfaces 2021, 22, 1–13. [Google Scholar] [CrossRef]
- Maruthapandi, M.; Saravanan, A.; Manohar, P.; Luong, J.H.T.; Gedanken, A. Photocatalytic Degradation of Organic Dyes and Antimicrobial Activities by Polyaniline–Nitrogen-Doped Carbon Dot Nanocomposite. Nanomaterials 2021, 11, 1128. [Google Scholar] [CrossRef]
- Zhu, J.; Chen, J.; Zhuang, P.; Zhang, Y.; Wang, Y.; Tan, H.; Feng, J.; Yan, W. Efficient adsorption of trace formaldehyde by polyaniline/TiO2 composite at room temperature and mechanism investigation. Atmos. Pollut. Res. 2021, 12, 1–11. [Google Scholar] [CrossRef]
- Khong, C.H.; Teh, G.B.; Phang, S.W. Effect of Titanium Dioxide and Carbon Nanotubes on Polyaniline Nanocomposites for Heavy Metals Removal. In POLYCHAR 25—World Forum on Advanced Materials; De Gruyter: Berlin, Germany, 2018; Volume 382, pp. 1–8. [Google Scholar] [CrossRef]
- Anjum, M.; Miandad, R.; Waqas, M.; Gehany, F.; Barakat, M. Remediation of wastewater using various nano-materials. Arab. J. Chem. 2019, 12, 4897–4919. [Google Scholar] [CrossRef] [Green Version]
- Azizi-Lalabadi, M.; Ehsani, A.; Divband, B.; Alizadeh-Sani, M. Antimicrobial activity of Titanium dioxide and Zinc oxide nanoparticles supported in 4A zeolite and evaluation the morphological characteristic. Sci. Rep. 2019, 9, 17439. [Google Scholar] [CrossRef] [Green Version]
- Parrino, F.; Palmisano, L. Titanium Dioxide (TiO2) and Its Applications, 1st ed.; Elsevier: Cambridge, MA, USA, 2021; pp. 13–666. [Google Scholar] [CrossRef]
- Fosso-Kankeu, E. Nano and Bio-Based Technologies for Wastewater Treatment: Prediction and Control Tools for the Dispersion of Pollutants in the Environment, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA; Beverly, NJ, USA, 2019; pp. 147–330. [Google Scholar] [CrossRef]
- Sato, N.; Aoyama, Y.; Yamanaka, J.; Toyotama, A.; Okuzono, T. Particle Adsorption on Hydrogel Surfaces in Aqueous Media due to van der Waals Attraction. Sci. Rep. 2017, 7, 6099. [Google Scholar] [CrossRef] [Green Version]
- Leite, F.L.; Bueno, C.C.; Da Róz, A.L.; Ziemath, E.C.; Oliveira, O.N., Jr. Theoretical Models for Surface Forces and Adhesion and Their Measurement Using Atomic Force Microscopy. Int. J. Mol. Sci. 2012, 13, 12773–12856. [Google Scholar] [CrossRef] [PubMed]
- Király, Z.; Turi, L.; Dékány, I.; Bean, K.; Vincent, B. Van der Waals attraction between Stöber silica particles in a binary solvent system. Colloid Polym. Sci. 1996, 274, 779–787. [Google Scholar] [CrossRef]
- Tolias, P. Lifshitz calculations of Hamaker constants for fusion relevant materials. Fusion Eng. Des. 2018, 133, 110–116. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Elsevier Inc.: Amsterdam, The Netherlands; Academic Press: Burlington, NJ, USA, 2011; ISBN 978-0-12-375182-9. [Google Scholar]
- Hamaker, H.C. The London-Van der waals attraction between spherical particles. Physica 1937, 4, 1058–1070. [Google Scholar] [CrossRef]
- London, F. The general theory of molecular forces. Trans. Faraday Soc. 1937, 33, 8–26. [Google Scholar] [CrossRef]
- Keesom, W.H. The cohesion forces in the theory of Van Der Waals. Phys. Z. 1921, 22, 129–141. [Google Scholar]
- Debye, P. Molecular forces and their electric explanation. Phys. Z. 1921, 22, 302–308. [Google Scholar]
- Lipkin, D.M.; Israelachvili, J.N.; Clarke, D.R. Estimating the metal-ceramic van der Waals adhesion energy. Philos. Mag. A 1997, 76, 715–728. [Google Scholar] [CrossRef]
- Karkkainen, K.K.; Sihvola, A.H.; Nikoskinen, K.I. Effective Permittivity of Mixtures: Numerical Validation by the FDTD Method. IEEE Trans. Geosci. Remote Sens. 2000, 38, 1303–1308. [Google Scholar] [CrossRef] [Green Version]
- Garnett, J.C.M. VII—Colours in Metal Glasses, in Metallic Films, and in Metallic Solutions–II; Series A Containing Papers of a Mathematical or Physical Character. Philos. Trans. Royal Soc. Lond. 1906, 205, 237–288. [Google Scholar]
- Saravanan, S.; Mathai, C.J.; Anantharaman, M.R.; Venkatachalam, S.; Prabhakaran, P.V. Investigations on the electrical and structural properties of polyaniline doped with camphor sulphonic acid. J. Phys. Chem. Solids 2006, 67, 1496–1501. [Google Scholar] [CrossRef]
- Dang, M.; Yongyao, L.; Kecheng, G.; Guiping, Z.; Renkuan, Y. Ellipsometric Spectra and Refractive Index of Polyaniline. Chin. Phys. Lett. 1993, 10374, 374–376. Available online: http://iopscience.iop.org/0256-307X/10/6/016 (accessed on 17 September 2021).
- Manke, F.; Frost, J.M.; Vaissier, V.; Nelson, J.; Barnes, P.R.F. Influence of a nearby substrate on the reorganization energy of hole exchange between dye molecules. Phys. Chem. Chem. Phys. 2015, 17, 7345–7354. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fernández, D.P.; Mulev, Y.; Goodwin, A.R.H.; Sengers, J.M.H.L. A Database for the Static Dielectric Constant of Water and Steam. J. Phys. Chem. Ref. Data 1995, 24, 33–70. [Google Scholar] [CrossRef]
- Al-Ghamdi, A.; Al-Saigh, Z.Y. Surface and thermodynamic characterization of conducting polymers by inverse gas chromatography: I. Polyaniline. J. Chromatogr. A 2002, 969, 229–243. [Google Scholar] [CrossRef]
- Govindaraj, Y.; Parida, S. Autogenous chemical and structural transition and the wettability of electropolymerized PANI surface. Appl. Surf. Sci. 2019, 481, 174–183. [Google Scholar] [CrossRef]
- Owens, D.K. Some thermodynamic aspects of polymer adhesion. J. Appl. Polym. Sci. 1970, 14, 1725–1730. [Google Scholar] [CrossRef]





| Material | Dielectric Constant at 1 MHz | Refractive Index at 600 nm |
|---|---|---|
| PANI | 68 [46] | 1.51 [47] |
| TiO2 (anatase) [48] | 86 | 2.6 |
| ZnO [48] | 8.5 | 2 |
| Water [49] | 78.4 | 1.33 |
| CdI2 (R = 348 nm) [11] | - | 2.145 |
| CdI2 (R = 136 nm) [11] | - | 2.1 |
| Φ | PANI/TiO2 | PANI/ZnO | ||
|---|---|---|---|---|
| ε | n | ε | n | |
| 0 | 68 | 1.51 | 68 | 1.51 |
| 0.2 | 71.3765 | 1.69352 | 49.5720 | 1.60203 |
| 0.4 | 74.8631 | 1.88852 | 34.8160 | 1.69644 |
| 0.6 | 78.4613 | 2.10002 | 23.3240 | 1.79379 |
| 0.8 | 82.1730 | 2.33429 | 14.6880 | 1.89476 |
| Φ (TiO2) | Rc = 348 nm | Rc = 136 nm | ||||
|---|---|---|---|---|---|---|
| HP (10−20J) | HD (10−20J) | H (10−20J) | HP (10−20J) | HD (10−20J) | H (10−20J) | |
| 0 | −0.02193 | 3.3126 | 3.14127 | −0.02193 | 3.1632 | 3.14127 |
| 0.2 | −0.01477 | 6.4547 | 4.62695 | −0.01477 | 6.1619 | 6.14713 |
| 0.4 | −0.00712 | 9.5229 | 6.08885 | −0.00712 | 9.0885 | 9.08138 |
| 0.6 | 0.00024 | 12.545 | 7,53285 | 0.00024 | 11.969 | 11.96924 |
| 0.8 | 0.00725 | 15.549 | 8.9665 | 0.00725 | 14.83 | 14.83725 |
| Φ (ZnO) | R (CdI2) = 348 nm | R (CdI2) = 136 nm | ||||
|---|---|---|---|---|---|---|
| HP (10−20J) | HD (10−20J) | H (10−20J) | HP (10−20J) | HD (10−20J) | H (10−20J) | |
| 0 | −0.02193 | 3.3126 | 3.29067 | −0.02193 | 3.1632 | 3.14127 |
| 0.2 | −0.069547 | 4.9191 | 4.84955 | −0.06954 | 4.6965 | 4.62695 |
| 0.4 | −0.11885 | 6.5027 | 6.38385 | −0.11885 | 6.2077 | 6.08885 |
| 0.6 | −0.16715 | 8.0670 | 7.89985 | −0.16715 | 7.7000 | 7.53285 |
| 0.8 | −0.21130 | 9.6165 | 9.4052 | −0.21130 | 9.1778 | 8.9665 |
| Material | Intercept a | Standard Error | Slope b | Standard Error |
|---|---|---|---|---|
| PANI/TiO2 | 1.040 | 0.00928 | 4.609 | 0.01694 |
| PANI/ZnO | 1.014 | 0.00392 | 2.302 | 0.00716 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahdhi, N.; Alsaiari, N.S.; Alzahrani, F.M.; Katubi, K.M.; Amari, A.; Hammami, S. Theoretical Investigation of the Adsorption of Cadmium Iodide from Water Using Polyaniline Polymer Filled with TiO2 and ZnO Nanoparticles. Water 2021, 13, 2591. https://doi.org/10.3390/w13182591
Mahdhi N, Alsaiari NS, Alzahrani FM, Katubi KM, Amari A, Hammami S. Theoretical Investigation of the Adsorption of Cadmium Iodide from Water Using Polyaniline Polymer Filled with TiO2 and ZnO Nanoparticles. Water. 2021; 13(18):2591. https://doi.org/10.3390/w13182591
Chicago/Turabian StyleMahdhi, Noureddine, Norah Salem Alsaiari, Fatimah Mohammed Alzahrani, Khadijah Mohammedsaleh Katubi, Abdelfattah Amari, and Saber Hammami. 2021. "Theoretical Investigation of the Adsorption of Cadmium Iodide from Water Using Polyaniline Polymer Filled with TiO2 and ZnO Nanoparticles" Water 13, no. 18: 2591. https://doi.org/10.3390/w13182591
APA StyleMahdhi, N., Alsaiari, N. S., Alzahrani, F. M., Katubi, K. M., Amari, A., & Hammami, S. (2021). Theoretical Investigation of the Adsorption of Cadmium Iodide from Water Using Polyaniline Polymer Filled with TiO2 and ZnO Nanoparticles. Water, 13(18), 2591. https://doi.org/10.3390/w13182591







