Abstract
In this work, two machine learning techniques, specifically decision trees (DTs) and support vector machines (SVMs), were applied to optimize the performance of a seawater reverse osmosis (SWRO) desalination plant with a capacity of 100 m3 per day. The input variables to the system were seawater pH, seawater conductivity, and three requirements: permeate flow rate, permeate conductivity, and total energy consumed by the desalination plant. These requirements were decided based on a cost function that prioritizes the water needs in a vessel and the maximum possible energy savings. The intelligent system modifies the actuators of the plant: feed flow rate control and high-pressure pump (HPP) operating pressure. This tool is proposed for the optimal use of desalination plants in marine vessels. Although both machine learning techniques output satisfactory results, it was concluded that the DTs technique (HPP pressure: root mean square error (RMSE) = 0.0104; feed flow rate: RMSE = 0.0196) is more accurate than SVMs (HPP pressure: RMSE = 0.0918; feed flow rate: RMSE = 0.0198) based on the metrics used. The final objective of the paper is to extrapolate the implementation of this smart system to other shipboard desalination plants and optimize their performance.
1. Introduction
Apart from energy, one of the pressing needs in a marine vessel is the water supply [1]. There are two main ways to obtain fresh water on the high seas: producing water through seawater desalination, and water bunkering in ports. Related to the first solution, certain variables have to be identified to operate a desalination plant in a way that provides the needs of a ship. The quality and quantity of daily water are important requirements to supply the needs of the crew and passengers of a marine vessel. However, the amount of energy consumed by a possible on-board desalination plant is an important and essential consideration as far as ships are concerned.
Regarding the quality of the water used in marine vessels, the World Health Organization’s (WHO) Guidelines for drinking-water quality (GDWQ) [2] have been followed. Another report also carried out by the WHO [3] makes clear the difference between countries of regulations and standards for drinking-water quality. In the GDWQ, regulations regarding inorganic, organic, radiological, microbiological aspects, etc., are studied. In this article, only the conductivity of the water obtained after desalination is controlled, which is directly related to total dissolved solids (TDS). The palatability of water with a TDS level of less than about 600 mg/L (938 µS/cm) is generally considered good. This is a reference value, as the WHO highlights that no health-based guideline value has been proposed for TDS. Concerning this, there is no international standard value, simply recommendations made by the organization.
In this case study, the desalination plant could be used both on land and on a ship. In particular, ships are isolated systems, where energy input and storage capacity are more limited than on land. One of the main reasons is that the stowage of the water tanks increases the weight and decreases the storage capacity.
Different investigations have studied the amount of water used on cruise ships. For example, a study carried out in Spain reports how each base port cruise recharged an average volume of 628 m3 per berth [4]. Another study says that the average consumption of drinking water on cruise ships is more than 984 m3 per day [1]. As can be seen, this depends on the number of passengers, size of the ship, etc. Therefore, this research is a useful tool to improve the control systems of desalination plants and save as much energy as possible.
On the other hand, this study opted for a reduced-size configuration of a desalination plant within a 20 ft shipping container, so that it could be integrated into the superstructure of a ship and at the same time allow its transfer to other ships without great effort.
Energy efficiency has been studied within the Water–Energy Nexus on many occasions in the last decades [5,6]. Ships always have significant restrictions regarding energy consumption, especially approached by the scientific community with the aim of introducing renewable energy into maritime transport. This is an essential objective for sustainability in the sector [7] since these energy sources have been deeply developed in other fields [8].
Artificial intelligence (AI) [9,10,11] is an important element in Industry 4.0 since it can offer higher quality in the control of plants, increasing their productivity, minimizing human errors, optimizing operation and production costs, and improving the general efficiency of the system [12]. Within the field of AI, both machine learning (ML) and deep learning (DL) techniques [13] have been developed to improve different stages in seawater treatment systems.
According to a recent study based on a search in the Google Scholar database, the number of publications with the keywords “desalination” and “artificial intelligence” for predicting, automating, controlling, and improving desalination performance [14] has increased notably in recent years.
Pohl et al. [15] proposed different control approaches for desalination plants. In our case, among the various alternative control strategies shown by these authors, a control strategy was chosen by varying the high-pressure pump operating pressure using a controller based on machine learning techniques. Note that the daily amount of water, the permeate conductivity, and the total energy consumption were the controlled output variables in this case.
On the other hand, it is important to note that the approach used is based on data-driven learning. Hence, the results obtained are strongly linked to the characteristics of this case.
It is important to note that phenomenological transport models are widely used in the scientific community. However, different authors (named below) have also opted for approaches based on AI techniques with good results. It should be noted that, in this work, the objective was focused on controlling the desalination plant in a stationary regime according to the different requirements of a particular desalination plant.
In this research, the application of AI techniques based on data-driven learning has been chosen, instead of using these models. AI techniques allow obtaining a control system based on an optimization process with acceptable efficiency, although other techniques could give more detailed models that contribute to a better understanding of physical processes. In fact, they could work in combination with AI techniques to provide other control architectures. The following paragraphs summarize some studies conducted with different AI techniques. This bibliographic study supports the innovation of this research.
Since the initial research [16], most of the studies conducted to improve desalination systems through AI, such as [17,18,19,20,21], have relied on the artificial neural networks (ANNs) method.
Pedro Cabrera et al. [22] concluded that in reverse osmosis (RO) desalination plants, artificial neural network-based algorithms have been widely used to simulate and/or predict the performance of plants when the operating parameters were altered. They carried out a study where three techniques were applied to predict the performance of a plant, with results that confirmed the improvement of support vector machines and random forests (RFs) over ANNs.
Another study developed a data-driven reverse osmosis plant performance model using support vector regression (SVR) with both steady and unsteady state operation [23]. Single output variable steady-state plant models for flow rates and conductivities of the permeate and retentate streams were highly accurate and suggested that short-term performance forecasting models based on plant data could be useful for advanced RO plant control algorithms with fault-tolerant control and process optimization.
Some of the disadvantages that ANNs exhibit are the need to specify the topology of the networks (number of nodes and layers), which slows down the process and complicates its implementation [14,24]. In contrast, one of the advantages of SVMs is that they avoid overfitting by controlling the number of support vectors [25].
After analyzing all these studies, in this work the focus was on the production of water on board a marine vessel. Therefore, it was essential to provide tools that allowed the operation of desalination plants with a detailed monitoring of the consumption foreseen for the specific needs of each process. Consequently, the main objective of this study was to propose an intelligent system that allows the optimal operation of an SWRO desalination plant. Various AI techniques have been studied to improve the control of certain output variables of desalination plants.
This work is novel since most of these techniques have been used in the context of land desalination plants. However, in the maritime sector, variables change to a greater extent as marine vessels move between different points where sea conditions continually change. Therefore, these techniques could contribute to improving the efficiency of desalination plants inside vessels. It is also important to highlight that the variables studied in this work play a key role in maritime transport, since, among other optimization objectives, the minimization of energy requirements and storage capacity are fundamental in the future of this sector.
This article is divided into four sections. The introduction (Section 1) describes the reasons that motivated the research. Subsequently, Section 2 is the most extensive in the work and explains in detail the process used to obtain the results. This section first describes the desalination plant, followed by an explanation of the table of optimal values, and then, of how the machine learning techniques were applied to the data. Section 3 and Section 4 of the article present the results obtained and the conclusions yielded by this work.
2. Materials and Methods
2.1. Description of the Equipment and Data Collection
This study was carried out using the operation data of a small-scale SWRO desalination pilot plant with a capacity of 80–100 m3/day. It is an industrial plant designed by the Canary Islands Institute of Technology (ITC) to be used in R&D projects within the DESAL + LIVING LAB platform. The plant is inside a 20 ft shipping container (Figure 1), which makes it enormously versatile in terms of its transport to warranty that could be moved to different locations for being fed with different seawater conditions. In terms of design and operationality, this plant should be similar to one on-board SWRO plant except for the high level of sensors installed and the possibility to move the nominal operation point, according to its research purposes. Some of its main characteristics are shown in Table 1.

Figure 1.
The 20 ft shipping container housing the SWRO desalination plant.

Table 1.
Main characteristics of the SWRO plant.
The plant has three possible configurations of high-pressure membrane vessels, from single element vessels to 2 + 5 or 7 in series element configurations. It allows us to operate the plant using different recovery rates and membrane configuration (Figure 2). Besides, other key element is plug and play technology which permits to test different devices in a simple and fast way.

Figure 2.
Interior view of the pilot plant used in the study.
The data used herein were taken at the plant described and provided by the ITC. Data were collected for 24 h at one-minute intervals. The 2 + 5 high-pressure vessel configuration was used for that with the Hydranautics SWC4 MAX membrane in service.
Finally, 1149 samples of different variables were obtained. These variables have been divided into two groups. The first one is determined by seawater conditions: seawater pH and conductivity. On the other hand, the second one corresponds to the rest of the variables. These variables modify their value depending on the variations in the desalination plant. They are feed flow rate, high-pressure pump operating pressure, permeate conductivity, permeate flow rate, and total energy consumption. Table 2 shows a sample of the data obtained. This table contains seven randomly decided rows that show a visual example of the entire database, which is 1149 pieces of data.

Table 2.
Sample of the data recorded during a 24 h measurement.
2.2. Table of Optimal Values and Application of Machine Learning Techniques
In the first part of the study, we obtained a table (based on established requirements and a cost function determined by the authors) with the optimal values of the variables mentioned earlier. This table resulted from three requirements regarding the feed flow rate, the permeate conductivity, and the total energy consumption of the desalination plant. After satisfying these requirements, a cost function was established to determine which of the three is most important.
In this case, the requirements chosen by the authors were intended to show an example that adapts to the conditions of the desalination plant used in the study. However, it should be noted that the final goal of the paper is to develop a smart system that can be extrapolated to other on-board desalination systems. The limits of the requirements and the cost function are explained in detail below.
- First requirement: the amount of water produced in 24 h (based on the need of a marine vessel). The amount of water produced was obtained from the permeate flow rate. For the authors, one of the main concerns was the amount of water available to the crew on a marine vessel.
- Second requirement: permeate conductivity. In this case, an affordable maximum was established, although this limit may vary for another case study. The maximum limit chosen was lower than the values recommended by the WHO’s GDWQ. Therefore, this water could be used for the consumption of the crew. If water was needed for other uses, this limit could be extended.
- Third requirement: total energy consumption of the plant. This was considered one of the most important aspects of this study and was focused on obtaining the maximum energy savings possible on the marine vessel.
The maximum and minimum limits of these requirements are detailed in Table 3. As explained previously, the values shown in this table are indicative. Therefore, they can vary depending on the needs of each maritime vessel.

Table 3.
Requirements applied to the initial dataset based on the needs of a marine vessel.
Once the variables were within the established range, a cost function was applied. This function is very simple, and its mission is the importance given in the system to each of the three requirements.
f(x) = 0.2 (daily amount of permeate water) + 0.3 (permeate conductivity) + 0.5 (total energy consumption)
In this case, different percentages were given for each requirement. The third one (total energy consumption) was considered a priority, since saving as much energy as possible is a fundamental concern in any marine vessel. In the case of the marine vessel used in the study, the highest importance was given to the energy consumption obtained in the desalination process, subsequently to the conductivity of the permeated water, and finally to the amount of water required.
The proportions of importance in the cost function are:
- Daily amount of permeate water: 20%;
- Permeate conductivity: 30%;
- Total energy consumption of the plant: 50%.
The methodology adopted in this work can be extrapolated to different marine vessels by modifying the proportions of the cost function. Another possibility could be to add new variables such as the temperature of the sea water, something that would be very useful in marine vessels because they are in continuous movement through the ocean.
Combining the requirements with the cost function yielded the table of optimal values. It had 828 samples for each variable (Table 4), meaning that those were the values that satisfied the specified requirements. It contains (like Table 3) seven rows that show a visual example of the entire database, which is 828 pieces of data.

Table 4.
Sample of the table of optimal values.
Once the table of optimal values was obtained, it was randomly divided into three groups of data. These were a training group (80% of the data), a validation group (10%), and a test group (10%). Note that the cross-validation method used the training data group and the validation group. It meant that a small data group (10%) was assuming the role of validation data through the training phase in an alternative way, while the test group (10%) was reserved for testing the model after completion of the training phase. It is important to note that the objective of the cross-validation technique was to obtain a result, which was independent of a particular choice of the distribution of the data in the different groups. Different machine learning models have been applied to this data group. Once the results were obtained, a verification was carried out with the test group to corroborate its reliability and ensure that these results were satisfactory.
In the second part of the work, the intelligent system that governs the operation of the plant was developed. In this case, a cascade system fed by the variables in the training and validation group were used (Figure 3). Two ML techniques were tested:
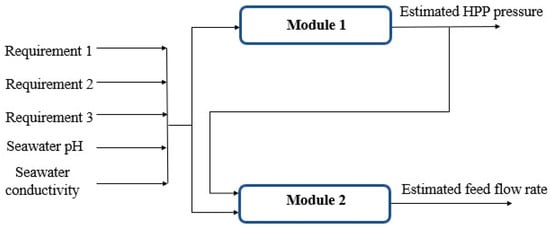
Figure 3.
Block diagram of the two first modules of the system, where ML techniques were applied.
- Support vector machines (regression), also known as support vector regression.
- Decision trees (regression), also known as regression trees.
Support vector machines are based on the idea of structural risk minimization (SRM) [26]. An SVM learns the decision surface from two distinct classes of input points. The support vector data description can form a decision boundary around the learned data domain with very little or no knowledge of data points outside the boundary. Utilizing a Gaussian kernel or another kind of kernel, these data points are mapped to a high dimensional feature space, where we search for the maximal separation between classes. This boundary function, when mapped back to the data space, can be separated into several components, each enclosing a separate cluster [27].
An SVM first maps the entry points to a feature space of a larger dimension, then finds a hyperplane that separates them and maximizes the margin “m” between classes in this space. Maximizing the margin “m” is a programming quadratic problem and can be solved by its dual problem by introducing Lagrange multipliers. Without any knowledge of the mapping, the SVM finds the optimal hyperplane using the dot product with functions in the feature space that are called kernels. The optimal hyperplane solution can be written as the combination of a few entry points that are called support vectors [27].
As explained in the first section of this article, in some applications, SVMs have been shown to perform better than other techniques such as ANNs [28] and were used to solve classification problems. In our case, SVMs were used in a regression problem.
Decision trees were the other technique used to solve this problem. DTs embody a supervised classification approach. The idea comes from the structure of an ordinary tree, made up of a root, nodes (the positions where places branches divide), branches, and leaves. Similarly, a decision tree is constructed from nodes that represent circles, and the branches are represented by the segments that connect the nodes. A decision tree starts from the root, moves downward, and is normally drawn from left to right. The node where the tree starts is called a root node. The node where the chain ends is known as the “leaf” node. Two or more branches can be extended from each internal node. A node represents a certain characteristic, while the branches represent a range of values. These ranges of values act as a partition point for the set of values of the given characteristic [29].
These two techniques were applied, compared, and analyzed to obtain models that improved the operation of the desalination plant. The two main actuators in any desalination plant are the feed flow rate control and the high-pressure pump operating pressure. For this reason, a cascade system was made, where the inputs to the system were the three requirements imposed, apart from seawater pH and conductivity (five input variables in total). From there, the AI techniques explained above were applied. The block diagram of the system is shown in Figure 3. It is a cascade system where the response variable of the first module (HPP operating pressure) is subsequently used as the input for the second module.
The cross-validation system, a data resampling method, was used to assess the generalization ability of the predictive models and to prevent overfitting [30,31]. Thanks to this method, we expect our model to be more generalizable [32]. In the chosen validation method, 10 folds were used in all cases. This number was decided by trial and error since the results were positive. Different subtypes of Regression Trees and SVMs were tested. Among them, the ones that yielded the best results were chosen.
Once the training was concluded in the first part, a new structure was designed to obtain the current values of the three requirement variables.
Note that modules 1 and 2 were used to train the system and to obtain the values for the plant’s actuators. In this case, these values, and the input variables used previously, were input to this new structure. This made it possible to obtain the current values of the daily amount of water, permeate conductivity, and total energy consumption of the desalination plant. This second system is shown in Figure 4, while the graphs and the results obtained from the training are given in the next section. It is important to point out that modules 3A, 3B, and 3C are also ML models trained using the values from the same table of optimal values (Table 4). In this case, the whole set of chosen output variables were different from the variables used in modules 1 and 2.
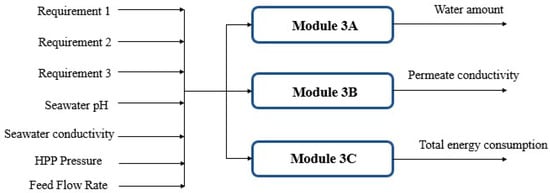
Figure 4.
Block diagram of modules 3A, 3B and 3C of the system.
3. Results and Discussion
The results obtained from comparing the two ML techniques are presented and discussed in this section to clarify which is the most appropriate to simulate the performance of the SWRO desalination plant.
The metrics used to quantify the errors in the models are standard metrics, such as the root mean square error (RMSE), mean absolute error (MAE), and coefficient of determination (R2) [32].
where n is the number of predictions, Y is the vector of observed values and is the vector of predicted values.
When choosing the metrics to analyze the results, we see that specially RMSE, but also MAE, have been widely used in the literature. However, there are several studies [33,34] that suggest that RMSE can be a misleading indicator of average error, which makes MAE a more natural measure of average error. Other references also demonstrate that RMSE performs better in some cases [35].
In light of this analysis, we decided to use a combination of the different metrics to obtain a more global vision of the model’s performance. Table 5 shows the errors using the different metrics mentioned before for each module that makes up the system. In this table, the best results (RMSE) obtained in the comparison between the two techniques are indicated in bold.

Table 5.
Comparison of results after the application of ML techniques.
The results reveal that the RMSE and R2 values obtained were satisfactory. The least accurate result obtained was for module 3B.
Subsequently, we can see in Figure 5 that the error obtained for modules 2 and 3C was very similar with both techniques. Note, however, the higher accuracy obtained in all three modules using the regression trees technique.
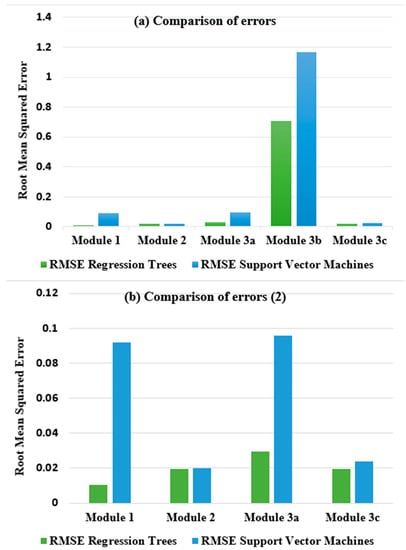
Figure 5.
(a) Errors according to the RMSE metric in the system’s five modules; (b) similar graph to the previous one, ignoring module 3B, to observe the error more clearly in the other modules.
Figure 6 shows the coefficient of determination in all five modules. In this case, the best results were obtained using DTs.
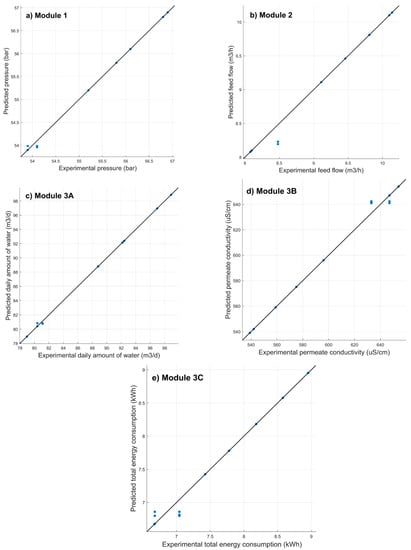
Figure 6.
Coefficients of determination of the modules. Note, as was identified in Table 5, that the correlation coefficients of the system modules had very satisfactory results.
The data that feed the modules were obtained from the training and validation group of data. Therefore, the training accuracy and generalization were subsequently checked with the remaining 10% of the data contained in the test group. The results are shown in Table 6. Note that the column “Maximum error” refers to the maximum difference between the system output and the real output. In this case, only the values of the models trained by regression trees are shown because these were the ones used in the work.

Table 6.
Error checking through the test group (remaining 10% of data).
The results in Table 6 show lower errors than those provided in Table 5, after training the system with the training and validation group of data. This confirms the correct operation of the developed model. In fact, the maximum errors are 2.77 × 10−13 Bar for the HPP operating pressure, 1.27 × 10−13 m3 for the amount of water, 6.82 × 10−13 µS/cm for permeate conductivity. That is, all errors are practically zero in the worst case. On the other hand, the worst-case errors are 0.67999 m3/h for feed flow and 0.00113 kWh for total energy consumption. These errors are acceptable since they are small values compared to the global values taken by these variables. These data show the goodness of the methods used.
As noted in previous paragraphs, we used in this case a training set of 80% of the data, a validation set of 10% of the data, and a test set of 10% of the data. To verify the performance of the method, new tests have been carried out, reducing the training set to 70% of the data. The generalization results using the new test dataset are shown in Table 7. As can be seen, the results are worse than in the previous case, given that a smaller training dataset has been used, although they are still satisfactory.

Table 7.
Error checking through the test group of data (remaining 20% of data).
Although the results of the generalization are worse than in the case shown in Table 6, the errors are still acceptable. They are small values compared to the global values taken by these variables.
At the end of the process, the “Smart System” function was created, which is similar to the modules used previously. This function is the final predictor developed in the study.
With this system, it is possible to optimize the operation of the desalination plant based on the initial requirements. These vary depending on each case study. The inputs to the function were the three requirements mentioned before, pH, and conductivity of the feed water. The function outputs the HPP operating pressure, the feed flow rate, and the actual values of the permeate conductivity, amount of water, and total energy consumption of the plant. This is shown in Figure 7.
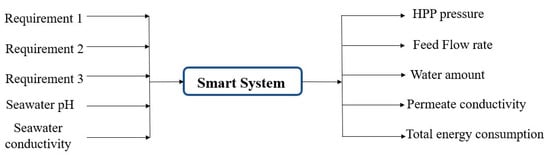
Figure 7.
Block diagram of the “Smart System” function.
Finally, Table 8 shows an example of the “Smart System” function. The three requirements and possible values for pH and seawater conductivity were entered in the input variables. It is observed that the intelligent system returns the values of the two actuators of the plant and an estimate of the permeate conductivity, amount of water, and total energy consumption of the plant. As has been commented previously, the values of the input variables can change depending on the needs of the system.

Table 8.
Sample of the “Smart System” function.
In this specific case, the marine vessel’s demands are a minimum of 75 m3 of water per day, a maximum conductivity of 600 µS/cm, and maximum energy consumption of the desalination plant of 9 kWh. For these initial data, the system was trained, and the results obtained were within the estimated parameters, so the results obtained were satisfactory.
Considering, as indicated before [1,4], that the average amount of water that is supplied to a typical cruise to ensure only the consumption of drinking water is much greater, it is important to remark that this case refers to a ship with a smaller number of passengers.
It is observed that Table 8 reveals how the smart system meets the requirements requested by the operator and indicates the HPP pressure and feed flow required to satisfy these values.
4. Conclusions
In this article, a table of optimal values was created, establishing different requirements and a cost function from the data for an SWRO desalination plant. Two machine learning techniques were applied to this table to determine the behavior of different variables. As we can see, the results achieved were satisfactory. Considering the values obtained, the regression trees techniques (HPP pressure: RMSE = 0.0104; feed flow rate: RMSE = 0.0196) yielded better results than support vector regression (HPP pressure: RMSE = 0.0918; feed flow rate: RMSE = 0.0198).
It is important to remark that the approach shown in this paper could be useful in the desalination world in general, and applications in marine vessels, especially, if the restrictions of the energy consumption inherent to small recreational vessels are considered. The system in question was designed to address three requirements of three key variables in marine transport. However, as was explained in previous sections, the idea of this study is to extrapolate it to other marine vessels with different characteristics and requirements.
Marine ships continually move through the ocean, changing seawater conditions (feed rate, temperature, conductivity, pH, etc.) to feed desalination plants. For these reasons, new techniques are necessary to improve its efficiency. It should be noted that the minimization of energy requirements and storage capacity are essential in the future of this sector, among other optimization processes with respect to the desalination process. Therefore, it is necessary to propose new methodologies to satisfy these objectives as far as possible.
The methodologies shown in this work contribute to improving desalination plants in this changing environment. As can be seen, the results obtained, shown in several tables of the article, present low errors in the prediction of the different variables of the plant.
Author Contributions
Conceptualization, J.C.-E. and G.N.M.P.; methodology, J.C.-E., G.N.M.P. and D.Á.P.; software, G.N.M.P. and J.C.-E.; validation, G.N.M.P.; formal analysis, G.N.M.P.; investigation, J.C.-E. and G.N.M.P.; resources, B.P.S.; data curation, B.P.S.; writing—original draft preparation, J.C.-E.; writing—review and editing, J.C.-E., D.Á.P. and G.N.M.P.; visualization, D.Á.P.; supervision, G.N.M.P.; project administration, J.C.-E., G.N.M.P., D.Á.P. and B.P.S.; funding acquisition, G.N.M.P. and B.P.S. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been co-funded by FEDER funds, INTERREG MAC 2014-2020 programme, within the E5DES project (MAC2/1.1a/309) and DESAL+ project (MAC/1.1a/094).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the support received by FEDER funds, INTERREGMAC 2014–2020 Program of the European Union, part of the DESAL+ Project [MAC/1.1a/094] and the E5DES project [MAC2/1.1a/309].
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Krile, S. Fresh Water Supply from Different Sources in the Shipping. Procedia Eng. 2016, 149, 190–196. [Google Scholar] [CrossRef][Green Version]
- World Health Organization. Guidelines for Drinking-Water Quality, 4th ed.; Incorporating the First Addendum; World Health Organization: Geneva, Switzerland, 2017. [Google Scholar]
- World Health Organization. A Global Overview of National Regulations and Standards for Drinking-Water Quality; World Health Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Garcia, C.; Mestre-Runge, C.; Morán-Tejeda, E.; Lorenzo-Lacruz, J.; Tirado, D. Impact of Cruise Activity on Freshwater Use in the Port of Palma (Mallorca, Spain). Water 2020, 12, 1088. [Google Scholar] [CrossRef]
- Macharia, P.; Kreuzinger, N.; Kitaka, N. Applying the Water-Energy Nexus for Water Supply—A Diagnostic Review on Energy Use for Water Provision in Africa. Water 2020, 12, 2560. [Google Scholar] [CrossRef]
- Shammi, M.; Mostafizur, M. (Eds.) Desalination technologies and potential mathematical modeling for sustainable water–energy nexus. In Water Engineering Modeling and Mathematic Tools, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2021; pp. 251–269. [Google Scholar]
- Balcombe, P.; Brierley, J.; Lewis, C.; Skatvedt, L.; Speirs, J.; Hawkes, A.; Staffell, I. How to decarbonise international shipping: Options for fuels, technologies. Energy Convers. Manag. 2019, 182, 72–88. [Google Scholar] [CrossRef]
- Padrón, I.; Avila, D.; Marichal, G.N.; Rodríguez, J.A. Assessment of Hybrid Renewable Energy Systems to supplied energy to Autonomous Desalination Systems in two islands of the Canary Archipelago. Renew. Sustain. Energy Rev. 2019, 101, 221–230. [Google Scholar] [CrossRef]
- Mitchell, T. Machine Learning; McGraw Hill: New York, NY, USA, 1997. [Google Scholar]
- Chen, C. Fuzzy Logic and Neural Network Handbook; McGraw Hill: New York, NY, USA, 1996. [Google Scholar]
- Marichal, G.N.; Acosta, L.; Moreno, L.; Méndez, J.A.; Rodrigo, J.J.; Sigut, M. Obstacle avoidance for a mobile robot: A neuro-fuzzy approach. Fuzzy Sets Syst. 2001, 124, 171–179. [Google Scholar] [CrossRef]
- Zhong, R.Y.; Xu, X.; Klotz, E.; Newman, S.T. Intelligent Manufacturing in the Context of Industry 4.0: A Review. Engineering 2017, 3, 616–630. [Google Scholar] [CrossRef]
- Alshehri, M.; Kumar, M.; Bhardwaj, A.; Mishra, S.; Gyani, J. Deep Learning Based Approach to Classify Saline Particles in Sea Water. Water 2021, 13, 1251. [Google Scholar] [CrossRef]
- Al Aani, S.; Bonny, T.; Hasan, S.W.; Hilal, N. Can machine language and artificial intelligence revolutionize process automation for water treatment and desalination? Desalination 2019, 458, 84–96. [Google Scholar] [CrossRef]
- Pohl, R.; Kaltschmitt, M.; Holländer, R. Investigation of different operational strategies for the variable operation of a simple reverse osmosis unit. Desalination 2009, 249, 1280–1287. [Google Scholar] [CrossRef]
- El-Hawary, M.E. Artificial neural networks and possible applications to desalination. Desalination 1993, 92, 125–147. [Google Scholar] [CrossRef]
- Murthy, Z.V.P.; Vora, M.M. Prediction of reverse osmosis performance using artificial neural network. Indian J. Chem. Technol. 2004, 11, 108–115. [Google Scholar]
- Abbas, A.; Al-Bastaki, N. Modeling of an RO water desalination unit using neural networks. Chem. Eng. J. 2005, 114, 139–143. [Google Scholar] [CrossRef]
- Aish, A.M.; Zaqoot, H.A.; Abdeljawad, S.M. Artificial neural network approach for predicting reverse osmosis desalination plants performance in the Gaza Strip. Desalination 2015, 367, 240–247. [Google Scholar] [CrossRef]
- Azad, A.; Aghaei, E.; Jalali, A.; Ahmadi, P. Multi-objective optimization of a solar chimney for power generation and water desalination using neural network. Energy Convers. Manag. 2021, 238, 114152. [Google Scholar] [CrossRef]
- Sadi, M.; Fakharian, H.; Ganji, H.; Kakavand, M. Evolving artificial intelligence techniques to model the hydrate-based desalination process of produced water. J. Water Reuse Desalination 2019, 9, 372–384. [Google Scholar] [CrossRef]
- Cabrera, P.; Carta, J.A.; González, J.; Melián, G. Wind-driven SWRO desalination prototype with and without batteries: A performance simulation using machine learning methods. Desalination 2018, 435, 77–96. [Google Scholar] [CrossRef]
- Pascual, X.; Gu, H.; Bartman, A.R.; Zhu, A.; Rahardianto, A.; Giralt, J.; Rallo, R.; Christofides, P.D.; Cohen, Y. Data-driven models of steady state and transient operations of spiral-wound RO plant. Desalination 2013, 316, 154–161. [Google Scholar] [CrossRef]
- Al Dhaifallah, M.; Nisar, K.S. Wiener modeling and identification of a reverse osmosis desalination process using least square support vector machine. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 7–19 March 2015. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Betancourt, G.A. Las máquinas de soporte vectorial (SVMs). Sci. Tech. 2005, 1, 27. [Google Scholar]
- Burges, C.J.C. A tutorial on Support Vector Machines for pattern recognition. Data Min. Knowl. Discov. 1998, 2, 121–167. [Google Scholar] [CrossRef]
- Ali, J.; Khan, R.; Ahmad, N.; Maqsood, I. Random Forests and Decision Trees. Int. J. Comput. Sci. Issues 2012, 9, 272–278. [Google Scholar]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning, 2nd ed.; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Mathworks, Statistics and Machine Learning Toolbox User’s Guide (MATLAB). 2020. Available online: https://www.mathworks.com/help/pdf_doc/stats/stats.pdf (accessed on 5 December 2020).
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K.; Robeson, S.M. Ambiguities inherent in sums-of-squares-based error statistics. Atmos. Environ. 2009, 43, 749–752. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?—Arguments against avoiding RMSE in the literatura. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).