Characterization of Bias during Meteorological Drought Calculation in Time Series Out-of-Sample Validation
Abstract
:1. Introduction
2. Theoretical Overview
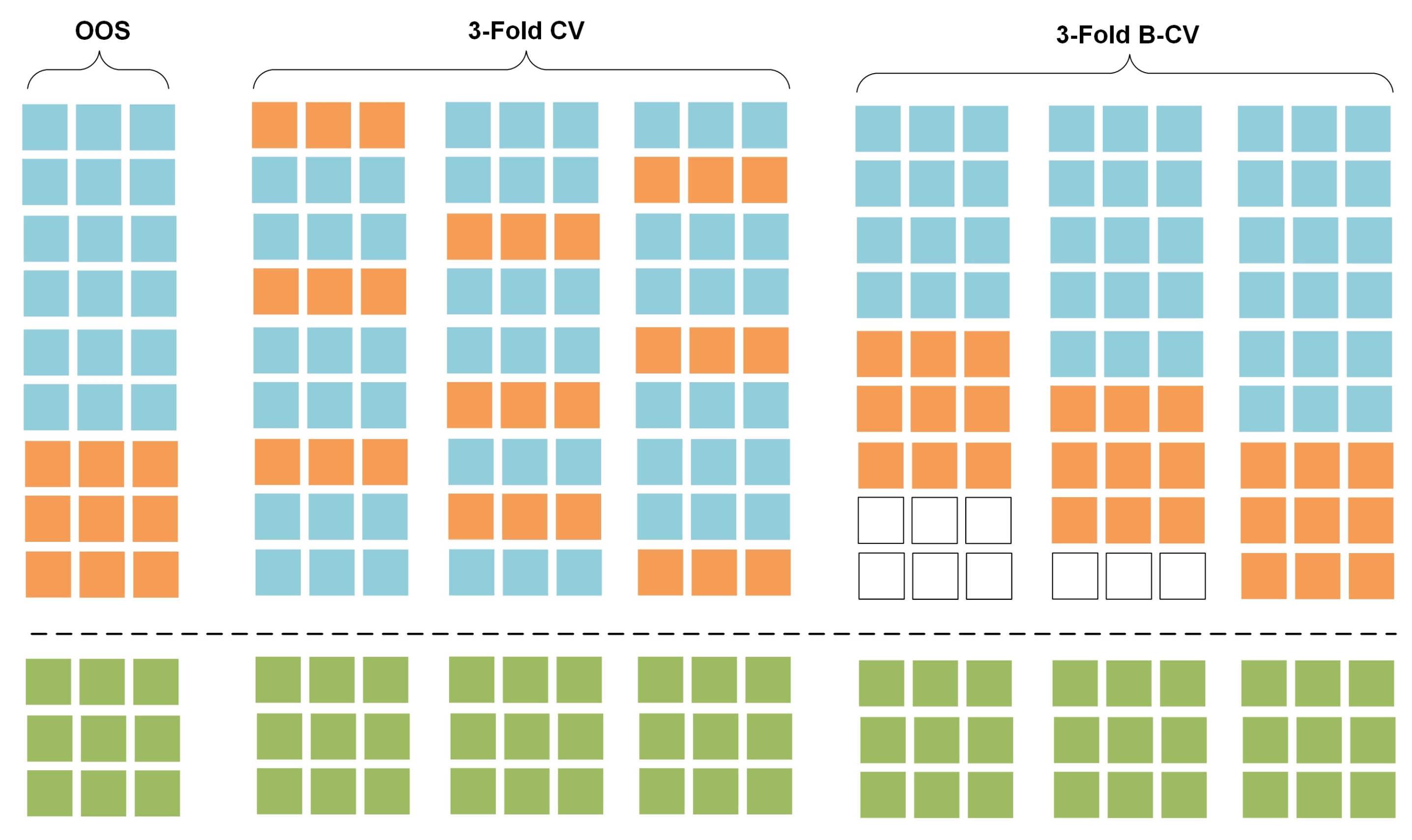
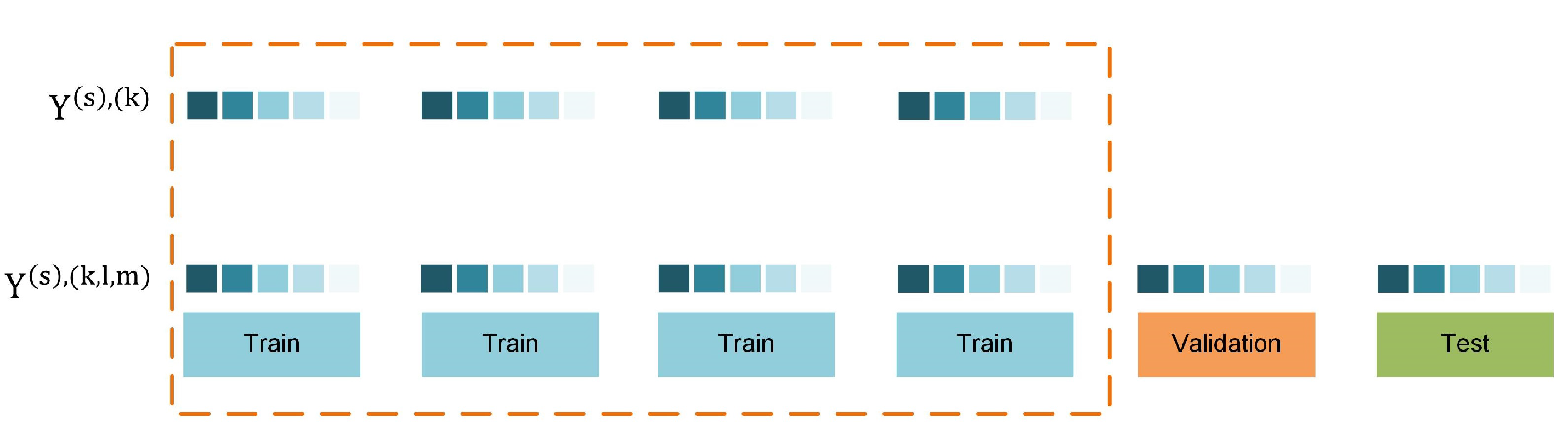
2.1. Data Separation in Model-Validation for Time Series Forecasting
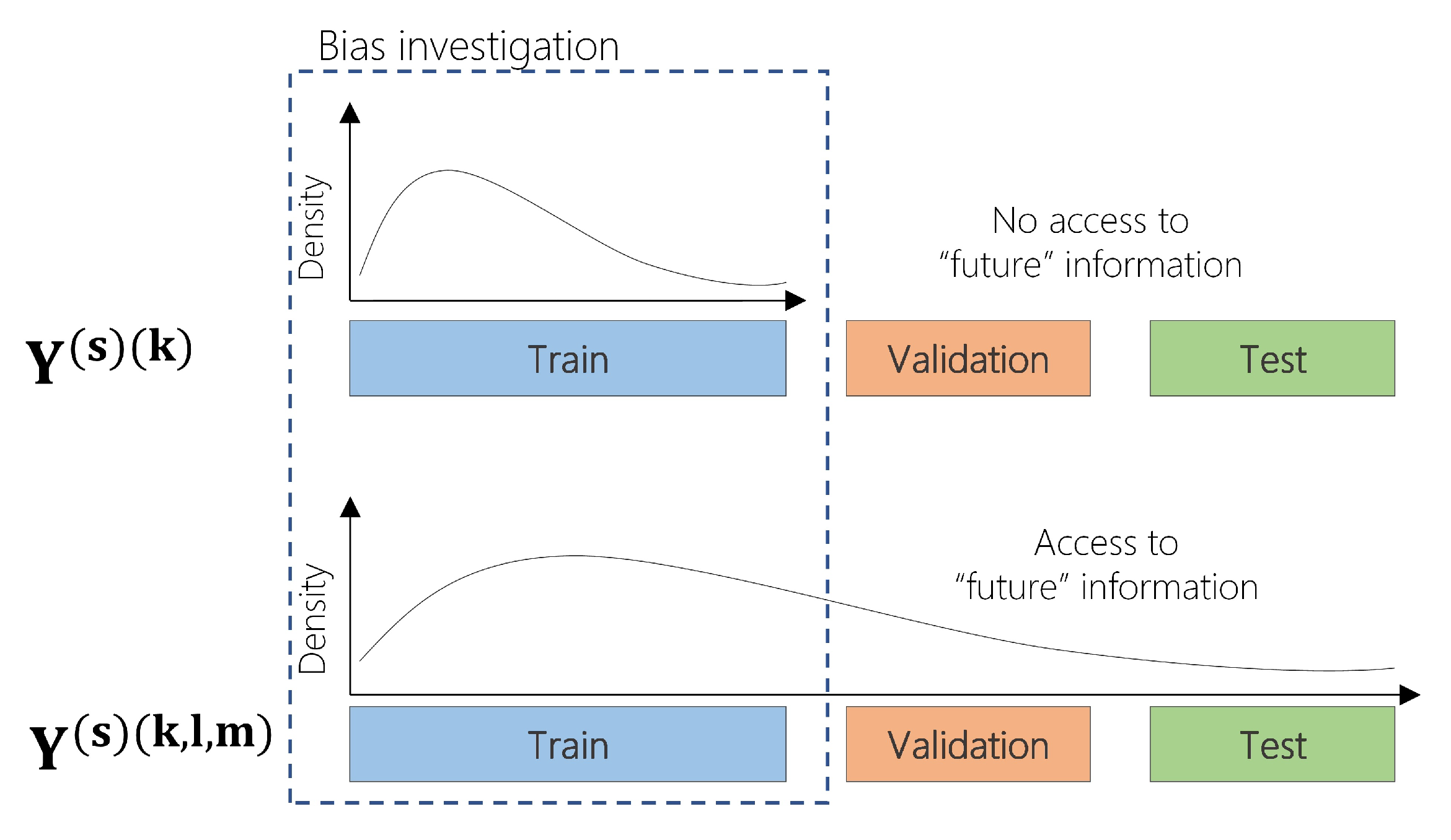
2.2. Addressing the Effect of Bias during Model-Validation in Drought Forecasting Applications
2.3. Estimating Bias during Model-Validation
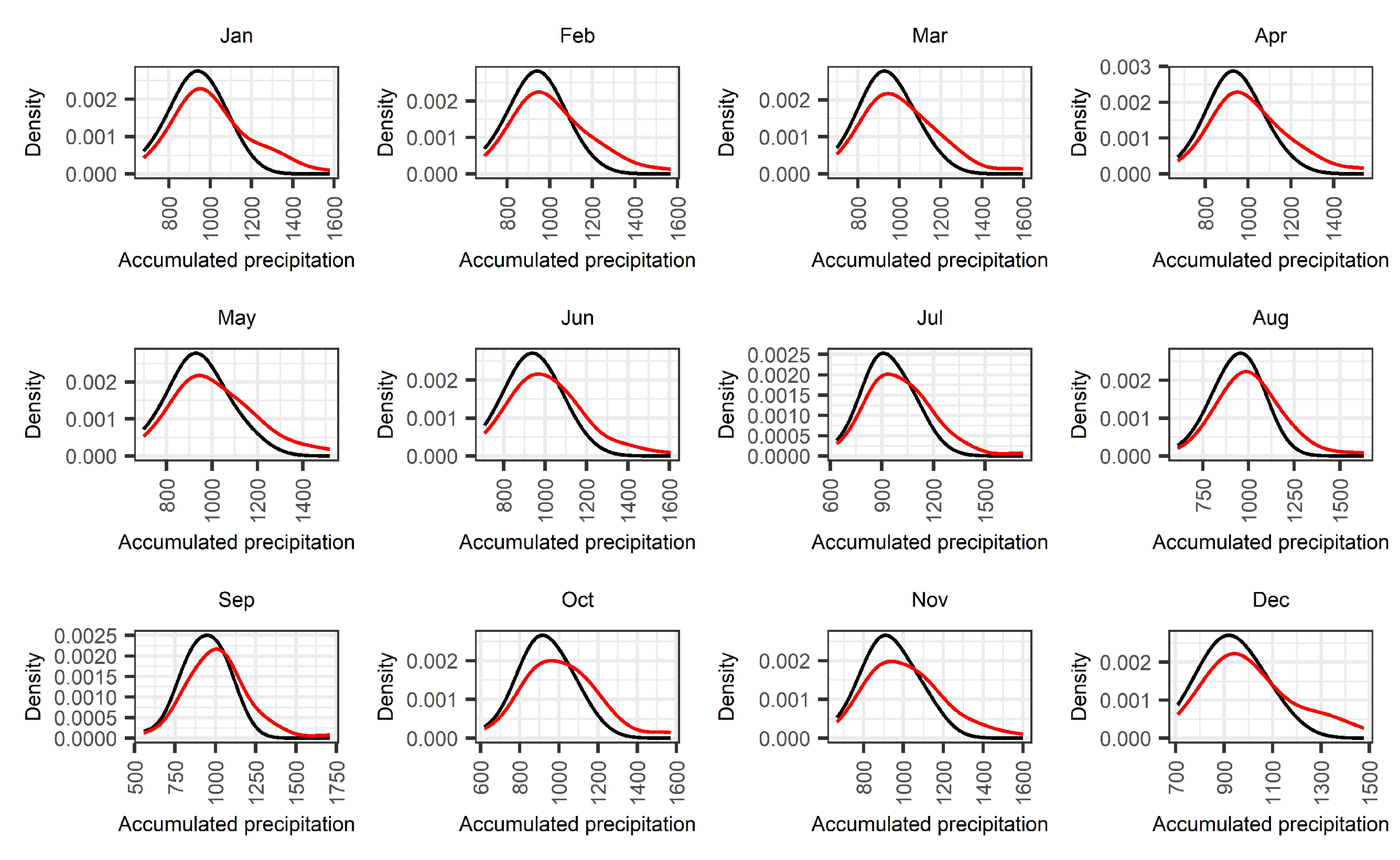
2.3.1. Comparison between the Distributions of Accumulated Precipitation
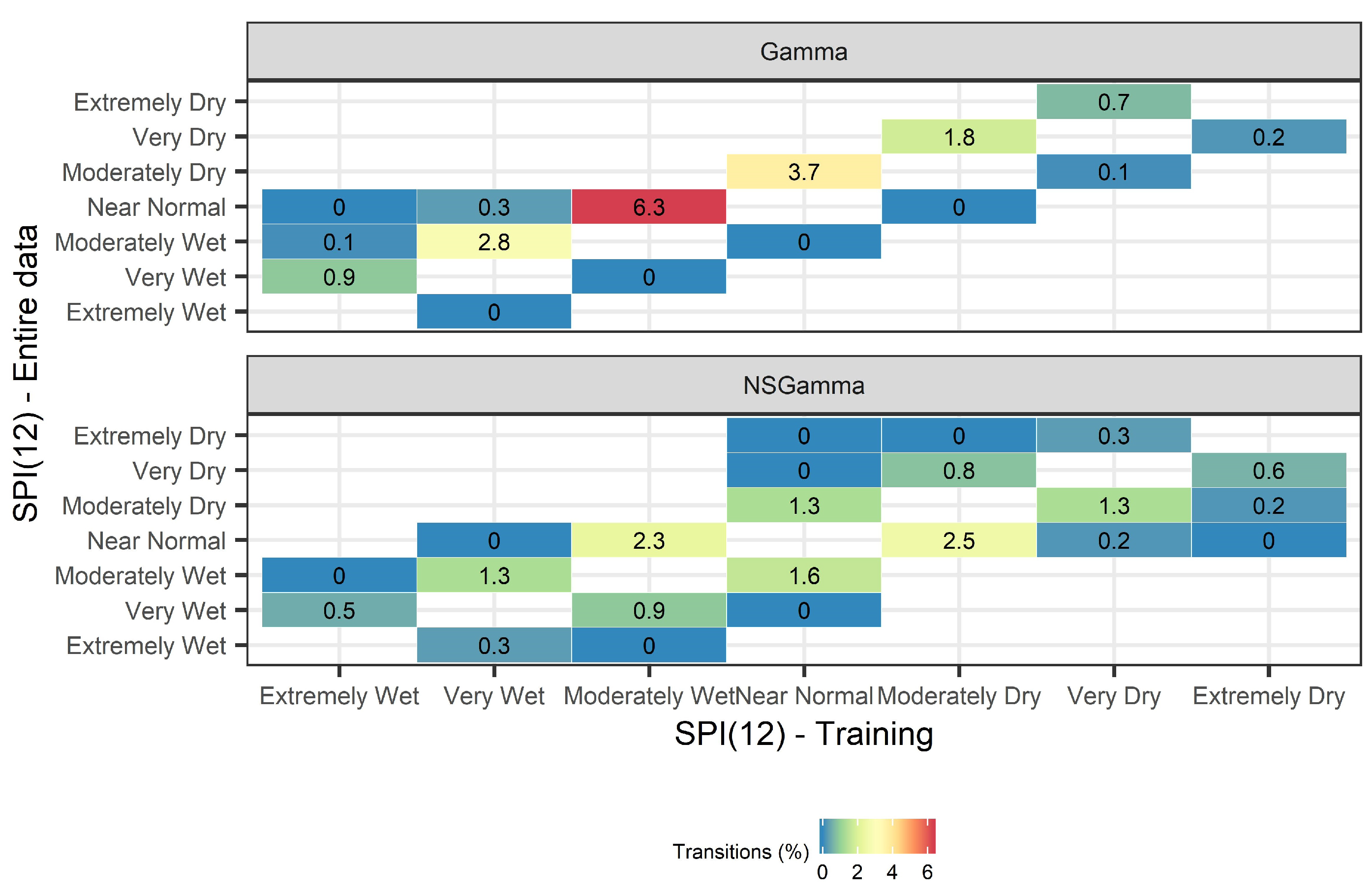
2.3.2. Drought Class Transition
2.3.3. Comparison between the Raw SPI Data
3. Methodology
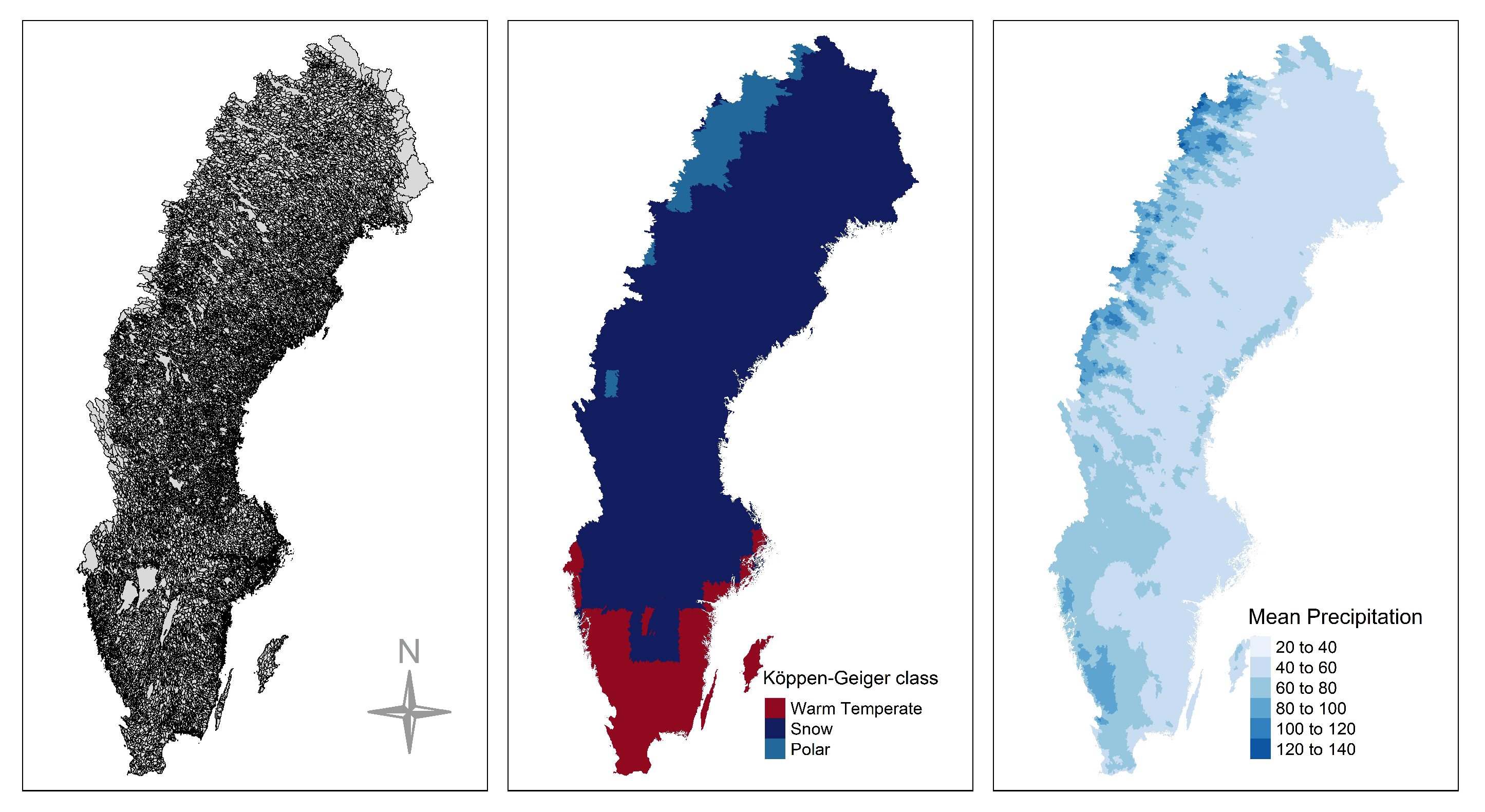
3.1. Data and Region of Interest
3.2. Experimental Setup
- Compare the densities of accumulated rainfall (see Section 2.3.1);
- Count the number of drought class transitions (see Section 2.3.2);
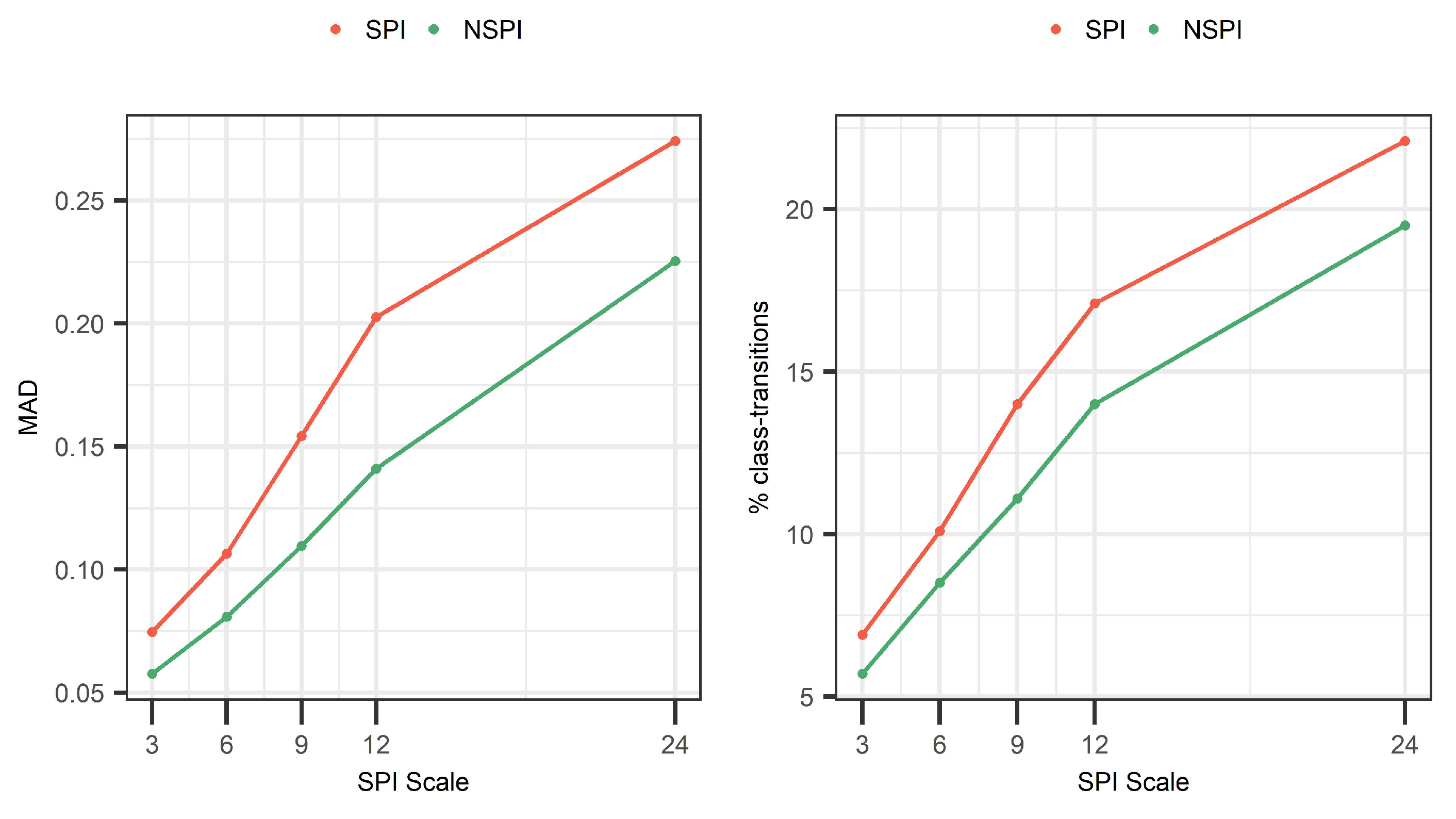
- Analyze the magnitude of the bias introduced at different SPI scales (see Section 2.3.3);
- Assess the variation of bias along Sweden’s climatic gradient. The error introduced to the model-validation is quantified based on one statistical metric; the mean absolute deviation (see Section 2.3.3).
4. Results
4.1. Comparison between the Distributions of Accumulated Precipitation
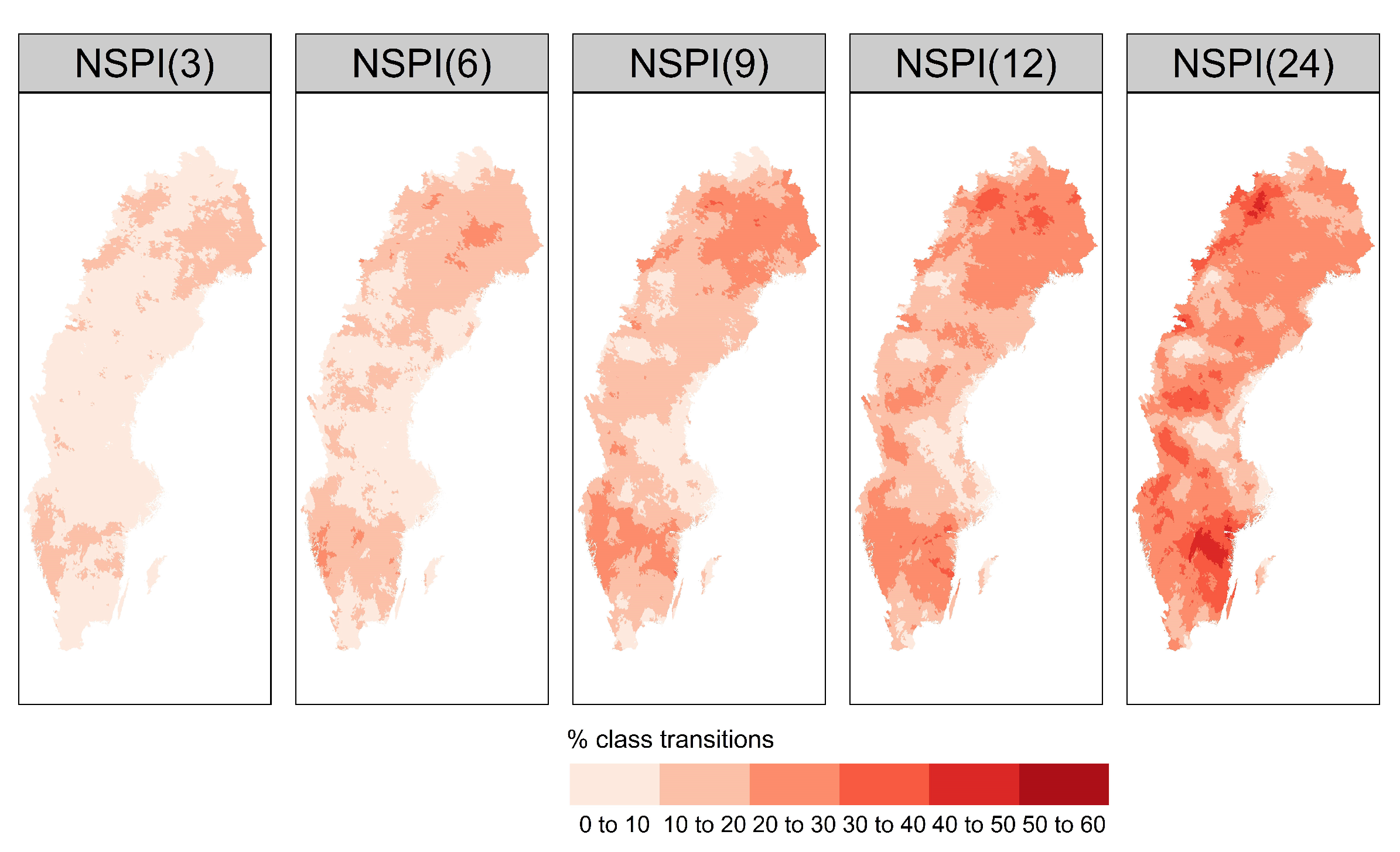
4.2. Drought Class Transitions
4.3. Comparison between the Raw SPI Data
4.4. Sensitivity Analysis of the Bias at Different SPI Scales
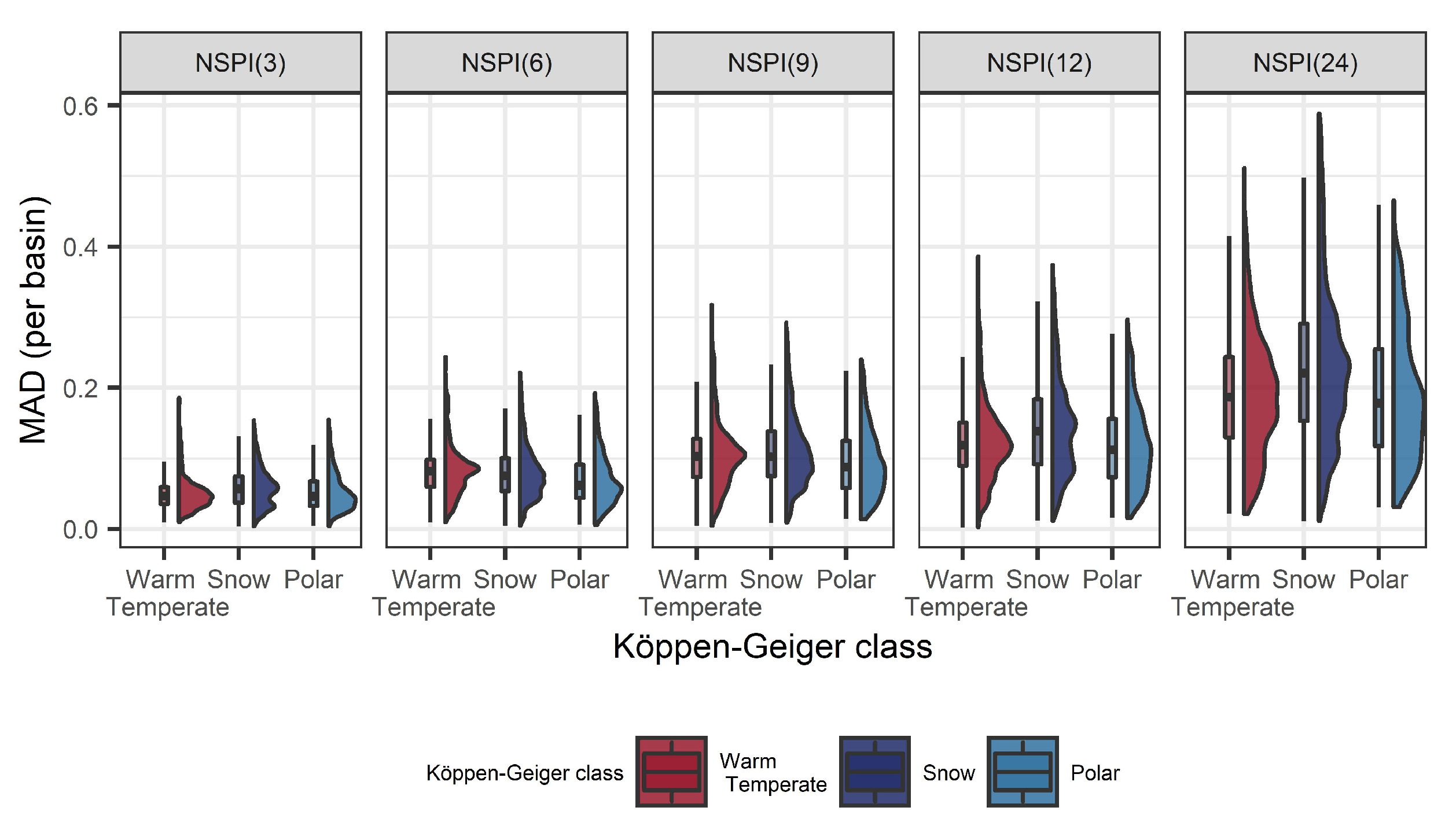
4.5. Bias along a Spatial Gradient
5. Discussion
5.1. Generalization over a Stronger Spatial Gradient
5.2. Applicability Using Different Drought Indices
6. Conclusions
- Climate change coupled with the computation of SPI prior to model-validation can be a significant source of bias in drought forecasting applications. In the case study presented, the increased precipitation during the last decades leads to changes in the distribution parameters of accumulated precipitation for different time scales of the stationary SPI. This phenomenon affects the estimation of drought in the training set and violates the fundamental principles of OOS model-validation;
- NSPI calculation using GAMLSS, involves the estimation of time-varying location and scale parameters of a Gamma distribution as a function of the increasing trend of accumulated precipitation over time. Although this property results to a trend-free index, still the misuse of the data, introduces biases to the training set;
- The bias introduced to the training data is larger when the stationary SPI is computed. This is mainly because SPI requires fitting the accumulated precipitation records to a time invariant probability density function that incorporates the increasing rainfall trend during SPI calculation. This property leads to a systematic underestimation of wet events in the training data consequently affecting future use of this data in forecasting applications;
- With increased SPI scale, the number of drought class transitions increases and affects up to 22.1% for SPI(24) and 19.3% for NSPI(24) of the available records. This finding is further supported by the MAD metric that indicates increased information leakage with larger SPI and NSPI scales. This is mainly due to the “memory” of the index to access longer sequences of future records during OOS model-validation, thus, leading to increased information leakage issue in the training data;
- The bias introduced due to the incorrect computation of NSPI has spatial dependence, especially in the large scales of the index. The regions affected most are located in the southern (snow climate) and northwest part of the Sweden that exhibit changes in the distribution of accumulated precipitation in the validation and test sets.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Stationary Standardized Precipitation Index
| SPI Values | Classification |
|---|---|
| Extremely Wet | |
| Very Wet | |
| Moderately Wet | |
| Near Normal | |
| Moderately Dry | |
| Very Dry | |
| Extremely Dry |
Appendix B. Non-Stationary Standardized Precipitation Index (NSPI)
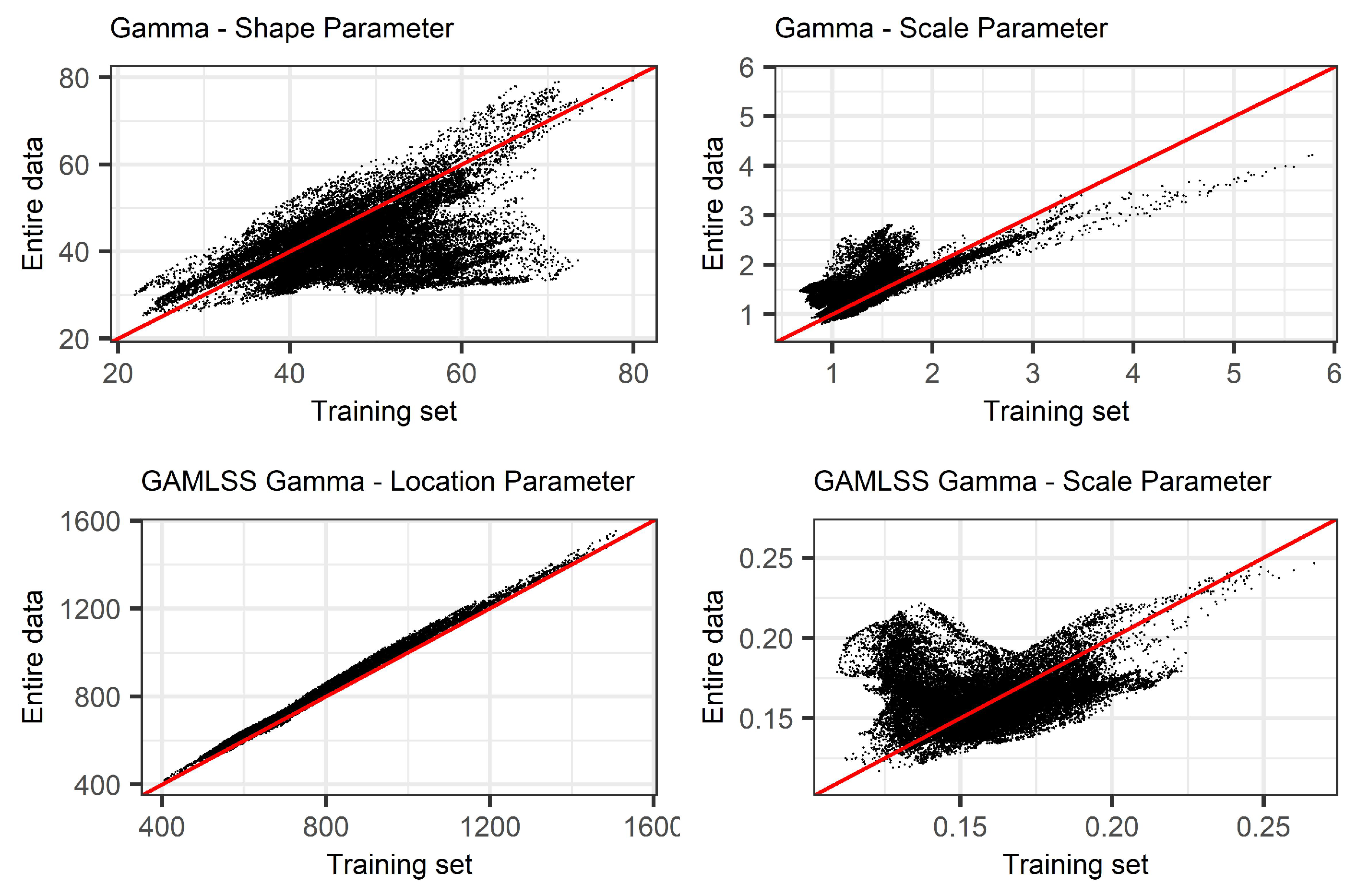
Appendix C. Comparison of Distribution Parameters

References
- FAO. The Impact of Disasters on Agriculture and Food Security; Technical Report; Food and Agriculture Organization of the United Nations: Rome, Italy, 2015. [Google Scholar]
- Cammalleri, C.; Naumann, G.; Mentaschi, L.; Formetta, G.; Forzieri, G.; Gosling, S.; Bisselink, B.; De Roo, A.; Feyen, L. Global Warming and Drought Impacts in the EU; Joint Research Centre (JRC): Brussels, Belgium, 2020. [Google Scholar]
- Vogt, J.; Sepulcre, G.; Magni, D.; Valentini, L.; Singleton, A.; Micale, F.; Barbosa, P. The European Drought Observatory (EDO): Current State and Future Directions; EGU General Assembly: Vienna, Austria, 2013; p. EGU2013-7374. [Google Scholar]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Hao, Z.; AghaKouchak, A.; Nakhjiri, N.; Farahmand, A. Global integrated drought monitoring and prediction system. Sci. Data 2014, 1, 1–10. [Google Scholar] [CrossRef]
- Sutanto, S.J.; Van Lanen, H.A.; Wetterhall, F.; Llort, X. Potential of pan-european seasonal hydrometeorological drought forecasts obtained from a multihazard early warning system. Bull. Am. Meteorol. Soc. 2020, 101, E368–E393. [Google Scholar] [CrossRef] [Green Version]
- Tsakiris, G.; Vangelis, H. Towards a drought watch system based on spatial SPI. Water Resour. Manag. 2004, 18, 1–12. [Google Scholar] [CrossRef]
- Livada, I.; Assimakopoulos, V. Spatial and temporal analysis of drought in Greece using the Standardized Precipitation Index (SPI). Theor. Appl. Climatol. 2007, 89, 143–153. [Google Scholar] [CrossRef]
- Patel, N.R.; Chopra, P.; Dadhwal, V.K. Analyzing spatial patterns of meteorological drought using standardized precipitation index. Meteorol. Appl. 2007, 14, 329–336. [Google Scholar] [CrossRef]
- Karavitis, C.; Alexandris, S.; Tsesmelis, D.; Athanasopoulos, G. Application of the standardized precipitation index (SPI) in Greece. Water 2011, 3, 787–805. [Google Scholar] [CrossRef]
- Van Loon, A.F.; Tijdeman, E.; Wanders, N.; Van Lanen, H.J.; Teuling, A.; Uijlenhoet, R. How climate seasonality modifies drought duration and deficit. J. Geophys. Res. Atmos. 2014, 119, 4640–4656. [Google Scholar] [CrossRef]
- Guenang, G.M.; Kamga, F.M. Computation of the standardized precipitation index (SPI) and its use to assess drought occurrences in Cameroon over recent decades. J. Appl. Meteorol. Climatol. 2014, 53, 2310–2324. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y.; Pan, Y.; Chen, Z.; Ren, Z. Assessment of candidate distributions for SPI/SPEI and sensitivity of drought to climatic variables in China. Int. J. Climatol. 2019, 39, 4392–4412. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Candidate distributions for climatological drought indices (SPI and SPEI). Int. J. Climatol. 2015, 35, 4027–4040. [Google Scholar] [CrossRef]
- Angelidis, P.; Maris, F.; Kotsovinos, N.; Hrissanthou, V. Computation of drought index SPI with alternative distribution functions. Water Resour. Manag. 2012, 26, 2453–2473. [Google Scholar] [CrossRef]
- Sienz, F.; Bothe, O.; Fraedrich, K. Monitoring and quantifying future climate projections of dryness and wetness extremes: SPI bias. Hydrol. Earth Syst. Sci. 2012, 16, 2143–2157. [Google Scholar] [CrossRef] [Green Version]
- Alam, N.; Raizada, A.; Jana, C.; Meshram, R.K.; Sharma, N. Statistical modeling of extreme drought occurrence in Bellary District of Eastern Karnataka. Proc. Natl. Acad. Sci. India Sect. B Biol. Sci. 2015, 85, 423–430. [Google Scholar] [CrossRef]
- Shiau, J.T. Effects of gamma-distribution variations on SPI-based stationary and nonstationary drought analyses. Water Resour. Manag. 2020, 34, 2081–2095. [Google Scholar] [CrossRef]
- Russo, S.; Dosio, A.; Sterl, A.; Barbosa, P.; Vogt, J. Projection of occurrence of extreme dry-wet years and seasons in Europe with stationary and nonstationary Standardized Precipitation Indices. J. Geophys. Res. Atmos. 2013, 118, 7628–7639. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Li, J.; Feng, P.; Hu, R. A time-dependent drought index for non-stationary precipitation series. Water Resour. Manag. 2015, 29, 5631–5647. [Google Scholar] [CrossRef]
- Box, G.; Jenkins, E.M. Time Series Analysis: Forecasting and Control; Holden-Day, Inc.: San Francisco, CA, USA, 1970. [Google Scholar]
- Mishra, A.K.; Desai, V.R. Drought forecasting using stochastic models. Stoch. Environ. Res. Risk Assess 2005, 19, 326–339. [Google Scholar] [CrossRef]
- Han, P.; Wang, P.; Tian, M.; Zhang, S.; Liu, J.; Zhu, D. Application of the ARIMA models in drought forecasting using the standardized precipitation index. IFIP Adv. Inf. Commun. Technol. 2013, 392, 352–358. [Google Scholar] [CrossRef] [Green Version]
- Yeh, H.F.; Hsu, H.L. Stochastic model for drought forecasting in the southern Taiwan basin. Water 2019, 11, 2041. [Google Scholar] [CrossRef] [Green Version]
- Sutanto, S.J.; Wetterhall, F.; Van Lanen, H.A. Hydrological drought forecasts outperform meteorological drought forecasts. Environ. Res. Lett. 2020, 15, 084010. [Google Scholar] [CrossRef]
- Vapnik, V.; Golowich, S.E.; Smola, A.J. Support Vector Method for Function Approximation, Regression Estimation and Signal Processing. In Proceedings of the NIPS’96 9th International Conference on Neural Information Processing Systems, Denver, CO, USA, 3–5 December 1996; MIT Press: Cambridge, MA, USA, 1996; pp. 281–287. [Google Scholar]
- McCulloch, W.; Pitts, W. A Logical Calculus of Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J. Drought forecasting using new machine learning methods. J. Water Land Dev. 2013, 18, 3–12. [Google Scholar] [CrossRef]
- Mokhtarzad, M.; Eskandari, F.; Vanjani, N.J.; Arabasadi, A. Drought forecasting by ANN, ANFIS, and SVM and comparison of the models. Environ. Earth Sci. 2017, 76, 729. [Google Scholar] [CrossRef]
- Wu, H.; Hayes, M.J.; Wilhite, D.A.; Svoboda, M.D. The effect of the length of record on the standardized precipitation index calculation. Int. J. Climatol. 2005, 25, 505–520. [Google Scholar] [CrossRef] [Green Version]
- Rezaeian-Zadeh, M.; Tabari, H. MLP-based drought forecasting in different climatic regions. Theor. Appl. Climatol. 2012, 109, 407–414. [Google Scholar] [CrossRef]
- Belayneh, A.; Adamowski, J.; Khalil, B.; Ozga-Zielinski, B. Long-term SPI drought forecasting in the Awash River Basin in Ethiopia using wavelet neural network and wavelet support vector regression models. J. Hydrol. 2014, 508, 418–429. [Google Scholar] [CrossRef]
- Deo, R.C.; Kisi, O.; Singh, V.P. Drought forecasting in eastern Australia using multivariate adaptive regression spline, least square support vector machine and M5Tree model. Atmos. Res. 2017, 184, 149–175. [Google Scholar] [CrossRef] [Green Version]
- Yaseen, Z.M.; Ali, M.; Sharafati, A.; Al-Ansari, N.; Shahid, S. Forecasting standardized precipitation index using data intelligence models: Regional investigation of Bangladesh. Sci. Rep. 2021, 11, 1–25. [Google Scholar] [CrossRef]
- Rhee, J.; Im, J. Meteorological drought forecasting for ungauged areas based on machine learning: Using long-range climate forecast and remote sensing data. Agric. For. Meteorol. 2017, 237, 105–122. [Google Scholar] [CrossRef]
- Tashman, L.J. Out-of-sample tests of forecasting accuracy: An analysis and review. Int. J. Forecast. 2004, 16, 437–450. [Google Scholar] [CrossRef]
- Bergmeir, C.; Benitez, J.M. On the Use of Cross-validation for Time Series Predictor Evaluation. Inf. Sci. 2012, 191, 192–213. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Prediction, Inference and Data Mining, 2nd ed.; Springer: New York, NY, USA, 2009; pp. 241–260. [Google Scholar]
- Mishra, A.K.; Desai, V.R.; Singh, V.P. Drought forecasting using a hybrid stochastic and neural network model. Hydrol. Eng. ASCE 2007, 12, 626–638. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Hydrol. Earth Syst. Sci 2006. [Google Scholar] [CrossRef]
- Girons Lopez, M.; Crochemore, L.; Pechlivanidis, I.G. Benchmarking an operational hydrological model for providing seasonal forecasts in Sweden. Hydrol. Earth Syst. Sci. 2021, 25, 1189–1209. [Google Scholar] [CrossRef]
- Guide, Svoboda, Hayes, and Wood; World Meteorological Organization: Geneva, Switzerland, 2012.
- Arheimer, B.; Lindström, G. Climate impact on floods: Changes in high flows in Sweden in the past and the future (1911–2100). Hydrol. Earth Syst. Sci. 2015, 19, 771–784. [Google Scholar] [CrossRef] [Green Version]
- Van Loon, A.; Van Huijgevoort, M.; Van Lanen, H. Evaluation of drought propagation in an ensemble mean of large-scale hydrological models. Hydrol. Earth Syst. Sci. 2012, 16, 4057–4078. [Google Scholar] [CrossRef] [Green Version]
- Van Loon, A.; Laaha, G. Hydrological drought severity explained by climate and catchment characteristics. J. Hydrol. 2015, 526, 3–14. [Google Scholar] [CrossRef] [Green Version]
- Blauhut, V.; Stahl, K.; Stagge, J.; Tallaksen, L.; De Stefano, L.; Vogt, J. Estimating drought risk across Europe from reported drought impacts, drought indices, and vulnerability factor. Hydrol. Earth Syst. Sci. 2016, 20, 2779–2800. [Google Scholar] [CrossRef] [Green Version]
- Hanel, M.; Rakovec, O.; Markonis, Y.; Maca, P.; Samaniego, L.; Kysely, J.; Kumar, R. Revisiting the recent European droughts from a long-term perspective. Sci. Rep. 2018, 8, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Dosio, A. Mean and Extreme Climate in Europe under 1.5, 2, and 3 °C Global Warming; JRC PESETA IV Project—Task 1; Publications Office of the European Union: Luxembourg, 2020. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; Lopez-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. Water Resour. Manag. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Byun, H.R.; Wilhite, D.A. Objective quantification of drought severity and duration. J. Clim. 1999, 12, 2747–2756. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M.; Reig, F.; Latorre, B. Standardized precipitation evapotranspiration index (SPEI) revisited: Parameter fitting, evapotranspiration models, tools, datasets and drought monitoring. Int. J. Climatol. 2014, 34, 3001–3023. [Google Scholar] [CrossRef] [Green Version]
- Deo, R.C.; Byun, H.R.; Adamowski, J.F.; Begum, K. Application of effective drought index for quantification of meteorological drought events: A case study in Australia. Theor. Appl. Climatol. 2017, 128, 359–379. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Silver Spring, MD, USA, 1965; Volume 30.
- Sepulcre-Canto, G.; Horion, S.; Singleton, A.; Carrao, H.; Vogt, J. Development of a Combined Drought Indicator to detect agricultural drought in Europe. Nat. Hazards Earth Syst. Sci. 2012, 12, 3519–3531. [Google Scholar] [CrossRef] [Green Version]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. Comment on “Characteristics and trends in various forms of the Palmer Drought Severity Index (PDSI) during 1900–2008” by Aiguo Dai. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Balint, Z.; Mutua, F.; Muchiri, P.; Omuto, C.T. Monitoring drought with the combined drought index in Kenya. In Developments in Earth Surface Processes; Elsevier: Amsterdam, The Netherlands, 2013; Volume 16, pp. 341–356. [Google Scholar]
- Sutanto, S.J.; Van Lanen, H.A. Streamflow drought: Implication of drought definitions and its application for drought forecasting. Hydrol. Earth Syst. Sci. Discuss. 2021, 25, 3991–4023. [Google Scholar] [CrossRef]
- Thom, H.C.S. A note on gamma distribution. Mon. Weather Rev. 1958, 86, 117–122. [Google Scholar] [CrossRef]
- Rigby, R.A.; Stasinopoulos, D.M. Generalized additive models for location, scale and shape. J. R. Stat. Soc. Ser. C (Appl. Stat.) 2005, 54, 507–554. [Google Scholar] [CrossRef] [Green Version]
- Villarini, G.; Smith, J.A.; Napolitano, F. Nonstationary modeling of a long record of rainfall and temperature over Rome. Adv. Water Resour. 2010, 33, 1256–1267. [Google Scholar] [CrossRef]
- Bazrafshan, J.; Hejabi, S. A non-stationary reconnaissance drought index (NRDI) for drought monitoring in a changing climate. Water Resour. Manag. 2018, 32, 2611–2624. [Google Scholar] [CrossRef]

| Station | Longitude | Latitude | Mean Monthly Rainfall (Train) | Mean Monthly Rainfall (Train, Valid, Test) |
|---|---|---|---|---|
| S-3357 | 67.37 | 22.28 | 77.6 mm | 84.2 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mammas, K.; Lekkas, D.F. Characterization of Bias during Meteorological Drought Calculation in Time Series Out-of-Sample Validation. Water 2021, 13, 2531. https://doi.org/10.3390/w13182531
Mammas K, Lekkas DF. Characterization of Bias during Meteorological Drought Calculation in Time Series Out-of-Sample Validation. Water. 2021; 13(18):2531. https://doi.org/10.3390/w13182531
Chicago/Turabian StyleMammas, Konstantinos, and Demetris F. Lekkas. 2021. "Characterization of Bias during Meteorological Drought Calculation in Time Series Out-of-Sample Validation" Water 13, no. 18: 2531. https://doi.org/10.3390/w13182531
APA StyleMammas, K., & Lekkas, D. F. (2021). Characterization of Bias during Meteorological Drought Calculation in Time Series Out-of-Sample Validation. Water, 13(18), 2531. https://doi.org/10.3390/w13182531







