1. Introduction
The estimation of streamflow time series on the watershed scale is of great importance in surface water hydrology. Accurate streamflow is the foundation of water resources planning and management, including river hydraulics modeling and engineering project design, water demand assessment and allocation, and water quality studies [
1,
2]. Data-driven methods have gained popularity in hydrologic and water quality (H/WQ) modeling in recent years due to their effectiveness in mapping connections between hydrologic inputs and outputs [
3]. Among these methods, the artificial neural network (ANN) has proven to be an effective tool in water resources modeling [
4,
5].
An ANN is a “parallel-distributed processor” that resembles the biological neural network structure of the human brain. The ANN acquires knowledge or information from a learning process and stores that knowledge in interneuron links using a weighted matrix. The early concept of ANNs as a computational tool was formalized in the 1940s. It went through gradual development in the ensuing decades as computers become more accessible and computational efficiency grew [
6]. ANN-based models hold some clear advantages over conventional conceptual models in H/WQ modeling. ANNs do not require
a priori knowledge of the physical characteristics of the study watershed as model input, thus significantly reducing the procedures for model setup and simulation [
7,
8]. When sufficient data have been provided, ANN models have produced satisfactory results for streamflow forecasting, according to a review provided by Yaseen et al. [
9]. However, some believe modeling hydrologic systems with ANNs without explaining the underlying physical processes is a significant drawback. For instance, the lack of capability to capture physical dynamics at the watershed level means that ANNs are not suitable for modeling streamflow under changing climate or land use conditions. In addition, the ANN’s predictive capability is often unreliable beyond the training data range due to the absence of physical explanation [
9,
10,
11,
12,
13]. Worland et al. [
3] further recommended that machine-learning models such as ANNs only be used for making predictions rather than gaining hydrological insights.
ANN application in hydrology began in the 1990s. Since then, many studies have applied ANNs in H/WQ modeling. Several studies have reported satisfactory results using ANNs for streamflow estimation. Karunanithi et al. [
13] demonstrated successful streamflow prediction at the Huron River in Michigan using neural network models in an early study. The predicted flow closely matched the timing and magnitude of the actual flow. Ahmed and Sarma [
14] used three data-driven models to generate synthetic streamflow for the Pagladia River in northeast India and concluded that the ANN-based model has the best performance. Birikundavyi et al. [
15] compared an ANN to an autoregressive model to forecast daily streamflow in the Mistassibi River in northeastern Quebec. They obtained results showing that the ANN model outperformed the autoregressive model. Similarly, Hu et al. [
16] showed an ANN-based model that simulated daily streamflow and annual reservoir inflow for two watersheds in northern China that outperformed an auto-regressive model. Humphrey et al. [
5] coupled an ANN model and a conceptual rainfall–runoff model to produce a monthly streamflow forecast for a drainage network in southeast Australia. They reported that the hybrid model outperformed the original conceptual model, especially for high flow periods. Isik et al. [
17] reported that accurate daily streamflow prediction was achieved using a hybrid model based on an ANN and the SCS (Soil Conservation Service, the US Department of Agriculture) curve number method. Kişi [
18] compared four different ANN algorithms for streamflow forecasting, all of which reached satisfactory statistical results with correlation coefficients of all four models close to one. Rezaeianzadeh et al. [
19] simulated daily watershed outflow at the Khosrow Shirin watershed in Iran, using an ANN and HEC-HMS, and concluded that the ANN model with a multi-layer perceptron was more efficient in forecasting daily streamflow.
Although the literature has demonstrated that ANN models can make satisfactory streamflow predictions, the ANN-based models often suffer from overfitting problems due to a relatively large number of parameters to be estimated compared with other statistical-based models [
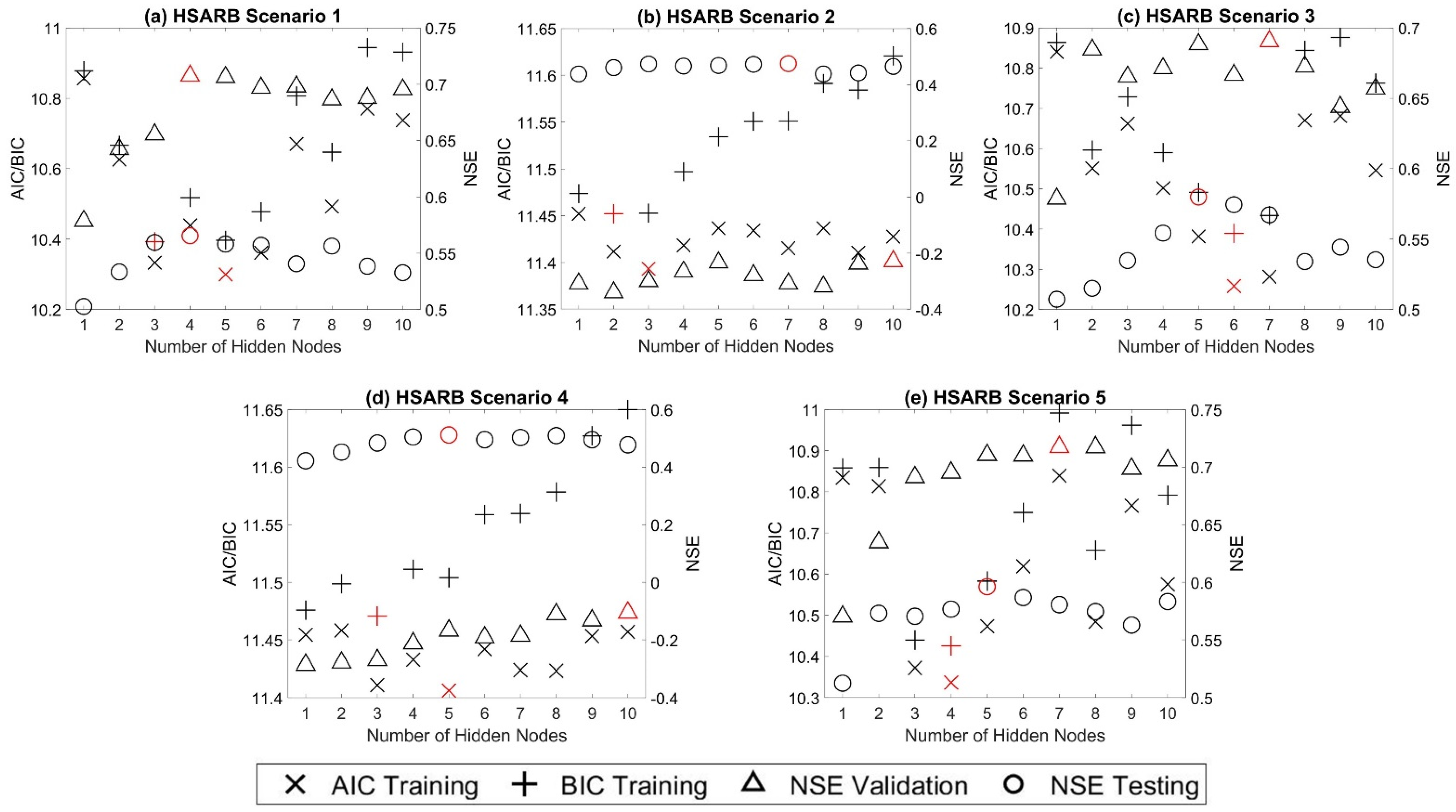
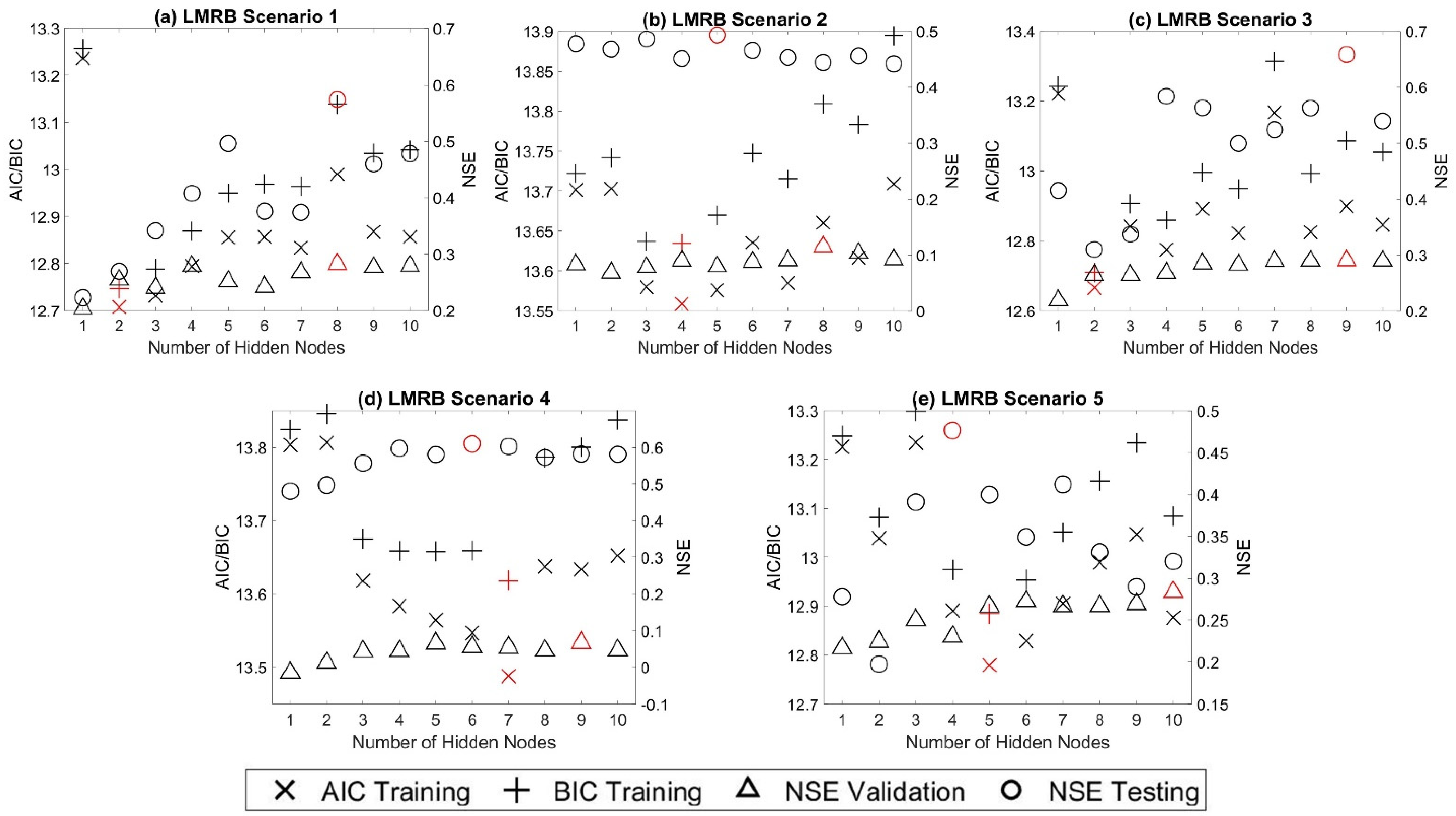
20]. Model overfitting often refers to ANNs fitting the in-sample data (training set) well but the out-of-sample data (testing set) poorly. Selecting the appropriate model structure is crucial for accurately simulating streamflow while ameliorating overfitting. Routinely, several ANN models are trained, and a model selection phase is applied to find the model with the best generalization capability [
21]. Two main types of model selection approaches are often adopted for this purpose. The out-of-sample approach, based on cross-validation, divides the available data into training, validation, and testing sets. The in-sample approach relies on in-sample criterion calculated on the training dataset, most notably Akaike’s information criterion (AIC) and Bayesian information criterion (BIC), for deciding the models’ generalization capability [
22]. Although it is generally accepted that the performance of statistical models should be assessed using out-of-sample tests rather than in-sample errors [
23], the in-sample model selection approach has the clear advantage of utilizing all available data for modeling training while avoiding data splitting. Previous studies have discussed the benefits and disadvantages of the two approaches. Arlot and Celisse [
24] argued that out-of-sample cross-validation is more applicable in many practical situations. Qi and Zhang [
22] showed that the results of a few in-sample model selection criteria were not consistent with the out-of-sample performance for three economic time series. On the other hand, a study conducted by Shao [
25] concluded that AIC and leave-one-out cross-validation (LOOCV) converge to the same model selection result. It is unclear how the out-of-sample and in-sample model selection approaches will perform on hydrological time series without actual experimentation. Additionally, as noted by Bergmeir and Benítez [
26], the distinct nature of different time series can cause a model selection method to work well with a particular type of time series but show poor performance on others. Hence, it is yet to be evaluated if the model selection outcomes of these two approaches converge for a hydrological time series.
The main objectives of this study are: (1) to create ANN rainfall–streamflow models on the watershed level, (2) determine the optimal model structure of the ANNs using both in-sample and out-of-sample model selection approaches, (3) compare the model selection results of these two approaches, and (4) empirically investigate their efficacy in selecting the optimal neural network. The task is to be accomplished using two small watersheds in the San Antonio region of south-central Texas, one of which is dominated by a well-developed urban landscape. An agricultural landscape primarily covers the other. The streamflow simulations are to be conducted on a daily time step for the outflows of both watersheds. The following sections will describe the details of the models.
4. Summary and Conclusions
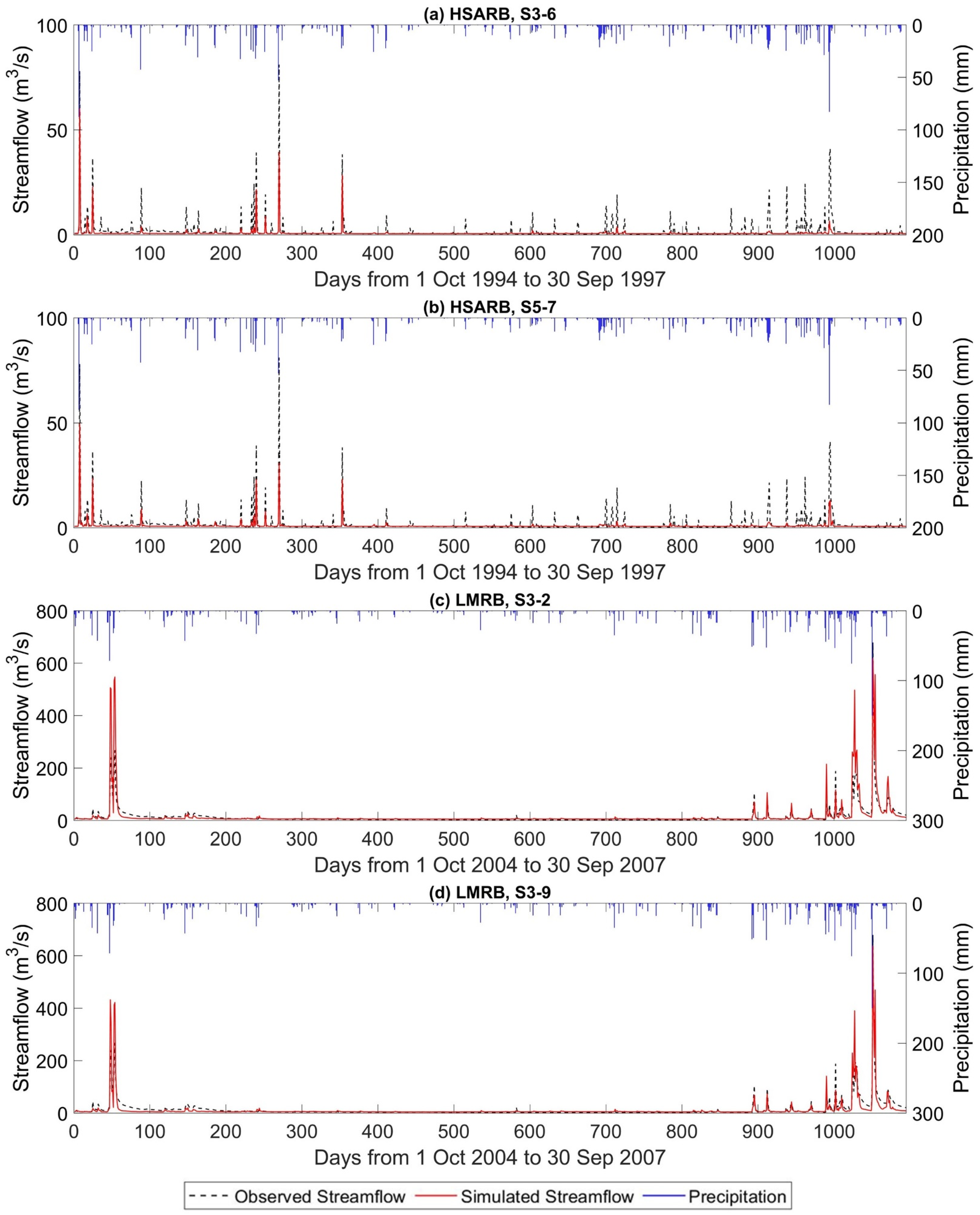
In this study, daily streamflow simulation models were developed for two small watersheds with distinctive land cover types in south-central Texas, using a three-layer feed-forward neural network. Five prediction scenarios using different combinations of meteorological and hydrological variables were considered, and for each prediction scenario a range of nodes in the hidden layer was evaluated. The results show that the best networks could produce “satisfactory” to “good” daily streamflow prediction performances for most of the considered input combinations. While plenty of studies have reported applying ANNs to H/WQ modeling, the model overfitting problem and model selection method for a hydrological time series simulation have not been adequately addressed.
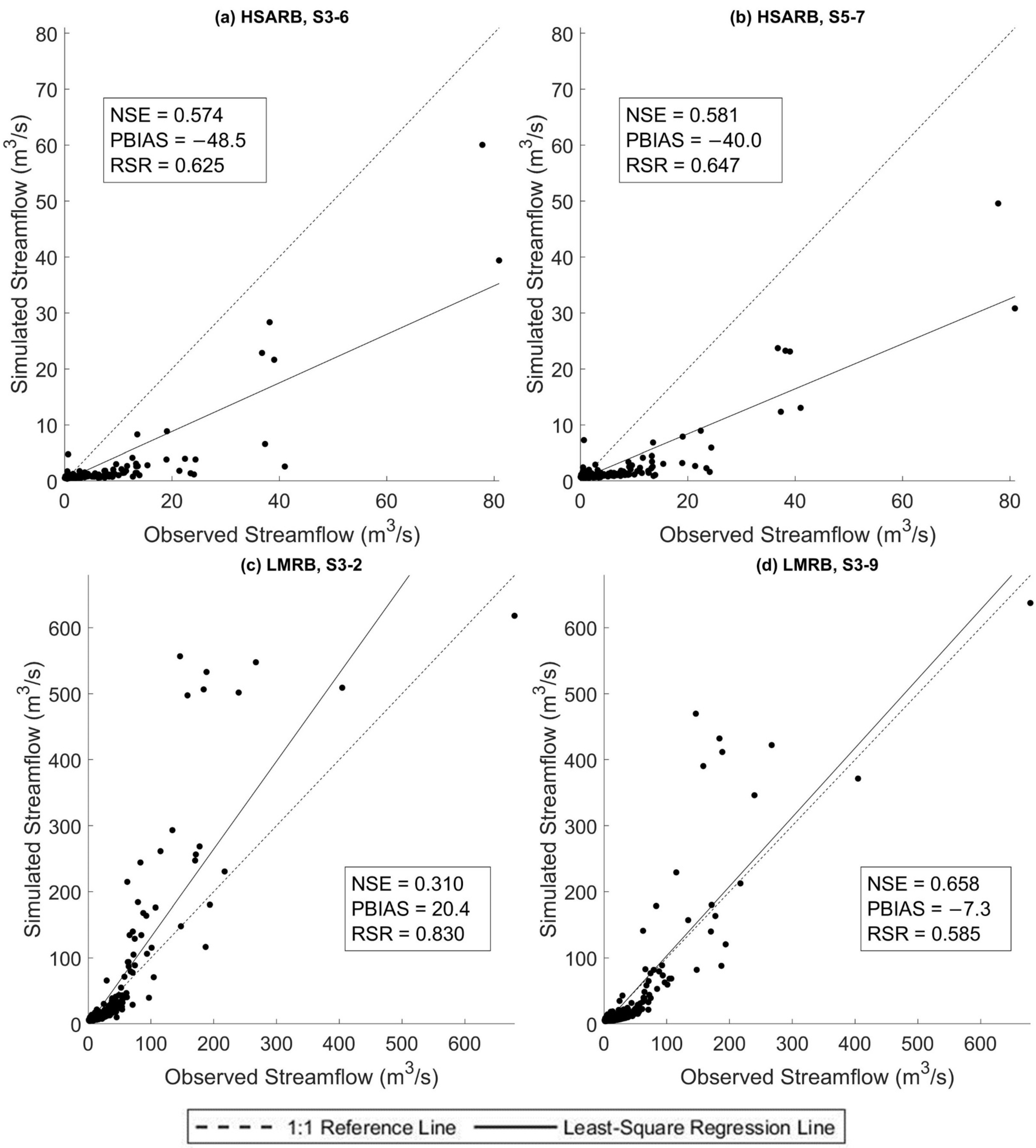
This study empirically investigated two main approaches for selecting the best ANN rainfall–streamflow models: the in-sample approach using AIC and BIC as criteria and the out-of-sample approach using BlockedCV. The evidence from this study suggests that none of the proposed approaches consistently select the model that has the best testing dataset predictive ability based on the criteria of optimum hidden layer size. However, when considering selecting among predictive scenarios where model structure difference is more notable, it is found that BlockedCV is more capable of identifying the best predictive model. Furthermore, the AIC and BIC are also found to select a simpler model structure than BlockedCV. Overall, this study strengthens the idea that the in-sample model selection criteria may over-penalize model complexity and select models that underfit the data for modeling a streamflow time series. The final best models in both study watersheds selected through BlockedCV are found to have “good” performance on the testing data. However, a closer inspection of the scatter plots and corresponding PBIAS values indicates that the models can perform very differently on low and high flow data, especially in the LMRB. This finding is also supported by the counter-intuitive result that the largely rural LMRB has better model performance than the urban HSARB, which could be explained by the fact that the HSARB has a much smaller average outflow discharge than the LMRB. Further studies could assess the model selection criteria separately on different quantiles and magnitudes of the flow data while choosing watersheds with closer average flow volume for comparison.