Toward Unified pH of Saline Solutions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Reagents and Solution Preparation
2.2. Measurement Methods
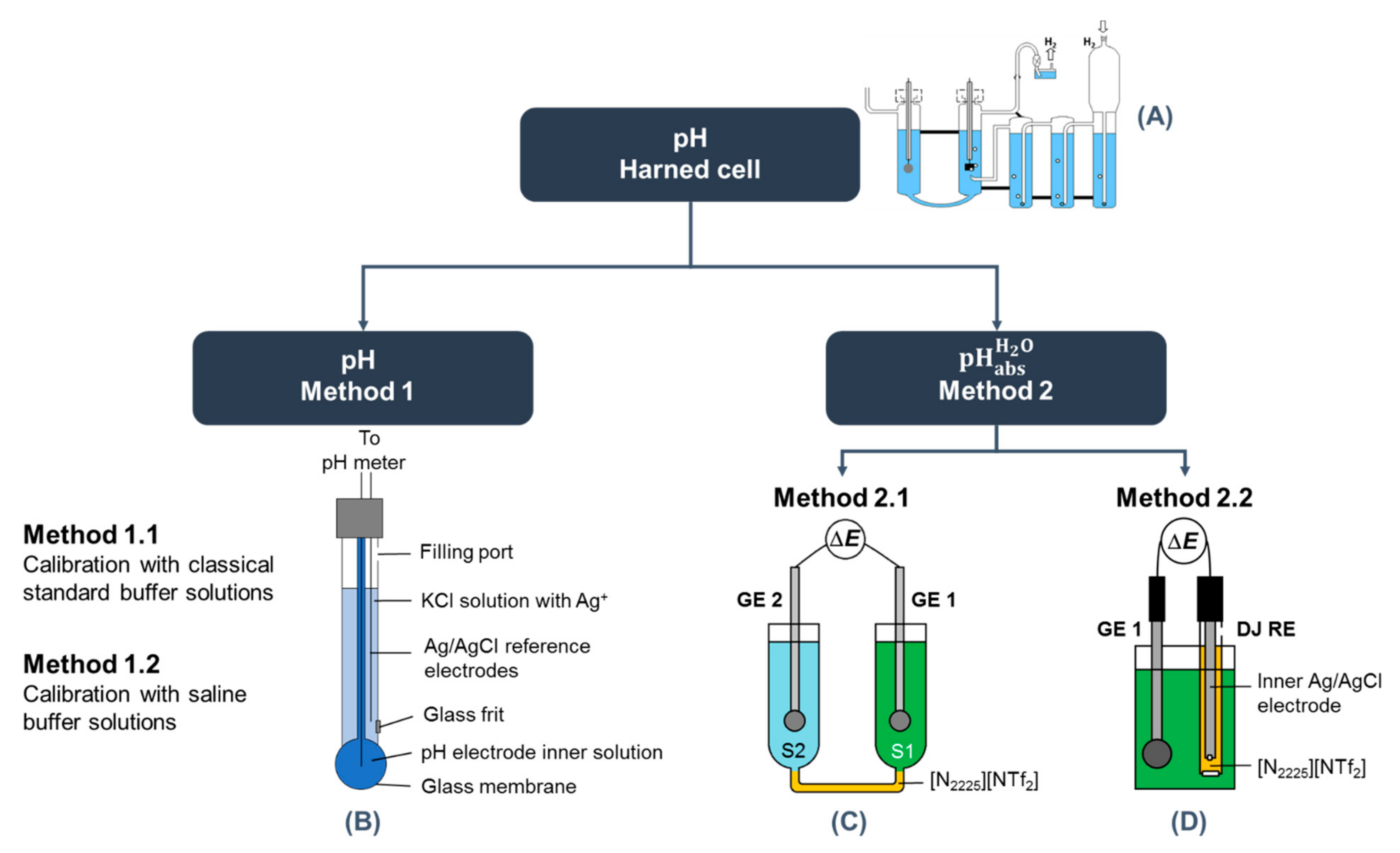
2.2.1. Primary Method Used to Assign Reference pH Values for Tris-Tris·HCl Buffer Solutions
2.2.2. pH Measurements with Classical Combination pH Electrodes
2.2.3. Measurements
2.2.4. Determination of RLJP
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Newton, J.A.; Feely, R.A.; Jewett, E.B.; Williamson, P.; Mathis, J. Global Ocean Acidification Observing Network: Requirements and Governance Plan, 2nd ed. GOA-ON. Available online: http://www.goa-on.org/documents/general/GOA-ON_2nd_edition_final.pdf (accessed on 22 July 2021).
- Tiwari, T.; Buffam, I.; Sponseller, R.A.; Laudon, H. Inferring scale-dependent processes influencing stream water biogeochemistry from headwater to sea. Limnol. Oceanogr. 2017, 62, S58–S70. [Google Scholar] [CrossRef]
- Buck, R.P.; Rondinini, S.; Covington, A.K.; Baucke, F.G.K.; Brett, C.M.A.; Camoes, M.F.; Milton, M.J.T.; Mussini, T.; Naumann, R.; Pratt, K.W.; et al. Measurement of pH. Definition, standards, and procedures. Pure Appl. Chem. 2002, 74, 2169–2200. [Google Scholar] [CrossRef] [Green Version]
- Dickson, A.G.; Camões, M.F.; Spitzer, P.; Fisicaro, P.; Stoica, D.; Pawlowicz, R.; Feistel, R. Metrological challenges for measurements of key climatological observables. Part 3: Seawater pH. Metrologia 2015, 53, R26. [Google Scholar] [CrossRef]
- Stoica, D.; Anes, B.; Fisicaro, P.; Camões, M.F. Feasibility of multifunction calibration of H+ responsive glass electrodes in seawater. J. Pure Appl. Chem. 2021. [Google Scholar] [CrossRef]
- Anes, B.; da Silva, R.J.B.; Oliveira, C.; Camões, M.F. Seawater pH measurements with a combination glass electrode and high ionic strength TRIS-TRIS HCl reference buffers—An uncertainty evaluation approach. Talanta 2019, 193, 118–122. [Google Scholar] [CrossRef] [PubMed]
- Naumann, R.; Alexander-Weber, C.; Eberhardt, R.; Giera, J.; Spitzer, P. Traceability of pH measurements by glass electrode cells: Performance characteristic of pH electrodes by multi-point calibration. Anal. Bioanal. Chem. 2002, 374, 778–786. [Google Scholar] [CrossRef] [PubMed]
- Kakiuchi, T. Salt bridge in electroanalytical chemistry: Past, present, and future. J. Solid State Electrochem. 2011, 15, 1661–1671. [Google Scholar] [CrossRef]
- Radtke, V.; Ermantraut, A.; Himmel, D.; Koslowski, T.; Leito, I.; Krossing, I. The Ideal ionic liquid salt bridge for the direct determination of gibbs energies of transfer of single ions, Part I: The concept. Angew. Chem. 2018, 57, 2344–2347. [Google Scholar] [CrossRef] [PubMed]
- Ermantraut, A.; Radtke, V.; Gebel, N.; Himmel, D.; Koslowski, T.; Leito, I.; Krossing, I. The ideal ionic liquid salt bridge for direct determination of gibbs energies of transfer of single ions, Part II: Evaluation of the role of ion solvation and ion mobilities. Angew. Chem. 2018, 57, 2348–2352. [Google Scholar] [CrossRef] [PubMed]
- Suu, A.; Jalukse, L.; Liigand, J.; Kruve, A.; Himmel, D.; Krossing, I.; Roses, M.; Leito, I. Unified pH values of liquid chromatography mobile phases. Anal. Chem. 2015, 87, 2623–2630. [Google Scholar] [CrossRef] [PubMed]
- Carstensen, J.; Duarte, C.M. Drivers of pH variability in coastal ecosystems. Environ. Sci. Technol. 2019, 53, 4020–4029. [Google Scholar] [CrossRef] [PubMed]
- Dickson, A.G. Standard potential of the reaction: AgCl (s)+ 12H2 (g)= Ag (s)+ HCl (aq), and the standard acidity constant of the ion HSO4- in synthetic sea water from 273.15 to 318.15 K. J. Chem. Thermodyn. 1990, 22, 113–127. [Google Scholar] [CrossRef]
- Heering, A.; Stoica, D.; Camões, F.; Anes, B.; Nagy, D.; Nagyné Szilágyi, Z.; Quendera, R.; Ribeiro, L.; Bastkowski, F.; Born, R.; et al. Symmetric potentiometric cells for the measurement of unified pH values. Symmetry 2020, 12, 1150. [Google Scholar] [CrossRef]
- Bastkowski, F.; Heering, A. EMPIR JRP FUN-09 realisation of a unified pH scale—Deliverable 2—Report on interlaboratory comparison to evaluate the performance of measurement procedures. (unpublished work).
- Anes, B.; da Silva, R.J.B.; Martins, H.F.; Oliveira, C.S.; Camoes, M.F. Compatibility of activity coefficients estimated experimentally and by Pitzer equations for the assessment of seawater pH. Accredit. Qual. Assur. 2016, 21, 1–7. [Google Scholar] [CrossRef]
- Camões, M.F.; Anes, B. Traceability of pH to the Mole. Water 2015, 7, 4247–4255. [Google Scholar] [CrossRef] [Green Version]
- Radtke, V.; Stoica, D.; Leito, I.; Camões, F.; Krossing, I.; Anes, B.; Roziková, M.; Deleebeeck, L.; Veltzé, S.; Näykki, T.; et al. A unified pH scale for all solvents Part I Intention and Reasoning. J. Pure Appl. Chem. 2021. [Google Scholar] [CrossRef]
- Lindner, E.; Guzinski, M.; Khan, T.A.; Pendley, B.D. Reference electrodes with ionic liquid salt bridge: When will these innovative novel reference electrodes gain broad acceptance? ACS Sens. 2019, 4, 549–561. [Google Scholar] [CrossRef] [PubMed]
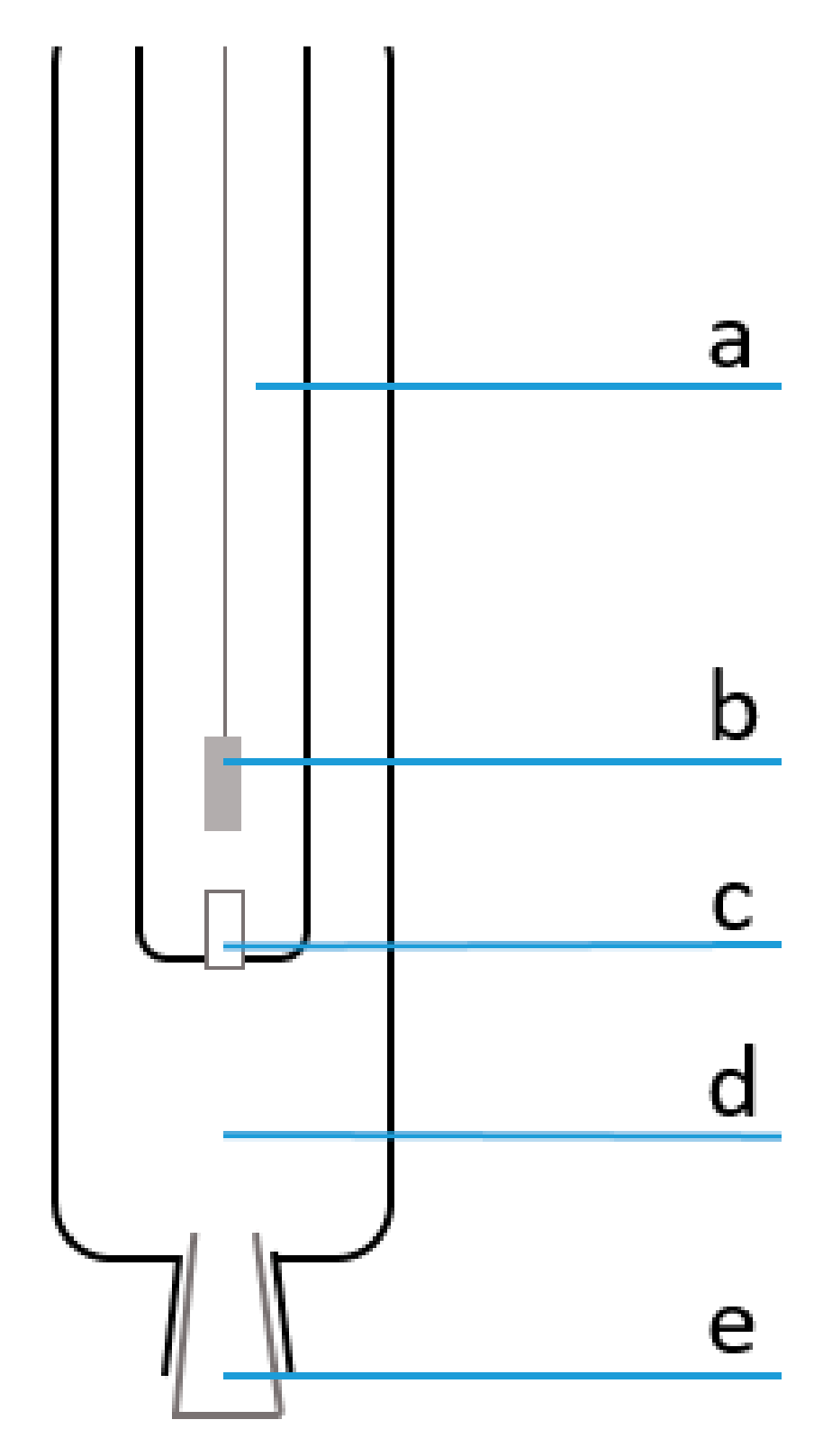
| m(Tris·HCl)/mol kg−1 | m(Tris) | m(HCl) | m(NaCl) | |
|---|---|---|---|---|
| /mol kg−1 | ||||
| buffer 1 | 0.03 | 0.079999 | 0.029999 | 0.376533 |
| buffer 2 | 0.04 | 0.080002 | 0.040000 | 0.366522 |
| buffer 3 | 0.05 | 0.079992 | 0.050001 | 0.356519 |
| Method 2.1 | Method 2.2 | |
|---|---|---|
| Scheme | SCGE2 | S2 | [N2225][NTf2] | S1 | SCGE1 R3 | UT: SCGE | Solution | [N2225][NTf2] | sat. KCl (aq) | AgCl | Ag LNE: SCGE | Solution | [N2225][NTf2] | 3 M KCl (aq) | AgCl | Ag R4 |
| Cell | UT: Special water-jacketed glass cell from Gebr. Rettberg (Göttingen, Germany) LNE: Special thermostating water jacket from Hubert Košt’ál, Czech | UT: The same cell was used as in method 2.1, but the whole cell was filled only with single solution LNE: Analyzed solutions and electrodes were placed in a PP tube, and the whole was immersed in a flow-through glass cell to enable temperature control |
| SCGE calibration | Aqueous standard buffers with nominal pH 4, 7, and 10. UT: Buffer solutions purchased from FlukaTM, Honeywell, Charlotte, NC, USA LNE: Buffer solutions purchased from Hach Lange (Radiometer) | |
| UT: Measurements against a Radiometer K401 (Copenhagen, Denmark) saturated calomel reference electrode LNE: Measurements against a Radiometer XR300 (Hach) saturated Ag/AgCl reference electrode | UT: Measurements against a double junction Methrom Ag/AgCl reference electrode 6.0729.100 LNE: Measurements against a double junction Methrom Ag/AgCl reference electrode 6.0729.100 | |
| Instrument for potential measurement | UT: Metrohm 713 pH meter. The cell and electrodes were all placed inside a Faraday cage (VistaShield™, Gamry Instruments, Warminster, PA, USA) LNE: Bio-Logic SP200 potentiostat equipped with a low current module. Analog filtering at 5 Hz was carried out to limit the electromagnetic noise and obtain a smooth signal. The cell and electrodes were all placed inside a Faraday cage (Bio-Logic) | |
| Data collection | UT: Collection over 1 h with a sampling interval of 5 s. Data collection started after the electrodes were inserted. LNE: Collection over at least 30 min with a sampling interval of 10 s. Data collection started after the electrodes were inserted | UT: Collection over 900 s with a sampling interval of 5 s. Data collection started after the electrodes were inserted. LNE: Collection over at least 30 min with a sampling interval of 10 s. Data collection started after the electrodes were inserted |
| Data analysis | UT: Average of data collected between 30 and 60 min (361 points) LNE: The most stable data over consecutively 15 min (91 points) | UT: Average of data collected between 300 and 360 s (13 points) LNE: The most stable data over consecutively 15 min (91 points) |
| Molality of NaCl Solution/mol kg−1 | |||
|---|---|---|---|
| 0.005 | 0.9276 | 0.0046 | −2.333 |
| 0.010 | 0.9028 | 0.0090 | −2.044 |
| 0.100 | 0.7771 | 0.0777 | −1.109 |
| 0.407 | 0.6909 | 0.2809 | −0.551 |
| 0.670 | 0.6680 | 0.4475 | −0.349 |
| 0.800 | 0.6622 | 0.5298 | −0.276 |
| Sample | pH | ||||||
|---|---|---|---|---|---|---|---|
| pHprimary | Method 1.1 | Method 1.2 | Method 2.1 | Method 2.2 | |||
| UT | LNE | UT | LNE | ||||
| buffer 1 | 8.494 ± 0.003 | 8.40 ± 0.01 | / | 8.40 ± 0.13 | 8.40 ± 0.12 | 8.39 ± 0.13 | 8.41 ± 0.12 |
| buffer 2 | 8.270 ± 0.003 | 8.18 ± 0.01 | 8.28 ± 0.01 | 8.21 ± 0.13 | 8.20 ± 0.12 | 8.17 ± 0.13 | 8.11 ± 0.12 |
| buffer 3 | 8.048 ± 0.003 | 7.96 ± 0.01 | / | 7.98 ± 0.13 | 7.98 ± 0.12 | 7.95 ± 0.13 | 7.98 ± 0.12 |
| Molality of NaCl Solution/mol kg−1 | ILSB | KClSB | ||||||
|---|---|---|---|---|---|---|---|---|
| ΔEmeas/mV | RLJP/mV | Effect on pH | ΔEmeas/mV | ϕ/mV | RLJP/mV | Effect on pH | ||
| 0.005 | −204.921 | −49.184 | 1.553 | 0.026 | 0.595 | 0.0101 | 3.0439 | 0.051 |
| 0.010 | −188.392 | −49.767 | 0.970 | 0.016 | −0.232 | −0.0039 | 2.2166 | 0.037 |
| 0.100 | −134.051 | −50.737 | 0 | 0 | −2.449 | −0.0414 | 0 | 0 |
| 0.407 | −106.439 | −56.134 | −5.397 | −0.091 | −4.595 | −0.0777 | −2.1455 | −0.036 |
| 0.670 | −94.462 | −56.129 | −5.392 | −0.091 | −5.204 | −0.0880 | −2.7553 | −0.046 |
| 0.800 | −91.170 | −57.169 | −6.432 | −0.109 | −6.112 | −0.1033 | −3.6632 | −0.062 |
| 0.005 (back) | −205.86 | 50.125 | 0.611 | 0.010 | 0.4036 | 0.0068 | 2.8526 | 0.048 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lainela, S.; Leito, I.; Heering, A.; Capitaine, G.; Anes, B.; Camões, F.; Stoica, D. Toward Unified pH of Saline Solutions. Water 2021, 13, 2522. https://doi.org/10.3390/w13182522
Lainela S, Leito I, Heering A, Capitaine G, Anes B, Camões F, Stoica D. Toward Unified pH of Saline Solutions. Water. 2021; 13(18):2522. https://doi.org/10.3390/w13182522
Chicago/Turabian StyleLainela, Silvie, Ivo Leito, Agnes Heering, Gaëlle Capitaine, Bárbara Anes, Filomena Camões, and Daniela Stoica. 2021. "Toward Unified pH of Saline Solutions" Water 13, no. 18: 2522. https://doi.org/10.3390/w13182522







