Evaluating the Performance of Machine Learning Approaches to Predict the Microbial Quality of Surface Waters and to Optimize the Sampling Effort
Abstract
:1. Introduction
- (1)
- We propose to compare the performance of six machine-learning models, including three traditional models and three ensemblist models, to predict the concentrations of the fecal indicator bacteria Escherichia coli. To train and test the models, meteorological data and river flow data should be aggregated with physico-chemical data.
- (2)
- For the chosen model, we propose to set up an alert system on the performance of the model in order to optimize the data collection. This alert should consist in identifying under which conditions the model fails to make the prediction and thus alerting the managers to carry out on site analysis in order to enrich the database.
- (3)
- The usefulness of a network of low-cost sensors for sampling optimization as a complementary strategy to improve the dataset is discussed.
2. Materials and Methods
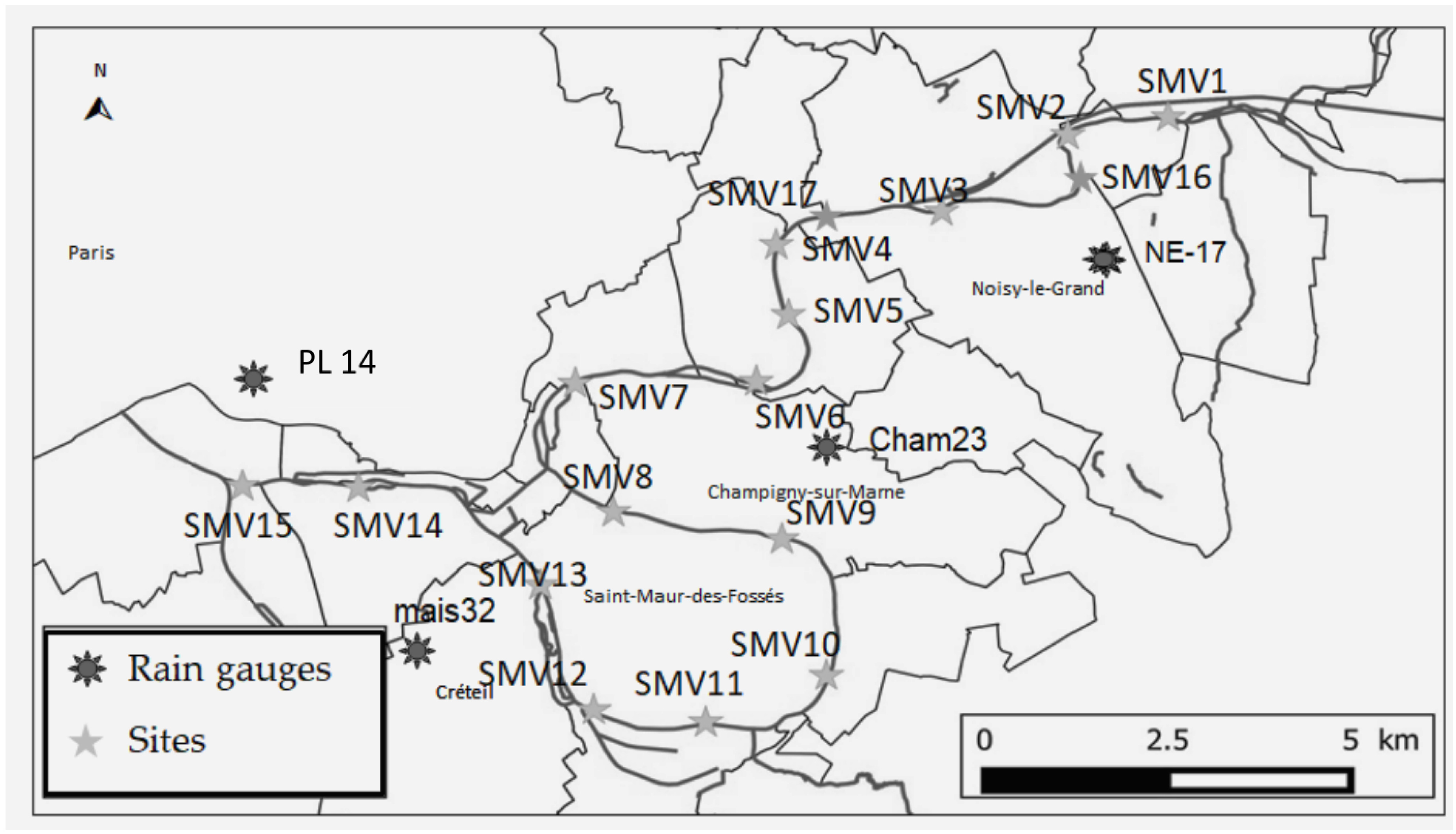
2.1. Study Site and Water Quality Data Collection
2.2. Data Preparation
2.3. Machine-Learning Models
2.3.1. KNN
2.3.2. SVM
2.3.3. DT
2.3.4. Bagging
2.3.5. RF
2.3.6. Adaboost
2.4. Models Evaluation
2.5. Identification of the Weakness Parts of the Dataset
3. Results and Discussion
3.1. The Dataset Used in This Study
3.2. ML-Based E. coli Prediction Comparison
3.3. Limits of ML-Based E. coli Estimation
3.4. Identification of the Weaknesses in the Dataset
4. Automated Data Collection
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
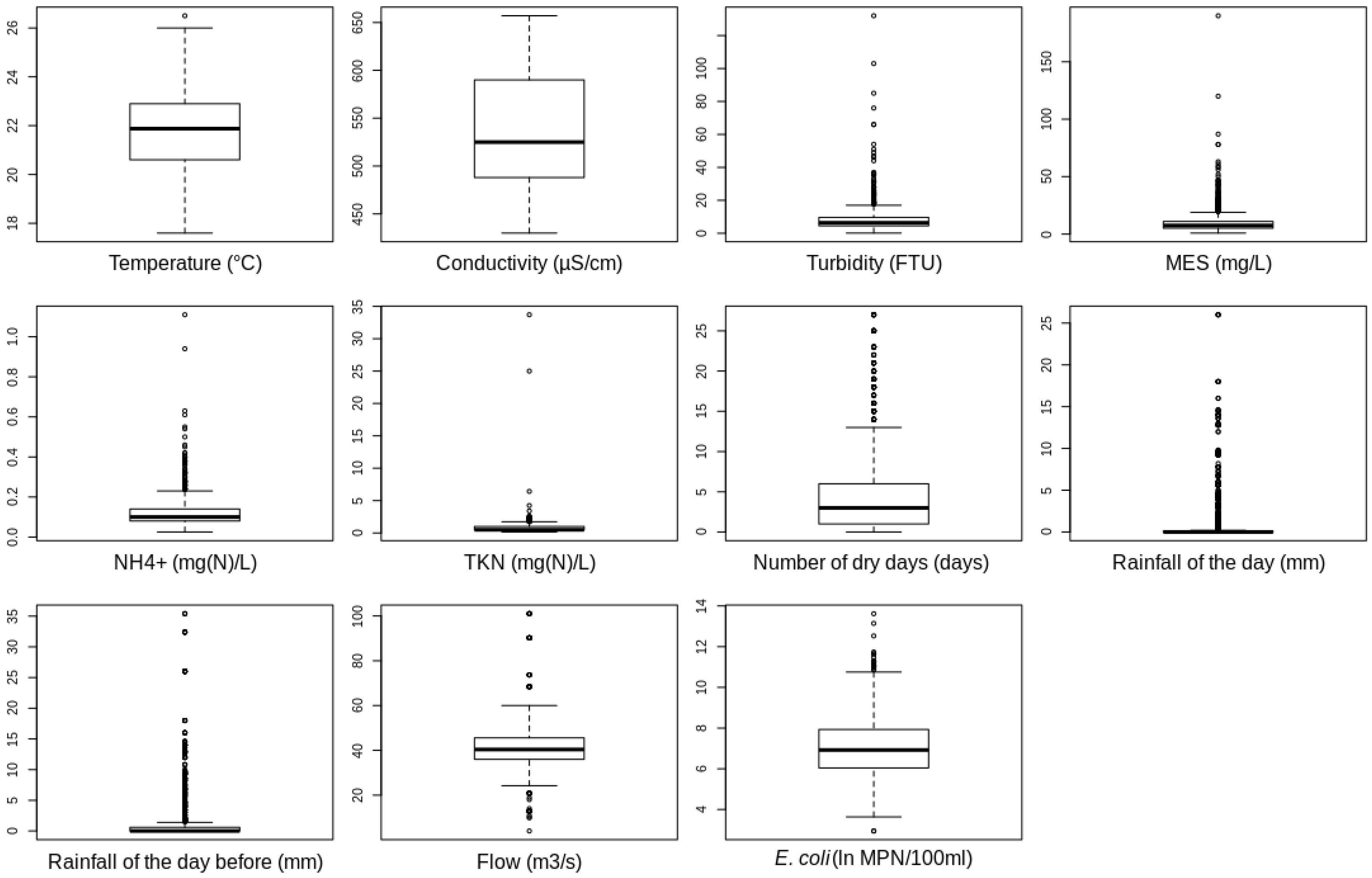
| Parameters | Mean | Standard Deviation | Minimum | Maximum |
|---|---|---|---|---|
| Water temperature | 21.77 | 1.59 | 17.60 | 26.50 |
| Conductivity | 537.36 | 56.09 | 430.00 | 657.00 |
| Turbidity | 7.91 | 7.33 | 0.12 | 132.00 |
| TSS | 9.76 | 9.13 | 0.90 | 190.00 |
| NH | 0.12 | 0.07 | 0.03 | 1.11 |
| TKN | 0.72 | 1.08 | 0.15 | 33.70 |
| Number of dry days | 4.80 | 5.72 | 0.00 | 27.00 |
| 24 h cumulative rainfall of the day | 0.97 | 2.90 | 0.00 | 26.00 |
| 24 h cumulative rainfall of the previous day | 1.86 | 4.69 | 0.00 | 35.40 |
| River flow | 41.68 | 10.59 | 4.00 | 101.00 |
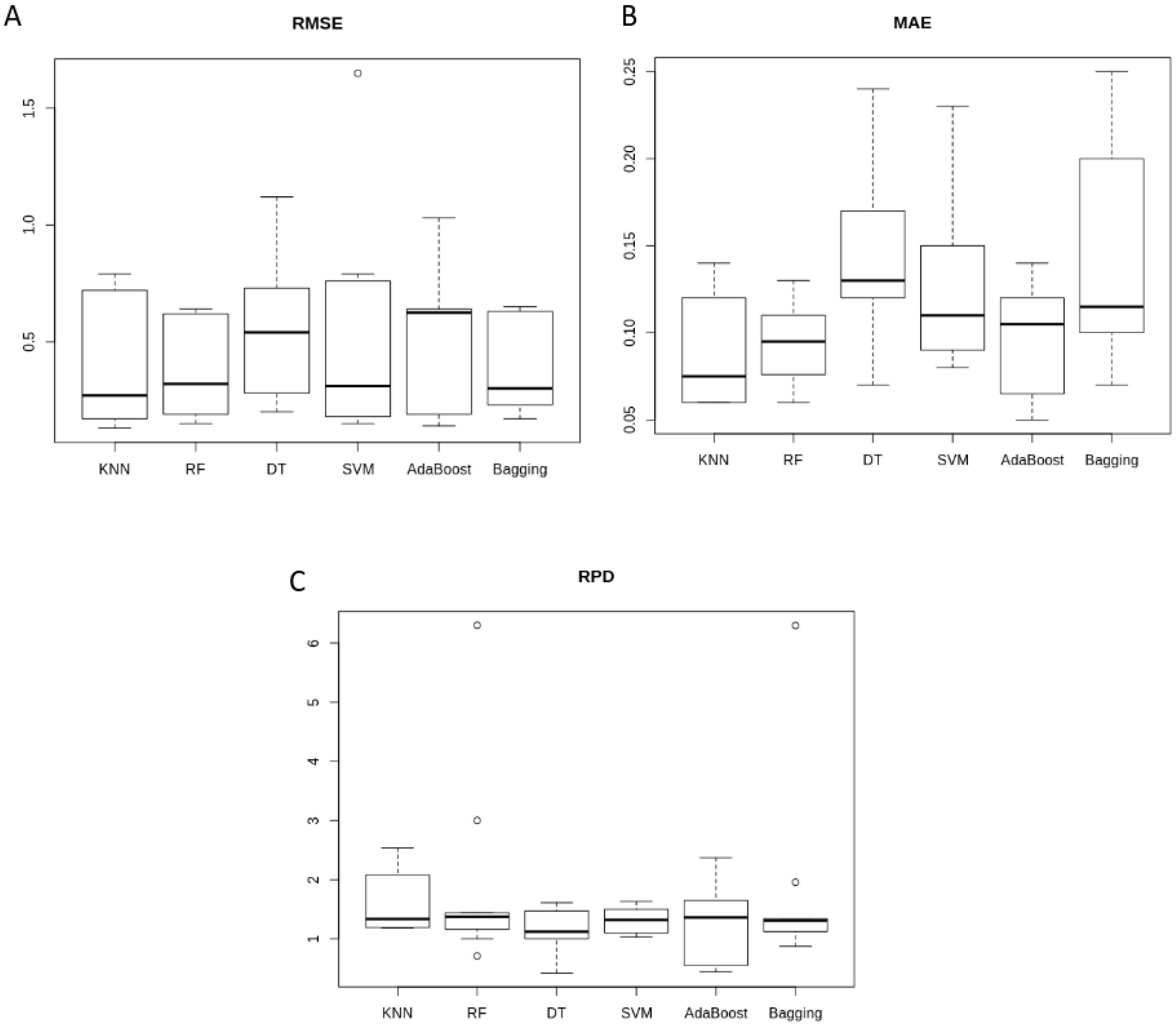
| Model | KNN | RF | DT | SVM | AdaBoost | Bagging |
|---|---|---|---|---|---|---|
| RMSE | 0.41 ± 0.28 | 0.37 ± 0.20 | 0.54 ± 0.29 | 0.53 ± 0.48 | 0.53 ± 0.28 | 0.38 ± 0.19 |
| MAE | 0.09 ± 0.03 | 0.09 ± 0.02 | 0.14 ± 0.05 | 0.13 ± 0.05 | 0.10 ± 0.03 | 0.14 ± 0.06 |
| RDP | 1.60 ± 0.49 | 1.91 ± 1.65 | 1.12 ± 0.36 | 1.32 ± 0.22 | 1.28 ± 0.62 | 1.77 ± 1.62 |
References
- Jang, C.S. Using probability-based spatial estimation of the river pollution index to assess urban water recreational quality in the Tamsui River watershed. Environ. Monit. Assess. 2015, 188, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Davies-Colley, R.; Valois, A.; Milne, J. Faecal pollution and visual clarity in New zealand rivers: Correlation of key variables affecting swimming suitability. J. Water Health 2018, 16, wh2018214. [Google Scholar] [CrossRef] [PubMed]
- Soller, J.A.; Schoen, M.E.; Bartrand, T.; Ravenscroft, J.E.; Ashbolt, N.J. Estimated human health risks from exposure to recreational waters impacted by human and non-human sources of faecal contamination. Water Res. 2010, 44, 4674–4691. [Google Scholar] [CrossRef]
- Mallin, M.A.; Williams, K.E.; Esham, E.C.; Lowe, R.P. Effect of human development on bacteriological water quality in coastal watersheds. Ecol. Appl. 2000, 10, 1047–1056. [Google Scholar] [CrossRef]
- Passerat, J.; Ouattara, N.K.; Mouchel, J.M.; Rocher, V.; Servais, P. Impact of an intense combined sewer overflow event on the microbiological water quality of the Seine River. Water Res. 2011, 45, 893–903. [Google Scholar] [CrossRef]
- Dueker, M.E.; O’Mullan, G.; Martínez, J.M.; Juhl, A.; Weathers, K. Onshore Wind Speed Modulates Microbial Aerosols along an Urban Waterfront. Atmosphere 2017, 8, 215. [Google Scholar] [CrossRef] [Green Version]
- Droppo, I.G.; Liss, S.N.; Williams, D.; Nelson, T.; Jaskot, C.; Trapp, B. Dynamic Existence of Waterborne Pathogens within River Sediment Compartments. Implications for Water Quality Regulatory Affairs. Environ. Sci. Technol. 2009, 43, 1737–1743. [Google Scholar] [CrossRef]
- Garcia-Armisen, T.; Servais, P. Partitioning and Fate of Particle-Associated E. coli in River Water. Water Environ. Res. Res. Publ. Water Environ. Fed. 2009, 81, 21–28. [Google Scholar] [CrossRef]
- Ahmed, W.; Hamilton, K.; Toze, S.; Cook, S.; Page, D. A review on microbial contaminants in stormwater runoff and outfalls: Potential health risks and mitigation strategies. Sci. Total Environ. 2019, 692, 1304–1321. [Google Scholar] [CrossRef]
- Whitehead, P.G.; Wilby, R.L.; Battarbee, R.W.; Kernan, M.; Wade, A.J. A review of the potential impacts of climate change on surface water quality. Hydrol. Sci. J. 2009, 54, 101–123. [Google Scholar] [CrossRef]
- WHO. World Health Organization. 2018. Available online: https://www.who.int/docs/default-source/wash-documents/who-recommendations-on-ec-bwd-august-2018.pdf (accessed on 16 July 2021).
- Weiskerger, C.J.; Phanikumar, M.S. Numerical Modeling of Microbial Fate and Transport in Natural Waters: Review and Implications for Normal and Extreme Storm Events. Water 2020, 12, 1876. [Google Scholar] [CrossRef]
- Jovanovic, D.; Gelsinari, S.; Bruce, L.; Hipsey, M.; Teakle, I.; Barnes, M.; Coleman, R.; Deletic, A.; Mccarthy, D.T. Modelling shallow and narrow urban salt-wedge estuaries: Evaluation of model performance and sensitivity to optimise input data collection. Estuar. Coast. Shelf Sci. 2019, 217, 9–27. [Google Scholar] [CrossRef]
- Nnane, D.E.; Ebdon, J.E.; Taylor, H.D. Integrated analysis of water quality parameters for cost-effective faecal pollution management in river catchments. Water Res. 2011, 45, 2235–2246. [Google Scholar] [CrossRef]
- Bui, D.T.; Khosravi, K.; Tiefenbacher, J.; Nguyen, H.; Kazakis, N. Improving prediction of water quality indices using novel hybrid machine-learning algorithms. Sci. Total Environ. 2020, 721, 137612. [Google Scholar] [CrossRef]
- Banda, T.; Kumarasamy, M. Application of Multivariate Statistical Analysis in the Development of a Surrogate Water Quality Index (WQI) for South African Watersheds. Water 2020, 12, 1584. [Google Scholar] [CrossRef]
- Ghahramani, Z. Probabilistic machine learning and artificial intelligence. Nature 2015, 521, 452–459. [Google Scholar] [CrossRef]
- Mälzer, H.J.; aus der Beek, T.; Müller, S.; Gebhardt, J. Comparison of different model approaches for a hygiene early warning system at the lower Ruhr River, Germany. Int. J. Hyg. Environ. Health 2016, 219, 671–680. [Google Scholar] [CrossRef] [PubMed]
- Qiu, X.; Ren, Y.; Suganthan, P.N.; Amaratunga, G.A. Empirical Mode Decomposition based ensemble deep learning for load demand time series forecasting. Appl. Soft Comput. 2017, 54, 246–255. [Google Scholar] [CrossRef]
- Chen, K.; Chen, H.; Zhou, C.; Huang, Y.; Qi, X.; Shen, R.; Liu, F.; Zuo, M.; Zou, X.; Wang, J.; et al. Comparative analysis of surface water quality prediction performance and identification of key water parameters using different machine learning models based on big data. Water Res. 2020, 171, 115454. [Google Scholar] [CrossRef] [PubMed]
- Qian, P.; Chen, Y.; Kuo, J.W.; Zhang, Y.D.; Jiang, Y.; Zhao, K.; Al Helo, R.; Friel, H.; Baydoun, A.; Zhou, F.; et al. mDixon-Based Synthetic CT Generation for PET Attenuation Correction on Abdomen and Pelvis Jointly Using Transfer Fuzzy Clustering and Active Learning-Based Classification. IEEE Trans. Med. Imaging 2020, 39, 819–832. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, J.; Wu, Q.; Jia, Y.; Zhou, B.; Wei, X.; Yu, P.S. Constrained Active Learning for Anchor Link Prediction Across Multiple Heterogeneous Social Networks. Sensors 2017, 17, 1786. [Google Scholar] [CrossRef]
- Bouneffouf, D. Exponentiated Gradient Exploration for Active Learning. Computers 2016, 5, 1. [Google Scholar] [CrossRef] [Green Version]
- Public Lab KnowFLow. Available online: https://www.eea.europa.eu/publications/european-bathing-water-quality-in-2018 (accessed on 30 June 2021).
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Swain, P.H.; Hauska, H. The decision tree classifier: Design and potential. IEEE Trans. Geosci. Electron. 1977, 15, 142–147. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Freund, Y.; Schapire, R. Experiments with a New Boosting Algorithm. In Proceedings of the Thirteenth International Conference on International Conference on Machine Learning, Bari, Italy, 3–6 July 1996; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1996; pp. 148–156. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Hastie, T. The Elements of Statistical Learning Data Mining, Inference, and Prediction, 2nd ed.; Springer Series in Statistics; Springer: New York, NY, USA, 2009. [Google Scholar]
- Barboza, F.; Kimura, H.; Altman, E. Machine learning models and bankruptcy prediction. Expert Syst. Appl. 2017, 83, 405–417. [Google Scholar] [CrossRef]
- Shrestha, D.; Solomatine, D. Experiments with AdaBoost.RT, an Improved Boosting Scheme for Regression. Neural Comput. 2006, 18, 1678–1710. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Ding, J. Evaluation of water quality based on a machine learning algorithm and water quality index for the Ebinur Lake Watershed, China. Sci. Rep. 2017, 7, 1–18. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lewis, C.D. Industrial and Business Forecasting Methods: A Practical Guide to Exponential Smoothing and Curve Fitting/Colin D. Lewis; Butterworth Scientific: London, UK, 1982; p. 143. [Google Scholar]
- Yan, J.; Gao, Y.; Yu, Y.; Xu, H.; Xu, Z. A Prediction Model Based on Deep Belief Network and Least Squares SVR Applied to Cross-Section Water Quality. Water 2020, 12, 1929. [Google Scholar] [CrossRef]
- Lu, H.; Ma, X. Hybrid decision tree-based machine learning models for short-term water quality prediction. Chemosphere 2020, 249, 126169. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018. [Google Scholar]
- Sylvestre, É.; Burnet, J.B.; Smeets, P.; Medema, G.; Prévost, M.; Dorner, S. Can routine monitoring of E. coli fully account for peak event concentrations at drinking water intakes in agricultural and urban rivers? Water Res. 2020, 170, 115369. [Google Scholar] [CrossRef]
- Avila, R.; Horn, B.; Moriarty, E.; Hodson, R.; Moltchanova, E. Evaluating statistical model performance in water quality prediction. J. Environ. Manag. 2018, 206, 910–919. [Google Scholar] [CrossRef]
- Ahmed, U.; Mumtaz, R.; Anwar, H.; Shah, A.A.; Irfan, R.; García-Nieto, J. Efficient Water Quality Prediction Using Supervised Machine Learning. Water 2019, 11, 2210. [Google Scholar] [CrossRef] [Green Version]
- Pachepsky, Y.A.; Allende, A.; Boithias, L.; Cho, K.; Jamieson, R.; Hofstra, N.; Molina, M. Microbial Water Quality: Monitoring and Modeling. J. Environ. Qual. 2018, 47, 931–938. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hameed, M.; Sharqi, S.S.; Yaseen, Z.M.; Afan, H.A.; Hussain, A.; Elshafie, A. Application of artificial intelligence (AI) techniques in water quality index prediction: A case study in tropical region, Malaysia. Neural Comput. Appl. 2017, 28, 893–905. [Google Scholar] [CrossRef]
- Muslea, I.; Minton, S.; Knoblock, C.A. Active Learning with Multiple Views. J. Artif. Intell. Res. 2006, 27, 203–233. [Google Scholar] [CrossRef]
- Abegaz, B.W.; Datta, T.; Mahajan, S.M. Sensor technologies for the energy-water nexus—A review. Appl. Energy 2018, 210, 451–466. [Google Scholar] [CrossRef]
- Kruse, P. Review on water quality sensors. J. Phys. D Appl. Phys. 2018, 51, 203002. [Google Scholar] [CrossRef] [Green Version]
- Cazals, M.; Stott, R.; Fleury, C.; Proulx, F.; Prévost, M.; Servais, P.; Dorner, S.; Burnet, J.B. Near real-time notification of water quality impairments in recreational freshwaters using rapid online detection of β-D-glucuronidase activity as a surrogate for Escherichia coli monitoring. Sci. Total Environ. 2020, 720, 137303. [Google Scholar] [CrossRef]
- Angelescu, D.; Huynh, V.; Hausot, A.; Yalkin, G.; Plet, V.; Mouchel, J.; Guérin-Rechdaoui, S.; Azimi, S.; Rocher, V. Autonomous system for rapid field quantification of Escherichia coli in surface waters. J. Appl. Microbiol. 2019, 126, 332–343. [Google Scholar] [CrossRef] [PubMed]
- Tryland, I.; Eregno, F.E.; Braathen, H.; Khalaf, G.; Sjølander, I.; Fossum, M. On-line monitoring of Escherichia coli in raw water at Oset drinking water treatment plant, Oslo (Norway). Int. J. Environ. Res. Public Health 2015, 12, 1788–1802. [Google Scholar] [CrossRef] [Green Version]
- Bramburger, A.J.; Brown, R.S.; Haley, J.; Ridal, J.J. A new, automated rapid fluorometric method for the detection of Escherichia coli in recreational waters. J. Great Lakes Res. 2015, 41, 298–302. [Google Scholar] [CrossRef]
- Rode, M.; Wade, A.J.; Cohen, M.J.; Hensley, R.T.; Bowes, M.J.; Kirchner, J.W.; Arhonditsis, G.B.; Jordan, P.; Kronvang, B.; Halliday, S.J.; et al. Sensors in the Stream: The High-Frequency Wave of the Present. Environ. Sci. Technol. 2016, 50, 10297–10307. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.A.; Moustahfid, H.; Mueller, A.V.; Michel, A.P.M.; Mowlem, M.; Glazer, B.T.; Mooney, T.A.; Michaels, W.; McQuillan, J.S.; Robidart, J.C.; et al. Advancing Observation of Ocean Biogeochemistry, Biology, and Ecosystems With Cost-Effective in situ Sensing Technologies. Front. Mar. Sci. 2019, 6, 519. [Google Scholar] [CrossRef]
- Nguyen, P.; Ferry, N.; Erdogan, G.; Song, H.; Lavirotte, S.; Tigli, J.Y.; Solberg, A. Advances in deployment and orchestration approaches for IoT-a systematic review. In Proceedings of the 2019 IEEE International Congress on Internet of Things (ICIOT), San Diego, CA, USA, 25–30 June 2019; pp. 53–60. [Google Scholar]
- Priyadarshi, R.; Gupta, B.; Anurag, A. Deployment techniques in wireless sensor networks: A survey, classification, challenges, and future research issues. J. Supercomput. 2020, 76, 7333–7373. [Google Scholar] [CrossRef]
- Senouci, M.R.; Mellouk, A. Deploying Wireless Sensor Networks: Theory and Practice; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Ciaponi, C.; Creaco, E.; Nardo, A.D.; Natale, M.D.; Giudicianni, C.; Musmarra, D.; Santonastaso, G.F. Optimal sensor placement in a partitioned water distribution network for the water protection from contamination. Proceedings 2018, 2, 670. [Google Scholar] [CrossRef] [Green Version]
- Ramesh, M.V.; Nibi, K.; Kurup, A.; Mohan, R.; Aiswarya, A.; Arsha, A.; Sarang, P. Water quality monitoring and waste management using IoT. In Proceedings of the IEEE Global Humanitarian Technology Conference (GHTC), San Jose, CA, USA, 19–22 October 2017; pp. 1–7. [Google Scholar]
- Mekki, K.; Bajic, E.; Chaxel, F.; Meyer, F. A comparative study of LPWAN technologies for large-scale IoT deployment. ICT Express 2019, 5, 1–7. [Google Scholar] [CrossRef]
- Rahimi, H.; Zibaeenejad, A.; Safavi, A.A. A novel IoT architecture based on 5G-IoT and next generation technologies. In Proceedings of the 2018 IEEE 9th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 1–3 November 2018; pp. 81–88. [Google Scholar]
- Betke, E.; Kunkel, J. Real-time I/O-monitoring of HPC applications with SIOX, elasticsearch, Grafana and FUSE. In International Conference on High Performance Computing; Springer: Cham, Switzerland, 2017; pp. 174–186. [Google Scholar]
- Protopsaltis, A.; Sarigiannidis, P.; Margounakis, D.; Lytos, A. Data visualization in internet of things: Tools, methodologies, and challenges. In Proceedings of the 15th International Conference on Availability, Reliability and Security, Virtual Event, Ireland, 25–28 August 2020; pp. 1–11. [Google Scholar]
- Chen, Y.; Han, D. Water quality monitoring in smart city: A pilot project. Autom. Constr. 2018, 89, 307–316. [Google Scholar] [CrossRef] [Green Version]

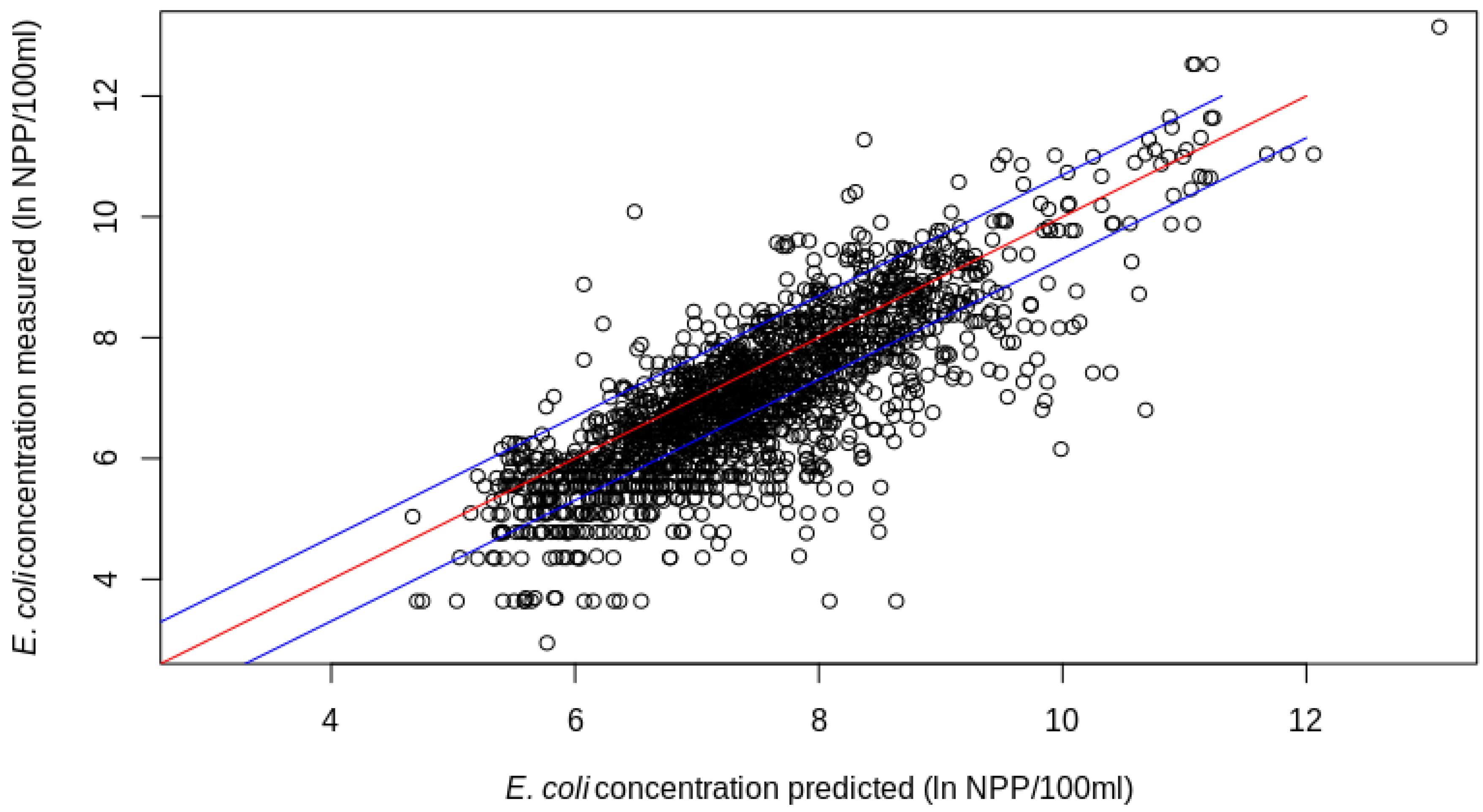
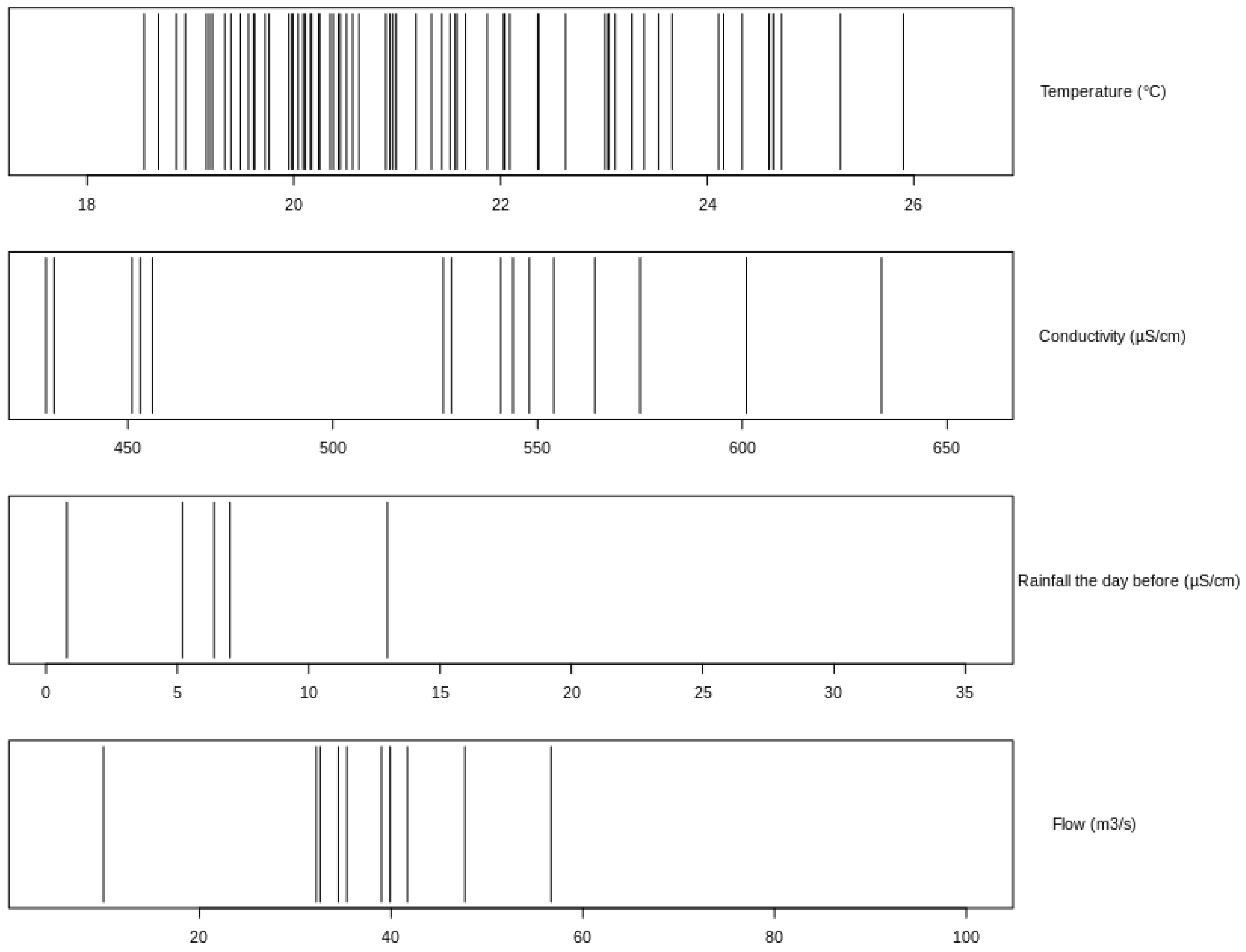
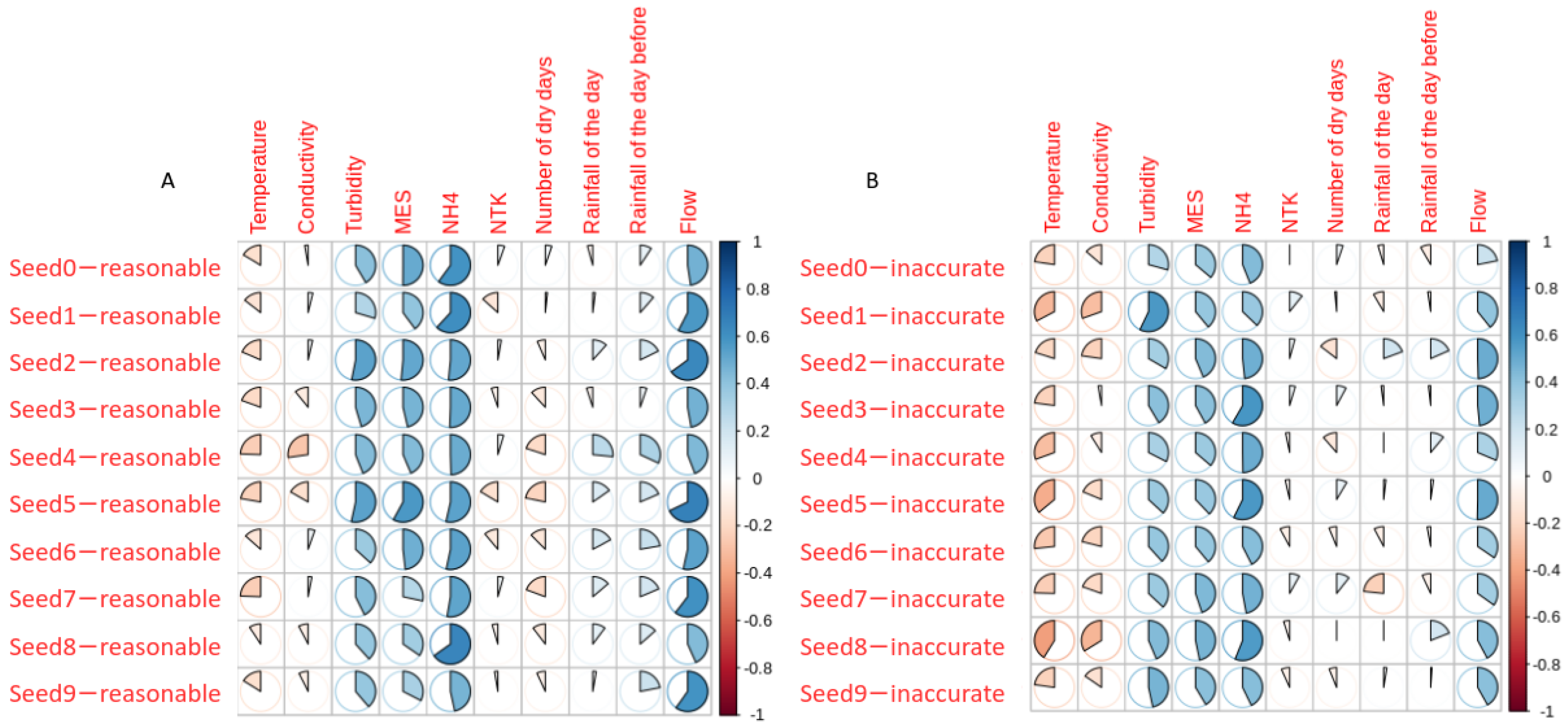
| Parameters | Reasonable Predictions r | Inaccurate Predictions r | p-Value |
|---|---|---|---|
| Water temperature | −0.17 ± 0.05 | −0.28 * ± 0.07 | 0.001 |
| Conductivity | −0.05 ± 0.11 | −0.18 ± 0.09 | 0.009 |
| Turbidity | 0.42 * ± 0.07 | 0.39 * ± 0.08 | 0.43 |
| TSS | 0.43 * ± 0.09 | 0.40 * ± 0.04 | 0.42 |
| NH | 0.54 * ± 0.06 | 0.48 * ± 0.07 | 0.05 |
| TKN | −0.03 ± 0.08 | 0.001 ± 0.06 | 0.26 |
| Number of dry days | −0.10 ± 0.09 | −0.01 ± 0.09 | 0.02 |
| 24 h cumulative rainfall of the day | 0.09 ± 0.10 | −0.02 ± 0.11 | 0.02 |
| 24 h cumulative rainfall of the previous day | 0.17 ± 0.08 | 0.03 ± 0.10 | 0.002 |
| River flow | 0.54 * ± 0.09 | 0.39 * ± 0.09 | 0.001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naloufi, M.; Lucas, F.S.; Souihi, S.; Servais, P.; Janne, A.; Wanderley Matos De Abreu, T. Evaluating the Performance of Machine Learning Approaches to Predict the Microbial Quality of Surface Waters and to Optimize the Sampling Effort. Water 2021, 13, 2457. https://doi.org/10.3390/w13182457
Naloufi M, Lucas FS, Souihi S, Servais P, Janne A, Wanderley Matos De Abreu T. Evaluating the Performance of Machine Learning Approaches to Predict the Microbial Quality of Surface Waters and to Optimize the Sampling Effort. Water. 2021; 13(18):2457. https://doi.org/10.3390/w13182457
Chicago/Turabian StyleNaloufi, Manel, Françoise S. Lucas, Sami Souihi, Pierre Servais, Aurélie Janne, and Thiago Wanderley Matos De Abreu. 2021. "Evaluating the Performance of Machine Learning Approaches to Predict the Microbial Quality of Surface Waters and to Optimize the Sampling Effort" Water 13, no. 18: 2457. https://doi.org/10.3390/w13182457
APA StyleNaloufi, M., Lucas, F. S., Souihi, S., Servais, P., Janne, A., & Wanderley Matos De Abreu, T. (2021). Evaluating the Performance of Machine Learning Approaches to Predict the Microbial Quality of Surface Waters and to Optimize the Sampling Effort. Water, 13(18), 2457. https://doi.org/10.3390/w13182457







