Aquifer Response to Stream-Stage Fluctuations: Field Tests and Analytical Solution for a Case Study of the Yangtze River in Wuhan, China
Abstract
:1. Introduction
2. Field Hydrological Monitoring Tests
2.1. Hydrological Monitoring Area
2.2. Hydrological Monitoring Plan
2.3. Hydrological Monitoring Results
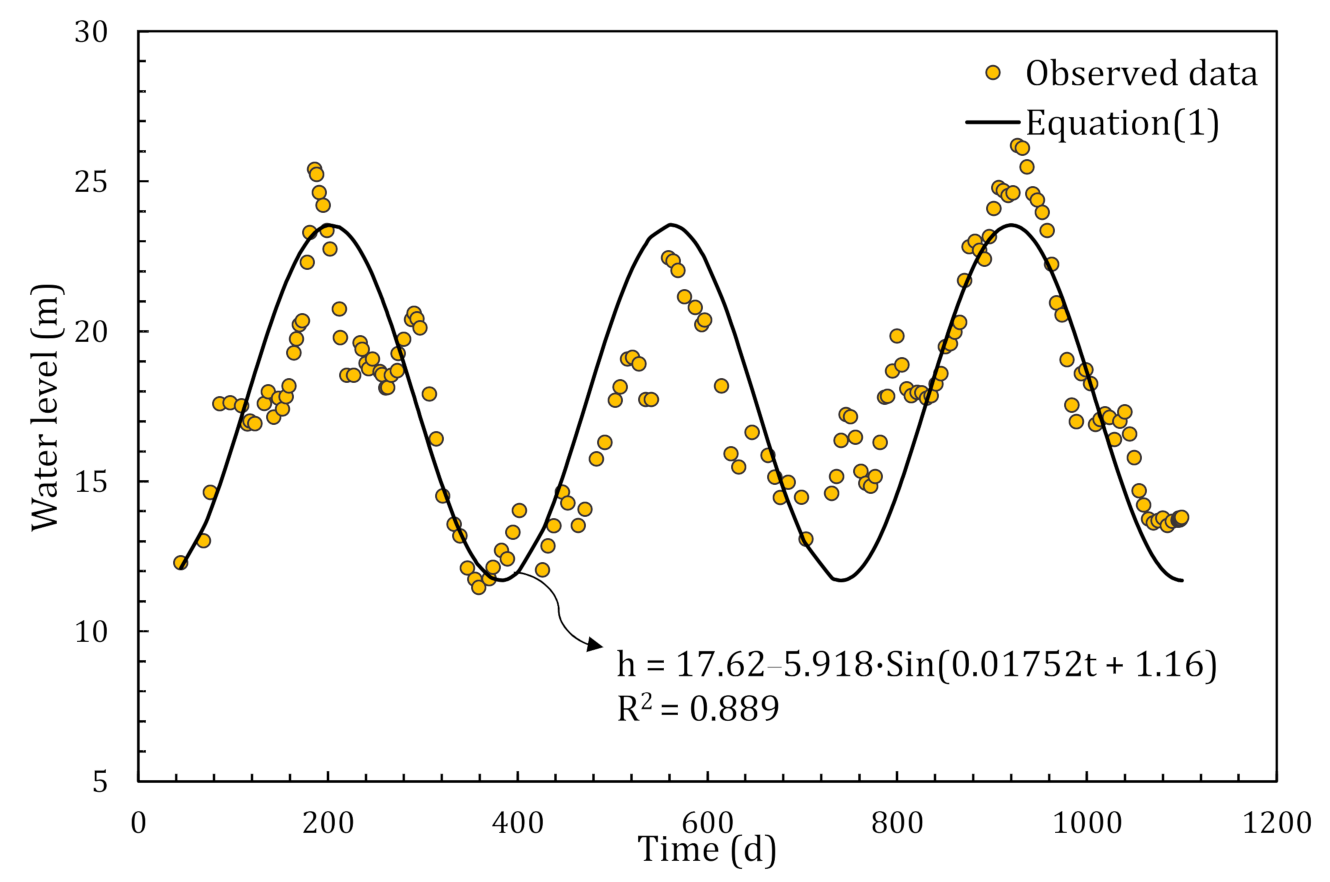
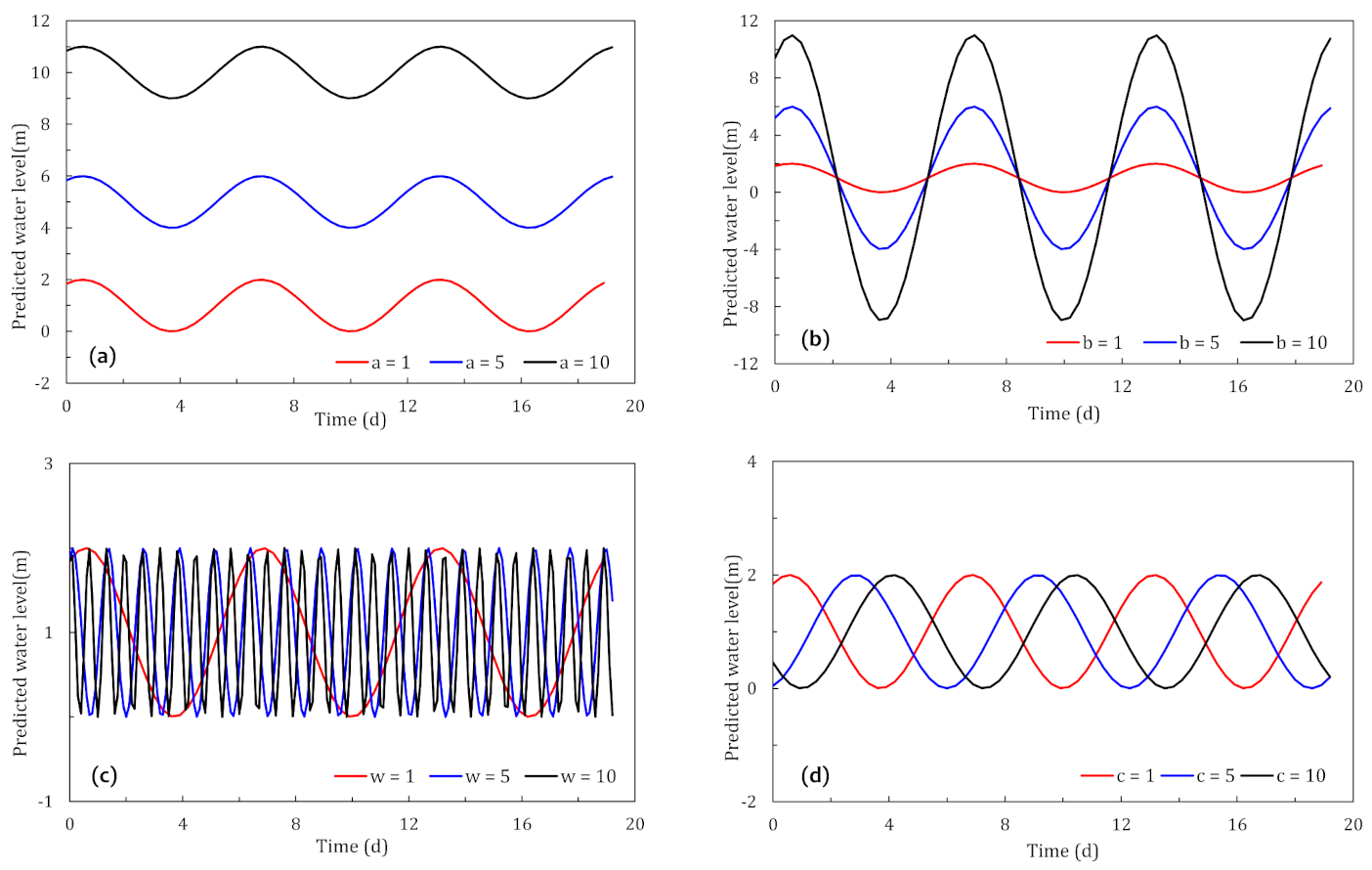
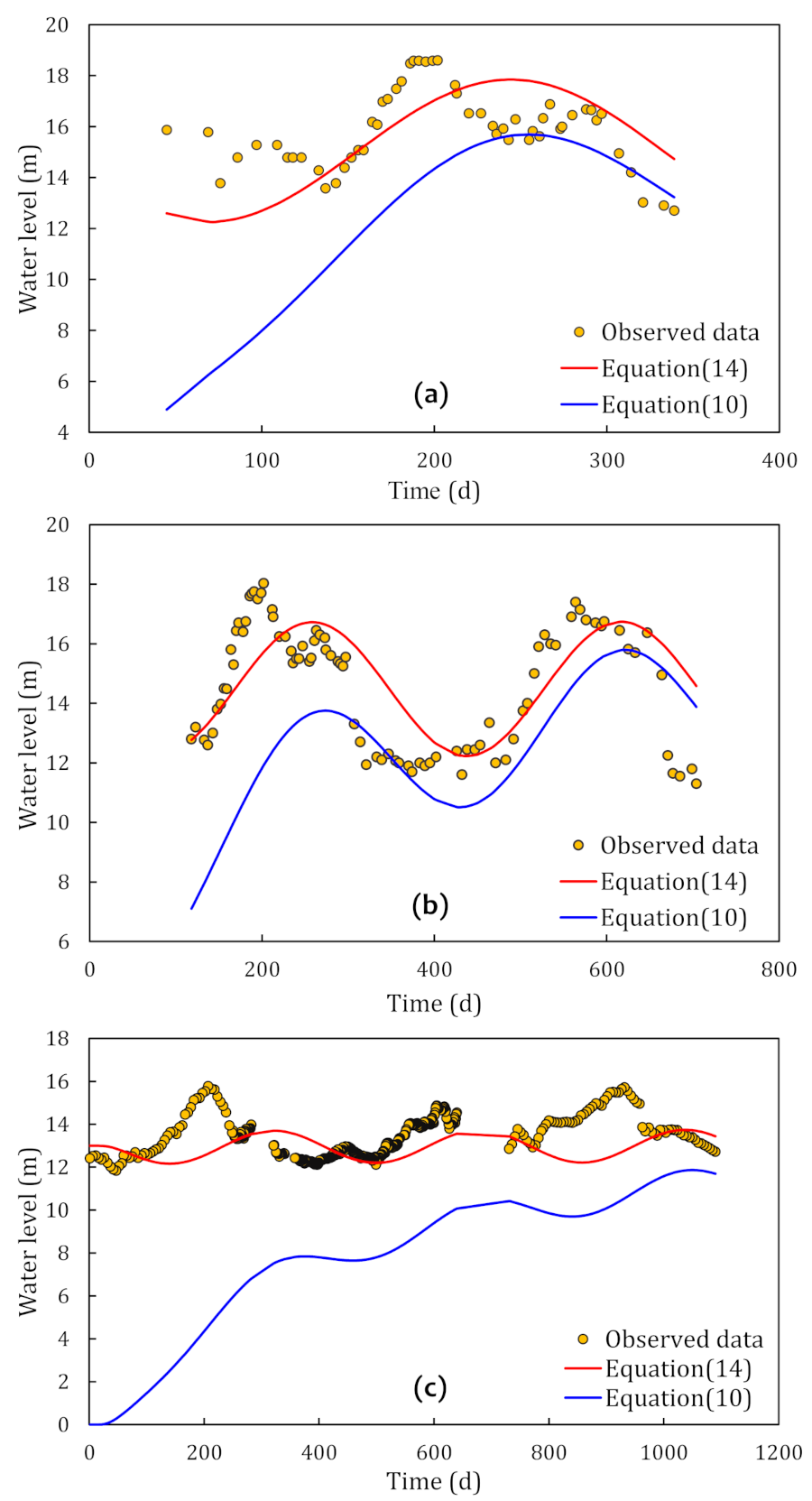
3. Yangtze River Water Level Fluctuation Model
4. Prediction of Confined Water Head
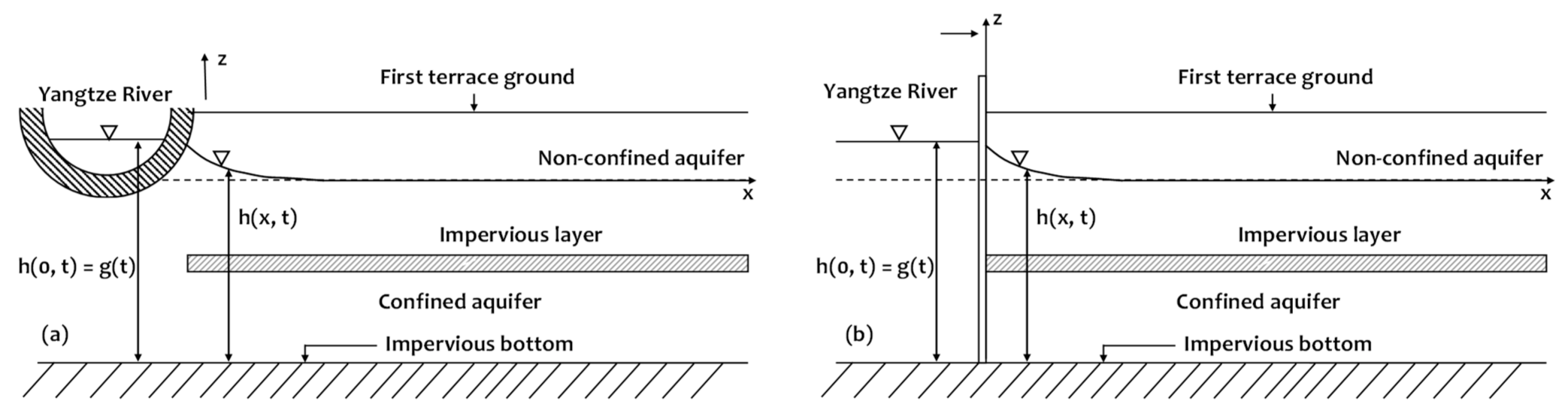
4.1. Analytical Derivation of Stream–Aquifer Interactions: Solution of the Ground Water Flow Equations
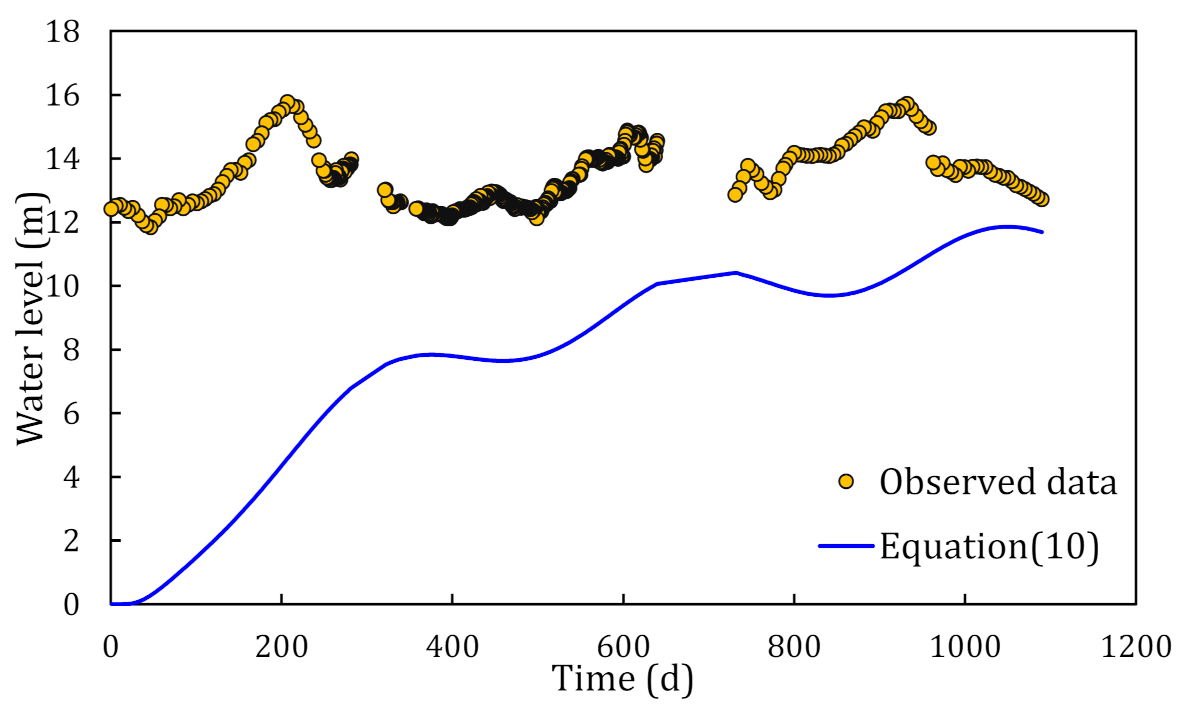
4.2. Calculation and Validation
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Spanoudaki, K.; Nanou-Giannarou, A.; Paschalinos, Y.; Memos, C.D.; Stamou, A.I. Analytical solutions to the stream-aquifer interaction problem: A critical review. Glob. Nest J. 2010, 12, 126–139. [Google Scholar] [CrossRef]
- Courbis, A.L.; Vayassade, B.; Martin, C.; Didon-Lescot, J.F. Modelling and simulation of a catchment in order to evaluate water resources. Glob. Nest J. 2008, 10, 301–309. [Google Scholar]
- Ma, S.l.; Kassinos, S.C.; Kassinos, D.F.; Akylas, E. Modeling the impact of water withdrawal schemes on the transport of pesticides in the Kouris Dam (Cyprus). Glob. Nest J. 2008, 10, 350–358. [Google Scholar]
- Castro, N.M.; Hornberger, G.M. Surface-subsurface water interactions in an alluviated mountain stream channel. Water Resour. Res. 1991, 27, 1613–1621. [Google Scholar] [CrossRef]
- Brunner, P.; Cook, P.G.; Simmons, C.T. Disconnected surface water and groundwater: From theory to practice. Ground Water 2011, 49, 460–467. [Google Scholar] [CrossRef] [Green Version]
- Medici, G.; Engdahl, N.B.; Langman, J.B. A basin-scale groundwater flow model of the columbia plateau regional aquifer system in the palouse (USA): Insights for aquifer vulnerability assessment. Int. J. Environ. Res. 2021, 15, 299–312. [Google Scholar] [CrossRef]
- Condon, L.E.; Maxwell, R.M. Simulating the sensitivity of evapotranspiration and streamflow to large-scale groundwater depletion. Sci. Adv. 2019, 5, 4574. [Google Scholar] [CrossRef] [Green Version]
- Konikow, L.F.; Kendy, E. Groundwater depletion: A global problem. Hydrogeol. J. 2005, 13, 317–320. [Google Scholar] [CrossRef]
- Hantush, M.S. Wells near streams with semipervious beds. J. Geophy. 1965, 70, 2829–2838. [Google Scholar] [CrossRef]
- Hunt, B. Unsteady stream depletion from groundwater pumping. Ground Water 1999, 37, 98–102. [Google Scholar] [CrossRef]
- Schmitz, G.H.; Edenhofer, J. Exact closed-form solution of the two-dimensional Laplace equation for steady groundwater flow with nonlinearized free-surface boundary condition. Water Resour. 2000, 36, 1975–1980. [Google Scholar] [CrossRef]
- Hantush, M.M. Modeling steam-aquifer interactions with linear response functions. J. Hydrol. 2005, 311, 59–79. [Google Scholar] [CrossRef]
- Dillon, P.J.; Liggett, A. An ephemeral steam- aquifer interaction model. Water Resour. 1983, 19, 621–626. [Google Scholar] [CrossRef]
- Chin, D.A. Leakage of clogged channels that partically penetrate surficial aquifers. J. Hydraul. 1991, 117, 467–488. [Google Scholar] [CrossRef]
- Sophocleous, M.A.; Koussis, A.; Martion, J.L.; Perkins, S.P. Evaluation of simplified stream-aquifer depletion models for water rights administration. Ground Water 1995, 33, 579–588. [Google Scholar] [CrossRef]
- Carabin, G.; Dassargues, A. Modeling ground water with ocean and river interaction. Water Resour. 1999, 35, 2347–2358. [Google Scholar] [CrossRef]
- Chen, X.H.; Yin, Y. Streamflow depletion: Modeling of reduced baseflow and induced stream infiltration from seasonally pumped wells. J. Am. Water Resour. 2001, 37, 185–195. [Google Scholar] [CrossRef]
- Intaraprasong, T.; Zhan, H. A general framework of stream-aquifer interaction caused by variable stream stages. J. Hydrol. 2009, 373, 112–121. [Google Scholar] [CrossRef]
- Sun, D.; Zhan, H. Flow to a horizontal well in an aquifer–aquitard system. J. Hydrol. 2006, 321, 364–376. [Google Scholar] [CrossRef]
- Sun, D.; Zhan, H. Pumping induced depletion from two streams. Water Resour. 2007, 30, 1016–1026. [Google Scholar] [CrossRef]
- Zhan, H.; Park, E. Horizontal well hydraulics in leaky aquifers. J. Hydrol. 2003, 281, 129–146. [Google Scholar] [CrossRef]
- Cooper, H.H., Jr.; Rorabaugh, M.I. Groundwater movements and bank storage due to flood stages in surface streams. USGS Water Supply Paper 1963, 1536, 343–366. [Google Scholar]
- Chen, X.; Chen, X.H. Stream water infiltration, bank storage, and storage zone changes due to stream-stage fluctuations. J. Hydrol. 2003, 280, 246–264. [Google Scholar] [CrossRef]
- Singh, S.K. Ramp kernels for aquifer responses to arbitrary stream stage. J. Irrig. Drain. 2004, 130, 460–467. [Google Scholar] [CrossRef]
- Moench, A.F.; Barlow, P.M. Aquifer response to stream-stage and recharge variations. I. Analytical step-response functions. J. Hydrol. 2000, 230, 192–210. [Google Scholar] [CrossRef]
- Barlow, P.M.; DeSimone, L.A.; Moench, A.F. Aquifer response to stream-stage and recharge variations. II. Convolution method and applications. J. Hydrol. 2000, 230, 211–229. [Google Scholar] [CrossRef]
- Sophocleous, M. Interactions between groundwater and surface water: The state of the science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, L.Z.; Gupta, A. Yangtze River, China: Introduction. Geomorphol. Spec. Issue 2001, 41, 248. [Google Scholar]
- Chen, Z.; Li, J.F.; Shen, H.T. Yangtze River, China, historical analysis of discharge variability and sediment flux. Geomorphology 2001, 41, 77–91. [Google Scholar] [CrossRef]
- Chen, Z.; Gupta, A.; Yin, H.F. Large monsoon rivers of Asia. Geomorphol. Spec. Issue 2007, 85, 316. [Google Scholar]
- Xiang, Y.; Bao, C. The Weather in the Middle and Lower Reaches of Yangtze River; Meteorological Press: Beijing, China, 1981; pp. 21–136. [Google Scholar]
- Zhang, Q.; Xu, C.Y.; Zhang, Z.; Chen, Y.D.; Liu, C.; Lin, H. Spatial and temporal variability of precipitation maxima during 1960–2005 in the Yangtze River Basin and possible association with large-scale circulation. J. Hydrol. 2008, 353, 215–227. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, B.; Xu, H. Effect of characteristics of ground water distribution and seepage on anti-uplift analysis of building foundations. China Civ. Eng. J. 2001, 1, 73–78. [Google Scholar]
- Liu, Y.; Wang, X. Analysis about influence of confined water level change near river on underground structures. Site Investig. Sci. Technol. 2009, 3, 39–41. [Google Scholar]
- Li, S.; Han, H. Method for getting the value of anti-uplift water level for construction—An exemplified project in Beijing. China Saf. Sci. J. 2005, 7, 58–62. [Google Scholar]
- Ren, X.; Santamarina, J.C. The hydraulic conductivity of sediments: A pore size perspective. Eng. Geol. 2018, 233, 48–54. [Google Scholar] [CrossRef] [Green Version]
- Ren, X.; Hong, N.; Li, L.; Kang, J.; Li, J. Effect of infiltration rate changes in urban soils on stormwater runoff process. Geoderma 2020, 363, 1–11. [Google Scholar] [CrossRef]
- Kamel, S.; Younes, H.; Chkir, N.; Zouari, K. The hydro geochemical characterization of ground waters in Tunisian Chott’s region. Environ. Geol. 2008, 54, 843–854. [Google Scholar] [CrossRef]
- Barzegar, R.; Moghaddam, A.A.; Najib, M.; Kazemian, N.; Adamowski, J. Characterization of hydrogeologic properties of the Tabriz plain multilayer aquifer system, NW Iran. Arab. J. Geosci. 2016, 9, 147. [Google Scholar] [CrossRef]
- Mao, Y.; Zhao, X.H. New characteristics of water level and discharge relationship at Jianli section in middle reaches of Yangtze River in past 10 years. Yangtze River 2020, 5, 89–93. [Google Scholar]
- Ren, X.; Zhao, Y.; Deng, Q.; Kang, J.; Li, D.; Wang, D. A relation of hydraulic conductivity-void ratio for soils based on Kozeny-Carman equation. Eng. Geol. 2016, 213, 89–97. [Google Scholar] [CrossRef]
- Shi, A.L.; Qin, J.; Chen, Z.H. Analysis of the long-term variation characteristics of water level in the upper reaches of Yangtze River. Resour. Environ. Yangtze Basin 2021, 2, 361–368. [Google Scholar]
- Colombera, L.; Mountney, N.P.; Medici, G.; West, L.J. The geometry of fluvial channel bodies: Empirical characterization and implications for object-based models of the subsurface. AAPG Bull. 2019, 103, 905–929. [Google Scholar] [CrossRef]
- Liu, Y.Z.; Zhang, X.Y. Groundwater value for the buoyancy design in the first terrace of Yangtze River in Wuhan. Soil Found. 2015, 29, 54–58. [Google Scholar]
- Rao, Q. Water level of anti-floating design and buoyancy reduction analysis for underground buildings in Wuhan area. Wuhan Surv. Des. 2012, 2, 36–38. [Google Scholar]
- Dong, L.; Luo, X.; Lin, Q.; Hu, B. Analytical solution to evaluate aquifer response to arbitrary water level variation. Eng. J. Wuhan Univ. 2019, 52, 847–853. [Google Scholar]
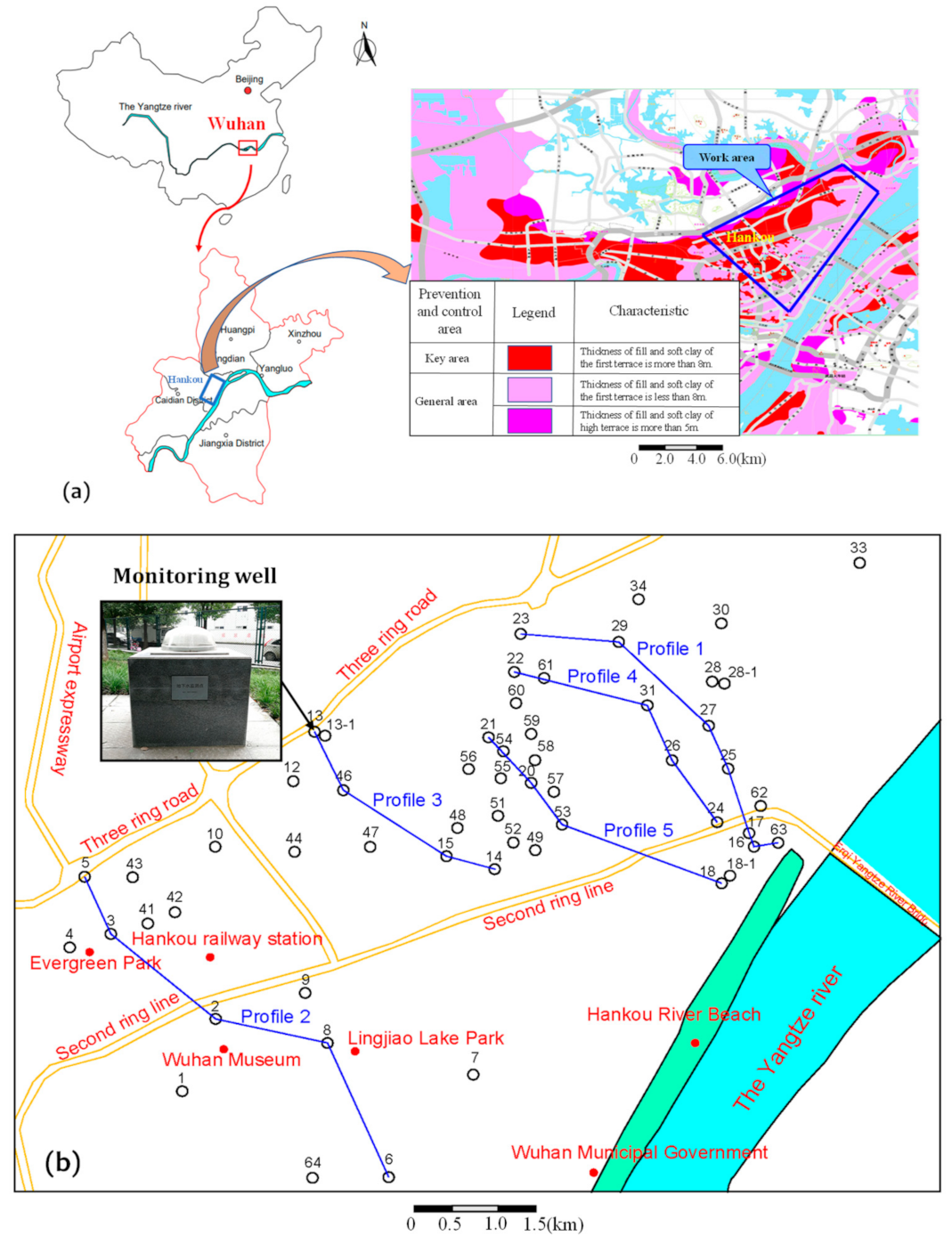
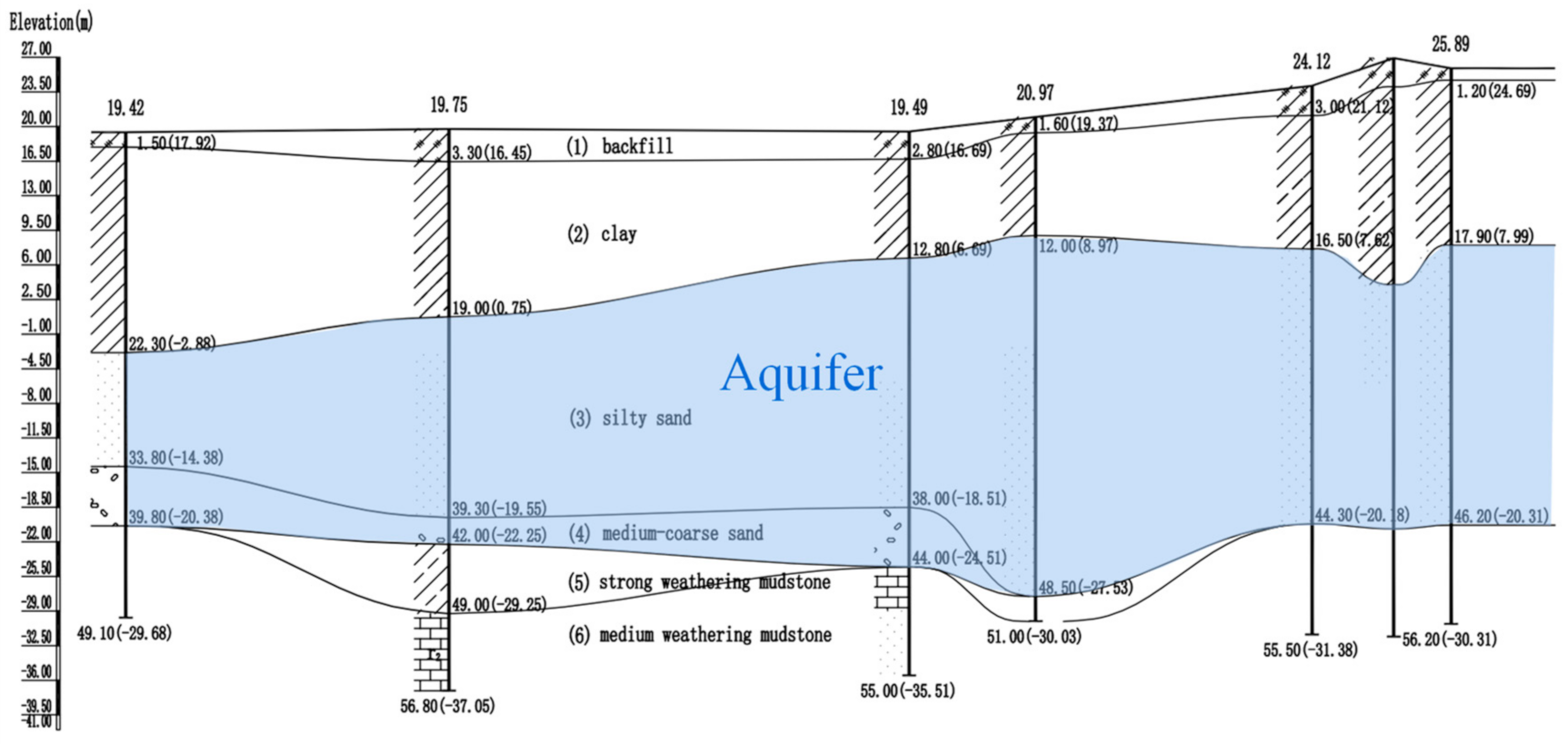
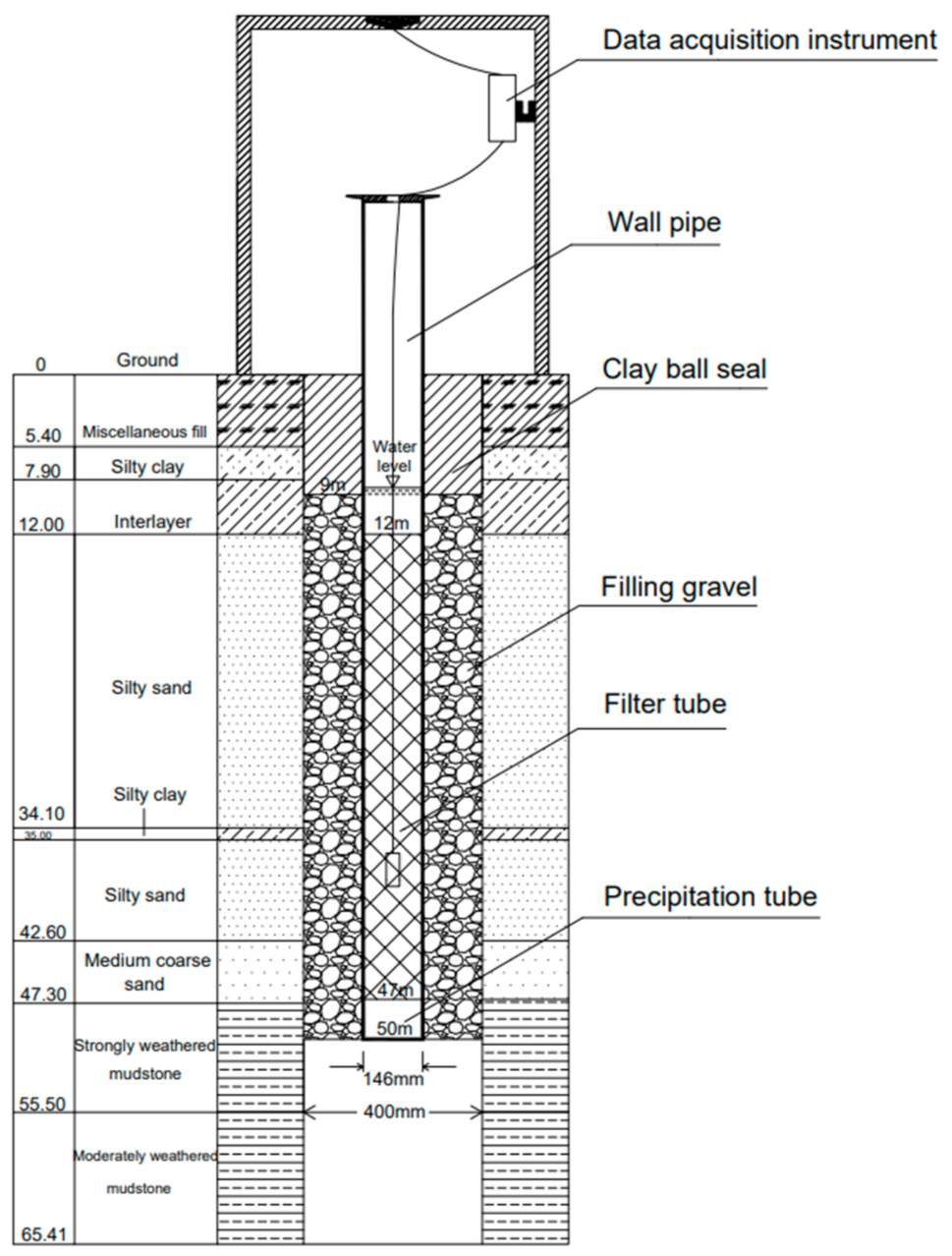
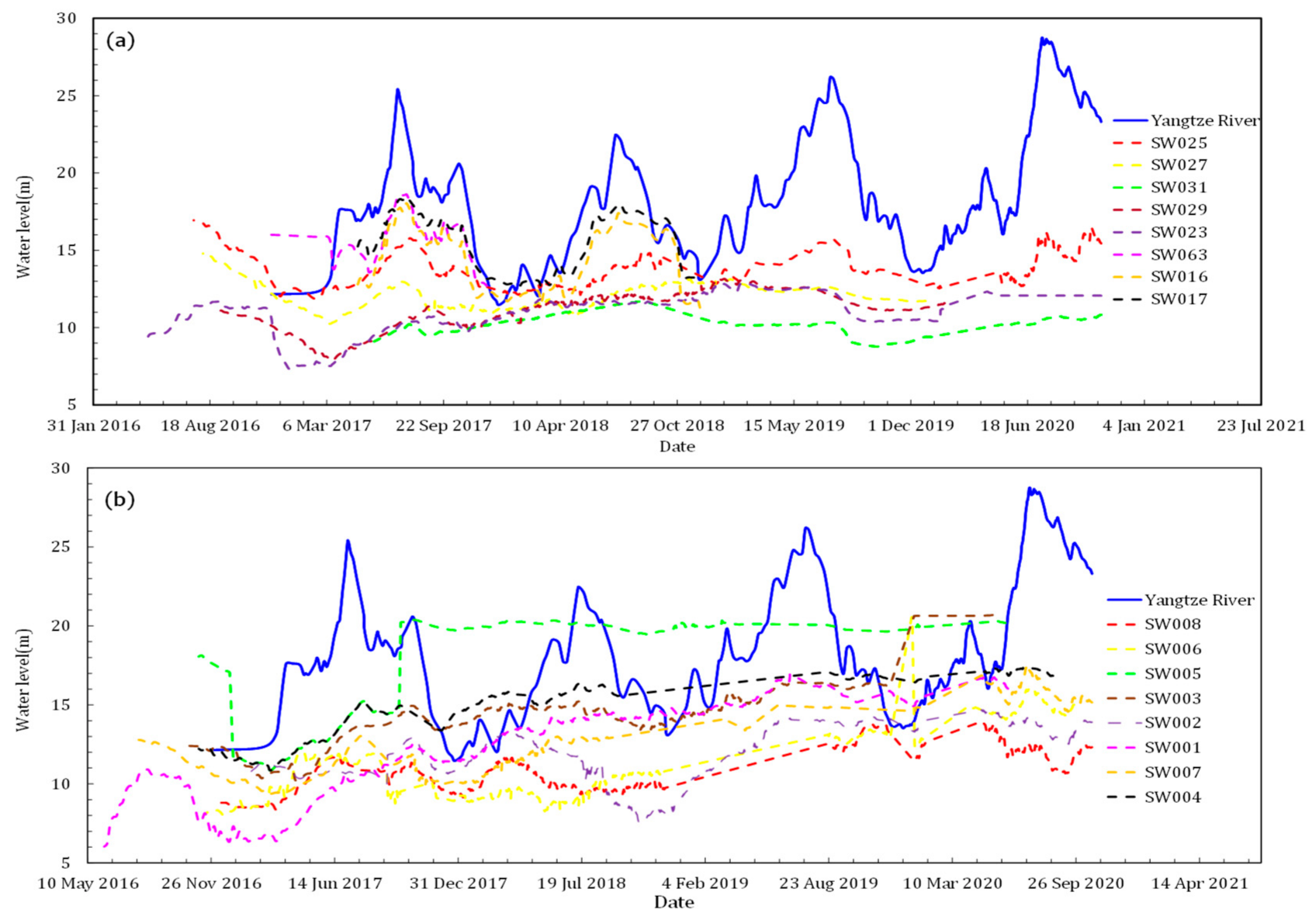
| Profile | Monitoring Well |
|---|---|
| Profile 1 | SW023- SW029- SW027- SW025- SW017- SW016- SW063- Yangtze River |
| Profile 2 | SW005- SW003- SW002- SW008- SW006- Yangtze River |
| Profile 3 | SW013- SW046- SW015- SW014- Yangtze River |
| Profile 4 | SW022- SW031- SW026- SW024- Yangtze River |
| Profile 5 | SW021- SW020- SW053- SW018- Yangtze River |
| Monitoring Wells | |||||||
|---|---|---|---|---|---|---|---|
| Profile 1 | SW063 | SW016 | SW017 | SW025 | SW027 | SW029 | SW023 |
| Distance/km | 0.6 | 0.8 | 0.9 | 1.7 | 2.2 | 3.8 | 4.8 |
| Profile 2 | SW06 | SW08 | SW02 | SW03 | SW05 | ||
| Distance/km | 2.6 | 4.1 | 5.5 | 7.2 | 8.0 | ||
| Parameter | Value | Unit |
|---|---|---|
| T | 30 | m2/d |
| S | 0.005 | Dimensionless |
| D | 6000 | m2/d |
| K | 1 | m/d |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Wang, H.; Wu, Y.; Zhao, Y.; Ren, X. Aquifer Response to Stream-Stage Fluctuations: Field Tests and Analytical Solution for a Case Study of the Yangtze River in Wuhan, China. Water 2021, 13, 2388. https://doi.org/10.3390/w13172388
Liu Y, Wang H, Wu Y, Zhao Y, Ren X. Aquifer Response to Stream-Stage Fluctuations: Field Tests and Analytical Solution for a Case Study of the Yangtze River in Wuhan, China. Water. 2021; 13(17):2388. https://doi.org/10.3390/w13172388
Chicago/Turabian StyleLiu, Yanmin, Hao Wang, Yungang Wu, Yuan Zhao, and Xingwei Ren. 2021. "Aquifer Response to Stream-Stage Fluctuations: Field Tests and Analytical Solution for a Case Study of the Yangtze River in Wuhan, China" Water 13, no. 17: 2388. https://doi.org/10.3390/w13172388
APA StyleLiu, Y., Wang, H., Wu, Y., Zhao, Y., & Ren, X. (2021). Aquifer Response to Stream-Stage Fluctuations: Field Tests and Analytical Solution for a Case Study of the Yangtze River in Wuhan, China. Water, 13(17), 2388. https://doi.org/10.3390/w13172388







