Local Meteoric Water Lines in a Semi-Arid Setting of Northwest China Using Multiple Methods
Abstract
:1. Introduction
2. Data and Method
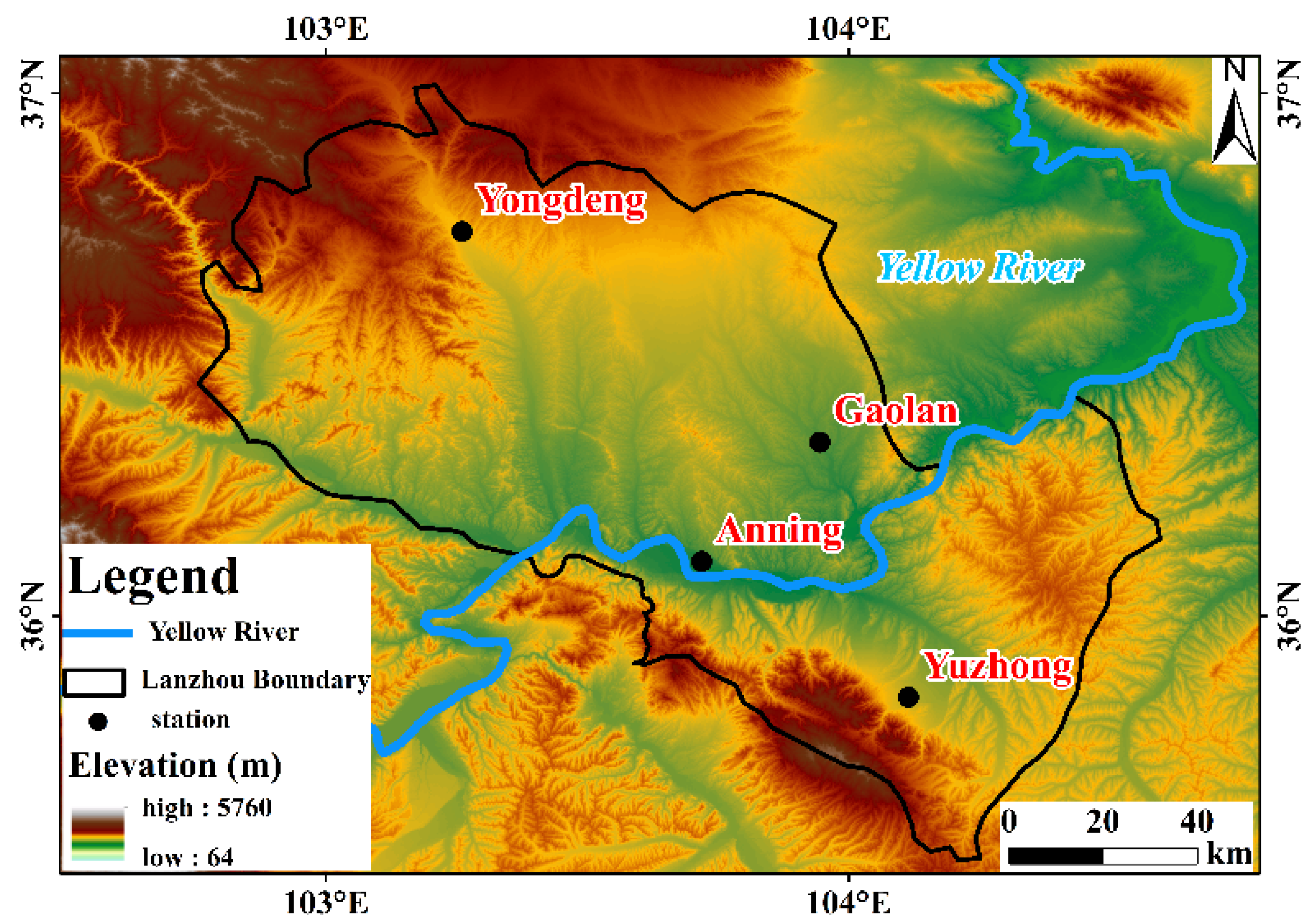
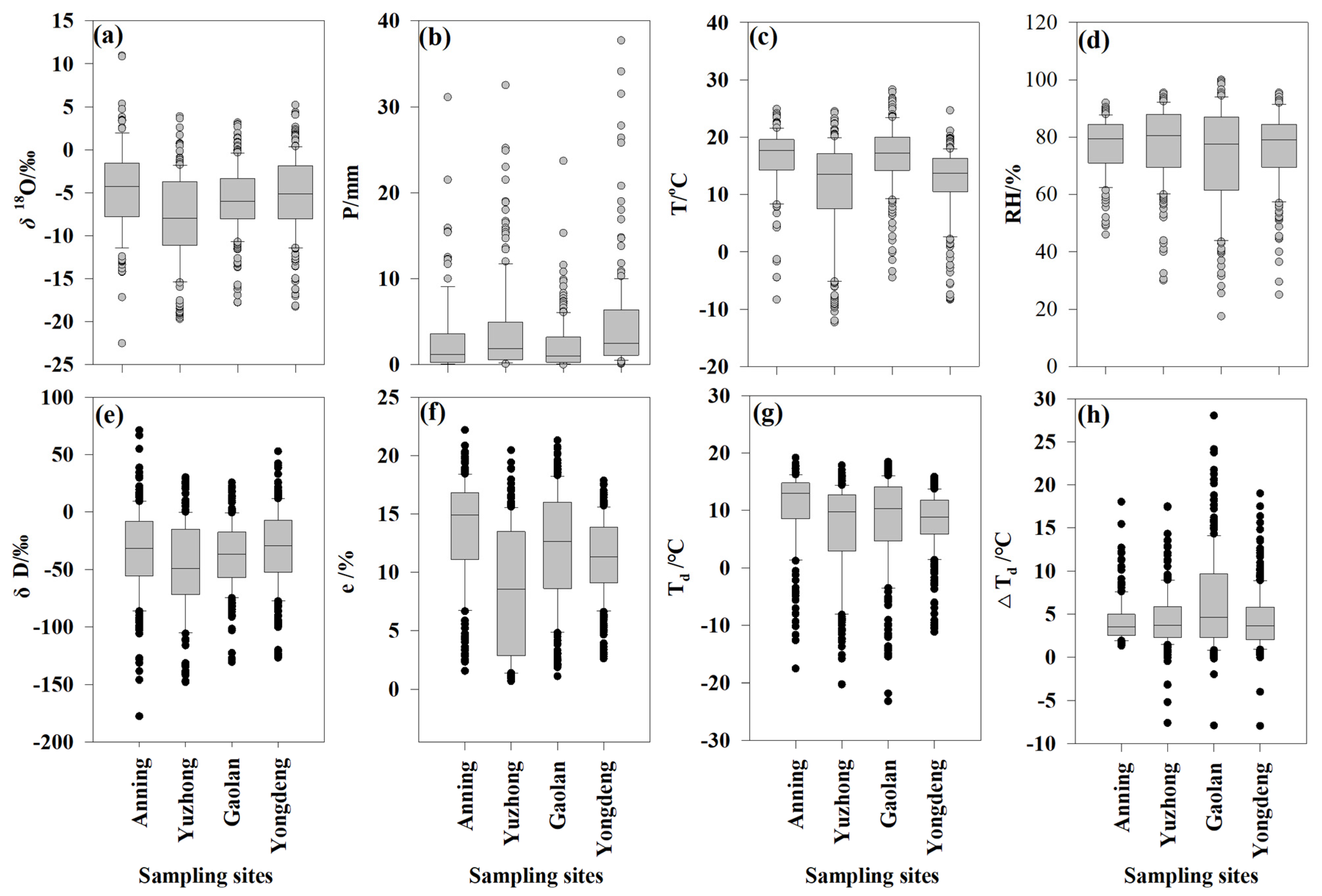
2.1. Data and Site Description
2.2. Local Meteoric Water Line Calculation
3. Results and Discussion
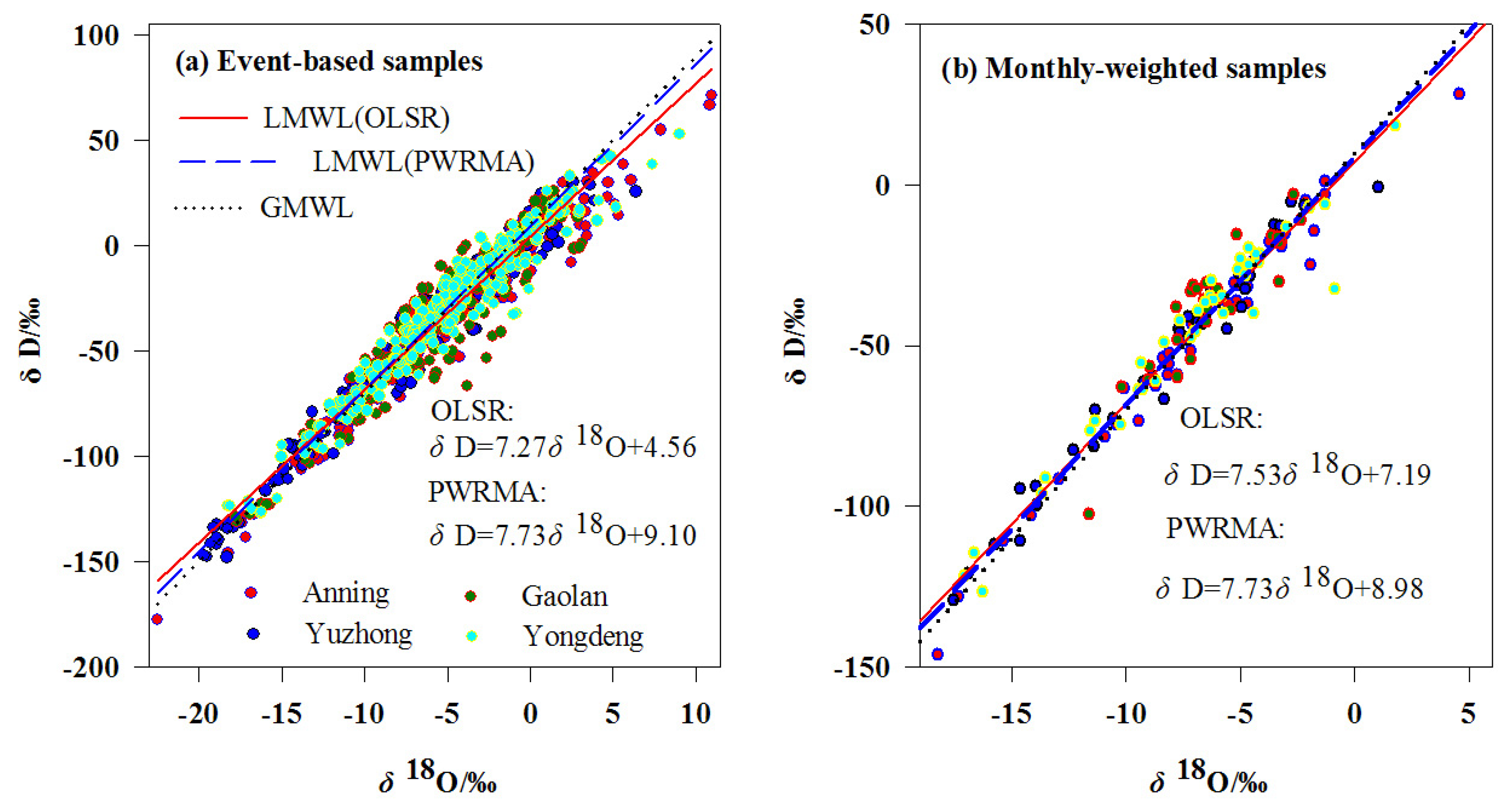
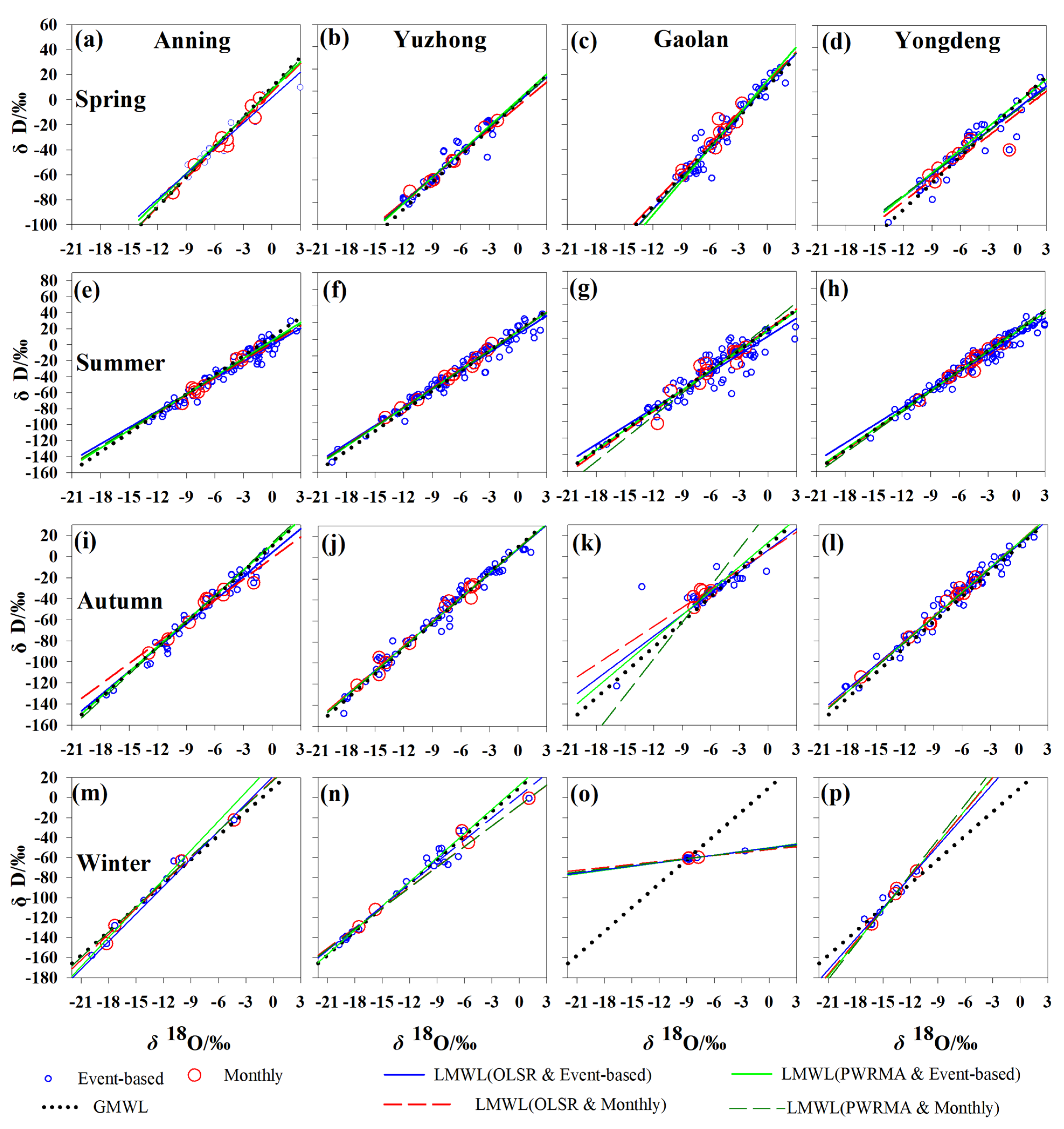
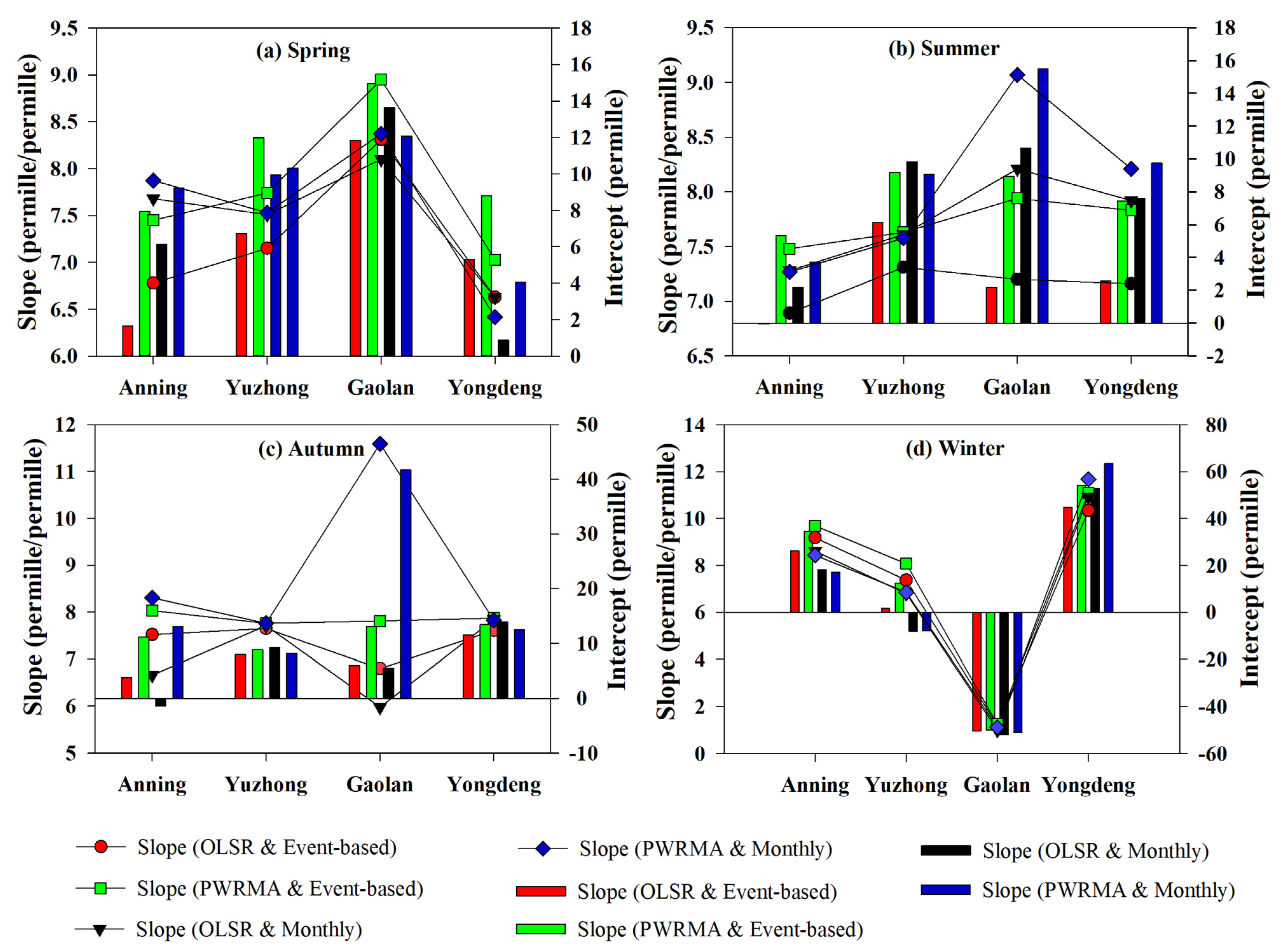
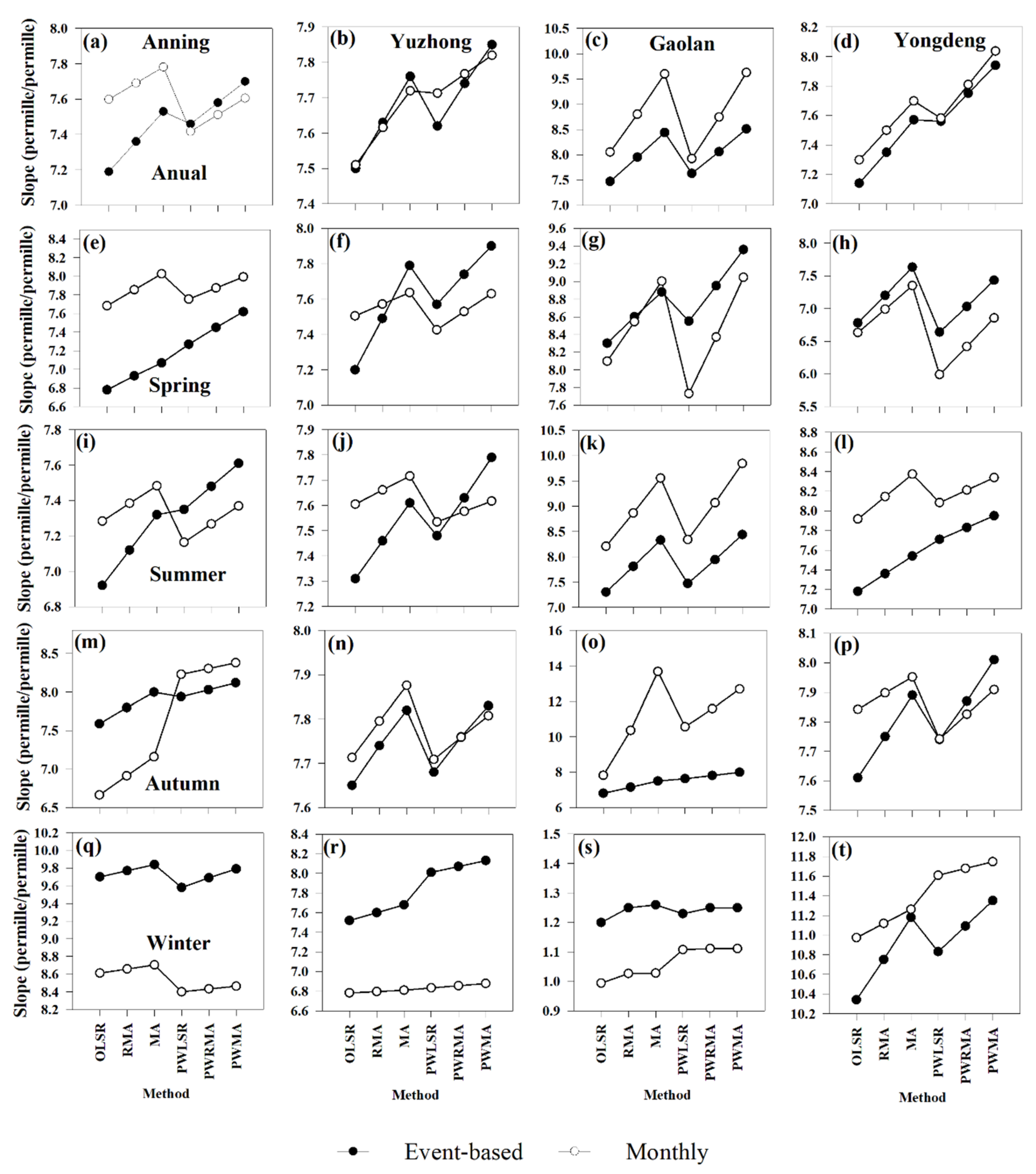
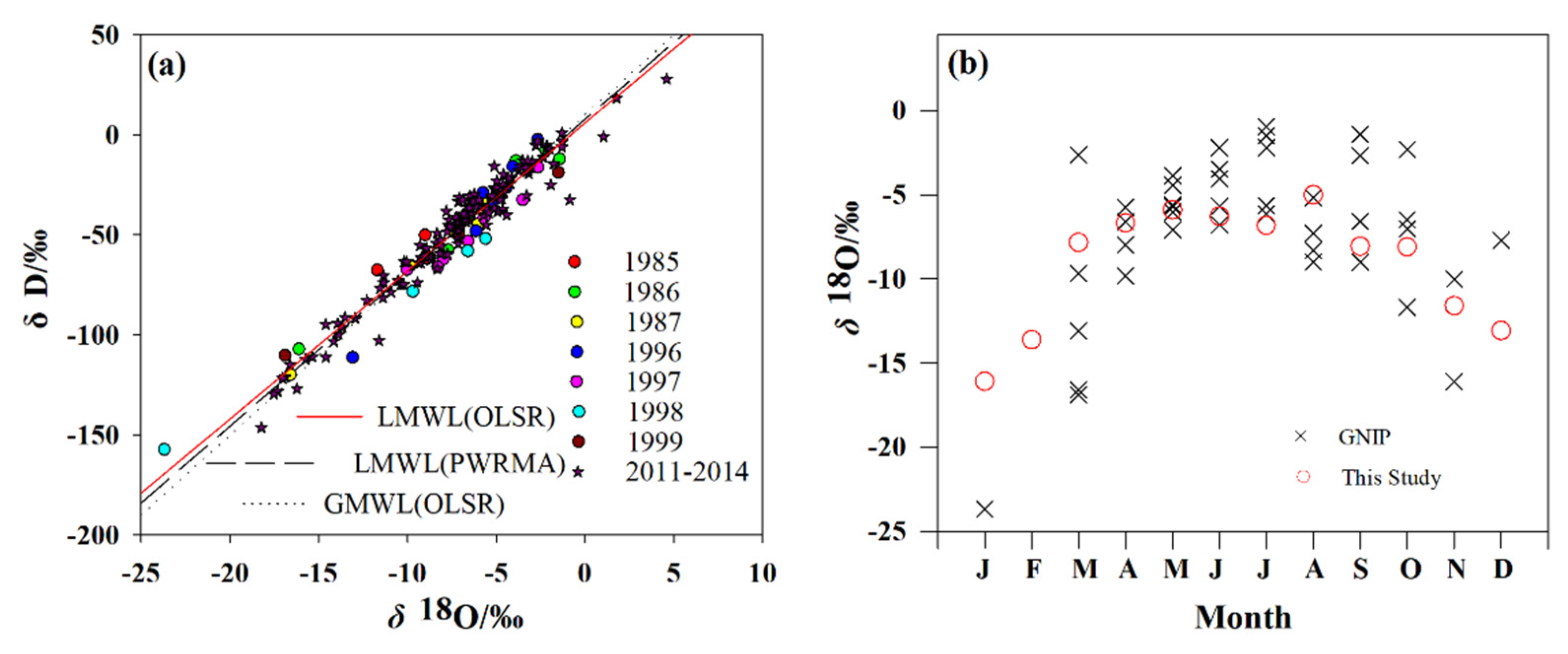
3.1. Basic Characteristics of LMWL
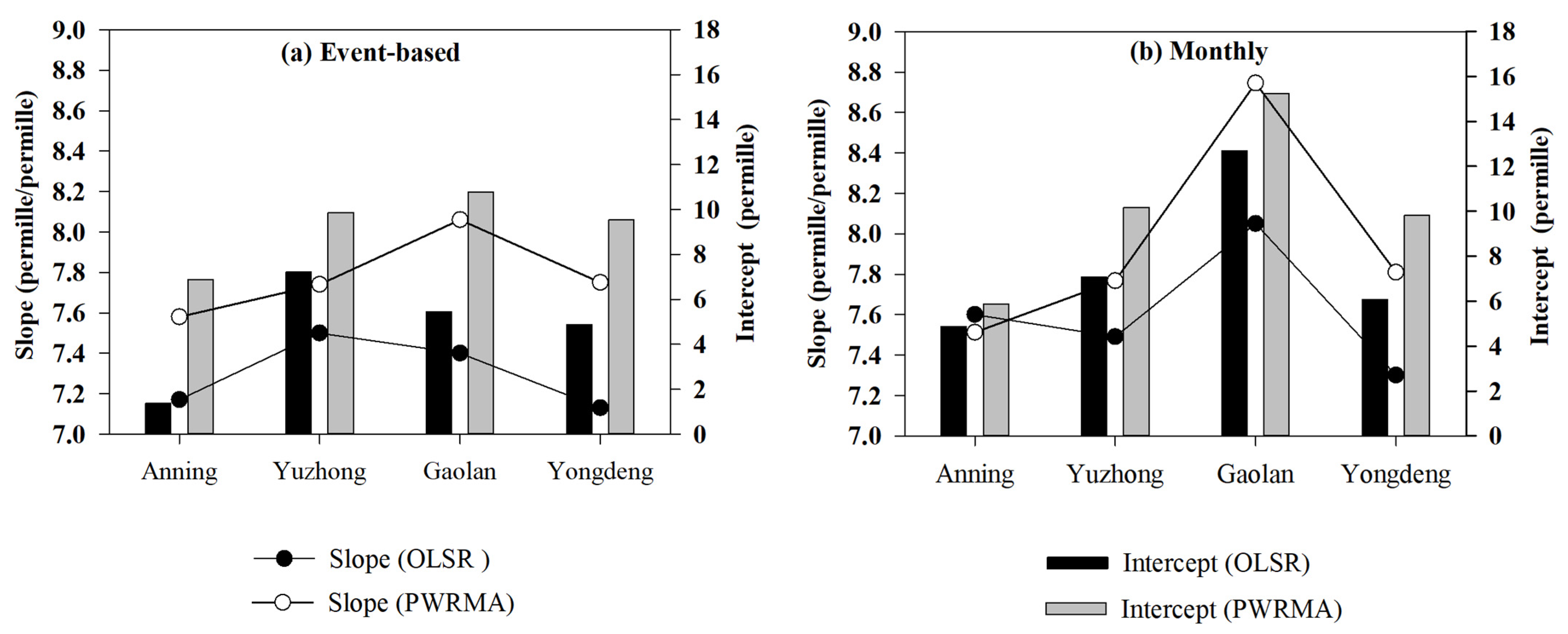
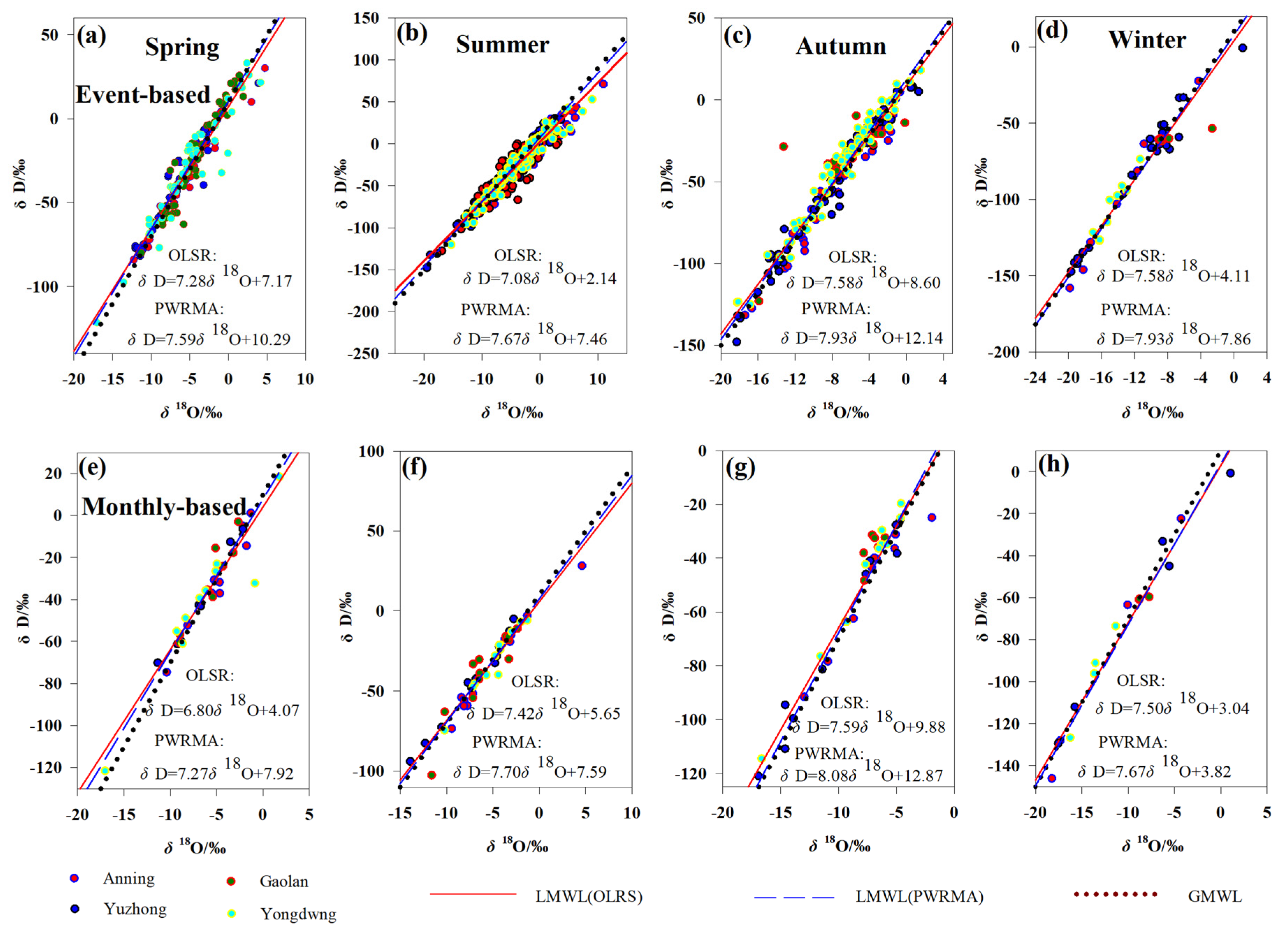
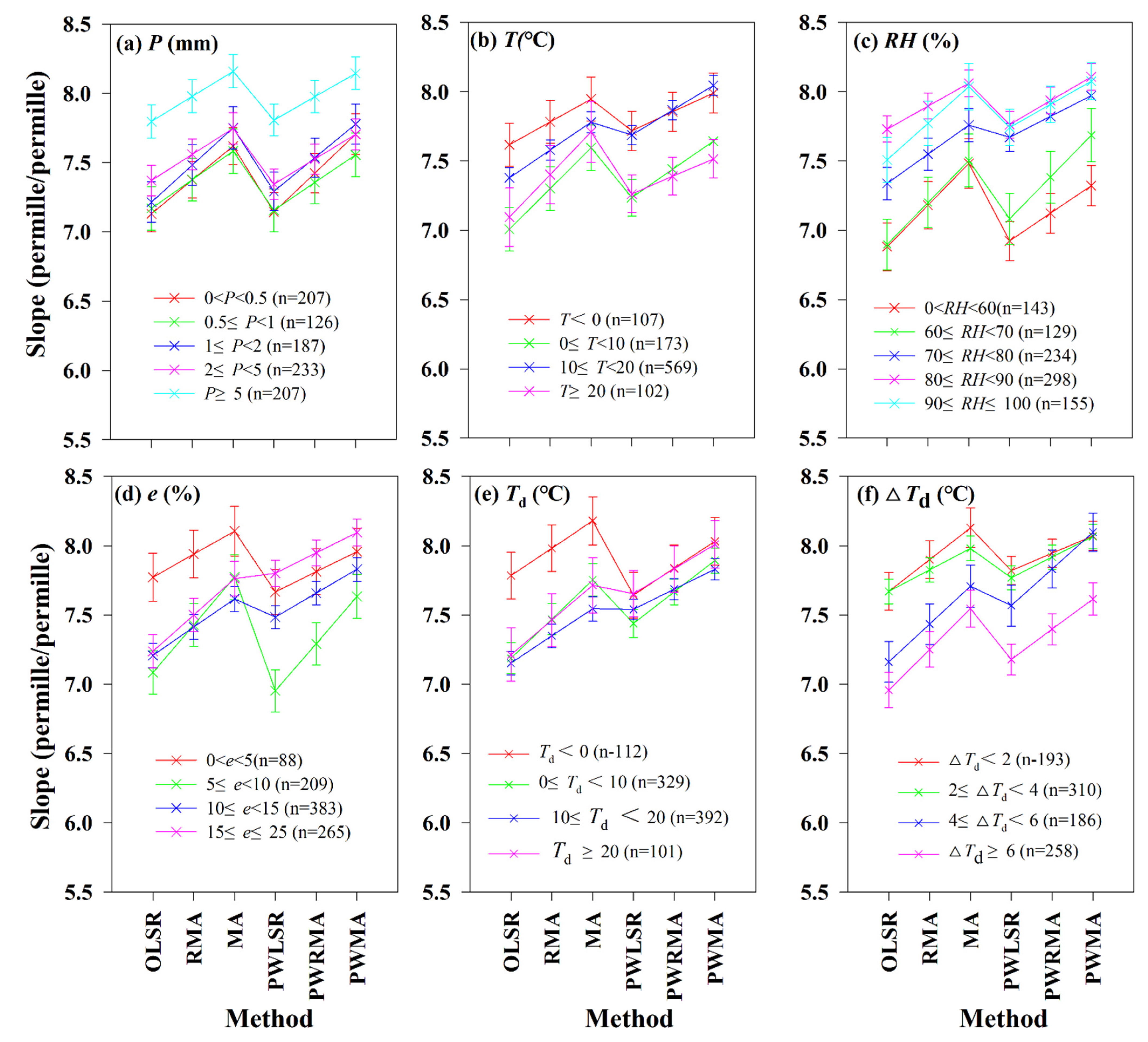
3.2. Meteorological Factors and LMWL
3.3. LMWL Sensitivity for Heavy and Small Events
3.4. Comparison between GNIP and Recent Observations
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chiang, J.C.H.; Herman, M.J.; Yoshimura, K.; Fung, I.Y. Enriched East Asian oxygen isotope of precipitation indicates reduced summer seasonality in regional climate and westerlies. Proc. Natl. Acad. Sci. USA 2020, 117, 14745–14750. [Google Scholar] [CrossRef]
- Putman, A.L.; Bowen, G.J.; Strong, C. Local and Regional Modes of Hydroclimatic Change Expressed in Modern Multidecadal Precipitation Oxygen Isotope Trends. Geophys. Res. Lett. 2021, 48, e2020GL092006. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, S. A review of precipitation isotope studies in China: Basic pattern and hydrological process. J. Geogr. Sci. 2016, 26, 921–938. [Google Scholar] [CrossRef] [Green Version]
- Craig, H. Isotopic Variations in Meteoric Waters. Science 1961, 133, 1702–1703. [Google Scholar] [CrossRef]
- Merlivat, L.; Jouzel, J. Global climatic interpretation of the deuterium-oxygen 18 relationship for precipitation. J. Geophys. Res. Space Phys. 1979, 84, 5029–5033. [Google Scholar] [CrossRef]
- Bedaso, Z.; Wu, S.-Y. Linking precipitation and groundwater isotopes in Ethiopia—Implications from local meteoric water lines and isoscapes. J. Hydrol. 2021, 596, 126074. [Google Scholar] [CrossRef]
- Smith, D.F.; Saelens, E.; Leslie, D.L.; Carey, A.E. Local meteoric water lines describe extratropical precipitation. Hydrol. Process. 2021, 35. [Google Scholar] [CrossRef]
- Putman, A.L.; Fiorella, R.P.; Bowen, G.J.; Cai, Z. A Global Perspective on Local Meteoric Water Lines: Meta-analytic Insight Into Fundamental Controls and Practical Constraints. Water Resour. Res. 2019, 55, 6896–6910. [Google Scholar] [CrossRef]
- Peng, H.; Mayer, B.; Harris, S.; Krouse, H.R. The influence of below-cloud secondary effects on the stable isotope composition of hydrogen and oxygen in precipitation at Calgary, Alberta, Canada. Tellus B Chem. Phys. Meteorol. 2007, 59, 698–704. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, M.; Che, Y.; Zhu, X.; Liu, X. Influence of Below-Cloud Evaporation on Deuterium Excess in Precipitation of Arid Central Asia and Its Meteorological Controls. J. Hydrometeorol. 2016, 17, 1973–1984. [Google Scholar] [CrossRef]
- Wang, S.; Jiao, R.; Zhang, M.; Crawford, J.; Hughes, C.E.; Chen, F. Changes in below-cloud evaporation affect precipitation isotopes during five decades of warming across China. J. Geophys. Res. Atmos. 2021, 126, e2020JD033075. [Google Scholar] [CrossRef]
- IAEA. Statistical Treatment of Data on Environmental Isotopes in Precipitation; IAEA: Vienna, Austria, 1992; pp. 1–781. ISBN 92-0-100892-9. [Google Scholar]
- IAEA/WMO. Global Network of Isotopes in Precipitation. 2021. Available online: http://www.iaea.org/water (accessed on 21 May 2021).
- Wang, S.; Zhang, M.; Hughes, C.; Crawford, J.; Wang, G.; Chen, F.; Du, M.; Qiu, X.; Zhou, S. Meteoric water lines in arid Central Asia using event-based and monthly data. J. Hydrol. 2018, 562, 435–445. [Google Scholar] [CrossRef]
- Hughes, C.; Crawford, J. A new precipitation weighted method for determining the meteoric water line for hydrological applications demonstrated using Australian and global GNIP data. J. Hydrol. 2012, 464–465, 344–351. [Google Scholar] [CrossRef]
- Harvey, F.E. Use of NADP Archive Samples to Determine the Isotope Composition of Precipitation: Characterizing the Meteoric Input Function for Use in Ground Water Studies. Ground Water 2001, 39, 380–390. [Google Scholar] [CrossRef] [PubMed]
- Crawford, J.; Hughes, C.E.; Lykoudis, S. Alternative least squares methods for determining the meteoric water line, demonstrated using GNIP data. J. Hydrol. 2014, 519, 2331–2340. [Google Scholar] [CrossRef]
- Araguás-Araguás, L.; Froehlich, K.; Rozanski, K. Stable isotope composition of precipitation over southeast Asia. J. Geophys. Res. Space Phys. 1998, 103, 28721–28742. [Google Scholar] [CrossRef]
- Tian, L.; Yao, T.; MacClune, K.; White, J.W.C.; Schilla, A.; Vaughn, B.; Vachon, R.; Ichiyanagi, K. Stable isotopic variations in west China: A consideration of moisture sources. J. Geophys. Res. Space Phys. 2007, 112. [Google Scholar] [CrossRef]
- Yao, T.; Masson-Delmotte, V.; Gao, J.; Yu, W.; Yang, X.; Risi, C.; Sturm, C.; Werner, M.; Zhao, H.; He, Y.; et al. A review of climatic controls on δ18O in precipitation over the Tibetan Plateau: Observations and simulations. Rev. Geophys. 2013, 51, 525–548. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, M.; Wang, S.; Ma, Q.; Zhu, X.; Dong, L. Relationship between sub-cloud secondary evaporation and stable isotopes in precipitation of Lanzhou and surrounding area. Quat. Int. 2015, 380-381, 68–74. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, M.; Wang, S.; Qiu, X.; Du, M. Environmental controls on stable isotopes of precipitation in Lanzhou, China: An enhanced network at city scale. Sci. Total. Environ. 2017, 609, 1013–1022. [Google Scholar] [CrossRef]
- Ma, Q.; Zhang, M.; Wang, S.; Wang, Q.; Liu, W.; Li, F.; Chen, F. An investigation of moisture sources and secondary evaporation in Lanzhou, Northwest China. Environ. Earth Sci. 2013, 71, 3375–3385. [Google Scholar] [CrossRef]
- Chen, F.; Zhang, M.; Ma, Q.; Wang, S.; Li, X.; Zhu, X. Stable isotopic characteristics of precipitation in Lanzhou City and its surrounding areas, Northwest China. Environ. Earth Sci. 2015, 73, 4671–4680. [Google Scholar] [CrossRef]
- Wu, J.; Ding, Y.; Ye, B.; Yang, Q.; Zhang, X.; Wang, J. Spatio-temporal variation of stable isotopes in precipitation in the Heihe River Basin, Northwestern China. Environ. Earth Sci. 2010, 61, 1123–1134. [Google Scholar] [CrossRef]
- Pang, Z.; Kong, Y.; Li, J.; Tian, J. An Isotopic Geoindicator in the Hydrological Cycle. Procedia Earth Planet. Sci. 2017, 17, 534–537. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, M.; Hughes, C.; Zhu, X.; Dong, L.; Ren, Z.; Chen, F. Factors controlling stable isotope composition of precipitation in arid conditions: An observation network in the Tianshan Mountains, central Asia. Tellus B Chem. Phys. Meteorol. 2016, 68. [Google Scholar] [CrossRef] [Green Version]
- Vodila, G.; Palcsu, L.; Futó, I.; Szántó, Z. A 9-year record of stable isotope ratios of precipitation in Eastern Hungary: Implications on isotope hydrology and regional palaeoclimatology. J. Hydrol. 2011, 400, 144–153. [Google Scholar] [CrossRef]
- Wu, P.; Ding, Y.; Liu, Y.; Li, X. The characteristics of moisture recycling and its impact on regional precipitation against the background of climate warming over Northwest China. Int. J. Clim. 2019, 39, 5241–5255. [Google Scholar] [CrossRef]
- Li, R.; Wang, C. Precipitation recycling using a new evapotranspiration estimator for Asian-African arid regions. Theor. Appl. Clim. 2020, 140, 1–13. [Google Scholar] [CrossRef]
| Year | Slope (Permille/Permille) | P (mm) | T (°C) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OLSR | RMA | MA | PWLSR | PWRMA | PWMA | Annual | DJF * | JJA ** | Annual | DJF | JJA | |
| 2011 | 7.33 ± 0.11 | 7.51 ± 0.11 | 7.70 ± 0.12 * | 7.65 ± 0.09 | 7.77 ± 0.09 ** | 7.90 ± 0.09 ** | 192.8 | 0.8 | 107.0 | 14.1 | −5.8 | 17.4 |
| 2012 | 7.38 ± 0.12 | 7.64 ± 0.12 | 7.89 ± 0.13 ** | 7.68 ± 0.12 | 7.91 ± 0.12 ** | 8.14 ± 0.12 ** | 247.0 | 5.7 | 135.5 | 12.4 | −7.4 | 18.9 |
| 2013 | 7.25 ± 0.12 | 7.48 ± 0.12 | 7.72 ± 0.12 ** | 7.29 ± 0.11 | 7.50 ± 0.11 | 7.71 ± 0.12 ** | 181.1 | 1.2 | 96.7 | 13.4 | −6.5 | 18.0 |
| 2014 | 7.13 ± 0.11 | 7.34 ± 0.11 | 7.56 ± 0.12 ** | 7.67 ± 0.11 ** | 7.84 ± 0.11 ** | 8.01 ± 0.11 ** | 229.5 | 5.2 | 116.7 | 12.5 | −5.2 | 16.6 |
| P (mm) | LMWL Slope (Permille/Permille) | n | |||||
|---|---|---|---|---|---|---|---|
| OLSR | RMA | MA | PWLSR | PWRMA | PWMA | ||
| All | 7.27 ± 0.06 | 7.51 ± 0.06 ** | 7.73 ± 0.06 ** | 7.55 ± 0.05 ** | 7.73 ± 0.05 ** | 7.91 ± 0.05 ** | 959 |
| <30 | 7.29 ± 0.06 | 7.51 ± 0.06 ** | 7.73 ± 0.06 ** | 7.51 ± 0.05 ** | 7.70 ± 0.05 ** | 7.88 ± 0.06 ** | 954 |
| <20 | 7.29 ± 0.06 | 7.51 ± 0.06 ** | 7.73 ± 0.06 ** | 7.53 ± 0.05 ** | 7.71 ± 0.06 ** | 7.90 ± 0.06 ** | 940 |
| <10 | 7.27 ± 0.06 | 7.50 ± 0.06 ** | 7.73 ± 0.06 ** | 7.47 ± 0.06 * | 7.68 ± 0.06 ** | 7.90 ± 0.06 ** | 880 |
| >0.5 | 7.36 ± 0.07 | 7.57 ± 0.07 * | 7.77 ± 0.07 ** | 7.56 ± 0.06 * | 7.74 ± 0.06 ** | 7.92 ± 0.06 ** | 719 |
| >1 | 7.45 ± 0.07 | 7.64 ± 0.07 | 7.83 ± 0.07 ** | 7.59 ± 0.07 | 7.76 ± 0.07 ** | 7.94 ± 0.07 ** | 604 |
| >5 | 7.79 ± 0.12 | 7.97 ± 0.12 | 8.14 ± 0.12 | 7.80 ± 0.11 | 7.97 ± 0.12 | 8.14 ± 0.12 * | 204 |
| Year | Summer Slope (Permille/Permille) | P (mm) | T (°C) | |||||
|---|---|---|---|---|---|---|---|---|
| OLSR | RMA | MA | PWLSR | PWRMA | PWMA | |||
| 2011 | 7.53 ± 0.35 | 7.74 ± 0.34 | 7.95 ± 0.36 | 7.82 ± 0.25 | 7.92 ± 0.25 | 8.03 ± 0.25 | 103 | 19.2 |
| 2012 | 6.90 ± 0.62 | 8.18 ± 0.57 | 8.45 ± 0.64 | 8.54 ± 0.69 | 8.84 ± 0.70 | 9.15 ± 0.72 | 54.4 | 19.5 |
| 2013 | 6.32 ± 0.32 | 6.50 ± 0.31 | 6.67 ± 0.33 | 6.67 ± 0.12 | 6.69 ± 0.12 | 6.71 ± 0.12 | 48 | 19.9 |
| 2014 | 6.70 ± 0.28 | 6.89 ± 0.27 | 7.07 ± 0.28 | 7.35 ± 0.35 | 7.63 ± 0.36 | 7.90 ± 0.37 * | 116 | 17.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, F.; Wang, S.; Wu, X.; Zhang, M.; Argiriou, A.A.; Zhou, X.; Chen, J. Local Meteoric Water Lines in a Semi-Arid Setting of Northwest China Using Multiple Methods. Water 2021, 13, 2380. https://doi.org/10.3390/w13172380
Chen F, Wang S, Wu X, Zhang M, Argiriou AA, Zhou X, Chen J. Local Meteoric Water Lines in a Semi-Arid Setting of Northwest China Using Multiple Methods. Water. 2021; 13(17):2380. https://doi.org/10.3390/w13172380
Chicago/Turabian StyleChen, Fenli, Shengjie Wang, Xixi Wu, Mingjun Zhang, Athanassios A. Argiriou, Xin Zhou, and Jufan Chen. 2021. "Local Meteoric Water Lines in a Semi-Arid Setting of Northwest China Using Multiple Methods" Water 13, no. 17: 2380. https://doi.org/10.3390/w13172380
APA StyleChen, F., Wang, S., Wu, X., Zhang, M., Argiriou, A. A., Zhou, X., & Chen, J. (2021). Local Meteoric Water Lines in a Semi-Arid Setting of Northwest China Using Multiple Methods. Water, 13(17), 2380. https://doi.org/10.3390/w13172380









