Identifying Hub Wastewater Propagation Chains in China’s National Economic System: A Model Coupled Input-Output Analysis with Graphical Theory
Abstract
:1. Introduction
2. Data and Methodology
2.1. Data
2.2. Methodology
3. Results
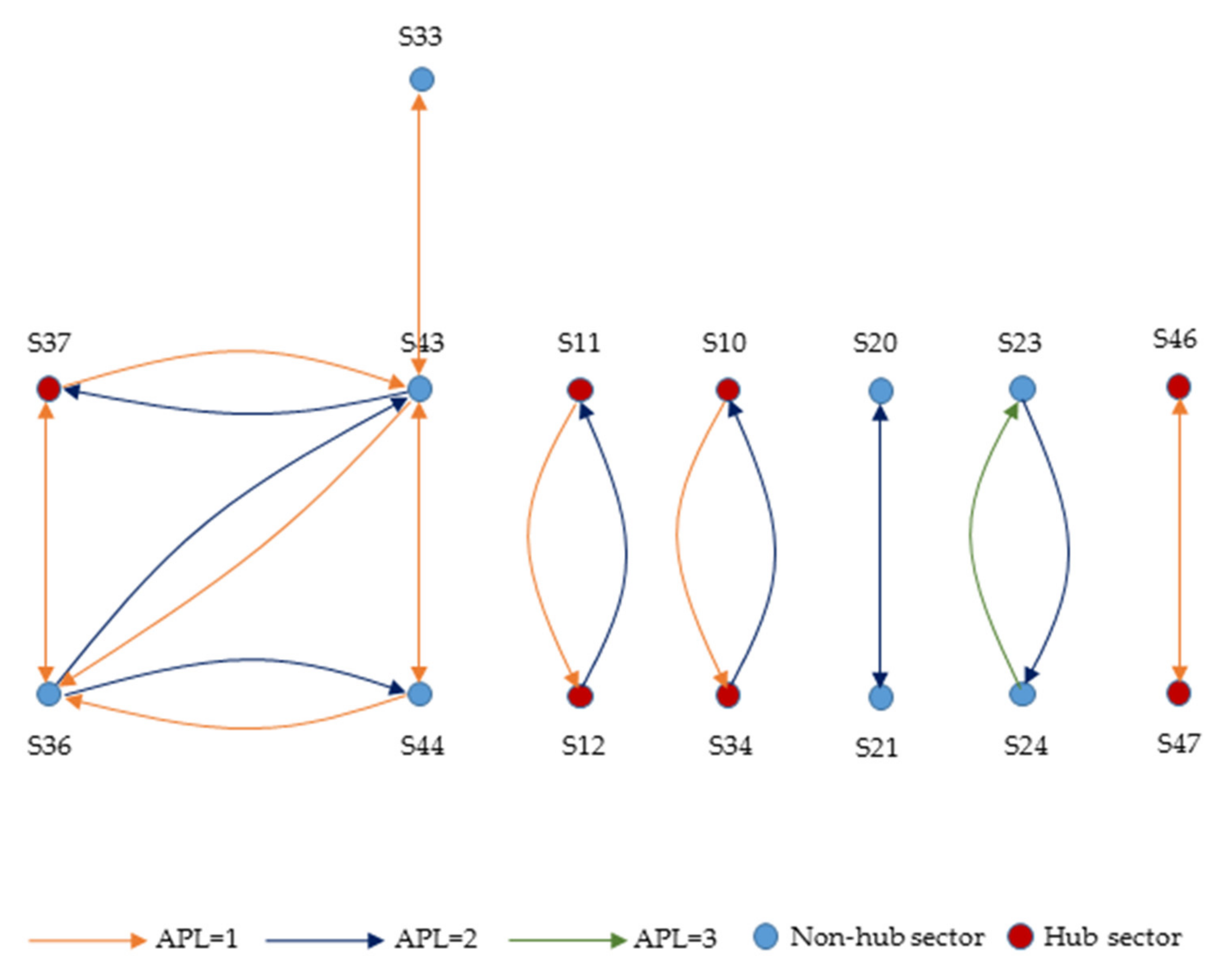
3.1. Hub Wastewater Propagation Chains by APL-HCG
3.2. Simulating the Wastewater Reduction Effects of HWPCs
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Output | ||||
|---|---|---|---|---|
| Intermediate Demand | Final Demand | Total Output | ||
| Input | Intermediate Input | |||
| Value-added | ||||
| Total Input | ||||
| Occupancy | Wastewater Discharge | |||
Appendix B
| Sector Code | Sector Name | Sector Code | Sector Name |
|---|---|---|---|
| S1 | Agricultural Products | S26 | Waste Resources and Waste Material Recycling Processed Products |
| S2 | Forest Products | S27 | Metal Products, Machinery and Equipment Repair Services |
| S3 | Animal Husbandry Products | S28 | Electricity, Steam and Hot Water Production and Supply (Excluding Water and Electricity) |
| S4 | Fishery Products | S29 | Gas Production and Supply |
| S5 | Agriculture, Forestry, Animal Husbandry and Fishery Service Products | S30 | Construction |
| S6 | Coal Mining and Washing Products | S31 | Merchandise Transportation and Storage (Excluding Water Transportation) |
| S7 | Oil and Gas Extraction Products | S32 | Postal Service |
| S8 | Metal Mining Products | S33 | Business |
| S9 | Non-metallic Mining Products | S34 | Catering |
| S10 | Food Manufacturing and Tobacco Processing | S35 | Information Transmission, Computer Services and Software |
| S11 | Textile | S36 | Finance and Insurance |
| S12 | Textile Clothing, Shoes, Hats, Leather, Down and Their Products | S37 | Real Estate |
| S13 | Wood Processing and Furniture | S38 | Scientific Research and Technical Services |
| S14 | Papermaking, Printing and Cultural, Educational and Sporting Goods | S39 | Environment and Public Facilities Management |
| S15 | Petroleum, Coking Products and Nuclear Fuel Processed Products | S40 | Resident Services, Repairs and Other Services |
| S16 | Chemical Products | S41 | Education |
| S17 | Non-metallic Mineral Products | S42 | Health and Social Work |
| S18 | Metal Smelting and Calendered Products | S43 | Culture, Sports and Entertainment |
| S19 | Metal Products | S44 | Public Administration, Social Security and Social Organization |
| S20 | Mechanical Equipment | S45 | Hydropower |
| S21 | Transportation Equipment | S46 | Water Supply |
| S22 | Electrical Machinery and Equipment | S47 | Sewage Treatment |
| S23 | Communication Equipment, Computers and Other Electronic Equipment | S48 | Water Transportation |
| S24 | Instrumentation | S49 | Water Management |
| S25 | Other Manufactured Products |
Appendix C

Appendix D
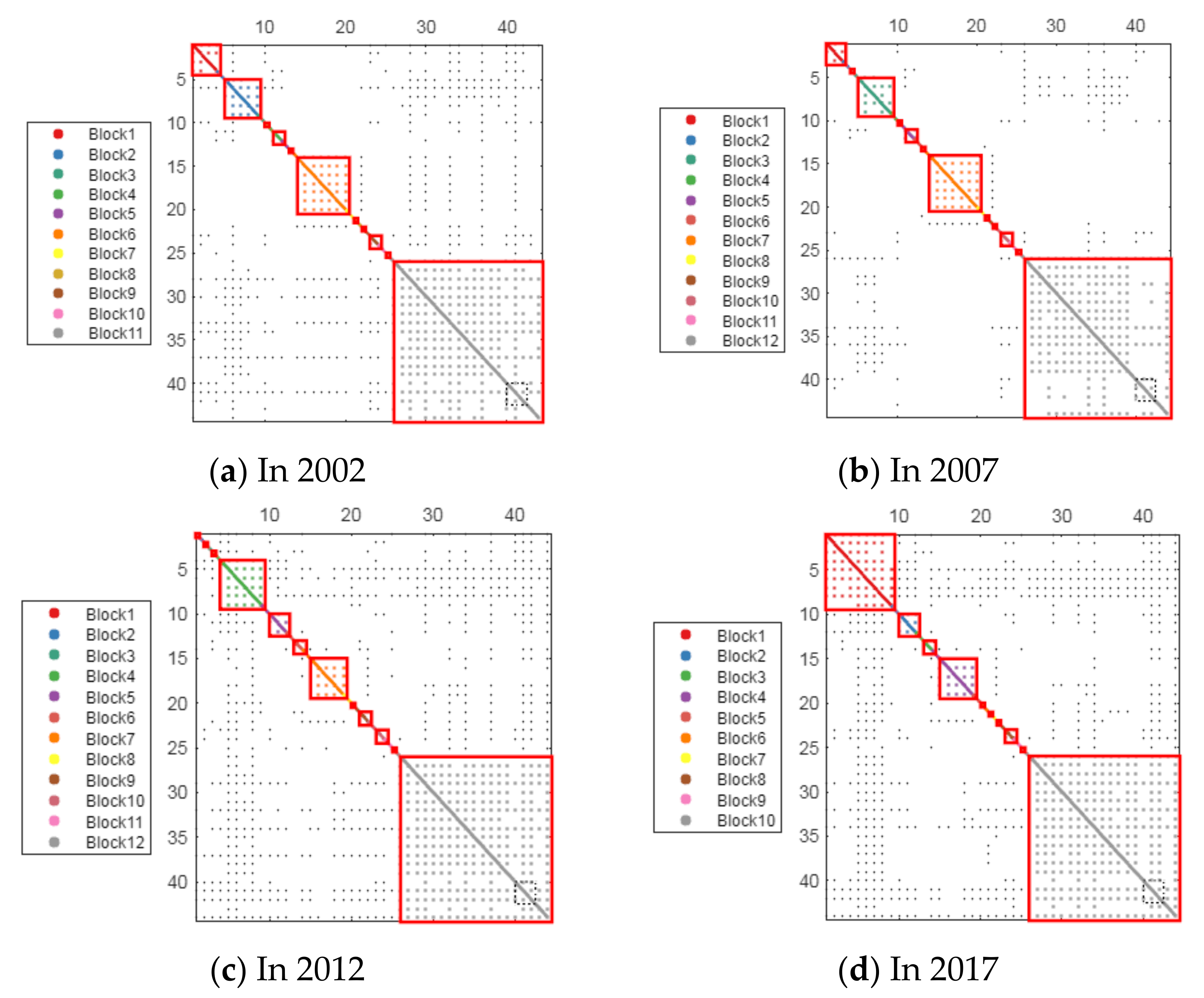
References
- China Environmental News Agency. Sewage Treatment Plants Should be Transformed into Energy Plants, 7th ed.; China Environment News: Beijing, China, 2021; p. 7982. Available online: http://epaper.cenews.com.cn/html/2021-03/09/content_63924.htm (accessed on 6 June 2021). (In Chinese)
- National Bureau of Statistics of China. China’s Environmental Statistics Yearbook; China Statistics Press: Beijing, China, 2017. (In Chinese) [Google Scholar]
- Xiao, L.S.; Lin, C.; Nakamura, S. Tracing the consumption origins of wastewater and sludge for a Chinese city based on waste input–output analysis. Environ. Sci. Technol. 2020, 54, 12560–12567. [Google Scholar] [CrossRef]
- Liu, J.G.; Zhao, D.D.; Mao, G.Q.; Cui, W.H.; Chen, H.; Yang, H. Environmental sustainability of water footprint in mainland China. Geo Sus 2020, 1, 8–17. [Google Scholar] [CrossRef]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China; Ministry of Ecology and Environment of the People’s Republic of China; Development and Reform Commission of the People’s Republic of China. Three-year Action Plan for Quality and Efficiency Improvement of Urban Sewage Treatment (2019–2021). In Official website of Ministry of Housing and Urban-Rural Development of the People’s Republic of China 2019. Available online: http://www.mohurd.gov.cn/wjfb/201905/t20190509_240490.html (accessed on 29 April 2019).
- National Development and Reform Commission of China; Ministry of Science and Technology of the People’s Republic of China; Ministry of Industry and Information Technology of the People’s Republic of China et al Guiding Opinions on Promoting the Utilization of Wastewater Resources. In Official website of National Development and Reform Commission of China 2021. Available online: https://www.ndrc.gov.cn/xwdt/tzgg/202101/t20210111_1264795_ext.html (accessed on 6 June 2021).
- Tu, Z.Z. Analysis and Evaluation of Water Environment in Beijing-Tianjin-Hebei Region. Master’s Thesis, The University of Chinese Academy of Sciences, Beijing, China, 2017. [Google Scholar]
- Deng, Z.G.; Chen, X.K. Analysis on Chinese product sectors′ production chains and their evolution based on APL model. Math. Prac. Theor. 2008, 38, 53–59. (In Chinese) [Google Scholar]
- Deng, Z.G.; Chen, X.K. Analysis of the evolvement trend and dynamic impact of sectors production chains in China. Oper. Res. Manag. Sci. 2009, 18, 19–23. (In Chinese) [Google Scholar]
- Dietzenbacher, E.; Luna, I.R.; Bosma, N. Using average propagation lengths to identify production chains in the Andalusian economy. Estudio Econ. Apl. 2005, 23, 405–422. [Google Scholar]
- Dietzenbacher, E.; Romero, I. Production chains in an interregional framework: Identification by means of average propagation lengths. Int. Reg. Sci. Rev. 2007, 30, 362–383. [Google Scholar] [CrossRef]
- Liu, X.L. A method to visualize the skeleton industrial structure with input-output analysis and its application in China, Japan and USA. J. Syst. Sci. Complex. 2018, 31, 1554–1570. [Google Scholar] [CrossRef]
- Wang, W.H.; Tang, X.; Yang, X.G.; Zhang, B.S.; Zhang, Y.Q.; Höök, M. Energy savings in China’s energy sectors and contributions to air pollution reduction in the 12th Five Year Plan. J. Clean Prod. 2018, 200, 305–317. [Google Scholar] [CrossRef]
- Wang, W.H.; Wang, S.Y.; Yang, X.G. Key sectors and reduction paths of embodied SO2 emission from coal consumption in Shandong province. J. Chin. Univ. Petr. (Edit. Soci. Scie.) 2019, 35, 9–15. (In Chinese) [Google Scholar]
- Zhao, Y.H.; Zhang, Z.H.; Wang, S.; Zhang, Y.F.; Liu, Y. Linkage analysis of sectoral CO2 emissions based on the hypothetical extraction method in South Africa. J. Clean. Prod. 2015, 103, 916–924. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Liu, Y.; Wang, S.; Zhang, Z.H.; Li, J.C. Inter-regional linkage analysis of industrial CO2 emissions in China: An application of a hypothetical extraction method. Ecol. Indic. 2016, 61, 428–437. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, Y.J.; Zhang, K.B. The key sectors for energy conservation and carbon emissions reduction in China: Evidence from the input-output method. J. Clean. Prod. 2018, 179, 180–190. [Google Scholar] [CrossRef]
- Romero, I.; Dietzenbacher, E.; Hewings, G. Fragmentation and complexity: Analyzing structural change in the Chicago regional economy. Rev. Econ. Mund. 2009, 15, 263–282. [Google Scholar]
- Antràs, P.; Chor, D.; Fally, T.; Hillberry, R. Measuring the upstreamness of production and trade flows. Am. Econ. Rev. Pap. Proc. 2012, 102, 412–416. [Google Scholar] [CrossRef]
- Lu, X.L.; Jian, X. Explaining the changes in ALPs by identifying ALPs important coefficients: An empirical application of China. J. Syst. Sci. Complex. 2013, 26, 383–406. [Google Scholar] [CrossRef]
- Chen, Q.R. The average propagation length: An extended analysis. In In Proceedings of the 22nd International Input-Output Conference, Lisbon, Portugal, 14–18 July 2014. [Google Scholar]
- Tan, K.M.; London, P.; Mohan, K.; Lee, S.I.; Fazel, M.; Witten, D. Learning graphical models with hubs. J. Mach. Learn. Res. 2014, 15, 3297–3331. [Google Scholar]
- Chaudhuri, S.; Drton, M.; Richardson, T. Estimation of a covariance matrix with zeros. Biometrika 2007, 94, 199–216. [Google Scholar] [CrossRef] [Green Version]
- Xue, L.Z.; Ma, S.Q.; Zou, H. Positive definite ℓ1 penalized estimation of large covariance matrices. J. Am. Stat. Assoc. 2012, 107, 1480–1491. [Google Scholar] [CrossRef] [Green Version]
- Zheng, S. The Study on China’s Household Consumption and Structure Prediction and Its Impacts on Resources Consumption. Master’s Thesis, The University of Chinese Academy of Sciences, Beijing, China, 2020. [Google Scholar]
- Zheng, B.Y.; Huang, G.H.; Liu, L.R.; Guan, Y.R.; Zhai, M.Y. Dynamic wastewater-induced research based on input-output analysis for Guangdong Province, China. Environ. Pollut. 2020, 256, 113502. [Google Scholar] [CrossRef]
- Zheng, Y.X.; Hong, J.K.; Xiao, C.L.; Li, Z.M. Unfolding the synergy and interaction of water-land-food nexus for sustainable resource management: A supernetwork analysis. Sci. Total Environ. 2021, 784, 147085. [Google Scholar]
- Liu, X.L.; Hewigns, G.J.D.; Wang, S.Y. Evaluating the impacts of waste treatment management modes on each sector’s price in a macro economic system. J. Clean. Prod. 2018, 200, 188–195. [Google Scholar] [CrossRef]
- Yu, C.; Shi, L.; Wang, Y.T.; Chang, Y.; Cheng, B.D. The eco-efficiency of pulp and paper industry in China: An assessment based on slacks-based measure and Malmquist-Luenberger index. J. Clean. Prod. 2016, 127, 511–521. [Google Scholar] [CrossRef]
- Lin, C. Hybrid input-output analysis of wastewater treatment and environmental impacts: A case study for the Tokyo Metropolis. Ecol. Econ. 2009, 68, 2096–2105. [Google Scholar] [CrossRef]
- Akao, P.K.; Singh, B.; Kaur, P.; Sor, A.; Avni, A.; Dhir, A.; Verma, S.; Kappoor, S.; Phutela, U.G.; Satpute, S.; et al. Coupled microalgal-bacterial biofilm for enhanced wastewater treatment without energy investment. J. Water Process. Eng. 2021, 41, 102029. [Google Scholar] [CrossRef]
- Paulu, A.; Bartacek, J.; Seresova, M.; Koci, V. Combining process modeling and LCA to assess the environmental impacts of wastewater treatment. Water 2021, 13, 1246. [Google Scholar] [CrossRef]
- Thirunavukkarasu, A.; Sivashankar, R.N.R. A review on the role of nanomaterials in the removal of organic pollutants from wastewater. Rev. Environ. Sci. Biotechnol. 2021, 19, 751–778. [Google Scholar] [CrossRef]
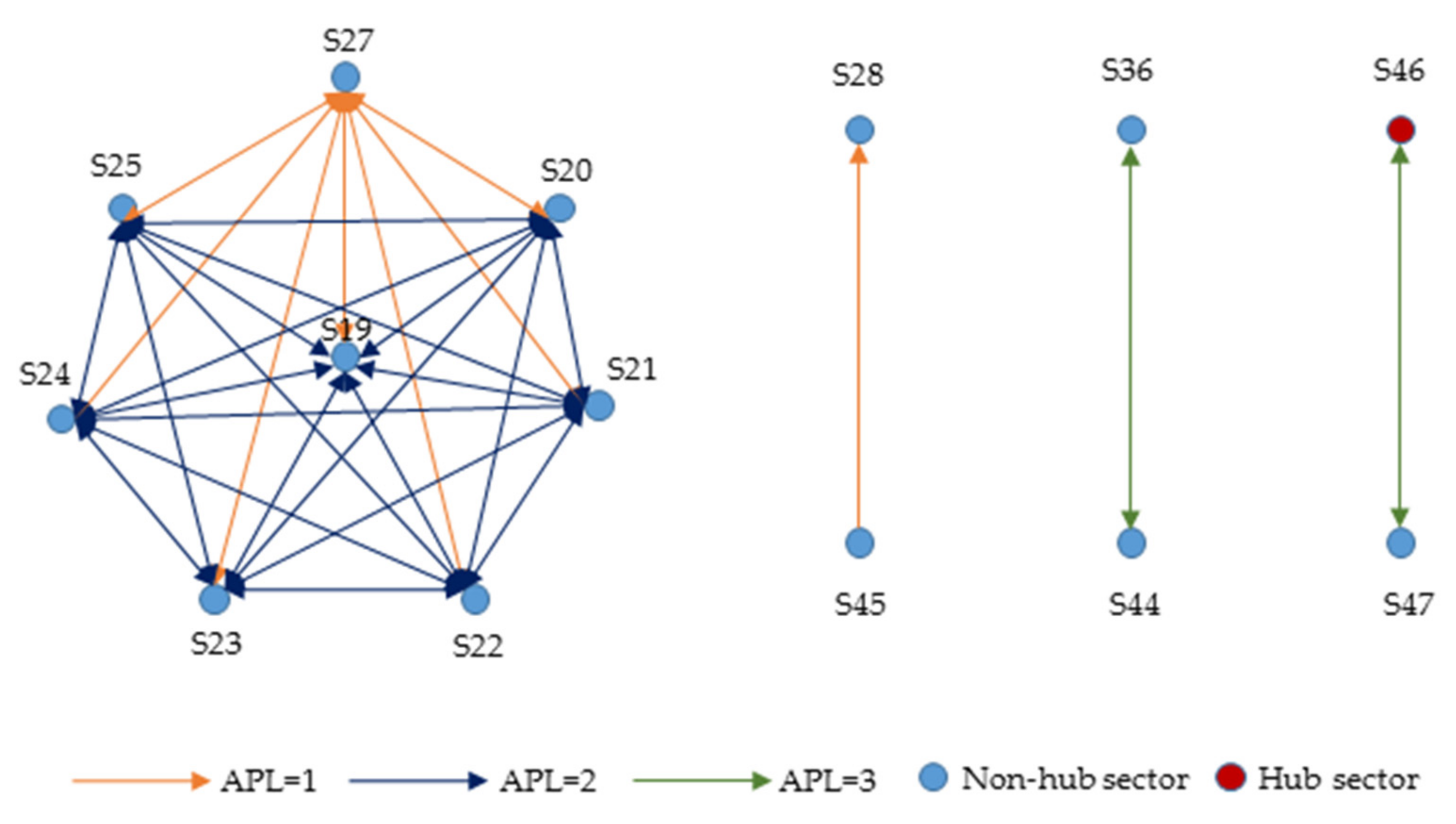
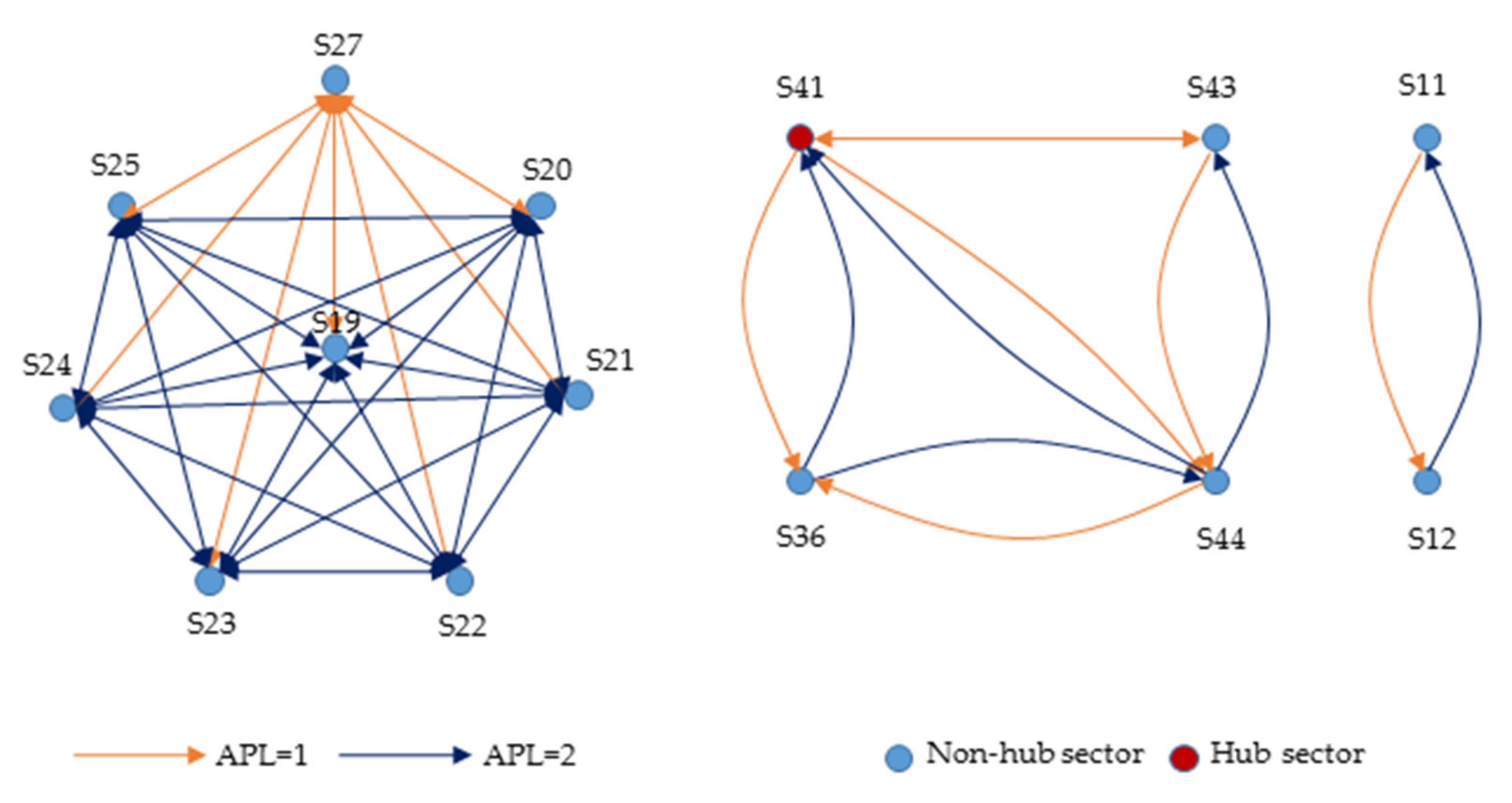
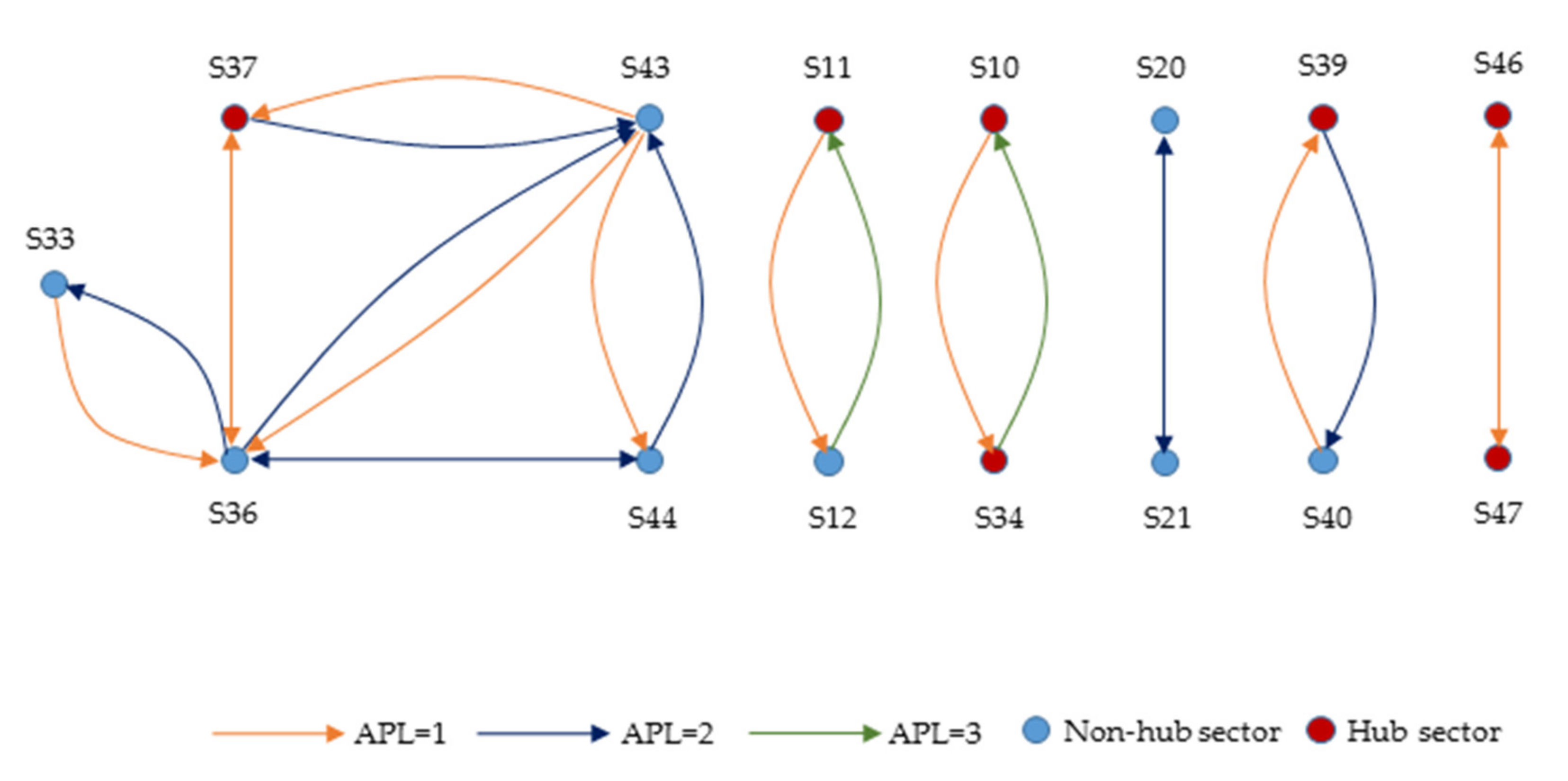
| Year | Decrease Rate (%) | |
|---|---|---|
| 2002 | 5.95 | 1.36 |
| 2007 | 14.07 | 2.53 |
| 2012 | 16.81 | 2.46 |
| 2017 | 14.73 | 2.11 |
| Year | Decrease Rate (%) | |
|---|---|---|
| 2002 | 5.35 | 1.22 |
| 2007 | 5.09 | 0.92 |
| 2012 | 13.64 | 1.99 |
| 2017 | 14.04 | 2.01 |
| Year | Decrease Rate (%) | |
|---|---|---|
| 2002 | 5.06 | 1.15 |
| 2007 | 10.30 | 1.85 |
| 2012 | 12.06 | 1.76 |
| 2017 | 12.06 | 1.76 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Liu, X. Identifying Hub Wastewater Propagation Chains in China’s National Economic System: A Model Coupled Input-Output Analysis with Graphical Theory. Water 2021, 13, 2351. https://doi.org/10.3390/w13172351
Li X, Liu X. Identifying Hub Wastewater Propagation Chains in China’s National Economic System: A Model Coupled Input-Output Analysis with Graphical Theory. Water. 2021; 13(17):2351. https://doi.org/10.3390/w13172351
Chicago/Turabian StyleLi, Xuefeng, and Xiuli Liu. 2021. "Identifying Hub Wastewater Propagation Chains in China’s National Economic System: A Model Coupled Input-Output Analysis with Graphical Theory" Water 13, no. 17: 2351. https://doi.org/10.3390/w13172351
APA StyleLi, X., & Liu, X. (2021). Identifying Hub Wastewater Propagation Chains in China’s National Economic System: A Model Coupled Input-Output Analysis with Graphical Theory. Water, 13(17), 2351. https://doi.org/10.3390/w13172351






