Revisiting the Gage–Bidwell Law of Dilution in Relation to the Effectiveness of Swimming Pool Filtration and the Risk to Swimming Pool Users from Cryptosporidium
Abstract
1. Introduction
2. Materials and Methods
- Disinfection using chlorine gas (0.45 mg L−1 free chlorine in the pool water).
- pH adjustment (pH 7.0 in the pool water).
- Flocculant dosing approx. 0.05 mg L−1 Al as poly-aluminium chloride (PAC).
- Dual media filter (0.5 m sand depth, 0.7–1.2 mm grain size), (0.5 m anthracite depth, 1.4–2.5 mm grain size).
- Filtration velocity 35 m h−1.
3. Results
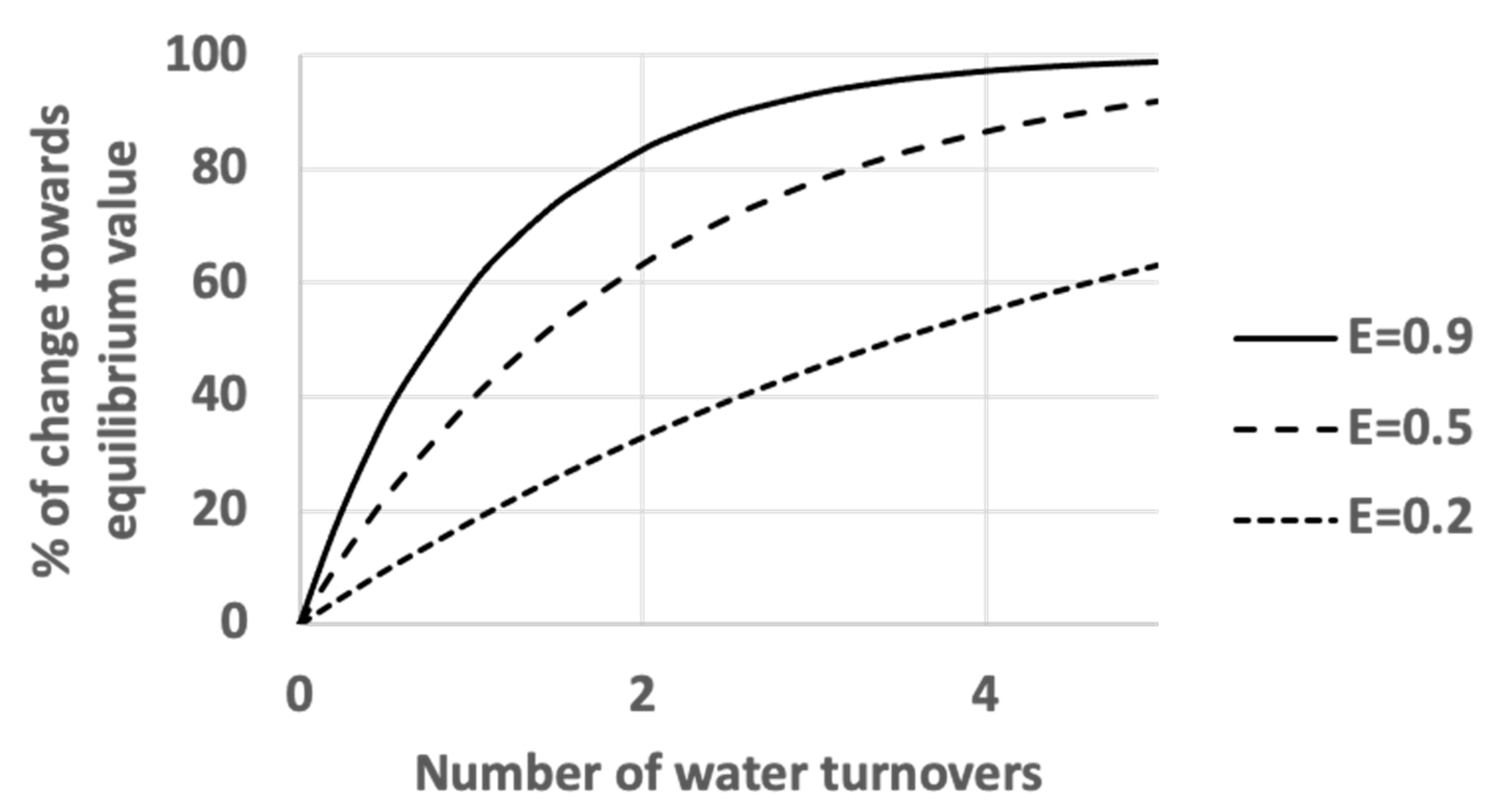
3.1. The Gage–Bidwell Law of Dilution: Empirical Approach
3.2. The Gage–Bidwell Law of Dilution: Computational Approach
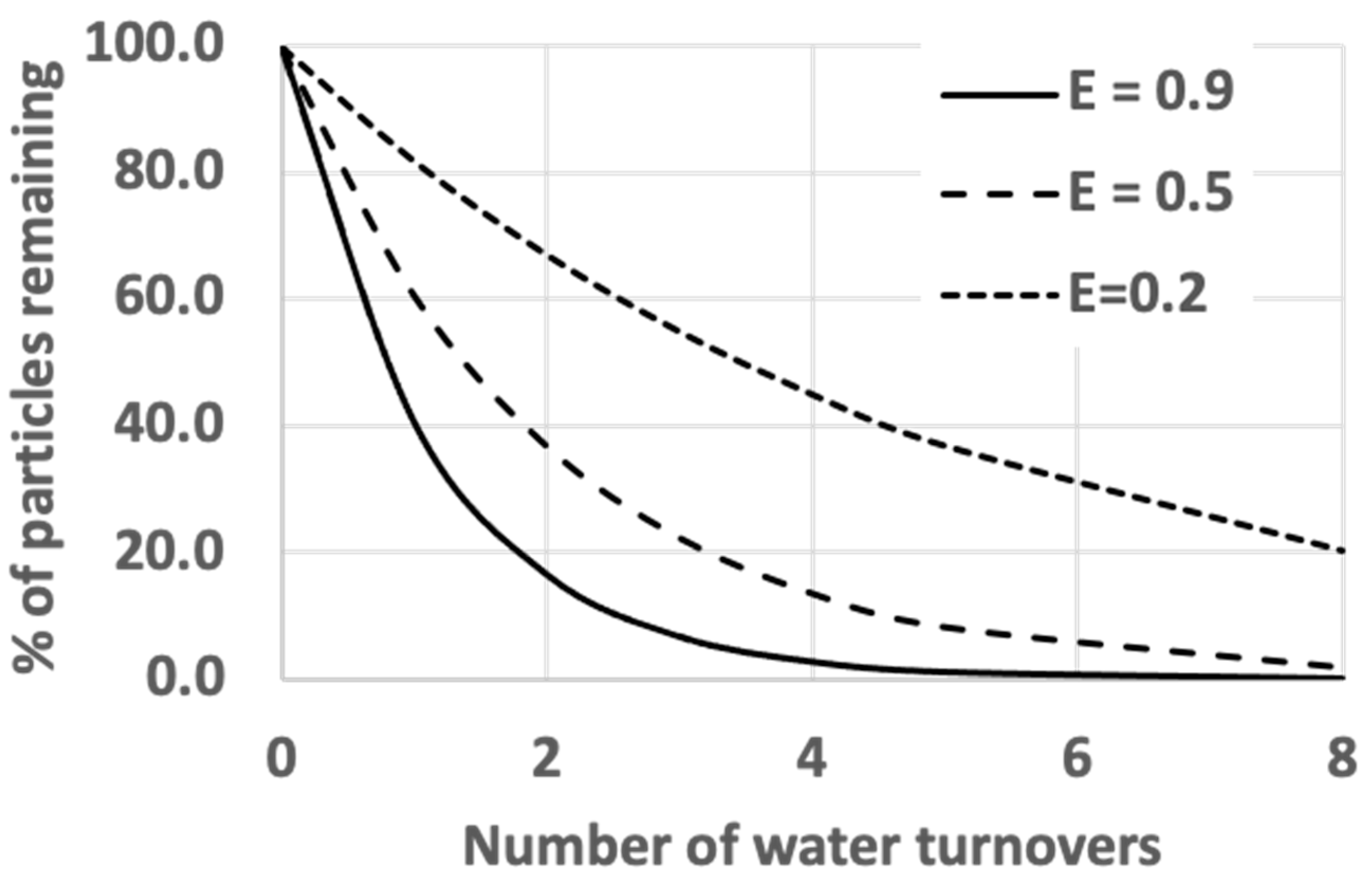
3.3. The Role of Filter Efficiency in Contaminant Removal
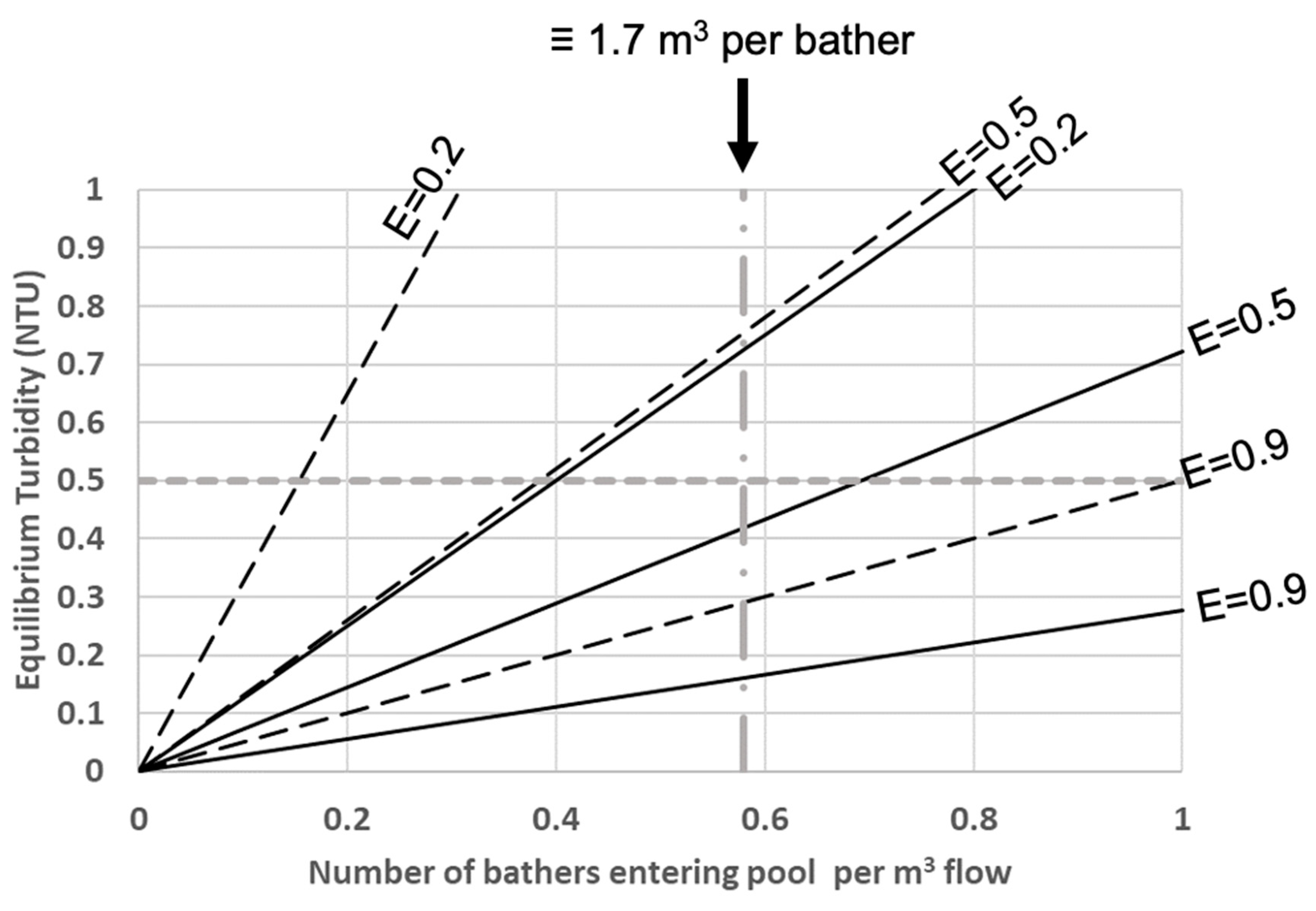
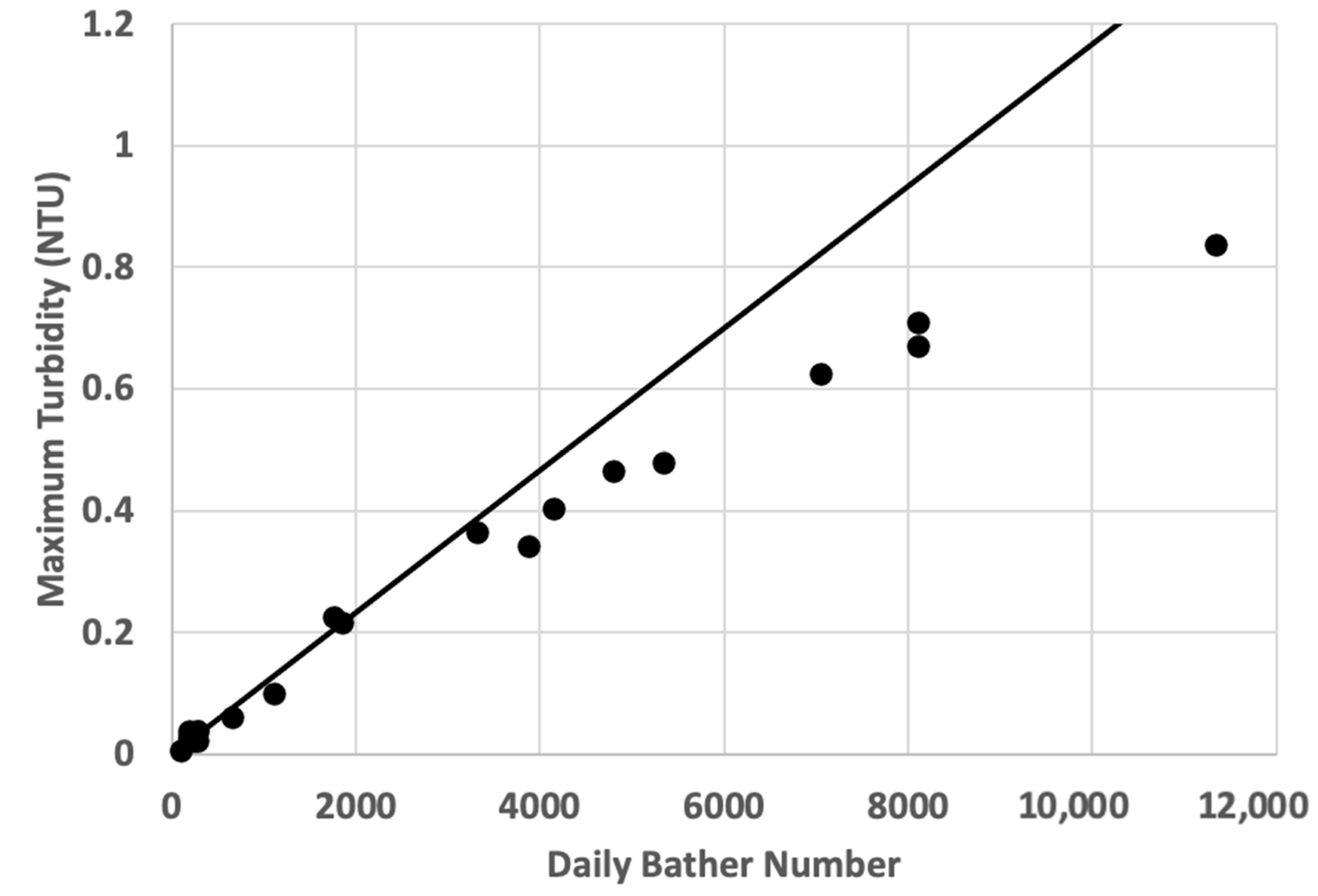
3.4. Application of the Gage–Bidwell Approach to Modelling the Peak Turbidity of Pool Water
- To establish the equilibrium turbidity likely to be achieved if a constant bathing load (in terms of numbers of bathers per hour) is maintained indefinitely.
- To establish the maximum turbidity likely to be achieved if a constant bathing load is sustained for a finite time that is too short for the equilibrium to be achieved.
3.4.1. Modelling the Maximum Turbidity Achievable If the Design Maximum Bathing Load for a Pool Is Sustained Indefinitely
3.4.2. Modelling the Maximum Turbidity Achievable If the Design Maximum Bathing Load for a Pool Is Sustained for a Finite Period
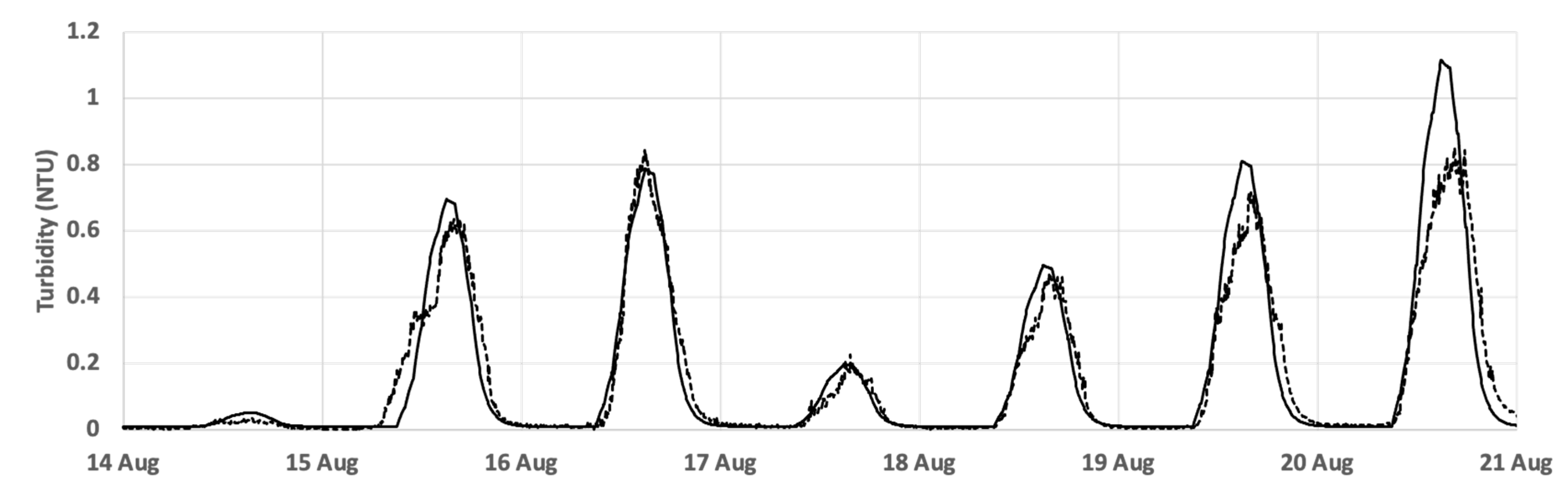
3.5. Modelling Observed Time Courses of NTU
3.6. Public Health Implications
- Prediction of the time it takes to achieve satisfactory removal of a contaminant (e.g., Cryptosporidium oocysts) following a single contamination event.
- Prediction of the maximum equilibrium concentration of a contaminant under conditions of a steady input of the contaminant (we considered the maximum turbidity achieved under conditions of a prolonged constant bathing load).
- Prediction of the amount of water that should be circulated per bather to ensure that water clarity remains excellent, even when there is a very prolonged period when bathers are entering the pool.
- Prediction of the peak turbidity likely to be achieved in practice from knowledge of the distribution of bathing load during the day.
- Depth ranging from 1–2 m (average depth 1.5 m).
- 4 m2 pool area allowed per bather at maximum bathing load following the UK guidelines [10], i.e., each bather occupies 6 m3 of water on average.
- 3 h water-turnover time.
- Average bathing time of 0.75 h.
3.7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lewis, L.; Chew, J.; Woodley, I.; Colbourne, J.; Pond, K. The application of computational fluid dynamics and small-scale physical models to assess the effects of operational practices on the risk to public health within large indoor swimming pools. J. Water Health 2015, 13, 939–952. [Google Scholar] [CrossRef] [PubMed]
- Ryan, U.; Lawler, S.; Reid, S. Limiting swimming pool outbreaks of cryptosporidiosis–the roles of regulations, staff, patrons and research. J. Water Health 2017, 15, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Chalmers, R.M. Waterborne outbreaks of cryptosporidiosis. Ann. dell’Istituto Super Sanità 2012, 48, 429–446. Available online: https://www.iss.it/documents/20126/45616/ANN_12_04_10.pdf (accessed on 26 April 2021). [CrossRef] [PubMed]
- Gregory, R. Bench-marking pool water treatment for coping with Cryptosporidium. J. Environ. Health Res. 2002, 1, 11–18. [Google Scholar]
- Messner, M.J.; Chappell, C.L.; Okhuysen, P.C. Risk assessment for Cryptosporidium: A hierarchical Bayesian analysis of human dose response data. Water Res. 2001, 35, 3934–3940. [Google Scholar] [CrossRef]
- World Health Organisation. Guidelines for Safe Recreational Water Environments. Volume 2: Swimming Pools and Similar Environments; World Health Organisation: Geneva, Switzerland, 2006; Available online: https://www.who.int/water_sanitation_health/publications/safe-recreational-water-guidelines-2/en/ (accessed on 26 April 2021).
- Wood, M.; Simmonds, L.; MacAdam, J.; Hassard, F.; Jarvis, P.; Chalmers, R.M. Role of filtration in managing the risk from Cryptosporidium in commercial swimming pools—A review. J. Water Health 2019, 17, 357–370. [Google Scholar] [CrossRef] [PubMed]
- Croll, B. Decontaminating swimming pools and managing Cryptosporidium. Recreation 2004, 2004, 32–35. Available online: https://poolsentry.co.uk/s/Croll-2004.pdf (accessed on 26 April 2021).
- Gage, S.D.; Ferguson, H.F.; Gillespie, C.G.; Messer, R.; Tisdale, E.S.; Hinman, J.J., Jr.; Green, H.W. Swimming Pools and other Public Bathing Places. Am. J. Public Health 1926, 16, 1186–1201. Available online: https://ajph.aphapublications.org/doi/pdf/10.2105/AJPH.16.12.1186 (accessed on 26 April 2021). [CrossRef] [PubMed]
- Pool Water Treatment Advisory Group. Code of Practice for Swimming Pool Water; Pool Water Treatment Advisory Group: Loughborough, UK, 2017; Available online: https://www.pwtag.org/code-of-practice/ (accessed on 26 April 2021).
- Kanan, A.; Karanfil, T. Formation of disinfection by-products in indoor swimming pool water: The contribution from filling water natural organic matter and swimmer body fluids. Water Res. 2011, 45, 926–932. [Google Scholar] [CrossRef] [PubMed]
- Ratajczak, K.; Pobudkowska, A. Pilot Test on Pre-Swim Hygiene as a Factor Limiting Trihalomethane Precursors in Pool Water by Reducing Organic Matter in an Operational Facility. Int. J. Environ. Res. Public Health 2020, 17, 7547. [Google Scholar] [CrossRef] [PubMed]
- Stauder, S.; Rodelsperger, M. Filtration particles and turbidity in pool water. Removal by in line filtration and modelling of daily courses. In Proceedings of the Fourth International Conference Swimming Pool and Spa, Porto, Portugal, 15–18 March 2011; pp. 71–77. Available online: https://poolsentry.co.uk/s/Stauder-S-and-Rodelsperger-M-2011-filtration-particles-and-turbidity-in-pool-water-removal-by-in-lin.pdf (accessed on 26 April 2021).
- Gordon, I.; Inglis, S. Great Lengths: The Historic Indoor Swimming Pools of Britain; English Heritage: Swindon, UK, 2009. [Google Scholar]
- Alansari, A.; Amburgey, J.; Madding, N. 2018 A quantitative analysis of swimming pool recirculation system efficiency. J. Water Health 2018, 16, 449–459. [Google Scholar] [CrossRef] [PubMed]
- Cloteaux, A.; Gérardin, F.; Midoux, N. Influence of swimming pool design on hydraulic behavior: A numerical and experimental study. Engineering 2013, 5, 511–524. [Google Scholar] [CrossRef][Green Version]
- Chappell, C.L.; Okhuysen, P.C.; Sterling, C.R.; DuPont, H.L. Cryptosporidium parvum: Intensity of infection and oocyst excretion patterns in healthy volunteers. J. Infect. Dis. 1996, 173, 232–236. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Lu, P.; Amburgey, J.E. A pilot-scale study of Cryptosporidium-sized microsphere removals from swimming pools via sand filtration. J. Water Health 2016, 14, 109–120. [Google Scholar] [CrossRef] [PubMed]
- Morais, I.P.; Tóth, I.V.; Rangel, A.O. Turbidimetric and nephelometric flow analysis: Concepts and applications. Spectrosc. Lett. 2006, 39, 547–579. [Google Scholar] [CrossRef]
- Amburgey, J.E. Optimization of the extended terminal subfluidization wash (ETSW) filter backwashing procedure. Water Res. 2005, 39, 314–330. [Google Scholar] [CrossRef] [PubMed]
- Keuten, M.G.A.; Schets, F.M.; Schijven, J.F.; Verberk, J.Q.J.C.; Van Dijk, J.C. Definition and quantification of initial anthropogenic pollutant release in swimming pools. Water Res. 2012, 46, 3682–3692. [Google Scholar] [CrossRef] [PubMed]
- Falk, R.A.; Blatchley, E.R.; Kuechler, T.C.; Meyer, E.M.; Pickens, S.R.; Suppes, L.M. Assessing the Impact of Cyanuric Acid on Bather’s Risk of Gastrointestinal Illness at Swimming Pools. Water 2019, 11, 1314. [Google Scholar] [CrossRef]
| State | Cumulative Fraction of Pool Volume Removed | Average Concentration (C) in Pool Water after Mixing |
|---|---|---|
| Starting state | 0 | C = Co |
| After first container | 1/3 | C = (1 − 1/3) Co |
| After second container | 2/3 | C = (1 − 1/3) (1 − 1/3) Co |
| After third container | 1 | C = (1 − 1/3) (1 − 1/3) (1 − 1/3) Co |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simmonds, L.P.; Simmonds, G.E.; Wood, M.; Marjoribanks, T.I.; Amburgey, J.E. Revisiting the Gage–Bidwell Law of Dilution in Relation to the Effectiveness of Swimming Pool Filtration and the Risk to Swimming Pool Users from Cryptosporidium. Water 2021, 13, 2350. https://doi.org/10.3390/w13172350
Simmonds LP, Simmonds GE, Wood M, Marjoribanks TI, Amburgey JE. Revisiting the Gage–Bidwell Law of Dilution in Relation to the Effectiveness of Swimming Pool Filtration and the Risk to Swimming Pool Users from Cryptosporidium. Water. 2021; 13(17):2350. https://doi.org/10.3390/w13172350
Chicago/Turabian StyleSimmonds, Lester P., Guy E. Simmonds, Martin Wood, Tim I. Marjoribanks, and James E. Amburgey. 2021. "Revisiting the Gage–Bidwell Law of Dilution in Relation to the Effectiveness of Swimming Pool Filtration and the Risk to Swimming Pool Users from Cryptosporidium" Water 13, no. 17: 2350. https://doi.org/10.3390/w13172350
APA StyleSimmonds, L. P., Simmonds, G. E., Wood, M., Marjoribanks, T. I., & Amburgey, J. E. (2021). Revisiting the Gage–Bidwell Law of Dilution in Relation to the Effectiveness of Swimming Pool Filtration and the Risk to Swimming Pool Users from Cryptosporidium. Water, 13(17), 2350. https://doi.org/10.3390/w13172350






