Assimilation of Piezometric Data to Calibrate Parsimonious Daily Hydrological Models
Abstract
:1. Introduction
2. Data Presentation
Study Sites
- ❖
- Meteorological data were obtained from the SAFRAN reanalysis developed by Meteo France. The SAFRAN reanalysis is based on an optimal interpolation method of meteorological data at the scale of massifs, defined from a division of France into climatologically homogeneous zones. It provided daily liquid and solid precipitation and temperature records, available on a regular 8 km × 8 km grid across France [26,27]. These data are available for the 1970–2020 period. The evapotranspiration data used in modelling were calculated using Oudin’s formula [1], depending only on air temperature.
- ❖
- Hydrometric data were presented as daily average flow records and were taken from the national data bank for hydrometry and hydrology (Hydro French database) [28]. Chronicle durations vary, depending on basins, over a reference period chosen between 1 January 1970 to 31 December 2020. This period was chosen because it is sufficiently broad, with wet years, such as 1977, and dry years, such as 1976, 1989, 2003, and 2011.
- ❖
- Groundwater data were extracted from the ADES (National Groundwater Data Access Portal), a french public site, which collects quantitative (water-level chronicles) and qualitative (geochemistry) data on groundwater in metropolitan France and overseas. It is an essential tool for optimal management of groundwater resources, to enhance our understanding of groundwater evolutions and contribute solutions for local, national pressing societal and European requirements. Values at variable time steps were aggregated at daily time steps so it could be compared with rainfall and flow data.
3. Data Processing
3.1. Computation of a Base Flow and Base Flow Index (BFI)
3.2. Method for Processing Temporal Signals: Cross-Correlations
- ;
- ;
- ;
- ;
- ;
3.3. Selecting the Most Representative Water Table Piezometer—Watercourse Exchange
- ⮚
- The smallest distance to the main watercourse (highest Strahler order);
- ⮚
- Belonging to the main water body in which the studied watershed is included;
- ⮚
- The highest correlation value between piezometry and base flow (r(Qb, H));
- ⮚
- The smallest distance to the watershed outlet.
4. Methodology
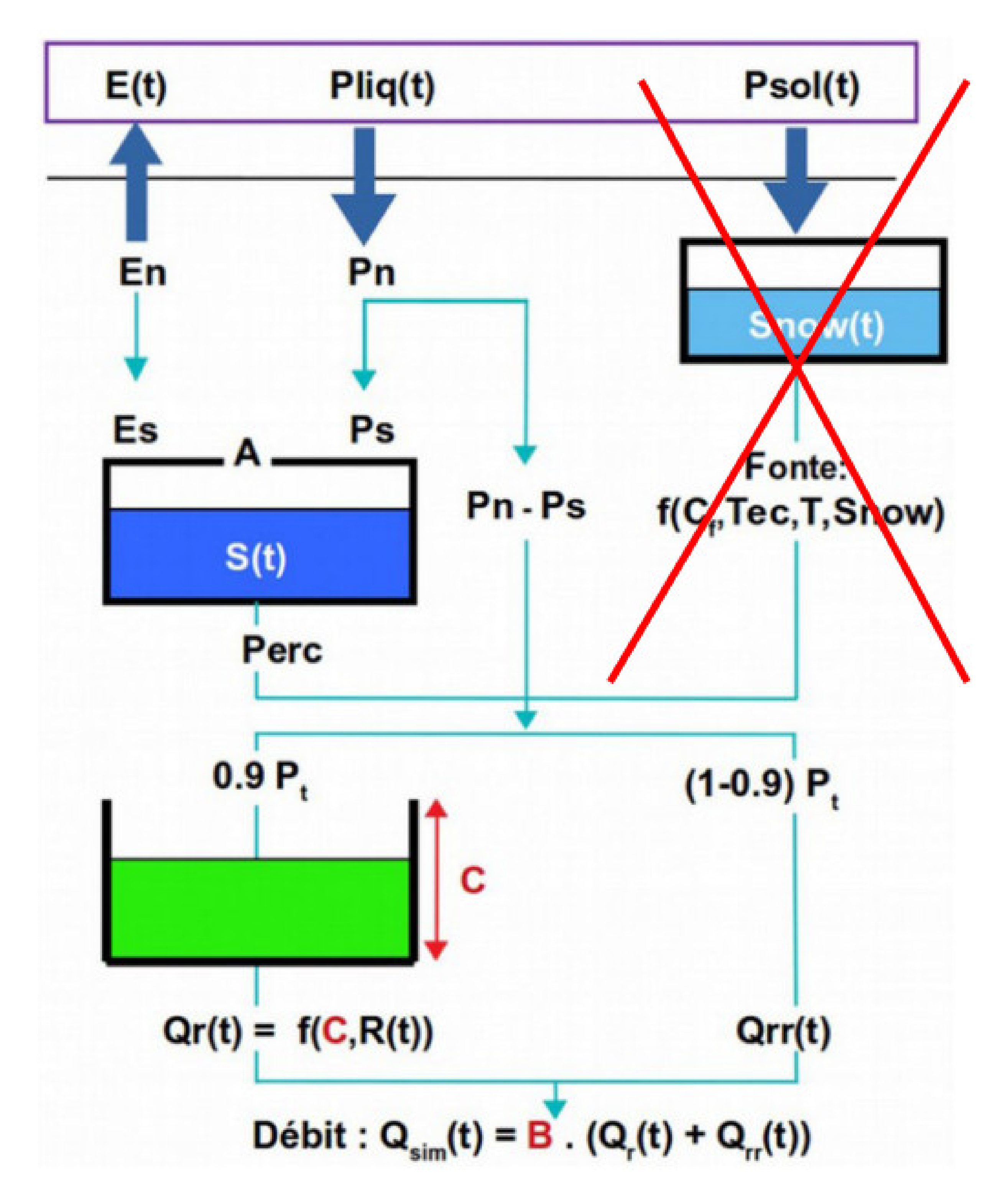
4.1. Hydrological Models
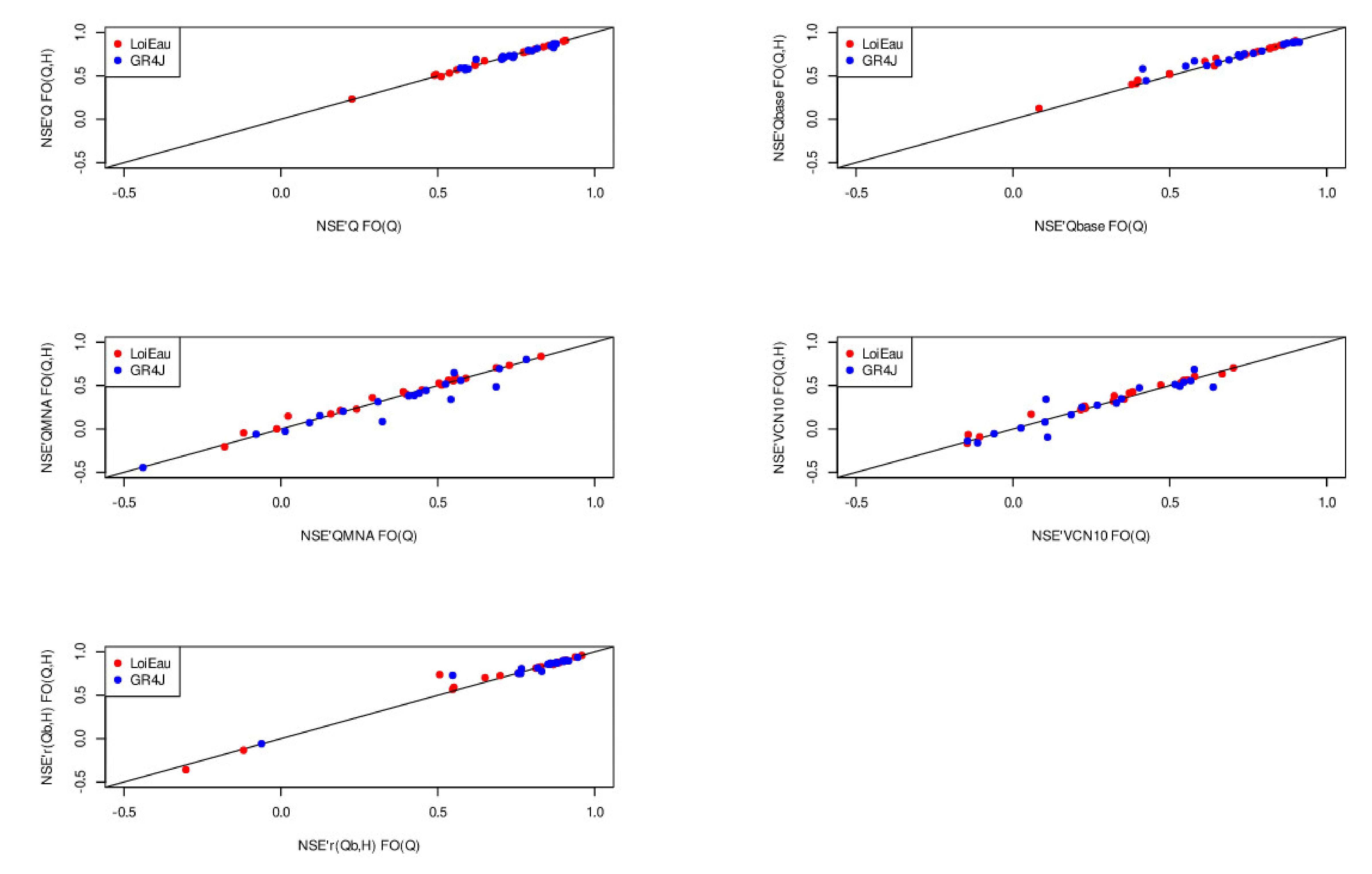
4.2. Multi-Criteria and Multi-Forcing Objective Function
- α is the ratio of simulated and observed flow variances;
- β is the model bias;
- r is the correlation coefficient between observed and simulated flows.
4.3. Evaluation Criteria
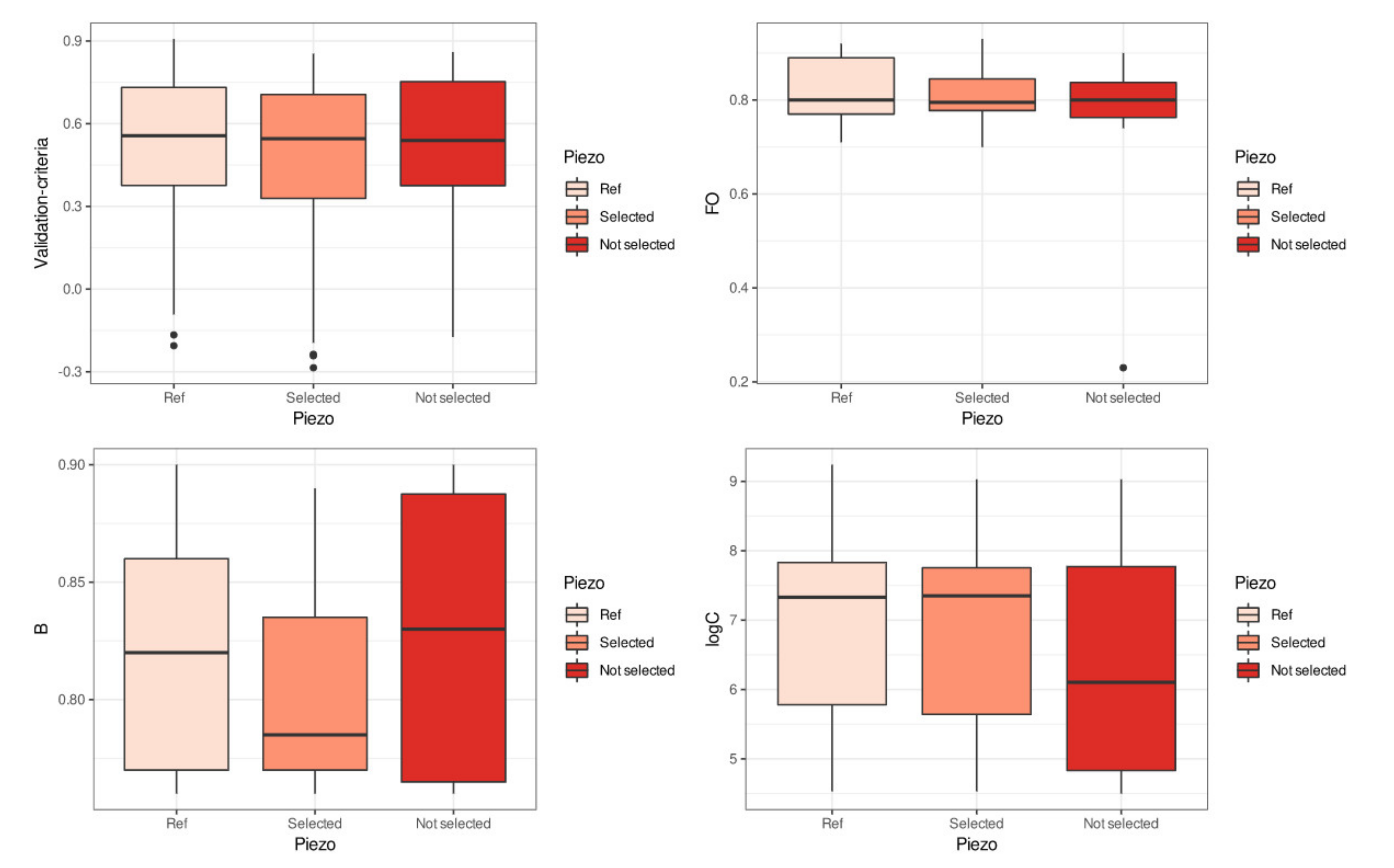
5. Results
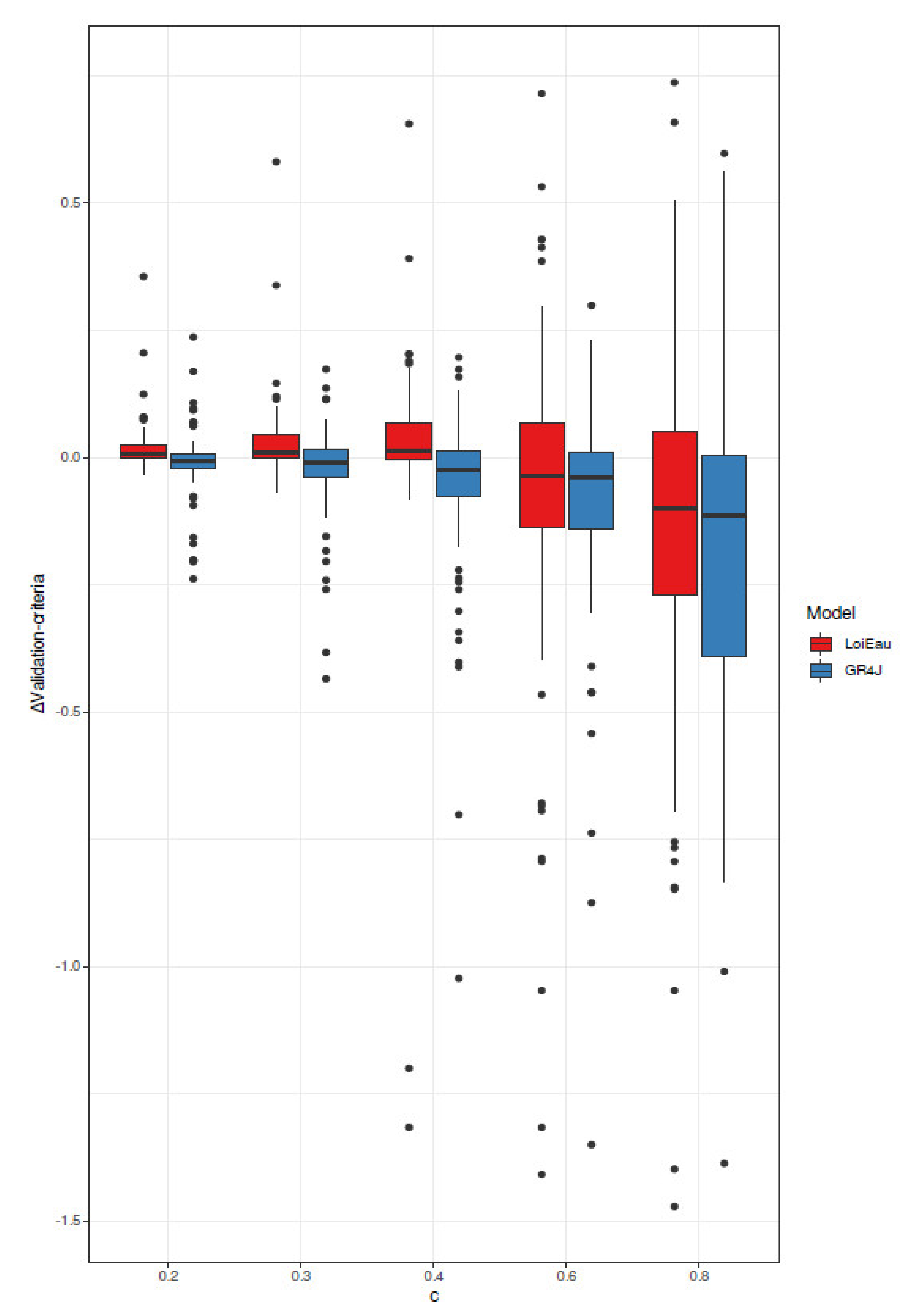
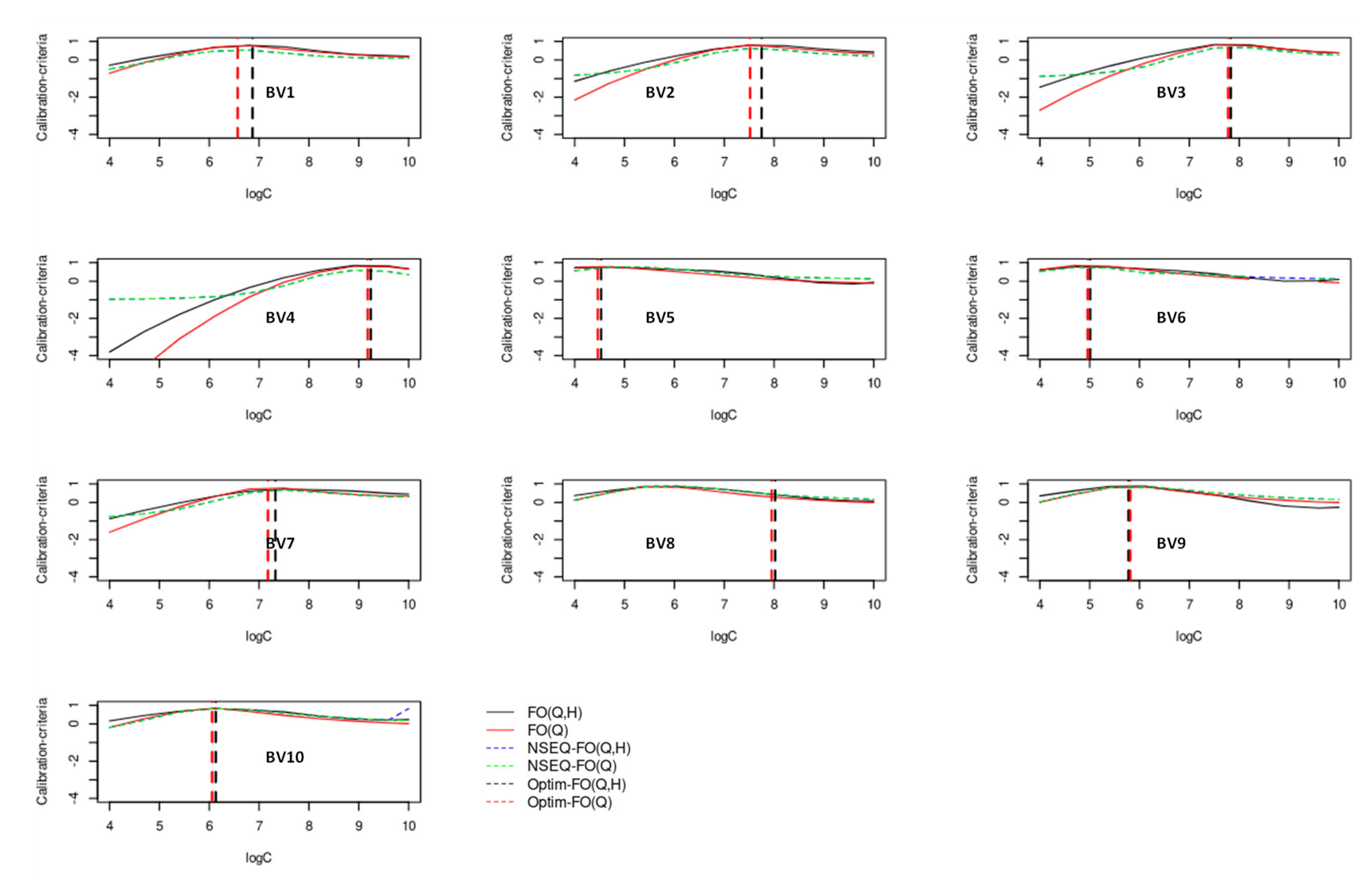
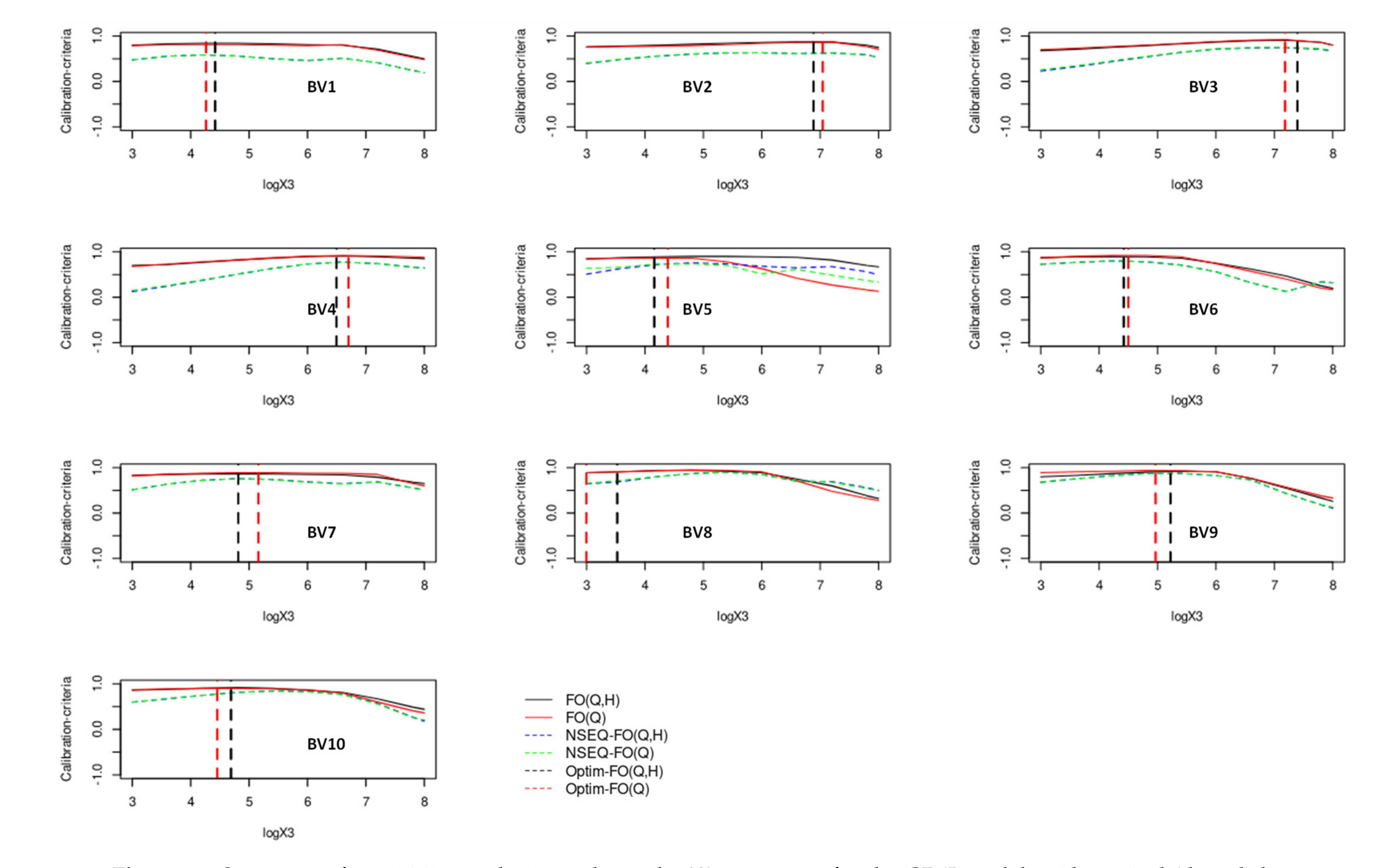
5.1. Analysis of Choosing Parameter Weights in the Multi-Criteria and Multi-Forcing Objective Function
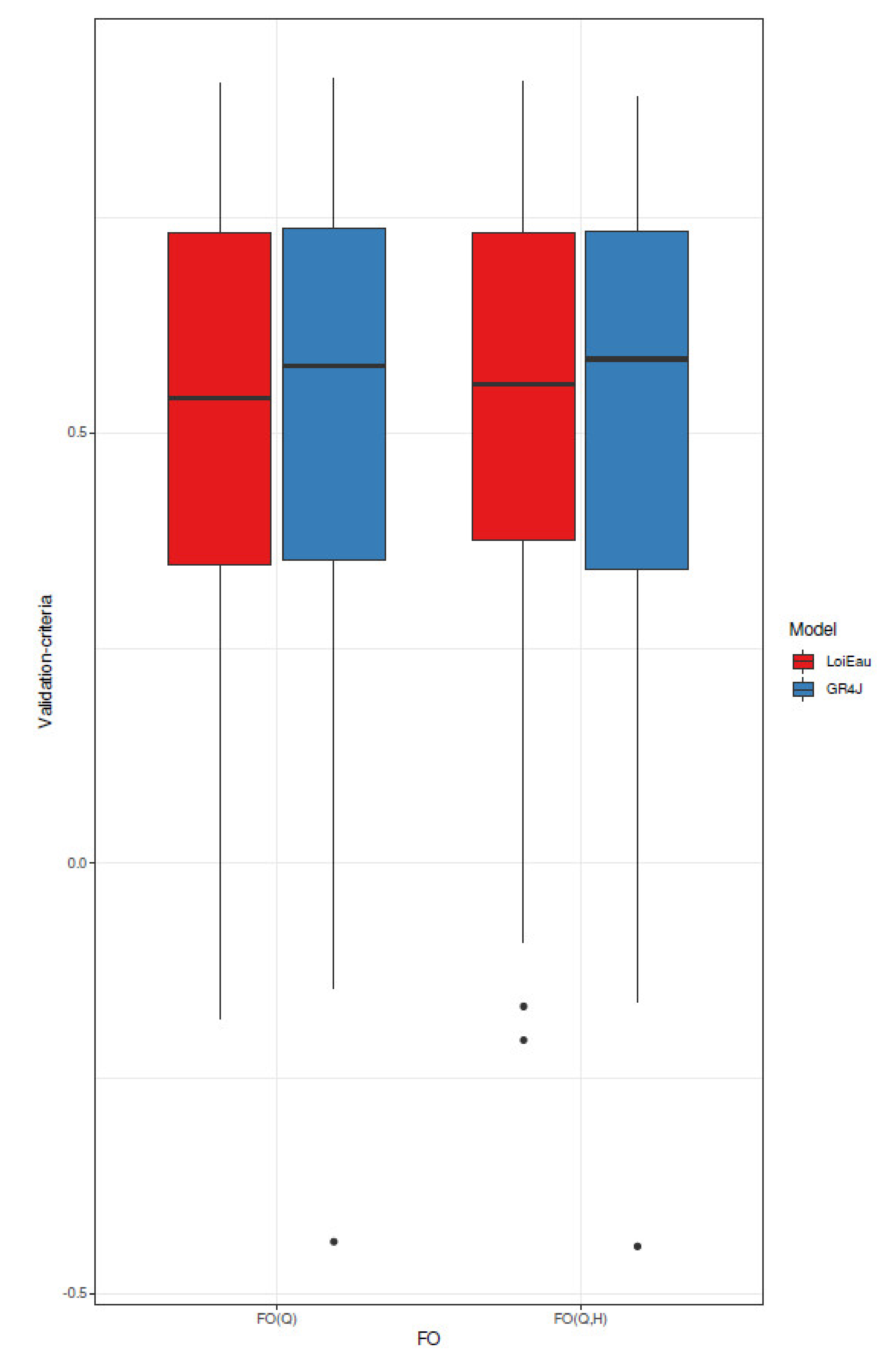
5.2. Temporal Robustness
6. Discussion
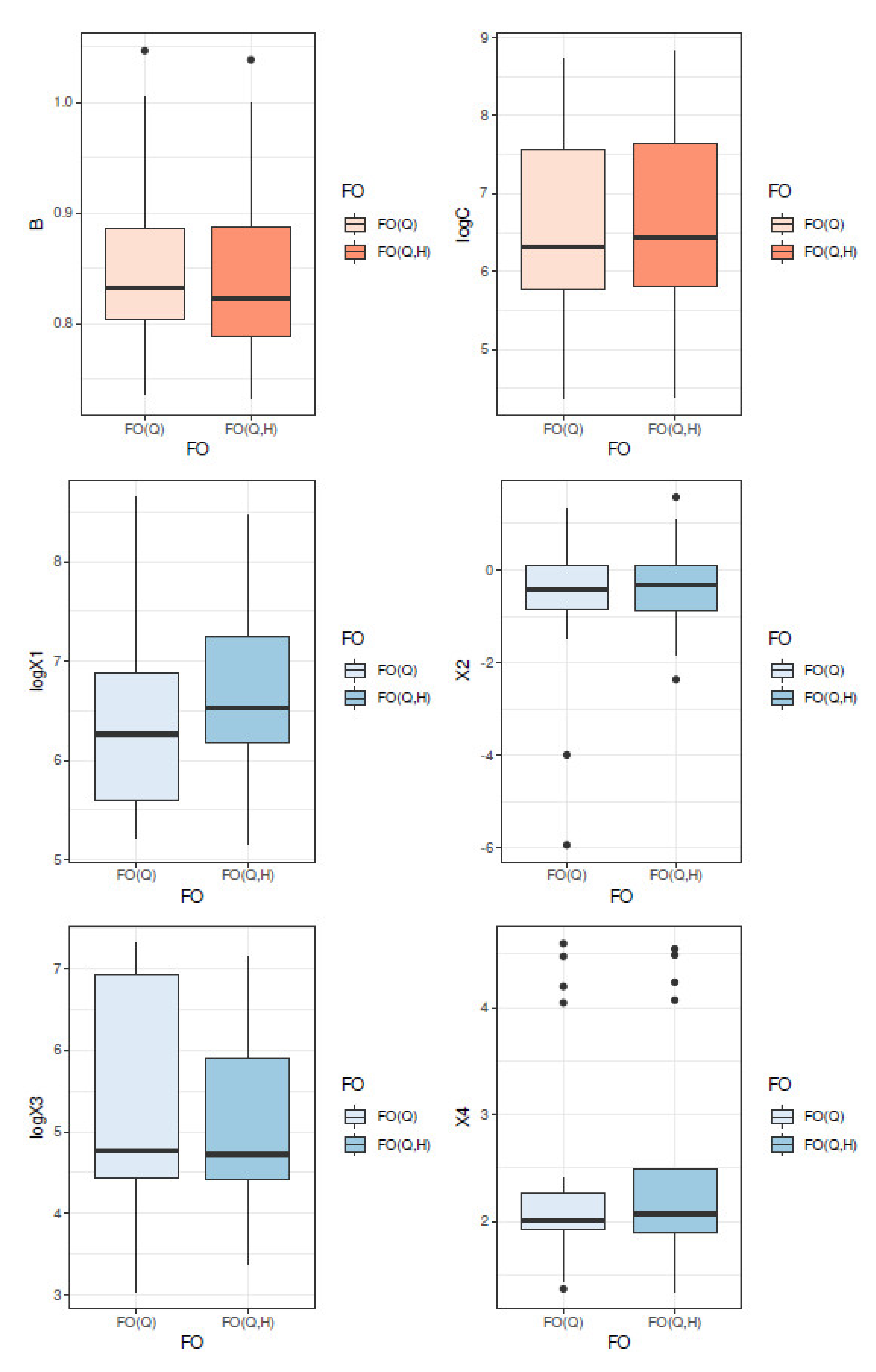
6.1. About Equifinality and FO
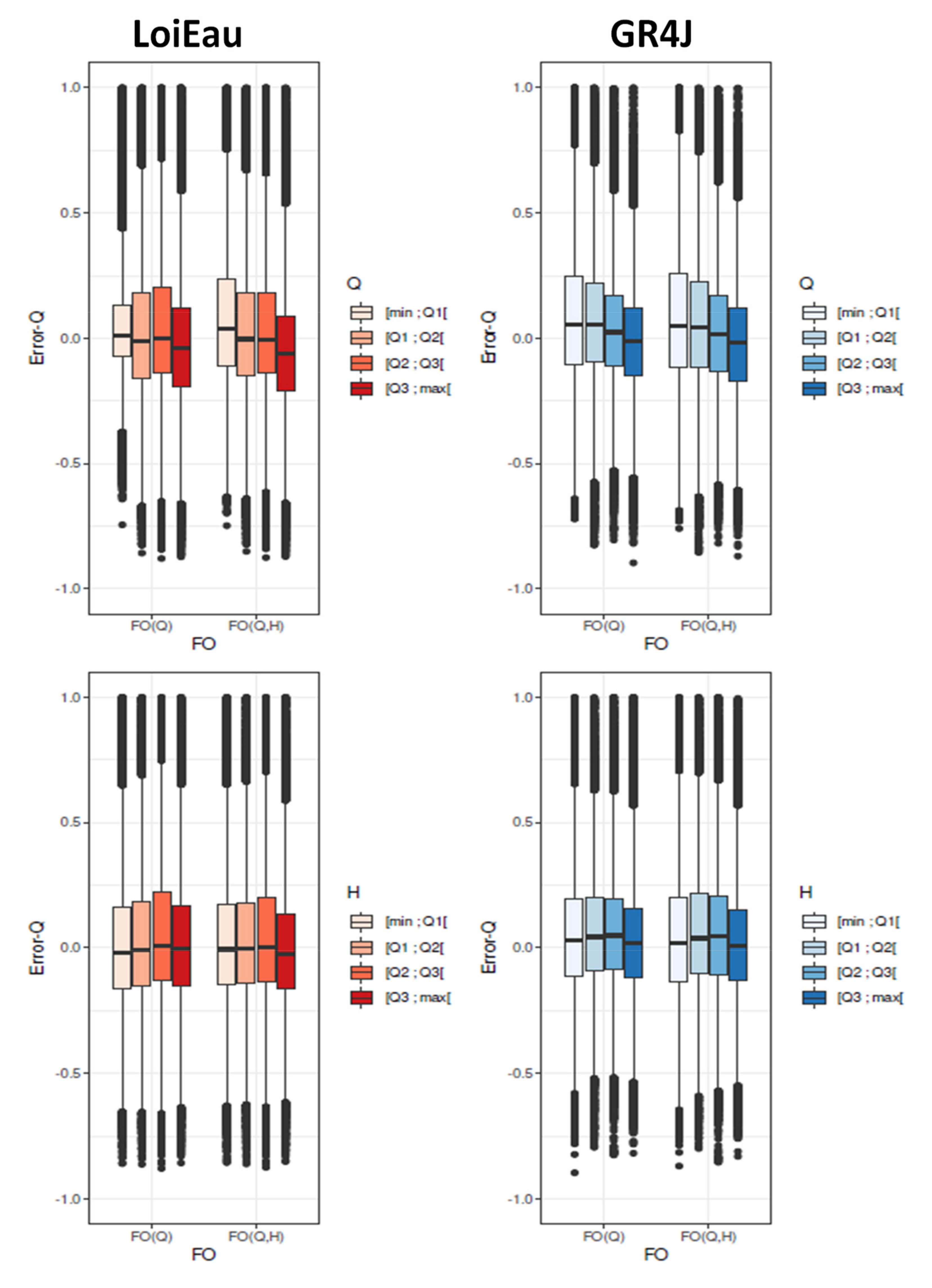
6.2. Analysis of Modelling Errors in Calibration
6.3. Influence of the Piezometer Choice on the Calibration Parameters of the GRLoiEau2J Model
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Oudin, L.; Michel, C.; Anctil, F. Which potential evapotranspiration input for a lumped rainfall-runoff model? J. Hydrol. 2005, 303, 275–289. [Google Scholar] [CrossRef]
- Gossel, W.; Ebraheem, A.M.; Wycisk, P. A very large scale GIS-based groundwater flow model for the Nubian sandstone aquifer in Eastern Sahara (Egypt, northern Sudan and eastern Libya). Hydrogeol. J. 2004, 12, 698–713. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Mace, R.E.; Barrett, M.E.; Smith, B. Can we simulate regional groundwater flow in a karst system using equivalent porous media models? Case study, Barton Springs Edwards aquifer, USA. J. Hydrol. 2003, 276, 137–158. [Google Scholar] [CrossRef]
- Smith, A.; Welsh, W.D. Review of Groundwater Models and Modelling Methodologies for the Great Artesian Basin; A technical report to the Australian Government from the CSIRO Great Artesian Basin Water Resource Assessment, CSIRO Water for a Healthy Country Flagship; CSIRO: Canberra, ACT, Australia, 2011. [Google Scholar]
- Harbaugh, A.W. MODFLOW-2005, the U.S. Geological Survey Modular Ground-Water Model—The Ground-Water Flow Process; U.S. Geological Survey Techniques and Methods 6-A16; U.S.G.S: Dublin, Ireland, 2005. [Google Scholar]
- Cooper, H.H.; Rorabaugh, M.I. Ground-Water Movements and Bank Storage Due to Flood Stages in Surface Streams. 1963. Available online: pubs.er.usgs.gov (accessed on 2 August 2021).
- Pinder, G.F.; Jones, J.F. Determination of the ground-water component of peak discharge from the chemistry of total runoff. Water Resour. Res. 1969, 5, 438–445. [Google Scholar] [CrossRef]
- Martel, E.A. Les Abîmes. Les Eaux Souterraines, Les Sources, Les Cavernes, la Spéléologie; Delagrave: Paris, France, 1984; 578p. [Google Scholar]
- Sophocleous, M. Interactions between groundwater and surface water: The state of the science. Hydrogeol. J. 2002, 10, 52–67. [Google Scholar] [CrossRef]
- Barlage, M.; Tewari, M.; Chen, F.; Miguez-Macho, G.; Yang, Z.L.; Niu, G.Y. The effect of groundwater interaction in North American regional climate simulations with WRF/Noah-MP. Clim. Chang. 2015, 129, 485–498. [Google Scholar] [CrossRef]
- Sulis, M.; Keune, J.; Shrestha, P.; Simmer, C.; Kollet, S.J. Quantifying the Impact of Subsurface-Land Surface Physical Processes on the Predictive Skill of Subseasonal Mesoscale Atmospheric Simulations. J. Geophys. Res. Atmos. 2018, 123, 9131–9151. [Google Scholar] [CrossRef]
- Ruelland, D.; Brisset, N.; Jourde, H.; Oyarzun, R. Modelingthe impact of climatic variability on the groundwater and surfaceflows from a mountainous catchment in the Chilean Andes. In Cold Regions Hydrology in a Changing Climate; IAHS Publication: Melbourne, VIC, Australia, 2011; Volume 346, pp. 171–179. [Google Scholar]
- Prudhomme, C.; Hannaford, J.; Harrigan, S.; Boorman, D.; Knight, J.; Bell, V.; Jackson, C.; Svensson, C.; Parry, S.; Bachiller-Jareno, N.; et al. Hydrological Outlook UK: An operational streamflow and groundwater level forecasting system at monthly to seasonal time scales. Hydrol. Sci. J. 2017, 62, 2753–2768. [Google Scholar] [CrossRef] [Green Version]
- Vergnes, J.P.; Roux, N.; Habets, F.; Ackerer, P.; Amraoui, N.; Besson, F.; Caballero, Y.; Courtois, Q.; Dreuzy, J.R.D.; Etchevers, P.; et al. The AquiFR hydrometeorological modelling platform as a tool for improving groundwater resource monitoring over France: Evaluation over a 60 year period. Hydrol. Earth Syst. Sci. 2020, 24, 633–654. [Google Scholar] [CrossRef] [Green Version]
- Mackay, J.D.; Jackson, C.R.; Wang, L. A lumped conceptual model to simulate groundwater level time-series. Environ. Model. Softw. 2014, 61, 229–245. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, R.M.; Condon, L.E.; Kollet, S.J. A high-resolution simulation of groundwater and surface water over most of the continental US with the integrated hydrologic model ParFlow v3. Geosci. Model Dev. 2015, 8, 923–937. [Google Scholar] [CrossRef] [Green Version]
- Thiéry, D. Forecast of changes in piezometric levels by a lumped hydrological model. J. Hydrol. 1988, 97, 129–148. [Google Scholar] [CrossRef]
- Thiéry, D. Logiciel GARDENIA, Version v8.2. Guide D’utilisation; BRGM: Orléans, France, 2014. [Google Scholar]
- Saleh, F.; Ducharne, A.; Flipo, N.; Oudin, L.; Ledoux, E. Impact of river bed morphology on discharge and water levels simulated by a 1D Saint–Venant hydraulic model at regional scale. J. Hydrol. 2013, 476, 169–177. [Google Scholar] [CrossRef]
- Thiéry, D. Code de calcul MARTHE—Modélisation 3D des écoulements dans les hydrosystèmes—Notice d’utilisation de la version 7.5 (MARTHE: Modeling Software for Groundwater Flows); BRGM/RP-64554-FR; BRGM: Orléans, France, 2015. [Google Scholar]
- Thiéry, D. Logiciel ÉROS version 7.1—Guide d’utilisation; Rapport Final, BRGM/RP-67704-FR; BRGM: Orléans, France, 2018. [Google Scholar]
- Keating, T. A lumped parameter model of a Chalk aquifer-stream system in Hampshire, United Kingdom. Groundwater 1982, 20, 430–436. [Google Scholar] [CrossRef]
- Rushton, K.R.; Rathod, K.S. Aquifer response due to zones of higher permeability and storage coefficient. J. Hydrol. 1981, 50, 299–316. [Google Scholar] [CrossRef]
- Rushton, K.R.; Smith, E.J.; Tomlinson, L.M. An improved understanding of flow in a limestone aquifer using field evidence and mathematical models. J. Inst. Water Eng. Sci. 1982, 36, 369–387. [Google Scholar]
- Beven, K.; Binley, A. The future of distributed models: Model calibration and uncertainty prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Quintana-Segui, P.; Le Moigne, P.; Durand, Y.; Martin, E.; Habets, F.; Baillon, M.; Canellas, C.; Franchisteguy, L.; Morel, S. Analysis of Near-Surface Atmospheric Variables: Validation of the SAFRAN Analysis over France. J. Appl. Meteorol. Climatol. 2008, 47, 92–107. [Google Scholar] [CrossRef]
- Vidal, J.P.; Martin, E.; Franchistéguy, L.; Baillon, M.; Soubeyroux, J.M. A 50-year high-resolution atmospheric reanalysis over France with the Safran system. Int. J. Climatol. 2010, 30, 1627–1644. [Google Scholar] [CrossRef] [Green Version]
- National data bank for hydrometry and hydrology (Hydro French database). Available online: http://www.hydro.eaufrance.fr/ (accessed on 2 August 2021).
- Institute of Hydrology. Low Flow Studies; Ress. Rep. I; Institute of Hydrology: Wallingford, UK, 1980. [Google Scholar]
- Lyne, V.; Hollick, M. Stochastic time-variable rainfall-runoff modelling. In Proceedings of the Hydrology and Water Resources Symposium, Perth, WA, Australia, 10–12 September 1979; Institution of Engineers National Conference Publication No. 79/10. : Canberra, ACT, Australia, 1979; pp. 89–92. [Google Scholar]
- Nathan, R.J.; McMahon, T.A. Evaluation of automated techniques for base flow and recession analyses. Water Resour. Res. 1990, 26, 1465–1473. [Google Scholar] [CrossRef]
- Gustard, A. Regional Variability of Soil Characteristics for Flood and Low Flow Estimation. Agric. Water Manag. 1983, 6, 255–268. [Google Scholar] [CrossRef]
- Jemcov, I.; Petric, M. Measured precipitation vs. effective infiltration and their influence on the assessment of karst systems based on results of the time series analysis. J. Hydrol. 2009, 379, 304–314. [Google Scholar] [CrossRef]
- Larocque, M. Intégration d’approches quantitatives de caractérisation et de simulation des aquifères calcaires fissurés. Application à l’aquifère karstique de la Rochefoucauld (Charente, France). BRGM. Ph.D. Thesis, Université de Poitiers, Orléans, France, 1997; 247p. [Google Scholar]
- Seguin, J.J.; Wuillemer, A. Exploitabilité des Ressources en eaux Souterraines en France. Résistance à la Sécheresse des Principaux Aquifères à Nappe Libre; BRGM/RP-55188-FR; BRGM: Orléans, France, 2006. [Google Scholar]
- Stollsteiner, P. Changement Climatique—EXPLORE 2070; BRGM/RP-61483-FR-vol1; BRGM: Orléans, France, 2012. [Google Scholar]
- Vernoux, J.F.; Seguin, J.J. Établissement D’un Téseau de Téférence Piézométrique Pour le Suivi de L’impact du Changement Climatique sur les Eaux Souterraines-Année 2; rapport BRGM/RP-61020-FR, 93 pages, 40 illustrations,3 tableaux, 3 annexes; BRGM: Orléans, France, 2012. [Google Scholar]
- Aubert, Y. Estimation des Valeurs Extrêmes de Débit par la Méthode Shyreg. Réflexions sur L’équifinalité Dans la ModéLisation de la Transformation Pluie en Débit. Ph.D. Thesis, IRSTEA, Aix-en-Provence, France, UPMC, Paris, France, 2012. [Google Scholar]
- Folton, N.; Arnaud, P. Indicateur sur la ressource en eau estimés par; une modélisation pluie-débit régionalisée: La base de données Web LoiEau. Houille Blanche Rev. Int. L’eau 2020, 106, 22–29. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Folton, N.; Arnaud, P. Régionalisation d’une modélisation hydrologique pour la cartographie des débits d’étiage. In Proceedings of the 9e Congrés International GRUTTEE, Aix-en-Provence, France, 29–31 October 2012. [Google Scholar]
- Pagano, T.; Hapuarachchi, P.; Wang, Q. Continuous Rainfallrunoff Model Comparison and Short-Term Daily Streamflow Forecast Skill Evaluation; Tech. Rep. EP103545; CSIRO: Water for a Healthy Country National Research Flagship: Canberra, ACT, Australia, 2010. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Garcia, F. Amélioration d’une modélisation hydrologique régionalisée pour estimer les statistiques d’étiage. Ph.D. Thesis, UPMC, Paris, France, 2016; 228p. [Google Scholar]
- Laaha, G. Zur Beurteilung der Genauigkeit von Niederwasserkennwerten. Mitt. Hydrogr. Dienstes Österr. 2000, 80, 61–68. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Mathevet, T.H.; Michel, C.L.; Andreassian, V.; Perrin, C. A bounded version of the Nash-Sutcliffe criterion for better model assessment on large sets of basins. IAHS-AISH Publ. 2006, 307, 211–219. [Google Scholar]
- Nascimento, N.D.; Yang, X.I.; Makhlouf, Z.; Michel, C. GR3J: A daily watershed model with three free parameters. Hydrol. Sci. J. 1999, 44, 263–277. [Google Scholar]
- Mathevet, T. Quels modèles pluie-débit globaux au pas de temps horaire ? Développement empiriques et comparaison de modèles sur un large échantillon de bassins versants. Ph.D. Thesis, Ecole Nationale du Génie Rural, des Eaux et des Forêts (ENGREF), Paris, France, 2005. [Google Scholar]
- Klemeš, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Pelletier, A.; Andréassian, V. Constraining a lumped rainfall-runoff model with piezometry to improve low-flow simulation. EGU General Assembly 2021, online, 19–30 April 2021, EGU21-4402. Available online: https://doi.org/10.5194/egusphere-egu21-4402 (accessed on 30 April 2021).
- Le Mesnil, M.; Charlier, J.-B.; Moussa, R.; Caballero, Y.; Dörfliger, N. Interbasin groundwater flow: Characterization, role of karst areas, impact on annual water balance and flood processes. J. Hydrol. 2020, 585, 124583. [Google Scholar] [CrossRef]
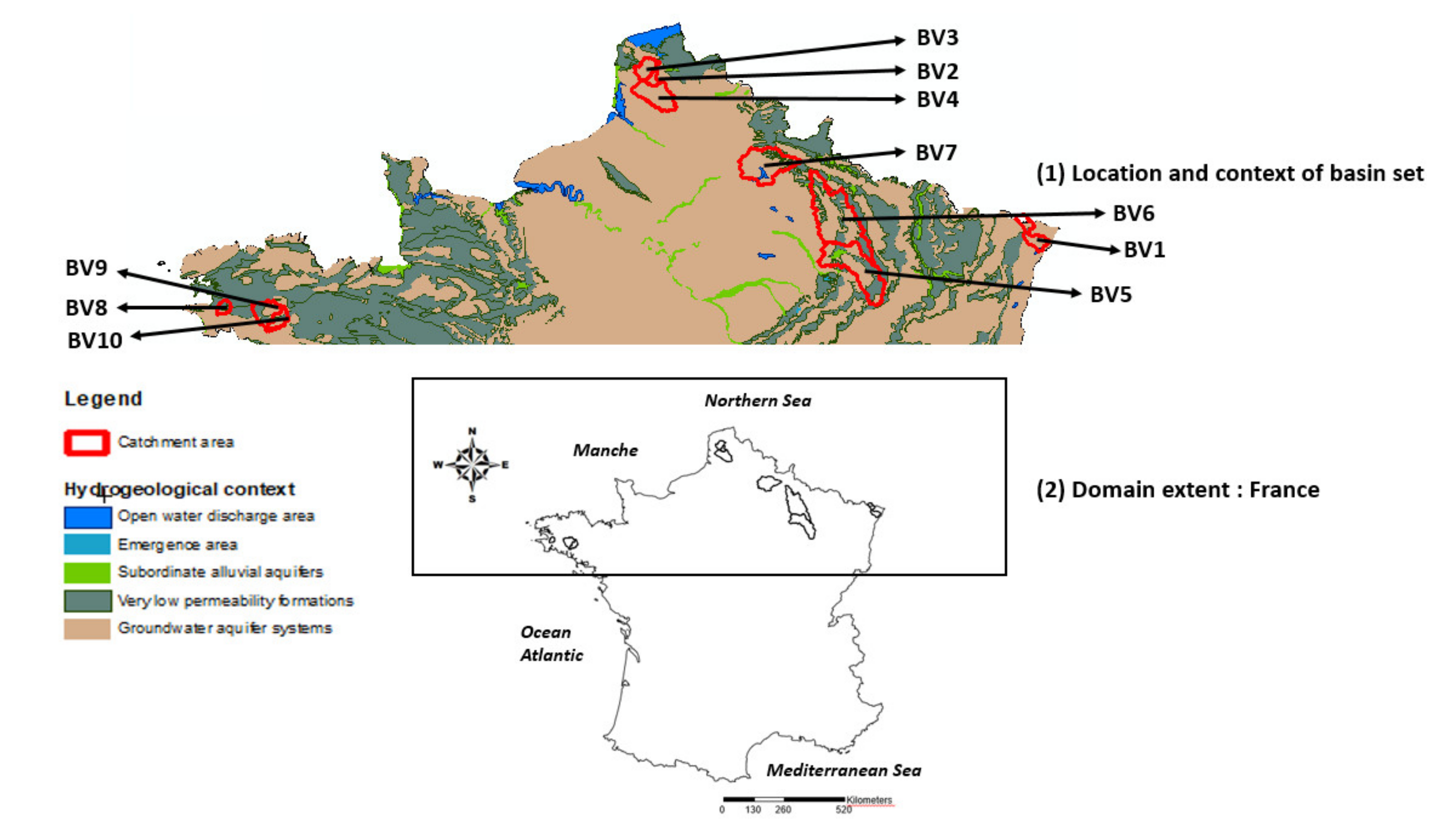
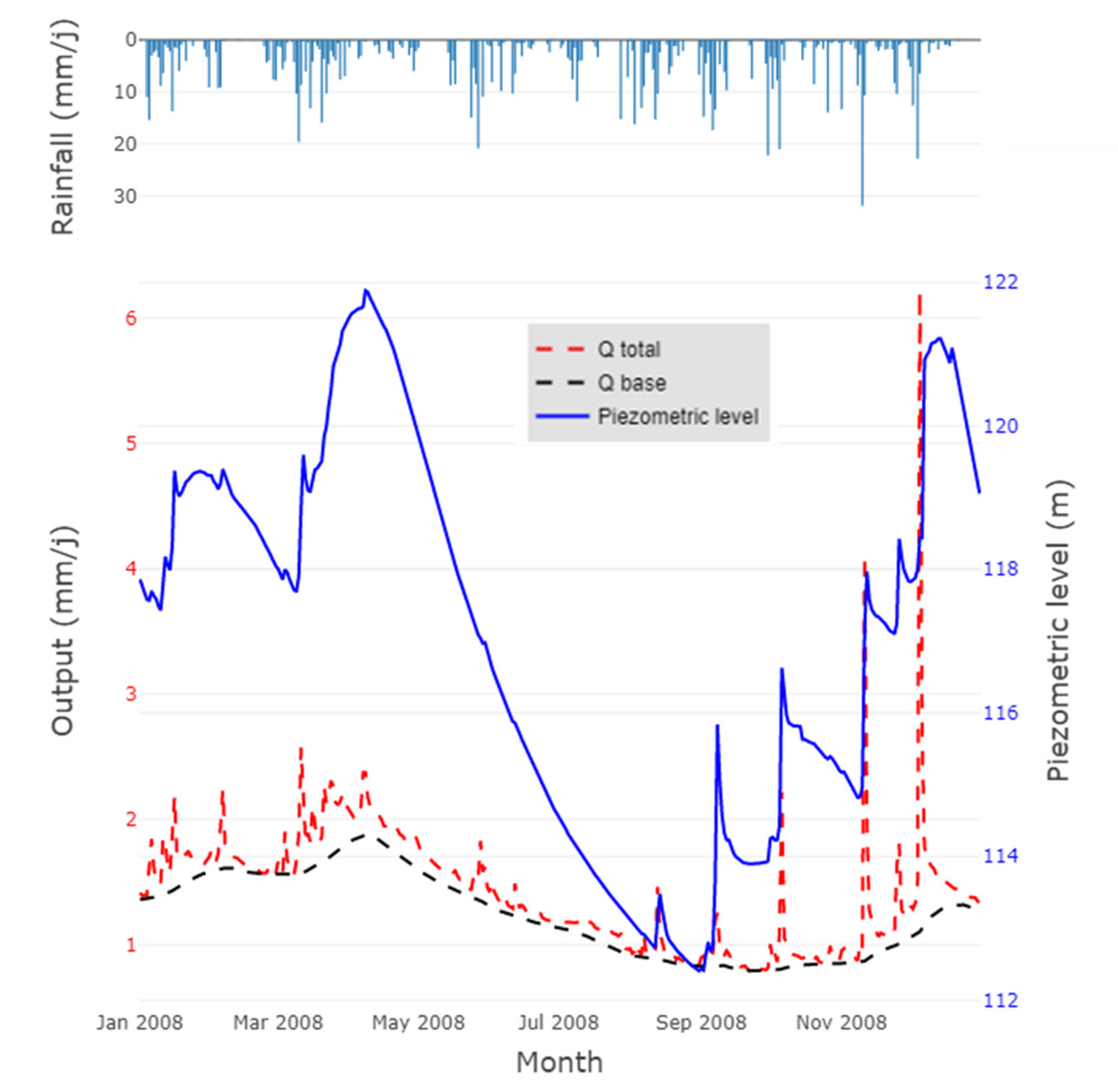
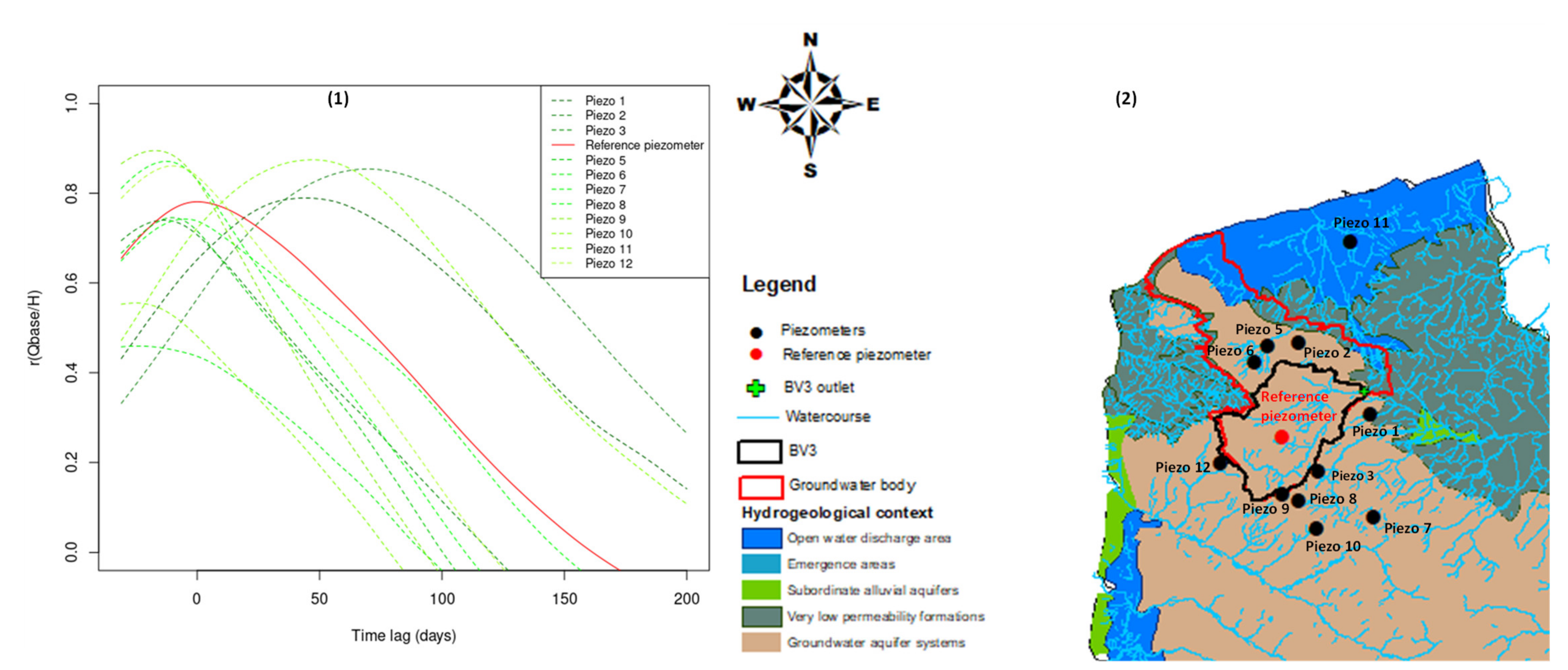
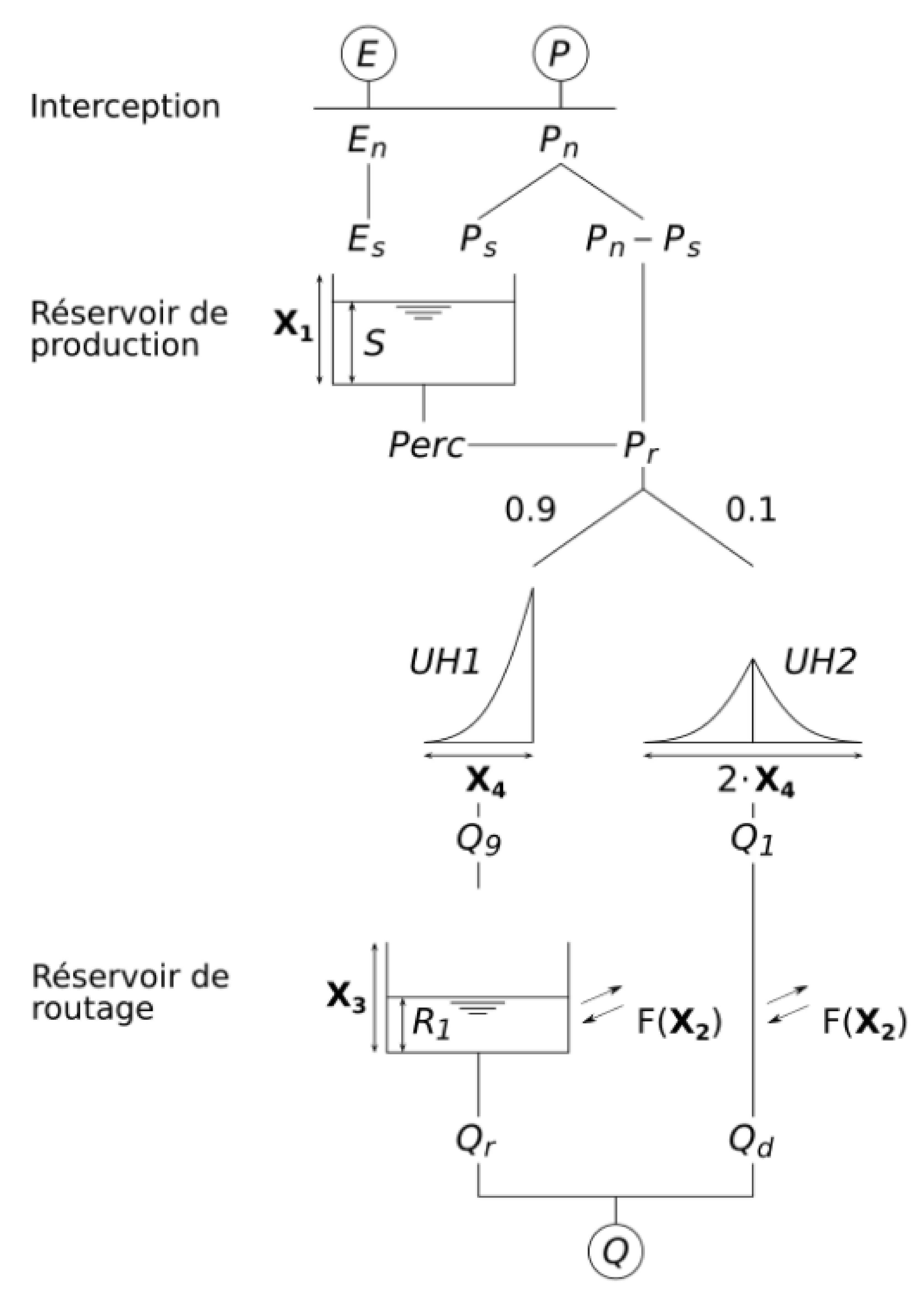
| Code | BV1 - A3792010 | BV2 - E3511220 | BV3 - E4035710 | BV4 - E5400310 | BV5 - H5172010 | BV6 - H6221010 | BV7 - H7162010 | BV8 - J4313010 | BV9 - J4742010 | BV10 - J5102210 |
|---|---|---|---|---|---|---|---|---|---|---|
| Watercourse | Sauer | Lys | Aa | Canche | Saulx | Aisne | Serre | Steir | Ellé | Scorff |
| Outlet | Beinheim | Lugy | Wizeres | Brimeux | Vitry-en-Pertrois | Givry | Pont à Bucy | Guengat | Arzano | Plouay |
| Area (km2) | 502.2 | 86.7 | 391.6 | 917.2 | 2109.1 | 2887.6 | 1637.4 | 179.9 | 575.7 | 299.3 |
| Average annual precipitation (mm/yr) (PA) | 808 | 1017 | 975 | 948 | 983 | 897 | 807 | 1191 | 1130 | 1126 |
| Average annual ETP (mm/yr) (ETPA) | 676 | 614 | 611 | 622 | 650 | 654 | 647 | 668 | 655 | 662 |
| Average annual flow (mm/yr) (QA) | 234 | 384 | 416 | 416 | 391 | 340 | 259 | 672 | 530 | 519 |
| Runoff Index (QA/PA) (%) | 28 | 38 | 43 | 44 | 40 | 38 | 32 | 56 | 47 | 46 |
| BFI | 0.67 | 0.83 | 0.84 | 0.9 | 0.53 | 0.52 | 0.78 | 0.6 | 0.6 | 0.61 |
| Geological context | Sandstone | Chalk | Chalk | Chalk | Chalk/Sand | Chalk/Sand | Chalk/Clay | Gneiss/Granite | Gneiss/Granite | Gneiss/Granite |
| Permeability | Low | High | High | High | Low | Low | Medium | Low | Low | Low |
| Watershed | BV1 | BV2 | BV3 | BV4 | BV5 | BV6 | BV7 | BV8 | BV9 | BV10 |
| r (P, H) | 0.17 | 0.14 | 0.13 | 0.14 | 0.13 | 0.08 | 0.07 | 0.31 | 0.25 | 0.19 |
| Time lag r (P, H) (j) | 8 | 92 | 118 | 24 | 9 | 107 | 28 | 8 | 12 | 27 |
| r (Q, H) | 0.27 | 0.8 | 0.74 | 0.81 | 0.76 | 0.54 | 0.71 | 0.86 | 0.83 | 0.72 |
| Time lag r (Q, H) (j) | 145 | 6 | 11 | 2 | 5 | 30 | 8 | 1 | 4 | 9 |
| r (Qb, H) | 0.38 | 0.88 | 0.78 | 0.81 | 0.84 | 0.75 | 0.74 | 0.91 | 0.87 | 0.84 |
| Time lag r (Qb, H) (j) | 140 | −6 | 0 | −19 | 3 | 16 | −4 | −6 | −2 | 4 |
| Name | Description |
|---|---|
| NSE′ (QMNA) | Bounded version of the NSE calculated on the QMNA |
| NSE′ (VCN10) | Bounded version of the NSE calculated on the VCN10 |
| NSE′ r(Qb,H) | Bounded version of the NSE calculated on the correlation between piezometry and the base flow (r(Qb,H)) |
| NSE′ (Qb) | Bounded version of the NSE calculated on base flows (Qb) |
| NSE′ (Q) | Bounded version of the NSE calculated on the flows (Q) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flinck, A.; Folton, N.; Arnaud, P. Assimilation of Piezometric Data to Calibrate Parsimonious Daily Hydrological Models. Water 2021, 13, 2342. https://doi.org/10.3390/w13172342
Flinck A, Folton N, Arnaud P. Assimilation of Piezometric Data to Calibrate Parsimonious Daily Hydrological Models. Water. 2021; 13(17):2342. https://doi.org/10.3390/w13172342
Chicago/Turabian StyleFlinck, Axel, Nathalie Folton, and Patrick Arnaud. 2021. "Assimilation of Piezometric Data to Calibrate Parsimonious Daily Hydrological Models" Water 13, no. 17: 2342. https://doi.org/10.3390/w13172342
APA StyleFlinck, A., Folton, N., & Arnaud, P. (2021). Assimilation of Piezometric Data to Calibrate Parsimonious Daily Hydrological Models. Water, 13(17), 2342. https://doi.org/10.3390/w13172342






