Influence of Pore Size Distribution on the Electrokinetic Coupling Coefficient in Two-Phase Flow Conditions
Abstract
:1. Introduction
2. Methodology
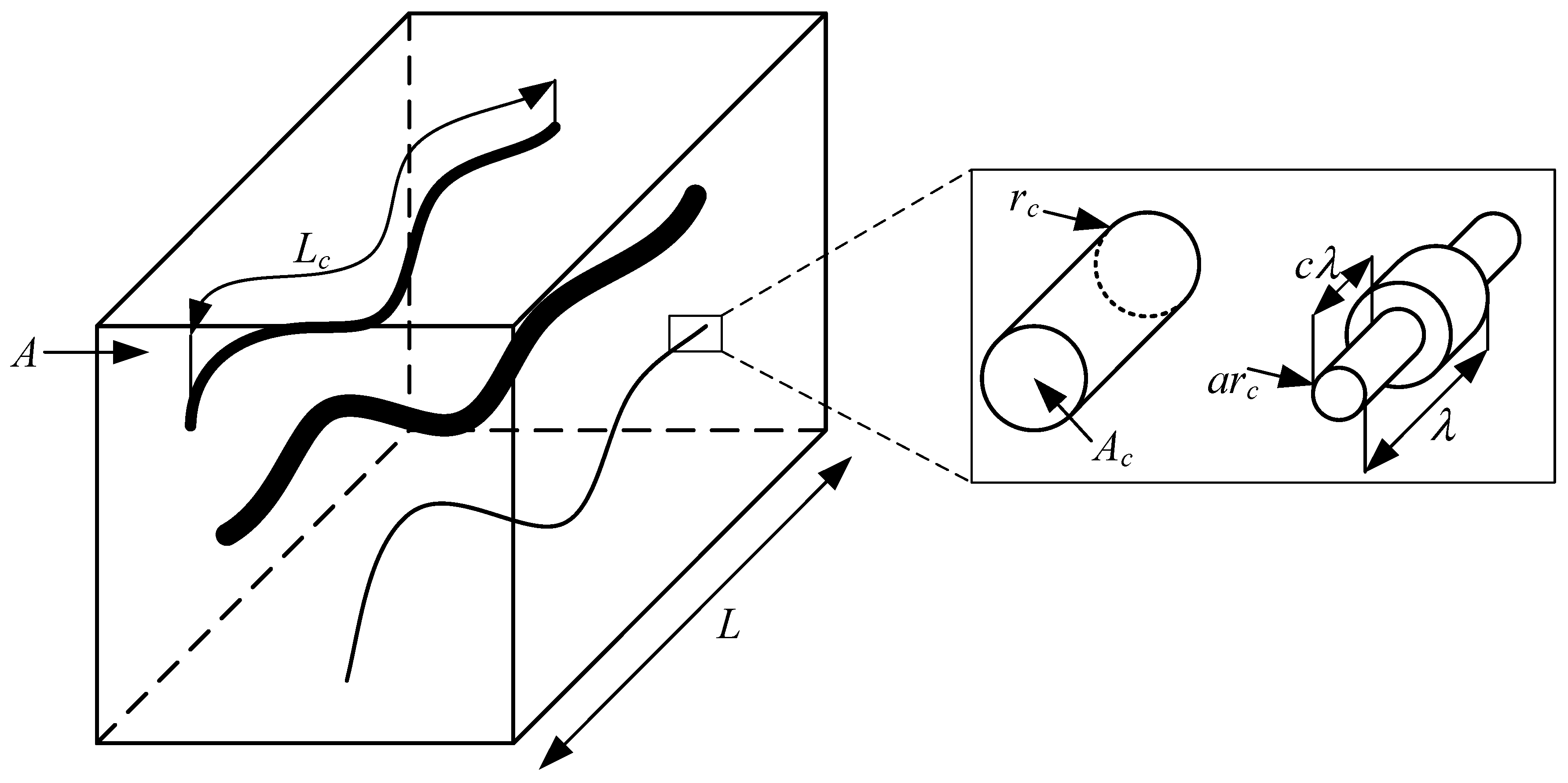
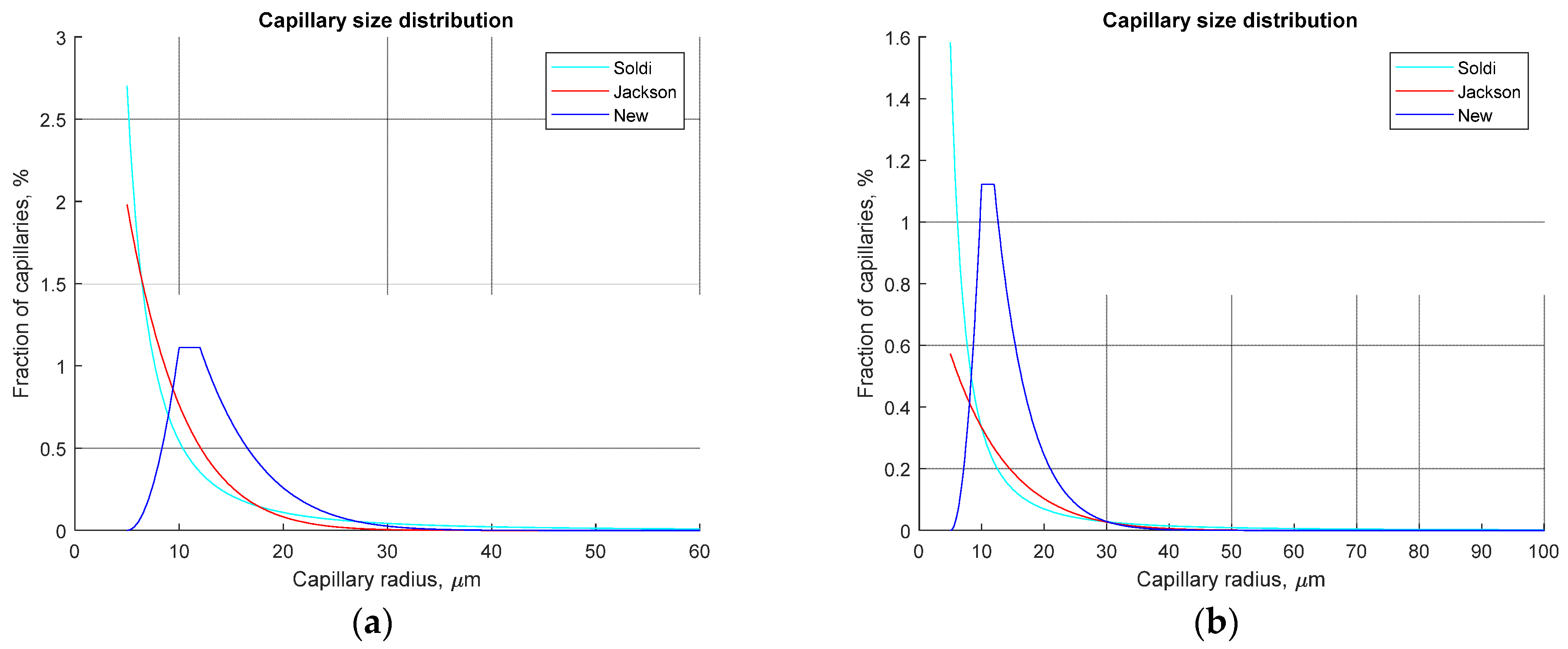
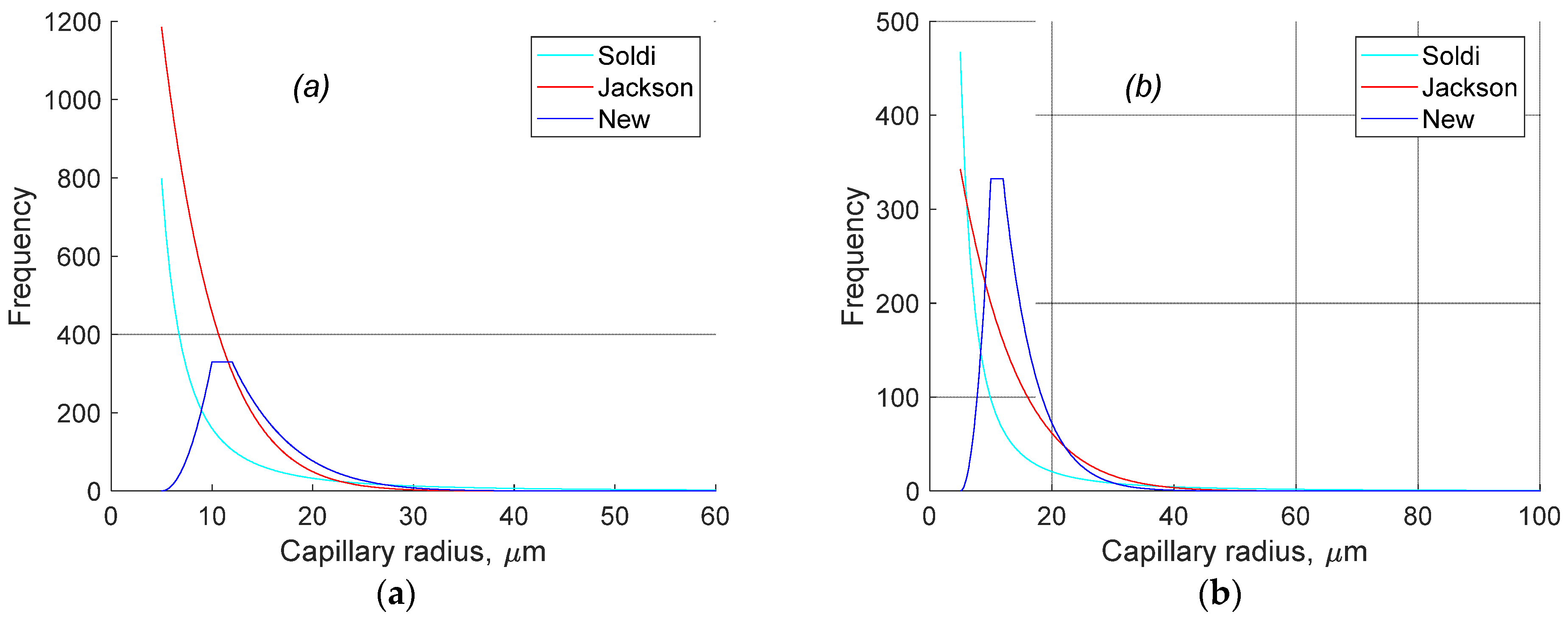
2.1. Basic Definitions and Capillary Size Distribution
2.2. Minimum and Maximum Capillary Radius
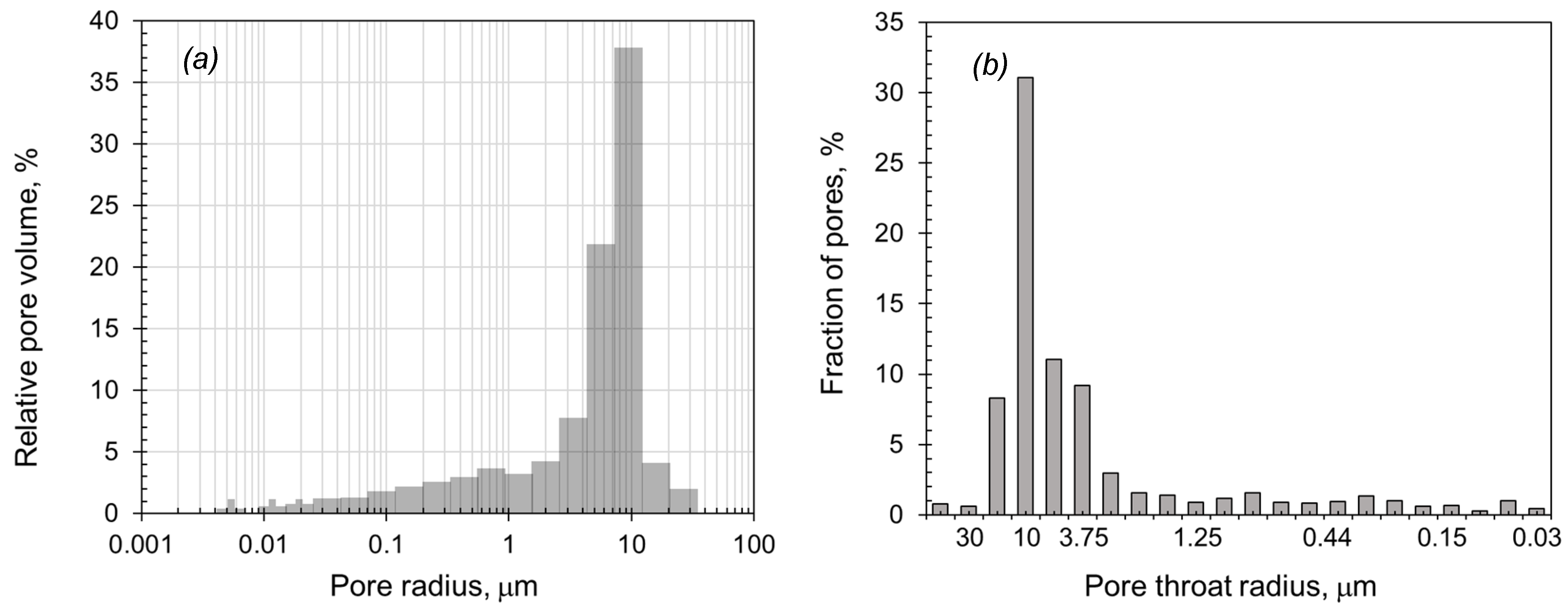
2.3. Matching Porosity and Permeability to Berea Sandstone
2.4. Constant Capillary Radius
2.5. Alternating Capillary Radius
2.6. Multi-Phase Flow Simulation
3. Results and Discussion
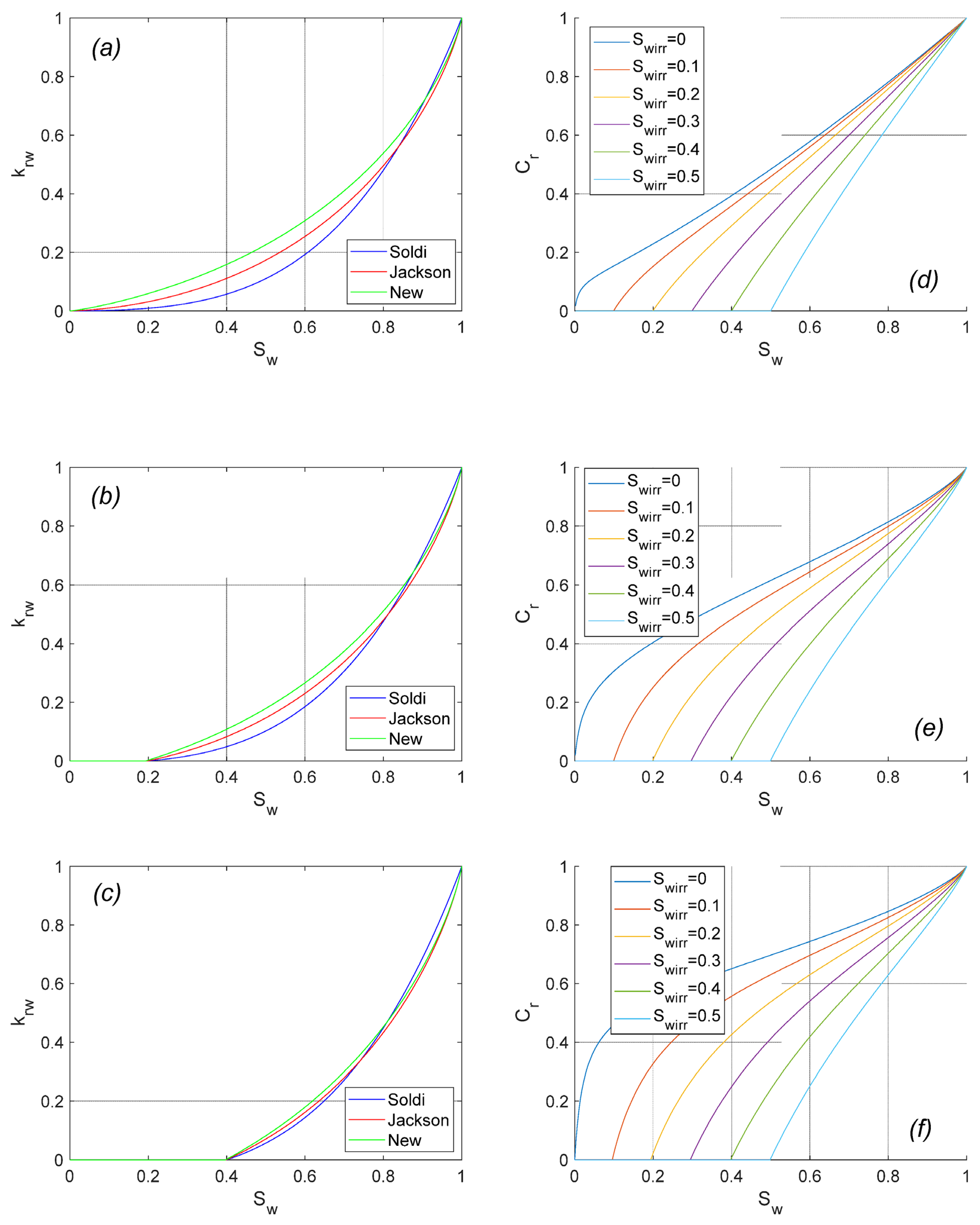
3.1. Relative Permeability to Water
3.2. Relative Streaming Potential Coupling Coefficient
3.3. Bundle of Capillary Tubes vs. Experimental Results of Moore et al. (2004)
4. Conclusions
- Unlike the previous bundle of parallel capillaries models, our approach to defining the pore and pore throat radii distribution is based on direct measurements, thus providing a more realistic description of porous rocks, in which pore and pore throat size distribution is non-monotonic;
- Our model was tested using constant and alternating capillary radii, with the latter being invoked in order to distinguish between pores and pore throats. Despite the alternating capillary radii model’s capability, we did not attempt to explicitly model residual trapping of the non-wetting phase in this work. Hence, we found no noticeable difference in the relative permeability and the relative streaming potential coupling coefficient modelled using either straight or variable radii capillary tubes;
- Our model produces considerably different relative permeability curves with small irreducible water saturation (<0.2) in comparison with previously published studies of Jackson [21] and Soldi et al. [37]. However, there is no noticeable difference between modelled curves using either of the approaches if irreducible water saturation is larger than 0.2;
- Compared with the results published by Jackson [21] and Soldi et al. [37], the relative streaming potential coupling coefficient simulated with our model appears to be more stable at high water saturation and to decrease more rapidly to zero as water saturation approaches the irreducible value. This behaviour is consistent with published experimental results, thus suggesting that the non-monotonic capillary size distribution should be used for more accurate characterisation of multi-phase flow in porous media;
- Our model was used to simulate measurements of the streaming potential coupling coefficient in sandstone samples saturated with aqueous solution and liquid CO2 [44]. The model assumed a thick double layer approach for computing the coupling coefficient, consistent with the use of tap water in the experiments. The modelling results suggest that true irreducible water saturation was not reached in the experiments reported by Moore et al. [44]. This conclusion is consistent with the hypothesis that explained a non-zero coupling coefficient in the experiments of Vinogradov and Jackson [18]. Moreover, since our model produces qualitatively more accurate behaviour of the coupling coefficient with decreasing water saturation, the discrepancy between the reported by Moore et al. [44] irreducible water saturation and the modelled true value was the smallest with our approach relative to that of Jackson [21] or Soldi et al. [37];
- To improve the quality of the here-developed bundle of capillary tubes model requires explicit representation of the residual (capillary) trapping of the non-wetting phase. This modification will be developed in a future study using the alternating capillary radii and will potentially allow a more accurate depiction of hysteretic behaviour of the streaming potential coupling coefficient during saturation and desaturation of the modelled rock with the non-wetting phase;
- Due to its simplicity, the here-reported and to-be-improved bundle of capillary tubes model can be used to accurately simulate the evolution of the streaming potential coupling coefficient during multi-phase flow in porous media, thus providing an efficient means for a variety of geophysical applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- WWAP United Nations World Water Assessment Programme. United Nations World Water Development Report 2014; UNESCO: Paris, France, 2014. [Google Scholar]
- Barlow, P.M.; Reichard, E.G. Saltwater intrusion in coastal regions of North America. Hydrogeol. J. 2010, 18, 247–260. [Google Scholar] [CrossRef]
- Binley, A.; Hubbard, S.S.; Huisman, J.A.; Revil, A.; Robinson, D.A.; Singha, K.; Slater, L.D. The emergence of hydrogeophysics for improved understanding of subsurface processes over multiple scales. Water Resour. Res. 2015, 51, 3837–3866. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jouniaux, L.; Maineult, A.; Naudet, V.; Pessel, M.; Sailhac, P. Review of self-potential methods in hydrogeophysics. Comptes Rendus Geosci. 2009, 341, 928–936. [Google Scholar] [CrossRef] [Green Version]
- Revil, A.; Jardani, A. The Self-Potential Method: Theory and Applications in Environmental Geosciences; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- MacAllister, D.J.; Jackson, M.D.; Butler, A.P.; Vinogradov, J. Remote detection of saline intrusion in a coastal aquifer using borehole measurements of self-potential. Water Resour. Res. 2018, 54, 1669–1687. [Google Scholar] [CrossRef] [Green Version]
- Jougnot, D.; Linde, N.; Haarder, E.B.; Looms, M.C. Monitoring of saline tracer movement with vertically distributed self-potential measurements at the HOBE agricultural site, Voulund, Denmark. J. Hydrol. 2015, 521, 314–327. [Google Scholar] [CrossRef] [Green Version]
- Voytek, E.; Barnard, H.; Jougnot, D.; Singha, K. Transpiration- and precipitation-induced subsurface water flow observed using the self-potential method. Hydrol. Process. 2019, 33, 1784–1801. [Google Scholar] [CrossRef] [Green Version]
- Roubinet, D.; Linde, N.; Jougnot, D.; Irving, J. Streaming potential modeling in fractured rocks: Insight into identification of hydraulically-active fractures. Geophys. Res. Lett. 2016, 43. [Google Scholar] [CrossRef] [Green Version]
- Hu, K.; Jougnot, D.; Huang, Q.; Looms, M.C.; Linde, N. Advancing quantitative understanding of self-potential signatures in the critical zone through long-term monitoring. J. Hydrol. 2020, 585, 124771. [Google Scholar] [CrossRef] [Green Version]
- Linde, N.; Doetsch, J.; Jougnot, D.; Genoni, O.; Duerst, Y.; Minsley, B.J.; Luster, J. Self-potential investigations of a gravel bar in a restored river corridor. Hydrol. Earth Syst. Sci. 2011, 15, 729–742. [Google Scholar] [CrossRef] [Green Version]
- Jackson, M.D.; Gulamali, M.Y.; Leinov, E.; Saunders, J.H.; Vinogradov, J. Spontaneous potentials in hydrocarbon reservoirs during waterflooding: Application to water-front monitoring. SPE J. 2012, 17, 53–69. [Google Scholar] [CrossRef]
- Leinov, E.; Jackson, M.D. Experimental measurements of the SP response to concentration and temperature gradients in sandstones with application to subsurface geophysical monitoring. J. Geophys. Res. Solid Earth 2014, 119, 6855–6876. [Google Scholar] [CrossRef] [Green Version]
- Hunter, R.J. Zeta Potential in Colloid Science; Academic: New York, NY, USA, 1981. [Google Scholar]
- Jougnot, D.; Roubinet, D.; Guarracino, L.; Maineult, A. Modeling streaming potential in porous and fractured media, description and benefits of the effective excess charge density approach. In Advances in Modeling and Interpretation in Near Surface Geophysics; Springer: Cham, Switzerland, 2020; pp. 61–96. [Google Scholar]
- Graham, M.; Macallister, D.; Vinogradov, J.; Jackson, M.; Butler, A. Self-potential as a predictor of seawater intrusion in coastal groundwater boreholes. Water Resour. Res. 2018, 54, 6055–6071. [Google Scholar] [CrossRef] [Green Version]
- Vinogradov, J.; Jackson, M.D.; Chamerois, M. Zeta potential in sandpacks: Effect of temperature, electrolyte pH, ionic strength and divalent cations. Colloids Surf. Physicochem. Eng. Asp. 2018, 553, 259–271. [Google Scholar] [CrossRef]
- Vinogradov, J.; Jackson, M.D. Multiphase streaming potential in sandstones saturated with gas/brine and oil/brine during drainage and imbibition. Geophys. Res. Lett. 2011, 38, L01301. [Google Scholar] [CrossRef]
- Guichet, X.; Jouniaux, L.; Pozzi, J.P. Streaming potential of a sand column in partial saturation conditions. J. Geophys. Res. Solid Earth 2003, 108, B3. [Google Scholar] [CrossRef]
- Revil, A.; Cerepi, A. Streaming potentials in two-phase flow conditions. Geophys. Res. Lett. 2004, 31, L11605. [Google Scholar] [CrossRef]
- Jackson, M.D. Multiphase electrokinetic coupling: Insights into the impact of fluid and charge distribution at the pore scale from a bundle of capillary tubes model. J. Geophys. Res. 2010, 115, B07206. [Google Scholar] [CrossRef]
- Zhang, J.; Vinogradov, J.; Leinov, E.; Jackson, M.D. Streaming potential during drainage and imbibition. J. Geophys. Res. Solid Earth 2017, 122, 4413–4435. [Google Scholar] [CrossRef]
- Blunt, M.J.; Bijeljic, B.; Dong, H.; Gharbi, O.; Iglauer, S.; Mostaghimi, P.; Paluszny, A.; Pentland, C. Pore-scale imaging and modelling. Adv. Water Resour. 2013, 51, 197–216. [Google Scholar] [CrossRef] [Green Version]
- Jougnot, D.; Mendieta, A.; Leroy, P.; Maineult, A. Exploring the effect of the pore size distribution on the streaming potential generation in saturated porous media, insight from pore network simulations. J. Geophys. Res. Solid Earth 2019, 124, 5315–5335. [Google Scholar] [CrossRef]
- Hao, L.; Cheng, P. Pore-scale simulations on relative permeabilities of porous media by lattice Boltzmann method. Int. J. Heat Mass Transfer. 2010, 53, 1908–1913. [Google Scholar] [CrossRef]
- Jackson, M.D. Characterization of multiphase electrokinetic coupling using a bundle of capillary tubes model. J. Geophys. Res. 2008, 113, B04201. [Google Scholar] [CrossRef] [Green Version]
- Jougnot, D.; Linde, N.; Revil, A. Doussan CDerivation of soil-specific streaming potential electrical parameters from hydrodynamic characteristics of partially saturated soils. Vadose Zone J. 2012, 11, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Tyler, S.W.; Wheatcraft, S.W. Fractal processes in soil water retention. Water Resour. Res. 1990, 26, 1047–1054. [Google Scholar] [CrossRef]
- Yu, B.; Li, J.; Li, Z.; Zou, M. Permeabilities of unsaturated fractal porous media. Int. J. Multiph. Flow 2003, 29, 1625–1642. [Google Scholar] [CrossRef]
- Guarracino, L. Estimation of saturated hydraulic conductivity Ks from the van Genuchten shape parameter α. Water Resour. Res. 2007, 43, W11502. [Google Scholar] [CrossRef]
- Pfannkuch, H.O. On the correlation of electrical conductivity properties of porous systems with viscous flow transport coefficients. In Developments in Soil Science; Elsevier: Amsterdam, The Netherlands, 1972; Volume 2, pp. 42–54. [Google Scholar] [CrossRef]
- Rembert, F.; Jougnot, D.; Guarracino, L. A fractal model for the electrical conductivity of water-saturated porous media during mineral precipitation-dissolution processes. Adv. Water Resour. 2020, 145, 103742. [Google Scholar] [CrossRef]
- Chu, Z.; Zhou, G.; Li, R. Enhanced fractal capillary bundle model for effective thermal conductivity of composite-porous geomaterials. Int. Commun. Heat Mass Transf. 2020, 113, 104527. [Google Scholar] [CrossRef]
- Dullien, F.A.L. Porous Media: Fluid Transport and Pore Structure, 2nd ed.; Academic Press: San Diego, CA, USA, 1992; p. 574. [Google Scholar]
- Soldi, M.; Guarracino, L.; Jougnot, D. A Simple Hysteretic Constitutive Model for Unsaturated Flow. Transport. Porous Media 2017, 120, 271–285. [Google Scholar] [CrossRef] [Green Version]
- Abou-Kassem, J.H.; Farouq Ali, S.M.; Rafiq Islam, M. Chapter 2—Single-Phase Fluid Flow Equations in Multidimensional Domain. In Petroleum Reservoir Simulations; Gulf Publishing Company: Huoston, TX, USA, 2006; pp. 7–41. [Google Scholar]
- Soldi, M.; Guarracino, L.; Jougnot, D. An effective excess charge model to describe hysteresis effects on streaming potential. J. Hydrol. 2020, 588, 124949. [Google Scholar] [CrossRef]
- Li, K.; Horne, R.N. Experimental Study and Fractal Analysis of Heterogeneity in Naturally Fractured Rocks. Fractal Characterization of the geysers rock. Transp. Porous Med. 2009, 78, 217–231. [Google Scholar] [CrossRef]
- Shi, J.Q.; Xue, Z.; Durucan, S. Supercritical CO2 core flooding and imbibition in Berea sandstone—CT imaging and numerical simulation. Energy Procedia 2011, 4, 5001–5008. [Google Scholar] [CrossRef] [Green Version]
- Soldi, M.; Jougnot, D.; Guarracino, L. An analytical effective excess charge density model to predict the streaming potential generated by unsaturated flow. Geophys. J. Int. 2019, 216, 380–394. [Google Scholar] [CrossRef] [Green Version]
- Kosugi, K. Three-parameter lognormal distribution model for soil water retention. Water Resour. Res. 1994, 30, 891–901. [Google Scholar] [CrossRef]
- Kosugi, K. Lognormal distribution model for unsaturated soil hydraulic properties. Water Resour. Res. 1996, 32, 2697–2703. [Google Scholar] [CrossRef]
- Malama, B.; Kuhlman, K.L. Unsaturated hydraulic conductivity models based on truncated lognormal pore-size distributions. Ground Water 2015, 53, 498–502. [Google Scholar] [CrossRef] [Green Version]
- Moore, J.R.; Glaser, S.D.; Morrison, F.H. The streaming potential of liquid carbon dioxide in Berea sandstone. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Hu, D.; Wyatt, D.; Chen, C.; Martysevich, V. Correlating Recovery Efficiency to Pore Throat Characteristics Using Digital Rock Analysis. In SPE Digital Energy Conference and Exhibition; Society of Petroleum Engineers: Texas, TX, USA, 2015. [Google Scholar]
- Minagawa, H.; Nishikawa, Y.; Ikeda, I.; Miyazaki, K. Characterization of sand sediment by pore size distribution and permeability using proton nuclear magnetic resonance measurement. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Ott, H.; Andrew, M.; Snippe, J.; Blunt, M.J. Microscale solute transport and precipitation in complex rock during drying. Geophys. Res. Lett. 2014, 41, 8369–8376. [Google Scholar] [CrossRef] [Green Version]
- Thomson, P.-R.; Aituar-Zhakupova, A.; Hier-Majumder, S. Image Segmentation and Analysis of Pore Network Geometry in Two Natural Sandstones. Front. Earth Sci. 2018, 6, 58. [Google Scholar] [CrossRef] [Green Version]
- Civan, F. Petrographic Characteristics of Petroleum-Bearing Formations. Reserv. Form. Damage 2007. [Google Scholar] [CrossRef]
- Tiab, D.; Donaldson, E.C. Formation Resistivity and Water Saturation. In Petrophysics (Fourth Edition): Theory and Practice of Measuring Reservoir Rock and Fluid Transport; Elsevier: Amsterdam, The Netherlands, 2016; pp. 187–278. [Google Scholar]
- Zecca, M.; Honari, A.; Vogt, S.J.; Bijeljic, B.; May, E.F.; Johns, M.L. Measurements of Rock Core Dispersivity and Tortuosity for Multi-Phase Systems. In International Symposium of the Society of Core Analysts; Snowmass: Colorado, CO, USA, 2016. [Google Scholar]
- Attia, A.M.; Fratta, D.; Bassiouni, Z. Irreducible Water Saturation from Capillary Pressure and Electrical Resistivity Measurements. Oil Gas. Sci. Technol. 2008, 63, 203–217. [Google Scholar] [CrossRef] [Green Version]
- Clennell, M.B. Tortuosity: A guide through the maze. Geol. Soc. Lond. Spec. Publ. 1997, 122, 299–344. [Google Scholar] [CrossRef]
- Ghanbarian, B.; Hunt, A.G.; Ewing, R.P.; Sahimi, M. Tortuosity in porous media: A critical review. Soil Sci. Soc. Am. J. 2013, 77, 1461–1477. [Google Scholar] [CrossRef]
- Sharqaway, M.H. Construction of pore network models for Berea and Fontainebleau sandstones using non-linear programing and optimization techniques. Adv. Water Resour. 2016, 98, 198–210. [Google Scholar] [CrossRef]
- Shehata, A.M.; Kumar, H.; Nasr-El-Din, H.A. New Insights on Relative Permeability and Initial Water Saturation Effects during Low-Salinity Waterflooding for Sandstone Reservoirs. In Proceedings of the SPE Trinidad and Tobago Section Energy Resources Conference, Port of Spain, Trinidad and Tobago, 13–15 June 2016. Society of Petroleum Engineers. [Google Scholar]
- Haeri, F.; Tapriyal, D.; Sanguinito, S.; Fuchs, S.J.; Shi, F.; Dalton, L.E.; Baltrus, J.; Howard, B.; Matranga, C.; Crandal, D.; et al. CO2-brine contact angle measurements on Navajo, Nugget, Bentheimer, Bandra Brown, Berea, and Mt. Simon Sandstones. Energy Fuels 2020, 34, 6085–6100. [Google Scholar] [CrossRef]
- Hirasaki, G.J. Wettability: Fundamentals and Surface Forces. SPE Form. Eval. 1991, 6, 217–226. [Google Scholar] [CrossRef]
- Revil, A.; Pezard, P.A.; Glover, P.W.J. Streaming potential in porous media 1. Theory of the zeta potential. J. Geophys. Res. Solid Earth 1999, 104, 20021–20031. [Google Scholar] [CrossRef]
- Vinogradov, J.; Jaafar, M.Z.; Jackson, M.D. Measurement of streaming potential coupling coefficient in sandstones saturated with natural and artificial brines at high salinity. J. Geophys. Res. 2010, 115, B12204. [Google Scholar] [CrossRef] [Green Version]
- Lorne, B.; Perrier, F.; Avouac, J.-P. Streaming potential measurements: 1. Properties of the electrical double layer from crushed rock samples. J. Geophys. Res. 1999, 104, 17857–17877. [Google Scholar] [CrossRef] [Green Version]
- Linde, N. Comment on “Characterization of multiphase electrokinetic coupling using a bundle of capillary tubes model”. J. Geophys. Res. 2009, 114, B06209. [Google Scholar] [CrossRef] [Green Version]
- Allègre, V.; Jouniaux, L.; Lehmann, F.; Sailhac, P. Streaming potential dependence on water-content in Fontainebleau sand. Geophys. J. Int. 2010, 182, 1248–1266. [Google Scholar] [CrossRef] [Green Version]
| Literature Reference | Method | Porosity (%) | Permeability (mD) | Pore Radius (μm) | Throat Radius (μm) |
|---|---|---|---|---|---|
| Hu et al. [45] | Micro-CT | 10–25 | 500–5000 | 15 | - |
| Li and Horne [38] | Mercury injection | 23 | 804 | 10 | - |
| Minagawa et al. [46] | NMR | - | - | 14 | 14 |
| Ott et al. [47] | Mercury injection | 22 | 500 | - | 20 |
| Thomson et al. [48] | Simulation (dry) | 19.9 | 132–167 | 2.72 | 1.29 |
| Thomson et al. [48] | Simulation (saturated) | 15.8 | 61.5–115 | 2.72 | 1.32 |
| Shi et al. [39] | Mercury injection | 18.7 | 330 | 10 | - |
| Distribution | Parameter | rmax = 60 μm | rmax = 100 μm |
|---|---|---|---|
| Soldi | DS | 1.31875 | 1.2565 |
| Jackson | DJ | 1185.32 | 342.74 |
| m | 10 | 10 | |
| New | D1 | 39,850 | 119,990 |
| m1 | 2 | 2 | |
| D2 | 978.4 | 1131 | |
| m2 | 8 | 16 |
| Distribution | rmax = 60 μm | rmax = 100 μm | ||
|---|---|---|---|---|
| Permeability (mD) | No. Capillaries | Permeability (mD) | No. Capillaries | |
| Soldi | 1313 | 29,532 | 3562 | 18,404 |
| Jackson | 263 | 59,861 | 686 | 29,772 |
| New | 409 | 29,638 | 434 | 29,393 |
| Distribution | Parameter | rmax = 60 μm | rmax = 100 μm |
|---|---|---|---|
| Soldi | DS | 1.3341 | 1.27275 |
| Jackson | DJ | 1319.82 | 381.57 |
| m | 10 | 10 | |
| New | D1 | 44,350 | 133,650 |
| m1 | 2 | 2 | |
| D2 | 1089.2 | 1259.3 | |
| m2 | 8 | 16 |
| Distribution | rmax = 60 μm | rmax = 100 μm | ||
|---|---|---|---|---|
| Permeability (mD) | No. Capillaries | Permeability (mD) | No. Capillaries | |
| Soldi | 227 | 33,355 | 615 | 20,926 |
| Jackson | 46 | 66,653 | 120 | 33,145 |
| New | 71 | 32,991 | 76 | 32,733 |
| Distribution | ||
|---|---|---|
| rmax = 60 μm | rmax = 100 μm | |
| Soldi | 2.8305 × 10−6 | 3.9592 × 10−6 |
| Jackson | 1.7221 × 10−6 | 2.5662 × 10−6 |
| New | 2.3668 × 10−6 | 2.38515 × 10−6 |
| Reported Swirr | Actual Irreducible Water Saturation When | ||
|---|---|---|---|
| Soldi CSD | Jackson CSD | New CSD | |
| 0.2 | 0.15 | 0.17 | 0.18 |
| 0.3 | 0.25 | 0.26 | 0.27 |
| 0.4 | 0.35 | 0.35 | 0.36 |
| 0.5 | 0.46 | 0.46 | 0.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vinogradov, J.; Hill, R.; Jougnot, D. Influence of Pore Size Distribution on the Electrokinetic Coupling Coefficient in Two-Phase Flow Conditions. Water 2021, 13, 2316. https://doi.org/10.3390/w13172316
Vinogradov J, Hill R, Jougnot D. Influence of Pore Size Distribution on the Electrokinetic Coupling Coefficient in Two-Phase Flow Conditions. Water. 2021; 13(17):2316. https://doi.org/10.3390/w13172316
Chicago/Turabian StyleVinogradov, Jan, Rhiannon Hill, and Damien Jougnot. 2021. "Influence of Pore Size Distribution on the Electrokinetic Coupling Coefficient in Two-Phase Flow Conditions" Water 13, no. 17: 2316. https://doi.org/10.3390/w13172316
APA StyleVinogradov, J., Hill, R., & Jougnot, D. (2021). Influence of Pore Size Distribution on the Electrokinetic Coupling Coefficient in Two-Phase Flow Conditions. Water, 13(17), 2316. https://doi.org/10.3390/w13172316








