Low Frequency Oscillations in a Hydroelectric Generating System to the Variability of Wind and Solar Power
Abstract
:1. Introduction
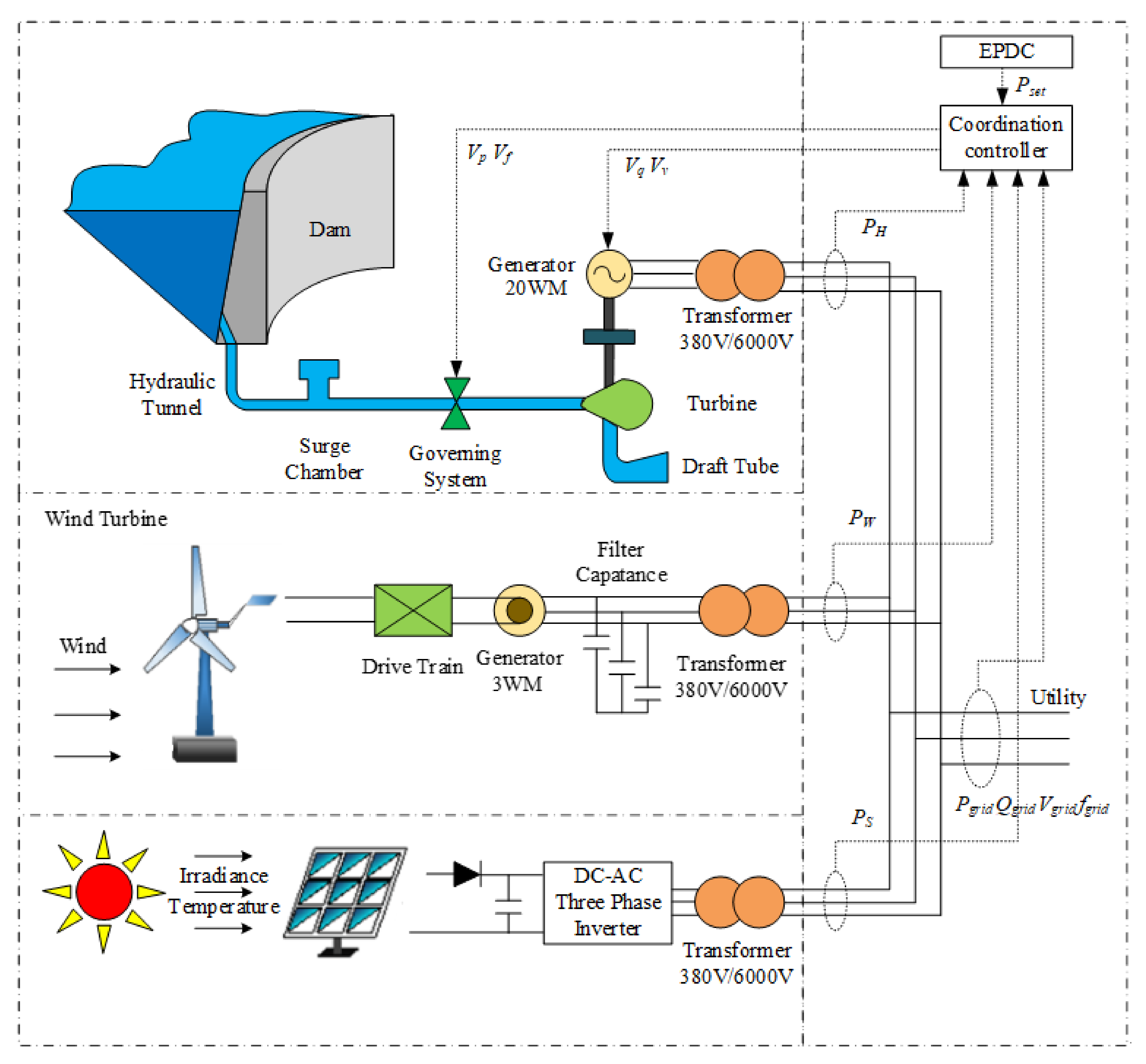
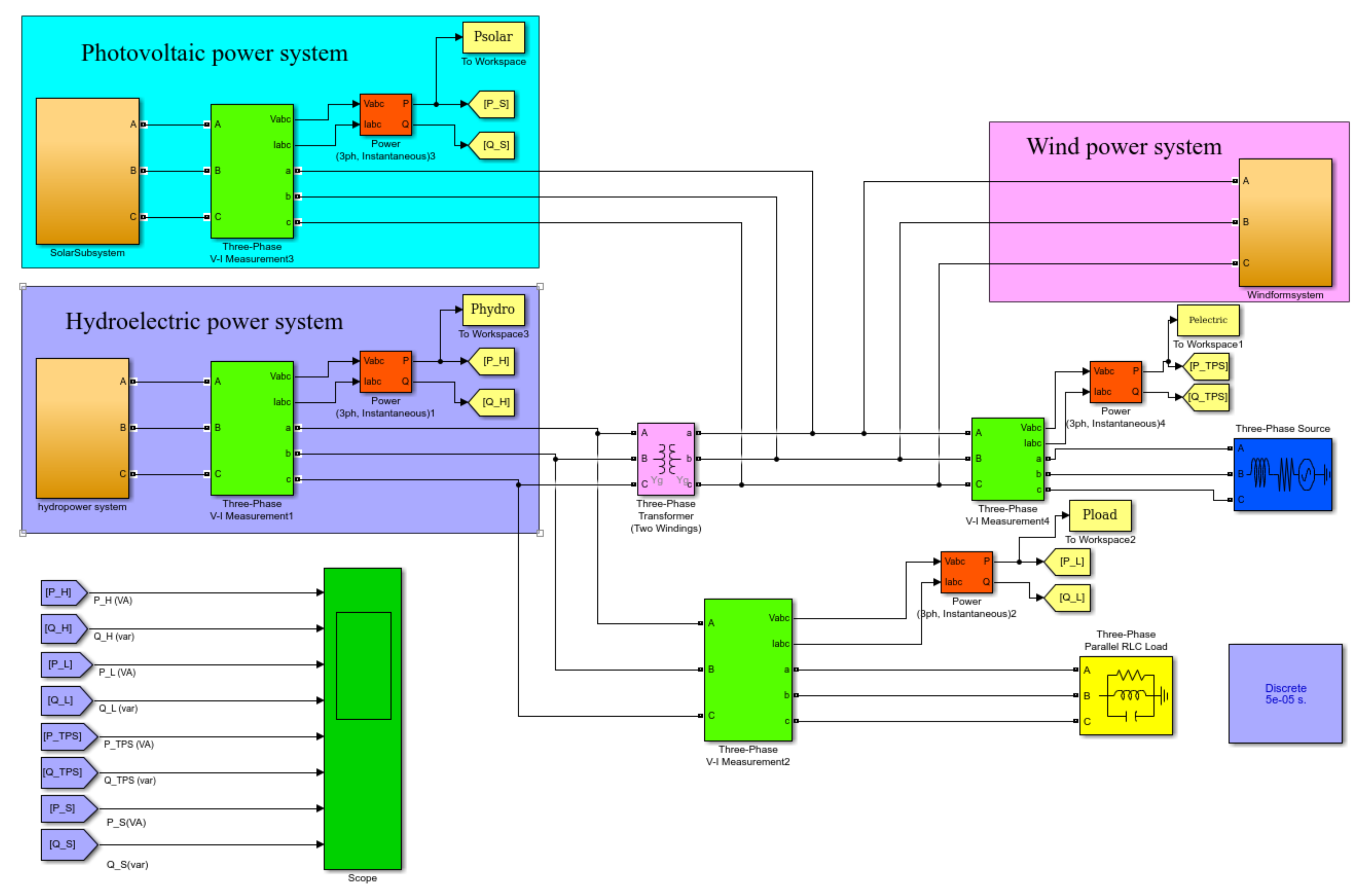
- A promising hybrid system of the hydropower generation integrating with wind farm and solar photovoltaic system is established using MATLAB/Simulink, in order to enable the stability analysis. This contributes to the current international pool of the integration modelling knowledge.
- The sensitivity of hydropower low frequency oscillations to its governor regulation capacity is quantified under the volatility influence of wind and solar energies. The main adopted methods include Nyquist response and root-locus analysis.
- To understand the stability conditions of the hybrid system, the influence of different wind/solar/hydropower quotas (i.e., W: S: H) and the various transmission line distance ratios on the low frequency oscillation mode of hydropower system are also quantified. The assessment indicators in this part include the three-phase parallel RLC load, the grounding transformer, the three-phase PI section line and the wind-farm transmission line, and the assessment criteria are oscillation frequency and damping ratio.
2. Mathematical Model of the Hybrid Power System
2.1. Hydropower System
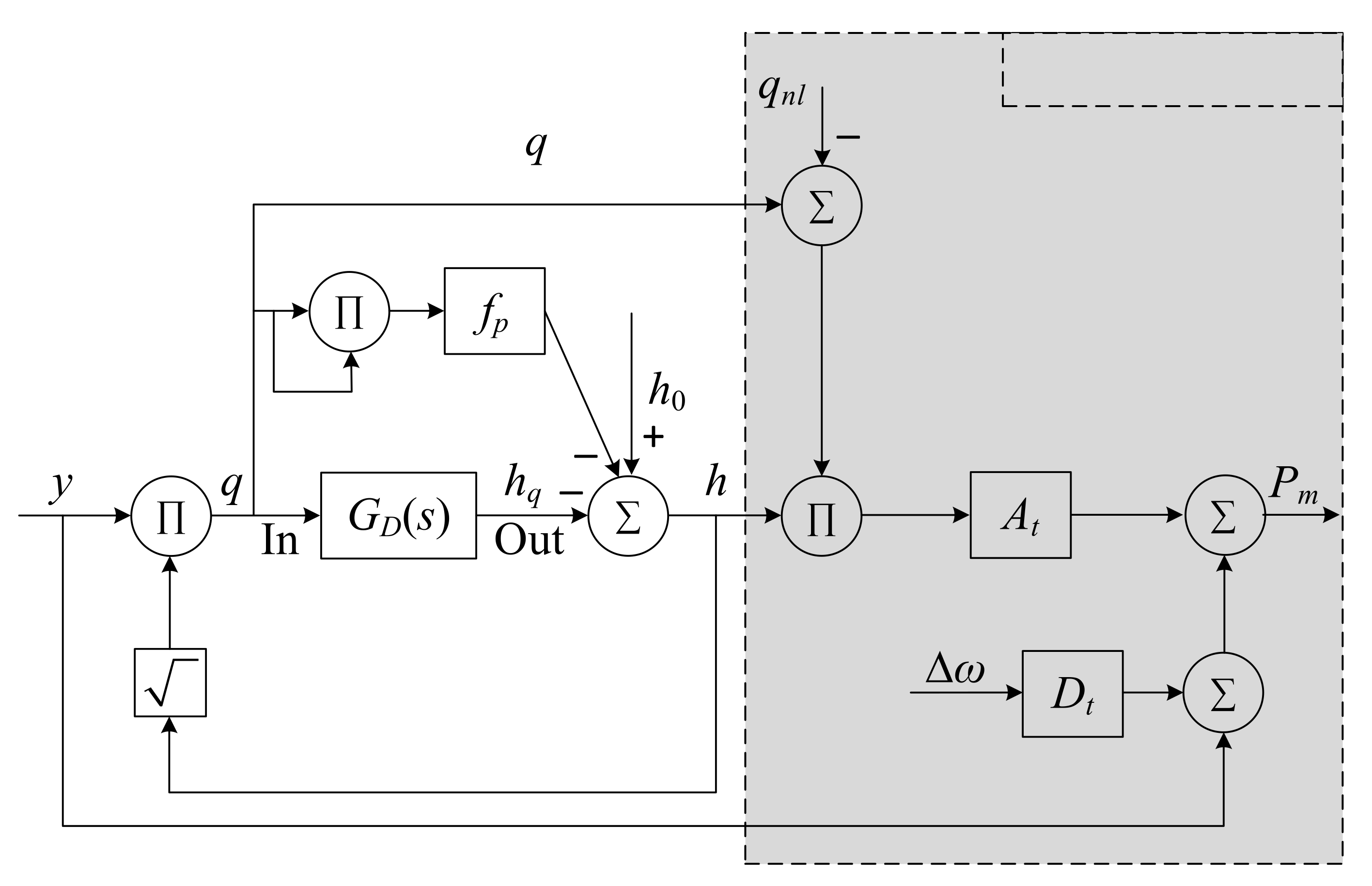
2.1.1. Penstock
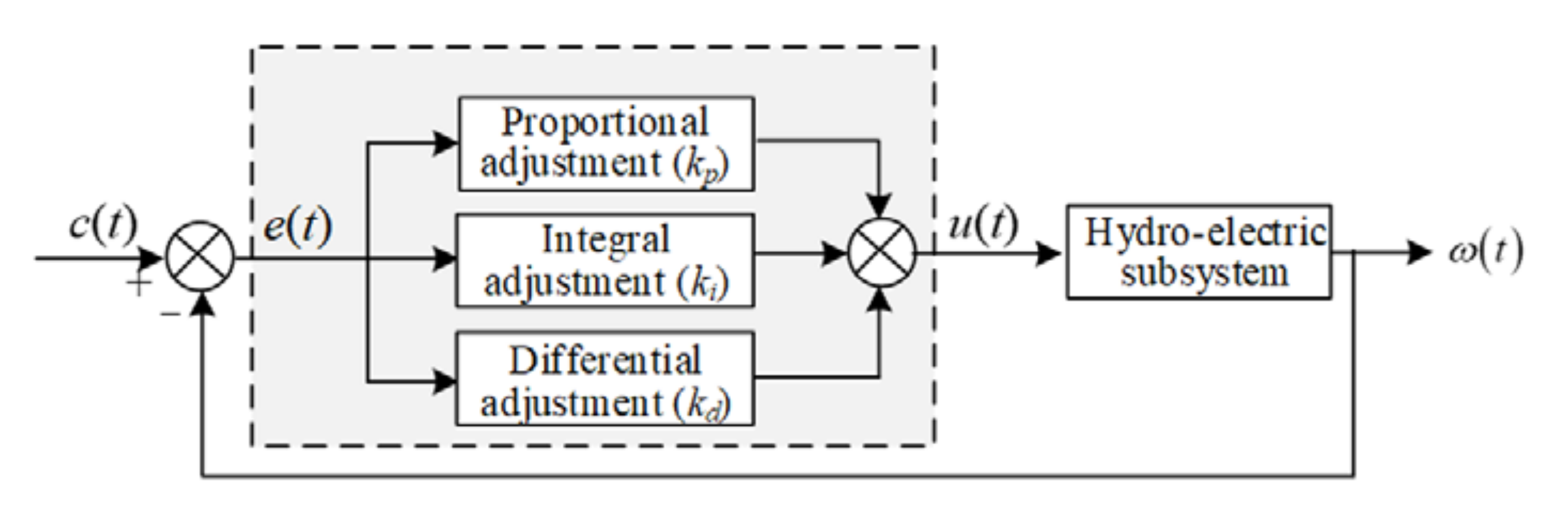
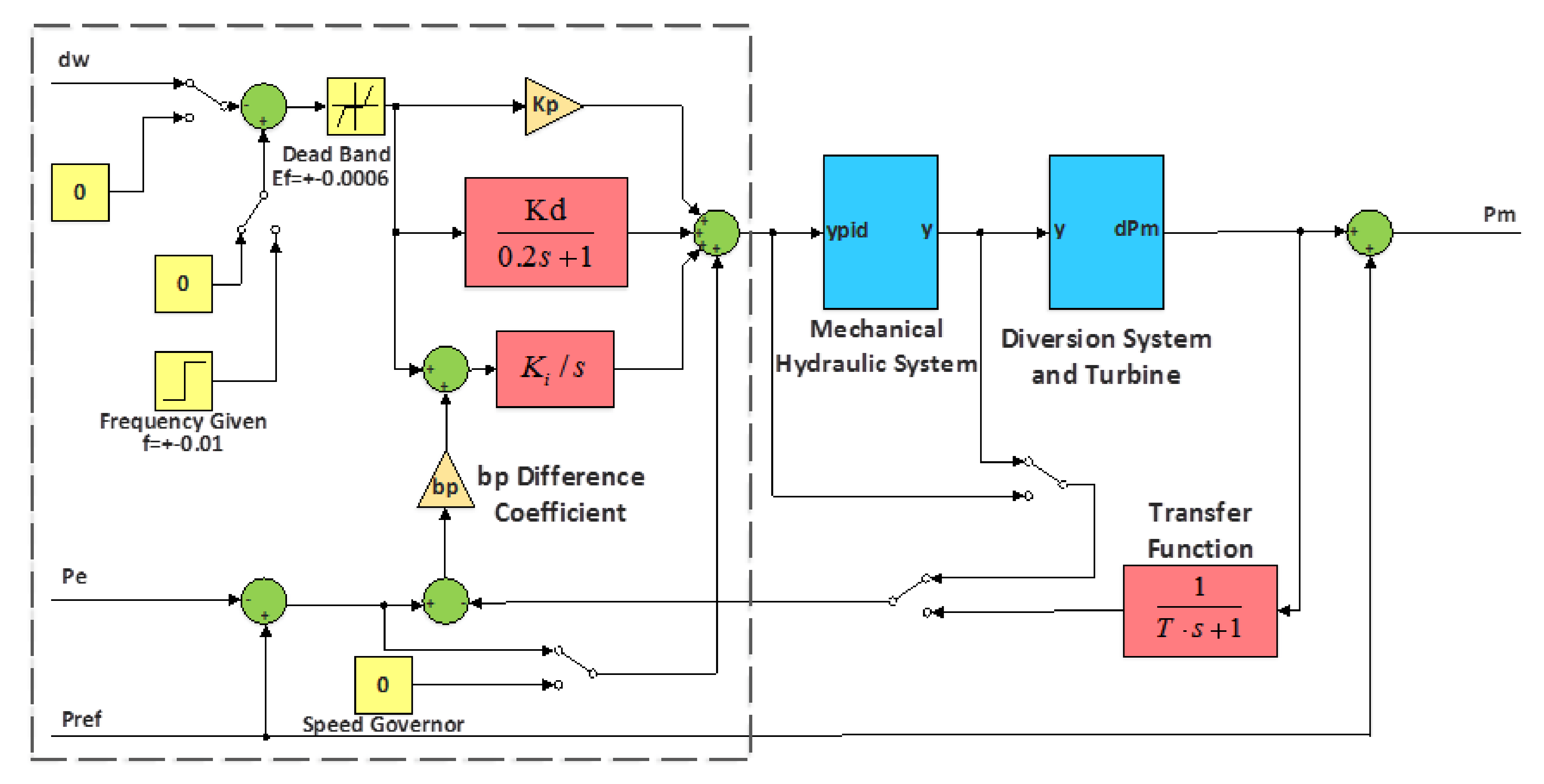
2.1.2. Governor
2.1.3. Hydro-Turbine
2.1.4. Synchronous Generator
2.1.5. Excitation Sector
2.2. Wind Farm
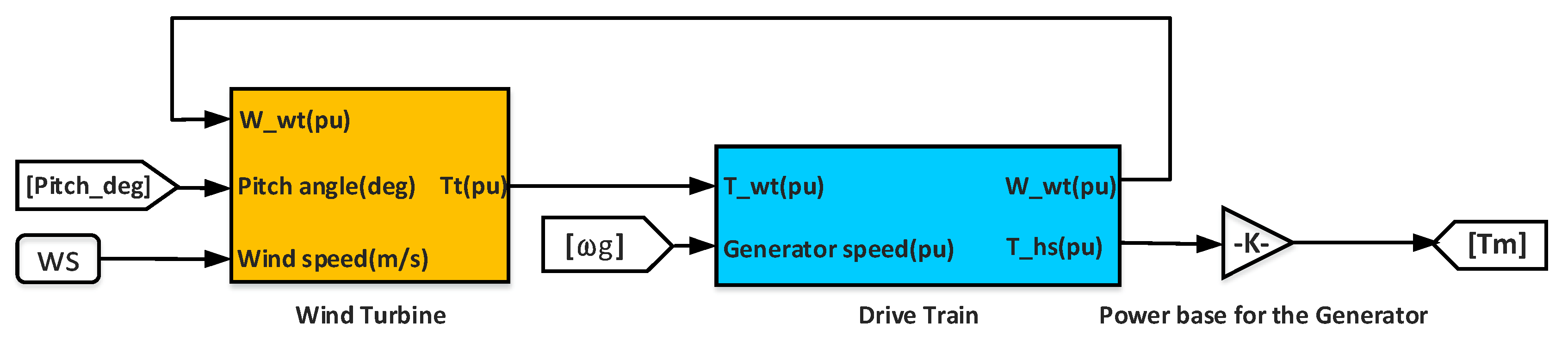
2.2.1. Wind Turbine Model
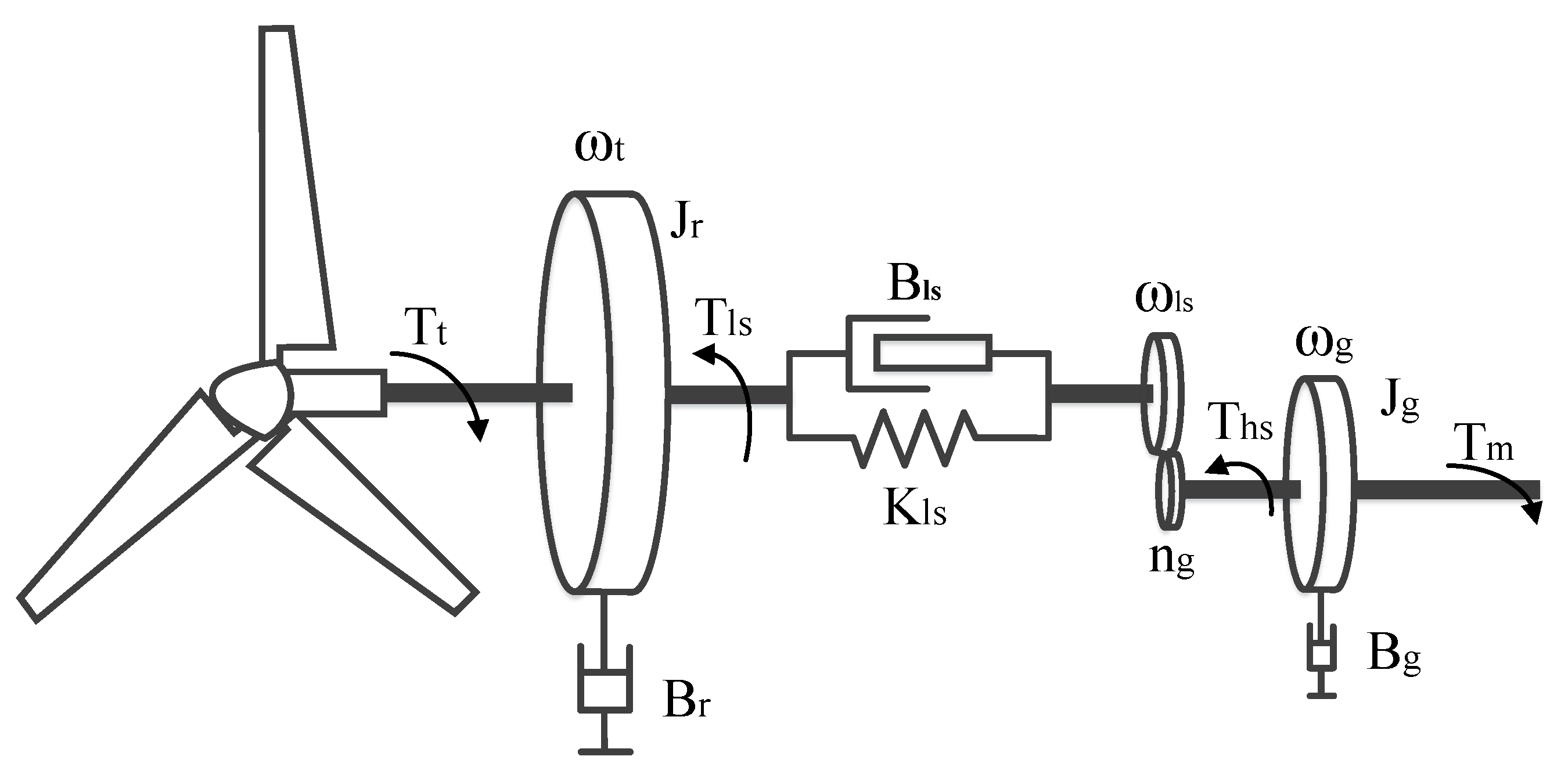
2.2.2. Mechanical Drive Shaft Model
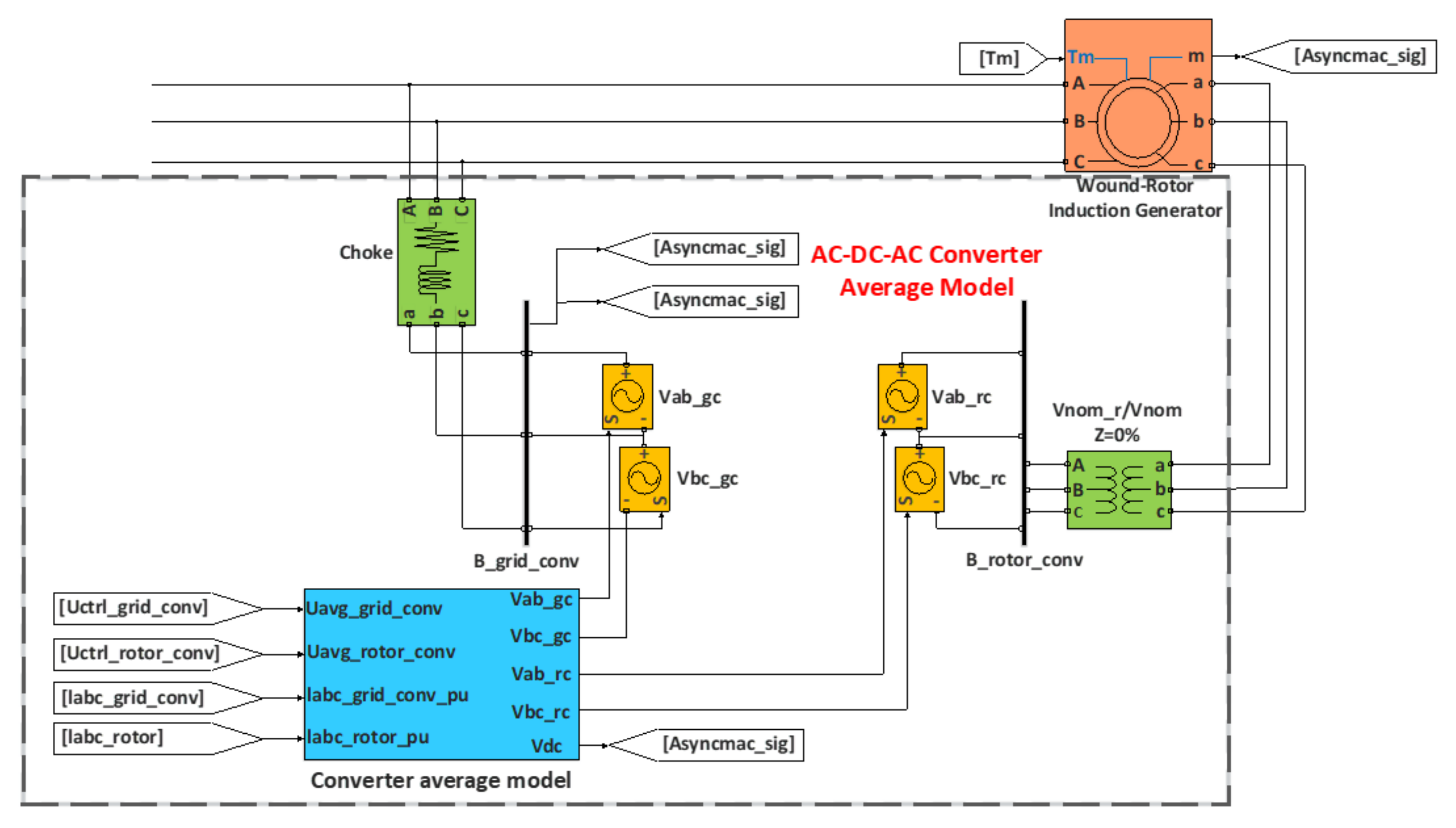
2.2.3. DFIG Model in dq Frame
2.2.4. PWM Converter Model
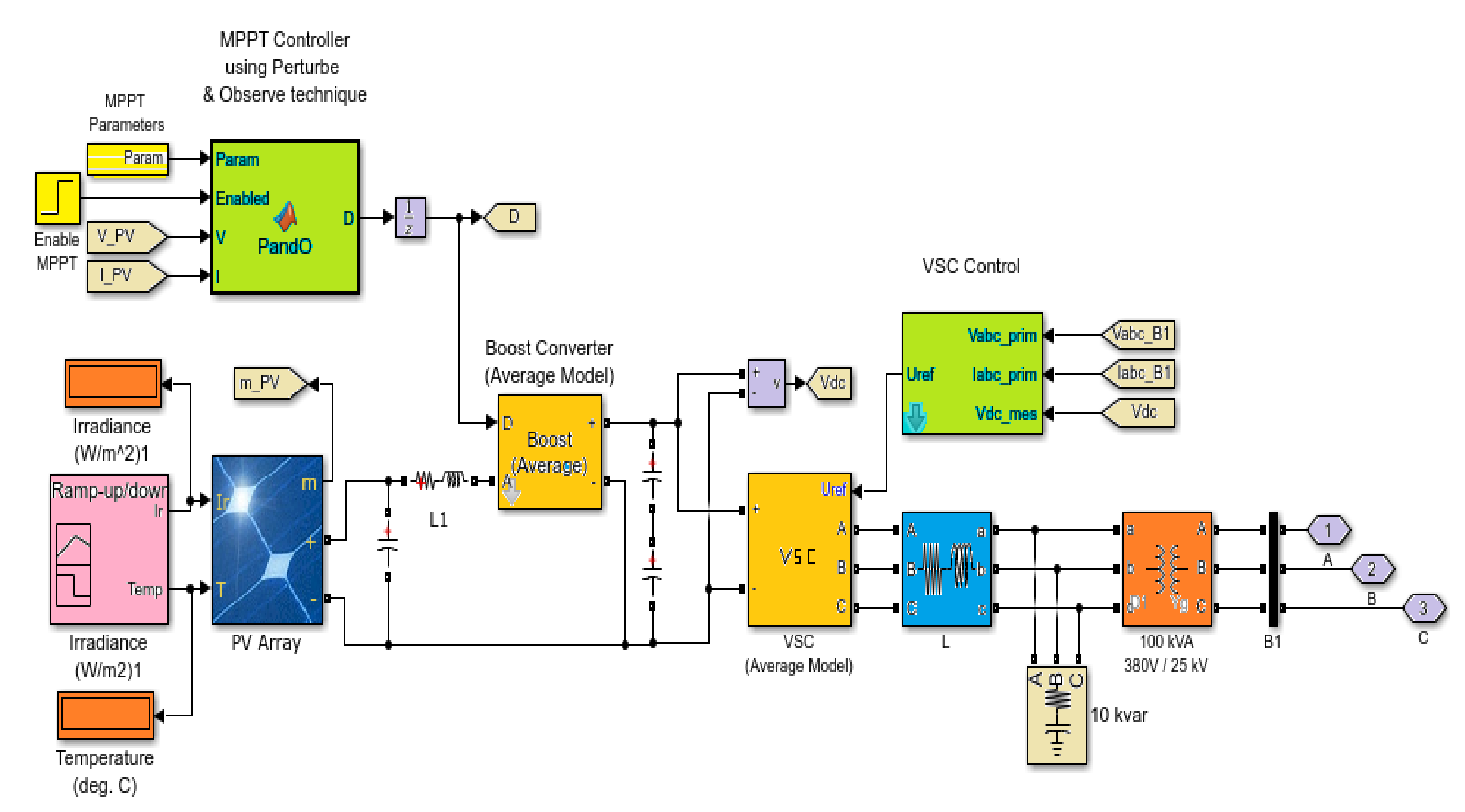
2.3. Solar Photovoltaic System
3. Low Frequency Oscillation Response to Hybrid Regulation
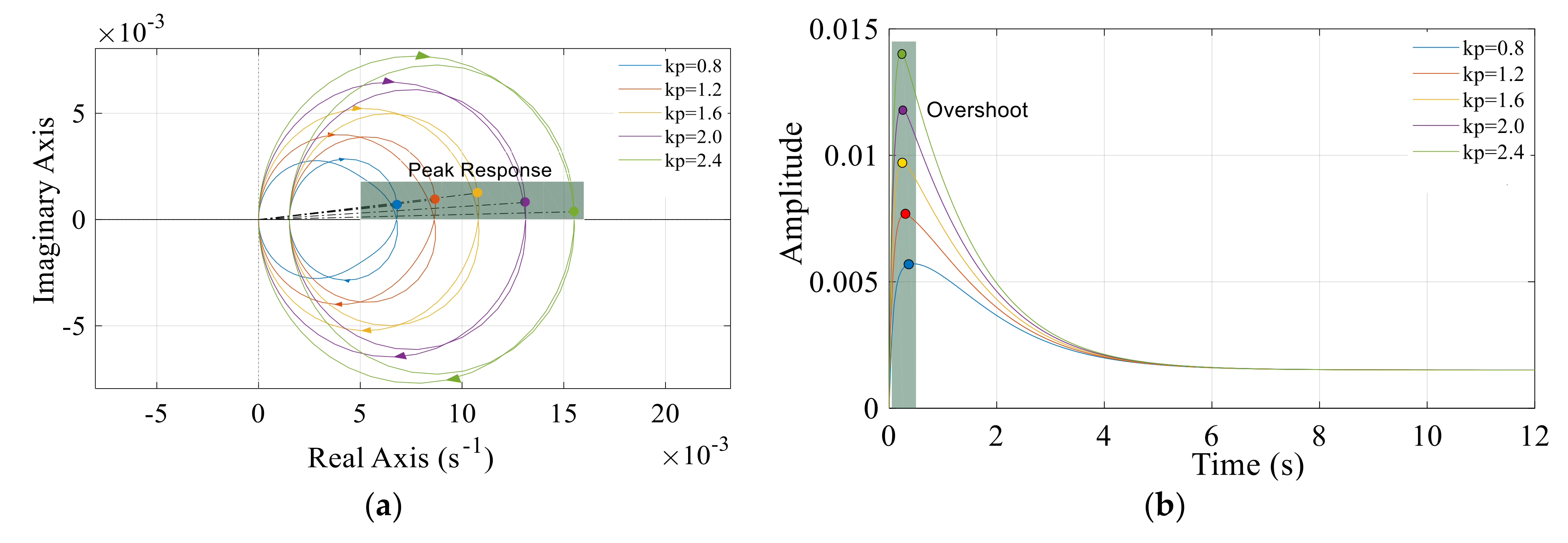
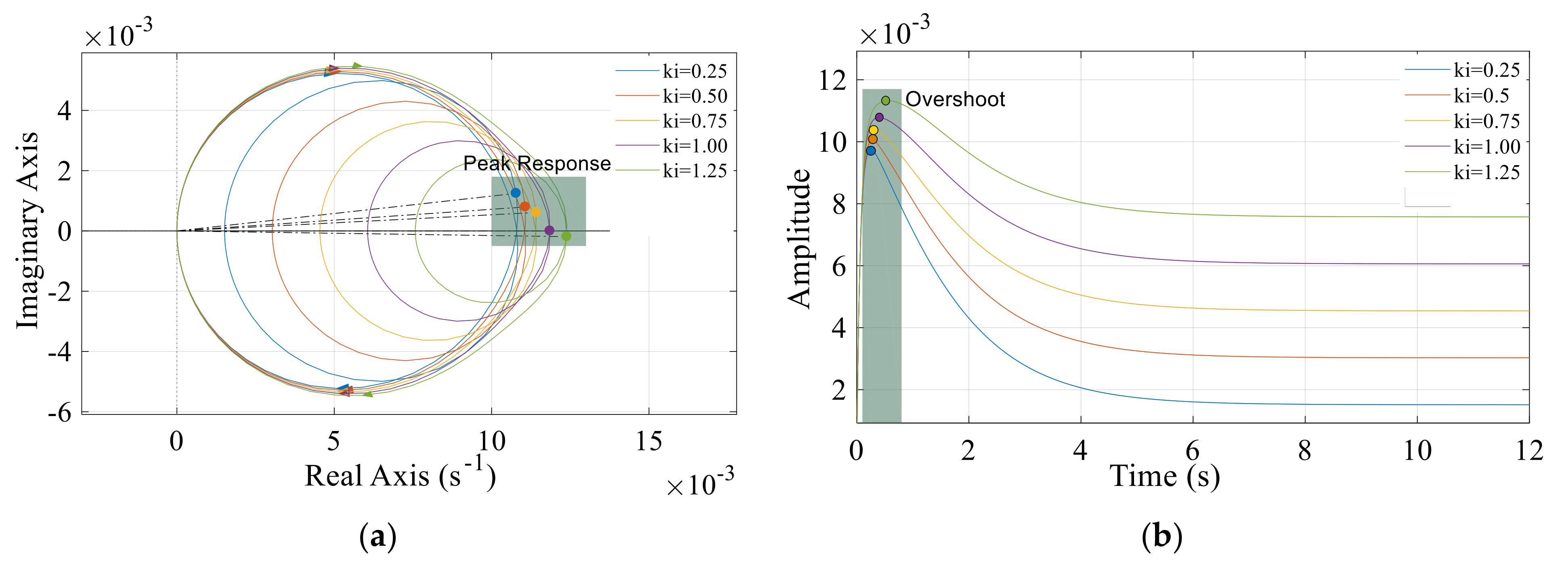
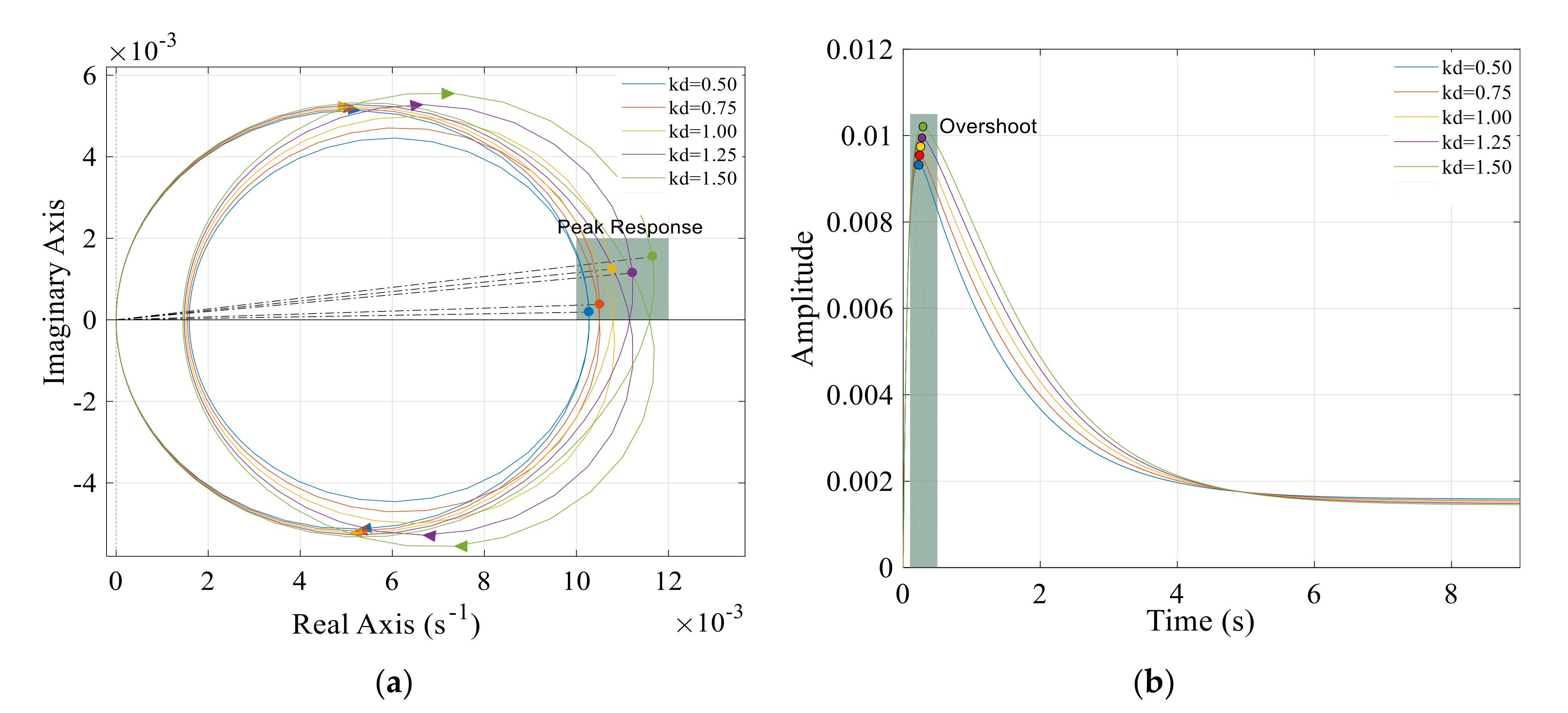
3.1. Nyquist Response to PID Regulation
3.1.1. Nyquist Profile
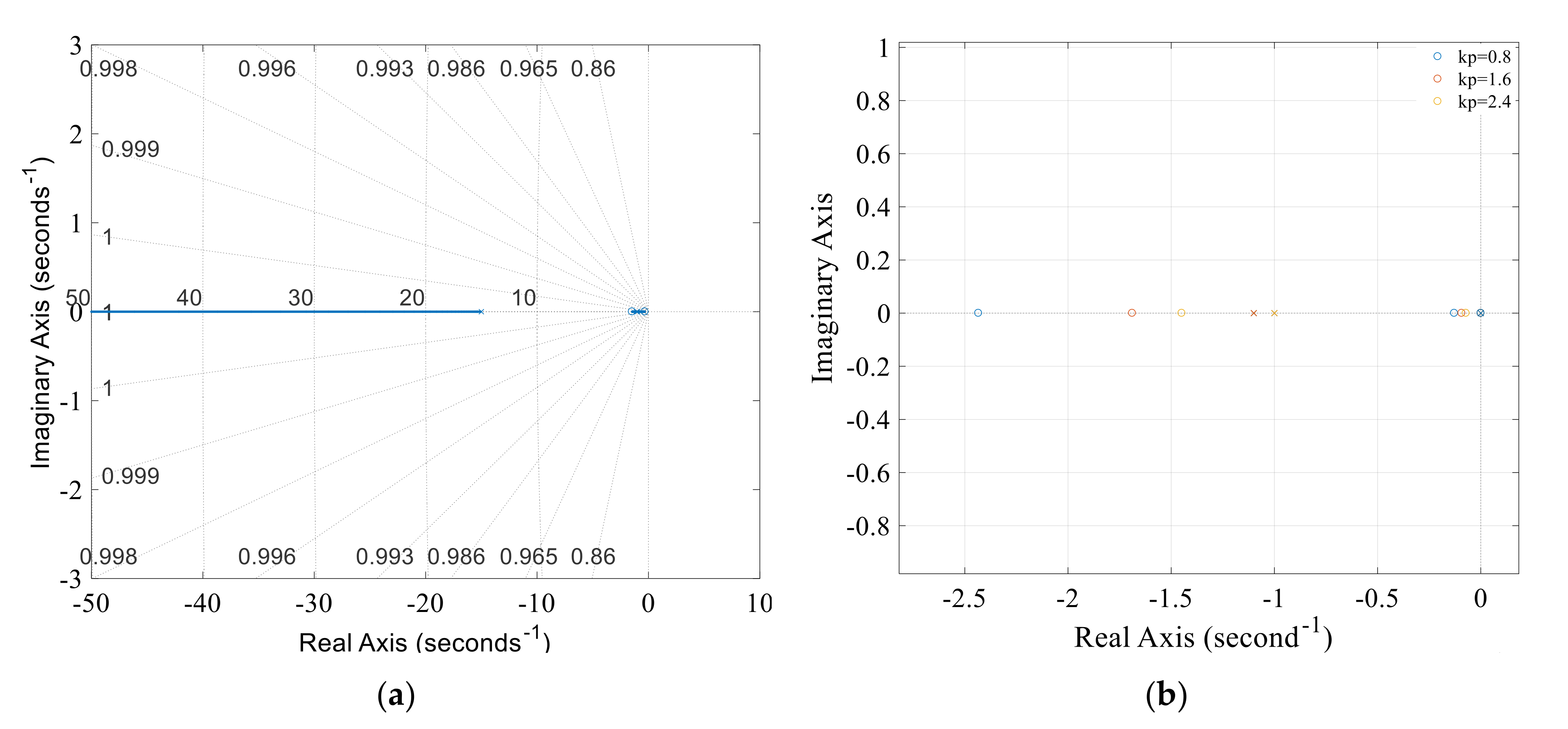
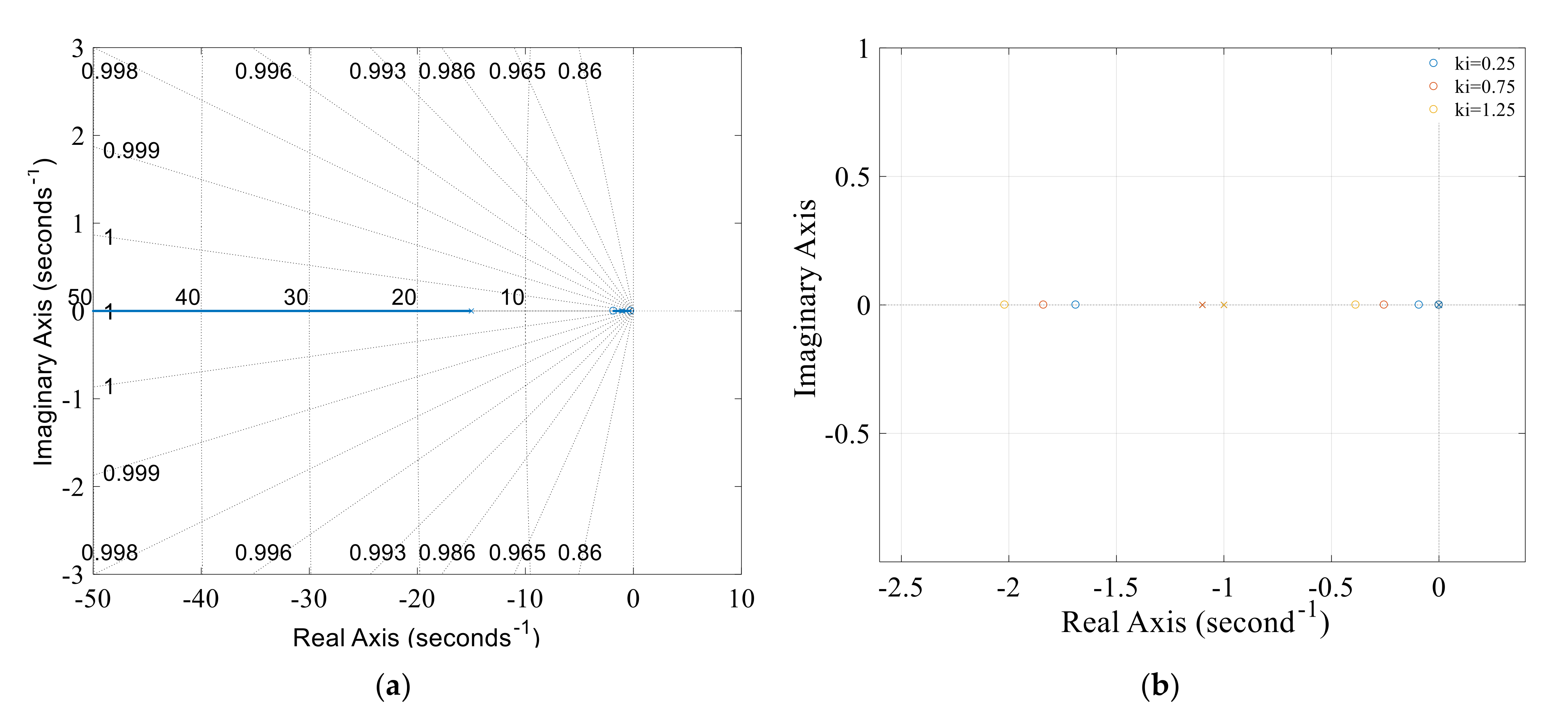
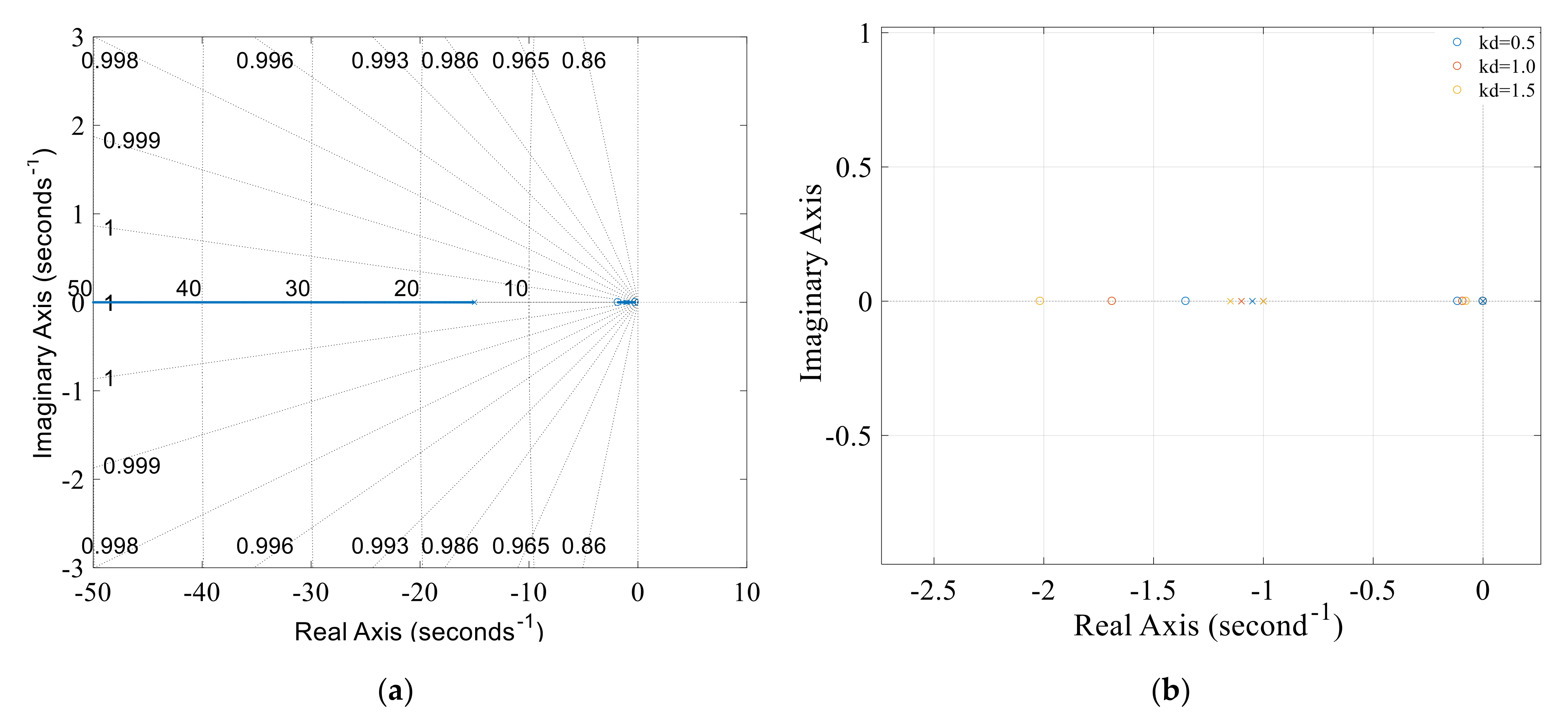
3.1.2. Influences of Governor Parameters on Nyquist and Step Responses
3.1.3. Root-Locus Profile
3.1.4. Influences of Governor Parameters on Root-Locus Response
4. Low Frequency Oscillation Response to Renewable-Quota
5. Conclusions
- Under the case where the wind, solar and hydropower ratio is 40:1:150, it is interesting that the smaller the governor parameters (kp, ki, and kd), the smaller the Nyquist overshoot and step fluctuation. Herein, the studied domains for kp, ki, and kd are [0.8, 2.4], [0.25, 1.25] and [0.5, 1.5], and thus the optimal values for maximally reducing hydropower low frequency oscillation are finally determined as kp = 0.8, ki = 0.25 and kd = 0.5.
- The wind/solar/hydropower hybrid system keeps global stability in the studied governor parameter domains since the Nyquist and root-locus low frequency oscillation responses meet the relevant stability criteria, i.e., the clockwise number around the point of −1/K equals to the negative pole numbers in the G(s)H(s) right half plane, as well as all root-locus trajectories are in the left half plane. Despite this merit, the overshoot problem is expected to arouse great attention and discussion to reduce the fatigue damage of hydropower components.
- Aiming at different wind/solar/hydropower quotas (i.e., 20: 1: 150, 30: 1: 150, and 40: 1: 150), the four quantified indicators (i.e., the three-phase parallel RLC load, the grounding transformer, the three-phase PI section line, and the wind-farm transmission line) show that it is beneficial to increase the wind farm installed capacity to maximize the electricity production without system stability defects under the solar-load and wind-load line ratios for 1:1 and 3:1 excepting for 2:1. This is contributed by the smaller quantified values of oscillation frequency and damping ratio.
- Regarding a certain wind/solar/hydropower quota, it is a promising strategy to increase the solar-load transmission line in order to achieve the safe and stable operation of the hybrid system and a relatively excellent dynamic regulation capacity of the hydropower governor.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hirth, L. The benefits of flexibility: The value of wind energy with hydropower. Appl. Energy 2016, 181, 210–223. [Google Scholar] [CrossRef]
- Lu, X.; McElroy, M.B.; Peng, W.; Liu, S.; Nielsen, C.P.; Wang, H. Challenges faced by China compared with the US in developing wind power. Nat. Energy 2016, 1, 16061. [Google Scholar] [CrossRef]
- Hart, E.K.; Stoutenburg, E.D.; Jacobson, M.Z. The Potential of Intermittent Renewables to Meet Electric Power Demand: Current Methods and Emerging Analytical Techniques. Proc. IEEE 2012, 100, 322–334. [Google Scholar] [CrossRef]
- Schaber, K.; Steinke, F.; Muehlich, P.; Hamacher, T. Parametric study of variable renewable energy integration in Europe: Advantages and costs of transmission grid extensions. Energy Policy 2012, 42, 498–508. [Google Scholar] [CrossRef] [Green Version]
- Kaur, A.; Nonnenmacher, L.; Coimbra, C.F.M. Net load forecasting for high renewable energy penetration grids. Energy 2016, 114, 1073–1084. [Google Scholar] [CrossRef]
- Talaat, M.; Farahat, M.A.; Elkholy, M.H. Renewable power integration: Experimental and simulation study to investigate the ability of integrating wave, solar and wind energies. Energy 2019, 170, 668–682. [Google Scholar] [CrossRef]
- Zhang, H.; Cao, Y.; Zhang, Y.; Terzija, V. Quantitative synergy assessment of regional wind-solar energy resources based on MERRA reanalysis data. Appl. Energy 2018, 216, 172–182. [Google Scholar] [CrossRef]
- Cao, Y.; Zhang, Y.; Zhang, H.; Shi, X.; Terzija, V. Probabilistic Optimal PV Capacity Planning for Wind Farm Expansion Based on NASA Data. IEEE Trans. Sustain. Energy 2017, 8, 1291–1300. [Google Scholar] [CrossRef]
- Zini, G.; Rosa, A.D. Hydrogen systems for large-scale photovoltaic plants: Simulation with forecast and real production data. Int. J. Hydrog. Energy 2014, 39, 107–118. [Google Scholar] [CrossRef]
- Wang, D.; Qiu, J.; Reedman, L.; Meng, K.; Lai, L.L. Two-stage energy management for networked microgrids with high renewable penetration. Appl. Energy 2018, 226, 39–48. [Google Scholar] [CrossRef]
- Vachirasricirikul, S.; Ngamroo, I. Robust LFC in a Smart Grid with Wind Power Penetration by Coordinated V2G Control and Frequency Controller. IEEE Trans. Smart Grid 2014, 5, 371–380. [Google Scholar] [CrossRef]
- Zhao, B.; Wang, X.; Lin, D.; Calvin, M.M.; Morgan, J.C.; Qin, R.; Wang, C. Energy Management of Multiple Microgrids Based on a System of Systems Architecture. IEEE Trans. Power Syst. 2018, 33, 6410–6421. [Google Scholar] [CrossRef]
- Etherden, N.; Bollen, M.H.J. Dimensioning of Energy Storage for Increased Integration of Wind Power. IEEE Trans. Sustain. Energy 2013, 4, 546–553. [Google Scholar] [CrossRef]
- Hill, C.A.; Such, M.C.; Chen, D.; Gonzalez, J.; Grady, W.M. Battery Energy Storage for Enabling Integration of Distributed Solar Power Generation. IEEE Trans. Smart Grid 2012, 3, 850–857. [Google Scholar] [CrossRef]
- Notton, G.; Mistrushi, D.; Stoyanov, L.; Berber, P. Operation of a photovoltaic-wind plant with a hydro pumping-storage for electricity peak-shaving in an island context. Sol. Energy 2017, 157, 20–34. [Google Scholar] [CrossRef]
- Corsini, A.; Rispoli, F.; Gamberale, M.; Tortora, E. Assessment of H-2- and H2O-based renewable energy-buffering systems in minor islands. Renew. Energy 2009, 34, 279–288. [Google Scholar] [CrossRef]
- Sternberg, A.; Bardow, A. Power-to-What?—Environmental assessment of energy storage systems. Energy Environ. Sci. 2015, 8, 389–400. [Google Scholar] [CrossRef]
- Fitzgerald, N.; Arantegui, R.L.; McKeogh, E.; Leahy, P. A GIS-based model to calculate the potential for transforming conventional hydropower schemes and non-hydro reservoirs to pumped hydropower schemes. Energy 2012, 41, 483–490. [Google Scholar] [CrossRef]
- Su, Y.; Kern, J.D.; Characklis, G.W. The impact of wind power growth and hydrological uncertainty on financial losses from oversupply events in hydropower-dominated systems. Appl. Energy 15 2017, 194, 172–183. [Google Scholar] [CrossRef]
- Xiong, H.; Xu, B.; Kheav, K.; Luo, X.; Zhang, X.; Patelli, E.; Guo, P.; Chen, D. Multiscale power fluctuation evaluation of a hydro-wind-photovoltaic system. Renew. Energy 2021, 175, 153–166. [Google Scholar] [CrossRef]
- Wang, X.; Mei, Y.; Kong, Y.; Lin, Y.; Wang, H. Improved multi-objective model and analysis of the coordinated operation of a hydro-wind-photovoltaic system. Energy 2017, 134, 813–839. [Google Scholar] [CrossRef]
- Xu, B.; Chen, D.; Venkateshkumar, M.; Xiao, Y.; Yue, Y.; Xing, Y.; Li, P. Modeling a pumped storage hydropower integrated to a hybrid power system with solar-wind power and its stability analysis. Appl. Energy 2019, 248, 446–462. [Google Scholar] [CrossRef]
- Martinez-Lucas, G.; Ignacio Sarasua, J.; Angel Sanchez-Fernandez, J.; Roman Wilhelmi, J. Frequency control support, of a wind-solar isolated system by a hydropower plant with long tail-race tunnel. Renew. Energy 2016, 90, 362–376. [Google Scholar] [CrossRef] [Green Version]
- Goyal, R.; Gandhi, B.K. Review of hydrodynamics instabilities in Francis turbine during off-design and transient operations. Renew. Energy 2018, 116, 697–709. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Y. Characteristic Analysis and Calculation of Frequencies of Voltages in Out-of-Step Oscillation Power System and a Frequency-Based Out-of-Step Protection. IEEE Trans. Power Syst. 2019, 34, 205–214. [Google Scholar] [CrossRef]
- Chen, C.-I.; Chang, G.W. An Efficient Prony-Based Solution Procedure for Tracking of Power System Voltage Variations. IEEE Trans. Ind. Electron. 2013, 60, 2681–2688. [Google Scholar] [CrossRef]
- Rintamaki, T.; Siddiqui, A.S.; Salo, A. Does renewable energy generation decrease the volatility of electricity prices? An analysis of Denmark and Germany. Energy Econ. 2017, 62, 270–282. [Google Scholar]
- Roozbehani, M.; Dahleh, M.A.; Mitter, S.K. Volatility of Power Grids under Real-Time Pricing. IEEE Trans. Power Syst. 2012, 27, 1926–1940. [Google Scholar] [CrossRef] [Green Version]
- El-Fadel, M.; Chedid, R.; Zeinati, M.; Hmaidan, W. Mitigating energy-related GHG emissions through renewable energy. Renew. Energy 2003, 28, 1257–1276. [Google Scholar] [CrossRef]
- Tripathi, L.; Mishra, A.K.; Dubey, A.K.; Tripathi, C.B.; Baredar, P. Renewable energy: An overview on its contribution in current energy scenario of India. Renew. Sustain. Energy Rev. 2016, 60, 226–233. [Google Scholar] [CrossRef]
- Perez-Diaz, J.I.; Jimenez, J. Contribution of a pumped-storage hydropower plant to reduce the scheduling costs of an isolated power system with high wind power penetration. Energy 2016, 109, 92–104. [Google Scholar] [CrossRef] [Green Version]
- Wang, B.; Guo, W.; Yang, J. Analytical solutions for determining extreme water levels in surge tank of hydropower station under combined operating conditions. Commun. Nonlinear Sci. Numer. Simul. 2017, 47, 394–406. [Google Scholar] [CrossRef]
- Lai, X.; Li, C.; Guo Wg Xu, Y.; Li, Y. Stability and dynamic characteristics of the nonlinear coupling system of hydropower station and power gird. Commun. Nonlinear Sci. Numer. Simul. 2019, 79, 104919. [Google Scholar] [CrossRef]
- Su, C.; Cheng, C.; Wang, P.; Shen, J.; Wu, X. Optimization model for long-distance integrated transmission of wind farms and pumped-storage hydropower plants. Appl. Energy 2019, 242, 285–293. [Google Scholar] [CrossRef]
- Helseth, A.; Gjelsvik, A.; Mo, B.; Linnet, U. A model for optimal scheduling of hydro thermal systems including pumped-storage and wind power. IET Gener. Transm. Distrib. 2013, 7, 1426–1434. [Google Scholar] [CrossRef]
- Wang, X.; Chen, L.; Chen, Q.; Mei, Y.; Wang, H. Model and Analysis of Integrating Wind and PV Power in Remote and Core Areas with Small Hydropower and Pumped Hydropower Storage. Energies 2018, 11, 3459. [Google Scholar] [CrossRef] [Green Version]
- Xu, B.B.; Chen, D.Y.; Zhang, H.; Wang, F.F.; Zhang, X.G.; Wu, Y.H. Hamiltonian model and dynamic analyses for a hydro-turbine governing system with fractional item and time-lag. Commun. Nonlinear Sci. Numer. Simul. 2017, 47, 35–37. [Google Scholar] [CrossRef] [Green Version]
- Arena, C.; Genco, M.; Lombardo, A.; Meli, I.; Mazzola, M.R. A Cost-Benefit Based, Parametric Procedure to Screen Existing Irrigation and Municipal Supply Reservoirs for Wind Energy Storage. Water 2018, 10, 1813. [Google Scholar] [CrossRef] [Green Version]
- Ouyang, W.; Hao, F.H.; Zhao, C.; Lin, C. Vegetation response to 30 years hydropower cascade exploitation in upper stream of Yellow River. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1928–1941. [Google Scholar] [CrossRef]
- Karhinen, S.; Huuki, H. Private and social benefits of a pumped hydro energy storage with increasing amount of wind power. Energy Econ. 2019, 81, 942–959. [Google Scholar] [CrossRef]
- Fahimi, A.; Upham, P. The renewable energy sector in Afghanistan: Policy and potential. Wiley Interdiscip. Rev. Energy Environ. 2018, 7, e280. [Google Scholar] [CrossRef]
- Jaime, R.H.; Mahmut, R.; Tang, H.; Erdal, K. Nonlinear control of fixed-wing UAVs in presence of stochastic winds. Commun. Nonlinear Sci. Numer. Simul. 2016, 33, 57–69. [Google Scholar]
- Emaminaeini, A.; Franklin, G.F.; Powell, J.D.; MathWorks, Inc. Feedback Control of Dynamic Systems/MATLAB & Simulink Student Version 2012a. J. De Gynécologie Obs. Et Biol. De La Reprod. 2012, 17, 67–74. [Google Scholar]
- Krause, P.C.; Wasynczuk, O.; Sudhoff, S.D. Analysis of Electric Machinery, Analysis of Electric Machinery and Drive; Wiley-IEEE Press: Piscataway, NJ, USA, 1986. [Google Scholar]
- Kamwa, I.; Pilote, M. Experience with computer-aided graphical analysis of sudden-short-circuit oscillograms of large synchronous machines. IEEE Trans. Energy Conver. 1995, 10, 407–414. [Google Scholar] [CrossRef]



| Line Length Ratio (S:W) | W:S:H | Eigenvalue | Frequency/HZ | Damping Ratio/% | Remark |
|---|---|---|---|---|---|
| 1:1 | 20:1:150 | −1.14 × 10−1 + j0 | 0.0182 | 100 | Three-Phase Parallel RLC Load |
| −1.26 × 101 + j0 | 2.01 | 100 | Grounding Transformer | ||
| −9.18 × 102 − j4.47 × 103 | 7.26 × 102 | 20.1 | Three-Phase PI Section Line | ||
| −3.15 × 103 − j9.43 × 103 | 1.58 × 103 | 31.7 | Windformsystem/30 km line | ||
| 30:1:150 | −1.13 × 10−1 + j0 | 0.018 | 100 | Three-Phase Parallel RLC Load | |
| −1.65 × 101 + j0 | 2.63 | 100 | Grounding Transformer | ||
| −9.47 × 102 − j4.61× 103 | 7.48 × 102 | 20.1 | Three-Phase PI Section Line | ||
| −3.15× 103 − j9.43× 103 | 1.58 × 103 | 31.7 | Windformsystem/30 km line | ||
| 40:1:150 | −1.13 × 10−1 + j0 | 0.018 | 100 | Three-Phase Parallel RLC Load | |
| −1.99 × 101 + j0 | 3.17 | 100 | Grounding Transformer | ||
| −9.77 × 102 − j4.74 × 103 | 7.71 × 102 | 20.2 | Three-Phase PI Section Line | ||
| −3.15 × 102 − j9.43 × 103 | 1.58 × 103 | 31.7 | Windformsystem/30 km line | ||
| 2:1 | 20:1:150 | −1.14 × 10−1 + j0 | 0.0182 | 100 | Three-Phase Parallel RLC Load |
| −1.26 × 101 − j0 | 2.01 | 100 | Grounding Transformer | ||
| −4.62 × 103 − j0 | 7.36 × 102 | 100 | Three-Phase PI Section Line | ||
| −3.23 × 102 − j7.11 × 103 | 1.13 × 103 | 4.54 | Windformsystem/30 km line | ||
| 30:1:150 | −1.13 × 10−1 + j0 | 0.018 | 100 | Three-Phase Parallel RLC Load | |
| −1.65 × 101 + j2.37 × 10−10 | 2.63 | 100 | Grounding Transformer | ||
| −9.67 × 102 − j4.58 × 103 | 7.45 × 102 | 20.7 | Three-Phase PI Section Line | ||
| −3.22 × 102 − j7.11 × 103 | 1.13 × 103 | 4.53 | Windformsystem/30 km line | ||
| 40:1:150 | −1.13 × 10−1 + j0 | 0.018 | 100 | Three-Phase Parallel RLC Load | |
| −1.99 × 101 + j0 | 3.17 | 100 | Grounding Transformer | ||
| −9.98 × 102 − j4.71 × 103 | 7.66 × 102 | 20.7 | Three-Phase PI Section Line | ||
| −3.22 × 102 − j7.11 × 103 | 1.13 × 103 | 4.52 | Windformsystem/30 km line | ||
| 3:1 | 20:1:150 | −1.14 × 10−1 + j0 | 0.0182 | 100 | Three-Phase Parallel RLC Load |
| −1.26 × 101 + j0 | 2.01 | 100 | |||
| −8.82 × 102 − j4.39 × 103 | 7.13 × 102 | 19.7 | Three-Phase PI Section Line | ||
| −5.85 × 102 + j627 × 103 | 1.00 × 103 | 9.28 | Windformsystem/30 km line | ||
| 30:1:150 | −1.13 × 10−1 + j0 | 0.018 | 100 | Three-Phase Parallel RLC Load | |
| −1.65 × 101 + j0 | 2.63 | 100 | Grounding Transformer | ||
| −1.72 × 102 − j4.48 × 103 | 7.13 × 102 | 3.85 | Three-Phase PI Section Line | ||
| −5.85 × 102 + j6.27 × 103 | 1.00 × 103 | 9.28 | Windformsystem/30 km line | ||
| 40:1:150 | −1.13 × 10−1 + j0 | 0.018 | 100 | Three-Phase Parallel RLC Load | |
| −1.99 × 101 − j0 | 3.17 | 100 | Grounding Transformer | ||
| −1.76 × 102 − j4.47 × 103 | 7.12 × 102 | 3.95 | Three-Phase PI Section Line | ||
| −5.85 × 102 + j6.27 × 103 | 1.00 × 103 | 9.28 | Windformsystem/30 km line |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, B.; Lei, L.; Zhao, Z.; Jiang, W.; Xiao, S.; Li, H.; Zhang, J.; Chen, D. Low Frequency Oscillations in a Hydroelectric Generating System to the Variability of Wind and Solar Power. Water 2021, 13, 1978. https://doi.org/10.3390/w13141978
Xu B, Lei L, Zhao Z, Jiang W, Xiao S, Li H, Zhang J, Chen D. Low Frequency Oscillations in a Hydroelectric Generating System to the Variability of Wind and Solar Power. Water. 2021; 13(14):1978. https://doi.org/10.3390/w13141978
Chicago/Turabian StyleXu, Beibei, Liuwei Lei, Ziwen Zhao, Wei Jiang, Shu Xiao, Huanhuan Li, Junzhi Zhang, and Diyi Chen. 2021. "Low Frequency Oscillations in a Hydroelectric Generating System to the Variability of Wind and Solar Power" Water 13, no. 14: 1978. https://doi.org/10.3390/w13141978





