Review and Comparison of Numerical Simulations of Secondary Flow in River Confluences
Abstract
:1. Introduction
2. Mathematical Description of the Main Flow and Secondary Circulation
3. Boundary Conditions
3.1. Wall Function Boundaries
| = | − | − | ε | (10) | |||
| convection owing to transport by mean flow | diffusion into mean flow | viscous dissipation rate | |||||
3.2. Free Surface
3.3. Inlet
3.4. Outlet
4. Numerical Research of River Confluence Flows
4.1. Secondary Flow in a 90° Confluent Channel with Bed Concordance
4.1.1. RANS Models
4.1.2. LES Models
4.1.3. ANN Models
4.2. Secondary Flow in Differently Angled Confluent Channels with Bed Concordance
4.2.1. RANS Models
4.2.2. DES Models
4.3. Secondary Flow in Confluent Channel with Bed Discordance
4.3.1. RANS Models
4.3.2. LES Models
4.3.3. DES Models
5. Discussion
6. Future Research Needs
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Best, J. Flow dynamics at river channel confluences: Implications for sediment transport and bed morphology. In Recent Developments in Fluvial Sedimentology; Ethridge, F.G., Flores, R.M., Harvey, M.D., Eds.; SEPM Society for Sedimentary Geology: Tulsa, OK, USA, 1987; pp. 27–35. [Google Scholar]
- Yang, Q.Y.; Liu, T.; Lu, W.; Wang, K. Numerical simulation of confluence flow in open channel with dynamic meshes techniques. Adv. Mech. Eng. 2013, 5, 860431. [Google Scholar] [CrossRef] [Green Version]
- Shakibaeinia, A.; Tabatabai, M.R.M.; Zarrati, A.R. Three-dimensional numerical study of flow structure in channel confluences. Can. J. Civ. Eng. 2010, 37, 772–781. [Google Scholar] [CrossRef]
- Weerakoon, S.B. Flow Structure and Bed Topography in River Confluences; University of Tokyo: Tokyo, Japan, 1990. [Google Scholar]
- Song, C.G.; Seo, I.W.; Do Kim, Y. Analysis of secondary current effect in the modeling of shallow flow in open channels. Adv. Water Resour. 2012, 41, 29–48. [Google Scholar] [CrossRef]
- Sivakumar, M.; Dissanayake, K.; Godbole, A. Numerical modeling of flow at an open-channel confluence. Environ. Eng. Res. Event. 2004, 97–106. [Google Scholar]
- Best, J.; Reid, I. Separation zone at open-channel junctions. J. Hydraul. Eng. 1984, 110, 1588–1594. [Google Scholar] [CrossRef]
- Bradbrook, K.F.; Lane, S.N.; Richards, K.S. Numerical simulation of three-dimensional, time-averaged flow structure at river channel confluences. Water Resour. Res. 2000, 36, 2731–2746. [Google Scholar] [CrossRef] [Green Version]
- Bradbrook, K.F.; Lane, S.N.; Richards, K.S.; Biron, P.M.; Roy, A. Large Eddy Simulation of periodic flow characteristics at river channel confluences. J. Hydraul. Res. 2000, 38, 207–215. [Google Scholar] [CrossRef]
- Bryan, R.B.; Kuhn, N.J. Hydraulic conditions in experimental rill confluences and scour in erodible soils. Water Resour. Res. 2002, 38, 211–214. [Google Scholar] [CrossRef]
- Biron, P.M.; Richer, A.; Kirkbride, A.D.; Roy, A.G.; Han, S. Spatial patterns of water surface topography at a river confluence. Earth Surf. Process. Landf. 2002, 27, 913–928. [Google Scholar] [CrossRef]
- Huang, J.; Weber, L.J.; Lai, Y.G. Three-dimensional numerical study of flows in open-channel junctions. J. Hydraul. Eng. 2002, 128, 268–280. [Google Scholar] [CrossRef]
- Biron, P.M.; Ramamurthy, A.S.; Han, S. Three-dimensional numerical modeling of mixing at River confluences. J. Hydraul. Eng. 2004, 130, 243–253. [Google Scholar] [CrossRef]
- Lane, S.N.; Bradbrook, K.F.; Richards, K.S.; Biron, P.A.; Roy, A.G. The application of computational fluid dynamics to natural river channels: Three-dimensional versus two-dimensional approaches. Geomorphology 1999, 29, 1–20. [Google Scholar] [CrossRef]
- Barkdoll, B. Experiments on flow at a 90-degree open-channel junction by larry j. weber, eric d. schumate, and nicola mawer. J. Hydraul. Eng. 2003, 129, 165–166. [Google Scholar] [CrossRef]
- Weber, L.J.; Schumate, E.D.; Mawer, N. Experiments on flow at a 90° open-channel junction. J. Hydraul. Eng. 2001, 127, 340–350. [Google Scholar] [CrossRef]
- Shaheed, R.; Mohammadian, A.; Gildeh, H.K. A comparison of standard k–ε and realizable k–ε turbulence models in curved and confluent channels. Environ. Fluid Mech. 2018, 19, 543–568. [Google Scholar] [CrossRef]
- Bradbrook, K.F.; Biron, P.M.; Lane, S.N.; Richards, K.S.; Roy, A.G. Investigation of controls on secondary circulation in a simple confluence geometry using a three-dimensional numerical model. Hydrol. Process. 1998, 12, 1371–1396. [Google Scholar] [CrossRef]
- Lane, S.N. Hydraulic modelling in hydrology and geomorphology: A review of high resolution approaches. Hydrol. Process. 1998, 12, 1131–1150. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comp. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Weerakoon, S.B.; Tamai, N. Three-dimensional calculation of flow in river confluences using boundary fitted coordinates. J. Hydrosci. Hydraul. Engng. 1989, 7, 51–62. [Google Scholar]
- Rhoads, B.L. Mean structure of transport-effective flows at an asymmetrical confluence when the main stream is dominant. In Coherent Flow Structures in Open Channels; Ashworth, P.J., Bennett, S.J., Best, J.L., McLelland, S.J., Eds.; John Wiley: New York, NY, USA, 1996; pp. 491–517. [Google Scholar]
- Liu, X.; Li, L.; Hua, Z.; Tu, Q.; Yang, T.; Zhang, Y. Flow dynamics and contaminant transport in y-shaped river channel confluences. Int. J. Environ. Res. Public Health 2019, 16, 572. [Google Scholar] [CrossRef] [Green Version]
- Bilal, A.; Xie, Q.; Zhai, Y. Flow, sediment, and morpho-dynamics of river confluence in tidal and non-tidal environments. J. Mar. Sci. Eng. 2020, 8, 591. [Google Scholar] [CrossRef]
- Zhang, T.; Xu, W.; Wu, C. Effect of discharge ratio on flow characteristics in 90° equal-width open-channel junction. J. Hydrodyn. 2009, 21, 541–549. [Google Scholar] [CrossRef]
- Zeng, C.; Li, C.W. A hybrid RANS-LES model for combining flows in open-channel T-junctions. J. Hydrodyn. 2010, 22, 154–159. [Google Scholar] [CrossRef]
- Yang, Q.; Sun, Y.; Wang, X.; Lu, W.; Wang, X. Effects of turbulence models on the numerical simulation of flow in open channel junction. Mech. Adv. Mater. Struct. 2011, 18, 566–571. [Google Scholar] [CrossRef]
- Mignot, E.; Bonakdari, H.; Knothe, P.; Lipeme Kouyi, G.; Bessette, A.; Rivière, N.; Bertrand-Krajewski, J.-L. Experiments and 3D simulations of flow structures in junctions and of their influence on location of flowmeters. Water Sci. Technol. 2012, 66, 1325–1332. [Google Scholar] [CrossRef] [PubMed]
- Mohammadiun, S.; Salehi Neyshabouri, S.A.A.; Naser, G.; Parhizkar, H.; Vahabi, H. Effects of open-channel geometry on flow pattern in a 90° junction. Iran. J. Sci. Technol. Trans. Civ. Eng. 2015, 39, 559–573. [Google Scholar]
- Tang, H.; Zhang, H.; Yuan, S. Hydrodynamics and contaminant transport on a degraded bed at a 90-degree channel confluence. Environ. Fluid Mech. 2018, 18, 443–463. [Google Scholar] [CrossRef]
- Luo, H.; Fytanidis, D.K.; Schmidt, A.R.; García, M.H. Comparative 1D and 3D numerical investigation of open-channel junction flows and energy losses. Adv. Water Resour. 2018, 117, 120–139. [Google Scholar] [CrossRef]
- Shumate, E.D. Experimental Description of Flow at An Open-Channel Junction; University of Iowa: Iowa, IO, USA, 1998. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD, 1st ed.; DCW Industries, Inc.: La Canada, CA, USA, 1993. [Google Scholar]
- Shumate, E.D.; Weber, L.J. Experimental description of combining flows at an open channel junction. In Proceedings of the Internationl Water Resources Engineering Conference, Memphis, TN, USA, 3–7 August 1998; American Society of Civil Engineers: Reston, VA, USA, 1998; pp. 1679–1684. [Google Scholar]
- Pouchoulin, S.; Ramos, P.X.; Emmanuel, M.; Schindfessel, L.; Tom, D.M.; Riviere, N. Discussion of “Tang, H., Zhang, H., & Yuan, S. (2018). Hydrodynamics and contaminant transport on a degraded bed at a 90-degree channel confluence. Environmental Fluid Mechanics, 18(2), 443–463”. Environ. Fluid Mech. 2018, 18, 1293–1295. [Google Scholar]
- Liu, H.; Zhou, J.G.; Burrows, R. Multi-block lattice Boltzmann simulations of subcritical flow in open channel junctions. Comput. Fluids 2009, 38, 1108–1117. [Google Scholar] [CrossRef]
- Schindfessel, L.; Creëlle, S.; De Mulder, T. Flow patterns in an open channel confluence with increasingly dominant tributary inflow. Water 2015, 7, 4724–4751. [Google Scholar] [CrossRef] [Green Version]
- Schindfessel, L.; Creëlle, S.; De Mulder, T. How different cross-sectional shapes influence the separation zone of an open-channel confluence. J. Hydraul. Eng. 2017, 143, 04017036. [Google Scholar] [CrossRef]
- Ramos, P.X.; Schindfessel, L.; Pêgo, J.P.; De Mulder, T. Flat vs. curved rigid-lid LES computations of an open-channel confluence. J. Hydroinformatics 2019, 21, 318–334. [Google Scholar] [CrossRef]
- Sun, S.; Yan, H.; Kouyi, G.L. Artificial neural network modelling in simulation of complex flow at open channel junctions based on large data sets. Environ. Model. Softw. 2014, 62, 178–187. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models. Part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Zaji, A.H.; Bonakdari, H. Efficient methods for prediction of velocity fields in open channel junctions based on the artifical neural network. Eng. Appl. Comput. Fluid Mech. 2015, 9, 220–232. [Google Scholar] [CrossRef]
- Weerakoon, S.B.; Kawahara, Y.; Tamai, N. Three-Dimensional Flow Structure in Channel Confluences of Rectangular Section. In Proceedings of the 25th IAHR Congress A, IAHR, Madrid, Spain, 9–13 September 1991; pp. 373–380. [Google Scholar]
- Brito, M.; Canelas, O.; Leal, J.; Cardoso, A. 3D Numerical Simulation of Flow at a 70° Open-Channel Confluence. In Proceedings of the V Conferencia Nacional de Mecanica Dos Fluidos, Termodinamica e Energía, MEFTE 2014, Porto, Portugal, 11–12 September 2014. [Google Scholar]
- Penna, N.; Marchis, M.D.; Canelas, O.B.; Napoli, E.; Cardoso, A.H.; Gaudio, R. Effect of the junction angle on turbulent flow at a hydraulic confluence. Water 2018, 10, 469. [Google Scholar] [CrossRef] [Green Version]
- Schneider, G.E.; Zedan, M. A modified strongly implicit procedure for the numerical solution of field problems. Numer. Heat Transf. 1981, 4, 1–19. [Google Scholar] [CrossRef]
- Gökçen, B. Hydrodynamics and Morphodynamics of River Confluences. In Proceedings of the 4th International Workshop on “River and Reservoir Hydrodynamics Ans Morphodynamics” & Summer School in “Measuring Techniques for Turbulent Open Channel Flows”, Bornova, Turkey, 29 July 2015. [Google Scholar]
- Bradbrook, K.F.; Lane, S.N.; Richards, K.S.; Biron, P.M.; Roy, A.G. Role of bed discordance at asymmetrical river confluences. J. Hydraul. Eng. 2001, 127, 351–368. [Google Scholar] [CrossRef]
- Yakhot, V.; Orzag, S.A.; Thangam, S.; Gatshi, T.B.; Speziale, C.G. Development of a turbulence model for shear flow by a double expansion technique. Phys. Fluids A 1992, 4, 1510–1520. [Google Scholar] [CrossRef] [Green Version]
- Biron, P.; Best, J.L.; Roy, A.G. Effects of bed discordance on flow dynamics at open channel confluences. J. Hydraul. Eng. 1996, 122, 676–682. [Google Scholar] [CrossRef]
- Biron, P.; Roy, A.G.; Best, J.L. Turbulent flow structure at concordant and discordant open-channel confluences. Exp. Fluids 1996, 21, 437–446. [Google Scholar] [CrossRef]
- Boxall, J.G.; Guymer, I.; Marion, A. Transverse mixing in sinuous natural open channel flows. J. Hydraul. Res. 2003, 41, 153–165. [Google Scholar] [CrossRef]
- Horna-Munoz, D.; Constantinescu, G.; Rhoads, B.; Lewis, Q.; Sukhodolov, A. Density effects at a concordant bed natural river confluence. Water Resour. Res. 2020, 56, e2019WR026217. [Google Scholar] [CrossRef]
- Kennedy, B.A. On Playfair’s law of accordant junctions. Earth Surf. Earth Surf. Process. Landf. 1984, 9, 153–173. [Google Scholar] [CrossRef]
- Sukhodolov, A.N.; Krick, J.; Sukhodolova, T.A.; Cheng, Z.; Rhoads, B.L.; Constantinescu, G.S. Turbulent flow structure at a discordant river confluence: Asymmetric jet dynamics with implications for channel morphology. J. Geophys. Res. Earth Surf. 2017, 122, 1278–1293. [Google Scholar] [CrossRef]
- Wang, X.; Yan, Z. Three-dimensional simulation for effects of bed discordance on flow dynamics at y-shaped open channel confluences. J. Hydrodyn. 2007, 19, 587–593. [Google Scholar] [CrossRef]
- Dordevica, D.; Stojnic, I. Numerical simulation of 3D flow in right-angled confluences with bed elevation discordance in both converging channels. Procedia Eng. 2016, 154, 1026–1033. [Google Scholar] [CrossRef] [Green Version]
- Boyer, C.; Roy, A.G.; Best, J.L. Dynamics of a river channel confluence with discordant beds: Flow turbulence, bed load sediment transport, and bed morphology. J. Geophys. Res. 2006, 111, F4. [Google Scholar] [CrossRef]
- Cheng, Z.; Constantinescu, G. Stratification effects on hydrodynamics and mixing at a river confluence with discordant bed. Environ. Fluid Mech. 2020, 20, 843–872. [Google Scholar] [CrossRef]
- Rhoads, B.L.; Kenworthy, S.T. Flow structure at an asymmetrical stream confluence. Geomorphology 1995, 11, 273–293. [Google Scholar] [CrossRef]
- Rhoads, B.L.; Kenworthy, S.T. Time-averaged flow structure in the central region of a stream confluence. Earth Surf. Process. Landf. 1998, 23, 171–191. [Google Scholar] [CrossRef]
- Mosley, M.P. An experimental study of channel confluences. J. Geol. 1976, 84, 535–562. [Google Scholar] [CrossRef]
- Riley, J.D.; Rhoads, B.L.; Parsons, D.R.; Johnson, K.K. Influence of junction angle on three-dimensional flow structure and bed morphology at confluent meander bends during di erent hydrological conditions. Earth Surf. Process. Landf. 2015, 40, 252–271. [Google Scholar] [CrossRef]
- Parsons, D.R.; Best, J.L.; Lane, S.N.; Kostaschuk, R.A.; Hardy, R.J.; Orfeo, O.; Amsler, M.L.; Szupiany, R.N. Large River Channel Confluences. In River Confluences, Tributaries and the Fluvial Network; JohnWiley & Sons: Chichester, UK, 2008. [Google Scholar]
- Constantinescu, G.; Miyawaki, S.; Rhoads, B.; Sukhodolov, A. Numerical analysis of the effect of momentum ratio on the dynamics and sediment-entrainment capacity of coherent flow structures at a stream confluence. J. Geophys. Res. Earth Surf. 2012, 117, 1–12. [Google Scholar] [CrossRef]
- Constantinescu, G.; Miyawaki, S.; Rhoads, B.; Sukhodolov, A.; Kirkil, G. Structure of turbulent flow at a river confluence with momentum and velocity ratios close to 1: Insight provided by an eddy-resolving numerical simulation. Water Resour. Res. 2011, 47, W05507. [Google Scholar] [CrossRef]
- De Serres, B.; Roy, A.G.; Biron, P.M.; Best, J.L. Three-dimensional structure of flow at a confluence of river channels with discordant beds. Geomorphology 1999, 26, 313–335. [Google Scholar] [CrossRef]
- Yan, X.; Rennie, C.D.; Mohammadian, A. A three-dimensional numerical study of flow characteristics in strongly curved channel bends with different side slopes. Environ. Fluid Mech. 2020, 20, 1491–1510. [Google Scholar] [CrossRef]
- Ferguson, R.; Hoey, T. Effects of Tributaries on Main-Channel Geomorphology; JohnWiley & Sons Ltd.: Chichester, UK, 2008. [Google Scholar]
- Biron, P.M.; Roy, A.G.; Best, J.L.; Boyer, C.J. Bed morphology and sedimentology at the confluence of unequal depth channels. Geomorphology 1993, 8, 115–129. [Google Scholar] [CrossRef]
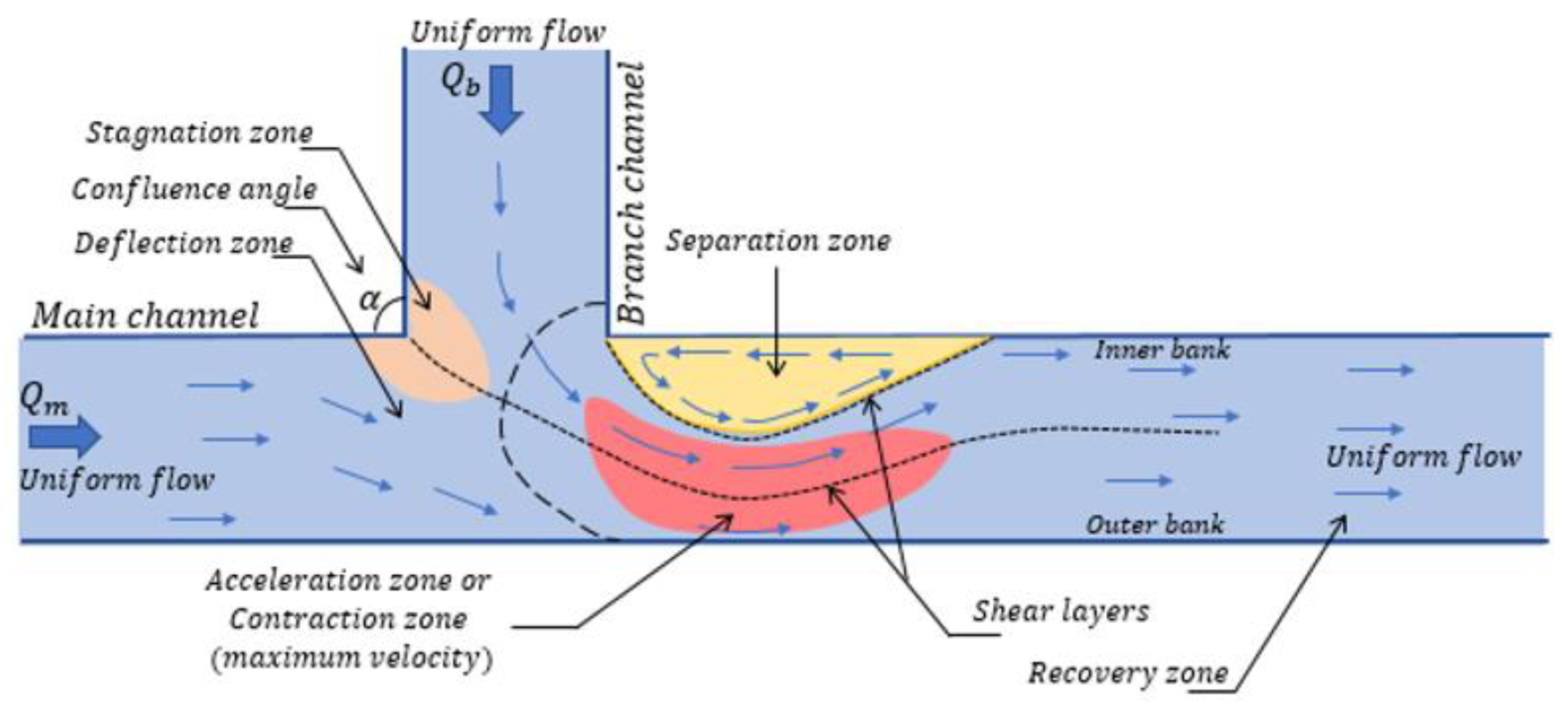
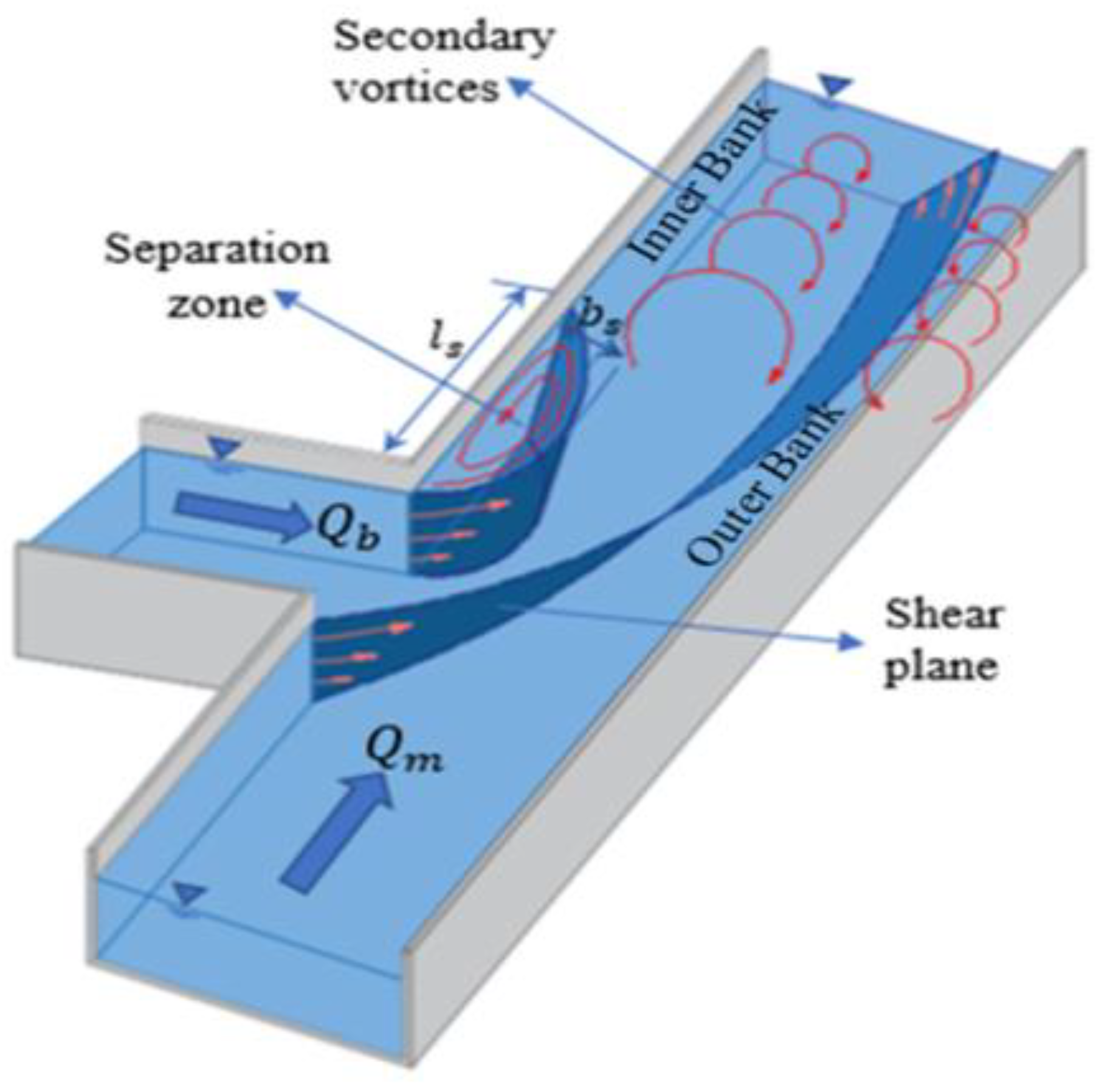

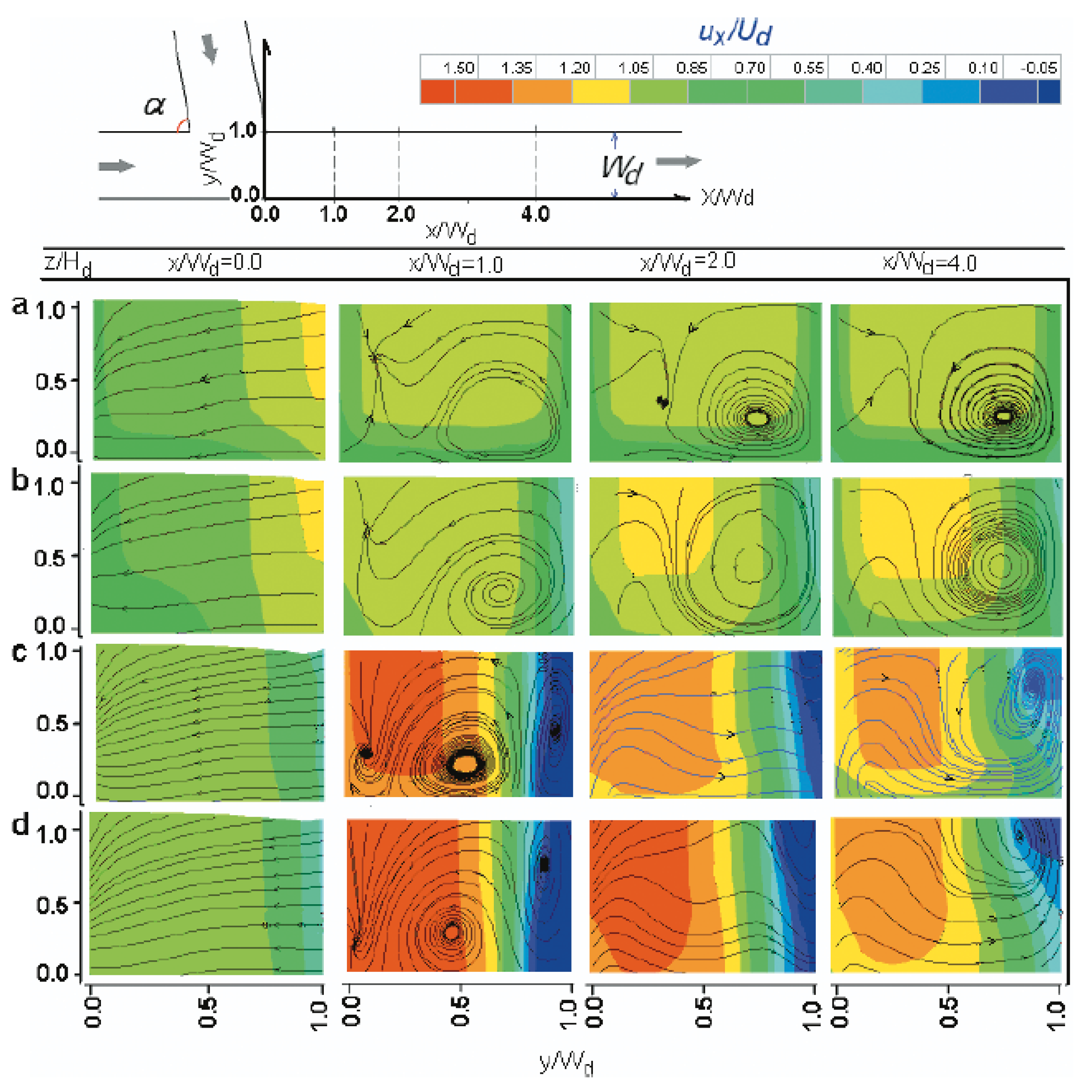
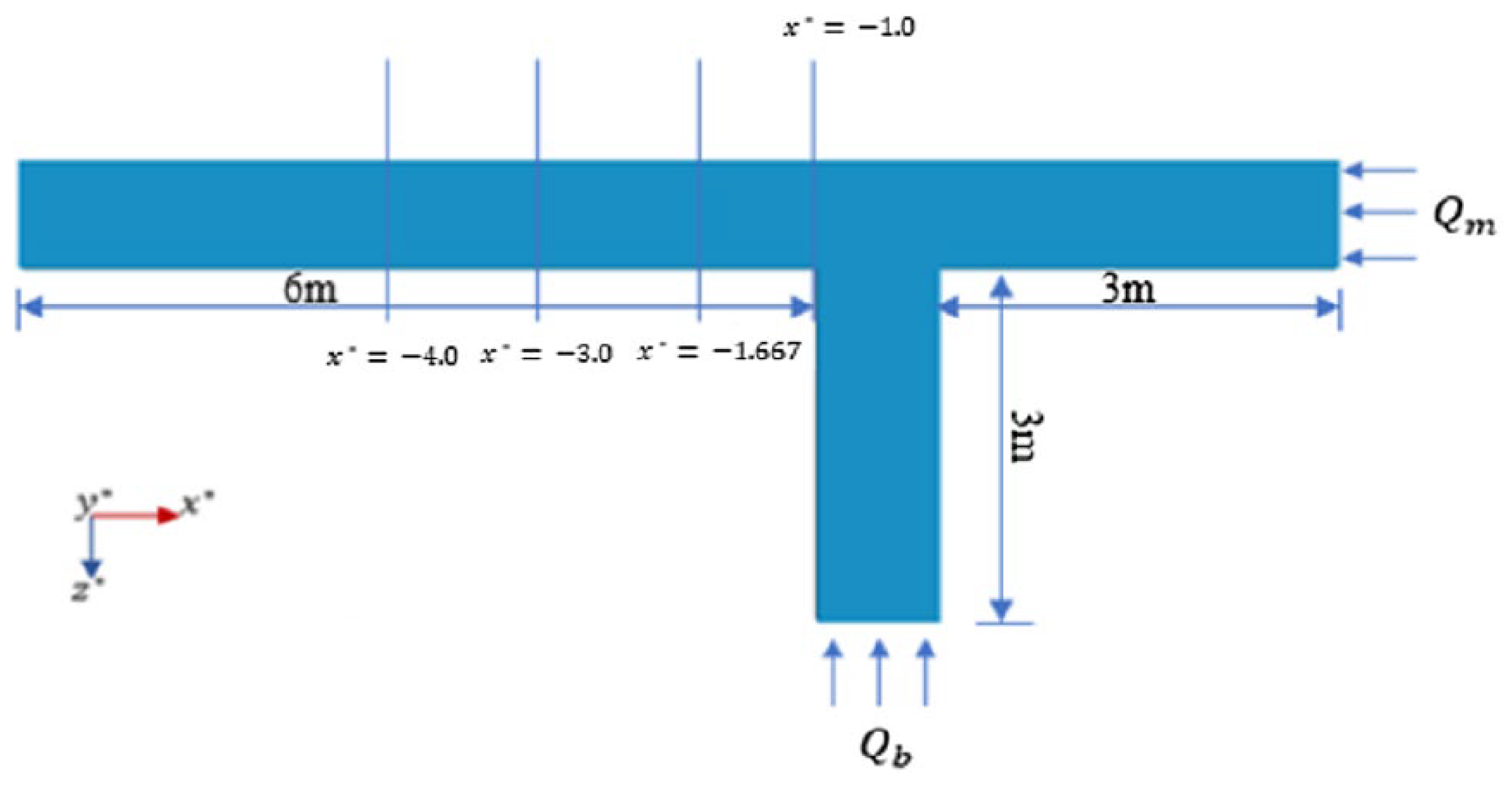
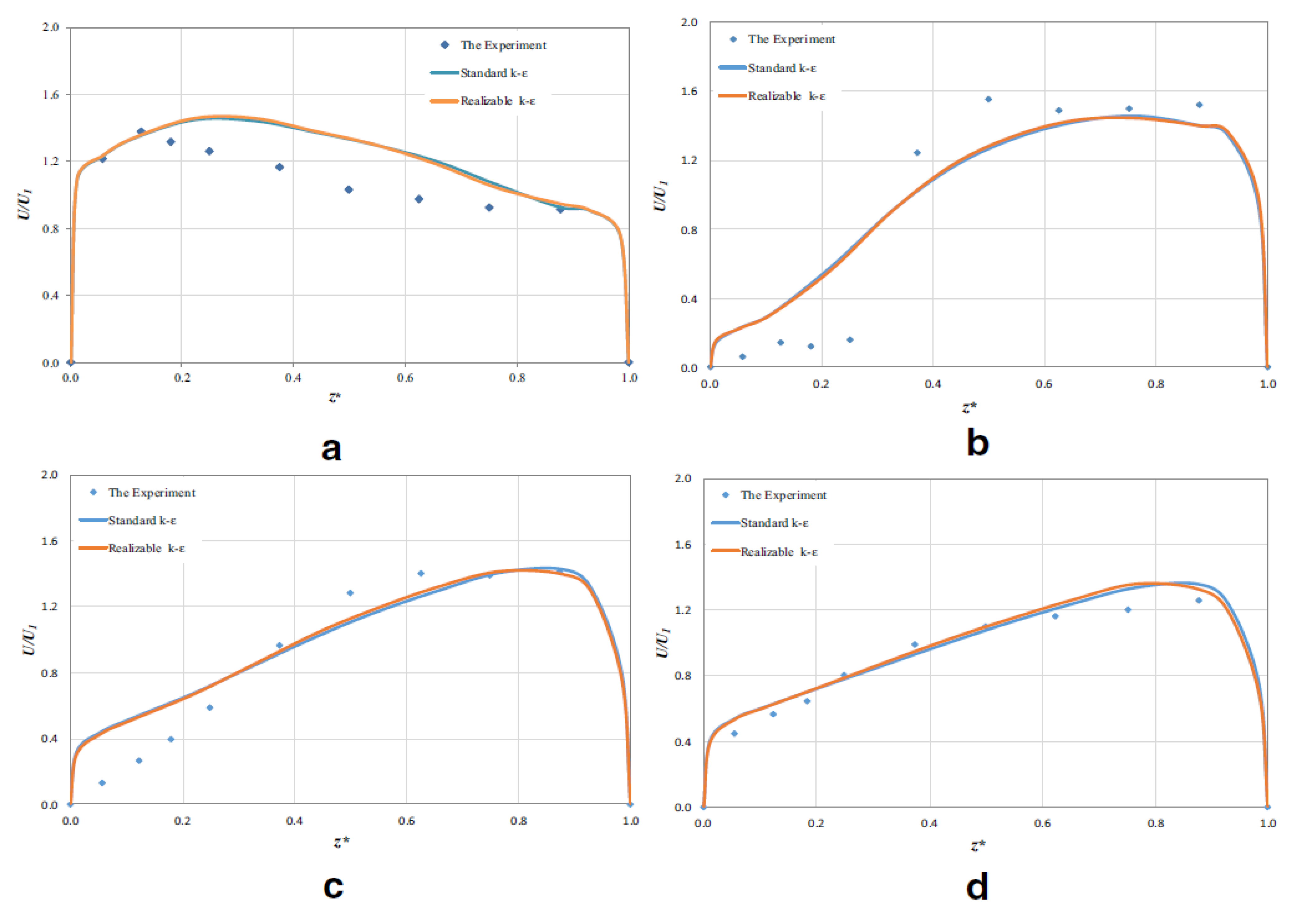
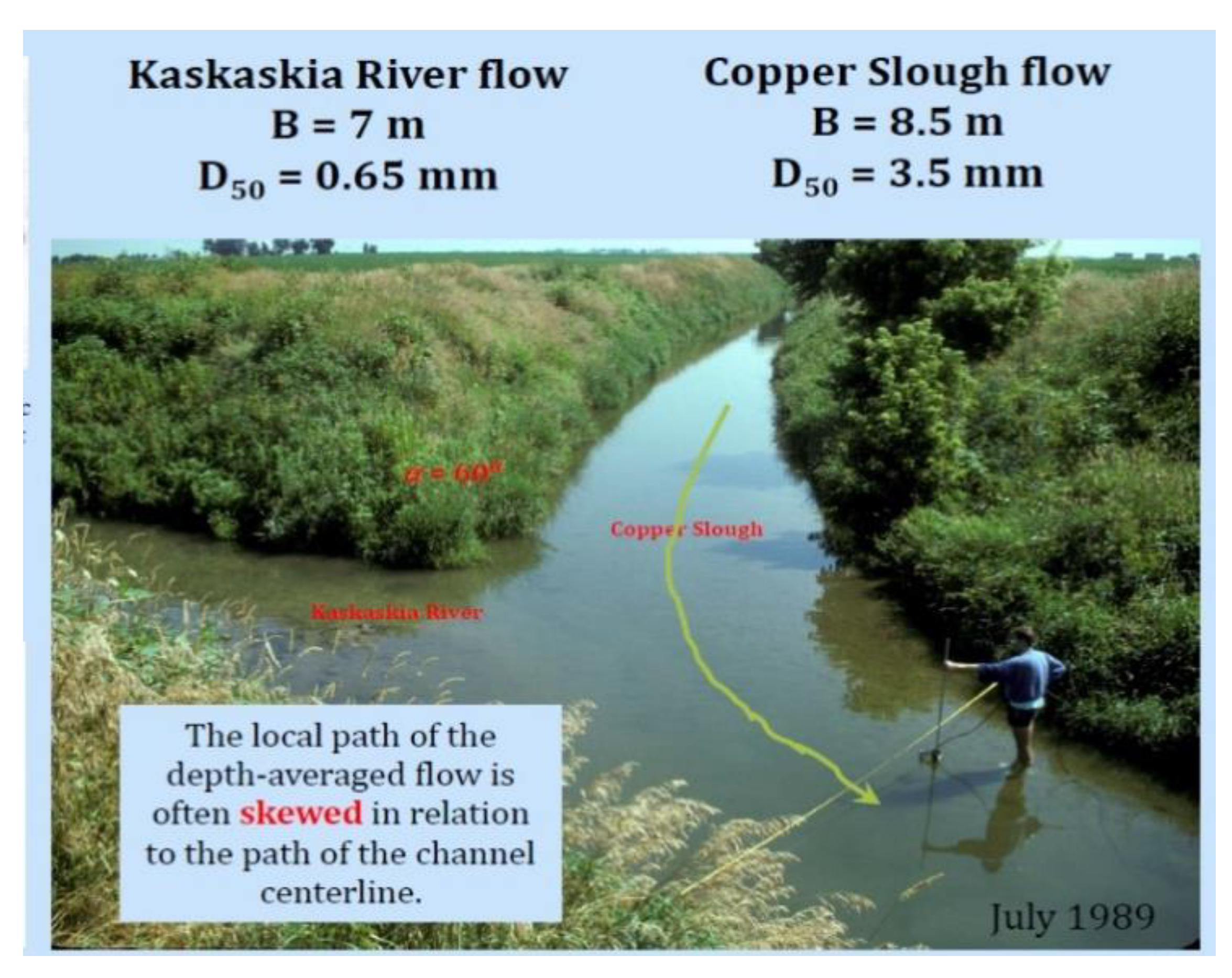
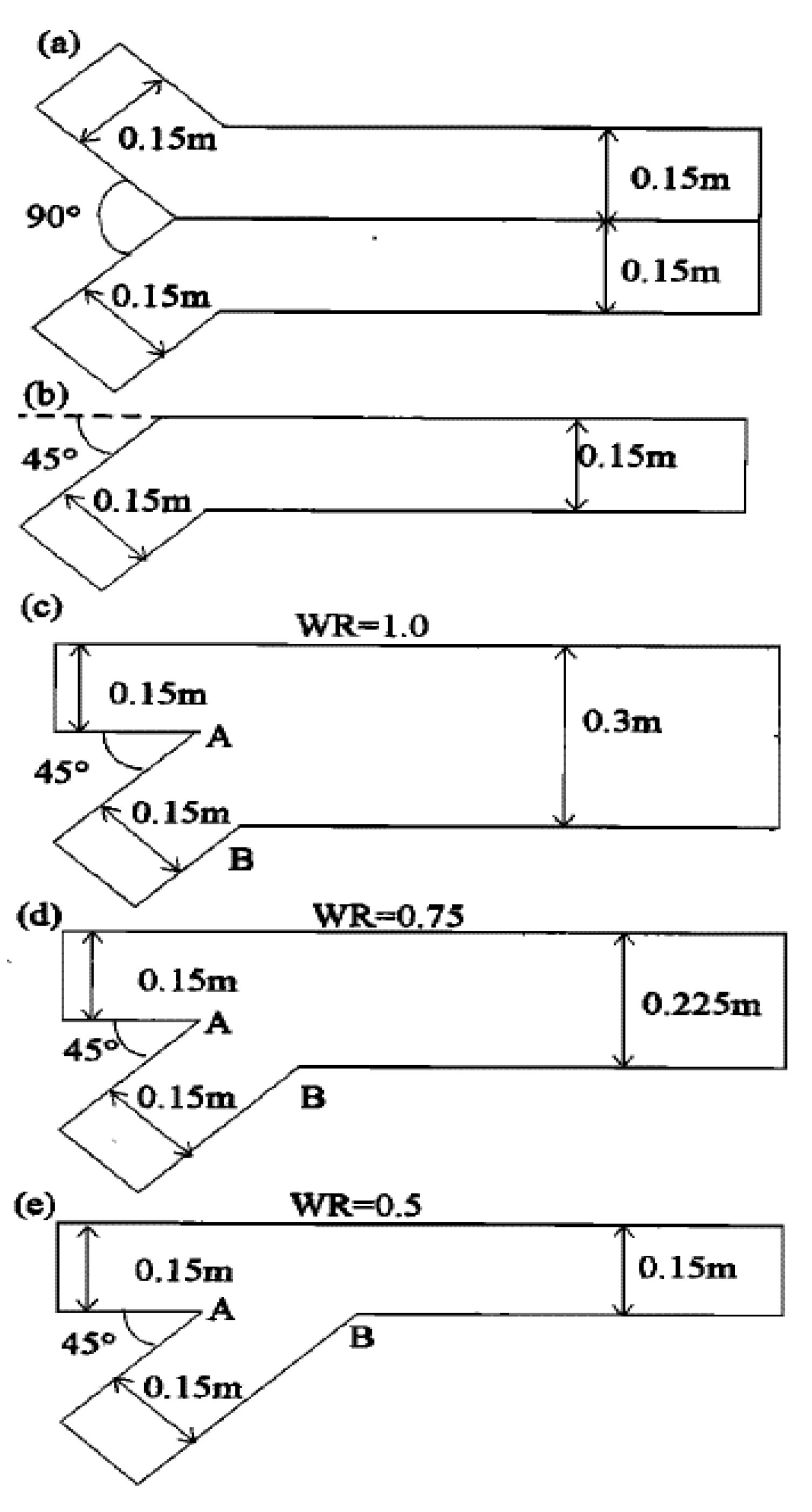
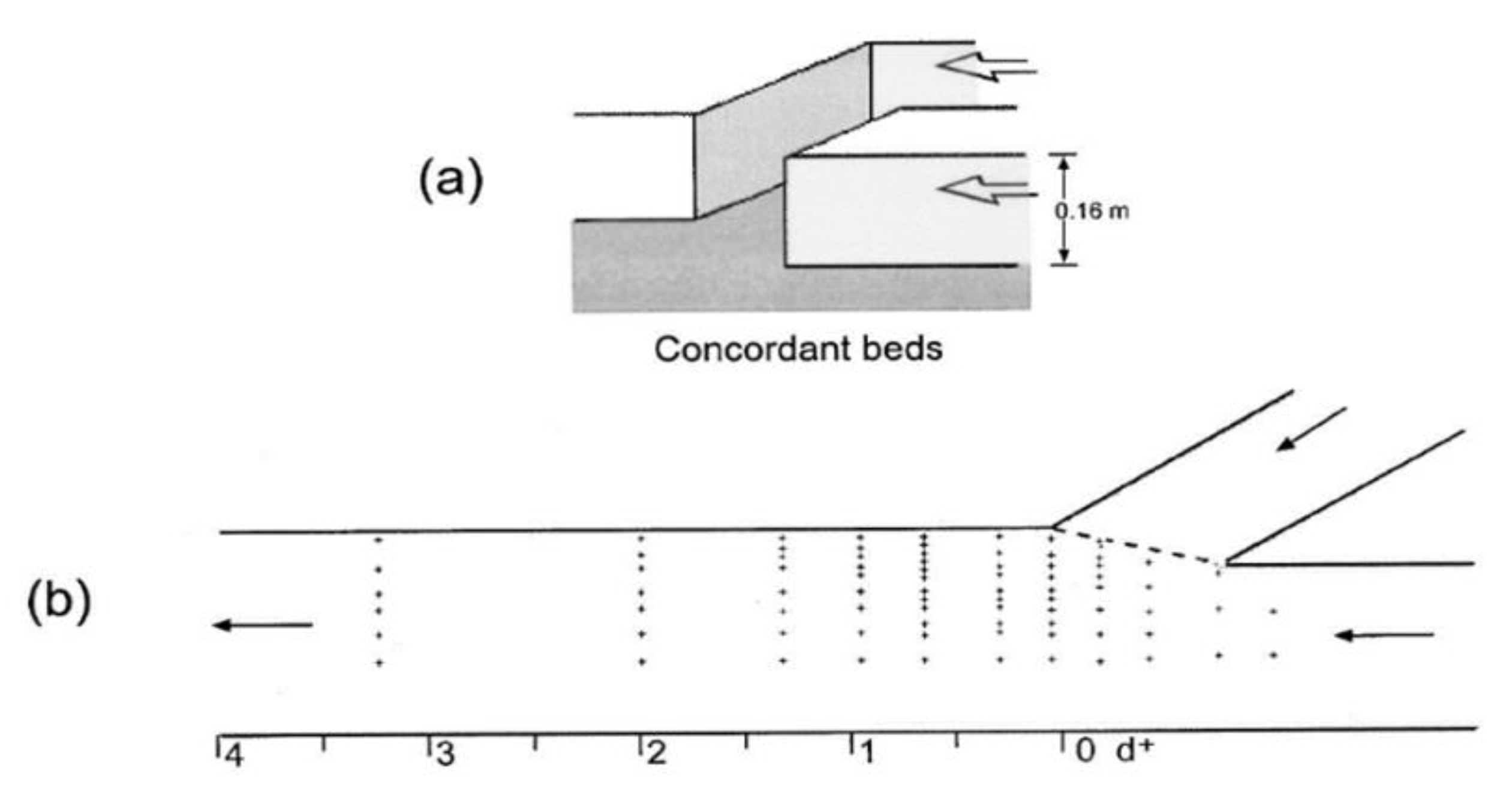
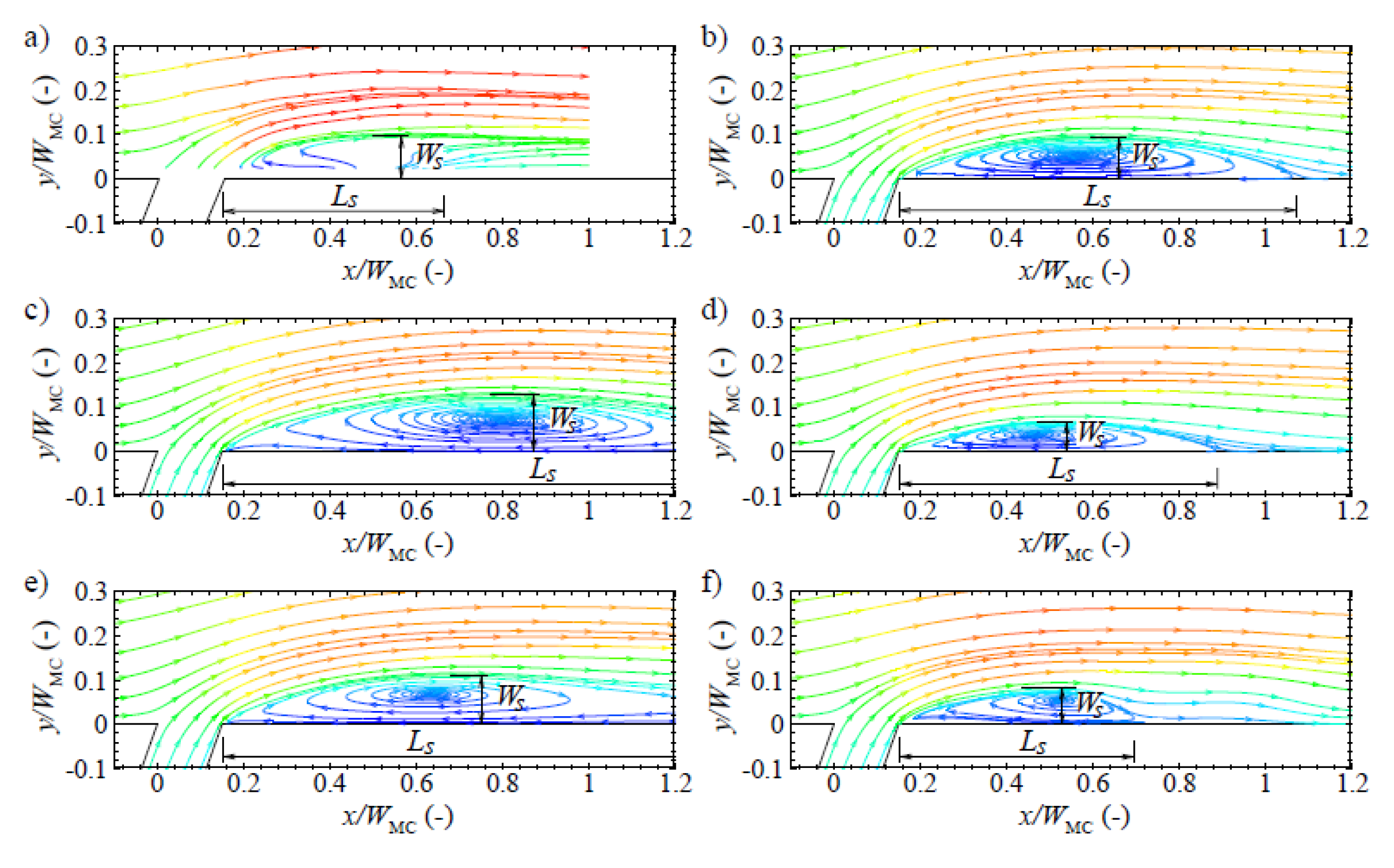


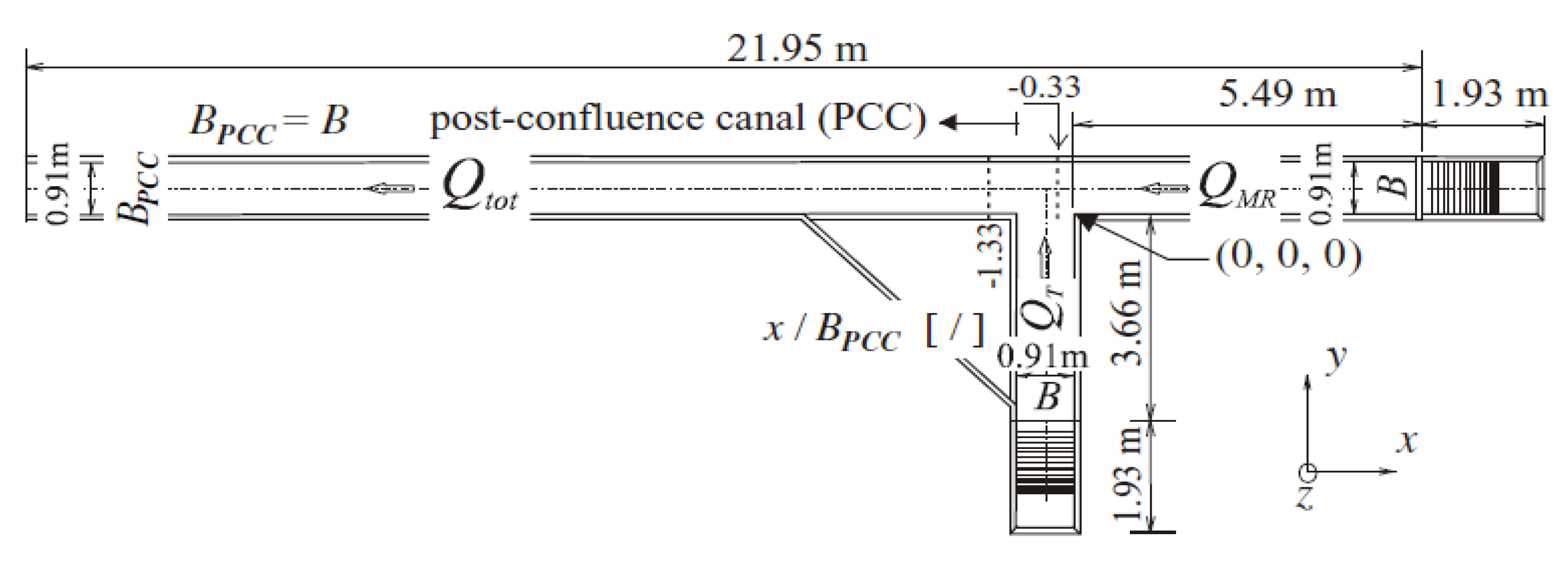
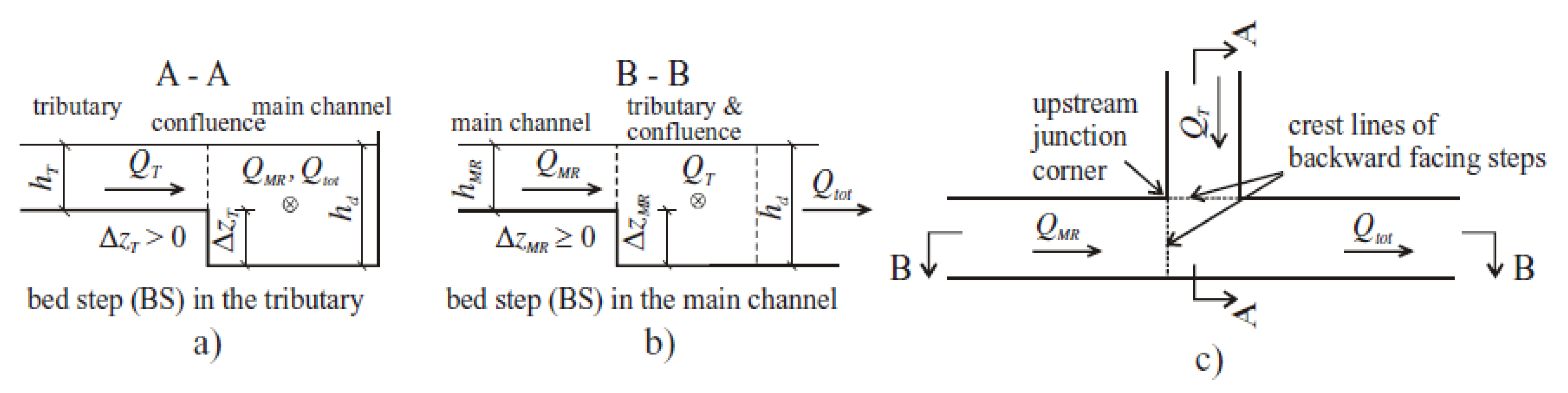

| Shape of Channel | Numerical Model | Key Findings | Reference |
|---|---|---|---|
Asymmetrical,  shaped shaped | k-ω model | The strength of the secondary flow was underpredicted | (Huang et al., 2002) [12] |
Asymmetrical,  shaped shaped | The CFD package, PHOENICS (version 3.5), the turbulence model was not specified in this paper | There was a good agreement at the upstream end of the junction, and the discrepancy increased at other downstream locations | (Sivakumar et al., 2004) [6] |
Asymmetrical,  shaped shaped | 3D k-ω model | The results of the numerical model agreed well with the experimental data | (Zhang et al., 2009 [25]) |
Asymmetrical,  shaped shaped | RNG form of k-ε model | The secondary flows appeared directly after the junction in approximately three counter-rotating helical cells | (Shakibaeinia et al., 2010) [3] |
Asymmetrical,  shaped shaped | A hybrid RANS-LES model was developed | The new modeling approach is more accurate than the RANS approach in addition to its ability of saving computational effort comparing to the LES approach | (Zeng and Li, 2010) [26] |
Asymmetrical,  shaped shaped | Standard k-ε, RNG k-ε, and RSM turbulence models | At the section immediately after the junction, the secondary flow predicted by the numerical models was smaller than that of the experiment | (Yang et al., 2011) [27] |
Asymmetrical,  shaped shaped | RNG form of k-ε model | The results showed good agreement between the simulation and the measured data | (Mignot et al., 2012) [28] |
Asymmetrical,  shaped shaped | Standard k-ε, realizable k-ε, and k-ω | The preferable model for the confluence flow simulation was k-ω | (Yang et al., 2013) [2] |
Asymmetrical,  shaped shaped | Reynolds Stress Modeling (RSM) | Flow pattern could be improved significantly by employing some geometrical adjustments | (Mohammadiun et al., 2015) [29] |
Asymmetrical,  shaped shaped | Standard k–ε model and the realizable k–ε model | The realizable k–ε model is better | (Shaheed et al., 2018) [17] |
Asymmetrical,  shaped shaped | Reynolds averaged Navier–Stokes equations and Reynolds stress turbulence model (RANS and RSM) | The contaminants mixing basically happens in the mixing layer at the interface of two confluent flows | (Tang et al., 2018) [30] |
Asymmetrical,  shaped shaped | A modified 1D nonlinear dynamic model and fully 3D non-hydrostatic, Reynolds-averaged Navier–Stokes equations (RANS) model | The strategies of 1D and 3D modeling could be applied to other flow diversion problems like river meander | (Luo et al., 2018) [31] |
| Flow Conditions in the Experiment | ||||||
| Runs | /s) | /s) | /s) | /s) | /s) | ) |
| 1 | 0.127 | 0.042 | 0.169 | 0.139 | 0.185 | 0.750 |
| Runs for Three Dimensional Simulation of Confluence Flow | ||||||
| Runs | Cases | Turbulence Model | Surface Treating | Meshes Adopted | Computing Time (hours) | |
| 1 | Standard k-ε | Dynamic meshes | 165,456 | 118 | ||
| 2 | Realizable k-ε | Dynamic meshes | 165,456 | 124 | ||
| 3 | k-ω | Dynamic meshes | 165,456 | 130 | ||
| 4 | k-ω | Rigid lid | 165,456 | 50 | ||
| 5 | k-ω | VOF | 232,200 | 245 | ||
| Shape of Channel | Numerical Model | Key Findings | Reference |
|---|---|---|---|
Asymmetrical,  shaped shaped | LES | A reasonable agreement with experimental data and analytical solutions was achieved. | (Liu et al., 2009) [36] |
Asymmetrical,  shaped shaped | LES | New features of the flow patterns were induced due to the flow of the tributary. | (Schindfessel et al., 2015) [37] |
Asymmetrical,  shaped shaped | LES | There was a significant difference in the separation zone dimensions for non-rectangular shapes. | (Schindfessel et al., 2017) [38] |
Asymmetrical,  shaped shaped | LES | Oversimplification of free surface numerical processing leads to lower accuracy of secondary flow and turbulent kinetic energy predictions. | (Ramos et al., 2019) [39] |
| Shape of Channel | Numerical Model | Key Findings | Reference |
|---|---|---|---|
| Asymmetrical, 60° angle | Standard k–ε turbulence model | The comparison between the numerical and experimental results was good | (Weerakoon and Tamai, 1989) [21] |
| Asymmetrical, 60° angle | Standard k–ε turbulence model | Experimental comparison good, but size of lateral separation zone underpredicted | (Weerakoon et al., 1991) [43] |
| Different styles of channels | Turbulence model based on a renormalized group (RNG) | As asymmetry increases, the structure of back-to-back helical cells thought to be less representative of the flow field | (Bradbrook et al., 2000a) [8] |
| Asymmetrical, 60° angle | Turbulence model based on a renormalized group (RNG) | As asymmetry increases, the structure of back-to-back helical cells thought to be less representative of the flow field | (Bradbrook et al., 2000a) [8] |
| Asymmetrical, 30° angle | RNG k-ε model | The mixing was faster at higher junction angles, especially for concordant beds | (Biron et al., 2004) [13] |
| Asymmetrical, 70° angle | k-ε, RNG k-ε, k-ω, SST k-ω, EARSM | The numerical results indicated the importance of simulating the secondary flows due to their great impact on the separation zone and velocity contour lines | (Brito et al., 2014) [44] |
| Ten different confluences from 45° to 90° | k-ε turbulence closure model | The increase in the confluence angle caused a wider and longer retardation zone at the corner of upstream junction and the separation zone | (Penna et al., 2018) [45] |
| Shape of Channel | Numerical Model | Key Findings | Reference |
|---|---|---|---|
| Asymmetrical, 30° angle | RNG k-ε model | The efficiency of secondary flows in the bend was less for mixing at the low flow than for the high flow. | (Biron et al., 2004) [13] |
| Asymmetrical, 60° angle | RNG k-ε model | The efficiency of secondary flows in the bend was less for mixing at the low flow than for the high flow. | (Biron et al., 2004) [13] |
Symmetrical,  shaped shaped | Linear Renormalization Group (RNG) 𝑘-ε turbulence model | The results appeared to be an accurate prediction by the numerical model. | (Wang and Yan, 2007) [56] |
Asymmetrical,  shaped shaped | Standard k–ε turbulence model | The perpendicular velocities were enhanced by the tributary bed steps along the side wall of the intersection and by the main channel bed steps along the opposite wall. | (Dordevica and Stojnic, 2016) [57] |
| Shape of Channel | Numerical Model | Key Findings | Reference |
|---|---|---|---|
| Asymmetrical, parallel channels | LES | The numerical simulation agreed well with the laboratory experiments. | (Bradbrook et al., 2000b) [9] |
| Asymmetrical, 65° angle | LES | The mixing data and the detailed flow provided by the model were helpful in understanding the production and evolution of large-scale turbulence features in confluence channels. | (Bradbrook et al., 2000b) [9] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shaheed, R.; Yan, X.; Mohammadian, A. Review and Comparison of Numerical Simulations of Secondary Flow in River Confluences. Water 2021, 13, 1917. https://doi.org/10.3390/w13141917
Shaheed R, Yan X, Mohammadian A. Review and Comparison of Numerical Simulations of Secondary Flow in River Confluences. Water. 2021; 13(14):1917. https://doi.org/10.3390/w13141917
Chicago/Turabian StyleShaheed, Rawaa, Xiaohui Yan, and Abdolmajid Mohammadian. 2021. "Review and Comparison of Numerical Simulations of Secondary Flow in River Confluences" Water 13, no. 14: 1917. https://doi.org/10.3390/w13141917
APA StyleShaheed, R., Yan, X., & Mohammadian, A. (2021). Review and Comparison of Numerical Simulations of Secondary Flow in River Confluences. Water, 13(14), 1917. https://doi.org/10.3390/w13141917









