The Decision of an Eco-Friendly Reservoir Operation Scheme Based on a Variable Set
Abstract
1. Introduction
2. Materials and Methods
2.1. Eco-Friendly Reservoir Operation Schemes
2.2. Evaluation Index System of Eco-Friendly Reservoir Operation Schemes
2.3. Optimal Decision-Making Principle Based on Variable Sets
2.3.1. The Fundamental of VS Theory—The Unity of Opposites
2.3.2. The Optimal Decision Principle Base on VS
3. Case Study
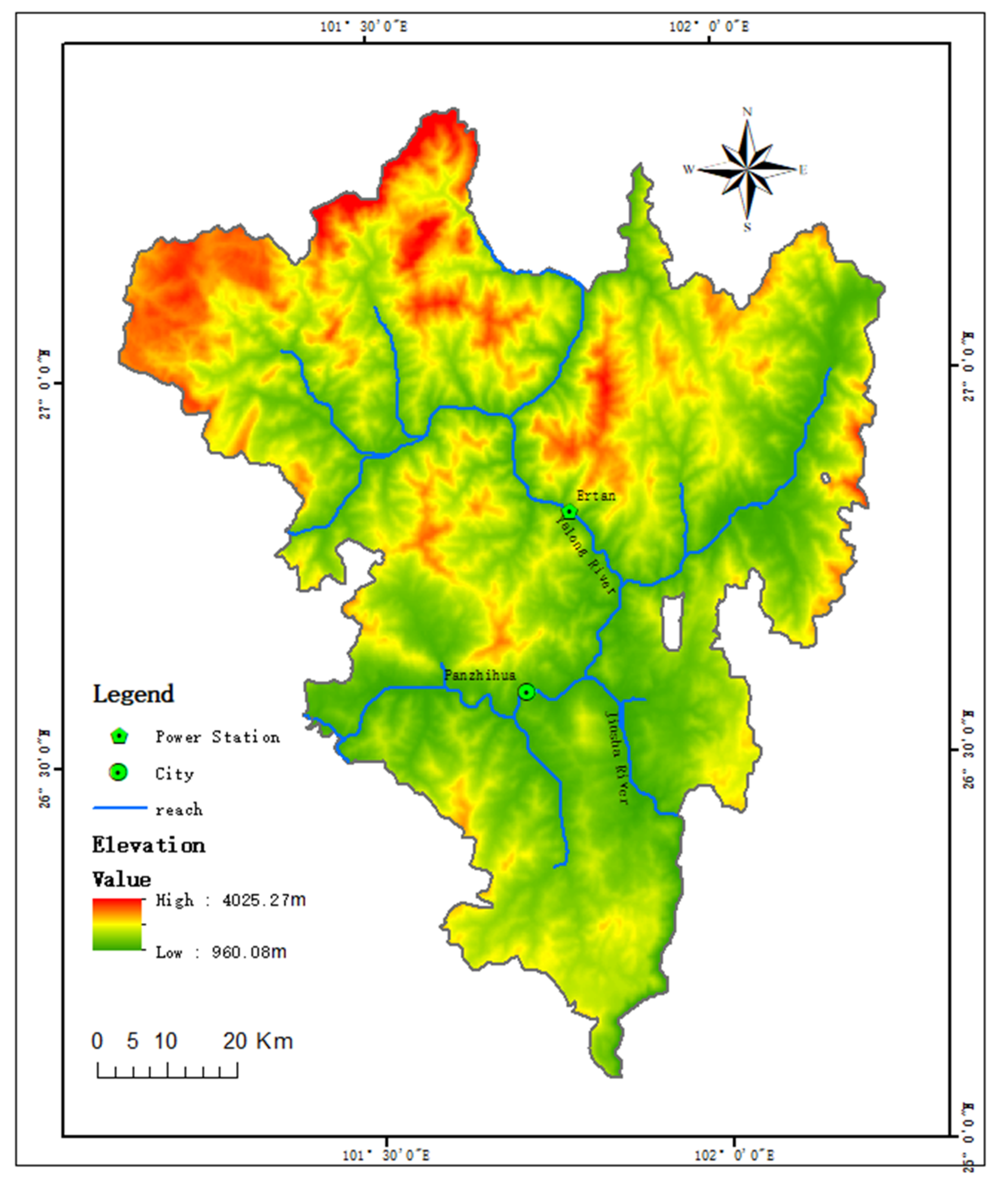
3.1. Study Area
3.2. Eco-Friendly Reservoir Operation
3.3. Optimization of Scheduling Schemes Based on Variable Fuzzy Sets
4. Discussions
4.1. Comparison and Analysis of the Results of Evaluation Methods with Fuzzy Sets
4.2. Comparison and Analysis of Composite Fuzzy Matter Element Methods
4.3. Stability Analysis of the Optimal Decision Model
4.4. Scope of Application
4.5. Engineering Application Prospects
5. Conclusions
- (1)
- The comparison with the evaluation results of the two evaluation methods shows that the method proposed in this paper is feasible, and has the characteristics of simple calculation and stable evaluation results. This method provides a new idea for the study of the decision of an eco-friendly reservoir operation scheme.
- (2)
- The method proposed in this paper is suitable for the decision-making study of eco-friendly reservoir scheduling under the condition that the basin area is relatively large and the water flow in the river is continuous all year. For smaller watersheds, the research methods proposed in this article need to be improved.
- (3)
- The research can provide new ideas for the decision-making research of engineering.
- (4)
- Ertan Hydropower Station should use the maximum and minimum values in the natural flow sequence at each period as the discharge constraints of the reservoir. Maintaining the natural characteristics of runoff as much as possible in controlling discharge can effectively take into account the needs of both power generation and the river’s ecological health.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Magilligan, F.J.; Nislow, K.H. Changes in hydrologic regime by dams. Geomorphology 2005, 71, 61–78. [Google Scholar] [CrossRef]
- Xu, Z.; Yin, X.; Sun, T.; Cai, Y.; Ding, Y.; Yang, W.; Yang, Z. Labyrinths in large reservoirs: An invisible barrier to fish migration and the solution through reservoir operation. Water Resour. Res. 2017, 53, 817–831. [Google Scholar] [CrossRef]
- Ma, D.; Luo, W.; Yang, G.; Lu, J.; Fan, Y. A study on a river health assessment method based on ecological flow. Ecol. Model. 2019, 401, 144–154. [Google Scholar] [CrossRef]
- Karimi, S.; Salarijazi, M.; Ghorbani, K.; Heydari, M. Comparative assessment of environmental flow using hydrological methods of low flow indexes, Smakhtin, Tennant and flow duration curve. Acta Geophys. 2021, 69, 285–293. [Google Scholar] [CrossRef]
- Poff, N.L. Beyond the natural flow regime? Broadening the hydro-ecological foundation to meet environmental flows challenges in a non-stationary world. Freshw. Biol. 2017, 63, 1011–1021. [Google Scholar] [CrossRef]
- Poff, N.L.; Allan, J.D.; Bain, M.B.; Karr, J.R.; Prestegaard, K.L.; Richter, B.D.; Sparks, R.E.; Stromberg, J.C. The Natural Flow Regime a paradigm for river conservation and restoration. Bioscience 1997, 47, 769–784. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, J.; Ou, Y.; Zhang, Y. TGC eco-friendly feneration multi-objective optimal dispatch modeland its solution algorithm. J. Hydraul. Eng. 2013, 44, 154–163. [Google Scholar] [CrossRef]
- Kuriqi, A.; Pinheiro, A.N.; Sordo-Ward, A.; Bejarano, M.D.; Garrote, L. Ecological impacts of run-of-river hydropower plants—Current status and future prospects on the brink of energy transition. Renew. Sustain. Energy Rev. 2021, 142, 110833. [Google Scholar] [CrossRef]
- Zhou, T.; Dong, Z.; Wang, W.; Shi, R.; Gao, X.; Huang, Z. Study on Multi-Scale Coupled Ecological Dispatching Model Based on the Decomposition-Coordination Principle. Water 2019, 11, 1443. [Google Scholar] [CrossRef]
- Shen, Q.; Mo, L.; Liu, G. Multi-objective Ecological Dispatching of Reservoir Based on MOCEA/D Algorithm. J. Coast. Res. 2019, 93, 460–465. [Google Scholar] [CrossRef]
- Ihunwo, O.C.; Ibezim-Ezeani, M.U. Distribution, Source Appropriation, and Human Health Risk Assessment of Polycyclic Aromatic Hydrocarbons due to Consumption of Callinectes amnicola from Woji Creek in Sambreiro River. Turk. J. Fish. Aquat. Sci. 2021, 21, 245–253. [Google Scholar] [CrossRef]
- Alric, B.; Dézerald, O.; Meyer, A.; Billoir, E.; Coulaud, R.; Larras, F.; Mondy, C.P.; Usseglio-Polatera, P. How diatom-, invertebrate- and fish-based diagnostic tools can support the ecological assessment of rivers in a multi-pressure context: Temporal trends over the past two decades in France. Sci. Total Environ. 2021, 762, 143915. [Google Scholar] [CrossRef]
- Shouyu, C.; Yu, G. Variable Fuzzy Sets and its Application in Comprehensive Risk Evaluation for Flood-control Engineering System. Fuzzy Optim. Decis. Mak. 2006, 5, 153–162. [Google Scholar] [CrossRef]
- Wang, X.J.; Zhao, R.H.; Hao, Y.W. Flood Control Operations Based on the Theory of Variable Fuzzy Sets. Water Resour. Manag. 2011, 25, 777–792. [Google Scholar] [CrossRef]
- Li, Q.; Zhou, J.; Liu, D.; Jiang, X. Research on flood risk analysis and evaluation method based on variable fuzzy sets and information diffusion. Saf. Sci. 2012, 50, 1275–1283. [Google Scholar] [CrossRef]
- Zou, Q.; Zhou, J.; Zhou, C.; Song, L.; Guo, J. Comprehensive flood risk assessment based on set pair analysis-variable fuzzy sets model and fuzzy AHP. Stoch. Environ. Res. Risk Assess. 2012, 27, 525–546. [Google Scholar] [CrossRef]
- Li, Q. Fuzzy approach to analysis of flood risk based on variable fuzzy sets and improved information diffusion methods. Nat. Hazards Earth Syst. Sci. 2013, 13, 239–249. [Google Scholar] [CrossRef]
- Wang, W.-C.; Xu, D.-M.; Chau, K.-W.; Lei, G.-J. Assessment of River Water Quality Based on Theory of Variable Fuzzy Sets and Fuzzy Binary Comparison Method. Water Resour. Manag. 2014, 28, 4183–4200. [Google Scholar] [CrossRef]
- He, G.; Chai, J.; Qin, Y.; Xu, Z.; Li, S. Coupled Model of Variable Fuzzy Sets and the Analytic Hierarchy Process and its Application to the Social and Environmental Impact Evaluation of Dam Breaks. Water Resour. Manag. 2020, 34, 2677–2697. [Google Scholar] [CrossRef]
- Kumar, K.; Garg, H. TOPSIS method based on the connection number of set pair analysis under interval-valued intuitionistic fuzzy set environment. Comput. Appl. Math. 2016, 37, 1319–1329. [Google Scholar] [CrossRef]
- Su, L.; Li, H.; Li, Z.; Cao, Y. Identification of unbalanced bids based on grey-fuzzy evaluation method. Can. J. Civ. Eng. 2020, 47, 272–278. [Google Scholar] [CrossRef]
- Herzog, S.; Tetzlaff, C.; Wörgötter, F. Evolving artificial neural networks with feedback. Neural Netw. 2020, 123, 153–162. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Xue, Z.; Li, M. Variable Sets principle and method for flood classification. Sci. China Ser. E Technol. Sci. 2013, 56, 2343–2348. [Google Scholar] [CrossRef]
- Ke, L.; Wang, Q.; Sun, X.; Sun, C.; Zhou, H.; Wang, F. The seawater environment quality evaluation research base on variable fuzzy pattern recognition model. Acta Ecol. Sin. 2013, 33, 1889–1899. [Google Scholar] [CrossRef]
- Peng, Y.; Chu, J.; Xue, Z. Basin flood control system risk evaluation based on variable sets. Sci. China Ser. E Technol. Sci. 2017, 60, 153–165. [Google Scholar] [CrossRef]
- Wan, X.-Y.; Zhong, P.-A.; Appiah-Adjei, E.K. Variable Sets and Fuzzy Rating Interval for Water Allocation Options Assessment. Water Resour. Manag. 2014, 28, 2833–2849. [Google Scholar] [CrossRef]
- Dong, Z.; Zhang, J.; Zhao, J. Comments upon progress of environmental flows assessments. J. Hydraul. Eng. 2017, 48, 670–677. [Google Scholar] [CrossRef]
- Vogel, R.M.; Sieber, J.; Archfield, S.A.; Smith, M.P.; Apse, C.D.; Huber-Lee, A. Relations among storage, yield, and instream flow. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Braun-Cruz, C.C.; Tritico, H.M.; Beregula, R.L.; Girard, P.; Zeilhofer, P.; Ribeiro, L.D.S.; Fantin-Cruz, I. Evaluation of Hydrological Alterations at the Sub-Daily Scale Caused by a Small Hydroelectric Facility. Water 2021, 13, 206. [Google Scholar] [CrossRef]
- Mei, Y.; Zhai, L.; Yang, N. Evaluation of control alternatives of release discharge for eco-friendly reservoir operation. Eng. J. Wuhan Univ. 2008, 41, 10–13. [Google Scholar]
- Richter, B.; Baumgartner, J.V.; Wigington, R.; Braun, D.P. How much water does a river need? Freshw. Biol. 1997, 37, 231–249. [Google Scholar] [CrossRef]
- Chen, S. Variable sets and the theorem and method of optimal decision- making for water resource system. J. Hydraul. Eng. 2012, 43, 1066–1074. [Google Scholar] [CrossRef]
- Chen, S.; Xue, Z.; Li, M.; Zhu, X. Variable sets method for urban flood vulnerability assessment. Sci. China Ser. E Technol. Sci. 2013, 56, 3129–3136. [Google Scholar] [CrossRef]
- Chen, S. Variable sets assessment theory and method of water resource system. J. Hydraul. Eng. 2013, 44, 134–142. [Google Scholar] [CrossRef]
- Wang, J.; Huang, W.; Ma, G.; Liu, G.; Guo, L. Evaluation of control alternatives of discharge for eco-friendly reservoir operation based on fuzzy set pair analysis and entropy weight fuzzy iteration method. J. Sichuan Univ. Eng. Sci. Ed. 2015, 47, 1–8. [Google Scholar] [CrossRef]
| Ecological Flow Patterns | Control Alternatives of Discharge |
|---|---|
| Do not consider ecological water requirements | M1: Reservoir discharge constraint: Qt ≥ 0 |
| Meet the minimum ecological water requirements: Qt ≥ Qst | M2: The driest monthly flow estimation method was adopted; Qst takes the annual average of the driest monthly flow |
| M3: Using the quarterly ecological flow estimation method, referring to the Tennant method, Qst takes 40% of the annual average flow in the non-flood season (November to May) and Qst takes 60% of the annual average flow in the flood season (June to October) | |
| M4: Monthly frequency calculation, Qst takes the flow rate at the 95% guaranteed rate for each month | |
| M5: Monthly frequency calculation, Qst takes the flow rate at the 90% guaranteed rate for each month | |
| Try to maintain the natural hydrological characteristics of runoff | M6: Reservoir discharge constraint: Qtrmin ≤ Qt ≤ Qtrmax. |
| Schemes | Multi-Year Average Power Generation (108 kW·h) | The Average Amount of Water Discarded over the Years (108 m3) | Power Generation Guarantee Rate (%) |
|---|---|---|---|
| M1 | 164.6769 | 59.5775 | 92 |
| M2 | 164.6769 | 59.5775 | 92 |
| M3 | 164.6374 | 59.5852 | 92 |
| M4 | 164.4720 | 59.5253 | 92 |
| M5 | 163.3475 | 59.9587 | 92 |
| M6 | 164.3399 | 59.2941 | 92 |
| Schemes | Evaluation Index | |||||
|---|---|---|---|---|---|---|
| M1 | 822.04 | 1096.70 | 722.39 | 0.2747 | 0.0161 | 0.8872 |
| M2 | 822.04 | 1096.70 | 722.39 | 0.2747 | 0.0161 | 0.8872 |
| M3 | 822.98 | 1096.70 | 738.76 | 0.2750 | 0.0125 | 0.8904 |
| M4 | 821.30 | 1098.29 | 786.94 | 0.2740 | 0.0156 | 0.8831 |
| M5 | 772.81 | 1097.89 | 1005.42 | 0.2553 | 0.0093 | 0.8305 |
| M6 | 793.76 | 426.66 | 725.62 | 0.2369 | 0.0164 | 0.8956 |
| Comprehensive Relative Membership | Grade | Grade Characteristic Values | Ranking | ||
|---|---|---|---|---|---|
| 1 | 2 | 3 | |||
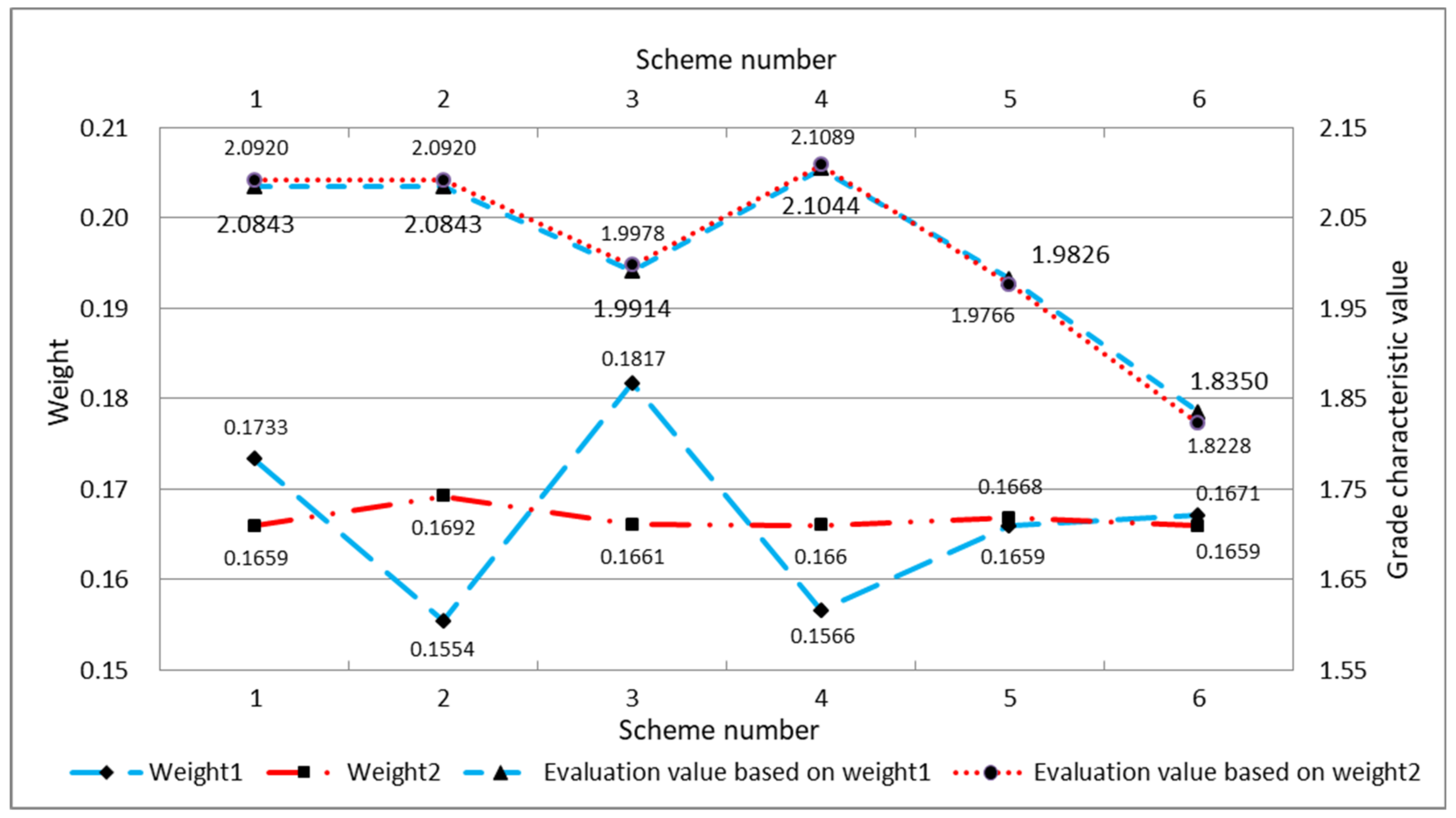
| 0.0355 | 0.8448 | 0.1197 | 2.0843 | 4 | |
| 0.0355 | 0.8448 | 0.1197 | 2.0843 | 4 | |
| 0.0798 | 0.8489 | 0.0713 | 1.9914 | 3 | |
| 0 | 0.8956 | 0.1044 | 2.1044 | 5 | |
| 0.1714 | 0.6746 | 0.1540 | 1.9826 | 2 | |
| 0.2325 | 0.7000 | 0.0675 | 1.8350 | 1 | |
| Fuzzy Set Pair Comprehensive Evaluation Method | Variable Sets Method | |||
|---|---|---|---|---|
| Contact Number | Ranking | Grade Characteristic Value | Ranking | |
| −0.1547 | 4 | 2.0843 | 4 | |
| −0.1547 | 4 | 2.0843 | 4 | |
| 0.0308 | 2 | 1.9914 | 3 | |
| −0.1950 | 5 | 2.1044 | 5 | |
| 0.0225 | 3 | 1.9826 | 2 | |
| 0.2006 | 1 | 1.8350 | 1 | |
| Schemes | Compound Fuzzy Matter Method | Variable Sets Method | ||
|---|---|---|---|---|
| Euclidean Closeness | Ranking | Grade Characteristic Values | Ranking | |
| 0.6880 | 5 | 2.0920 | 4 | |
| 0.6880 | 5 | 2.0920 | 4 | |
| 0.7194 | 3 | 1.9978 | 3 | |
| 0.6904 | 4 | 2.1089 | 5 | |
| 0.7220 | 2 | 1.9766 | 2 | |
| 0.8204 | 1 | 1.8228 | 1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.-T.; Li, A.-L.; Wang, W.-C.; Zhao, Z. The Decision of an Eco-Friendly Reservoir Operation Scheme Based on a Variable Set. Water 2021, 13, 1694. https://doi.org/10.3390/w13121694
Chen H-T, Li A-L, Wang W-C, Zhao Z. The Decision of an Eco-Friendly Reservoir Operation Scheme Based on a Variable Set. Water. 2021; 13(12):1694. https://doi.org/10.3390/w13121694
Chicago/Turabian StyleChen, Hai-Tao, A-Long Li, Wen-Chuan Wang, and Zhao Zhao. 2021. "The Decision of an Eco-Friendly Reservoir Operation Scheme Based on a Variable Set" Water 13, no. 12: 1694. https://doi.org/10.3390/w13121694
APA StyleChen, H.-T., Li, A.-L., Wang, W.-C., & Zhao, Z. (2021). The Decision of an Eco-Friendly Reservoir Operation Scheme Based on a Variable Set. Water, 13(12), 1694. https://doi.org/10.3390/w13121694






