Graph Convolutional Networks: Application to Database Completion of Wastewater Networks
Abstract
1. Introduction
2. Background and State of the Art
2.1. Machine Learning and Graphs
2.2. Graph Embedding
2.3. Graph Neural Networks
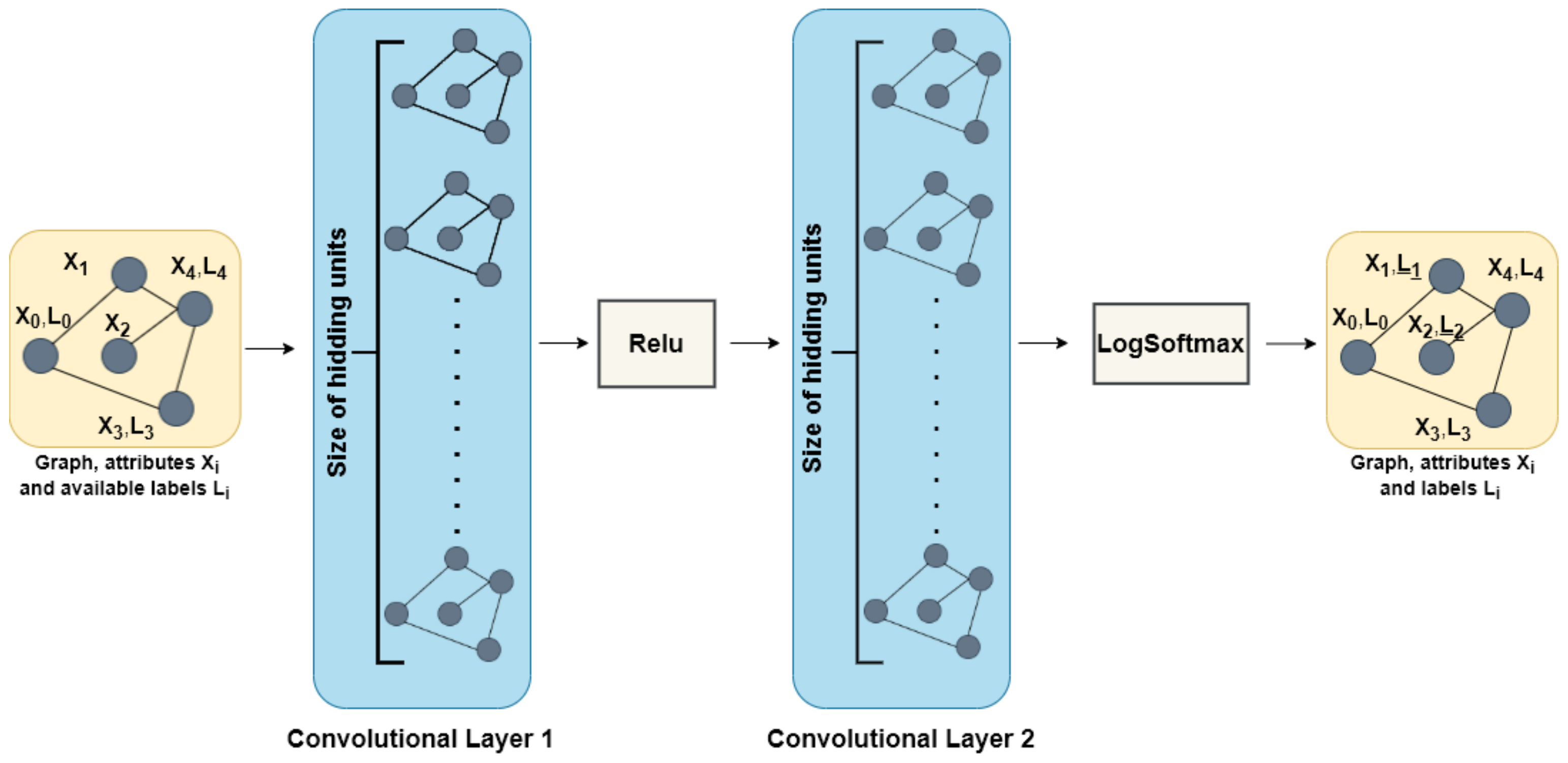
2.4. GCN for Semi-Supervised Learning
3. Materials and Methods
3.1. Models and Test Configurations
- Configuration 1: The network graph, a portion of the values of the targeted attribute, and domain knowledge are provided.
- Configuration 2: The network graph, a portion of the values of the targeted attribute, domain knowledge, and other fields of the attribute table are provided.
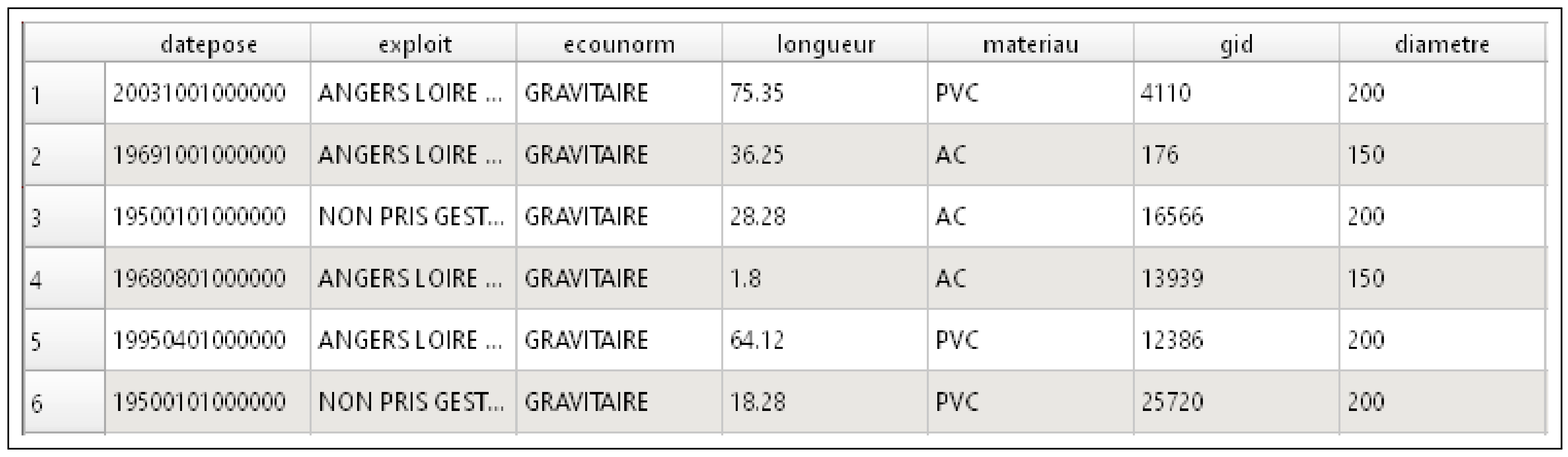
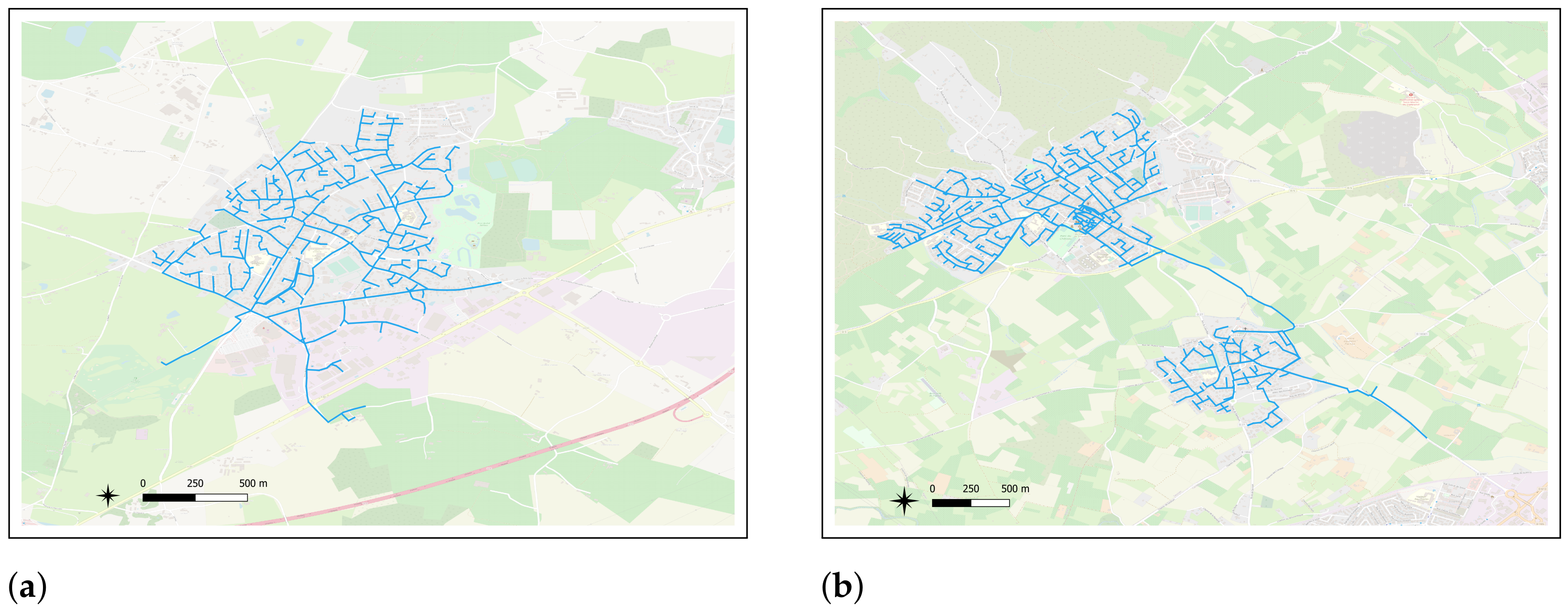
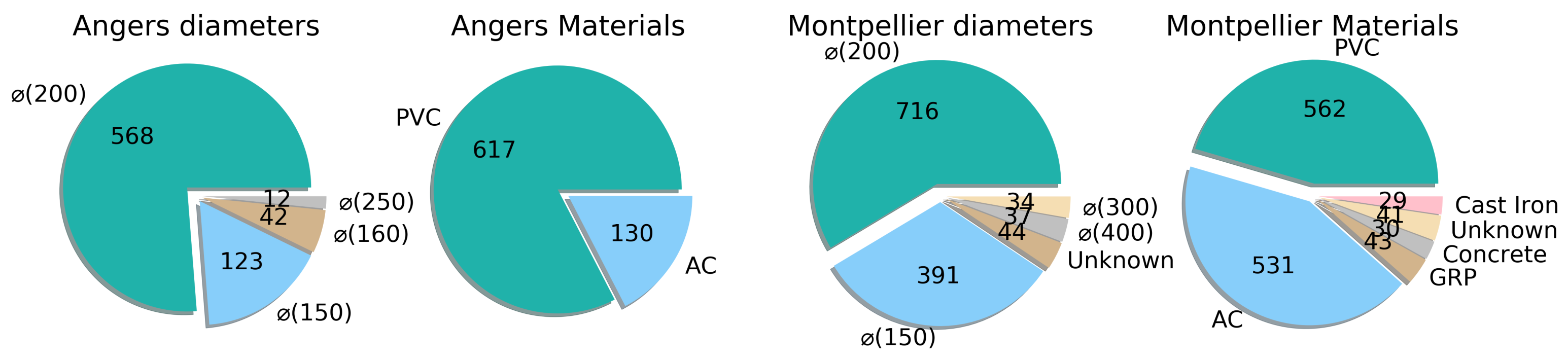
3.2. Datasets
3.3. Testing Procedure
4. Experimental Results
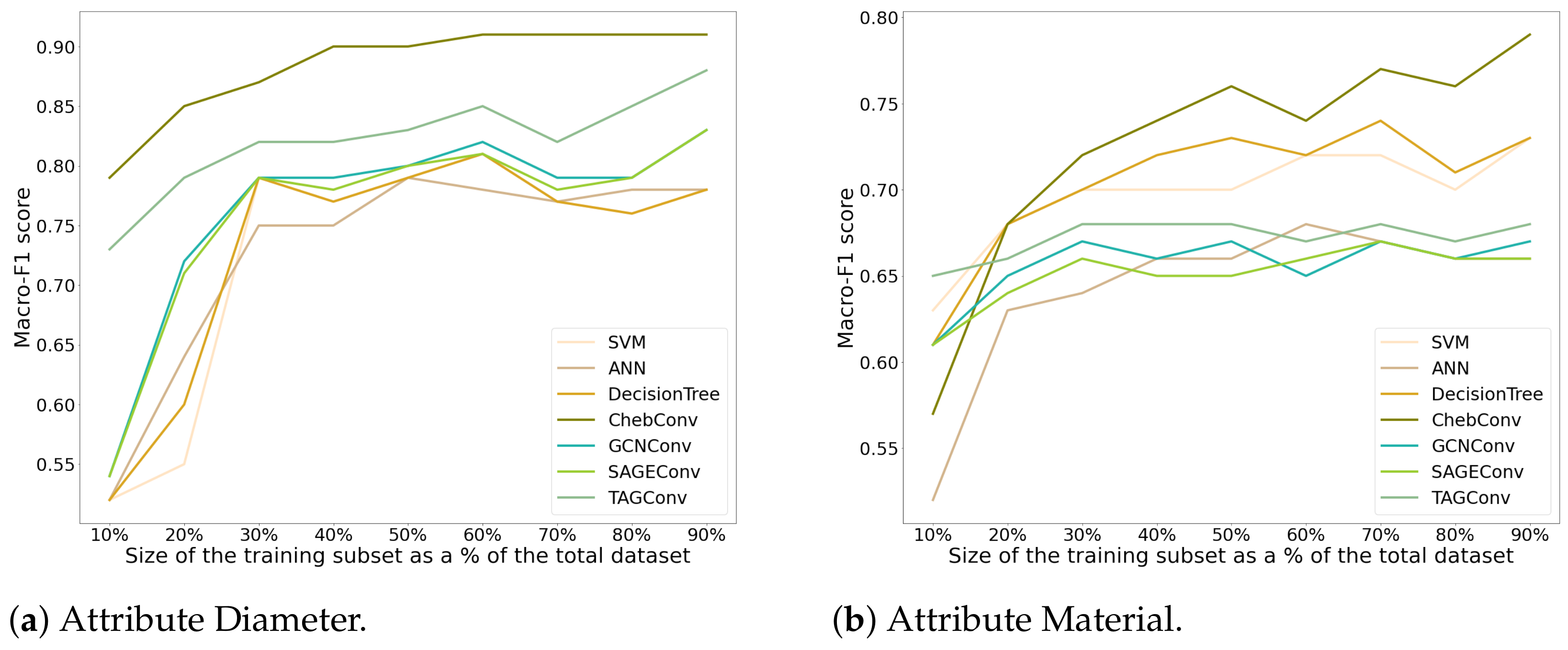
4.1. Configuration 1
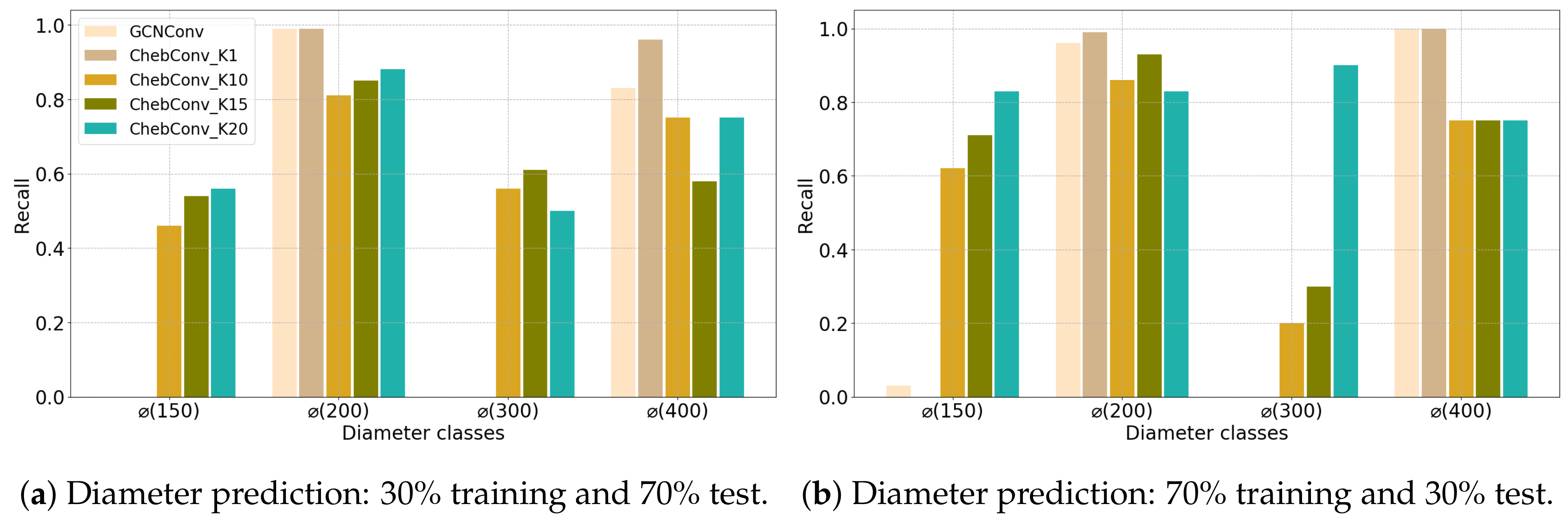
4.2. Configuration 2
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- UN. Population Division of the Department of Economic and Social Affairs of the United Nations: World Urbanization Prospects: The 2018 Revision; Technical Report (ST/ESA/SER.A/420); UN: New York, NY, USA, 2019. [Google Scholar]
- OECD. OECD Environmental Outlook to 2050: The Consequences of Inaction; OECD Editions: Paris, France, 2012; p. 350. [Google Scholar] [CrossRef]
- Yuan, Z.; Olsson, G.; Cardell-Oliver, R.; van Schagen, K.; Marchi, A.; Deletic, A.; Urich, C.; Rauch, W.; Liu, Y.; Jiang, G. Sweating the assets—The role of instrumentation, control and automation in urban water systems. Water Res. 2019, 155, 381–402. [Google Scholar] [CrossRef]
- Harrison, C.; Eckman, B.; Hamilton, R.; Hartswick, P.; Kalagnanam, J.; Paraszczak, J.; Williams, P. Foundations for Smarter Cities. IBM J. Res. Dev. 2010, 54, 1–16. [Google Scholar] [CrossRef]
- Nie, X.; Fan, T.; Wang, B.; Li, Z.; Shankar, A.; Manickam, A. Big Data analytics and IoT in Operation safety management in Under Water Management. Comput. Commun. 2020, 154, 188–196. [Google Scholar] [CrossRef]
- Chen, Y.; Han, D. Water quality monitoring in smart city: A pilot project. Autom. Constr. 2018, 89, 307–316. [Google Scholar] [CrossRef]
- Kofinas, D.T.; Spyropoulou, A.; Laspidou, C.S. A methodology for synthetic household water consumption data generation. Environ. Model. Softw. 2018, 100, 48–66. [Google Scholar] [CrossRef]
- Zeng, Z.; Yuan, X.; Liang, J.; Li, Y. Designing and implementing an SWMM-based web service framework to provide decision support for real-time urban stormwater management. Environ. Model. Softw. 2021, 135, 104887. [Google Scholar] [CrossRef]
- Gibert, K.; Sànchez-Marrè, M.; Rodríguez-Roda, I. GESCONDA: An intelligent data analysis system for knowledge discovery and management in environmental databases. Environ. Model. Softw. 2006, 21, 115–120. [Google Scholar] [CrossRef]
- Lin, P.; Yuan, X.X. A two-time-scale point process model of water main breaks for infrastructure asset management. Water Res. 2019, 150, 296–309. [Google Scholar] [CrossRef]
- Junninen, H.; Niska, H.; Tuppurainen, K.; Ruuskanen, J.; Kolehmainen, M. Methods for imputation of missing values in air quality data sets. Atmos. Environ. 2004, 38, 2895–2907. [Google Scholar] [CrossRef]
- Schneider, T. Analysis of incomplete climate data: Estimation of Mean Values and covariance matrices and imputation of Missing values. J. Clim. 2001, 14, 853–871. [Google Scholar] [CrossRef]
- ASTEE. Gestion Patrimoniale des Réseaux D’assainissement; ASTEE: Nanterre, France, 2015. [Google Scholar]
- Chen, H.; Cohn, A.G. Buried utility pipeline mapping based on multiple spatial data sources: A Bayesian data fusion approach. In Twenty-Second International Joint Conference on Artificial Intelligence; IJCAI: Barcelona, Catalonia, Spain, 2011; pp. 2411–2417. ISBN 978-1-57735-516-8. [Google Scholar]
- Bilal, M.; Khan, W.; Muggleton, J.; Rustighi, E.; Jenks, H.; Pennock, S.R.; Atkins, P.R.; Cohn, A. Inferring the most probable maps of underground utilities using Bayesian mapping model. J. Appl. Geophys. 2018, 150, 52–66. [Google Scholar] [CrossRef]
- Hafsi, M.; Bolon, P.; Dapoigny, R. Detection and localization of underground networks by fusion of electromagnetic signal and GPR images. In Proceedings SPIE 10338, Thirteenth International Conference on Quality Control by Artificial Vision 2017, Tokyo, Japan; Nagahara, H., Umeda, K., Yamashita, A., Eds.; International Society for Optics and Photonics: Bellingham, WA, USA, 2017; Volume 10338, pp. 7–14. [Google Scholar] [CrossRef]
- Commandre, B.; En-Nejjary, D.; Pibre, L.; Chaumont, M.; Delenne, C.; Chahinian, N. Manhole Cover Localization in Aerial Images with a Deep Learning Approach. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42W1, 333–338. [Google Scholar] [CrossRef]
- Kabir, G.; Tesfamariam, S.; Hemsing, J.; Sadiq, R. Handling incomplete and missing data in water network database using imputation methods. Sustain. Resilient Infrastruct. 2020, 5, 365–377. [Google Scholar] [CrossRef]
- Tsai, C.F.; Chang, F.Y. Combining instance selection for better missing value imputation. J. Syst. Softw. 2016, 122, 63–71. [Google Scholar] [CrossRef]
- García-Laencina, P.J.; Sancho-Gómez, J.L.; Figueiras-Vidal, A.R.; Verleysen, M. K nearest neighbours with mutual information for simultaneous classification and missing data imputation. Neurocomputing 2009, 72, 1483–1493. [Google Scholar] [CrossRef]
- Liew, A.W.C.; Law, N.F.; Yan, H. Missing value imputation for gene expression data: Computational techniques to recover missing data from available information. Briefings Bioinform. 2010, 12, 498–513. [Google Scholar] [CrossRef] [PubMed]
- García-Laencina, P.J.; Sancho-Gómez, J.L.; Figueiras-Vidal, A.R. Pattern classification with missing data: A review. Neural Comput. Appl. 2010, 19, 263–282. [Google Scholar] [CrossRef]
- Ngouna, R.H.; Ratolojanahary, R.; Medjaher, K.; Dauriac, F.; Sebilo, M.; Junca-Bourié, J. A data-driven method for detecting and diagnosing causes of water quality contamination in a dataset with a high rate of missing values. Eng. Appl. Artif. Intell. 2020, 95, 103822. [Google Scholar] [CrossRef]
- Bischof, S.; Harth, A.; Kämpgen, B.; Polleres, A.; Schneider, P. Enriching integrated statistical open city data by combining equational knowledge and missing value imputation. J. Web Semant. 2018, 48, 22–47. [Google Scholar] [CrossRef]
- Yadav, M.L.; Roychoudhury, B. Handling missing values: A study of popular imputation packages in R. Knowl. Based Syst. 2018, 160, 104–118. [Google Scholar] [CrossRef]
- Serrano-Notivoli, R.; de Luis, M.; Beguería, S. An R package for daily precipitation climate series reconstruction. Environ. Model. Softw. 2017, 89, 190–195. [Google Scholar] [CrossRef]
- Murtojärvi, M.; Suominen, T.; Uusipaikka, E.; Nevalainen, O.S. Optimising an observational water monitoring network for Archipelago Sea, South West Finland. Comput. Geosci. 2011, 37, 844–854. [Google Scholar] [CrossRef]
- Belda, S.; Pipia, L.; Morcillo-Pallarés, P.; Rivera-Caicedo, J.P.; Amin, E.; De Grave, C.; Verrelst, J. DATimeS: A machine learning time series GUI toolbox for gap-filling and vegetation phenology trends detection. Environ. Model. Softw. 2020, 127, 104666. [Google Scholar] [CrossRef]
- Ma, J.; Cheng, J.C.; Ding, Y.; Lin, C.; Jiang, F.; Wang, M.; Zhai, C. Transfer learning for long-interval consecutive missing values imputation without external features in air pollution time series. Adv. Eng. Inform. 2020, 44, 101092. [Google Scholar] [CrossRef]
- Giustarini, L.; Parisot, O.; Ghoniem, M.; Hostache, R.; Trebs, I.; Otjacques, B. A user-driven case-based reasoning tool for infilling missing values in daily mean river flow records. Environ. Model. Softw. 2016, 82, 308–320. [Google Scholar] [CrossRef]
- Nelwamondo, F.V.; Golding, D.; Marwala, T. A dynamic programming approach to missing data estimation using neural networks. Inf. Sci. 2013, 237, 49–58. [Google Scholar] [CrossRef]
- Spinelli, I.; Scardapane, S.; Uncini, A. Missing data imputation with adversarially-trained graph convolutional networks. Neural Netw. 2020, 129, 249–260. [Google Scholar] [CrossRef]
- Collobert, R.; Weston, J. A Unified Architecture for Natural Language Processing: Deep Neural Networks with Multitask Learning. In Proceedings of the 25th International Conference on Machine Learning, ICML’08, Helsinki, Finland, 5–9 July 2008; Association for Computing Machinery: New York, NY, USA, 2008; pp. 160–167. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Graves, A.; Mohamed, A.r.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6645–6649. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. ImageNet Classification with Deep Convolutional Neural Networks. Commun. ACM 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef]
- Zhou, J.; Cui, G.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph Neural Networks: A Review of Methods and Applications. arXiv 2019, arXiv:cs.LG/1812.08434. [Google Scholar]
- Cai, H.; Zheng, V.W.; Chang, K.C.C. A comprehensive survey of graph embedding: Problems, techniques, and applications. IEEE Trans. Knowl. Data Eng. 2018, 30, 1616–1637. [Google Scholar] [CrossRef]
- Grover, A.; Leskovec, J. node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2008, 20, 61–80. [Google Scholar] [CrossRef]
- Li, Y.; Tarlow, D.; Brockschmidt, M.; Zemel, R. Gated Graph Sequence Neural Networks. arXiv 2017, arXiv:cs.LG/1511.05493. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-Supervised Classification with Graph Convolutional Networks. arXiv 2017, arXiv:cs.LG/1609.02907. [Google Scholar]
- Thekumparampil, K.K.; Wang, C.; Oh, S.; Li, L.J. Attention-Based Graph Neural Network for Semi-Supervised Learning. arXiv 2017, arXiv:stat.ML/1803.03735. [Google Scholar]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral Networks and Locally Connected Networks on Graphs. arXiv 2014, arXiv:cs.LG/1312.6203. [Google Scholar]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering. arXiv 2017, arXiv:cs.LG/1606.09375. [Google Scholar]
- Hammond, D.K.; Vandergheynst, P.; Gribonval, R. Wavelets on graphs via spectral graph theory. Appl. Comput. Harmon. Anal. 2011, 30, 129–150. [Google Scholar] [CrossRef]
- Duvenaud, D.; Maclaurin, D.; Aguilera-Iparraguirre, J.; Gómez-Bombarelli, R.; Hirzel, T.; Aspuru-Guzik, A.; Adams, R.P. Convolutional Networks on Graphs for Learning Molecular Fingerprints. arXiv 2015, arXiv:cs.LG/1509.09292. [Google Scholar]
- Hamilton, W.; Ying, Z.; Leskovec, J. Inductive representation learning on large graphs. arXiv 2017, arXiv:1706.02216. [Google Scholar]
- Du, J.; Zhang, S.; Wu, G.; Moura, J.M.; Kar, S. Topology adaptive graph convolutional networks. arXiv 2017, arXiv:1710.10370. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Safavian, S.R.; Landgrebe, D. A survey of decision tree classifier methodology. IEEE Trans. Syst. Man Cybern. 1991, 21, 660–674. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Strahler, A. Quantitative analysis of watershed geomorphology. Eos Trans. Am. Geophys. Union 1957, 38, 913–920. [Google Scholar] [CrossRef]
- Paszke, A.; Gross, S.; Chintala, S.; Chanan, G.; Yang, E.; DeVito, Z.; Lin, Z.; Desmaison, A.; Antiga, L.; Lerer, A. Automatic Differentiation in PyTorch. arXiv 2017, arXiv:1706.02216. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Rahimi, A.; Cohn, T.; Baldwin, T. Semi-supervised User Geolocation via Graph Convolutional Networks. arXiv 2018, arXiv:cs.CL/1804.08049. [Google Scholar]
- Tsiami, L.; Makropoulos, C. Cyber—Physical Attack Detection in Water Distribution Systems with Temporal Graph Convolutional Neural Networks. Water 2021, 13, 1247. [Google Scholar] [CrossRef]
- Jepsen, T.S.; Jensen, C.S.; Nielsen, T.D. Graph Convolutional Networks for Road Networks. In Proceedings of the 27th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Chicago, IL, USA, 5–8 November 2019. [Google Scholar] [CrossRef]
- Kumar, A.; Rizvi, S.M.A.A.; Brooks, B.; Vanderveld, R.A.; Wilson, K.H.; Kenney, C.; Edelstein, S.; Finch, A.; Maxwell, A.; Zuckerbraun, J.; et al. Using Machine Learning to Assess the Risk of and Prevent Water Main Breaks. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018. [Google Scholar]
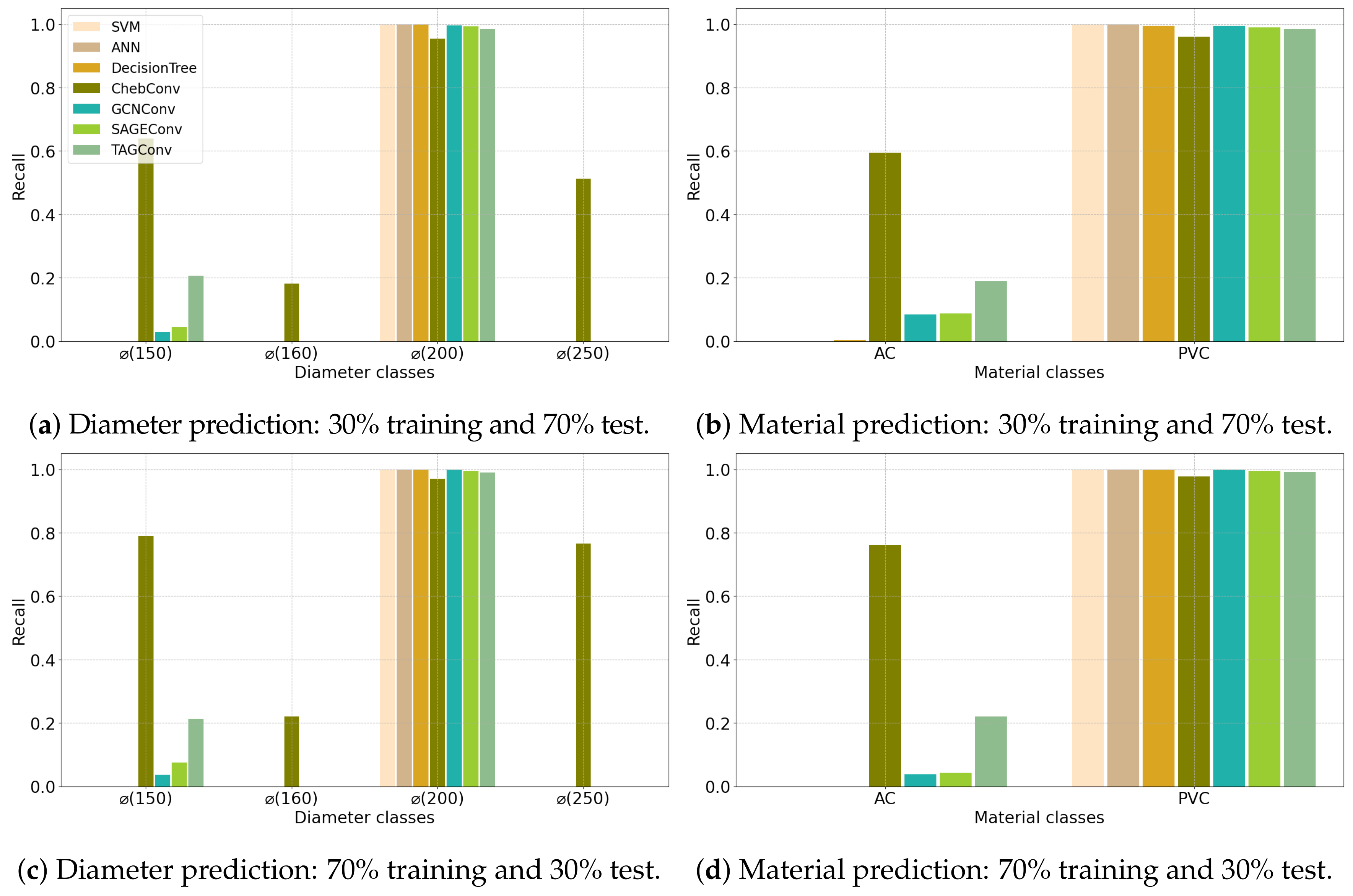
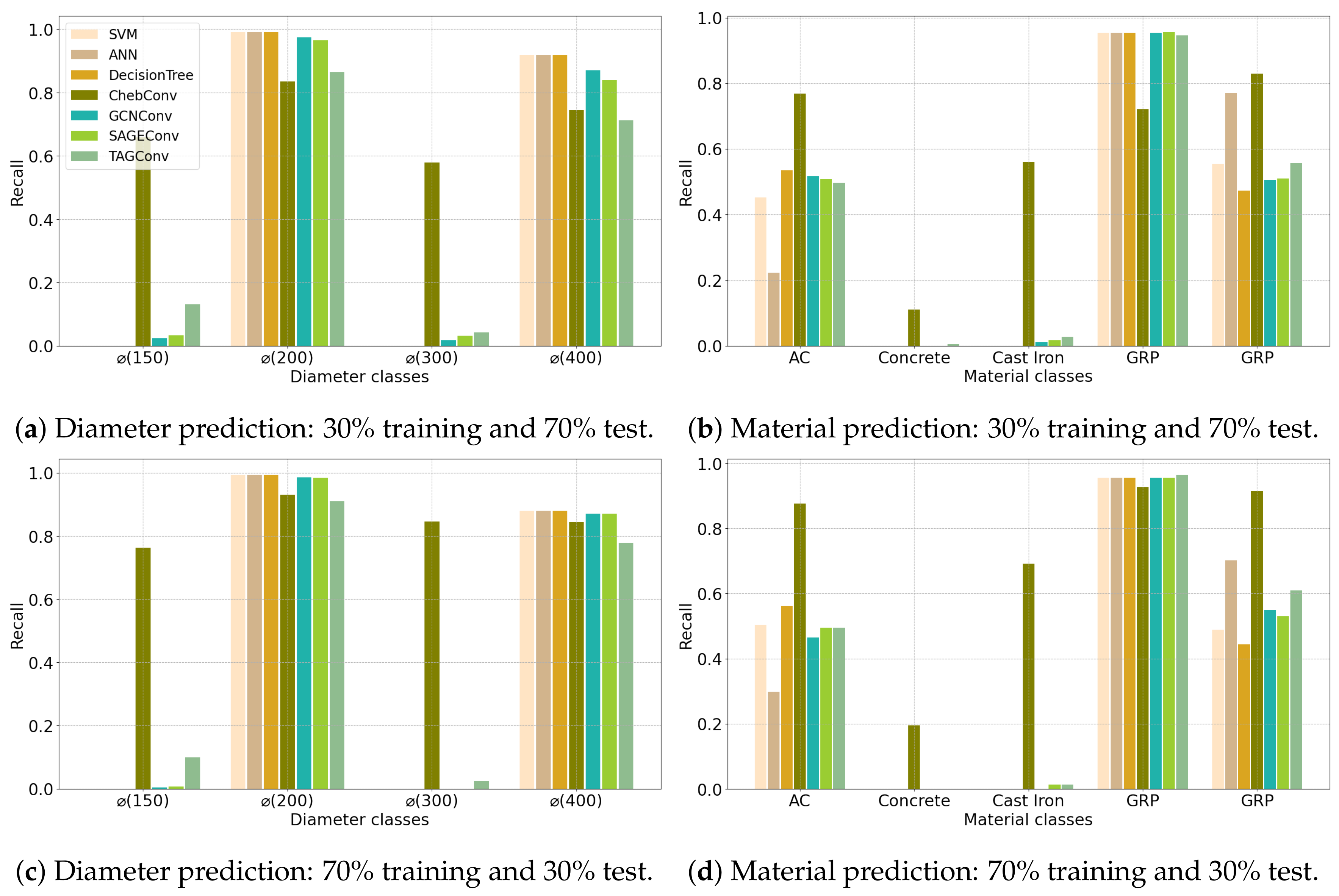
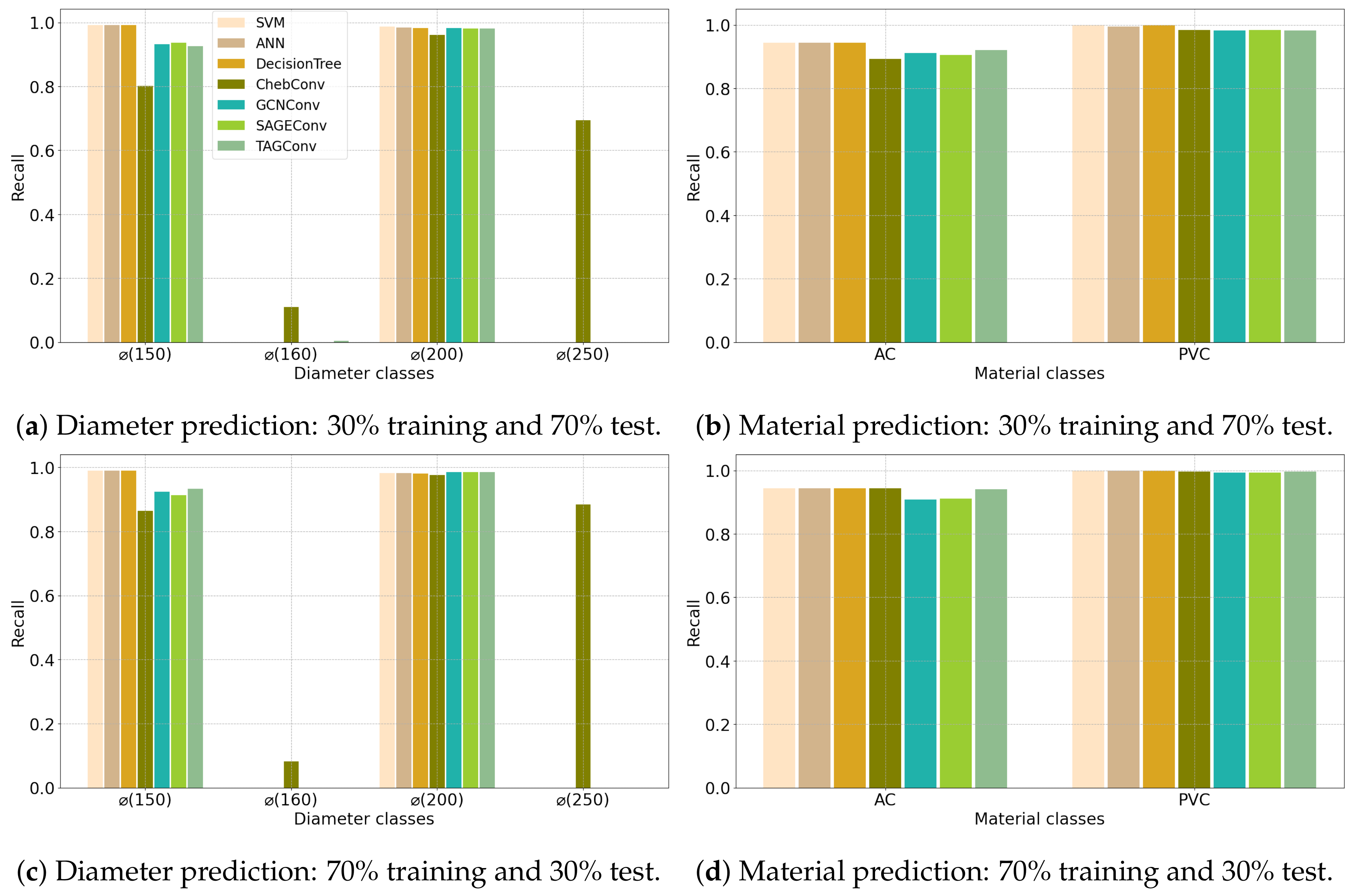
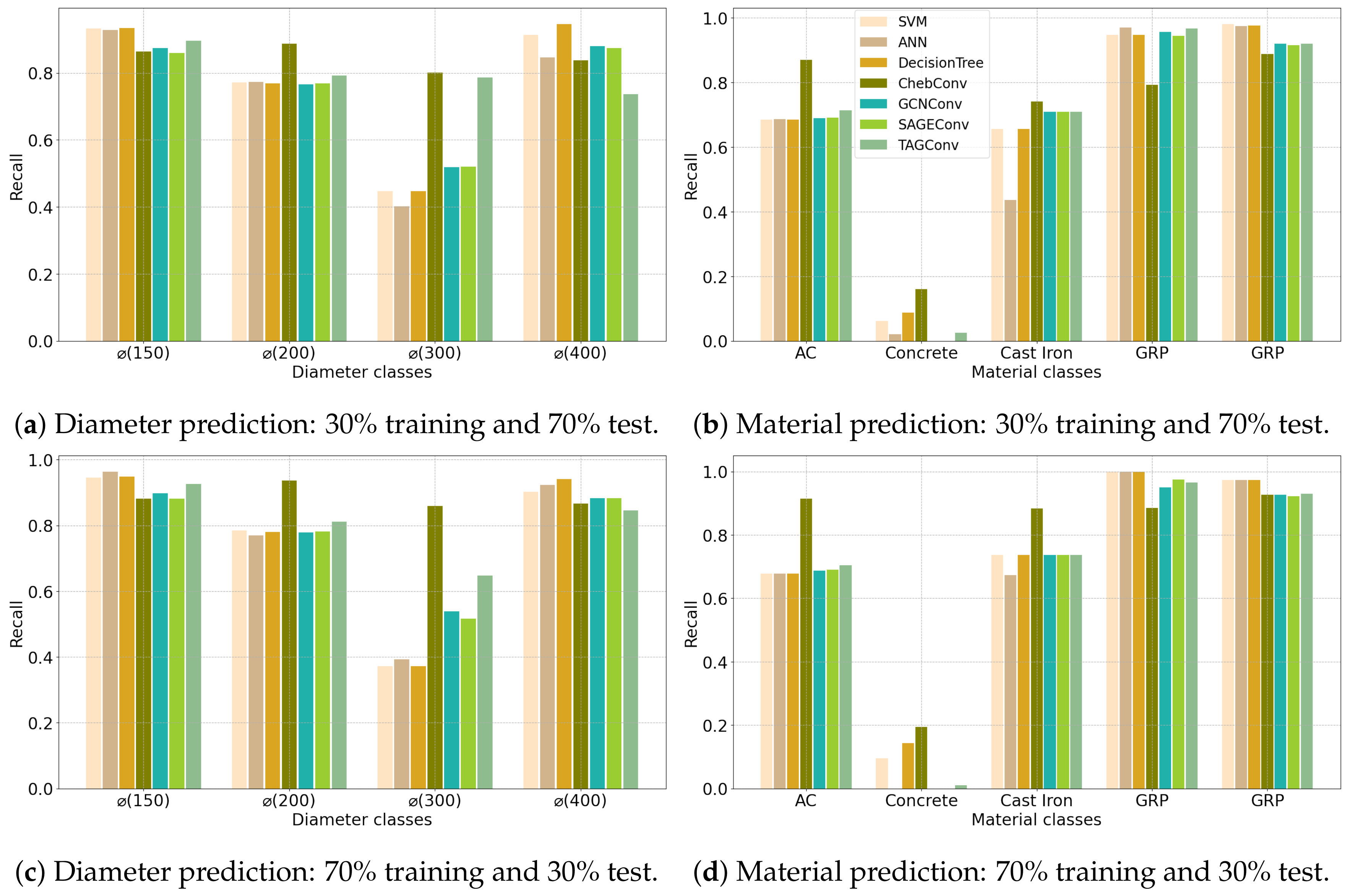
| (a) Angers Dataset | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SVM | ANN | DT | ChebConv | GCNConv | SAGEConv | TAGConv | ||||||||||||||||
| Attribute | % | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 |
| Diameter | 10 | 0.25 | 0.19 | 0.22 | 0.25 | 0.19 | 0.21 | 0.25 | 0.19 | 0.22 | 0.41 | 0.6 | 0.45 | 0.26 | 0.28 | 0.23 | 0.25 | 0.21 | 0.22 | 0.27 | 0.34 | 0.26 |
| 20 | 0.25 | 0.19 | 0.22 | 0.25 | 0.19 | 0.22 | 0.25 | 0.19 | 0.22 | 0.51 | 0.69 | 0.56 | 0.26 | 0.28 | 0.24 | 0.26 | 0.24 | 0.23 | 0.29 | 0.38 | 0.29 | |
| 30 | 0.25 | 0.19 | 0.22 | 0.25 | 0.19 | 0.22 | 0.25 | 0.19 | 0.22 | 0.57 | 0.77 | 0.63 | 0.26 | 0.26 | 0.23 | 0.26 | 0.27 | 0.23 | 0.3 | 0.4 | 0.3 | |
| 40 | 0.25 | 0.19 | 0.22 | 0.25 | 0.19 | 0.22 | 0.25 | 0.19 | 0.22 | 0.61 | 0.79 | 0.66 | 0.26 | 0.26 | 0.23 | 0.26 | 0.26 | 0.23 | 0.3 | 0.42 | 0.3 | |
| 50 | 0.25 | 0.19 | 0.22 | 0.25 | 0.19 | 0.22 | 0.25 | 0.19 | 0.22 | 0.66 | 0.8 | 0.7 | 0.26 | 0.28 | 0.24 | 0.27 | 0.31 | 0.25 | 0.3 | 0.41 | 0.3 | |
| 60 | 0.25 | 0.19 | 0.22 | 0.25 | 0.19 | 0.22 | 0.25 | 0.19 | 0.22 | 0.68 | 0.81 | 0.71 | 0.25 | 0.23 | 0.23 | 0.27 | 0.36 | 0.26 | 0.3 | 0.41 | 0.31 | |
| 70 | 0.25 | 0.19 | 0.22 | 0.25 | 0.19 | 0.22 | 0.25 | 0.19 | 0.22 | 0.69 | 0.77 | 0.71 | 0.26 | 0.29 | 0.23 | 0.27 | 0.35 | 0.25 | 0.3 | 0.4 | 0.3 | |
| 80 | 0.25 | 0.19 | 0.22 | 0.25 | 0.19 | 0.22 | 0.25 | 0.19 | 0.22 | 0.69 | 0.78 | 0.72 | 0.26 | 0.28 | 0.23 | 0.26 | 0.29 | 0.24 | 0.3 | 0.41 | 0.3 | |
| 90 | 0.25 | 0.19 | 0.22 | 0.25 | 0.19 | 0.22 | 0.25 | 0.19 | 0.22 | 0.75 | 0.76 | 0.74 | 0.27 | 0.29 | 0.24 | 0.26 | 0.27 | 0.23 | 0.31 | 0.43 | 0.31 | |
| Material | 10 | 0.5 | 0.42 | 0.45 | 0.5 | 0.41 | 0.45 | 0.49 | 0.43 | 0.45 | 0.62 | 0.78 | 0.66 | 0.54 | 0.69 | 0.53 | 0.52 | 0.63 | 0.5 | 0.56 | 0.73 | 0.57 |
| 20 | 0.5 | 0.41 | 0.45 | 0.5 | 0.41 | 0.45 | 0.5 | 0.41 | 0.45 | 0.71 | 0.82 | 0.75 | 0.53 | 0.66 | 0.51 | 0.53 | 0.6 | 0.5 | 0.59 | 0.83 | 0.61 | |
| 30 | 0.5 | 0.41 | 0.45 | 0.5 | 0.41 | 0.45 | 0.5 | 0.42 | 0.45 | 0.78 | 0.86 | 0.81 | 0.54 | 0.74 | 0.53 | 0.54 | 0.71 | 0.53 | 0.59 | 0.81 | 0.6 | |
| 40 | 0.5 | 0.41 | 0.45 | 0.5 | 0.41 | 0.45 | 0.5 | 0.41 | 0.45 | 0.85 | 0.89 | 0.86 | 0.54 | 0.76 | 0.53 | 0.54 | 0.74 | 0.53 | 0.6 | 0.82 | 0.63 | |
| 50 | 0.5 | 0.41 | 0.45 | 0.5 | 0.41 | 0.45 | 0.5 | 0.41 | 0.45 | 0.86 | 0.88 | 0.87 | 0.54 | 0.76 | 0.53 | 0.55 | 0.77 | 0.54 | 0.6 | 0.87 | 0.63 | |
| 60 | 0.5 | 0.41 | 0.45 | 0.5 | 0.41 | 0.45 | 0.5 | 0.41 | 0.45 | 0.87 | 0.9 | 0.89 | 0.53 | 0.64 | 0.5 | 0.54 | 0.73 | 0.53 | 0.6 | 0.83 | 0.63 | |
| 70 | 0.5 | 0.41 | 0.45 | 0.5 | 0.41 | 0.45 | 0.5 | 0.41 | 0.45 | 0.87 | 0.92 | 0.89 | 0.52 | 0.6 | 0.49 | 0.52 | 0.61 | 0.49 | 0.61 | 0.85 | 0.63 | |
| 80 | 0.5 | 0.42 | 0.45 | 0.5 | 0.42 | 0.45 | 0.5 | 0.42 | 0.45 | 0.88 | 0.93 | 0.9 | 0.53 | 0.75 | 0.52 | 0.53 | 0.75 | 0.52 | 0.6 | 0.87 | 0.63 | |
| 90 | 0.5 | 0.41 | 0.45 | 0.5 | 0.41 | 0.45 | 0.5 | 0.41 | 0.45 | 0.91 | 0.95 | 0.93 | 0.53 | 0.64 | 0.5 | 0.53 | 0.64 | 0.5 | 0.62 | 0.91 | 0.65 | |
| (b) Montpellier Dataset | ||||||||||||||||||||||
| SVM | ANN | DT | ChebConv | GCNConv | SAGEConv | TAGConv | ||||||||||||||||
| Attribute | % | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 |
| Diameter | 10 | 0.22 | 0.16 | 0.18 | 0.23 | 0.16 | 0.19 | 0.22 | 0.17 | 0.19 | 0.48 | 0.62 | 0.52 | 0.23 | 0.38 | 0.23 | 0.23 | 0.37 | 0.23 | 0.38 | 0.52 | 0.41 |
| 20 | 0.25 | 0.17 | 0.2 | 0.36 | 0.24 | 0.29 | 0.38 | 0.26 | 0.31 | 0.63 | 0.74 | 0.67 | 0.39 | 0.44 | 0.37 | 0.39 | 0.47 | 0.37 | 0.43 | 0.5 | 0.43 | |
| 30 | 0.48 | 0.31 | 0.38 | 0.48 | 0.31 | 0.38 | 0.48 | 0.31 | 0.38 | 0.7 | 0.78 | 0.73 | 0.47 | 0.39 | 0.39 | 0.47 | 0.43 | 0.4 | 0.44 | 0.47 | 0.42 | |
| 40 | 0.48 | 0.32 | 0.38 | 0.48 | 0.32 | 0.38 | 0.48 | 0.32 | 0.38 | 0.76 | 0.85 | 0.79 | 0.46 | 0.37 | 0.39 | 0.46 | 0.37 | 0.39 | 0.44 | 0.52 | 0.42 | |
| 50 | 0.48 | 0.31 | 0.38 | 0.48 | 0.31 | 0.38 | 0.48 | 0.31 | 0.38 | 0.8 | 0.88 | 0.83 | 0.47 | 0.34 | 0.39 | 0.47 | 0.35 | 0.39 | 0.47 | 0.53 | 0.43 | |
| 60 | 0.48 | 0.32 | 0.38 | 0.48 | 0.32 | 0.38 | 0.48 | 0.32 | 0.38 | 0.83 | 0.88 | 0.84 | 0.48 | 0.33 | 0.39 | 0.48 | 0.35 | 0.39 | 0.46 | 0.53 | 0.42 | |
| 70 | 0.47 | 0.32 | 0.38 | 0.47 | 0.32 | 0.38 | 0.47 | 0.32 | 0.38 | 0.85 | 0.91 | 0.87 | 0.47 | 0.34 | 0.38 | 0.47 | 0.34 | 0.38 | 0.45 | 0.46 | 0.41 | |
| 80 | 0.49 | 0.34 | 0.4 | 0.49 | 0.34 | 0.4 | 0.49 | 0.34 | 0.4 | 0.85 | 0.91 | 0.87 | 0.48 | 0.34 | 0.4 | 0.48 | 0.35 | 0.4 | 0.48 | 0.55 | 0.44 | |
| 90 | 0.47 | 0.33 | 0.38 | 0.47 | 0.33 | 0.38 | 0.47 | 0.33 | 0.38 | 0.87 | 0.91 | 0.88 | 0.47 | 0.33 | 0.38 | 0.47 | 0.33 | 0.38 | 0.46 | 0.5 | 0.41 | |
| Material | 10 | 0.36 | 0.33 | 0.33 | 0.35 | 0.29 | 0.31 | 0.36 | 0.33 | 0.32 | 0.43 | 0.55 | 0.45 | 0.36 | 0.33 | 0.34 | 0.36 | 0.33 | 0.33 | 0.35 | 0.36 | 0.34 |
| 20 | 0.39 | 0.33 | 0.34 | 0.39 | 0.31 | 0.33 | 0.39 | 0.32 | 0.34 | 0.55 | 0.68 | 0.57 | 0.39 | 0.35 | 0.35 | 0.4 | 0.36 | 0.36 | 0.39 | 0.37 | 0.36 | |
| 30 | 0.39 | 0.32 | 0.35 | 0.39 | 0.28 | 0.32 | 0.39 | 0.33 | 0.35 | 0.6 | 0.69 | 0.62 | 0.4 | 0.37 | 0.36 | 0.4 | 0.35 | 0.36 | 0.41 | 0.39 | 0.37 | |
| 40 | 0.39 | 0.33 | 0.35 | 0.39 | 0.31 | 0.33 | 0.39 | 0.33 | 0.35 | 0.64 | 0.75 | 0.65 | 0.39 | 0.33 | 0.35 | 0.39 | 0.34 | 0.35 | 0.41 | 0.38 | 0.38 | |
| 50 | 0.39 | 0.32 | 0.34 | 0.39 | 0.27 | 0.31 | 0.39 | 0.33 | 0.34 | 0.68 | 0.84 | 0.71 | 0.39 | 0.33 | 0.35 | 0.39 | 0.33 | 0.34 | 0.42 | 0.4 | 0.38 | |
| 60 | 0.39 | 0.33 | 0.34 | 0.39 | 0.3 | 0.32 | 0.39 | 0.33 | 0.34 | 0.72 | 0.85 | 0.76 | 0.39 | 0.33 | 0.35 | 0.39 | 0.34 | 0.35 | 0.42 | 0.38 | 0.38 | |
| 70 | 0.39 | 0.32 | 0.34 | 0.39 | 0.3 | 0.33 | 0.39 | 0.32 | 0.34 | 0.72 | 0.83 | 0.75 | 0.39 | 0.33 | 0.35 | 0.4 | 0.35 | 0.35 | 0.42 | 0.36 | 0.38 | |
| 80 | 0.38 | 0.33 | 0.33 | 0.38 | 0.29 | 0.32 | 0.38 | 0.33 | 0.33 | 0.72 | 0.88 | 0.75 | 0.37 | 0.31 | 0.33 | 0.38 | 0.32 | 0.34 | 0.41 | 0.36 | 0.37 | |
| 90 | 0.39 | 0.33 | 0.33 | 0.38 | 0.28 | 0.31 | 0.39 | 0.34 | 0.32 | 0.74 | 0.78 | 0.75 | 0.4 | 0.35 | 0.36 | 0.39 | 0.33 | 0.34 | 0.44 | 0.4 | 0.41 | |
| (a) Angers Dataset | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SVM | ANN | DT | ChebConv | GCNConv | SAGEConv | TAGConv | ||||||||||||||||
| Attribute | % | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 |
| Diameter | 10 | 0.49 | 0.46 | 0.47 | 0.49 | 0.46 | 0.48 | 0.49 | 0.46 | 0.48 | 0.58 | 0.76 | 0.62 | 0.48 | 0.45 | 0.46 | 0.47 | 0.45 | 0.46 | 0.48 | 0.5 | 0.47 |
| 20 | 0.49 | 0.46 | 0.48 | 0.49 | 0.46 | 0.48 | 0.49 | 0.46 | 0.48 | 0.64 | 0.74 | 0.66 | 0.48 | 0.45 | 0.46 | 0.48 | 0.45 | 0.46 | 0.48 | 0.46 | 0.47 | |
| 30 | 0.49 | 0.46 | 0.48 | 0.49 | 0.46 | 0.48 | 0.49 | 0.46 | 0.48 | 0.64 | 0.73 | 0.66 | 0.48 | 0.45 | 0.47 | 0.48 | 0.45 | 0.47 | 0.48 | 0.46 | 0.47 | |
| 40 | 0.49 | 0.46 | 0.48 | 0.49 | 0.46 | 0.47 | 0.49 | 0.46 | 0.47 | 0.68 | 0.76 | 0.7 | 0.48 | 0.45 | 0.47 | 0.48 | 0.45 | 0.47 | 0.49 | 0.46 | 0.47 | |
| 50 | 0.49 | 0.46 | 0.48 | 0.49 | 0.46 | 0.48 | 0.49 | 0.46 | 0.48 | 0.67 | 0.79 | 0.69 | 0.48 | 0.45 | 0.47 | 0.48 | 0.45 | 0.47 | 0.48 | 0.46 | 0.47 | |
| 60 | 0.49 | 0.46 | 0.48 | 0.49 | 0.46 | 0.48 | 0.49 | 0.46 | 0.48 | 0.68 | 0.8 | 0.7 | 0.48 | 0.45 | 0.47 | 0.48 | 0.45 | 0.47 | 0.48 | 0.46 | 0.47 | |
| 70 | 0.49 | 0.46 | 0.48 | 0.49 | 0.46 | 0.47 | 0.49 | 0.46 | 0.48 | 0.7 | 0.77 | 0.71 | 0.48 | 0.46 | 0.47 | 0.47 | 0.46 | 0.47 | 0.48 | 0.46 | 0.47 | |
| 80 | 0.5 | 0.46 | 0.48 | 0.5 | 0.46 | 0.48 | 0.5 | 0.46 | 0.48 | 0.66 | 0.71 | 0.66 | 0.48 | 0.45 | 0.46 | 0.48 | 0.45 | 0.46 | 0.48 | 0.46 | 0.47 | |
| 90 | 0.49 | 0.46 | 0.48 | 0.49 | 0.46 | 0.48 | 0.49 | 0.46 | 0.48 | 0.74 | 0.77 | 0.74 | 0.48 | 0.45 | 0.47 | 0.48 | 0.46 | 0.47 | 0.48 | 0.46 | 0.47 | |
| Material | 10 | 0.96 | 0.99 | 0.97 | 0.96 | 0.99 | 0.97 | 0.97 | 0.99 | 0.98 | 0.87 | 0.93 | 0.9 | 0.93 | 0.95 | 0.94 | 0.92 | 0.95 | 0.94 | 0.9 | 0.94 | 0.92 |
| 20 | 0.96 | 0.99 | 0.98 | 0.97 | 0.99 | 0.98 | 0.97 | 0.99 | 0.98 | 0.91 | 0.94 | 0.92 | 0.94 | 0.96 | 0.95 | 0.94 | 0.95 | 0.95 | 0.94 | 0.96 | 0.95 | |
| 30 | 0.97 | 0.99 | 0.98 | 0.97 | 0.99 | 0.98 | 0.97 | 0.99 | 0.98 | 0.94 | 0.96 | 0.95 | 0.95 | 0.95 | 0.95 | 0.94 | 0.96 | 0.95 | 0.95 | 0.96 | 0.96 | |
| 40 | 0.97 | 0.99 | 0.98 | 0.97 | 0.99 | 0.98 | 0.97 | 0.99 | 0.98 | 0.94 | 0.96 | 0.95 | 0.94 | 0.96 | 0.95 | 0.94 | 0.95 | 0.95 | 0.95 | 0.96 | 0.96 | |
| 50 | 0.97 | 0.99 | 0.98 | 0.97 | 0.99 | 0.98 | 0.97 | 0.99 | 0.98 | 0.95 | 0.97 | 0.96 | 0.95 | 0.96 | 0.95 | 0.94 | 0.96 | 0.95 | 0.96 | 0.98 | 0.97 | |
| 60 | 0.98 | 0.99 | 0.98 | 0.98 | 0.99 | 0.98 | 0.98 | 0.99 | 0.98 | 0.97 | 0.97 | 0.97 | 0.96 | 0.97 | 0.96 | 0.96 | 0.97 | 0.96 | 0.97 | 0.98 | 0.97 | |
| 70 | 0.97 | 0.99 | 0.98 | 0.97 | 0.99 | 0.98 | 0.97 | 0.99 | 0.98 | 0.97 | 0.99 | 0.98 | 0.95 | 0.97 | 0.96 | 0.95 | 0.97 | 0.96 | 0.97 | 0.99 | 0.98 | |
| 80 | 0.96 | 0.99 | 0.98 | 0.96 | 0.99 | 0.98 | 0.96 | 0.99 | 0.98 | 0.95 | 0.98 | 0.96 | 0.94 | 0.96 | 0.95 | 0.94 | 0.96 | 0.95 | 0.96 | 0.98 | 0.97 | |
| 90 | 0.95 | 0.99 | 0.97 | 0.95 | 0.99 | 0.97 | 0.95 | 0.99 | 0.97 | 0.97 | 0.97 | 0.97 | 0.93 | 0.96 | 0.94 | 0.93 | 0.96 | 0.94 | 0.95 | 0.99 | 0.97 | |
| (b) Montpellier Dataset | ||||||||||||||||||||||
| SVM | ANN | DT | ChebConv | GCNConv | SAGEConv | TAGConv | ||||||||||||||||
| Attribute | % | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 | MR | MP | MF1 |
| Diameter | 10 | 0.5 | 0.64 | 0.52 | 0.51 | 0.58 | 0.52 | 0.51 | 0.6 | 0.52 | 0.75 | 0.86 | 0.79 | 0.52 | 0.64 | 0.54 | 0.52 | 0.61 | 0.54 | 0.67 | 0.83 | 0.73 |
| 20 | 0.54 | 0.64 | 0.55 | 0.64 | 0.69 | 0.64 | 0.59 | 0.68 | 0.6 | 0.82 | 0.89 | 0.85 | 0.7 | 0.81 | 0.72 | 0.68 | 0.82 | 0.71 | 0.77 | 0.84 | 0.79 | |
| 30 | 0.77 | 0.86 | 0.79 | 0.74 | 0.81 | 0.75 | 0.77 | 0.85 | 0.79 | 0.85 | 0.9 | 0.87 | 0.76 | 0.85 | 0.79 | 0.76 | 0.84 | 0.79 | 0.8 | 0.86 | 0.82 | |
| 40 | 0.77 | 0.85 | 0.77 | 0.77 | 0.81 | 0.75 | 0.78 | 0.84 | 0.77 | 0.88 | 0.92 | 0.9 | 0.79 | 0.83 | 0.79 | 0.78 | 0.82 | 0.78 | 0.81 | 0.85 | 0.82 | |
| 50 | 0.77 | 0.86 | 0.79 | 0.78 | 0.85 | 0.79 | 0.79 | 0.85 | 0.79 | 0.88 | 0.92 | 0.9 | 0.79 | 0.83 | 0.8 | 0.79 | 0.84 | 0.8 | 0.81 | 0.88 | 0.83 | |
| 60 | 0.8 | 0.86 | 0.81 | 0.77 | 0.83 | 0.78 | 0.8 | 0.85 | 0.81 | 0.9 | 0.93 | 0.91 | 0.82 | 0.83 | 0.82 | 0.82 | 0.83 | 0.81 | 0.85 | 0.86 | 0.85 | |
| 70 | 0.75 | 0.85 | 0.77 | 0.76 | 0.84 | 0.77 | 0.76 | 0.85 | 0.77 | 0.89 | 0.93 | 0.91 | 0.77 | 0.82 | 0.79 | 0.77 | 0.82 | 0.78 | 0.81 | 0.86 | 0.82 | |
| 80 | 0.75 | 0.81 | 0.76 | 0.77 | 0.86 | 0.78 | 0.75 | 0.81 | 0.76 | 0.89 | 0.93 | 0.91 | 0.79 | 0.82 | 0.79 | 0.79 | 0.82 | 0.79 | 0.85 | 0.87 | 0.85 | |
| 90 | 0.79 | 0.81 | 0.78 | 0.79 | 0.8 | 0.78 | 0.79 | 0.8 | 0.78 | 0.89 | 0.96 | 0.91 | 0.84 | 0.85 | 0.83 | 0.84 | 0.83 | 0.83 | 0.9 | 0.87 | 0.88 | |
| Material | 10 | 0.6 | 0.72 | 0.63 | 0.54 | 0.52 | 0.52 | 0.6 | 0.68 | 0.61 | 0.54 | 0.73 | 0.57 | 0.6 | 0.65 | 0.61 | 0.6 | 0.64 | 0.61 | 0.63 | 0.7 | 0.65 |
| 20 | 0.66 | 0.73 | 0.68 | 0.63 | 0.65 | 0.63 | 0.66 | 0.76 | 0.68 | 0.65 | 0.78 | 0.68 | 0.64 | 0.68 | 0.65 | 0.63 | 0.68 | 0.64 | 0.65 | 0.71 | 0.66 | |
| 30 | 0.67 | 0.79 | 0.7 | 0.62 | 0.71 | 0.64 | 0.67 | 0.81 | 0.7 | 0.69 | 0.81 | 0.72 | 0.65 | 0.7 | 0.67 | 0.65 | 0.69 | 0.66 | 0.67 | 0.73 | 0.68 | |
| 40 | 0.67 | 0.77 | 0.7 | 0.64 | 0.7 | 0.66 | 0.68 | 0.82 | 0.72 | 0.71 | 0.82 | 0.74 | 0.65 | 0.69 | 0.66 | 0.64 | 0.68 | 0.65 | 0.66 | 0.72 | 0.68 | |
| 50 | 0.68 | 0.76 | 0.7 | 0.65 | 0.7 | 0.66 | 0.7 | 0.83 | 0.73 | 0.73 | 0.85 | 0.76 | 0.67 | 0.7 | 0.67 | 0.65 | 0.67 | 0.65 | 0.67 | 0.71 | 0.68 | |
| 60 | 0.69 | 0.81 | 0.72 | 0.67 | 0.72 | 0.68 | 0.69 | 0.84 | 0.72 | 0.72 | 0.81 | 0.74 | 0.64 | 0.69 | 0.65 | 0.65 | 0.69 | 0.66 | 0.66 | 0.71 | 0.67 | |
| 70 | 0.7 | 0.83 | 0.72 | 0.66 | 0.7 | 0.67 | 0.71 | 0.87 | 0.74 | 0.76 | 0.81 | 0.77 | 0.66 | 0.7 | 0.67 | 0.66 | 0.69 | 0.67 | 0.67 | 0.72 | 0.68 | |
| 80 | 0.67 | 0.78 | 0.7 | 0.65 | 0.71 | 0.66 | 0.68 | 0.82 | 0.71 | 0.73 | 0.84 | 0.76 | 0.65 | 0.69 | 0.66 | 0.65 | 0.69 | 0.66 | 0.66 | 0.72 | 0.67 | |
| 90 | 0.72 | 0.78 | 0.73 | 0.65 | 0.69 | 0.66 | 0.72 | 0.78 | 0.73 | 0.79 | 0.8 | 0.79 | 0.68 | 0.69 | 0.67 | 0.68 | 0.67 | 0.66 | 0.68 | 0.7 | 0.68 | |
| Angers Dataset | |||
|---|---|---|---|
| Attributes | Diameter | Material | Strahler |
| Diameter | 1 | 0.74 | 0.06 |
| Material | 0.74 | 1 | 0.01 |
| Strahler | 0.06 | 0.01 | 1 |
| Montpellier Dataset | |||
| Attributes | Diameter | Material | Strahler |
| Diameter | 1 | 0.43 | 0.31 |
| Material | 0.43 | 1 | 0.08 |
| Strahler | 0.31 | 0.08 | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belghaddar, Y.; Chahinian, N.; Seriai, A.; Begdouri, A.; Abdou, R.; Delenne, C. Graph Convolutional Networks: Application to Database Completion of Wastewater Networks. Water 2021, 13, 1681. https://doi.org/10.3390/w13121681
Belghaddar Y, Chahinian N, Seriai A, Begdouri A, Abdou R, Delenne C. Graph Convolutional Networks: Application to Database Completion of Wastewater Networks. Water. 2021; 13(12):1681. https://doi.org/10.3390/w13121681
Chicago/Turabian StyleBelghaddar, Yassine, Nanee Chahinian, Abderrahmane Seriai, Ahlame Begdouri, Reda Abdou, and Carole Delenne. 2021. "Graph Convolutional Networks: Application to Database Completion of Wastewater Networks" Water 13, no. 12: 1681. https://doi.org/10.3390/w13121681
APA StyleBelghaddar, Y., Chahinian, N., Seriai, A., Begdouri, A., Abdou, R., & Delenne, C. (2021). Graph Convolutional Networks: Application to Database Completion of Wastewater Networks. Water, 13(12), 1681. https://doi.org/10.3390/w13121681






