Dynamics of Volumetric Moisture in Sand Caused by Injection Irrigation—Physical Model
Abstract
1. Introduction
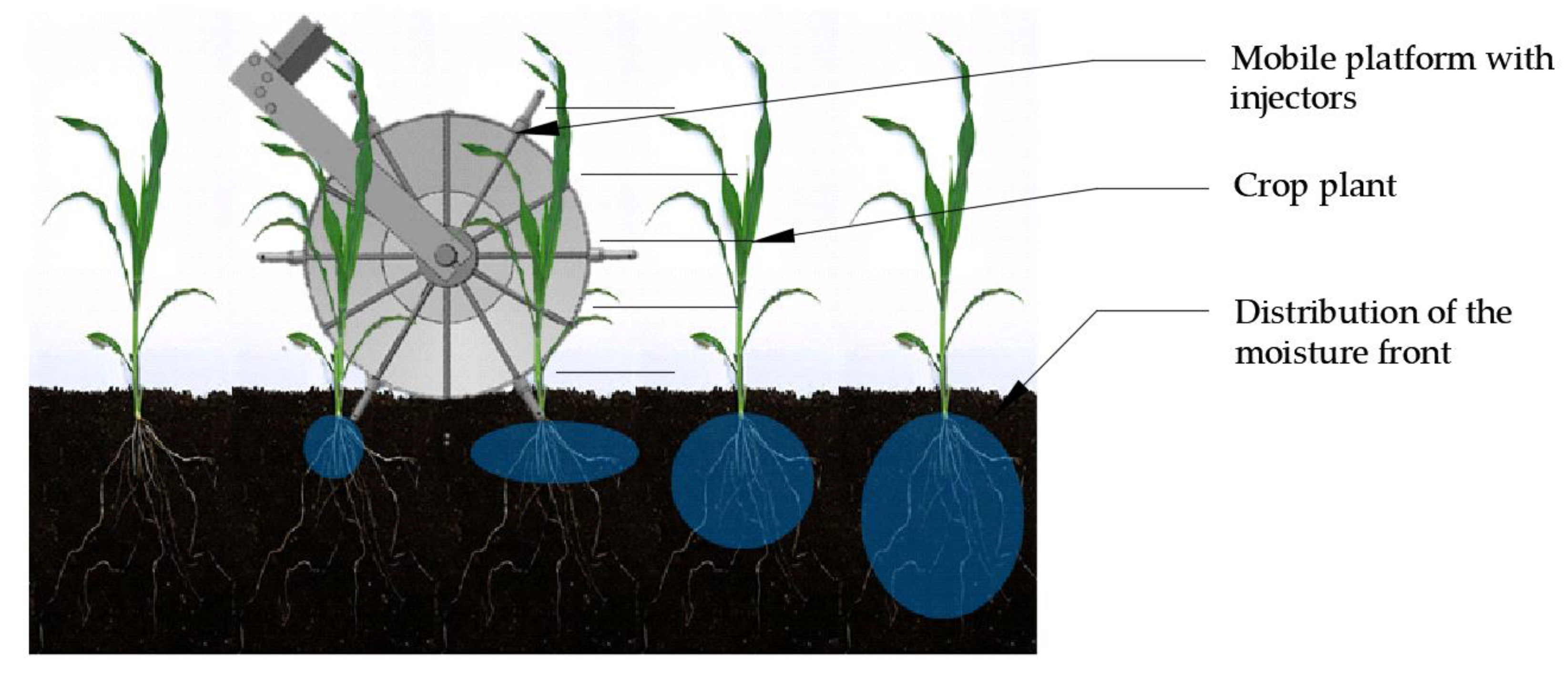
1.1. Distribution of Soil Moisture Dynamics during Injection Irrigation
1.2. Standards of Injection Irrigation of Field Cultivations
1.2.1. Plant Spacing in Cultivations Dedicated for Injection Irrigation
1.2.2. Irrigation Dose in the Case of Injection Irrigation
1.2.3. Depth of Water Injection Relative to Ground Surface
1.3. Research Objective
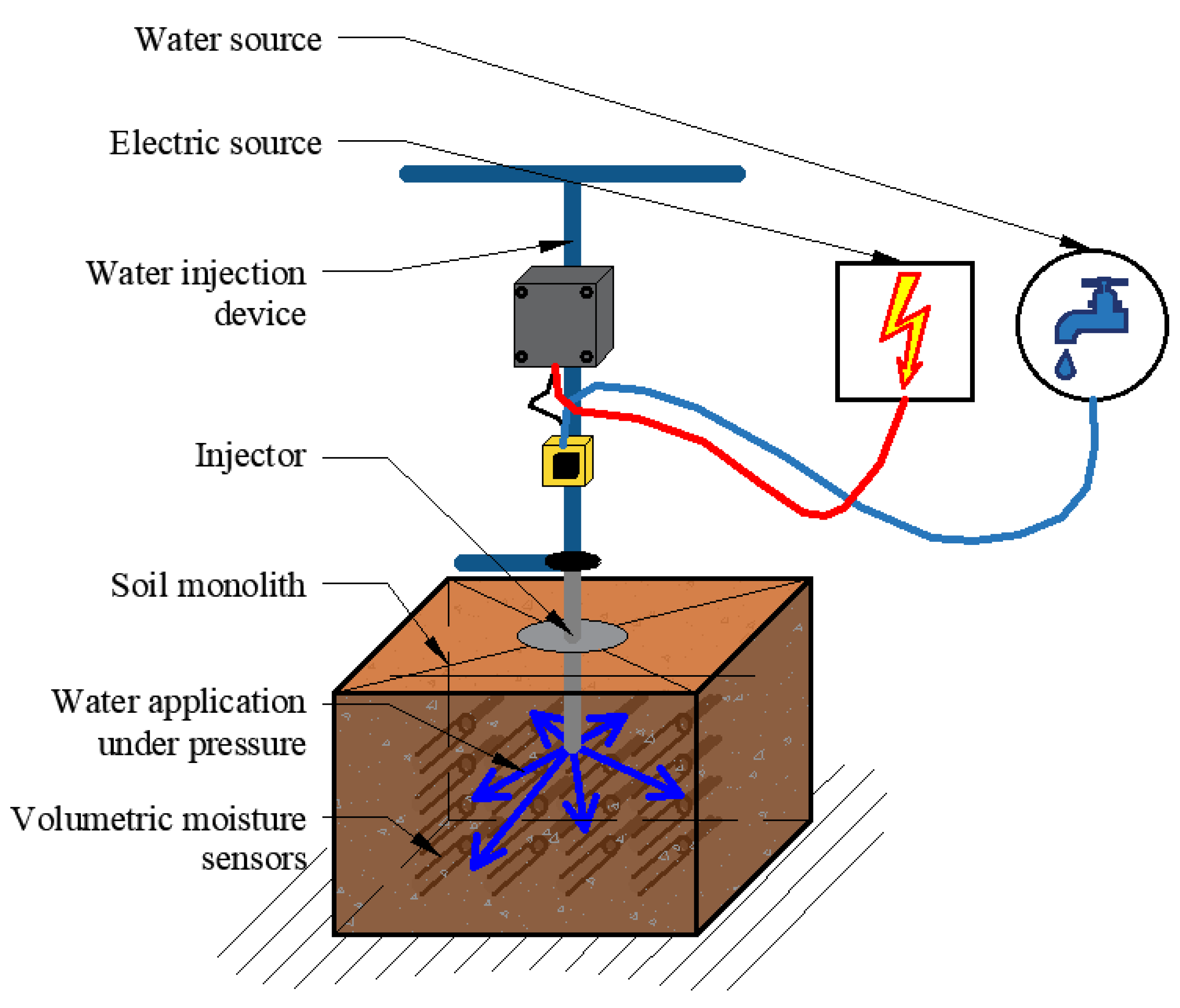
2. Materials and Methods
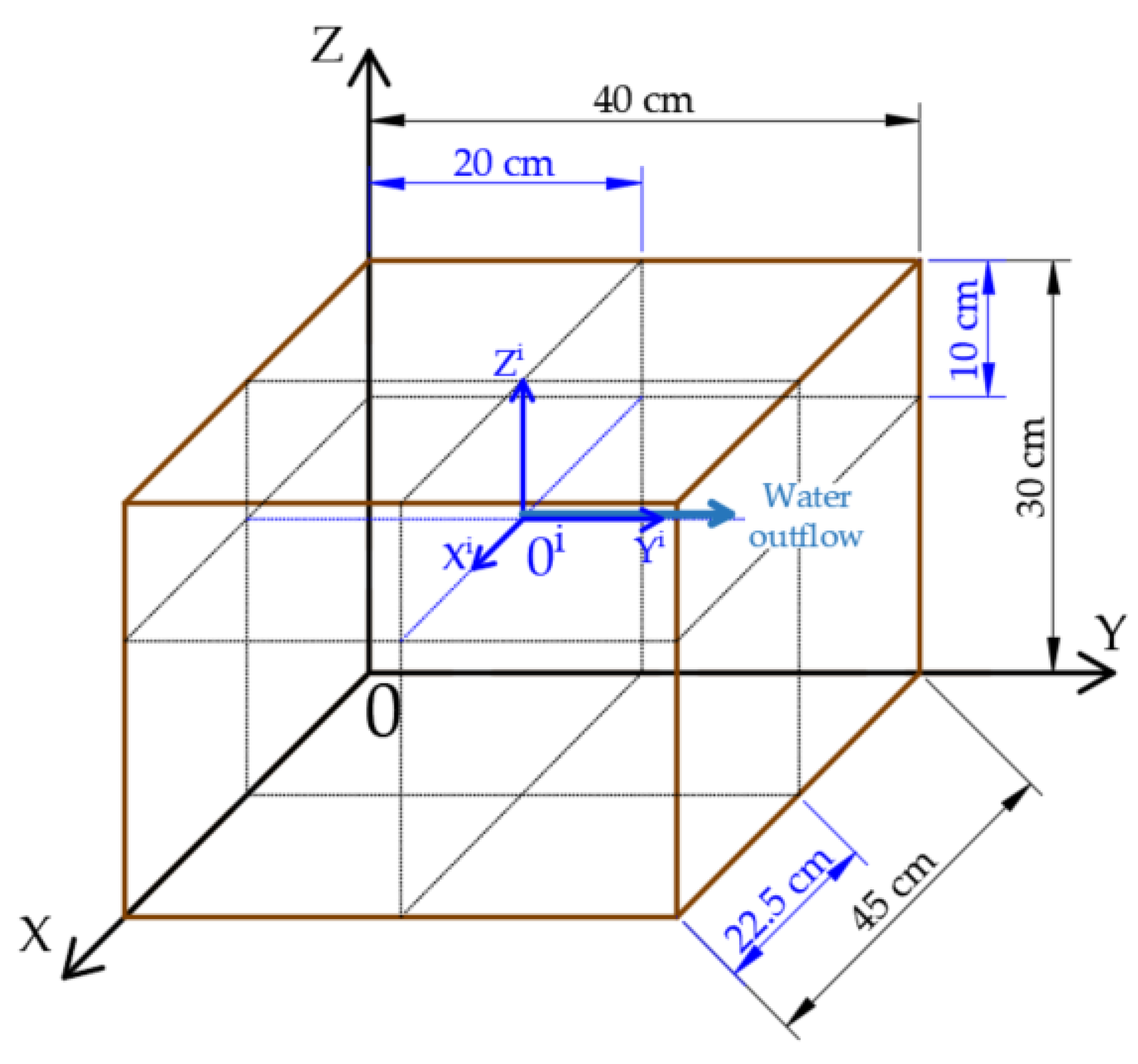
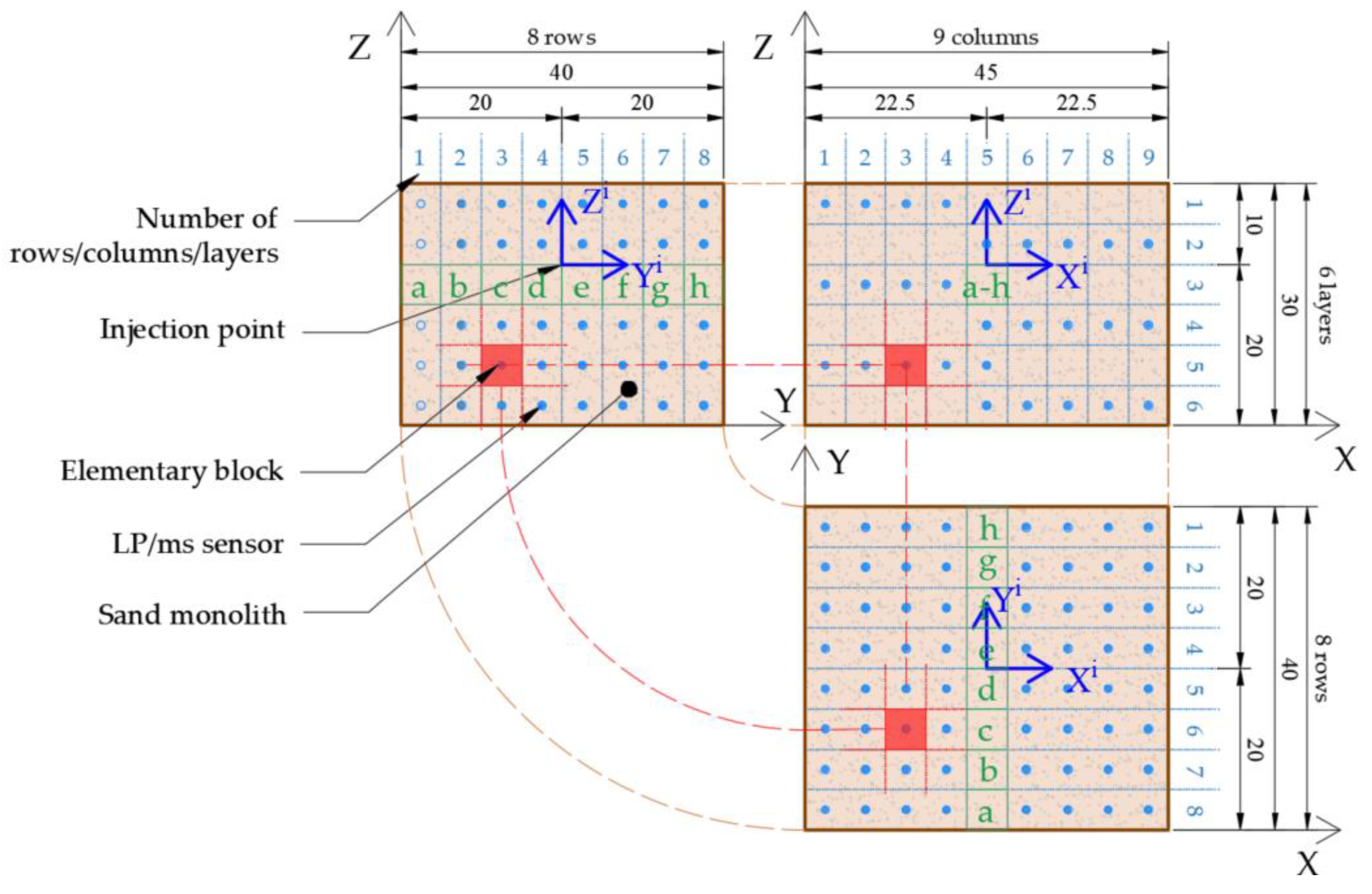
2.1. Scope and Run of the Experiment
2.2. Monitoring of Volumetric Water Content
2.3. Water Balance
3. Results and Discussion
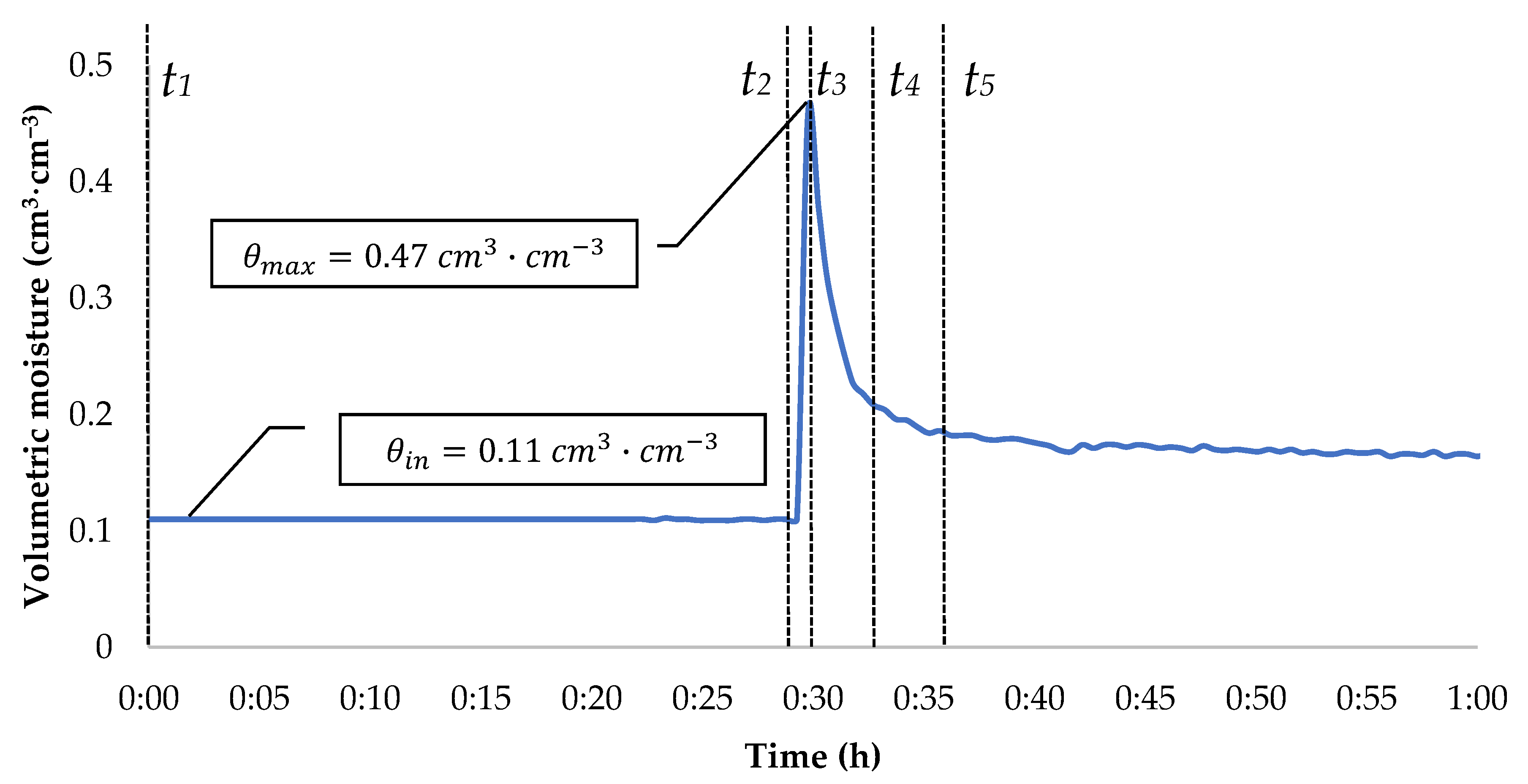
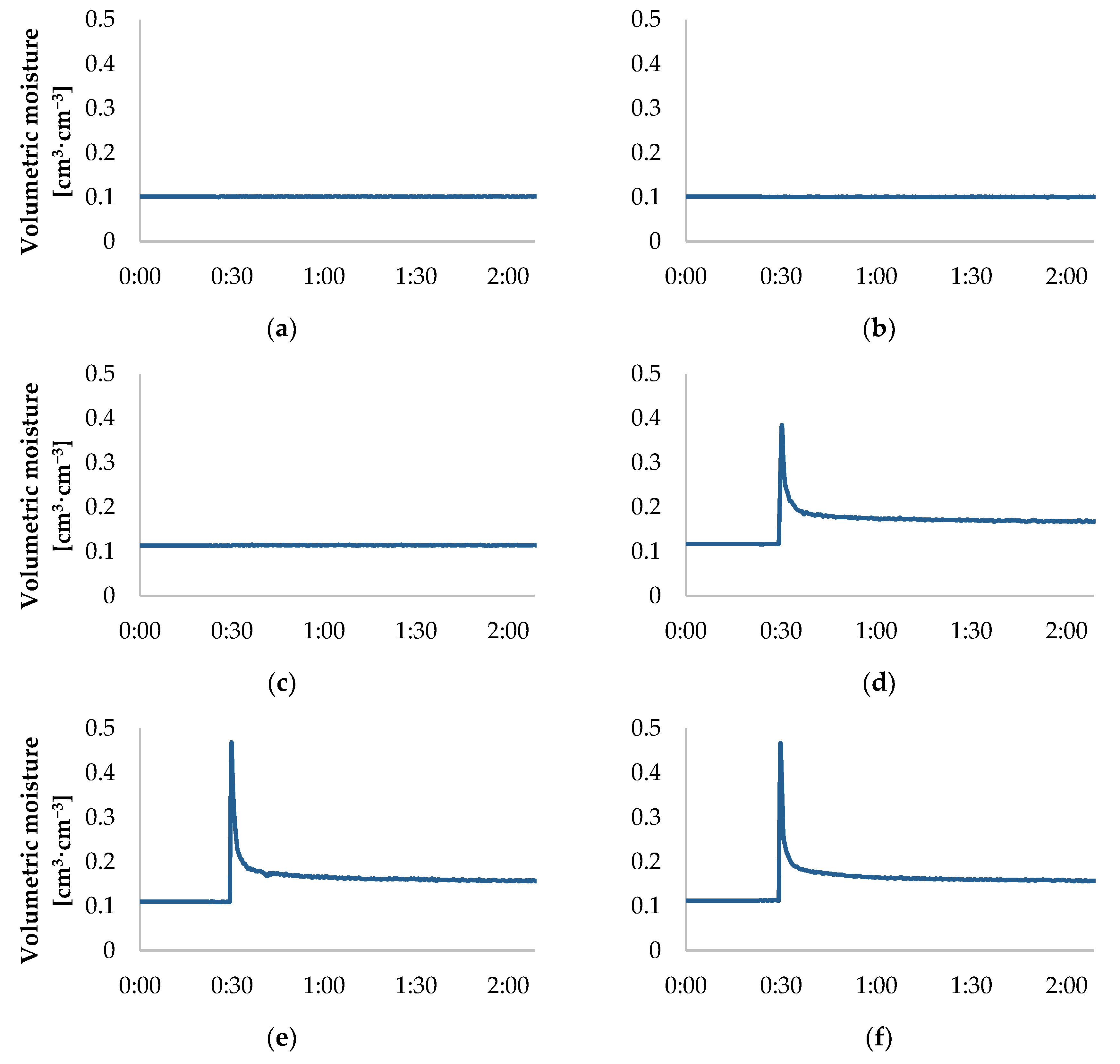
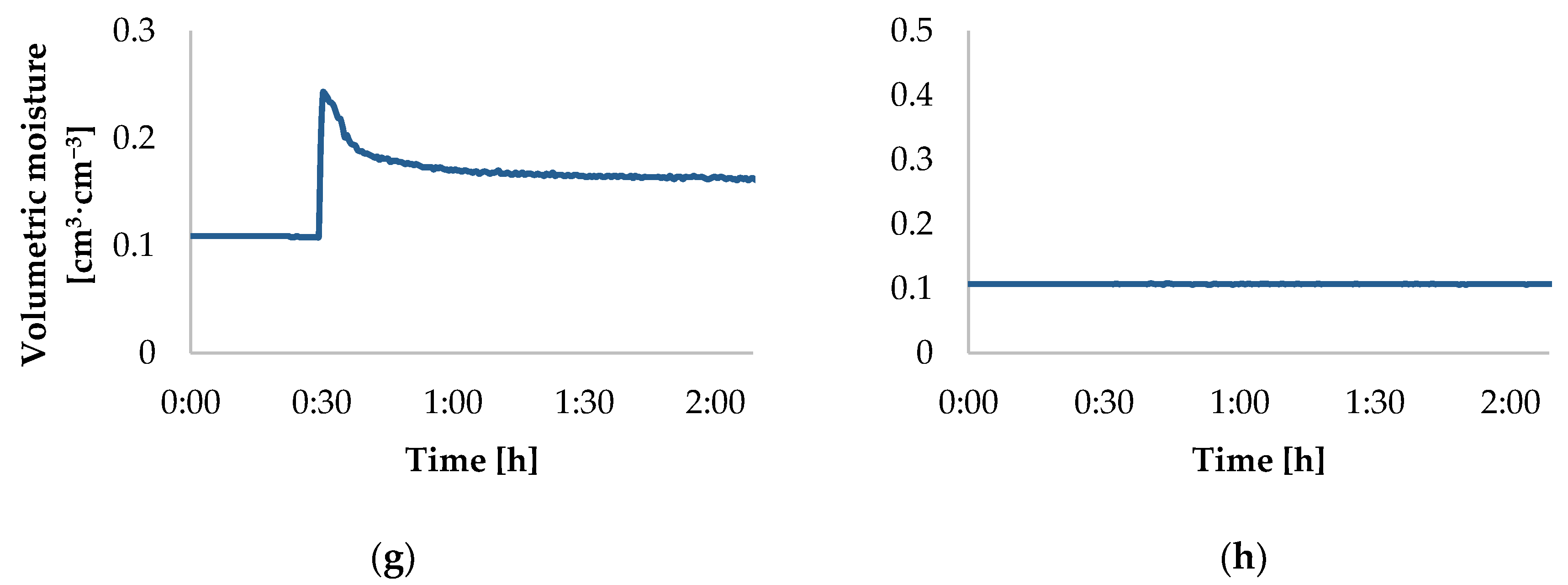
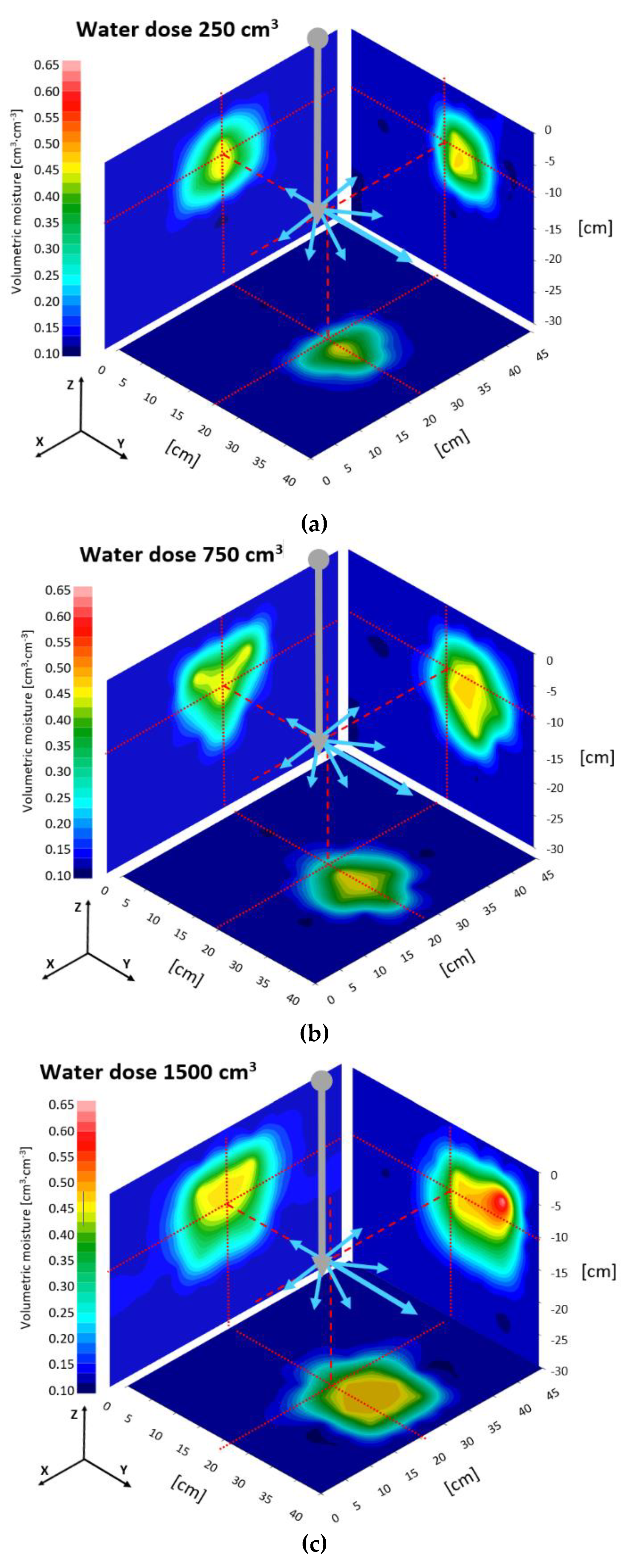
3.1. Dynamics of the Volumetric Moisture
3.2. Water Balance in the Physical Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jackson, R.B.; Carpenter, S.R.; Dahm, C.N.; McKnight, D.M.; Naiman, R.J.; Postel, S.L.; Running, S.W. Issues in Ecology. WATER A Chang. WORLD 2001, 11, 1027–1045. [Google Scholar]
- Wada, Y.; Bierkens, M.F.P. Sustainability of global water use: Past reconstruction and future projections. Environ. Res. Lett. 2014, 9, 104003–104020. [Google Scholar] [CrossRef]
- Walczak, A. The Use of World Water Resources in the Irrigation of Field Cultivations. J. Ecol. Eng. 2021, 22, 186–206. [Google Scholar] [CrossRef]
- Ünlü, M.; Kanber, R.; Şenyigit, U.; Onaran, H.; Diker, K. Trickle and sprinkler irrigation of potato (Solanum tuberosum L.) in the Middle Anatolian Region in Turkey. Agric. Water Manag. 2006, 79, 43–71. [Google Scholar] [CrossRef]
- Kang, Y.; Wang, F.X.; Liu, H.J.; Yuan, B.Z. Potato evapotranspiration and yield under different drip irrigation regimes. Irrig. Sci. 2004, 23, 133–143. [Google Scholar] [CrossRef]
- Dyśko, J.; Kaniszewski, S. Effect of drip irrigation, n-fertigation and cultivation methods on the yield and quality of carrot. Veg. Crop. Res. Bull. 2007, 67, 25–33. [Google Scholar] [CrossRef]
- Kulkarni, S. Innovative Technologies for Water Saving in Irrigated Agriculture. Int. J. Water Resour. Arid Environ. 2011, 1, 226–231. [Google Scholar]
- Sauer, T.; Havlík, P.; Schneider, U.A.; Schmid, E.; Kindermann, G.; Obersteiner, M. Agriculture and resource availability in a changing world: The role of irrigation. Water Resour. Res. 2010, 46, 1–12. [Google Scholar] [CrossRef]
- Janik, G.; Walczak, A.; Dawid, M.; Pokładek, R.; Adamczewska-Sowińska, K.; Wolski, K.; Sowiński, J.; Gronostajski, Z.; Reiner, J.; Kaszuba, M.; et al. Innovative Conception of Irrigation and Fertilization—Section in Monography; Agricultural Advisory Center in Brwinów: Brwinów, Poland, 2013; ISBN 978-83-88082-18-4. [Google Scholar]
- Janik, G.; Kłosowicz, I.; Walczak, A.; Adamczewska-Sowińska, K.; Jama-Rodzeńska, A.; Sowiński, J. Application of the TDR technique for the determination of the dynamics of the spatial and temporal distribution of water uptake by plant roots during injection irrigation. Agric. Water Manag. 2021, 252, 106911–106923. [Google Scholar] [CrossRef]
- Walczak, A.; Lipiński, M.; Janik, G. Application of the tdr sensor and the parameters of injection irrigation for the estimation of soil evaporation intensity. Sensors 2021, 21, 2309. [Google Scholar] [CrossRef]
- Kaczyński, P.; Kaszuba, M.; Dworzak, Ł. Obrotowy Rozdzielacz Hydrauliczny Obrotowy do Iniekcyjnego Nawadniania Gruntów. Polish Patent P.436556, 2021. [Google Scholar]
- McBratney, A.; Whelan, B.; Ancev, T.; Bouma, J. T. Future Directions of Precision Agriculture. Precis. Agric. 2005, 6, 7–23. [Google Scholar] [CrossRef]
- Gebbers, R.; Adamchuk, V.I. Precision Agriculture and Food Security Published by: American Association for the Advancement. Precis. Agric. Food Secur. 2017, 327, 828–831. [Google Scholar]
- Shock, C.C.; Wang, F.X. Soil water tension, a powerful measurement for productivity and stewardship. HortScience 2011, 46, 178–185. [Google Scholar] [CrossRef]
- Bittelli, M. Measuring soil water potential forwater management in agriculture: A review. Sustainability 2010, 2, 1226–1251. [Google Scholar] [CrossRef]
- King, B.A.; Bjorneberg, D.L. Characterizing droplet kinetic energy applied by moving spray-plate center-pivot irrigation sprinklers. Trans. ASABE 2010, 53, 137–145. [Google Scholar] [CrossRef]
- Richards, L.A. A pressure-membrane extraction apparatus for soil solution. Soil Sci. 1941, 51, 377–386. [Google Scholar] [CrossRef]
- Šimůnek, J.; Van Genuchten, M.T.; Šejna, M. Hydrus: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1261–1274. [Google Scholar]
- List, F.; Radu, F.A. A study on iterative methods for solving Richards’ equation. Comput. Geosci. 2016, 20, 341–353. [Google Scholar] [CrossRef]
- Naglič, B.; Kechavarzi, C.; Coulon, F.; Pintar, M. Numerical investigation of the influence of texture, surface drip emitter discharge rate and initial soil moisture condition on wetting pattern size. Irrig. Sci. 2014, 32, 421–436. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Bowman, B.T.; Drury, C.F.; Tan, C.S.; Lu, X. Indicators of good soil physical quality: Density and storage parameters. Geoderma 2002, 110, 131–146. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Puértolas, J.; Alcobendas, R.; Alarcón, J.J.; Dodd, I.C. Long-distance abscisic acid signalling under different vertical soil moisture gradients depends on bulk root water potential and average soil water content in the root zone. Plant Cell Environ. 2013, 36, 1465–1475. [Google Scholar] [CrossRef] [PubMed]
- Badr, A.E.; Abuarab, M.E. Soil moisture distribution patterns under surface and subsurface drip irrigation systems in sandy soil using neutron scattering technique. Irrig. Sci. 2013, 31, 317–332. [Google Scholar] [CrossRef]
- Elfstrand, S.; Båth, B.; Mårtensson, A. Influence of various forms of green manure amendment on soil microbial community composition, enzyme activity and nutrient levels in leek. Appl. Soil Ecol. 2007, 36, 70–82. [Google Scholar] [CrossRef]
- Baumann, D.T.; Bastiaans, L.; Kropff, M.J. Competition and crop performance in a leek-celery intercropping system. Crop Sci. 2001, 41, 764–774. [Google Scholar] [CrossRef]
- Smilde, D. Phytophthora Porri in Leek: Epidemiology and Resistance; Wageningen University & Research: Wageningen, Netherlands, 1996; ISBN 9789054855071. [Google Scholar]
- Borowy, A. Effect of Celeriac-Leek Intercropping on Weeds, Insects and Plant Growth. In Second European Allelopathy Symposium “Allelopathy—from understanding to application”; Institute of Soil Science and Plant Cultivation State Research Institute: Puławy, Poland, 2003; pp. 119–120. [Google Scholar]
- Niemiec, M.; Cupiał, M.; Szeląg-Sikora, A. Efficiency of Celeriac Fertilization with Phosphorus and Potassium Under Conditions of Integrated Plant Production. Agric. Agric. Sci. Procedia 2015, 7, 184–191. [Google Scholar] [CrossRef]
- Sogut, T.; Arioglu, H. Plant density and sowing date effects on sugarbeet yield and quality. J. Agron. 2004, 3, 215–218. [Google Scholar] [CrossRef]
- Yang, X.; You, X. Estimating parameters of van genuchten model for soil water retention curve by intelligent algorithms. Appl. Math. Inf. Sci. 2013, 7, 1977–1983. [Google Scholar] [CrossRef]
- Elmaloglou, S.; Diamantopoulos, E. Soil water dynamics under surface trickle irrigation as affected by soil hydraulic properties, discharge rate, dripper spacing and irrigation duration. Irrig. Drain. 2010, 59, 254–263. [Google Scholar] [CrossRef]
- Arbat, G.; Cufí, S.; Duran-Ros, M.; Pinsach, J.; Puig-Bargués, J.; Pujol, J.; de Cartagena, F.R. Modeling approaches for determining dripline depth and irrigation frequency of subsurface drip irrigated rice on different soil textures. Water 2020, 12, 1724. [Google Scholar] [CrossRef]
- Li, J.; Liu, Y. Water and nitrate distributions as affected by layered-textural soil and buried dripline depth under subsurface drip fertigation. Irrig. Sci. 2011, 29, 469–478. [Google Scholar] [CrossRef]
- Mali, S.S.; Jha, B.K.; Singh, R.; Meena, M. Bitter Gourd Response to Surface and Subsurface Drip Irrigation under Different Fertigation Levels. Irrig. Drain. 2017, 66, 615–625. [Google Scholar] [CrossRef]
- Gliński, J.; Horabik, J.L.J. Encyclopedia of Agrophyscis; Springer: Berlin, Germany, 2011. [Google Scholar]
- Smit, A.L.; Zuin, A. Root growth dynamics of Brussels sprouts (Brassica olearacea van gemmifera ) and leeks (Allium porrum L.) as reflected by root length, root colour and UV fluorescence. Plant Soil 2021, 185, 271–280. [Google Scholar] [CrossRef]
- Hossne, A.J.; Jesus Méndez, N.; Leonett, F.A.; Meneses, J.E.; Gil, J.A. Maize root growth under regular water content, subjected to compaction, irrigation frequencies, and shear stress. Rev. Fac. Nac. Agron. Medellin 2016, 69, 7867–7880. [Google Scholar] [CrossRef]
- García-Gaines, R.A.; Frankenstein, S. USCS and the USDA Soil Classification System: Development of a Mapping Scheme. United States Army Corps of Engineers: Washington DC, USA, 2015; 37. [Google Scholar]
- Sulewska, M.J. Neural modelling of compactibility characteristics of cohesionless soil. Comput. Assist. Mech. Eng. Sci. 2010, 17, 27–40. [Google Scholar]
- Kaczyński, P.J.; Kaszuba, M.D.; Dworzak, Ł.J.; Hawryluk, M. Iniektor do Nawadniania Gruntu 2019. nr W.128720, Polish Patent Office: Warszawa, Poland. Available online: https://ewyszukiwarka.pue.uprp.gov.pl/search/pwp-details/W.128720?lng=en.
- Isweek.com. YF-B Series Water Flow Sensor Description. Available online: https://www.isweek.com/product/water-flow-sensor-yf-b1-b2-b3-b7_2430.html (accessed on 5 June 2021).
- Bianchi, A.; Masseroni, D.; Thalheimer, M.; de Medici, L.O.; Facchi, A. Field irrigation management through soil water potential measurements: A review. Ital. J. Agrometeorol. 2017, 22, 25–38. [Google Scholar]
- Evett, S. Coaxial Multiplexer for time domain rflectometry measurement of soil water content and bulk electrical conductivity. Encylopedia Water Sci. 2003, 41, 181–190. [Google Scholar]
- Jones, S.B.; Sheng, W.; Xu, J.; Robinson, D.A. Electromagnetic Sensors for Water Content: The Need for International Testing Standards. In Proceedings of the 2018 12th International Conference on Electromagnetic Wave Interaction with Water and Moist Substances (ISEMA), Lublin, Poland, 4–7 June 2018. [Google Scholar]
- Šarec, P.; Šarec, O.; Prošek, V.; Dobek, T.K. Description of new design of an instrument measuring soil humidity. Inżynieria Rol. 2008, 11, 219–225. [Google Scholar]
- Susha Lekshmi, S.U.; Singh, D.N.; Shojaei Baghini, M. A critical review of soil moisture measurement. Meas. J. Int. Meas. Confed. 2014, 54, 92–105. [Google Scholar]
- Malicki, M.A.; Plagge, R.; Roth, C.H. Improving the calibration of dielectric TDR soil moisture determination taking into account the solid soil. Eur. J. Soil Sci. 1996, 47, 357–366. [Google Scholar] [CrossRef]
- Skierucha, W. Accuracy of soil moisture measurement by TDR technique. Int. Agrophys. 2000, 14, 417–426. [Google Scholar]
- Skierucha, W.; Wilczek, A.; Alokhina, O. Calibration of a TDR probe for low soil water content measurements. Sens. Actuators A Phys. 2008, 147, 544–552. [Google Scholar] [CrossRef]
- Skierucha, W.; Wilczek, A.; Szypłowska, A.; Sławiński, C.; Lamorski, K. A TDR-based soil moisture monitoring system with simultaneous measurement of soil temperature and electrical conductivity. Sensors 2012, 12, 13545–13566. [Google Scholar] [CrossRef]
- Manoel, C.; Vaz, P.; Hopmans, J.W. with a Combined Penetrometer—TDR Moisture Probe. Soil Sci. Soc. Am. J. 2001, 65, 4–12. [Google Scholar]
- Gong, Y.; Cao, Q.; Sun, Z. The effects of soil bulk density, clay content and temperature on soil water content measurement using time-domain reflectometry. Hydrol. Process. 2003, 17, 3601–3614. [Google Scholar] [CrossRef]
- Chen, R.P.; Chen, Y.M.; Xu, W.; Yu, X. Measurement of electrical conductivity of pore water in saturated sandy soils using time domain reflectometry (TDR) measurements. Can. Geotech. J. 2012, 47, 197–206. [Google Scholar] [CrossRef]
- Telichenko, V.; Rimshin, V.; Eremeev, V.; Kurbatov, V. Mathematical modeling of groundwaters pressure distribution in the underground structures by cylindrical form zone. MATEC Web Conf. 2018, 196, 02025. Available online: https://www.matec-conferences.org/articles/matecconf/abs/2018/55/matecconf_rsp2018_02025/matecconf_rsp2018_02025.html (accessed on 6 January 2021).
- Karlberg, L.; Jansson, P.E.; Gustafsson, D. Model-based evaluation of low-cost drip-irrigation systems and management strategies using saline water. Irrig. Sci. 2007, 25, 387–399. [Google Scholar] [CrossRef]
- Koumanov, K.S.; Hopmans, J.W.; Schwankl, L.W. Soil Water Dynamics in the Root Zone of a Micro-Sprikler Irrigated Almond Tree. Available online: https://www.ishs.org/ishs-article/664_46 (accessed on 6 June 2021).
- Alomran, A.M. Management of Irrigation Water Salinity in Greenhouse Tomato Production under Calcareous Sandy Soil and Drip Irrigation. J. Agric. Sci. Technol. 2012, 14, 939–950. [Google Scholar]
- Simionesei, L.; Ramos, T.B.; Brito, D.; Jauch, E.; Leitão, P.C.; Almeida, C.; Neves, R. Numerical Simulation of Soil Water Dynamics Under Stationary Sprinkler Irrigation With Mohid-Land. Irrig. Drain. 2016, 65, 98–111. [Google Scholar] [CrossRef]
- Elnesr, M.N.; Alazba, A.A. Computational evaluations of HYDRUS simulations of drip irrigation in 2D and 3D domains (i-Surface drippers). Comput. Electron. Agric. 2019, 162, 189–205. [Google Scholar] [CrossRef]
- Shan, G.; Sun, Y.; Zhou, H.; Schulze Lammers, P.; Grantz, D.A.; Xue, X.; Wang, Z. A horizontal mobile dielectric sensor to assess dynamic soil water content and flows: Direct measurements under drip irrigation compared with HYDRUS-2D model simulation. Biosyst. Eng. 2019, 179, 13–21. [Google Scholar] [CrossRef]
- Lipnikov, K.; Manzini, G.; Shashkov, M. Mimetic finite difference method. J. Comput. Phys. 2014, 257, 1163–1227. [Google Scholar] [CrossRef]
- Chávez-Negrete, C.; Domínguez-Mota, F.J.; Santana-Quinteros, D. Numerical solution of Richards’ equation of water flow by generalized finite differences. Comput. Geotech. 2018, 101, 168–175. [Google Scholar] [CrossRef]
- Curry, C.W.; Bennett, R.H.; Hulbert, M.H.; Curry, K.J.; Faas, R.W. Comparative study of sand porosity and a technique for determing porosity of undisturbed marine sediment. Mar. Georesources Geotechnol. 2004, 22, 231–252. [Google Scholar] [CrossRef]
- E-TEST Sp. z o.o. Innovative Measurement Techniques for Environment and Soil Science. Available online: https://www.e-test.eu/ (accessed on 20 January 2021).
- Douh, B.; Boujelben, A.; Khila, S.; Bel Haj Mguidiche, A. Effect of Subsurface Drip Irrigation System Depth on Soil Water Content Distribution At Different Depths and Different Times After Irrigation. Larhyss. J. 2013, 13, 7–16. [Google Scholar]
- Barker, J.B.; Franz, T.E.; Heeren, D.M.; Neale, C.M.U.; Luck, J.D. Soil water content monitoring for irrigation management: A geostatistical analysis. Agric. Water Manag. 2017, 188, 36–49. [Google Scholar] [CrossRef]
- Bear, J. The General Conservation Principle. In Dynamics of fluids in porous media; Courier Corporation: Chelmsford, MA, USA, 2013; pp. 74–113. [Google Scholar]
- Sahimi, M. The Mass Conservation Equation. In Flow and Transport in Porous Media and Fractured Rock: From Classical Methods to Modern Approaches; John Wiley and Sons: Weinheim, Germany, 2011. [Google Scholar]
- Quinones, H.; Ruelle, P.; Nemeth, I. Comparison of three calibration procedures for tdr soil moisture sensors. Irrig. Drain. 2003, 52, 203–217. [Google Scholar] [CrossRef]
- Pfletschinger, H.; Engelhardt, I.; Piepenbrink, M.; Königer, F.; Schuhmann, R.; Kallioras, A.; Schüth, C. Soil column experiments to quantify vadose zone water fluxes in arid settings. Environ. Earth Sci. 2012, 65, 1523–1533. [Google Scholar] [CrossRef]
- Janik, G.; Wolski, K.; Daniel, A.; Albert, M.; Skierucha, W.; Wilczek, A.; Szyszkowski, P.; Walczak, A. TDR technique for estimating the intensity of evapotranspiration of turfgrasses. Sci. World J. Hindawi 2015, 2015, 626545. [Google Scholar] [CrossRef] [PubMed]
- Mmolawa, K.; Or, D. Root zone solute dynamics under drip irrigation: A review. Plant Soil 2000, 222, 163–190. [Google Scholar] [CrossRef]
- Janik, G.; Dawid, M.; Walczak, A.; Słowińska-Osypiuk, J.; Skierucha, W.; Wilczek, A.; Daniel, A. Application of the TDR technique for the detection of changes in the internal structure of an earthen flood levee. J. Geophys. Eng. 2017, 14, 292–302. [Google Scholar] [CrossRef]
- Elaiuy, M.L.C.; Dos Santos, L.N.S.; De Sousa, A.C.M.; Souza, C.F.; Matsura, E.E. Wet bulbs from the subsurface drip irrigation with water supply and treated sewage effluent. Eng. Agric. 2015, 35, 242–253. [Google Scholar] [CrossRef]
- Saefuddin, R.; Saito, H.; Šimůnek, J. Experimental and numerical evaluation of a ring-shaped emitter for subsurface irrigation. Agric. Water Manag. 2019, 211, 111–122. [Google Scholar] [CrossRef]
- Wysocka, M.; Szypcio, Z.; Tymosiak, D. The speed of capillary raise in granular soils. Civ. Environ. Eng. 2013, 4, 167–172. [Google Scholar]
- Hewelke, P.; Gnatowski, T.; Hewelke, E.; Tyszka, J.; Żakowicz, S. Analysis of water retention capacity for select forest soils in Poland. Polish J. Environ. Stud. 2015, 24, 1013–1019. [Google Scholar] [CrossRef]
- Janik, G.; Szpila, M.; Slowinska, J.; Brej, G.; Turkiewicz, M.; Skierucha, W.; Pastuszka, T. Method for the determination of the sensitivity zone of the probe. Acta Agrophys. 2011, 18, 269–286. [Google Scholar]
- Subbaiah, R. A review of models for predicting soil water dynamics during trickle irrigation. Irrig. Sci. 2013, 31, 225–258. [Google Scholar] [CrossRef]
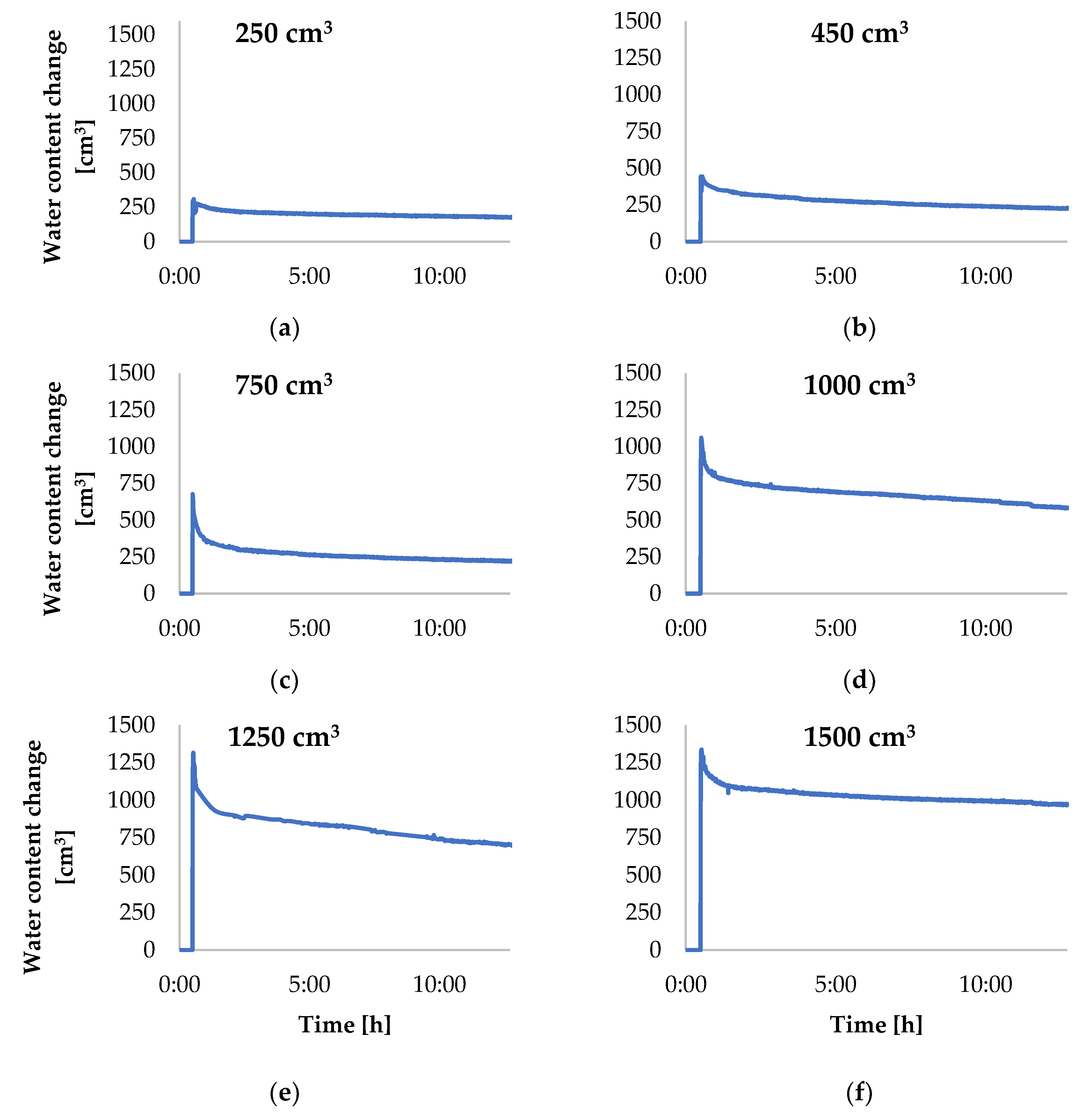
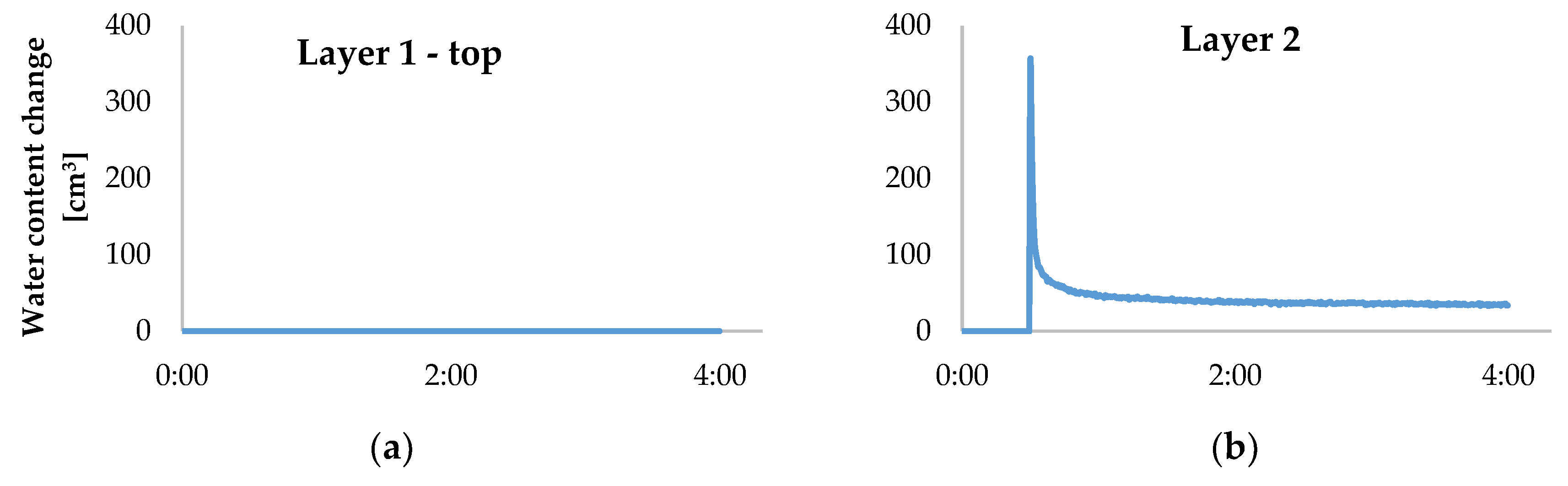
| Planned Water Dose | Calculated Water Dose | Relative Error |
|---|---|---|
| 250 | 285 | 14 |
| 450 | 435 | 3 |
| 750 | 675 | 10 |
| 1000 | 950 | 5 |
| 1250 | 1200 | 4 |
| 1500 | 1315 | 12 |
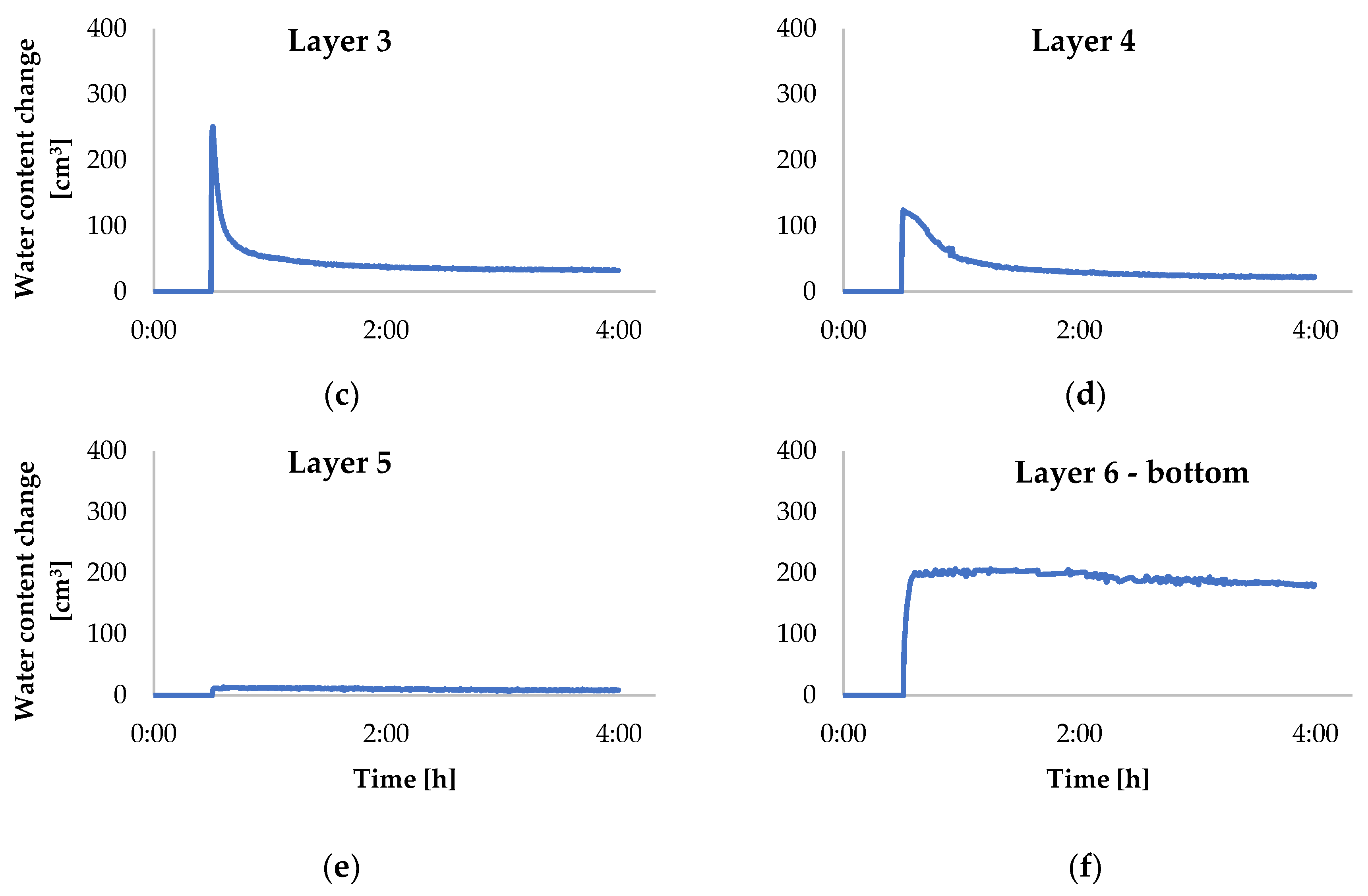
| Planned Water Dose | Calculated Water Dose at Injection Moment | Calculated Water Content after 12 h | |||
|---|---|---|---|---|---|
| 250 | 285 | 175 | 110 | 15 | 274 |
| 450 | 435 | 226 | 209 | 17 | 311 |
| 750 | 675 | 222 | 453 | 22 | 402 |
| 1000 | 950 | 589 | 361 | 25 | 457 |
| 1250 | 1200 | 705 | 495 | 27 | 493 |
| 1500 | 1315 | 969 | 346 | 33 | 603 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Walczak, A.; Szypłowska, A.; Janik, G.; Pęczkowski, G. Dynamics of Volumetric Moisture in Sand Caused by Injection Irrigation—Physical Model. Water 2021, 13, 1603. https://doi.org/10.3390/w13111603
Walczak A, Szypłowska A, Janik G, Pęczkowski G. Dynamics of Volumetric Moisture in Sand Caused by Injection Irrigation—Physical Model. Water. 2021; 13(11):1603. https://doi.org/10.3390/w13111603
Chicago/Turabian StyleWalczak, Amadeusz, Agnieszka Szypłowska, Grzegorz Janik, and Grzegorz Pęczkowski. 2021. "Dynamics of Volumetric Moisture in Sand Caused by Injection Irrigation—Physical Model" Water 13, no. 11: 1603. https://doi.org/10.3390/w13111603
APA StyleWalczak, A., Szypłowska, A., Janik, G., & Pęczkowski, G. (2021). Dynamics of Volumetric Moisture in Sand Caused by Injection Irrigation—Physical Model. Water, 13(11), 1603. https://doi.org/10.3390/w13111603






