Application of SWAT in Hydrological Simulation of Complex Mountainous River Basin (Part I: Model Development)
Abstract
1. Introduction
2. Materials and Methods
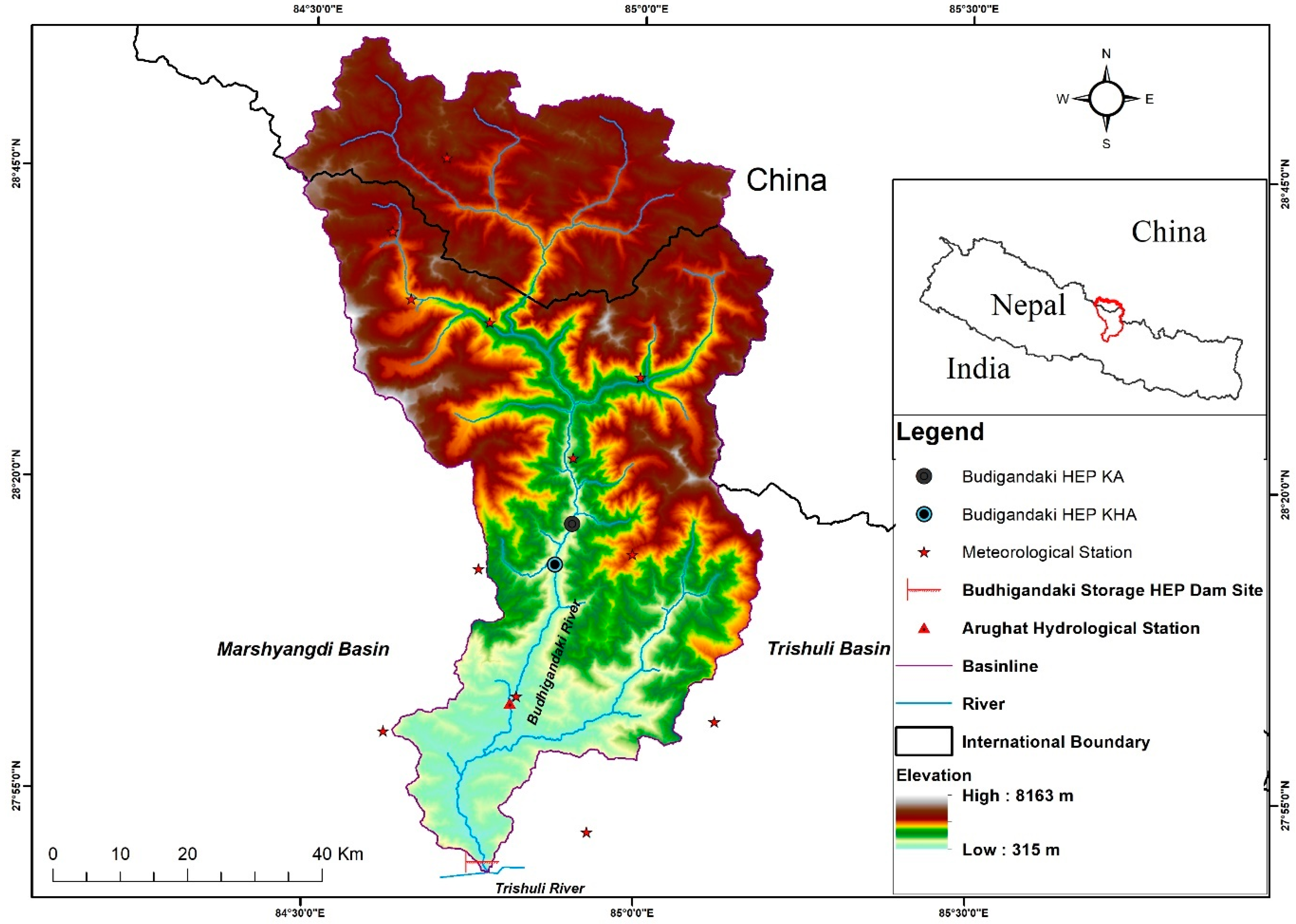
2.1. Study Area
2.2. Data Used
2.2.1. Meteorological Data
2.2.2. Flow Data
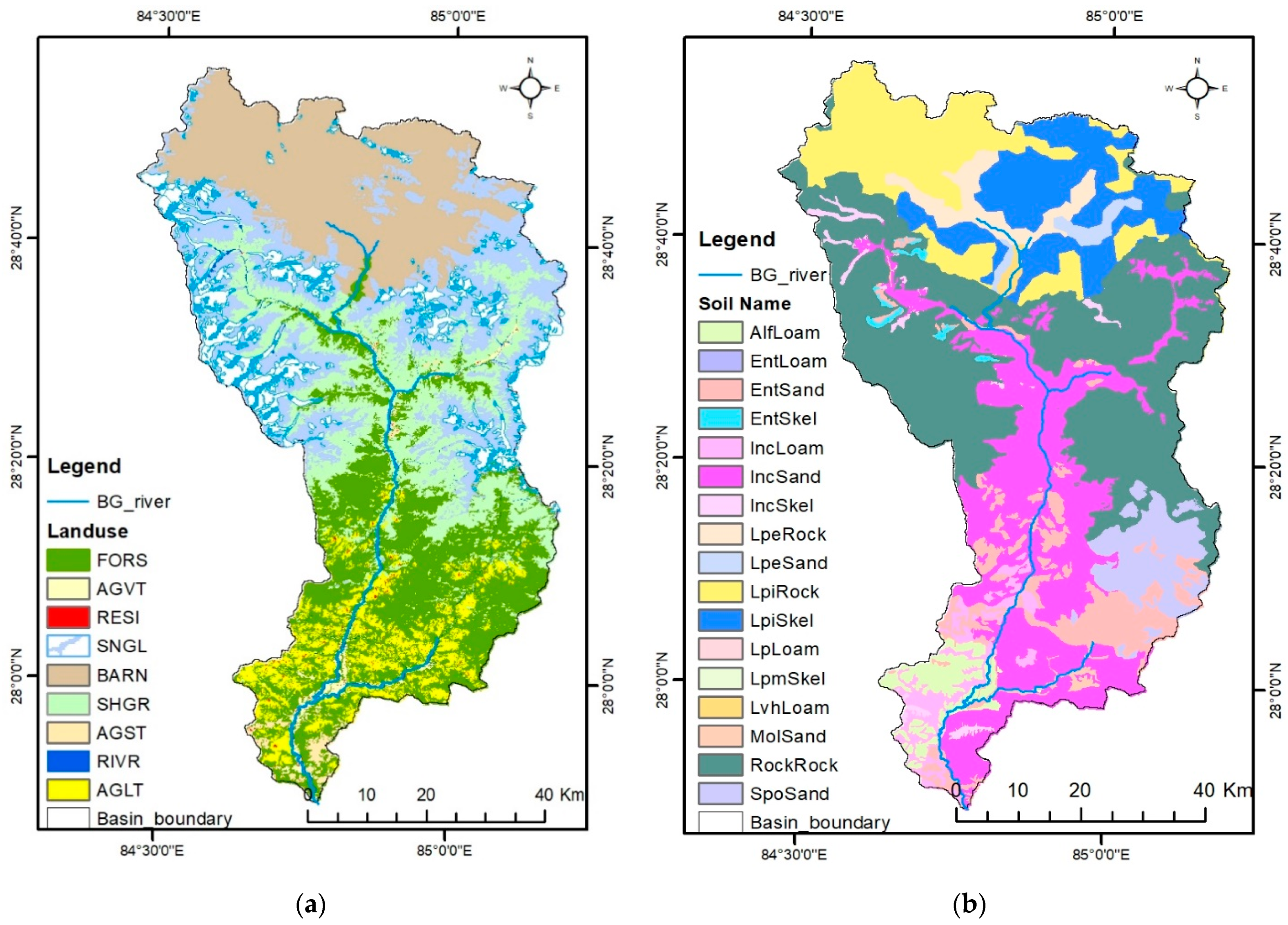
2.2.3. Spatial Data
2.3. SWAT Model
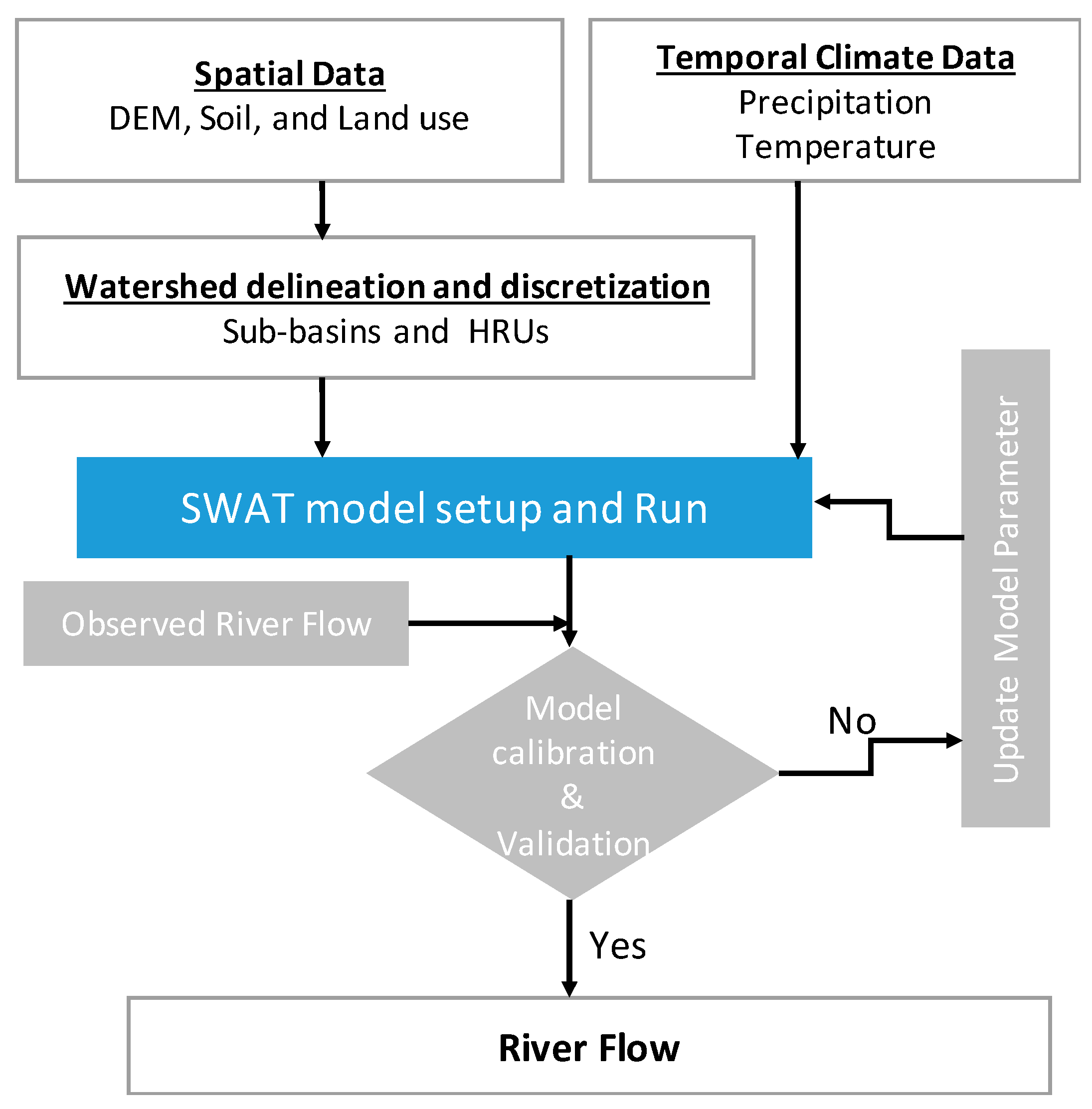
2.4. Model Setup and Simulation
Performance Evaluation Criteria
3. Results
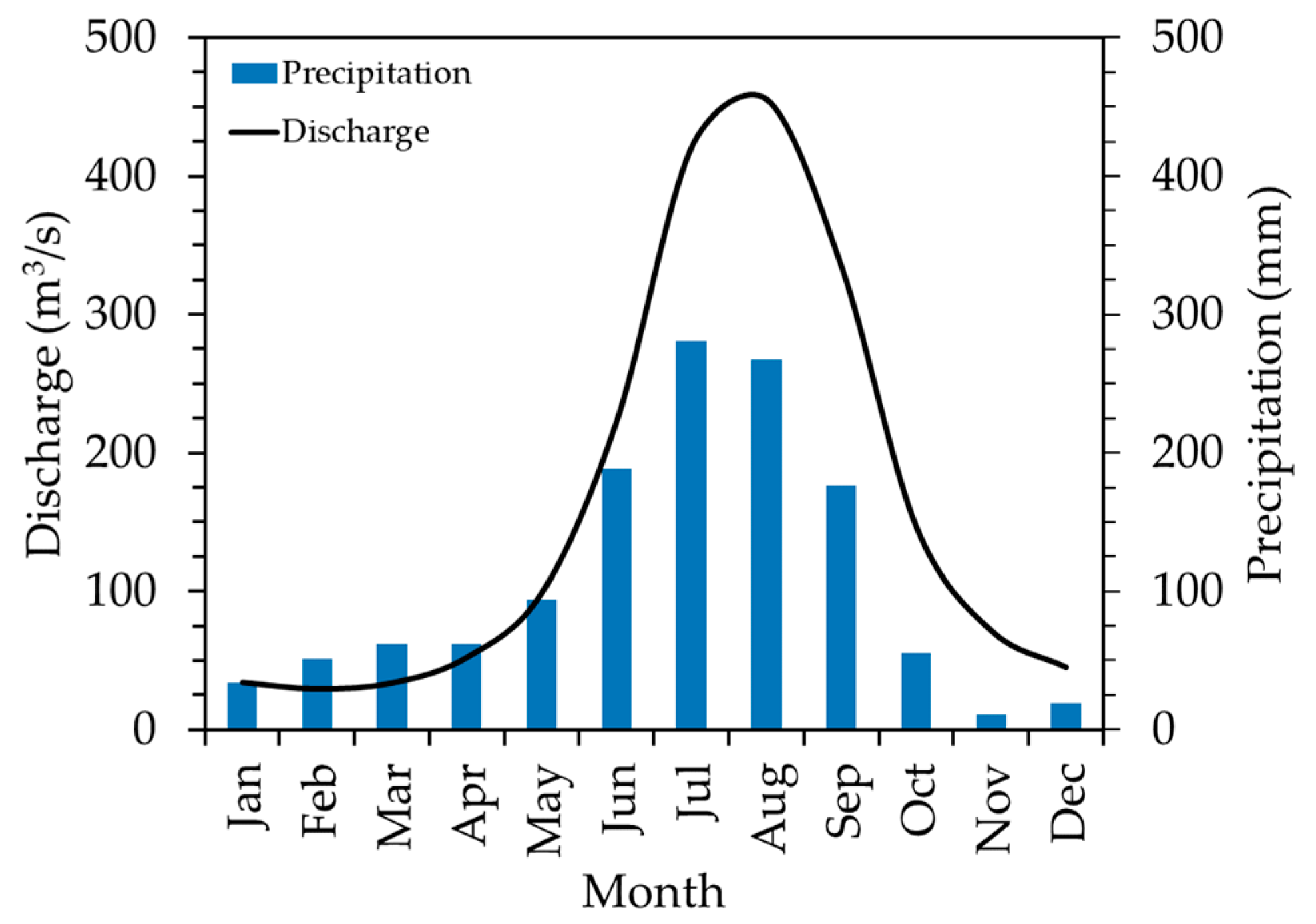
3.1. Observed Rainfall-Runoff Characteristics
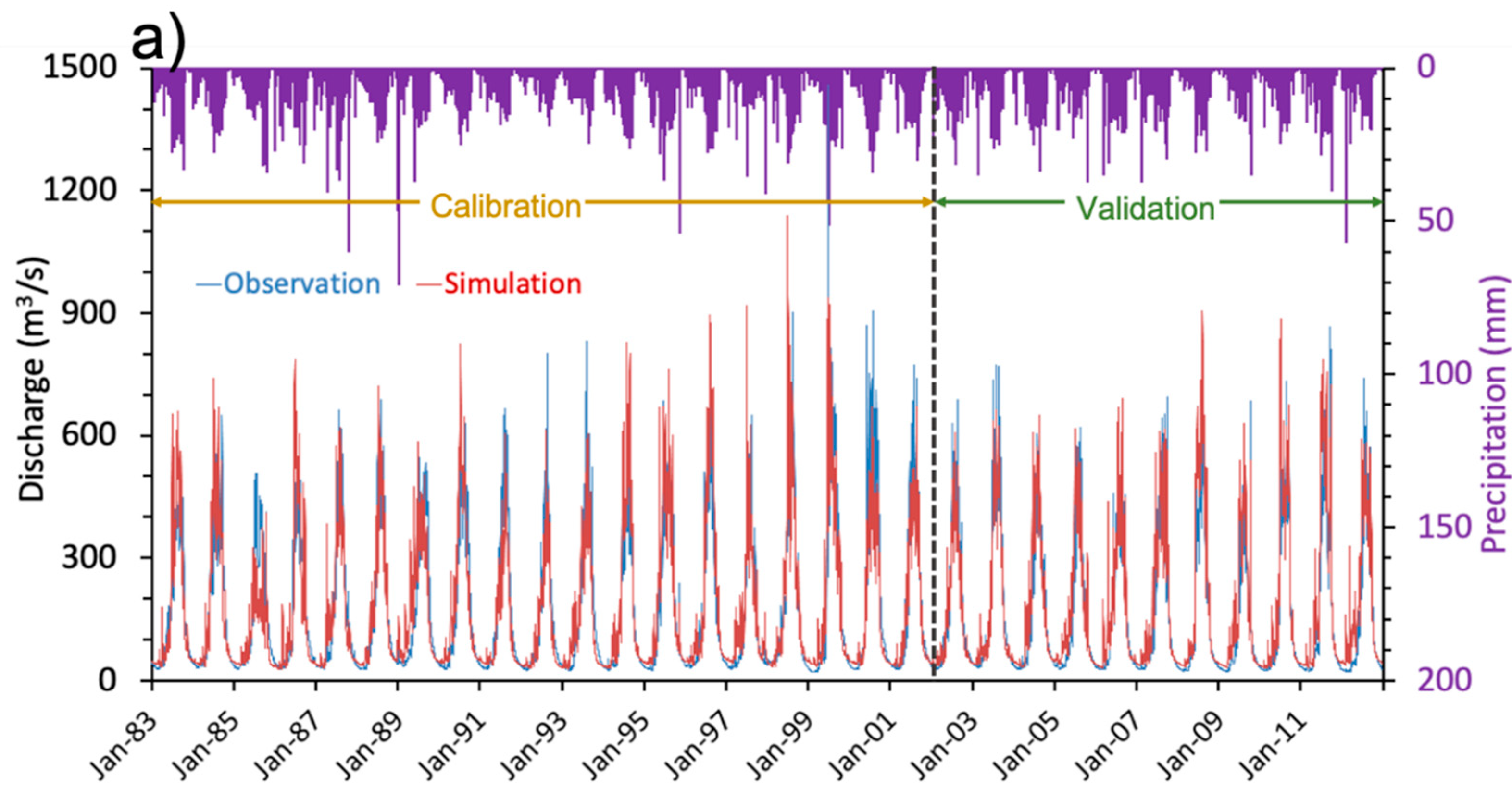
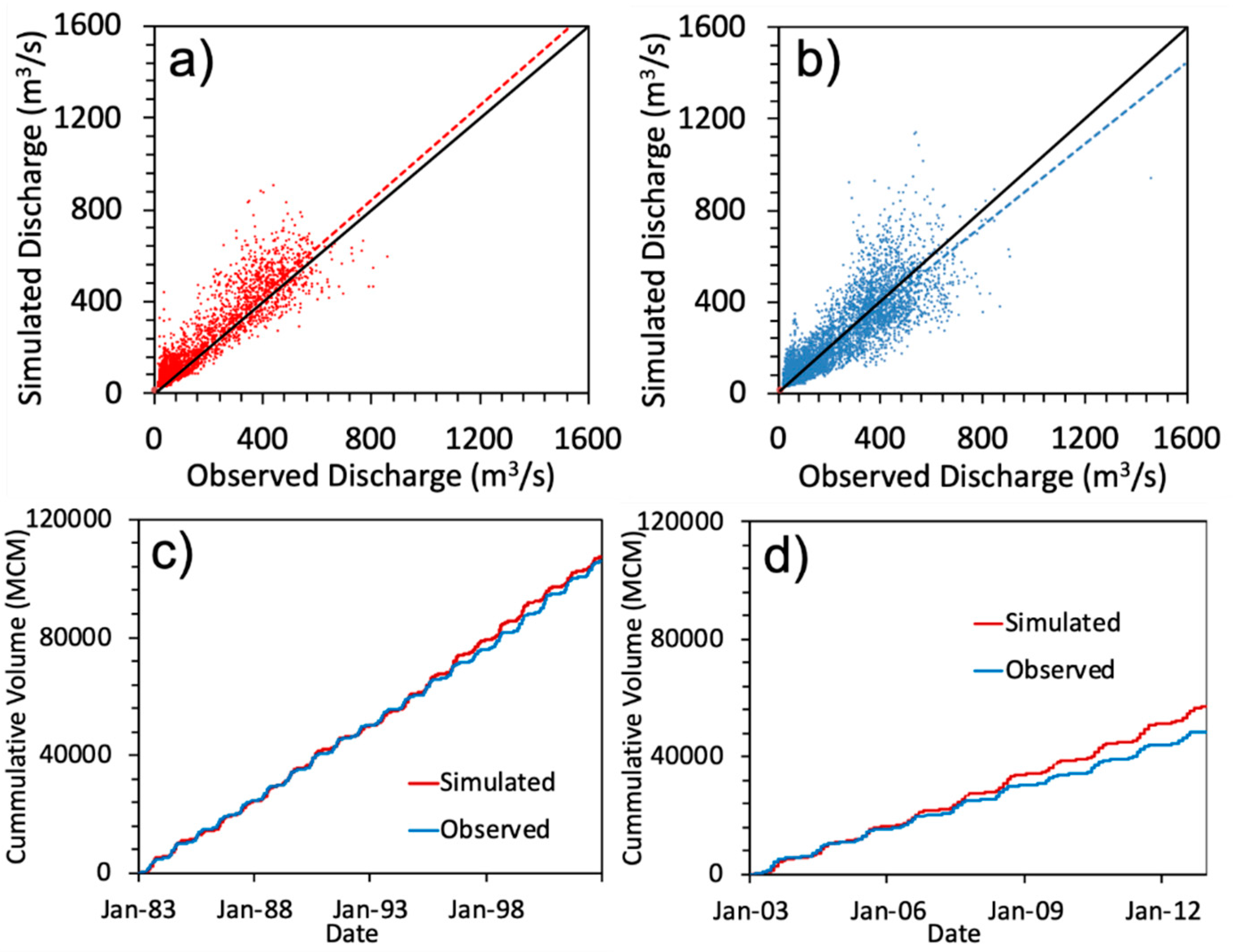
3.2. SWAT Model Performance
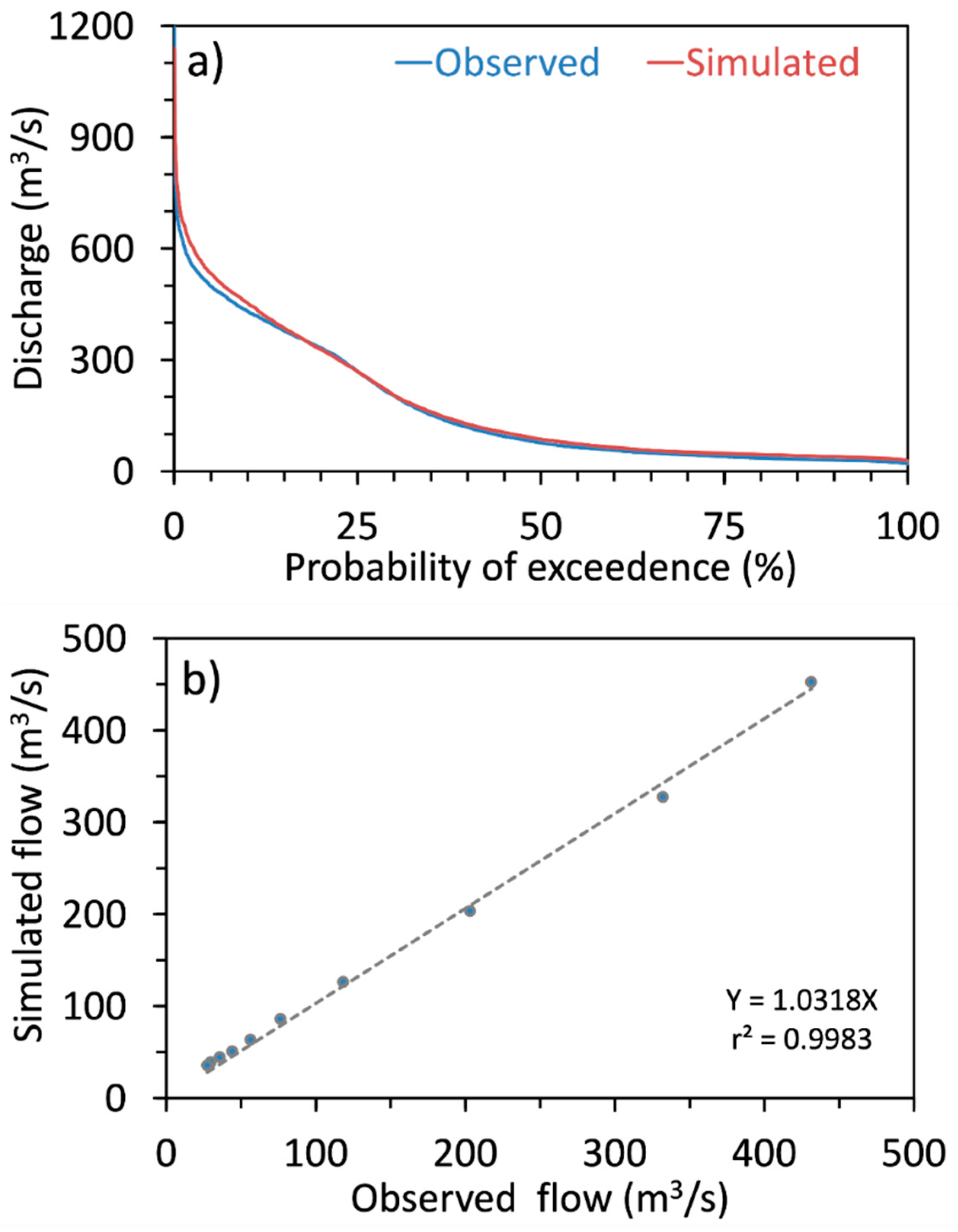
3.3. Additional Validation of SWAT at Supplementary Stations
3.4. Flow Duration Curve
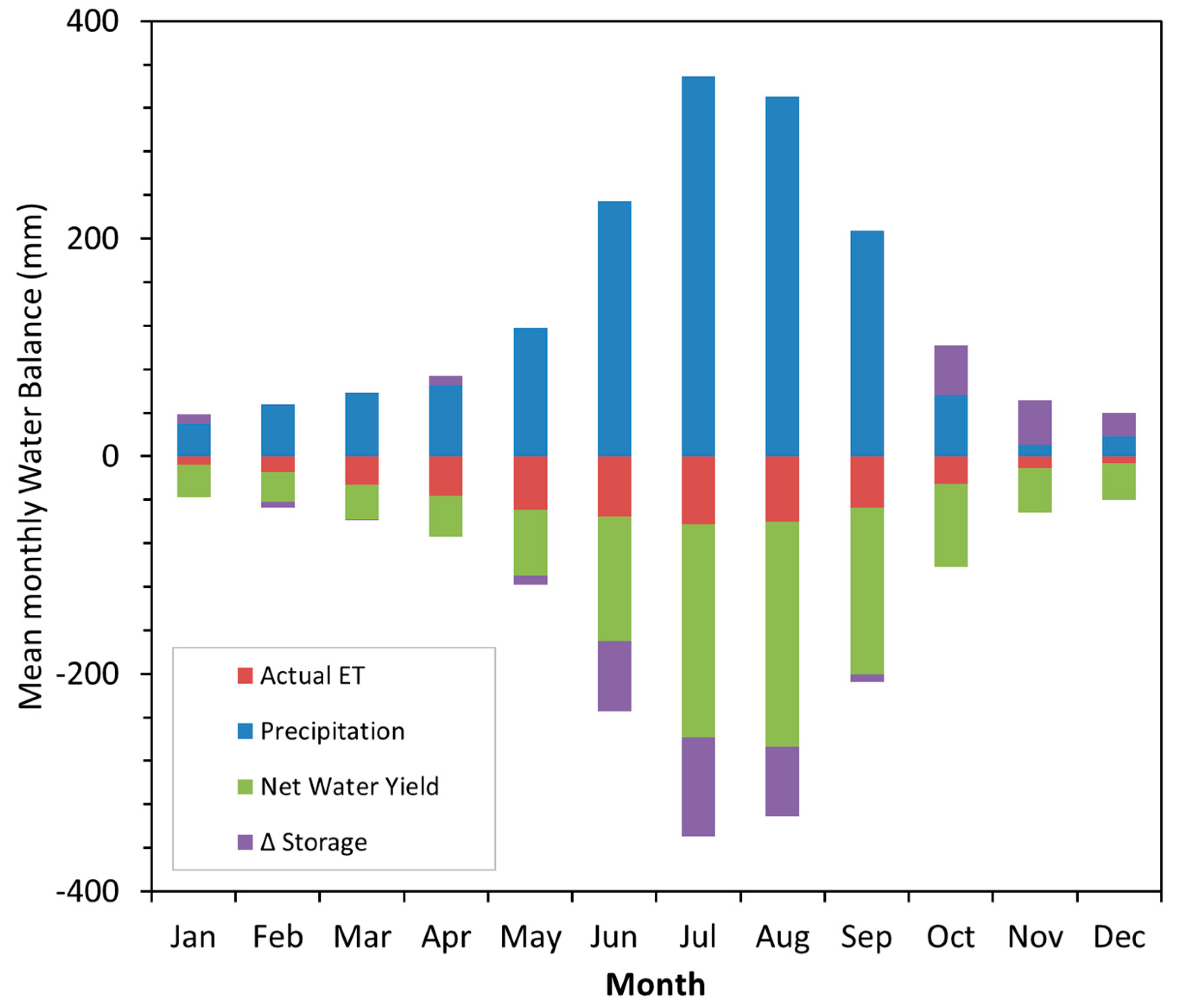
3.5. Water Balance of the Budhigandaki Basin
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; TATA McGrawHill Inc.: New York, NY, USA, 1988. [Google Scholar]
- Zhang, Q.; Knowles, J.F.; Barnes, R.T.; Cowie, R.M.; Rock, N.; Williams, M.W. Surface and subsurface water contributions to streamflow from a mesoscale watershed in complex mountain terrain. Hydrol. Process. 2018, 32, 954–967. [Google Scholar] [CrossRef]
- Tallaksen, L.M. A review of baseflow recession analysis. J. Hydrol. 1995, 165, 349–370. [Google Scholar] [CrossRef]
- Dobriyal, P.; Badola, R.; Tuboi, C.; Hussain, S.A. A review of methods for monitoring streamflow for sustainable water resource management. Appl. Water Sci. 2017, 7, 2617–2628. [Google Scholar] [CrossRef]
- Loukas, A.; Vasiliades, L. Streamflow simulation methods for ungauged and poorly gauged watersheds. Nat. Hazards Earth Syst. Sci. 2014, 14, 1641–1661. [Google Scholar] [CrossRef]
- Shin, S.; Pokhrel, Y.; Talchabhadel, R.; Panthi, J. Spatio-temporal dynamics of hydrologic changes in the Himalayan river basins of Nepal using high-resolution hydrological-hydrodynamic modeling. J. Hydrol. 2021, 598, 126209. [Google Scholar] [CrossRef]
- Alford, D.; Armstrong, R.; Racoviteanu, A. Glacier Retreat in the Nepal Himalaya: The role of glaciers in stream flow from the Nepal Himalaya. World Bank Tech. Rep. Forthcom. 2011. [Google Scholar] [CrossRef]
- Hishinuma, S.; Takeuchi, K.; Magome, J. Challenges of hydrological analysis for water resource development in semi-arid mountainous regions: Case study in Iran. Hydrol. Sci. J. 2014, 59, 1718–1737. [Google Scholar] [CrossRef]
- Viviroli, D.; Dürr, H.H.; Messerli, B.; Meybeck, M.; Weingartner, R. Mountains of the world, water towers for humanity: Typology, mapping, and global significance. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Horton, R.E. Drainage-basin characteristics. EOS Trans. Am. Geophys. Union 1932, 13, 350–361. [Google Scholar] [CrossRef]
- Kale, V.S. Fluvial geomorphology of Indian rivers: An overview. Prog. Phys. Geogr. 2002, 26, 400–433. [Google Scholar] [CrossRef]
- Higuchi, K.; Ageta, Y.; Yasunari, T.; Inoue, J. Characteristics of precipitation during the monsoon season in high-mountain areas of the Nepal Himalaya. IAHS Publ. 1982, 138, 21–30. [Google Scholar]
- Shrestha, A.B.; Wake, C.P.; Dibb, J.E.; Mayewski, P.A. Precipitation fluctuations in the Nepal Himalaya and its vicinity and relationship with some large scale climatological parameters. Int. J. Climatol. J. R. Meteorol. Soc. 2000, 20, 317–327. [Google Scholar] [CrossRef]
- Kansakar, S.R.; Hannah, D.M.; Gerrard, J.; Rees, G. Spatial pattern in the precipitation regime of Nepal. Int. J. Climatol. J. R. Meteorol. Soc. 2004, 24, 1645–1659. [Google Scholar] [CrossRef]
- Putkonen, J.K. Continuous Snow and Rain Data at 500 to 4400 m Altitude near Annapurna, Nepal, 1999–2001. Arct. Antarct. Alp. Res. 2004, 36, 244–248. [Google Scholar] [CrossRef]
- Ichiyanagi, K.; Yamanaka, M.D.; Muraji, Y.; Vaidya, B.K. Precipitation in Nepal between 1987 and 1996. Int. J. Climatol. J. R. Meteorol. Soc. 2007, 27, 1753–1762. [Google Scholar] [CrossRef]
- Devkota, R.P.; Pandey, V.P.; Bhattarai, U.; Shrestha, H.; Adhikari, S.; Dulal, K.N. Climate change and adaptation strategies in Budhi Gandaki River Basin, Nepal: A perception-based analysis. Clim. Chang. 2017, 140, 195–208. [Google Scholar] [CrossRef]
- Pokharel, B.; Wang, S.S.; Meyer, J.; Marahatta, S.; Nepal, B.; Chikamoto, Y.; Gillies, R. The east–west division of changing precipitation in Nepal. Int. J. Climatol. 2020, 40, 3348–3359. [Google Scholar] [CrossRef]
- WMO. Calculation of Monthly and Annual 30-Year Standard Normals, Prepared by a Meeting of Experts, Washington, DC, USA, March 1989; WCDP-No. 10, WMO-TD/No. 341; World Meteorological Organization: Geneva, Switzerland, 1989. [Google Scholar]
- Jain, S.K.; Jain, S.K.; Jain, N.; Xu, C.-Y. Hydrologic modeling of a Himalayan mountain basin by using the SWAT mode. Hydrol. Earth Syst. Sci. Discuss. 2017, 1–26. [Google Scholar] [CrossRef]
- Woolridge, D.D.; Niemann, J.D. Mountain Basin Hydrologic Study. 2018. Available online: https://dnrweblink.state.co.us/dwr/0/edoc/3377613/DWR_3377613.pdf?searchid=10250736-fd55-4a8f-a43f-b9270fad6e92 (accessed on 22 December 2020).
- Meng, F.; Sa, C.; Liu, T.; Luo, M.; Liu, J.; Tian, L. Improved Model Parameter Transferability Method for Hydrological Simulation with SWAT in Ungauged Mountainous Catchments. Sustainability 2020, 12, 3551. [Google Scholar] [CrossRef]
- Marahatta, S.; Devkota, L.; Aryal, D. Hydrological Modeling: A Better Alternative to Empirical Methods for Monthly Flow Estimation in Ungauged Basins. J. Water Resour. Prot. 2021, 254–270. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef]
- Pandey, V.P.; Dhaubanjar, S.; Bharati, L.; Thapa, B.R. Spatio-temporal distribution of water availability in Karnali-Mohana Basin, Western Nepal: Hydrological model development using multi-site calibration approach (Part-A). J. Hydrol. Reg. Stud. 2020, 29, 100690. [Google Scholar] [CrossRef]
- Zhou, X.; Helmers, M.; Qi, Z. Modeling of subsurface tile drainage using MIKE SHE. Appl. Eng. Agric. 2013, 29, 865–873. [Google Scholar]
- Devkota, L.P.; Gyawali, D.R. Impacts of climate change on hydrological regime and water resources management of the Koshi River Basin, Nepal. J. Hydrol. Reg. Stud. 2015, 4, 502–515. [Google Scholar] [CrossRef]
- Sitterson, J.; Knightes, C.; Parmar, R.; Wolfe, K.; Avant, B.; Muche, M. An Overview of Rainfall-Runoff Model Types. 2018. Available online: https://cfpub.epa.gov/si/si_public_record_report.cfm?dirEntryId=339328&Lab=NERL (accessed on 12 January 2021).
- Hossain, S.; Hewa, G.A.; Wella-Hewage, S. A Comparison of continuous and event-based rainfall–runoff (RR) modelling using EPA-SWMM. Water 2019, 11, 611. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R.; Ramanarayanan, T.S.; Arnold, J.G.; Bednarz, S.T.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large area hydrologic modeling and assessment part I: Model development 1. JAWRA J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Williams, J.R.; Arnold, J.G.; Kiniry, J.R.; Gassman, P.W.; Green, C.H. History of model development at Temple, Texas. Hydrol. Sci. J. 2008, 53, 948–960. [Google Scholar] [CrossRef]
- Douglas-Mankin, K.R.; Srinivasan, R.; Arnold, J.G. Soil and Water Assessment Tool (SWAT) model: Current developments and applications. Trans. ASABE 2010, 53, 1423–1431. [Google Scholar] [CrossRef]
- Tan, M.L.; Gassman, P.W.; Srinivasan, R.; Arnold, J.G.; Yang, X. A review of SWAT studies in Southeast Asia: Applications, challenges and future directions. Water 2019, 11, 914. [Google Scholar] [CrossRef]
- Das, B.; Jain, S.; Singh, S.; Thakur, P. Evaluation of multisite performance of SWAT model in the Gomti River Basin, India. Appl. Water Sci. 2019, 9, 1–10. [Google Scholar] [CrossRef]
- Van Griensven, A.; Ndomba, P.; Yalew, S.; Kilonzo, F. Critical review of SWAT applications in the upper Nile basin countries. Hydrol. Earth Syst. Sci. 2012, 16, 3371–3381. [Google Scholar] [CrossRef]
- Fukunaga, D.C.; Cecílio, R.A.; Zanetti, S.S.; Oliveira, L.T.; Caiado, M.A.C. Application of the SWAT hydrologic model to a tropical watershed at Brazil. Catena 2015, 125, 206–213. [Google Scholar] [CrossRef]
- Anand, J.; Gosain, A.K.; Khosa, R.; Srinivasan, R. Regional scale hydrologic modeling for prediction of water balance, analysis of trends in streamflow and variations in streamflow: The case study of the Ganga River basin. J. Hydrol. Reg. Stud. 2018, 16, 32–53. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, J.; Gao, C.; Ruben, G.B.; Wang, G. Assessing the uncertainties of four precipitation products for swat modeling in Mekong River basin. Remote Sens. 2019, 11, 304. [Google Scholar] [CrossRef]
- CARD (Center for Agricultural and Rural Development). Swat Lit. Database Peer-Reviewed J. Artic; Center for Agricultural and Rural Development—Iowa State University: Ames, IA, USA, 2020; Available online: https://www.card.iastate.edu/swatarticles (accessed on 13 January 2021).
- Shrestha, S.; Shrestha, M.; Shrestha, P.K. Evaluation of the SWAT model performance for simulating river discharge in the Himalayan and tropical basins of Asia. Hydrol. Res. 2018, 49, 846–860. [Google Scholar] [CrossRef]
- Bharati, L.; Gurung, P.; Jayakody, P.; Smakhtin, V.; Bhattarai, U. The projected impact of climate change on water availability and development in the Koshi Basin, Nepal. Mt. Res. Dev. 2014, 34, 118–130. [Google Scholar] [CrossRef]
- Omani, N.; Srinivasan, R.; Karthikeyan, R.; Smith, P.K. Hydrological modeling of highly glacierized basins (Andes, Alps, and Central Asia). Water 2017, 9, 111. [Google Scholar] [CrossRef]
- Talchabhadel, R.; Nakagawa, H.; Kawaike, K.; Yamanoi, K.; Aryal, A.; Bhatta, B.; Karki, S. SWAT modeling for assessing future scenarios of soil erosion in West Rapti River Basin of Nepal. In Proceedings of the EGU General Assembly Conference Abstracts, Online, 4–8 May 2020; p. 1853. [Google Scholar]
- Dhami, B.; Himanshu, S.K.; Pandey, A.; Gautam, A.K. Evaluation of the SWAT model for water balance study of a mountainous snowfed river basin of Nepal. Environ. Earth Sci. 2018, 77. [Google Scholar] [CrossRef]
- Mishra, Y.; Nakamura, T.; Babel, M.S.; Ninsawat, S.; Ochi, S. Impact of climate change on water resources of the Bheri River Basin, Nepal. Water 2018, 10, 220. [Google Scholar] [CrossRef]
- Dahal, P.; Shrestha, M.L.; Panthi, J.; Pradhananga, D. Modeling the future impacts of climate change on water availability in the Karnali River Basin of Nepal Himalaya. Environ. Res. 2020, 185, 109430. [Google Scholar] [CrossRef]
- Bajracharya, A.R.; Bajracharya, S.R.; Shrestha, A.B.; Maharjan, S.B. Climate change impact assessment on the hydrological regime of the Kaligandaki Basin, Nepal. Sci. Total Environ. 2018, 625, 837–848. [Google Scholar] [CrossRef]
- Lamichhane, S.; Shakya, N.M. Integrated assessment of climate change and land use change impacts on hydrology in the Kathmandu Valley watershed, Central Nepal. Water 2019, 11, 2059. [Google Scholar] [CrossRef]
- Dahal, V.; Shakya, N.M.; Bhattarai, R. Estimating the impact of climate change on water availability in Bagmati Basin, Nepal. Environ. Process. 2016, 3, 1–17. [Google Scholar] [CrossRef]
- Pandey, V.P.; Dhaubanjar, S.; Bharati, L.; Thapa, B.R. Spatio-temporal distribution of water availability in Karnali-Mohana Basin, Western Nepal: Climate change impact assessment (Part-B). J. Hydrol. Reg. Stud. 2020, 29, 100691. [Google Scholar] [CrossRef]
- Bhatta, B.; Shrestha, S.; Shrestha, P.K.; Talchabhadel, R. Evaluation and application of a SWAT model to assess the climate change impact on the hydrology of the Himalayan River Basin. Catena 2019, 181, 104082. [Google Scholar] [CrossRef]
- Bharati, L.; Gurung, P.; Maharjan, L.; Bhattarai, U. Past and future variability in the hydrological regime of the Koshi Basin, Nepal. Hydrol. Sci. J. 2016, 61, 79–93. [Google Scholar] [CrossRef]
- BGHEP. Feasibility Study and Detailed Design of Budhigandaki Hydropower Project Part 1; Budhigandaki Hydroelectric Project Development Committee, Government of Nepal: Kathmandu, Nepal, 2015.
- Khatri, H.B.; Jain, M.K.; Jain, S.K. Modelling of streamflow in snow dominated Budhigandaki catchment in Nepal. J. Earth Syst. Sci. 2018, 127, 1–14. [Google Scholar] [CrossRef]
- Pangali Sharma, T.P.; Zhang, J.; Khanal, N.R.; Prodhan, F.A.; Paudel, B.; Shi, L.; Nepal, N. Assimilation of snowmelt runoff model (SRM) using satellite remote sensing data in Budhi Gandaki River Basin, Nepal. Remote Sens. 2020, 12, 1951. [Google Scholar] [CrossRef]
- Shrestha, M.L. Interannual variation of summer monsoon rainfall over Nepal and its relation to Southern Oscillation Index. Meteorol. Atmos. Phys. 2000, 75, 21–28. [Google Scholar] [CrossRef]
- Marahatta, S.; Dangol, B.S.; Gurung, G.B. Temporal and Spatial Variability of Climate Change over Nepal, 1976–2005; Practical Action Nepal Office: Kathmandu, Nepal, 2009; ISBN 9937813522. [Google Scholar]
- MoCTCA. Mountaineering in Nepal Facts and Figures; Ministry of Culture, Tourism and Civil Aviation (MoCTCA), Government of Nepal: Kathmandu, Nepal, 2014.
- DHM. Study of Climate and Climatic Variation over Nepal; Technical Report; Department of Hydrology and Meteorology, Government of Nepal: Kathmandu, Nepal, 2015.
- DHM. Institutional Development of Department of Hydrology and Meteorology; Technical Report No.7 (Basin Study); DHM: Kathmandu, Nepal, 2002. [Google Scholar]
- DHM. Streamflow Summary (1962–2015); Department of Hydrology and Meteorology, Government of Nepal: Kathmandu, Nepal, 2018.
- NNH. Hydrology, Hydraulics and Sediment Studies of Budhigandaki KA HEP; Naulo Nepal Hydro-electric (P) Ltd.: Kaski District, Nepal, 2010. [Google Scholar]
- NNH. Hydrology, Hydraulics and Sediment Studies of Budhigandaki KHA HEP; Naulo Nepal Hydro-electric (P) Ltd.: Kaski District, Nepal, 2010. [Google Scholar]
- Yang, K.; He, J. China Meteorological Forcing Dataset (1979−2018). National Tibetan Plateau Data Center, 2019. Available online: https://doi:10.11888/AtmosphericPhysics.tpe.249369.file (accessed on 29 May 2021).
- DoWRI Irrigation Master Plan Preparation through Integrated River Basin Planning (Dataset), Water Resources Project Preparatory Facility; Department of Water Resources and Irrigation, Ministry of Energy, Water Resources and Irrigation (MoEWRI): Kathmandu, Nepal, 2019.
- ICIMOD. Land Cover of Nepal 2010 [Dataset]; International Center for Integrated Mountain Development (ICIMOD): Kathmandu, Nepal, 2010; Available online: http://rds.icimod.org/Home/DataDetail (accessed on 3 December 2020).
- Thiessen, A.H. Precipitation averages for large areas. Mon. Weather Rev. 1911, 39, 1082–1089. [Google Scholar] [CrossRef]
- Srinivasan, R.; Ramanarayanan, T.S.; Arnold, J.G.; Bednarz, S.T. Large area hydrologic modeling and assessment part II: Model application 1. J. Am. Water Resour. Assoc. 1998, 34, 91–101. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Wilson, B.N.; Douglas-Mankin, K.R.; Arnold, J.G.; Gowda, P.H. Hydrologic and water quality models: Use, calibration, and validation. Trans. ASABE 2012, 55, 1241–1247. [Google Scholar] [CrossRef]
- Van Liew, M.W.; Arnold, J.G.; Bosch, D.D. Problems and potential of autocalibrating a hydrologic model. Trans. ASAE 2005, 48, 1025–1040. [Google Scholar] [CrossRef]
- Neitsch, S.L.; Arnold, J.G.; Kiniry, J.R.; Williams, J.R. Soil and Water Assessment Tool Theoretical Documentation Version 2009; Texas Water Resources Institute: College Station, TX, USA, 2011. [Google Scholar]
- WMO. The Role of Climatological Normals in a Changing Climate; WCDMP-No. 61, WMO-TD No. 1377; World Meteorological Organization: Geneva, Switzerland, 2007. [Google Scholar]
- WMO. Guide to Climatological Practices; 2011 Edition, WMO Number 100; World Meteorological Organization: Geneva, Switzerland, 2011. [Google Scholar]
- WMO. Guidelines on the Calculation of Climate Normals; 2017 Edition WMO-No. 1203; World Meteorological Organization: Geneva, Switzerland, 2017. [Google Scholar]
- Mockus, V. National Engineering Handbook; Soil Conservation Service: Washington, DC, USA, 1964; Volume 4. [Google Scholar]
- Hargreaves, G.H.; Samani, Z.A. Estimating potential evapotranspiration. J. Irrig. Drain. Div. 1982, 108, 225–230. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and water quality models: Performance measures and evaluation criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar]
- Schaefli, B.; Gupta, H.V. Do Nash values have value? Hydrol. Process. An Int. J. 2007, 21, 2075–2080. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Knoben, W.J.M.; Freer, J.E.; Woods, R.A. Inherent benchmark or not? Comparing Nash–Sutcliffe and Kling–Gupta efficiency scores. Hydrol. Earth Syst. Sci. 2019, 23, 4323–4331. [Google Scholar] [CrossRef]
- Pool, S.; Vis, M.; Seibert, J. Evaluating model performance: Towards a non-parametric variant of the Kling-Gupta efficiency. Hydrol. Sci. J. 2018, 63, 1941–1953. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Arnold, J.G.; Kiniry, J.R.; Srinivasan, R.; Williams, J.R.; Haney, E.B.; Neitsch, S.L. Soil & Water Assessment Tool: Input/Output Documentation; Version 2012; TR-439; Texas Water Resources Institute: Forney, TX, USA, 2013; p. 650. [Google Scholar]
- Bharati, L.; Bhattarai, U.; Khadka, A.; Gurung, P.; Neumann, L.E.; Penton, D.J.; Dhaubanjar, S.; Nepal, S. From the Mountains to the Plains: Impact of Climate Change on Water Resources in the Koshi River Basin; International Water Management Institute (IWMI): Colombo, Sri Lanka, 2019; Volume 187, ISBN 9290908858. [Google Scholar]
- Pandey, V.P.; Dhaubanjar, S.; Bharati, L.; Thapa, B.R. Hydrological response of Chamelia watershed in Mahakali Basin to climate change. Sci. Total Environ. 2019, 650, 365–383. [Google Scholar] [CrossRef]
- Palazzoli, I.; Maskey, S.; Uhlenbrook, S.; Nana, E.; Bocchiola, D. Impact of prospective climate change on water resources and crop yields in the Indrawati basin, Nepal. Agric. Syst. 2015, 133, 143–157. [Google Scholar] [CrossRef]
- Tegegne, G.; Park, D.K.; Kim, Y.-O. Comparison of hydrological models for the assessment of water resources in a data-scarce region, the Upper Blue Nile River Basin. J. Hydrol. Reg. Stud. 2017, 14, 49–66. [Google Scholar] [CrossRef]
- Sharannya, T.M.; Mudbhatkal, A.; Mahesha, A. Assessing climate change impacts on river hydrology–A case study in the Western Ghats of India. J. Earth Syst. Sci. 2018, 127, 1–11. [Google Scholar] [CrossRef]
- Duan, Y.; Liu, T.; Meng, F.; Luo, M.; Frankl, A.; De Maeyer, P.; Bao, A.; Kurban, A.; Feng, X. Inclusion of modified snow melting and flood processes in the swat model. Water 2018, 10, 1715. [Google Scholar] [CrossRef]
- Le Coz, J. A Literature Review of Methods for Estimating the Uncertainty Associated with Stage-Discharge Relations. WMO Rep. PO6a 2012, 21. Available online: https://www.semanticscholar.org/paper/A-literature-review-of-methods-for-estimating-the-Coz-Cemagref/b685243d91acd17a64c3e31ecff08ea39d5b279d (accessed on 14 January 2021).
- Subramanayam, K. Engineering Hydrology; TATA McGraw Hills Publications Ltd.: New Delhi, India, 1994; ISBN 0-07-462449-8. [Google Scholar]
- Domeneghetti, A.; Castellarin, A.; Brath, A. Assessing rating-curve uncertainty and its effects on hydraulic model calibration. Hydrol. Earth Syst. Sci. 2012, 16, 1191–1202. [Google Scholar] [CrossRef]
- Manfreda, S.; Pizarro, A.; Moramarco, T.; Cimorelli, L.; Pianese, D.; Barbetta, S. Potential advantages of flow-area rating curves compared to classic stage-discharge-relations. J. Hydrol. 2020, 585, 124752. [Google Scholar] [CrossRef]
- Kayastha, R.B.; Steiner, N.; Kayastha, R.; Mishra, S.K.; Forster, R.R. Comparative Study of Hydrology and Icemelt in Three Nepal River Basins Using the Glacio-Hydrological Degree-Day Model (GDM) and Observations from the Advanced Scatterometer (ASCAT). Front. Earth Sci. 2020, 7, 354. [Google Scholar] [CrossRef]
- Mishra, S.K.; Hayse, J.; Veselka, T.; Yan, E.; Kayastha, R.B.; LaGory, K.; McDonald, K.; Steiner, N. An integrated assessment approach for estimating the economic impacts of climate change on River systems: An application to hydropower and fisheries in a Himalayan River, Trishuli. Environ. Sci. Policy 2018, 87, 102–111. [Google Scholar] [CrossRef]
- Pradhananga, N.S.; Kayastha, R.B.; Bhattarai, B.C.; Adhikari, T.R.; Pradhan, S.C.; Devkota, L.P.; Shrestha, A.B.; Mool, P.K. Estimation of discharge from Langtang River basin, Rasuwa, Nepal, using a glacio-hydrological model. Ann. Glaciol. 2014, 55, 223–230. [Google Scholar] [CrossRef]
- Khadka, M.; Kayastha, R.B.; Kayastha, R. Future projection of cryospheric and hydrologic regimes in Koshi River basin, Central Himalaya, using coupled glacier dynamics and glacio-hydrological models. J. Glaciol. 2020. [Google Scholar] [CrossRef]


| Data | Data Source |
|---|---|
| River flow | [53,61,62,63] |
| Precipitation and temperature | Nepal- Department of Hydrology and Meteorology (DHM), Tibet—[64] https://data.tpdc.ac.cn/, assessed on 24 July 2020 |
| Digital elevation model (DEM)-30 m resolution | Shuttle Radar Topography Mission (SRTM) (www.earthexplorer.usgs.gov, accessed on 25 July 2020) |
| Soil | SOTER (2019) for Tibet (http://www.isric.org/data/data-download, assessed on 24 July 2020) Nepal—[65] |
| Land use | [65,66] |
| Parameter | Unit | Final Value | Allowable Range * | Impacted Component of Flow |
|---|---|---|---|---|
| ALPHA_BF | day | 0.01 | 0–1 | Baseflow |
| CN2 | 50–93 | 35–98 | Surface runoff | |
| GW_DELAY | day | 55 | 0–500 | Baseflow |
| GWQMIN | mm | 200 | 0–5000 | Baseflow |
| LAT_TIME | day | 18 | 0–180 | Lateral flow |
| OV_N | s/m1/3 | 0.5 | 0.01–0.41 | Surface runoff |
| SFTMP | °C | 4.5 | −5–5 | Snow |
| SMFMN | mm/°C/day | 2.5 | 1.7–6.5 | Snow |
| SMFMX | mm/°C/day | 4.5 | 1.7–6.5 | Snow |
| SMTMP | °C | 2.5 | −5–5 | Snow |
| SNOCOVMX | mm | 400 | 0–1.0 | Snow |
| SOL_AWC | mm/mm | 0–0.3 | 0–1.0 | Baseflow |
| SOL_Z | mm | 0–50 | 0–3500 | Baseflow |
| SURLAG | day | 0.1 | 1–10 | Lateral flow |
| TLAPS | °C/km | −6.5 | −10–10 | Snow |
| Statistic (Years) | Mean Flow (m3/s) | Standard Deviation (m3/s) | Performance Indicators | |||||
|---|---|---|---|---|---|---|---|---|
| Observed | Simulated | Observed | Simulated | NSE | PBIAS | RSR | KGE | |
| Calibration (1983–2002) | 168 | 170 | 167 | 168 | 0.78 | −1.46% | 0.47 | 0.89 |
| Validation (2003–2012) | 154 | 181 | 163 | 180 | 0.81 | −17.1% | 0.44 | 0.79 |
| Entire Simulation (1983–2012) | 163 | 174 | 166 | 172 | 0.79 | −6.38% | 0.46 | 0.88 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marahatta, S.; Devkota, L.P.; Aryal, D. Application of SWAT in Hydrological Simulation of Complex Mountainous River Basin (Part I: Model Development). Water 2021, 13, 1546. https://doi.org/10.3390/w13111546
Marahatta S, Devkota LP, Aryal D. Application of SWAT in Hydrological Simulation of Complex Mountainous River Basin (Part I: Model Development). Water. 2021; 13(11):1546. https://doi.org/10.3390/w13111546
Chicago/Turabian StyleMarahatta, Suresh, Laxmi Prasad Devkota, and Deepak Aryal. 2021. "Application of SWAT in Hydrological Simulation of Complex Mountainous River Basin (Part I: Model Development)" Water 13, no. 11: 1546. https://doi.org/10.3390/w13111546
APA StyleMarahatta, S., Devkota, L. P., & Aryal, D. (2021). Application of SWAT in Hydrological Simulation of Complex Mountainous River Basin (Part I: Model Development). Water, 13(11), 1546. https://doi.org/10.3390/w13111546





