Detecting Groundwater Temperature Shifts of a Subsurface Urban Heat Island in SE Germany
Abstract
:1. Introduction
1.1. Subsurface Urban Heat Island and Its Technical Use
1.2. Groundwater Monitoring for Sustainable Development
2. Materials and Methods
2.1. Geographic Setting
2.2. Data Collection
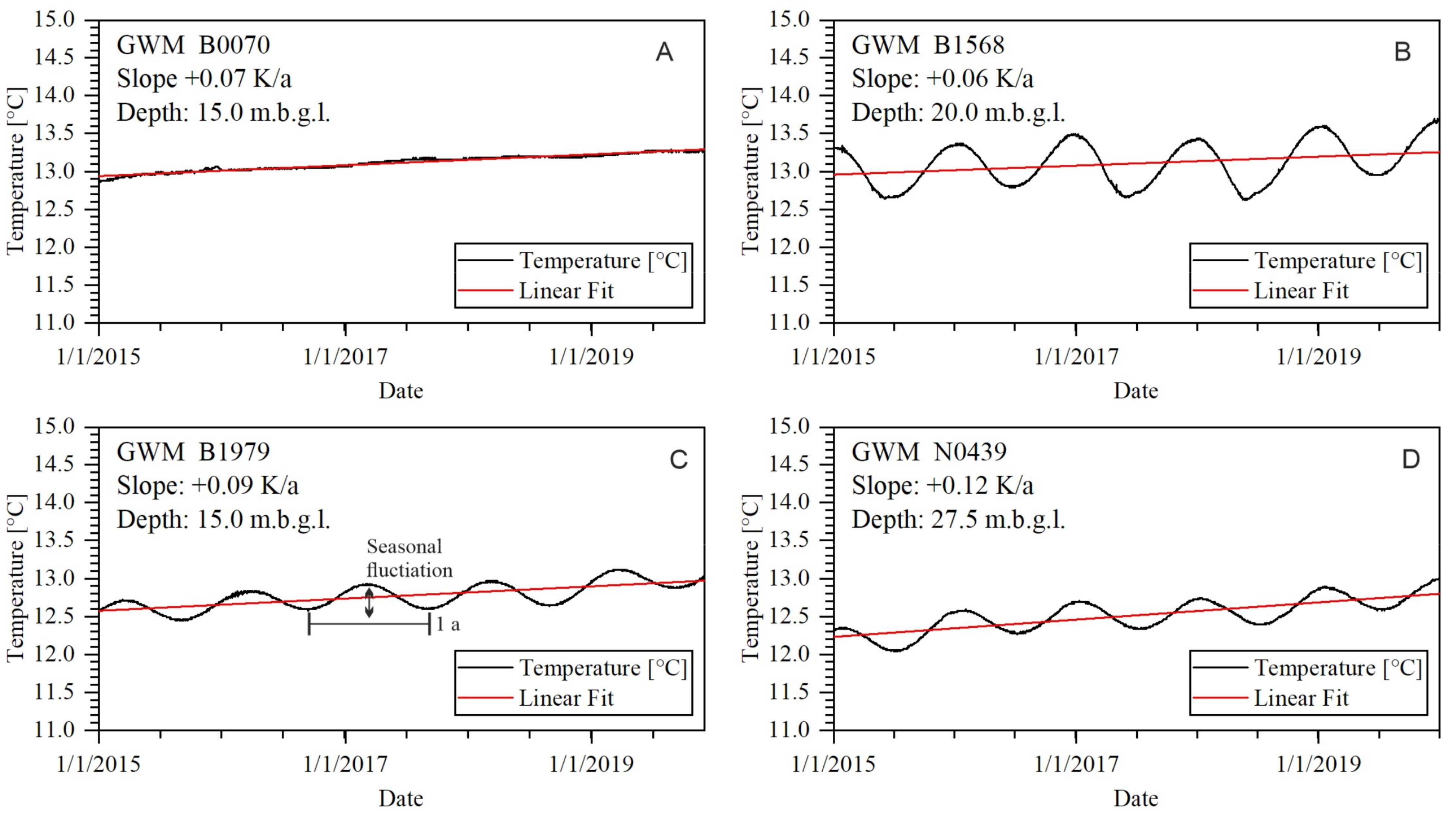
2.3. Analysis of Groundwater Temperatures
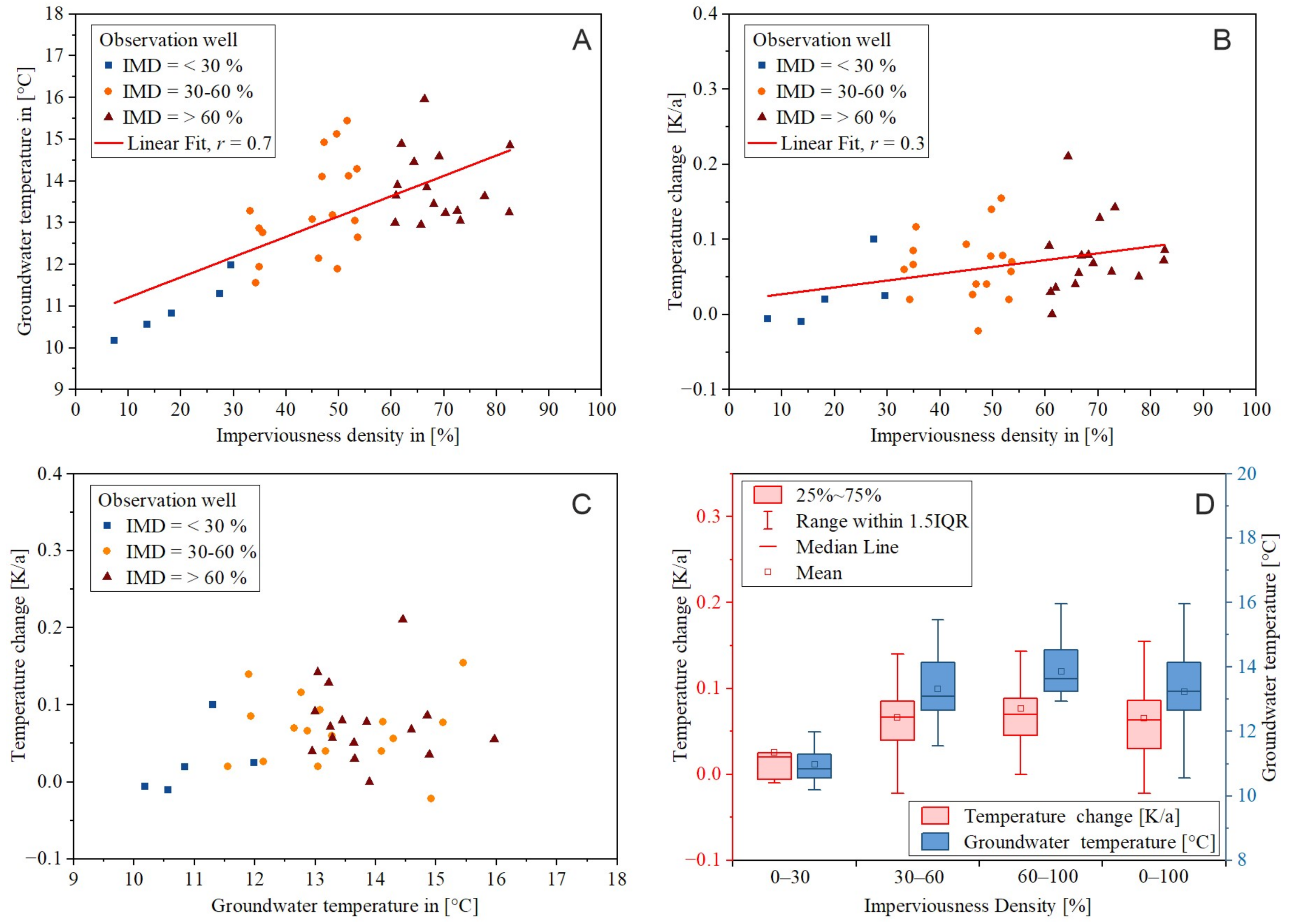
2.4. Urban Classification for Groundwater Temperature Shifts
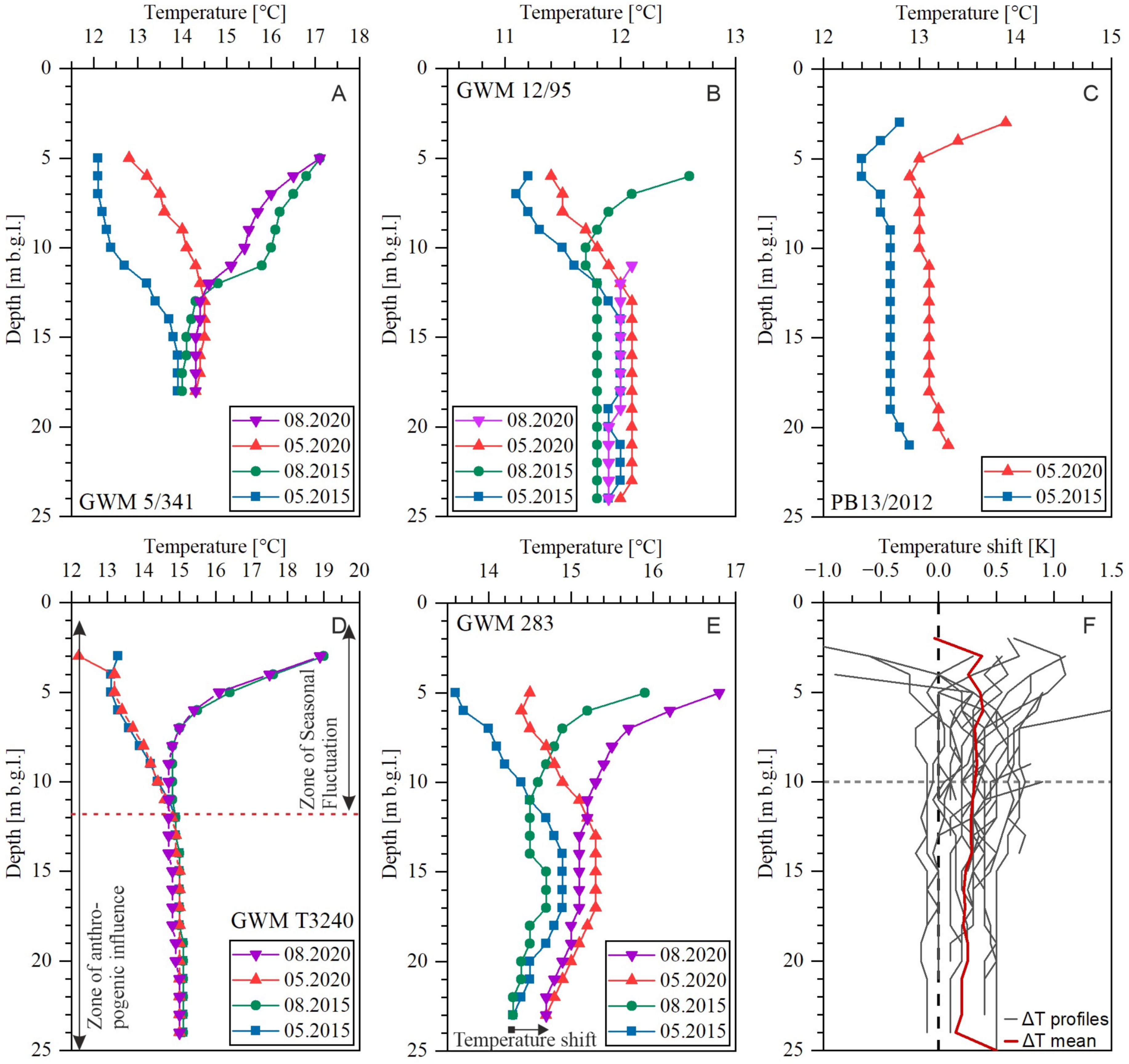
3. Results
3.1. Groundwater Temperature and Temperature Shifts
3.2. Linking Groundwater Temperatures to Surface Sealing
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saitoh, T.S.; Shimada, T.; Hoshi, H. Modeling and simulation of the Tokyo urban heat island. Atmos. Environ. 1996, 30, 3431–3442. [Google Scholar] [CrossRef]
- Velazquez-Lozada, A.; Gonzalez, J.E.; Winter, A. Urban heat island effect analysis for San Juan, Puerto Rico. Atmos. Environ. 2006, 40, 1731–1741. [Google Scholar] [CrossRef]
- Farr, G.; Patton, A.; Boon, D.; Schofield, D.; James, D.; Williams, B. Mapping shallow urban groundwater temperatures, a case study from Cardiff, UK. Q. J. Eng. Geol. Hydrogeol. 2017, 50, 187–198. [Google Scholar] [CrossRef]
- Tissen, C.; Benz, S.; Menberg, K.; Bayer, P.; Blum, P. Groundwater temperature anomalies in central Europe. Environ. Res. Lett. 2019, 14, 104012. [Google Scholar] [CrossRef] [Green Version]
- Ferguson, G.; Woodbury, A. Urban heat island in the subsurface. Geophys. Res. Lett. 2007, 34, L23713. [Google Scholar] [CrossRef]
- Huang, S.; Taniguchi, M.; Yamano, M.; Wang, C. Detecting urbanization effects on surface and subsurface thermal environment—A case study of Osaka. Sci. Total Environ. 2009, 407, 3142–3152. [Google Scholar] [CrossRef]
- Shi, B.; Tang, C.; Gao, L.; Liu, C.; Wang, B. Observation and analysis of the urban heat island effect on soil in Nanjing, China. Environ. Earth Sci. 2012, 67, 215–229. [Google Scholar] [CrossRef]
- Benz, S.; Bayer, P.; Blum, P.; Hamamoto, H.; Arimoto, H.; Taniguchi, M. Comparing anthropogenic heat input and heat accumulation in the subsurface of Osaka, Japan. Sci. Total Environ. 2018, 643, 1127–1136. [Google Scholar] [CrossRef]
- Hemmerle, H.; Hale, S.; Dressel, I.; Benz, S.; Attard, G.; Blum, P.; Bayer, P. Estimation of Groundwater Temperatures in Paris, France. Geofluids 2019, 5246307, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Menberg, K.; Bayer, P.; Zosseder, K.; Rumohr, S.; Blum, P. Subsurface urban heat islands in German cities. Sci. Total Environ. 2013, 442, 123–133. [Google Scholar] [CrossRef]
- Taha, H. Urban climates and heat islands: Albedo, evapotranspiration, and anthropogenic heat. Energy Build. 1997, 25, 99–103. [Google Scholar] [CrossRef] [Green Version]
- Dědeček, P.; Šafanda, J.; Rajver, D. Detection and quantification of local anthropogenic and regional climatic transient signals in temperature logs from Czechia and Slovenia. Clim. Chang. 2012, 113, 787–801. [Google Scholar] [CrossRef]
- Menberg, K.; Blum, P.; Schaffitel, A.; Bayer, P. Long Term Evolution of Anthropogenic Heat Fluxes into a Subsurface Urban Heat Island. Environ. Sci. Technol. 2013, 47, 9747–9755. [Google Scholar] [CrossRef] [PubMed]
- Cermak, V.; Bodri, L.; Kresl, M.; Dedecek, P.; Safanda, J. Eleven years of ground–air temperature tracking over different land cover types. Int. J. Climatol. 2017, 37, 1084–1099. [Google Scholar] [CrossRef]
- Benz, S.; Bayer, P.; Winkler, G.; Blum, P. Recent trends of groundwater temperatures in Austria. Hydrol. Earth Syst. Sci. 2018, 22, 3143–3154. [Google Scholar] [CrossRef] [Green Version]
- Riedel, T. Temperature-associated changes in groundwater quality. J. Hydrol. 2019, 572, 206–212. [Google Scholar] [CrossRef]
- Hemmerle, H.; Bayer, P. Climate Change Yields Groundwater Warming in Bavaria, Germany. Front. Earth Sci. 2020, 8, 523. [Google Scholar] [CrossRef]
- Nitoiu, D.; Beltrami, H. Subsurface thermal effects of land use changes. J. Geophys. Res. Earth Surface 2005, 110, F01005. [Google Scholar] [CrossRef] [Green Version]
- Lalosevic, M.D.; Komatina, M.S.; Milos, M.V.; Rudonja, N.R. Green roofs and cool materials as retrofitting strategies for urban heat Island mitigation—Case study in Belgrade, Serbia. Therm. Sci. 2018, 22, 2309–2324. [Google Scholar] [CrossRef]
- Luo, Z.; Asproudi, C. Subsurface urban heat island and its effects on horizontal ground-source heat pump potential under climate change. Appl. Therm. Eng. 2015, 90, 530–537. [Google Scholar] [CrossRef]
- Zhu, K.; Blum, P.; Ferguson, G.; Balke, K.-D.; Bayer, P. The geothermal potential of urban heat islands. Environ. Res. Lett. 2011, 6, 019501. [Google Scholar] [CrossRef]
- Arola, T.; Korkka-Niemi, K. The effect of urban heat islands on geothermal potential: Examples from Quaternary aquifers in Finland. Hydrogeol. J. 2014, 22, 1953–1967. [Google Scholar] [CrossRef]
- Barla, M.; Di Donna, A. Energy tunnels: Concept and design aspects. Undergr. Space 2018, 3, 268–276. [Google Scholar] [CrossRef]
- Baralis, M.; Barla, M.; Bogusz, W.; Di Donna, A.; Ryżyński, G.; Żeruń, M. Geothermal Potential of the NE Extension Warsaw Metro Tunnels. Environ. Geotech. 2018, 7, 282–294. [Google Scholar] [CrossRef]
- Baumgärtel, S.; Rohn, J.; Luo, J. Experimental study of road deicing by using the urban groundwater under the climatic condition of Nuremberg city, Germany. SN Appl. Sci. 2020, 2, 537. [Google Scholar] [CrossRef] [Green Version]
- Ongen, A.; Erguler, Z. The effect of urban heat island on groundwater located in shallow aquifers of Kutahya city center and shallow geothermal energy potential of the region. Bull. Miner. Res. Explor. 2020, 1–24. [Google Scholar]
- Jung, Y.-J.; Kim, H.-J.; Choi, B.-E.; Jo, J.-H.; Cho, Y.-H. A Study on the Efficiency Improvement of Multi-Geothermal Heat Pump Systems in Korea Using Coefficient of Performance. Energies 2016, 9, 356. Energies 2016, 9, 356. [Google Scholar] [CrossRef] [Green Version]
- Galgaro, A.; Cultrera, M. Thermal short circuit on groundwater heat pump. Appl. Therm. Eng. 2013, 57, 107–115. [Google Scholar] [CrossRef]
- Brielmann, H.; Griebler, C.; Schmidt, S.I.; Michel, R.; Lueders, T. Effects of thermal energy discharge on shallow groundwater ecosystems. FEMS Microbiol. Ecol. 2009, 68, 273–286. [Google Scholar] [CrossRef] [Green Version]
- Hähnlein, S.; Bayer, P.; Ferguson, G.; Blum, P. Sustainability and policy for the thermal use of shallow geothermal energy. Energy Policy 2013, 59, 914–925. [Google Scholar] [CrossRef]
- Kløve, B.; Ala-Aho, P.; Bertrand, G.; Gurdak, J.; Kupfersberger, H.; Kværner, J.; Muotka, T.; Mykrä, H.; Preda, E.; Rossi, P.; et al. Climate change impacts on groundwater and dependent ecosystems. J. Hydrol. 2014, 518, 250–266. [Google Scholar] [CrossRef]
- Saito, T.; Hamamoto, S.; Ueki, T.; Ohkubo, S.; Moldrup, P.; Kawamoto, K.; Komatsu, T. Temperature change affected groundwater quality in a confined marine aquifer during long-term heating and cooling. Water Res. 2016, 94, 120–127. [Google Scholar] [CrossRef]
- Welch, S.A.; Ullman, W.J. The temperature dependence of bytownite feldspar dissolution in neutral aqueous solutions of inorganic and organic ligands at low temperature (5–35 °C). Chem. Geol. 2000, 167, 337–354. [Google Scholar] [CrossRef]
- Smedley, P.L.; Kinniburgh, D.G. A review of the source, behaviour and distribution of arsenic in natural waters. Appl. Geochem. 2002, 17, 517–568. [Google Scholar] [CrossRef] [Green Version]
- Bonte, M.; van Breukelen, B.M.; Stuyfzand, P.J. Temperature-induced impacts on groundwater quality and arsenic mobility in anoxic aquifer sediments used for both drinking water and shallow geothermal energy production. Water Res. 2013, 47, 5088–5100. [Google Scholar] [CrossRef]
- Zhou, Q. A Review of Sustainable Urban Drainage Systems Considering the Climate Change and Urbanization Impacts. Water 2014, 6, 976–992. [Google Scholar] [CrossRef]
- Kourtis, I.; Tsihrintzis, V.; Baltas, E. Simulation of Low Impact Development (LID) Practices and Comparison with Conventional Drainage Solutions. Proceedings 2018, 2, 640. [Google Scholar] [CrossRef] [Green Version]
- Li, C.; Liu, M.; Hu, Y.; Han, R.; Shi, T.; Qu, X.; Wu, Y. Evaluating the Hydrologic Performance of Low Impact Development Scenarios in a Micro Urban Catchment. Int. J. Environ. Res. Public Health 2018, 15, 273. [Google Scholar] [CrossRef] [Green Version]
- Yamano, M.; Goto, S.; Miyakoshi, A.; Hamamoto, H.; Lubis, R.-F.; Monyrath, V.; Taniguchi, M. Reconstruction of the thermal environment evolution in urban areas from underground temperature distribution. Sci. Total Environ. 2009, 407, 3120–3128. [Google Scholar] [CrossRef]
- Gunawardhana, L.N.; Kazama, S. Climate change impacts on groundwater temperature change in the Sendai plain, Japan. Hydrol. Process. 2011, 25, 2665–2678. [Google Scholar] [CrossRef]
- Lee, B.; Hamm, S.-Y.; Jang, S.; Cheong, J.-Y.; Kim, G.-B. Relationship between groundwater and climate change in South Korea. Geosci. J. 2014, 18, 209–218. [Google Scholar] [CrossRef]
- GEO-NET, U.G. Stadtklimagutachten—Analyse der Klimaökologischen Funktionen für das Stadtgebiet von Nürnberg; GEO-NET: Hannover, Germany, 2014; p. 131. [Google Scholar]
- Baier, A.; van Geldern, R.; Löhr, G.; Subert, H.L.; Barth, J.A.C. Grundwasser in Nürnberg: Wichtige Einheiten und deren Nutzbarkeit. Grundwasser 2016, 21, 253–266. [Google Scholar] [CrossRef]
- Schweighofer, J.A.V.; Wehrl, M.; Baumgärtel, S.; Rohn, J. Calculating Energy and Its Spatial Distribution for a Subsurface Urban Heat Island Using a GIS-Approach. Geosciences 2021, 11, 24. [Google Scholar] [CrossRef]
- de Wall, H.; Schaarschmidt, A.; Kämmlein, M.; Gabriel, G.; Bestmann, M.; Scharfenberg, L. Subsurface granites in the Franconian Basin as the source of enhanced geothermal gradients: A key study from gravity and thermal modeling of the Bayreuth Granite. Int. J. Earth Sci. 2019, 108, 1913–1936. [Google Scholar] [CrossRef]
- Verein Deutscher Ingenieure e.V. VDI 4640 Blatt 1: 2010-06: Thermal Use of the Underground; VDI-Gesellschaft Energie und Umwelt: Berlin, Germany, 2010; p. 33. [Google Scholar]
- Berthold, S.; Börner, F. Detection of free vertical convection and double-diffusion in groundwater monitoring wells with geophysical borehole measurements. Environ. Geol. 2008, 54, 1547–1566. [Google Scholar] [CrossRef]
- Andujar Marquez, J.; Bohórquez, M.A.; Melgar, S. Ground Thermal Diffusivity Calculation by Direct Soil Temperature Measurement. Application to very Low Enthalpy Geothermal Energy Systems. Sensors 2016, 16, 306. [Google Scholar] [CrossRef] [Green Version]
- Lo Russo, S.; Glenda, T.; Vittorio, V. Development of the thermally affected zone (TAZ) around a groundwater heat pump (GWHP) system: A sensitivity analysis. Geothermics 2012, 43, 66–74. [Google Scholar] [CrossRef]
- Epting, J.; Händel, F.; Huggenberger, P. Thermal management of an unconsolidated shallow urban groundwater body. Hydrol. Earth Syst. Sci. 2013, 17, 1851–1869. [Google Scholar] [CrossRef] [Green Version]
- Epting, J.; Händel, F.; Huggenberger, P. The thermal impact of subsurface building structures on urban groundwater resources—A paradigmatic example. Sci. Total Environ. 2017, 596–597, 87–96. [Google Scholar] [CrossRef]
- Arthur, S.; Streetly, H.; Valley, S.; Streetly, M.; Herbert, A. Modelling large ground source cooling systems in the Chalk aquifer of central London. Q. J. Eng. Geol. Hydrogeol. 2010, 43, 289–306. [Google Scholar] [CrossRef]
- Galgaro, A.; Farina, Z.; Emmi, G.; De Carli, M. Feasibility analysis of a Borehole Heat Exchanger (BHE) array to be installed in high geothermal flux area: The case of the Euganean Thermal Basin, Italy. Renew. Energy 2015, 78, 93–104. [Google Scholar] [CrossRef]
- Ma, W.; Kim, M.K.; Hao, J. Numerical Simulation Modeling of a GSHP and WSHP System for an Office Building in the Hot Summer and Cold Winter Region of China: A Case Study in Suzhou. Sustainability 2019, 11, 3282. [Google Scholar] [CrossRef] [Green Version]
- Sanchez-Lorenzo, A.; Calbó, J.; Martin-Vide, J. Spatial and Temporal Trends in Sunshine Duration over Western Europe (1938–2004). J. Clim. 2008, 21, 6089–6098. [Google Scholar] [CrossRef]
- Salthammer, T.; Schieweck, A.; Gu, J.; Ameri, S.; Uhde, E. Future trends in ambient air pollution and climate in Germany—Implications for the indoor environment. Build. Environ. 2018, 143, 661–670. [Google Scholar] [CrossRef]
- Bartoszek, K.; Matuszko, D.; Węglarczyk, S. Trends in sunshine duration in Poland (1971–2018). Int. J. Climatol. 2021, 41, 73–91. [Google Scholar] [CrossRef]
| System | Chronostratigraphy | Lithostratigraphy | Lithology | Hydrogeology | λsat [W/(m × K)] | Thickness [m] | |
|---|---|---|---|---|---|---|---|
| Quaternary | - | Sediments | q | clay-gravel | Aquifer 3 | 2.4 5 | 0–30 4 |
| Triassic | Norian | Löwenstein-F. 1 | kmBO 1 | Sst 1 | Aquifer 3 | 3.0 2 | 90 4 |
| kmBM 1 | SSt | 3.0 2 | |||||
| kmBU 1 | Sst | 2.9 2 | |||||
| Carnian | Mainhardt-F. | 2.9 2 | |||||
| Hassberge-F. | kmBl + C 1 | Sst | 3.0 2 | 40 4 | |||
| Steigerwald-F. | kmL 1 | Clst 1 | Aquifer 3 | 2.5 2 | 30 4 | ||
| Stuttgart-F. | kmS 1 | SSt | Aquifer 3 | 2.6 2 | 4–30 4 | ||
| Ladinian/Carnian | Benk-F. | kmE 1 | Clst | Aquiclude 3 | 2.1 2 | 20–30 4 | |
| kmBe 1 | Sst | Aquifer 3 | - | 90 4 | |||
| Type | Device | Accuracy | Interval of Measurement | Depth of Data Acquisition | No. of Sampling Well |
|---|---|---|---|---|---|
| TLC-meter | Solinst/HT Hydrotechnik | ±0.1 K | ≤5 a | Vertical log, 0–30 m | 27 |
| Data logger | Aquitronic Beaver ATP10 | ±0.2 K | 12–24 h | Discrete depth, 10–27.5 m | 11 |
| Parameter | Unit | Total Database | Temperature Logs | Data Logger |
|---|---|---|---|---|
| Observation well, count | [–] | 38 | 27 | 11 |
| Depth of Data Acquisition | [m b.g.l.] | 10–27.5 | 10–26 | 10–27.05 |
| Min Temperature shift | [K/a] | −0.02 | −0.02 | +0.05 |
| Max Temperature shift | [K/a] | +0.21 | +0.21 | +0.15 |
| Mean Temperature shift | [K/a] | +0.07 | +0.05 | +0.10 |
| Median Temperature shift | [K/a] | +0.06 | +0.04 | +0.08 |
| Raster Re-Calculation | Focal Statistics Radius in [m] | ||
|---|---|---|---|
| Original data set | Original data set | −0.12 | +0.18 |
| Mean/Circular | 50 | −0.13 | +0.32 |
| Mean/Circular | 100 | −0.06 | +0.36 |
| Mean/Circular | 250 | +0.11 | +0.60 |
| Mean/Circular | 500 | +0.35 | +0.67 |
| Mean/Circular | 750 | +0.33 | +0.68 |
| Mean/Circular | 1000 | +0.31 | +0.63 |
| Parameter | Unit | IMDr = 500 in [%] | ||||
|---|---|---|---|---|---|---|
| 0–30 | 30–60 | 60–100 | 0–100 | |||
| Observation well | count | [–] | 5 | 17 | 16 | 38 |
| Temperature shift | Mean | [K/a] | +0.03 | +0.07 | +0.08 | +0.07 |
| Median | [K/a] | +0.02 | +0.07 | +0.07 | +0.06 | |
| Min | [K/a] | −0.01 | −0.02 | −0.00 | −0.02 | |
| Max | [K/a] | +0.10 | +0.15 | +0.21 | +0.21 | |
| Std Dev | [K/a] | +0.04 | +0.04 | +0.05 | +0.05 | |
| Groundwater temperature | Mean | [°C] | 11.0 | 13.3 | 13.9 | 13.2 |
| Median | [°C] | 10.8 | 13.1 | 13.6 | 13.2 | |
| Min | [°C] | 10.2 | 11.6 | 13.0 | 10.2 | |
| Max | [°C] | 12.0 | 15.5 | 16.0 | 16.0 | |
| Std Dev | [°C] | 0.7 | 1.2 | 0.9 | 1.3 | |
| Location | Period | Land Use Classification | Temperature Shift | No. of Sampling Locations | Data Acquisition | Depth | Sampling Location |
|---|---|---|---|---|---|---|---|
| Germany/Baden-Württemberg [16] | 2000–2015 | - | 0.012 K/a | 1468 | - | <40 m | well |
| Germany/Bavaria [17] | 1992/’94–2019 | - | 0.28 K/(10 a) (median) | ≤32 | TCL-meter | 20 m | well |
| Austria [15] | 1994–2013 | CLC | 0.7 K/(19 a) (~0.04 K/a) | 227 | - | <30 m | well |
| Germany/Nuremberg | 2015–2020 | IMD | 0.07 K/a | 38 | TCL-meter | <30 m | well |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schweighofer, J.A.V.; Wehrl, M.; Baumgärtel, S.; Rohn, J. Detecting Groundwater Temperature Shifts of a Subsurface Urban Heat Island in SE Germany. Water 2021, 13, 1417. https://doi.org/10.3390/w13101417
Schweighofer JAV, Wehrl M, Baumgärtel S, Rohn J. Detecting Groundwater Temperature Shifts of a Subsurface Urban Heat Island in SE Germany. Water. 2021; 13(10):1417. https://doi.org/10.3390/w13101417
Chicago/Turabian StyleSchweighofer, Julian A. V., Michael Wehrl, Sebastian Baumgärtel, and Joachim Rohn. 2021. "Detecting Groundwater Temperature Shifts of a Subsurface Urban Heat Island in SE Germany" Water 13, no. 10: 1417. https://doi.org/10.3390/w13101417
APA StyleSchweighofer, J. A. V., Wehrl, M., Baumgärtel, S., & Rohn, J. (2021). Detecting Groundwater Temperature Shifts of a Subsurface Urban Heat Island in SE Germany. Water, 13(10), 1417. https://doi.org/10.3390/w13101417






