The Effect of Phragmites australis Dieback on Channel Sedimentation in the Mississippi River Delta: A Conceptual Modeling Study
Abstract
1. Introduction
2. Methodology
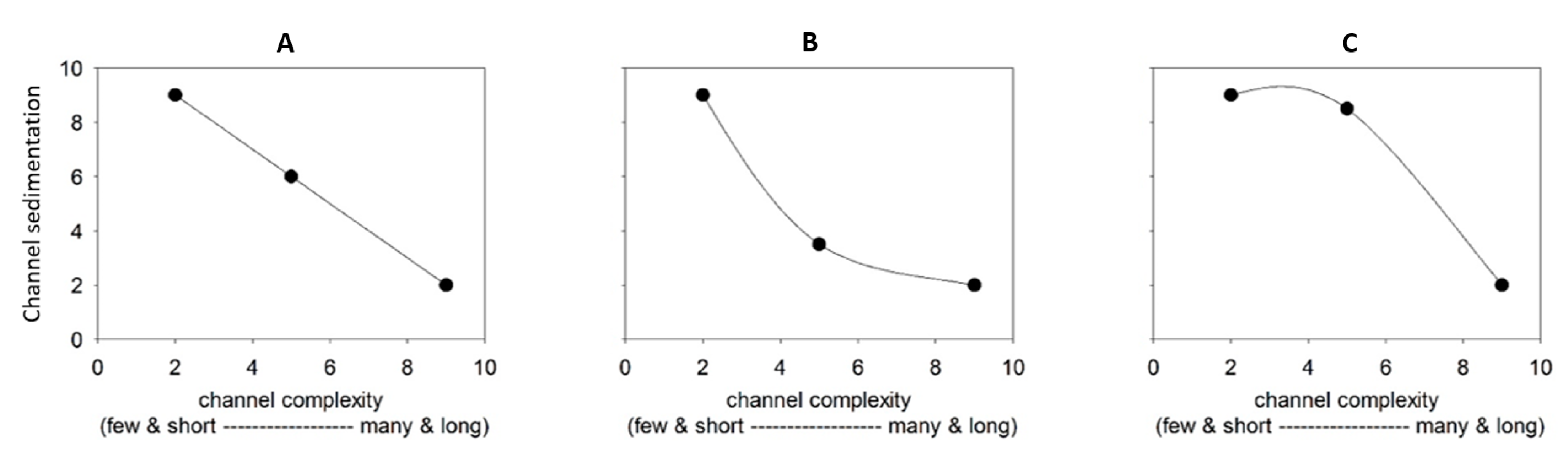
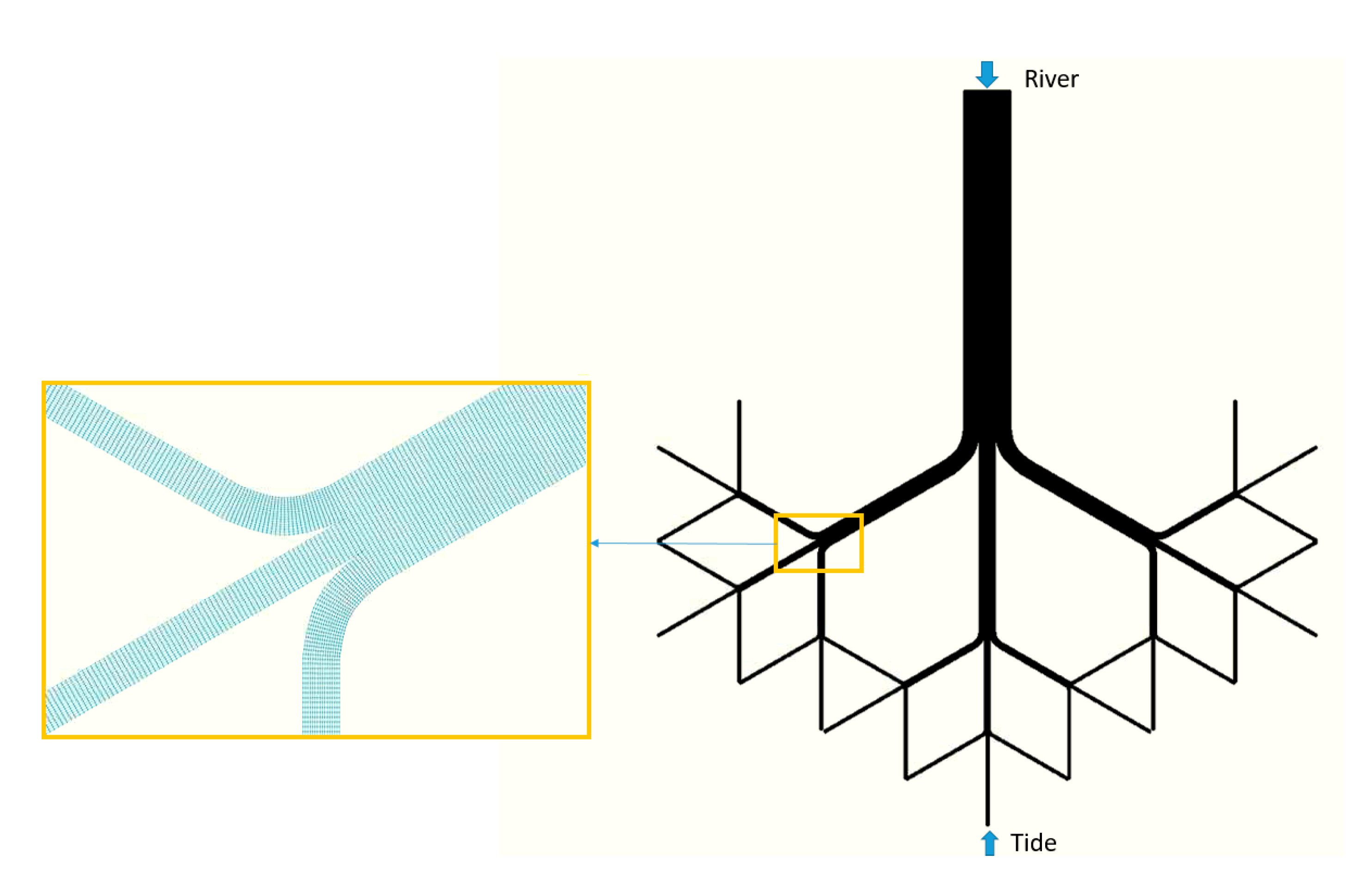
2.1. Conceptual Multichannel Deltaic Systems
- (i)
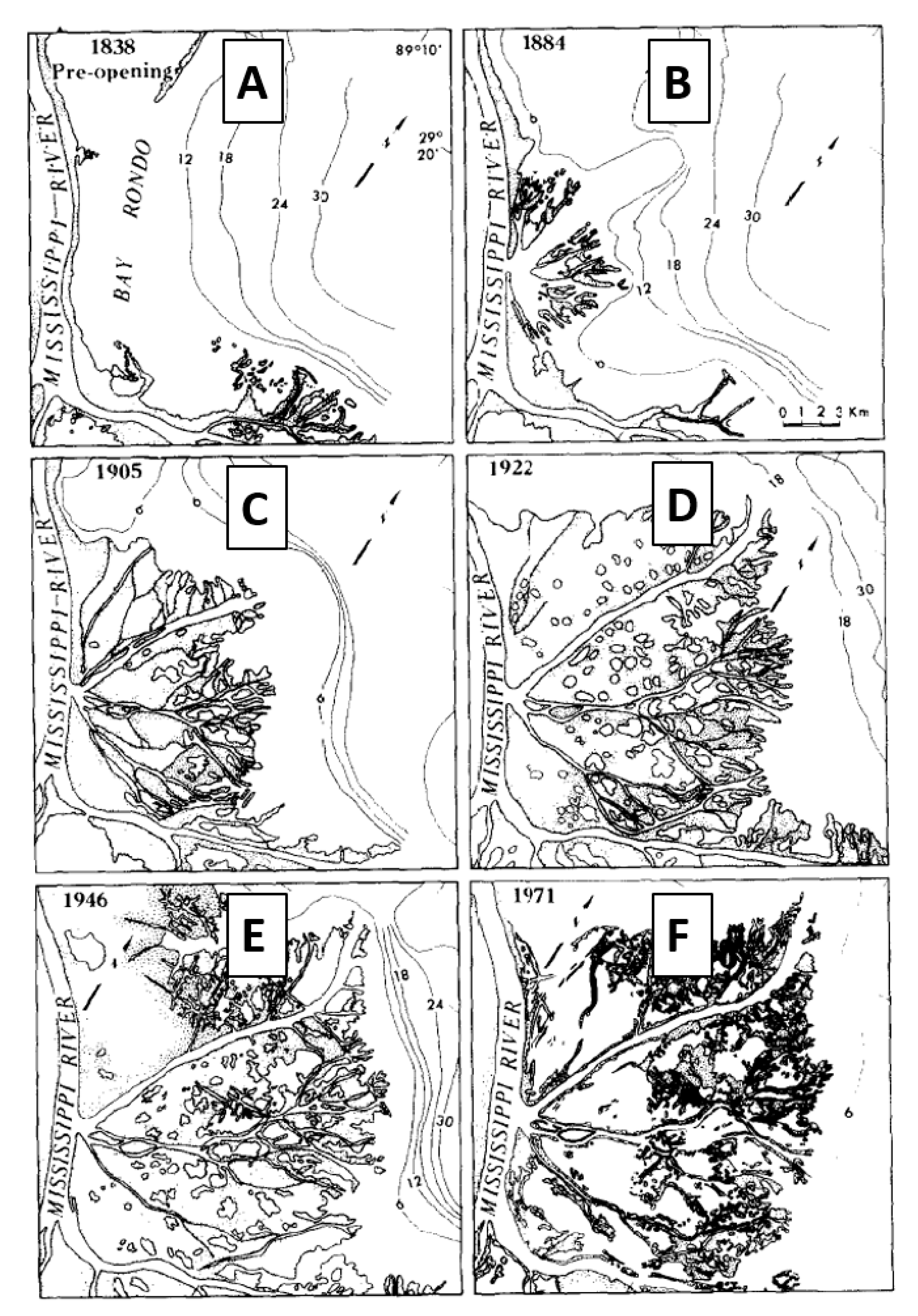
- Extensive P. australis. In this landscape, the discharge is constrained by long, narrow channels that bifurcate repeatedly. This landscape is intended to represent conditions similar to what in the Bird’s Foot Delta has occurred in Main Pass from 1922 to the present [8] that may persist if P. australis dieback is a temporary phenomenon (Figure 4D–F).
- (ii)
- Minimum P. australis extent. In this landscape, the discharge is constrained only by short, wide channels that rarely bifurcate. This landscape is intended to represent conditions similar to what occurred in Main Pass during 1884 [17] that may occur again if P. australis dieback is extreme and persistent (Figure 4B).
- (iii)
- Poor P. australis extent. In this landscape, the discharge is constrained by channels that are approximately one-third as complex, in terms of length and bifurcation, as in condition (i). This landscape is intended to represent the conditions that occurred in Main Pass during 1905 [8] and that may occur if the P. australis dieback is fairly severe and persistent (Figure 4C).
- (iv)
- Good P. australis extent. In this landscape, the discharge is constrained by channels that are approximately two-thirds as complex, in terms of length and bifurcation, as in condition (i) (Figure 4D–F). This landscape is intended to represent conditions that may occur if the P. australis dieback is moderately severe and persistent.
2.2. Conceptual Multichannel Process-Based Model
3. Results
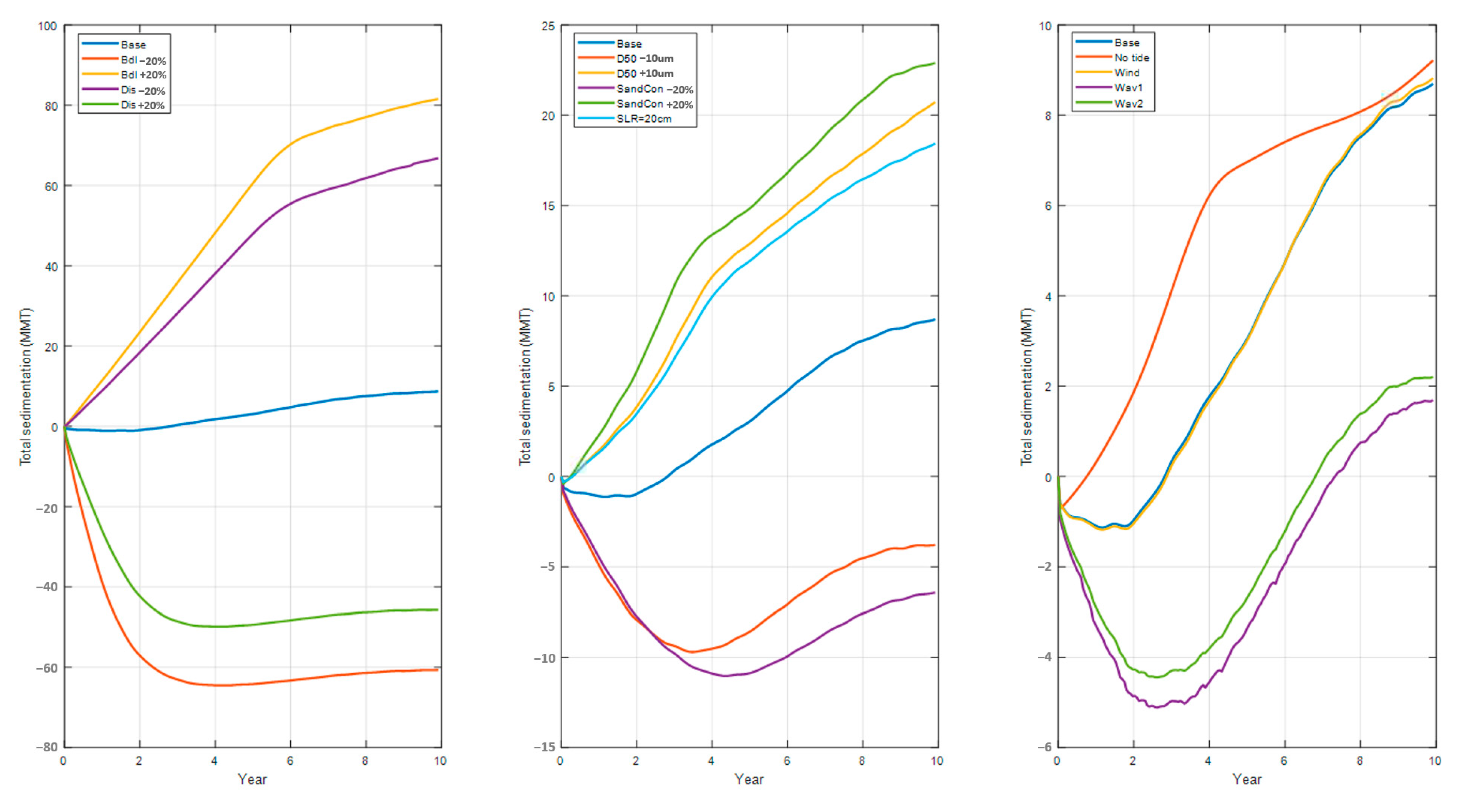
4. Sensitivity Analysis
- Tide: With no tides, the sedimentation rate, compared with the base case, increased for the first several years but then decreased afterwards. Interestingly, the final sedimentation was very close to the base case with the tide turned on. The tide affected the evolution of the system, but this effect diminished over decades.
- Wind: There was no significant difference between the wind case and the base case with no wind. It seems that the normal wind fields (excluding extreme events such as hurricanes and cold fronts) have little effect on long-term sedimentation processes.
- Waves: The effect of the waves was substantial. Both scenarios showed a reduction of sedimentation when the waves were turned on. The most likely explanation is that enhanced bottom shear stresses by the waves made the bed material more erodible.
- Sea level rise: The sea level rise caused an increase of the water level and, equivalently, a decrease of the river current speed given the same river discharge. The reduced current velocity increased the sedimentation in the system.
- River discharge: The system was very sensitive to river discharge. An increase of discharge accelerated the current, which moved more sediment out of the system and caused less sedimentation and more erosion.
- River sediment concentration: A change of the river sediment concentration changed the riverine sediment supply. It was obvious that the more sediment supply came with more sedimentation and vice versa.
- Sediment median grain size (D50): Under the same hydrodynamic conditions, the transport rate for coarser sediments was smaller than for finer sediments, which can result in more sedimentation for coarser sediments.
- Bed level: Similar to the river discharge, the system was also very sensitive to a bed level change. Given the same river discharge, an increase in the bed level decreased the current velocity, which increased the sedimentation.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kleinhaus, M.G.; van Dijk, W.M.; van de Lageweg, W.I.; Hoyal, D.C.; Markies, H.; van Maarseveen, M.; Roosendaal, C.; van Weesep, W.; van Breemen, D.; Hoendervoogt, R.; et al. Quantifiable effectiveness of experimental scaling of river- and delta morpholdynamics and stratigraphy. Earth-Sci. Rev. 2014, 133, 43–61. [Google Scholar] [CrossRef]
- Hiatt, M.; Passalacqua, P. What controls the transition from confined to unconfined flow? Analysis of Hydraulics in a coastal river delta. J. Hydraul. Eng. 2017, 143, 03117003. [Google Scholar] [CrossRef]
- Knight, I.A.; Wilson, B.E.; Gill, M.; Aveles, L.; Cronin, J.T.; Nyman, J.A.; Schneider, S.A.; Diaz, R. Invasion of Nipponaclerda biwakoensis (Hemiptera: Aclerdidae) and associated Phragmites australis dieback in southern Louisiana, USA. Biol. Invasions 2018, 20, 2739–2744. [Google Scholar] [CrossRef]
- Knight, I.A.; Cronin, J.T.; Gill, M.; Nyman, J.A.; Wilson, B.E.; Diaz, R. Investigating plant phenotype, salinity, and infestation by the Roseau Cane Scale as factors in the die-back of Phragmites australis in the Mississippi River Delta, USA. Wetlands 2020, 40, 1327–1337. [Google Scholar] [CrossRef]
- Benoit, L.K.; Askins, R.A. Impact of the spread of Phragmites on the distribution of birds in the Connecticut tidal marshes. Wetlands 1999, 19, 194–208. [Google Scholar] [CrossRef]
- Saltonstall, K. Cyrptic invasion by a non-native genotype of the common reed, Phragmites australis, into North America. Proc. Natl. Acad. Sci. USA 2002, 99, 2445–2449. [Google Scholar] [CrossRef] [PubMed]
- Chambers, R.M.; Myerson, L.A.; Saltonstall, K. Expansion of Phragmites into tidal wetlands of North America. Aquat. Bot. 1999, 64, 261–273. [Google Scholar] [CrossRef]
- Lloyd, F.E.; Tracy, S.M. The insular flora of Mississippi and Louisiana. Bull. Torrey Bot. Club 1901, 28, 61–101. [Google Scholar] [CrossRef]
- Hauber, D.P.; White, D.A.; Powers, S.P.; DeFrancesch, F.R. Isozyme variation and correspondence with unusual infrared reflectance patterns in Phragmites australis (Poaceae). Plant Syst. Evol. 1991, 178, 1–8. [Google Scholar] [CrossRef]
- Hauber, D.P.; Saltonstall, K.; White, D.A.; Hood, C.S. Genetic variation in the Common Reed, Phragmites australis, in the Mississippi River Delta Marshes: Evidence for multiple introductions. Estuar. Coasts 2011, 34, 851–862. [Google Scholar] [CrossRef]
- White, D.A. Vascular plant community development on mudflats in the Mississippi River delta, Louisiana, USA. Aquat. Bot. 1993, 45, 171–194. [Google Scholar] [CrossRef]
- Cahoon, D.R.; White, D.A.; Lynch, J.C. Sediment infilling and wetland formation dynamics in an active crevasse splay of the Mississippi River delta. Geomorphology 2011, 131, 57–68. [Google Scholar] [CrossRef]
- Englonger, A.I. Structure, growth dynamics and biomass of reed (Phragmites australis)—A review. Flora 2009, 204, 331–346. [Google Scholar] [CrossRef]
- O’Neil, T. The Muskrat in the Louisiana Coastal Marshes; Louisiana Department of Wild Life and Fisheries: New Orleans, LA, USA, 1949; pp. 12–18. [Google Scholar]
- Achenback, L.; Brix, H. Can differences in salinity tolerance explain the distribution of four genetically distinct lineages of Phragmites australis in the Mississippi River Delta? Hydrobiologia 2014, 737, 5–23. [Google Scholar] [CrossRef]
- Lambertini, C.; Mendelssohn, I.A.; Gustafsson, M.H.; Olesen, B.; Riis, T.; Sorrell, B.K.; Brix, H. Tracing the origin of Gulf Coast Phragmites (Poaceae): A story of long-distance dispersal and hybridization. Am. J. Bot. 2012, 99, 538–551. [Google Scholar] [CrossRef] [PubMed]
- Wells, J.T.; Coleman, J.M. Wetland loss and the subdelta life cycle. Estuar. Coast. Shelf Sci. 1987, 25, 111–125. [Google Scholar] [CrossRef]
- Kemp, G.P.; Day, J.W.; Freeman, A.M. Restoring the sustainability of the Mississippi River Delta. Ecol. Eng. 2014, 64, 131–146. [Google Scholar] [CrossRef]
- Wingate, M. Current and Future Dredging along the Lower Mississippi River. Pdf File. 2019. Available online: https://albl.org/wp-content/uploads/2019/12/Mark-Wingate.pdf (accessed on 17 May 2021).
- Tejedor, A.; Longjas, A.; Zaliapin, I.; Foufoula-Georgiou, E. Delta channel networks: 2. Metrics of topologic and dynamic complexity for delta comparison, physical inference, and vulnerability assessment. Water Resour. Res. 2015, 51, 4019–4045. [Google Scholar] [CrossRef]
- Edmonds, D.A.; Slingerland, R.L. Mechanics of river mouth bar formation: Implications for the morphodynamics of delta distributary networks. J. Geophys. Res. 2007, 112, F02034. [Google Scholar] [CrossRef]
- Tejedor, A.; Longjas, A.; Caldwell, R.; Edmonds, D.A.; Zaliapin, I.; Foufoula-Georgiou, E. Quantifying the signature of sediment composition on the topologic and dynamic complexity of river delta channel networks and inferences toward delta classification. Geophys. Res. Lett. 2016, 43, 3280–3287. [Google Scholar] [CrossRef]
- Kernkamp, H.W.; van Dam, A.; Stelling, G.S.; de Goede, E.D. Efficient scheme for the shallow water equations on unstructured grids with application to the Continental Shelf. Ocean Dyn. 2011, 61, 1175–1188. [Google Scholar] [CrossRef]
- Green, R.H.; Lowe, R.J.; Buckley, M.L. Hydrodynamics of a Tidally Forced Coral Reef Atoll. J. Geophys. Res. Ocean. 2018, 123, 7084–7101. [Google Scholar] [CrossRef]
- Bloemendaal, N.; Muis, S.; Haarsma, R.J.; Verlaan, M.; Irazoqui Apecechea, M.; de Moel, H.; Ward, P.J.; Aerts, J.C. Global modeling of tropical cyclone storm surges using high-resolution forecasts. Clim. Dyn. 2019, 52, 5031–5044. [Google Scholar] [CrossRef]
- Hoch, J.M.; van Beek, R.; Winsemius, H.C.; Bierkens, M.F. Benchmarking flexible meshes and regular grids for large-scale fluvial inundation modelling, Elsevier. Adv. Water Resour. 2018, 121, 350–360. [Google Scholar] [CrossRef]
- Eslami, S.; Hoekstra, P.; Nguyen Trung, N.; Kantoush, S.A.; van Binh, D.; Duc Dung, D.; Tran Quang, T.; van der Vegt, M. Tidal amplification and salt intrusion in the Mekong Delta driven by anthropogenic sediment starvation. Sci. Rep. 2019, 9, 18746. [Google Scholar] [CrossRef]
- Achete, F.M.; van der Wegen, M.; Roelvink, D.; Jaffe, B. How can climate change and engineered water conveyance affect sediment dynamics in the San Francisco Bay-Delta system? Clim. Chang. 2017, 142, 375–389. [Google Scholar] [CrossRef]
- Barrera Crespo, P.D.; Mosselman, E.; Giardino, A.; Becker, A.; Ottevanger, W.; Nabi, M.; Arias-Hidalgo, M. Sediment budget analysis of the Guayas River using a process-based model. Hydrol. Earth Syst. Sci. 2019, 23, 2763–2778. [Google Scholar] [CrossRef]
- Deltares. RGFGRID User Manual. Pdf File. 2021. Available online: https://content.oss.deltares.nl/delft3d/manuals/RGFGRID_User_Manual.pdf (accessed on 17 May 2021).
- Thorne, C.R.; Harmar, O.P.; Wallerstein, N. Sediment Transport in the Lower Mississippi River; Final Report; U.S. Army Research, Development, and Standardisation Group: London, UK, 2000; p. 71. Available online: https://apps.dtic.mil/sti/pdfs/ADA460627.pdf (accessed on 17 May 2021).
- van Rijn, L.C. Unified view of sediment transport by currents and waves. I: Initiation of motion, bed roughness, and bed-load transport. J. Hydraul. Eng. 2007, 133, 649–667. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. On the Partial Difference Equations of Mathematical Physics. IBM J. Res. Dev. 1967, 11, 215–234. [Google Scholar] [CrossRef]
- Bentley, S.J., Sr.; Blum, M.D.; Maloney, J.; Pond, L.; Paulsell, R. The Mississippi River source-to-sink system: Perspectives on tectonic, climatic, and anthropogenic influences, Miocene to Anthropocene. Earth-Sci. Rev. 2016, 153, 139–174. [Google Scholar] [CrossRef]
- Ameen, A.D.; Kolker, A.S.; Taylor, C.M. Vegetation and shear strength in a delta-splay mouth bar. Wetlands 2017, 37, 1159–1168. [Google Scholar] [CrossRef]
- Allison, M.A.; Meselhe, E.A. The use of large water and sediment diversions in the Lower Mississippi River (Louisiana) for coastal restoration. J. Hydrol. 2010, 387, 346–360. [Google Scholar] [CrossRef]
- White, E.D.; Reed, D.J.; Meselhe, E.A. Modeled sediment availability, deposition, and decadal land change in coastal Louisiana marshes under future sea level rise scenarios. Wetlands 2019, 39, 1233–1248. [Google Scholar] [CrossRef]
- Meselhe, E.A.; Roelvink, D.; Wackerman, C.; Xing, F.; Vo, Q.T. Modeling the process response of coastal and deltaic systems to human and global changes. Oceanography 2017, 30, 84–97. [Google Scholar] [CrossRef]
- Allison, M.; Weathers, D.; Meselhe, E.A. Bottom morphology in the Song Hau Distributary Channel, Mekong River Delta, Vietnam. Cont. Shelf Res. 2017, 147, 51–61. [Google Scholar] [CrossRef]


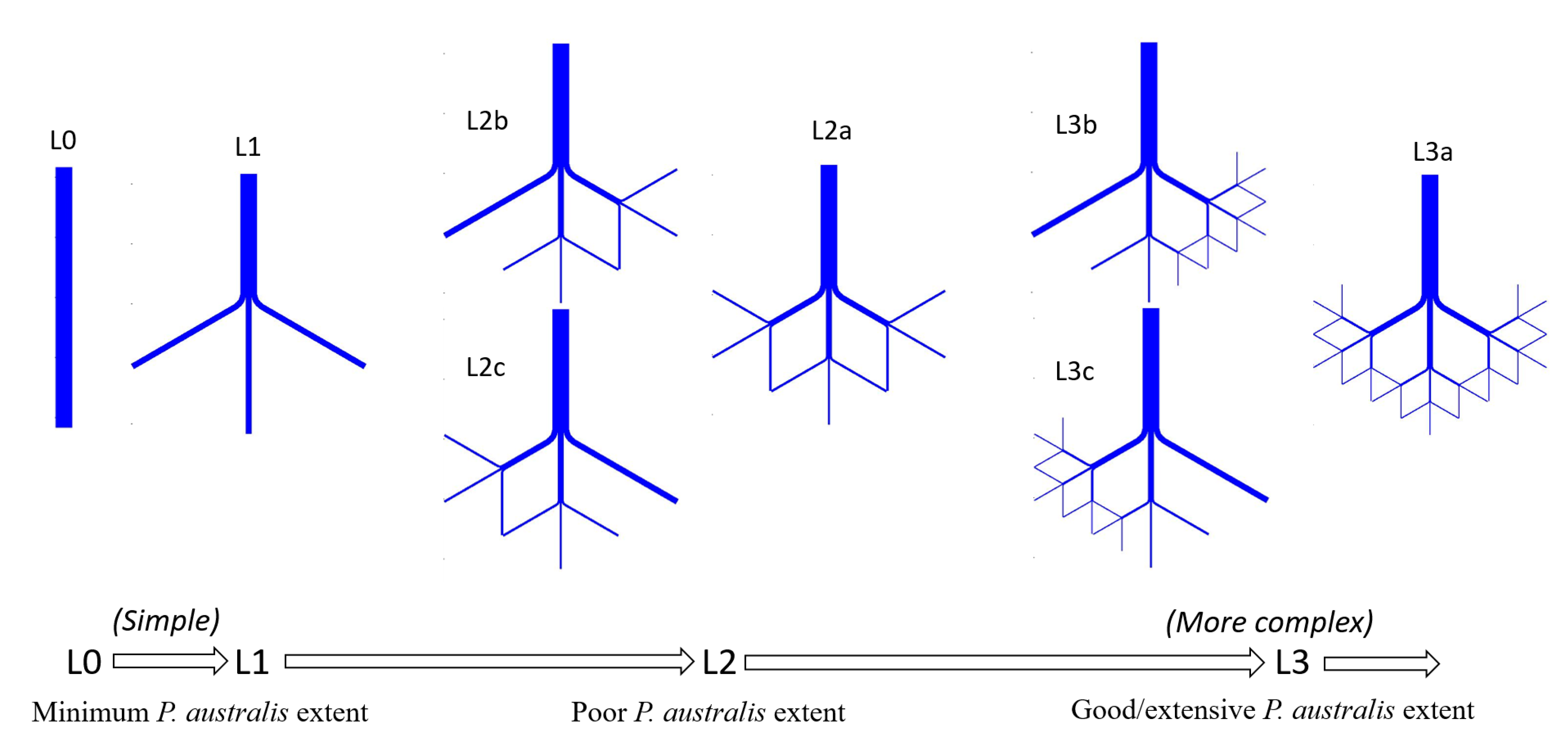
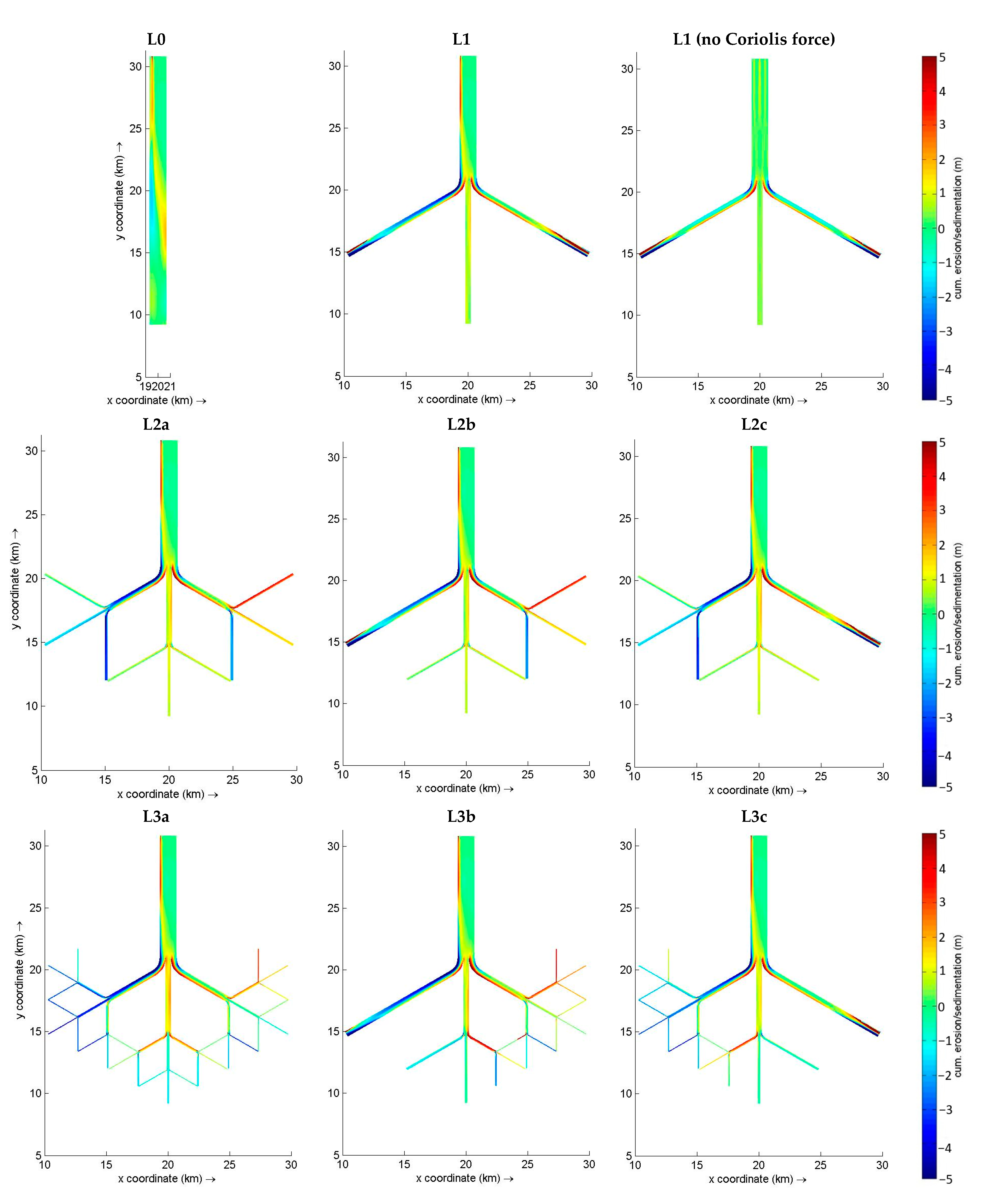
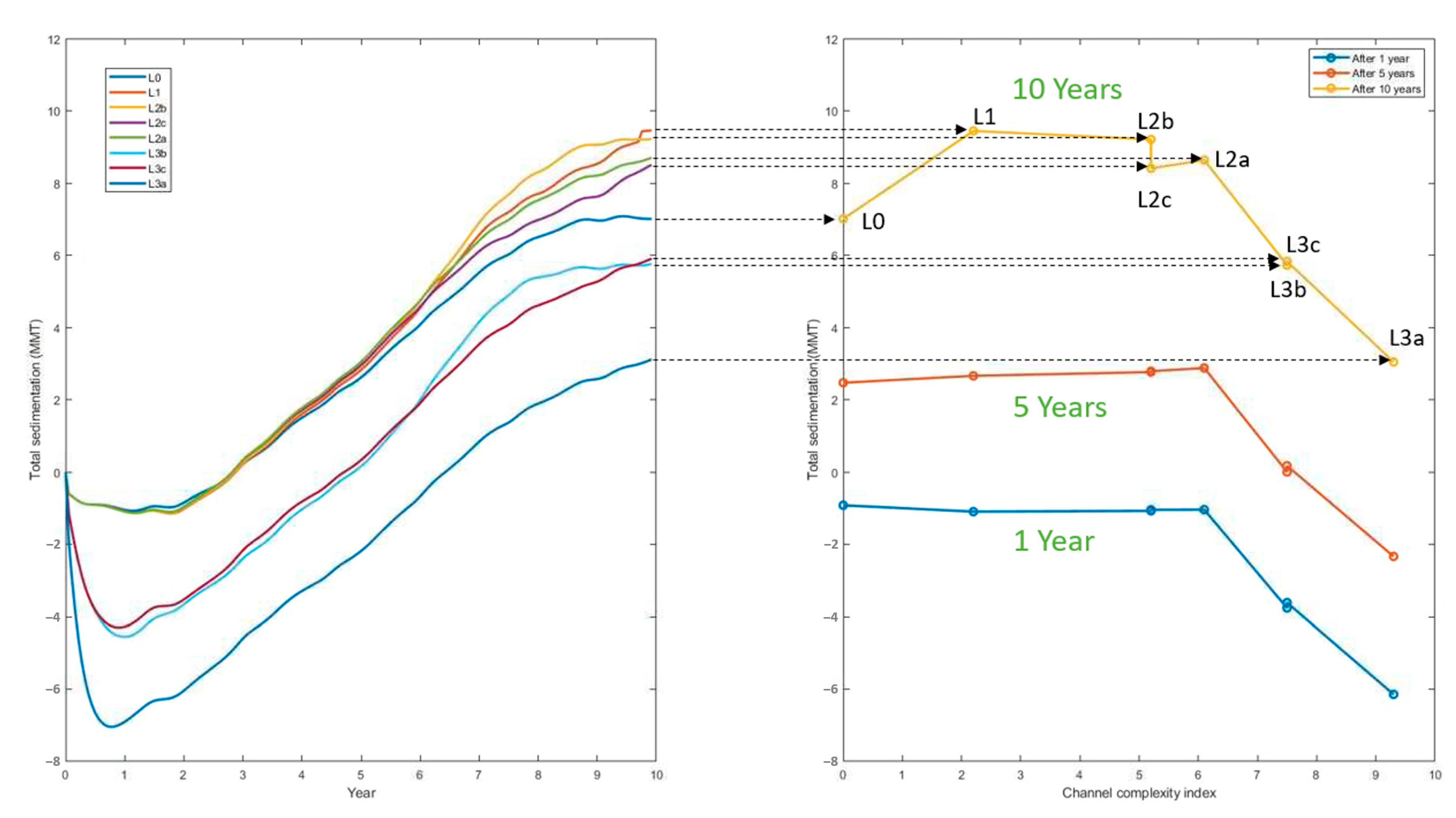
| Level | NL (# of Links) | NV (# of Vertices) | NO (# of Outlets) | Complexity Index |
|---|---|---|---|---|
| L0 | 1 | 1 | 1 | 0 |
| L1 | 3 | 1 | 3 | 2.2 |
| L2b/L2c | 9 | 3 | 7 | 5.2 |
| L2a | 12 | 4 | 9 | 6.1 |
| L3b/L3c | 20 | 7 | 13 | 7.5 |
| L3a | 36 | 13 | 23 | 9.3 |
| Factor | Base Case | Option 1 | Option 2 | Impact on Sedimentation | |
|---|---|---|---|---|---|
| (Option 1) | (Option 2) | ||||
| Tide | On | Off | / | Neutral | / |
| Wind 1 | Off | On | / | Neutral | / |
| Waves 2 | Off | On (Fetch/depth limited) | On (Young–Verhagen) | Decrease | Decrease |
| Sea level rise 3 | Off (0 m) | On (+0.2 m) | / | Increase | / |
| River discharge | 10,800 m3/s | 12,960 m3/s (+20%) | 8640 m3/s (−20%) | Decrease | Increase |
| River sediment concentration | 50 mg/L | 60 mg/L (+20%) | 40 mg/L (−20%) | Increase | Decrease |
| D50 | 150 µm | 160 µm | 140 µm | Increase | Decrease |
| Bed level | 8.0 m | 9.6 m (+20%) | 6.4 m (−20%) | Increase | Decrease |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, K.; Meselhe, E.; Nyman, J.A. The Effect of Phragmites australis Dieback on Channel Sedimentation in the Mississippi River Delta: A Conceptual Modeling Study. Water 2021, 13, 1407. https://doi.org/10.3390/w13101407
Hu K, Meselhe E, Nyman JA. The Effect of Phragmites australis Dieback on Channel Sedimentation in the Mississippi River Delta: A Conceptual Modeling Study. Water. 2021; 13(10):1407. https://doi.org/10.3390/w13101407
Chicago/Turabian StyleHu, Kelin, Ehab Meselhe, and J. Andrew Nyman. 2021. "The Effect of Phragmites australis Dieback on Channel Sedimentation in the Mississippi River Delta: A Conceptual Modeling Study" Water 13, no. 10: 1407. https://doi.org/10.3390/w13101407
APA StyleHu, K., Meselhe, E., & Nyman, J. A. (2021). The Effect of Phragmites australis Dieback on Channel Sedimentation in the Mississippi River Delta: A Conceptual Modeling Study. Water, 13(10), 1407. https://doi.org/10.3390/w13101407







