Evaluation of Drought Stress in Cereal through Probabilistic Modelling of Soil Moisture Dynamics
Abstract
1. Introduction
2. Materials and Methods
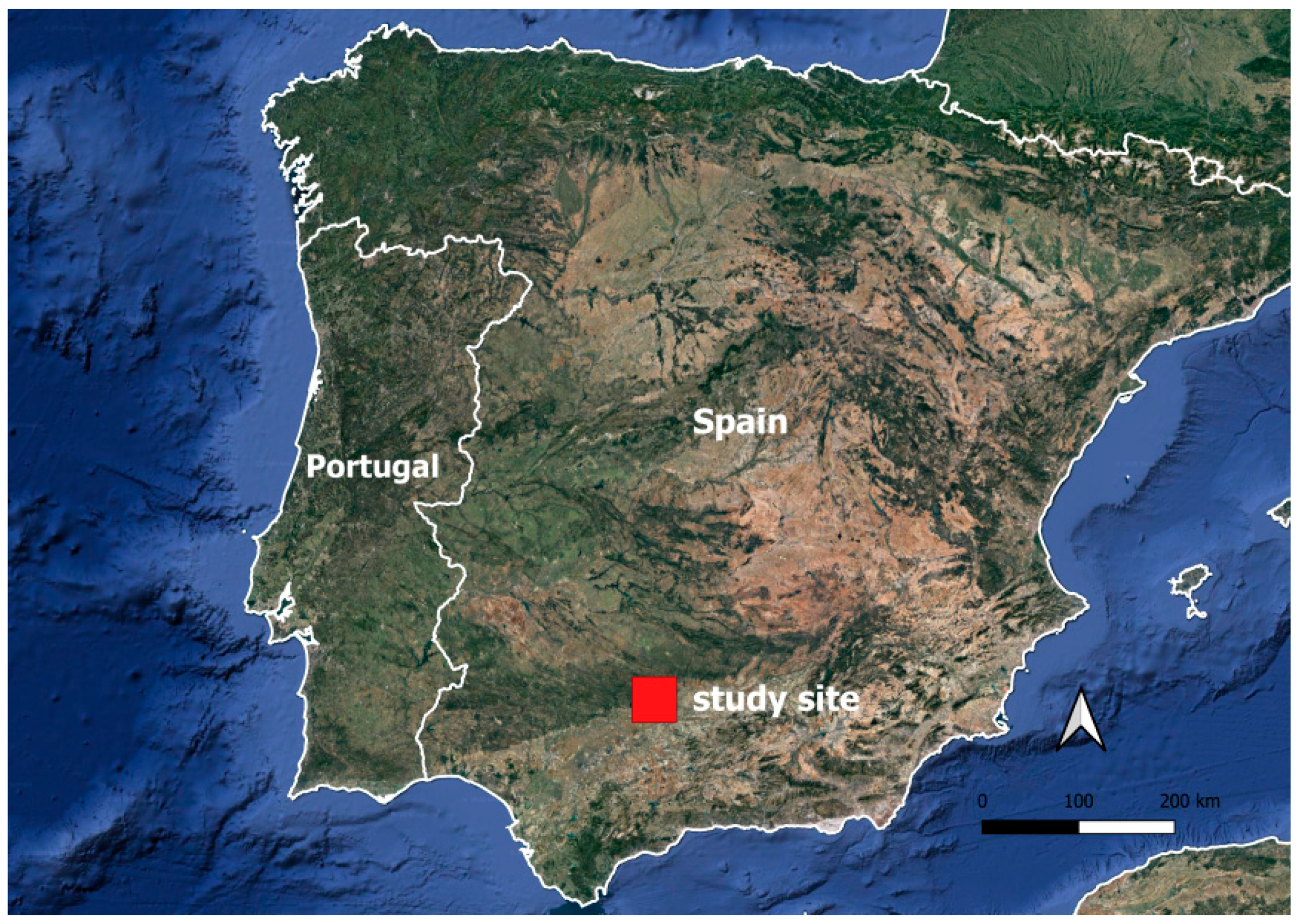
2.1. Study Area
2.2. Calculation of Static and Dynamic Stress Indicators
2.3. Soil Water Balance
2.4. Crop Yield Data
3. Results
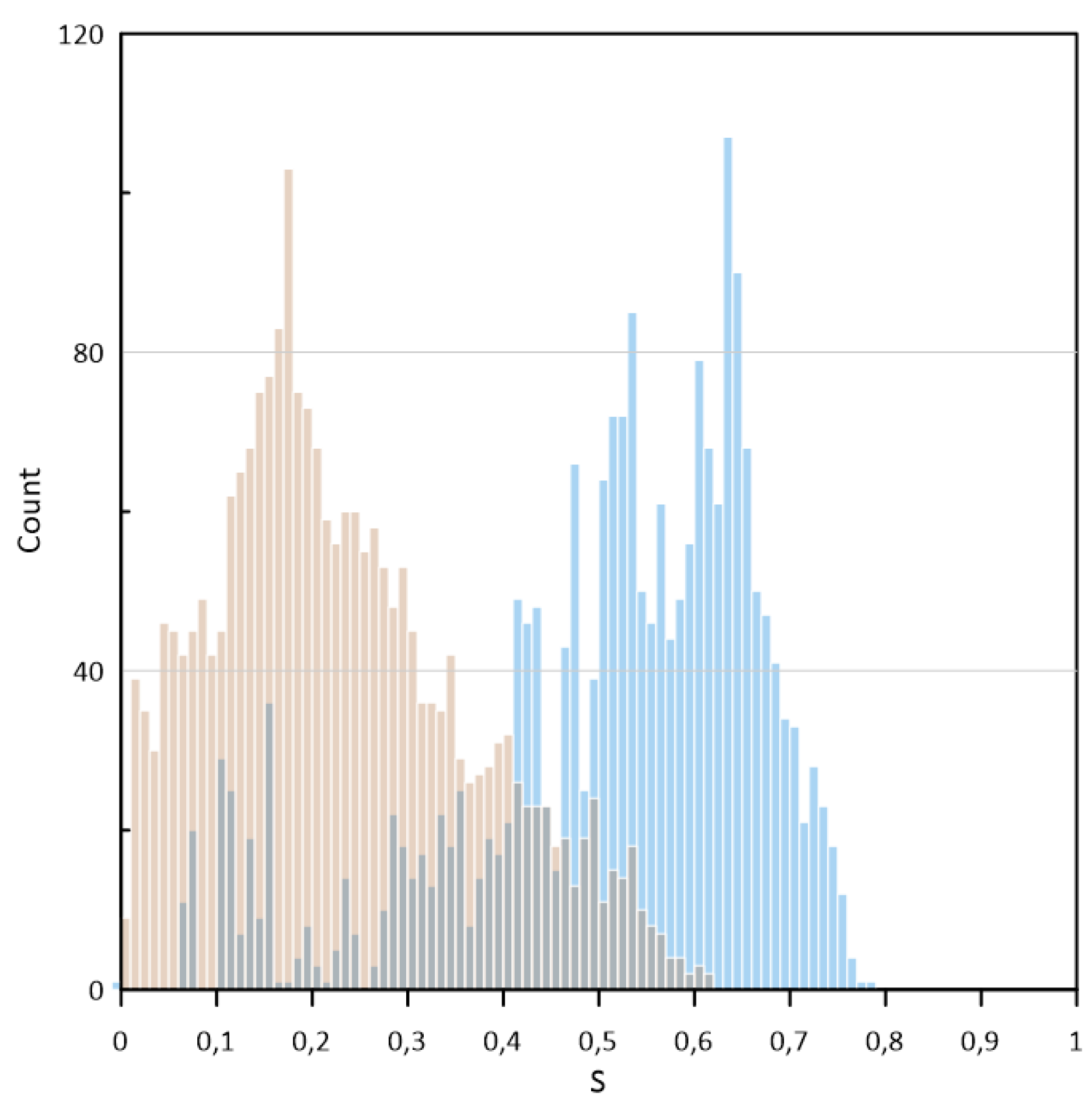
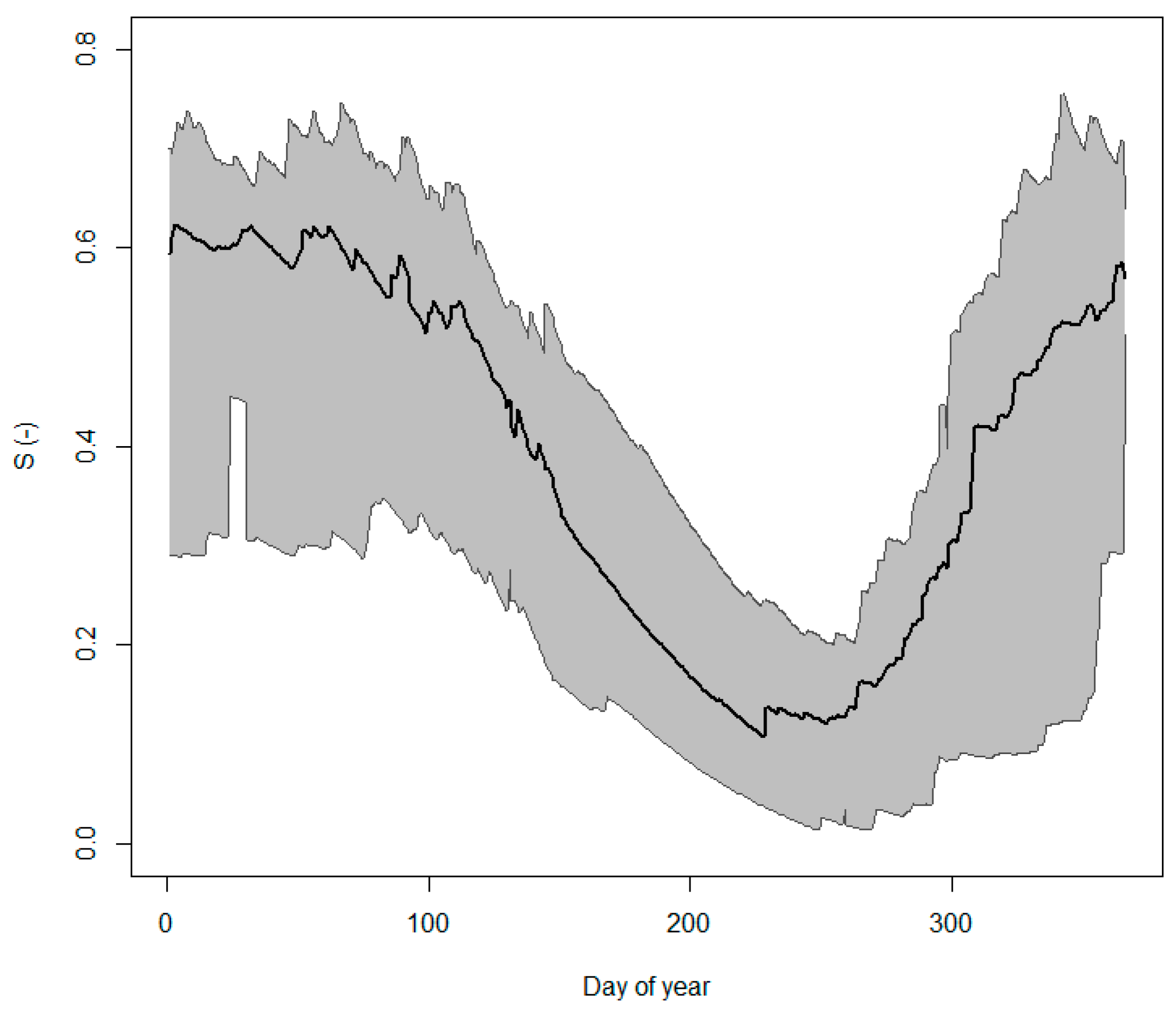
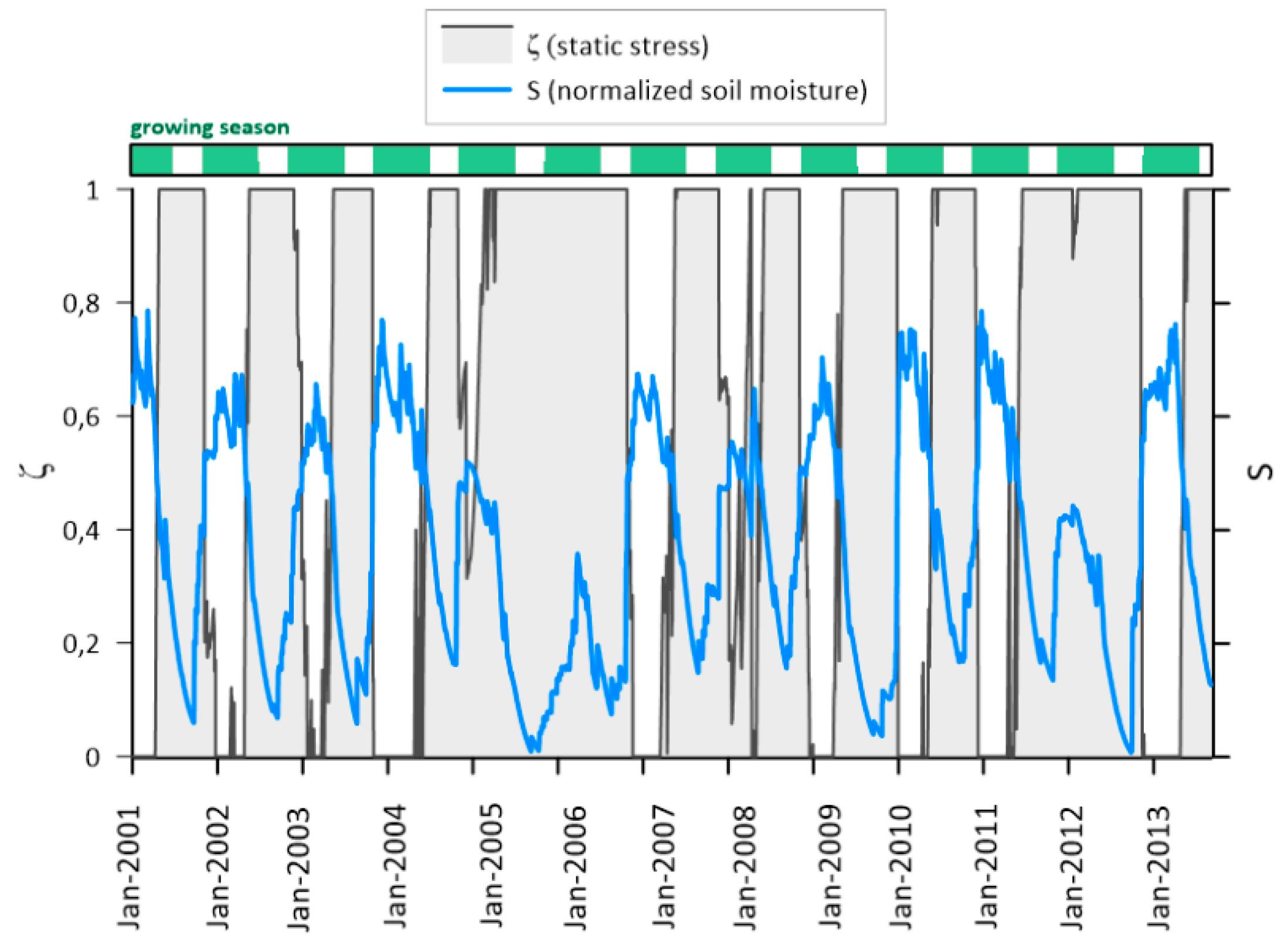
3.1. Soil Moisture Dynamics
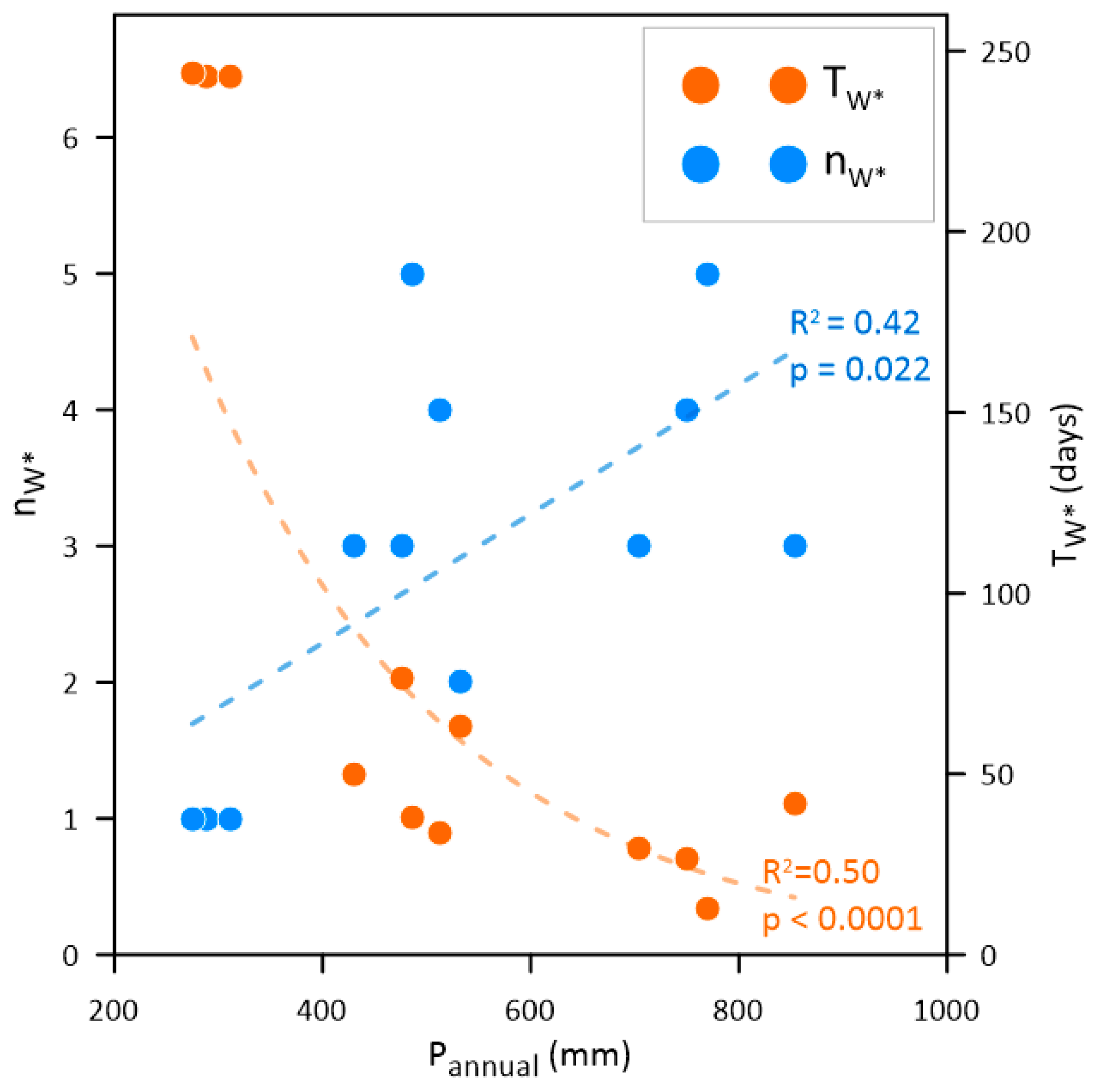
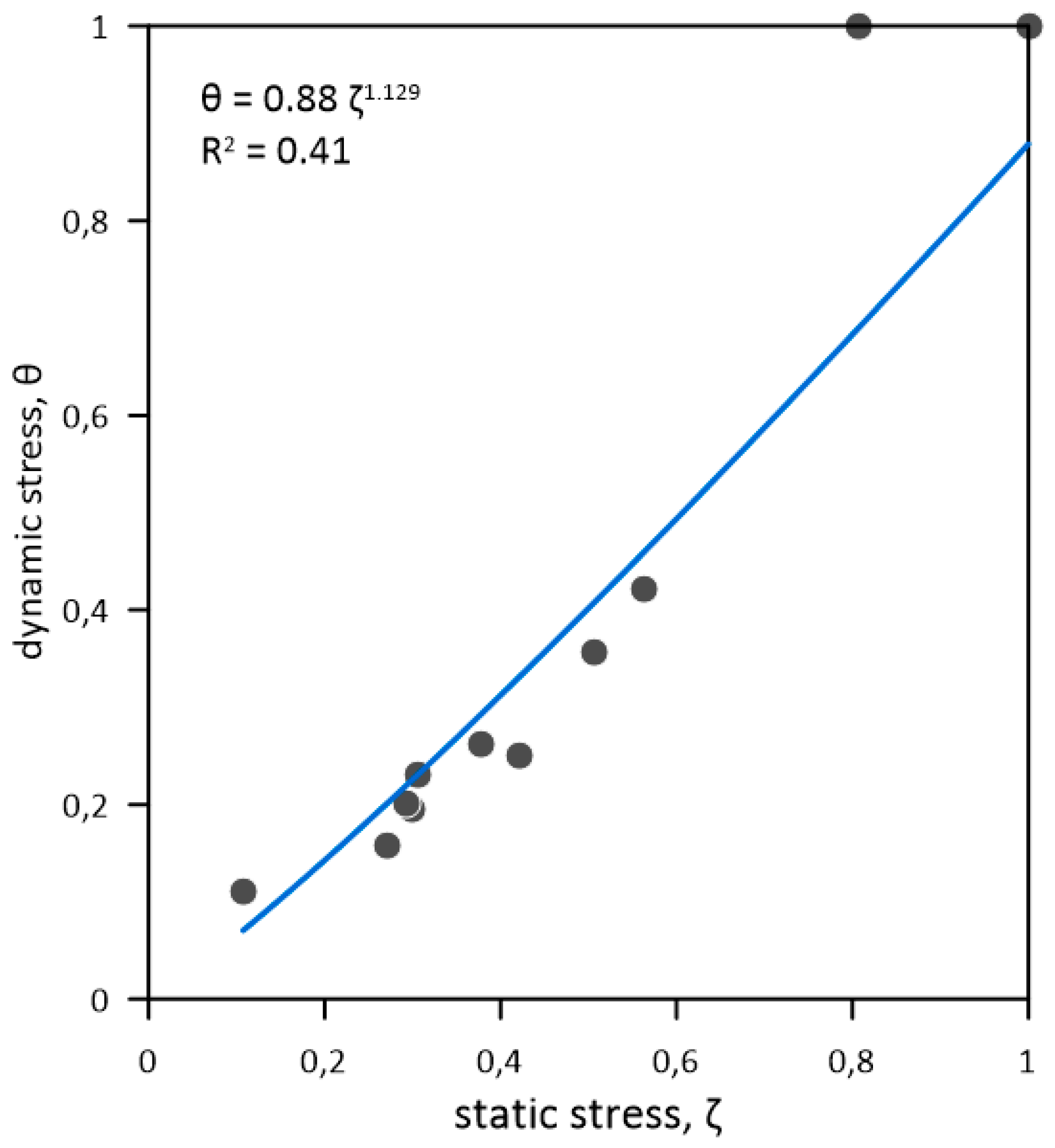
3.2. Static and Dynamic Stress Indicators
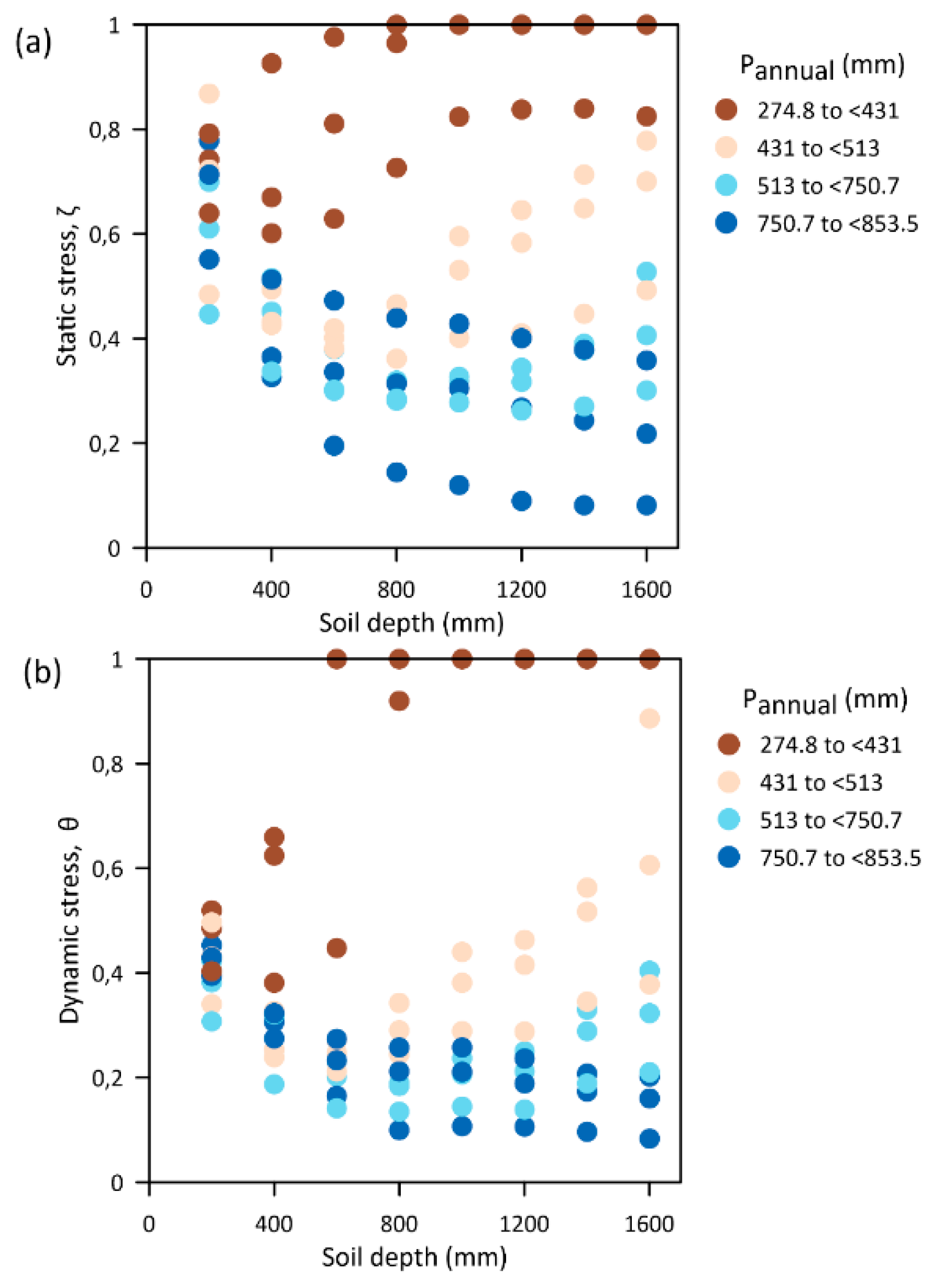
3.3. Sensitivity of Static and Dynamic Stress Indicators to Soil Depth
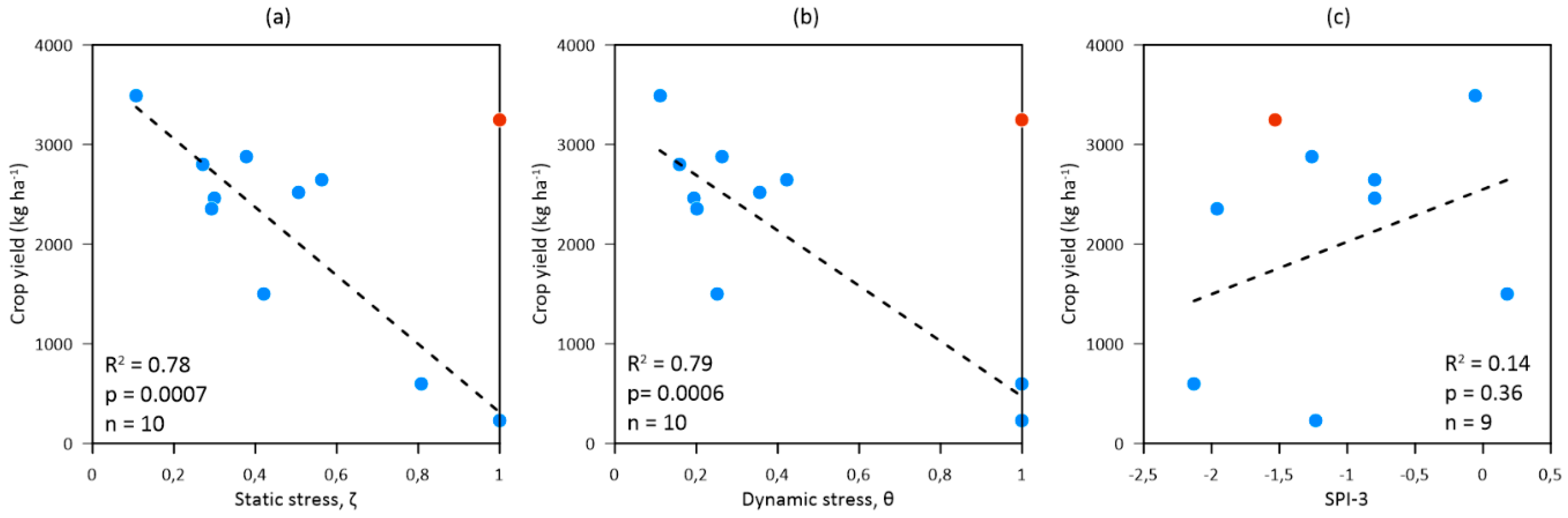
3.4. Validation of Static and Dynamic Stresses for Prediction of Crop Yield
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Porporato, A.; Laio, F.; Ridolfi, L.; Rodriguez-Iturbe, I. Plants in water-controlled ecosystems: Active role in hydrologic processes and response to water stress: III. Vegetation water stress. Adv. Water Resour. 2001, 24, 725–744. [Google Scholar] [CrossRef]
- Enenkel, M.; See, L.; Bonifacio, R.; Boken, V.; Chaney, N.; Vinck, P.; You, L.; Dutra, E.; Anderson, M. Drought and food security—Improving decision-support via new technologies and innovative collaboration. Glob. Food Secur. 2015, 4, 51–55. [Google Scholar] [CrossRef]
- Kim, W.; Iizumi, T.; Nishimori, M. Global Patterns of Crop Production Losses Associated with Droughts from 1983 to 2009. J. Appl. Meteorol. Climatol. 2019, 58, 1233–1244. [Google Scholar] [CrossRef]
- Leng, G.; Hall, J. Crop yield sensitivity of global major agricultural countries to droughts and the projected changes in the future. Sci. Total Environ. 2019, 654, 811–821. [Google Scholar] [CrossRef]
- Ortiz-Bobea, A.; Wang, H.; Carrillo, C.M.; Ault, T.R. Unpacking the climatic drivers of US agricultural yields. Environ. Res. Lett. 2019, 14, 064003. [Google Scholar] [CrossRef]
- Dai, A. Drought under global warming: A review. WIREs Clim. Chang. 2011, 2, 45–65. [Google Scholar] [CrossRef]
- Hussain, H.A.; Men, S.; Hussain, S.; Chen, Y.; Ali, S.; Zhang, S.; Zhang, K.; Li, Y.; Xu, Q.; Liao, C.; et al. Interactive effects of drought and heat stresses on morpho-physiological attributes, yield, nutrient uptake and oxidative status in maize hybrids. Sci. Rep. 2019, 9, 3890. [Google Scholar] [CrossRef] [PubMed]
- Lesk, C.; Rowhani, P.; Ramankutty, N. Influence of extreme weather disasters on global crop production. Nature 2016, 529, 84–87. [Google Scholar] [CrossRef]
- Spinoni, J.; Barbosa, P.; Bucchignani, E.; Cassano, J.; Cavazos, T.; Christensen, J.H.; Christensen, O.B.; Coppola, E.; Evans, J.; Geyer, B.; et al. Future Global Meteorological Drought Hot Spots: A Study Based on CORDEX Data. J. Clim. 2020, 33, 3635–3661. [Google Scholar] [CrossRef]
- Rey, D.; Holman, I.P.; Knox, J.W. Developing drought resilience in irrigated agriculture in the face of increasing water scarcity. Reg. Environ. Chang. 2017, 17, 1527–1540. [Google Scholar] [CrossRef]
- Daccache, A.; Ciurana, J.S.; Diaz, J.A.R.; Knox, J.W. Water and energy footprint of irrigated agriculture in the Mediterranean region. Environ. Res. Lett. 2014, 9, 124014. [Google Scholar] [CrossRef]
- Mann, M.L.; Warner, J.M.; Malik, A.S. Predicting high-magnitude, low-frequency crop losses using machine learning: An application to cereal crops in Ethiopia. Clim. Chang. 2019, 154, 211–227. [Google Scholar] [CrossRef]
- Mckee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Gao, X.-D.; Katsumoto, T.; Onodera, K. Purification and Characterization of Chitin Deacetylase from Absidia coerulea. J. Biochem. 1995, 117, 257–263. [Google Scholar] [CrossRef]
- Sepulcre-Canto, G.; Horion, S.; Singleton, A.; Carrao, H.; Vogt, J. Development of a Combined Drought Indicator to detect agricultural drought in Europe. Nat. Hazards Earth Syst. Sci. 2012, 12, 3519–3531. [Google Scholar] [CrossRef]
- Jiménez-Donaire, M.D.P.; Tarquis, A.; Giráldez, J.V. Evaluation of a combined drought indicator and its potential for agricultural drought prediction in southern Spain. Nat. Hazards Earth Syst. Sci. 2020, 20, 21–33. [Google Scholar] [CrossRef]
- Peña-Gallardo, M.; Vicente-Serrano, S.M.; Domínguez-Castro, F.; Beguería, S. The impact of drought on the productivity of two rainfed crops in Spain. Nat. Hazards Earth Syst. Sci. 2019, 19, 1215–1234. [Google Scholar] [CrossRef]
- García-León, D.; Contreras, S.; Hunink, J. Comparison of meteorological and satellite-based drought indices as yield predictors of Spanish cereals. Agric. Water Manag. 2019, 213, 388–396. [Google Scholar] [CrossRef]
- Laio, F.; Porporato, A.; Ridolfi, L.; Rodriguez-Iturbe, I. Plants in water-controlled ecosystems: Active role in hydrologic processes and response to water stress: II. Probabilistic soil moisture dynamics. Adv. Water Resour. 2001, 24, 707–723. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Porporato, A.; Laio, F.; Ridolfi, L. Plants in water-controlled ecosystems: Active role in hydrologic processes and response to water stress: I. Scope and general outline. Adv. Water Resour. 2001, 24, 695–705. [Google Scholar] [CrossRef]
- Peel, M.C.; Finlayson, B.L.; McMahon, T.A. Updated world map of the Köppen-Geiger climate classification. Hydrol. Earth Syst. Sci. 2007, 11, 1633–1644. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T. On the estimation of antecedent wetness conditions in rainfall–runoff modelling. Hydrol. Process. 2008, 22, 629–642. [Google Scholar] [CrossRef]
- Georgakakos, K.P. A generalized stochastic hydrometeorological model for flood and flash-flood forecasting: 1. Formulation. Water Resour. Res. 1986, 22, 2083–2095. [Google Scholar] [CrossRef]
- Brooks, R.H.; Corey, A.T. Properties of Porous Media Affecting Fluid Flow. J. Irrig. Drain. Div. 1966, 92, 61–88. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998; ISBN 978-92-5-104219-9. [Google Scholar]
- Doorenbos, J.; Pruitt, W.O. Guidelines for Predicting Crop Water Requirements; FAO Irrigation and Drainage Paper 24; Rev; Food and Agriculture Organization of the United Nations: Rome, Italy, 1977; ISBN 978-92-5-100279-7. [Google Scholar]
- Rawls, W.J.; Brakensiek, D.L. Estimation of Soil Water Retention and Hydraulic Properties. In Unsaturated Flow in Hydrologic Modeling: Theory and Practice; NATO ASI Series; Morel-Seytoux, H.J., Ed.; Springer: Dordrecht, The Netherlands, 1989; pp. 275–300. ISBN 978-94-009-2352-2. [Google Scholar]
- Rawls, W.J.; Brakensiek, D.L.; Soni, B. Agricultural Management Effects on Soil Water Processes Part I: Soil Water Retention and Green and Ampt Infiltration Parameters. Trans. ASAE 1983, 26, 1747–1752. [Google Scholar] [CrossRef]
- Vanderlinden, K. Análisis de Procesos Hidrológicos a Diferentes Escalas Espacio-Temporales; University of Córdoba, Dept. of Agronomy: Córdoba, Spain, 2001. [Google Scholar]
- Fan, J.; McConkey, B.; Wang, H.; Janzen, H. Root distribution by depth for temperate agricultural crops. Field Crop. Res. 2016, 189, 68–74. [Google Scholar] [CrossRef]
- Ministerio de Agricultura, Pesca y Alimentación Anuario de Estadística. Available online: https://www.mapa.gob.es/es/estadistica/temas/publicaciones/anuario-de-estadistica/ (accessed on 15 August 2020).
- Espejo-Pérez, A.J.; Brocca, L.; Moramarco, T.; Giráldez, J.V.; Triantafilis, J.; Vanderlinden, K. Analysis of soil moisture dynamics beneath olive trees. Hydrol. Process. 2016, 30, 4339–4352. [Google Scholar] [CrossRef]
- Narasimhan, B.; Srinivasan, R. Development and evaluation of Soil Moisture Deficit Index (SMDI) and Evapotranspiration Deficit Index (ETDI) for agricultural drought monitoring. Agric. For. Meteorol. 2005, 133, 69–88. [Google Scholar] [CrossRef]
- Sohrabi, M.M.; Ryu, J.H.; Abatzoglou, J.; Tracy, J. Development of Soil Moisture Drought Index to Characterize Droughts. J. Hydrol. Eng. 2015, 20, 04015025. [Google Scholar] [CrossRef]
- Martínez-Fernández, J.; González-Zamora, A.; Sánchez, N.; Gumuzzio, A.; Herrero-Jiménez, C.M. Satellite soil moisture for agricultural drought monitoring: Assessment of the SMOS derived Soil Water Deficit Index. Remote Sens. Environ. 2016, 177, 277–286. [Google Scholar] [CrossRef]
- Sánchez, N.; González-Zamora, Á.; Piles, M.; Martínez-Fernández, J. A New Soil Moisture Agricultural Drought Index (SMADI) Integrating MODIS and SMOS Products: A Case of Study over the Iberian Peninsula. Remote Sens. 2016, 8, 287. [Google Scholar] [CrossRef]
- Reichle, R.H.; De Lannoy, G.J.M.; Liu, Q.; Ardizzone, J.V.; Colliander, A.; Conaty, A.; Crow, W.; Jackson, T.J.; Jones, L.A.; Kimball, J.S.; et al. Assessment of the SMAP Level-4 Surface and Root-Zone Soil Moisture Product Using In Situ Measurements. J. Hydrometeorol. 2017, 18, 2621–2645. [Google Scholar] [CrossRef]
- Velpuri, N.M.; Senay, G.B.; Morisette, J.T. Evaluating New SMAP Soil Moisture for Drought Monitoring in the Rangelands of the US High Plains. Rangelands 2016, 38, 183–190. [Google Scholar] [CrossRef]
- Zhuang, R.; Zeng, Y.; Manfreda, S.; Su, Z. Quantifying Long-Term Land Surface and Root Zone Soil Moisture over Tibetan Plateau. Remote Sens. 2020, 12, 509. [Google Scholar] [CrossRef]
- Baldwin, D.; Manfreda, S.; Keller, K.; Smithwick, E.A.H. Predicting root zone soil moisture with soil properties and satellite near-surface moisture data across the conterminous United States. J. Hydrol. 2017, 546, 393–404. [Google Scholar] [CrossRef]
| Parameter | Value | Source |
|---|---|---|
| m (-) | 0.1 | Mean value of the interval proposed by Brocca et al. [23] |
| Ks (mm day−1) | 38.4 | Estimate of soil water properties by Rawls and Brakensiek [28]; representative value for clay soil according to USDA classification |
| λ (-) | 0.15 | Derived from graphics of the parameter l of Brooks and Corey [25] as a function of soil texture, organic matter content and increase in soil porosity above the reference [29] |
| Ws (m3/m3) | 0.45 | As proposed by Vanderlinden [30] calculated from the soil map of Andalusia |
| Wfc (m3/m3) | 0.32 | |
| Wpwp (m3/m3) | 0.22 | |
| Wr (m3/m3) | 0.05 | |
| W* (m3/m3) | 0.275 | Following Doorenbos en Pruitt [27], taken as 55% of the total available water for cereal |
| q (-) | 1 | Porporato et al. [1] |
| k (-) | 0.5 | Porporato et al. [1] |
| h (m) | 1 | Fan et al. [31] |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiménez-Donaire, M.d.P.; Giráldez, J.V.; Vanwalleghem, T. Evaluation of Drought Stress in Cereal through Probabilistic Modelling of Soil Moisture Dynamics. Water 2020, 12, 2592. https://doi.org/10.3390/w12092592
Jiménez-Donaire MdP, Giráldez JV, Vanwalleghem T. Evaluation of Drought Stress in Cereal through Probabilistic Modelling of Soil Moisture Dynamics. Water. 2020; 12(9):2592. https://doi.org/10.3390/w12092592
Chicago/Turabian StyleJiménez-Donaire, María del Pilar, Juan Vicente Giráldez, and Tom Vanwalleghem. 2020. "Evaluation of Drought Stress in Cereal through Probabilistic Modelling of Soil Moisture Dynamics" Water 12, no. 9: 2592. https://doi.org/10.3390/w12092592
APA StyleJiménez-Donaire, M. d. P., Giráldez, J. V., & Vanwalleghem, T. (2020). Evaluation of Drought Stress in Cereal through Probabilistic Modelling of Soil Moisture Dynamics. Water, 12(9), 2592. https://doi.org/10.3390/w12092592





