Abstract
Extreme precipitation events are often localized, difficult to predict, and available records are often sparse. Improving frequency analysis and describing the associated uncertainty are essential for regional hazard preparedness and infrastructure design. Our primary goal is to evaluate incorporating Bayesian model averaging (BMA) within a spatial Bayesian hierarchical model framework (BHM). We compare results from two distinct regions in Oregon with different dominating rainfall generation mechanisms, and a region of overlap. We consider several Bayesian hierarchical models from relatively simple (location covariates only) to rather complex (location, elevation, and monthly mean climatic variables). We assess model predictive performance and selection through the application of leave-one-out cross-validation; however, other model assessment methods were also considered. We additionally conduct a comprehensive assessment of the posterior inclusion probability of covariates provided by the BMA portion of the model and the contribution of the spatial random effects term, which together characterize the pointwise spatial variation of each model’s generalized extreme value (GEV) distribution parameters within a BHM framework. Results indicate that while using BMA may improve analysis of extremes, model selection remains an important component of tuning model performance. The most complex model containing geographic and information was among the top performing models in western Oregon (with relatively wetter climate), while it performed among the worst in the eastern Oregon (with relatively drier climate). Based on our results from the region of overlap, site-specific predictive performance improves when the site and the model have a similar annual maxima climatology—winter storm dominated versus summer convective storm dominated. The results also indicate that regions with greater temperature variability may benefit from the inclusion of temperature information as a covariate. Overall, our results show that the BHM framework with BMA improves spatial analysis of extremes, especially when relevant (physical and/or climatic) covariates are used.
1. Introduction
The ability to estimate the magnitude and frequency of extreme precipitation events is an essential part of infrastructure planning and flood prediction [1,2,3]. Extreme events directly affect infrastructure and residents of a region, while also having an economic effect [3,4,5]. In some regions, extreme events can be localized and difficult to predict, especially when gauge data is sparse [6]. In regions that do have relatively dense observational networks, integrating spatial information (i.e., multiple extremes across space) for frequency is not straightforward [6].
Following the early contributions by Gumbel [7], which expanded upon the work of Fisher and Tippett [8], frequency analysis became widely used for estimating rainfall or streamflow corresponding to different return periods [5,9,10,11]. The process generally involves fitting a representative parametric distribution function (e.g., generalized extreme value distribution, Log-Pearson, exponential) to extreme values (e.g., exceeding 95th percentile) [1,8,12,13]. The fitted distribution is then used to estimate the probability of occurrence of different events (e.g., precipitation and/or streamflow) [14]. The further out on the tail of the distribution inference is made, the greater the uncertainty [14,15,16].
Precipitation is a spatial process and several methods have been developed to integrate spatial information into frequency analysis [17]. One approach for spatial extreme precipitation analysis is spatial Bayesian hierarchical modeling (BHM) [6,18]. BHM distributes extremal model parameters in space using covariate information pertaining to geographical and climatological factors that influence regional precipitation extremes [15,19,20,21]. The advantages of a BHM-based spatial analysis of extremes include (a) that BHM does not require the decomposition of the study region into homogeneous subregions [6]; (b) it is robust in the treatment of uncertainty [6,19]; (c) BHM can be easily adapted to accommodate treatments of non-stationarity [19,22,23]; and (d) it allows the inclusion of physical features (e.g., elevation) of the region and other relevant climatic variables (e.g., temperature, moisture transport) [6,24]. Moreover, the Bayesian inference methodological framework readily supports the inclusion of additional data types relevant to the analysis—for example, information derived via elicitation and climate indices [23,24,25,26,27]. A potential challenge with applying spatial BHM, however, is either locating or developing relevant covariate data to support its deployment. Past spatial BHM extreme value studies incorporate covariate information from gridded model outputs or interpolated data sets (i.e., ERA-interim reanalysis data, VIC, ECHAM4.5, interpolated data sets from the Spatial Climate Analysis Service, and the Hulme data set) [6,26,27,28,29,30,31].
In this study, we incorporate the parameter-elevation relationships on independent slopes model (PRISM) data set [32,33,34] as a source of covariate information within a BHM framework that includes Bayesian model averaging (BMA) for each parameter’s general linear model. We consider a wide range of models from relatively simple (location covariates only) to rather complex (location, elevation, and monthly mean climatic variables). The climatic variables used include mean daily temperature and dewpoint temperature, which goes beyond the inclusion of precipitation of previous studies in the western US. [35]. We compare model choice, complexity, and covariates in two distinct regions in Oregon with different dominating rainfall generation mechanisms and a region of overlap. We apply BMA to account for model uncertainty and to access covariate selection across models and domains. We analyze the posterior inclusion probabilities (PIP) generated using BMA for the model covariates, model performance, and the contribution of the spatial random effects term to the parameter estimates. The overarching goal of this paper is to determine the effectiveness of including BMA within a spatial BHM framework across climatically varying regions.
2. Materials and Methods
In this study, we model annual maxima (AM) daily precipitation data from Oregon using the generalized extreme value (GEV) family of distribution functions. The GEV family of distribution functions are of the form [14]
defined on where The location , scale , and shape parameters of the distribution specify the center of the distribution, the size of the deviation around , and the tail behavior of the distribution, respectively. The GEV family incorporates the three possible extreme value distributions which correspond to (Weibull), interpreted as the limit as (Gumbel), and (Fréchet).
The spatial BHM extreme rainfall analysis was performed using a framework that implements a Markov Chain Monte Carlo (MCMC) sampling methodology to estimate the spatially dependent parameters of the GEV distribution, along with BMA, to account for and assess model uncertainty related to the covariates employed [36,37]. Each GEV spatially dependent parameter is defined by a general linear model (GLM) of the covariates plus a spatial random effects term () that accounts for residual spatial association not captured by the covariates. Ideally, if the covariates sufficiently capture the latent processes, the term should be minimal. The precipitation AM for a specific location is represented as (within the spatial region of study ) and for a year , where
and
where . The covariates, regression parameters, and spatial random effects terms are denoted by , , and , respectively, where . The spatial random effects term is assumed to be a zero-centered Gaussian spatial process defined by an isotropic exponential covariance function with a sill ( and range . In particular,
where is the Euclidean distance between locations and . The current framework does not allow user defined covariance functions and could be an area for future development, especially for regions that display anisotropic covariance. The likelihood is given by
where denotes the entire set of block maxima observations. The likelihood definition does imply that and are conditionally independent for anywhere . This independence assumption may influence our results, particularly in the denser network of stations within the Willamette River Basin (WRB) where larger-scale winter storms off the Pacific Ocean dominate the AM events. However, for the sparser network of stations within the eastern Oregon region (EOR), where more localized thunderstorms dominate several sites, this is less likely to influence performance.
Model inference is performed using MCMC methods, wherein the algorithm returns a chain of length N, where the th iteration contains the set of elements
for each from which the joint posterior distribution is estimated after discarding the initial burn-in period. The Gaussian proposal distributions are tuned using second-order Taylor expansions of Equation (6).
The BMA feature within the framework makes use of conditional Bayes factors and an MC3-within-Gibbs style of sampling to account for model uncertainty [36]. For each iteration a subset of model covariates is randomly sampled, let us call this model subset M. A conditional Bayes factor evaluation is used, where the full conditional probability of M is compared with that of the proposal M’. If the proposal M’ is accepted, then the regression parameters corresponding to each of the covariates used in M’ are updated. If rejected, the previous M is used. Each time M is accepted, the covariates it contains are assigned a one; conversely, each is assigned zero when rejected or not used within M. After all iterations have completed, the posterior inclusion probability (PIP) can be calculated using the number of times a covariate received a one out of the total post-burnin iterations.
The covariate information we employed for our models pertains to the geographical and climatological factors that we assume influence regional precipitation extremes within the study regions. To improve inference, all covariates were standardized prior to model simulation. We evaluated the predictive performance of each model through application of leave-one-out cross validation (LOO-CV) and minimization of the continuous ranked probability score (CRPS) and root mean squared error (RMSE). RMSE was applied as
where N is the site-specific number of AM events and is precipitation in inches.
The CRPS compares the predicted and observed cumulative distribution functions and can be defined as
where represents the predicted precipitation, and the observed precipitation [38,39]. For the median of the predicted GEV cumulative distributions (Equation (2)) was used across all iterations (post burn-in). is the Heaviside step function where
As the distributions become increasingly similar, the CRPS approaches zero [38]. A small (100ths) change in CRPS corresponds with a substantial difference in performance, which is why we chose to also use RMSE to help further differentiate between models with similar CRPS. For this study, we used a derivation of CRPS, which can be written as
where is the number of predicted values and is the number of observed values.
2.1. Study Regions and Storm Climatology
The Willamette River Basin (WRB) is located along the western part of Oregon (Figure 1). The region is bounded by the Coastal Range to the west, the Columbia River to the north, and the Cascade Range to the east. Extreme precipitation in the WRB primarily is a result of winter storms that occur between October and March and which typically account for 75–80% of the region’s annual precipitation [40,41]. Temperature fluctuations are relatively small due to the basin’s proximity to the Pacific Ocean; however, elevation plays a major role in its variability [41,42]. Elevations within the WRB range from near sea level along the Columbia River to over 3048 m in the Cascade Range [32]. The orographic effect of the Cascade Range results in relatively high amounts of precipitation along the Columbia River Gorge [32]. Overall, the Pacific northwest region experiences warm, dry summers due to intensification of the Pacific subtropical high and cool, wet winters as the polar jet stream dips southward bringing storms from the Gulf of Alaska [43].
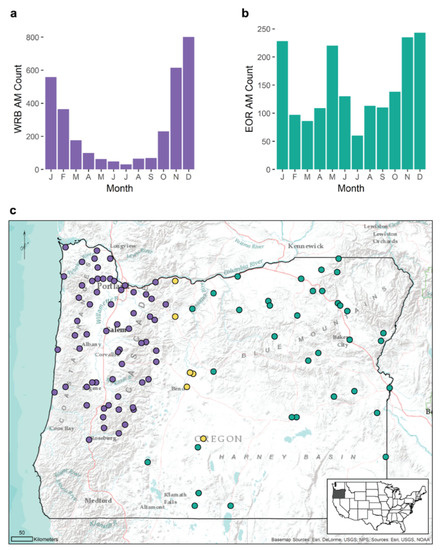
Figure 1.
Study regions with location reference numbers, and annual maxima (AM) climatology where (a) is the count of AM events by month for the Willamette River Basin (WRB) and (b) is the count of AM events by month for the eastern Oregon (EOR) study region. Within the study region map (c), the purple markers indicate locations included exclusively within the WRB, while green markers indicate those within the EOR. The yellow markers are the locations that were included within both study regions. Basemap Source: ESRI [44].
We also focus on eastern Oregon (EOR), which encompasses the region east of the Cascade Range crest-line, the high desert of southeastern Oregon, north-central Deschutes-Umatilla Plateau, and the Blue Mountains in the northeast. We chose this additional region since it varies climatically from the WRB. In general, EOR is drier than western Oregon with approximately four times less precipitation falling east of the Cascade Range than to the west [45]. During the early summer months, areas within the EOR region often experience increases in precipitation due to thunderstorms which develop as cool marine air pushes inland east of the Cascade Range and interacts with warmer inland air [42,43,46]. As the summer months progress, decreases in precipitation are widespread as the Pacific subtropical high continues to increase in intensity and extent while the polar jet stream shifts northward, with a few localized exceptions due to thunderstorms [43].
2.2. Annual Maxima Data and Covariates
The time series of annual maxima (AM) data for the WRB and EOR regions was produced for the Oregon Department of Transportation (ODOT) by Schaefer et al. [47], which was conducted due to the lack of a National Oceanic and Atmospheric Administration (NOAA) precipitation atlas update for the region [10]. The data set is comprised of 24 h annual precipitation maxima for 128 stations throughout Oregon, where annual is defined as the period between 1 January and 31 December [47]. The length of record for each station ranges from 10 years to 66 years, with a combined 2912 AM for the WRB and 1620 AM for EOR. We used the stations which fall within our specific study regions; 68 stations fall within the WRB region, while 41 stations fall within the bounds of EOR (Figure 1). Six of the stations (along the Columbia River Gorge and east of the Cascade Range crest) were included in both the WRB and EOR regions for additional model comparison. The remaining stations from the original data set fall within the Umpqua and Rogue River watersheds, which were not included in this analysis. Schaefer et al. [47] performed quality checks on the station records for errors, incomplete records, and any anomalous precipitation amounts relative to neighboring gages. The station data was also checked for stationarity and temporal independence using a null hypothesis of zero slope and zero serial correlation, respectively; the null hypothesis could not be rejected at a significance level of 0.05. Based on the dominance of larger-scale winter storms across the WRB, there is likely some spatial dependence between stations. However, the spatial dependence across the EOR region should be less since there are fewer stations spread over a larger region with several dominated by local convective storms.
The covariates we employed include the site-specific geographical information of longitude, latitude, elevation, and climatological information including monthly and annual precipitation, mean temperature, and mean dew point temperature from the PRISM Norm81m long-term (1981–2010) mean monthly gridded data set. The covariates were selected based on the literature on the impacts of physical information (e.g., elevation, climatology) on local extreme precipitation [16,48,49]. Temperature and dewpoint temperature were included since their interaction with precipitation extremes, primarily because of rainfall–temperature thermodynamic relations, have been recognized in previous publications [50,51,52].
The PRISM data set not only has the advantage of being extensively peer-reviewed but also has a relatively fine spatial resolution across the contiguous United States (~800 m) [34]. From the PRISM data set we also derived the seasonal mean (November–March and April–October means) of the climatological variables monthly precipitation (P), monthly mean daily temperature (T), and monthly dew point temperature (Td) for use in our models. Our choice of specific covariate data used for each of the models varies from simple (longitude and latitude; model XY) to more complex (longitude, latitude, elevation, monthly P, monthly Td, and monthly T; model XYZPT6) (Table 1).

Table 1.
Model acronyms and covariates employed.
3. Results
3.1. Model Selection
The selection of the best performing models for each region was based upon the comparison of the mean, median and spread of the CRPS and RMSE across sites (Figure 2 and Figure S1, Tables S1 and S2). Additionally, we inspected individual location predicted CDFs (Figure S2) and mapped model performance to determine whether there was any noticeable difference between models (Figure S3). The results of our LOO-CV analysis suggest that, from the eight models tested for each region, XYZPT2, XYZPT4, XYZPT5, and XYZPT6 were the top performing models for the WRB (Figure 2b), while XYZPT1 and XYZPT3 were the top for EOR (Figure 2a). We argue that these top performing models within a given region are equally good since their mean and median scores and their spatial distributions are similar. Therefore, our choice for the best model is the simplest model out of the top performing models for each region. For the WRB, the simplest top-performing model includes location, elevation, and mean wet-season P, T, and as covariates (model XYZPT2); while the simplest for the EOR contains location, elevation and mean annual P (model XYZPT1).
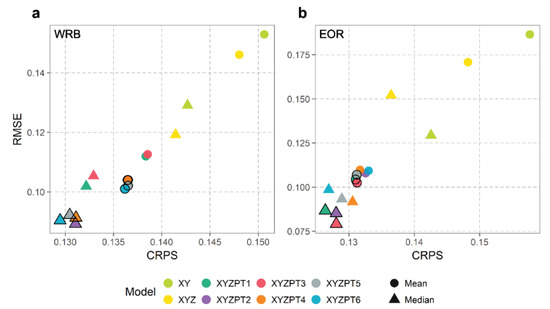
Figure 2.
Comparison of mean and median continuous ranked probability score (CRPS) and root mean squared error (RMSE) for (a) the WRB region and (b) the EOR region. The top performing three or four models are closely clustered where one may perform better with respect to CRPS, while another may have a slightly better RMSE. The top performing models across both mean and median results in (a) are XYZPT2, XYZPT4, XYZPT5, and XYZPT6, while the top performing in (b) are XYZPT1 and XYZPT3.
We also performed a spatial GEV analysis for each model to assess model fit, which is commonly used to fine-tune covariate selection when cross validation and/or BMA are not used. The GLM for each parameter contained the full set of covariates for each model. The Takeuchi information criterion (TIC) for each model was assessed relative to model complexity (Figure 3, Table S3). The results confirm our selection of best model, and that the inclusion of climatic covariates greatly improves model fit. For the WRB, model XYZPT2 has a lower TIC relative to XYZPT1 and XYZPT3. For the EOR region, model XYZPT1 has a lower TIC relative to XYZPT2 and is close to the TIC result for the more complex XYZPT3. While XYZPT6 has the lowest TIC, we chose not to use it to avoid overfitting.
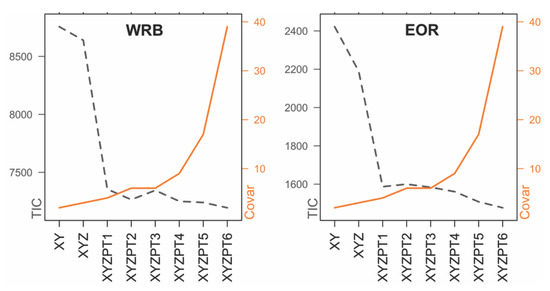
Figure 3.
Spatial generalized extreme value (GEV) model fit for both regions. Grey dashed line represents TIC, while the solid orange line represents the number of model covariates.
3.2. Posterior Inclusion Probability by Region
As noted previously, the methodology used here includes a BMA functionality that provides an estimate of the posterior inclusion probability (PIP) for the linear terms of each GEV parameter. While most model covariates have a non-negligible PIP, mean wet-season precipitation (November–March) has the greatest influence on the location parameter, μ, of the GEV distribution for both regions (Figure 4). Longitude (x), latitude (y), and elevation (z) have slightly greater μ PIP for the WRB models than for the EOR models, which could be due to the greater variability in elevation and mean precipitation across the relatively small WRB region.
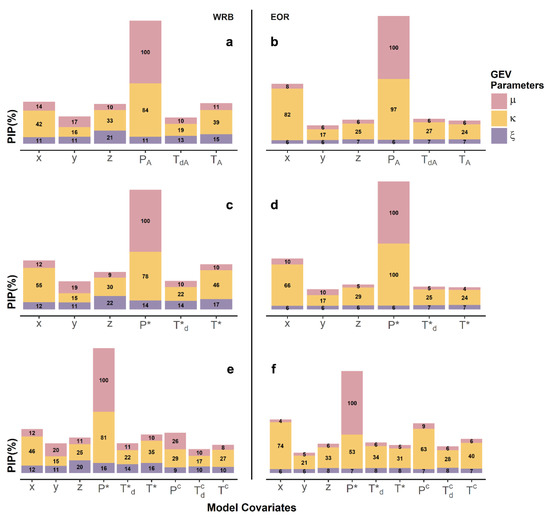
Figure 4.
Posterior inclusion probability for the GEV location, inverse scale, and shape parameters (μ, , ) for the three simpler models. Model XYZPT3 for (a) the WRB and (b) EOR, model XYZPT2 for (c) the WRB and (d) EOR, and model XYZPT4 for (e) the WRB and (f) EOR. For all models and regions, the uppermost color (pink) represents μ, the middle color (orange) displays the results for , and the bottommost color (purple) shows the results for .
Precipitation and longitude have the largest PIP for the inverse-scale parameter, , across the simpler models for both regions (Figure 4), with longitude appearing to be more important for the EOR models relative to the WRB models. Mean daily temperature (T) has a slightly higher PIP in the WRB models, relative to EOR, with wet-season T receiving a higher PIP than dry-season T. The climatic difference between the regions can also be seen when P is separated into wet- and dry-seasons (Figure 4e,f), with the WRB showing a greater PIP for wet-season P and the EOR displaying similar PIPs for both seasons (dry-season P displaying a slightly higher PIP). The PIP results nicely echo the AM climatology of both regions, with precipitation in the WRB being driven by large synoptic systems originating from the Pacific during winter months, while precipitation in the EOR is generally driven by convective systems resulting in short duration, high intensity events in the early summer. Latitude consistently has one of the lowest PIP across models and regions.
For the WRB, elevation (z) appears to have the most influence on the shape parameter, , of the simpler models (Figure 4a,e). However, this is not the case for the simpler EOR models where does not depend on any single covariate for the region’s top performing models (XYZPT1 and XYZPT3 shown in Figure 4b); it is only seen with model XYZPT6 (Figure 5b), which did not perform as well within the EOR region.
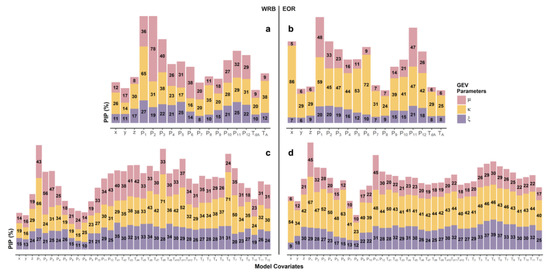
Figure 5.
Posterior inclusion probability for the GEV parameters (μ, , ) for the two most complex models. Model XYZPT5 for (a) the WRB and (b) EOR, and model XYZPT6 for (c) the WRB and (d) EOR. For both models and regions, the upper-most color (pink) represent μ, the middle color (orange) displays the results for , and the bottom-most color (purple) shows the results for .
In the more complex models (XYZPT5 and XYZPT6), PIP results mostly reflect those of the simpler models, although in finer detail given that the covariates are on a monthly scale (Figure 5). Again, XYZPT5 and XYZPT6 where both among the top preforming stations for the WRB region; however, they were not among the top performing for the EOR region. In the WRB model XYZPT5 (Figure 5a), February precipitation (P2) dominates μ PIP; while for the EOR XYZPT5, January and November precipitation (P1 and P11) dominate μ PIP (Figure 5b). For the WRB XYZPT6 (Figure 5c), February μ PIP remains the highest with December, January, and March μ PIP following close behind. For the EOR XYZPT6 (Figure 5d), January and November precipitation still stand out with the highest μ PIP.
Within these more complex models, the PIP results again reflect the differences in each region’s primary storm mechanism. For both XYZPT5 and XYZPT6 in the WRB region, January precipitation is among the covariates with the highest PIP. In the WRB XYZPT6 model, August dewpoint temperature (Td8) and June mean daily temperature (T6) have the highest PIP, exceeding that of the January precipitation. In the EOR XYZPT5 model (Figure 5b), longitude and June precipitation have the highest PIP; while for the EOR XYZPT6 model (Figure 5d), January and June precipitation standout with the highest PIP. Latitude has one of the lowest PIP for both WRB models in Figure 5, which reflects the PIP results of the simpler WRB models in Figure 4. Both EOR models display a relatively higher PIP for latitude compared with the models in Figure 4.
Most noticeable of all is the difference in the PIP of the more complex models in comparison with those of the simpler models. While the simpler models had negligible to near-negligible PIP, these more complex models display higher PIP with more variability across covariates. For model XYZPT5 (Figure 5a,b), it generally appears that precipitation of wet-season months tends to have a higher PIP for both regions; the exception to this being the May precipitation PIP of the WRB XYZPT5 model. Model XYZPT6 (Figure 5c,d) mirrors the PIP results for monthly P seen in XYZPT5 for the WRB region and has the same distribution but with higher PIPs for the EOR region. The EOR XYZPT6 model (Figure 5d), unlike the better performing EOR models, has a relatively high PIP for elevation, Td, and T.
The contribution of the spatial random effects () term relative to the general linear model (GLM) component of each GEV parameter (Figure 6), when used in combination with PIP results, can provide additional insight into relevant model covariates. While the inclusion of climatic covariates decreases the term contribution for the location parameter of both regions, the inclusion of monthly T and Td further greatly reduces across the majority of sites. This is demonstrated by the sizeable decrease in seen for model XYZPT6 relative to the other models (Figure 6a). For the WRB, comparison of models XYZPT5 and XYZPT6 reveals that winter and fall monthly P along with monthly T and Td reduces the term contribution more than winter P only. For the EOR region, the inclusion of winter monthly P, monthly T and Td, and elevation reduce the contribution of more than winter monthly P alone.
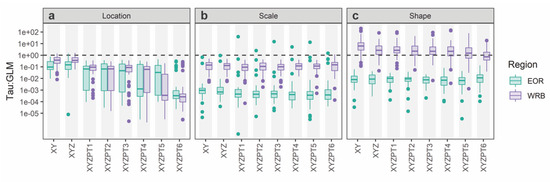
Figure 6.
The contribution of the spatial random effects term relative to the general linear model (GLM) term for each GEV parameter and model. The dashed horizontal line is placed at one, representing a 1:1 ratio of the spatial random effects term to GLM. (a) is location, (b) is scale and (c) is shape.
For the scale parameter (Figure 6b), most sites in the EOR region have a smaller term than sites in the WRB, with the exception of a few EOR outliers where the term is similar in contribution or larger (southwestern-most site near Crater Lake) than the GLM term. Although the WRB sites have a higher contribution from the term relative to EOR, none of the sites have a term that contributes more than the GLM term. There is a slight reduction in the term contribution with the inclusion of climatic covariates for the scale parameter, but the change is less noticeable relative to the results for the location parameter. The inclusion of the monthly T and Td of model XYZPT6 appears to increase some of the term contributions for the WRB. The main differences, when comparing PIPs for models XYZPT5 and XYZPT6 (Figure 5a,c), are a higher PIP for TA relative to TdA seen for the XYZPT5 model that is not seen for XYZPT6. Additionally, model XYZPT6 gave the highest PIPs to August Td and June T, even higher than January P, which had a relatively high PIP in both models. For the EOR, the term contributions of both models XYZPT5 and XYZPT6 are very similar with the exception of the outliers (Figure 6b). The term contribution of the EOR region’s largest outlier’s decreases by an order of magnitude with the inclusion of monthly T and Td. The main differences, besides T and Td, between the two models in PIP for the EOR region is the reduced PIP of longitude and the increased PIP of elevation for model XYZPT6 relative to XYZPT5 (Figure 5b,d).
The term contribution to the shape parameter for the EOR sites is much lower than that of the WRB sites (Figure 6c). For the majority of the WRB sites, the contribution of the term exceeds that of the GLM term, in some cases by a large proportion (y-axis in log scale). This could indicate that there are additional covariates not included in this study that influence the shape of the GEV distribution within the WRB. The main difference in shape parameter PIP results between model XYZPT6 and the other models, for both regions, is the large increase in the contribution of T and Td. The XYZPT6 model had the lowest contribution of all the models for the WRB with a median contribution less than 1:1, indicating that including monthly T and Td was beneficial. However, in the EOR region, the XYZPT6 model has a greater median term contribution to the shape parameter relative to all other models. This is the only potential indication of a term contribution link with the EOR predictive performance results where XYZPT6 was among the worst models.
3.3. Model Performance at Stations within Region of Overlap
For the locations east of the Cascade Range, which were included in both regions (hereafter referred to as “overlapping stations”), the AM temporal distribution of each station appears to correspond well with which region’s models performed best at that location (Figure 7 and Figure S5). This could be due to the different storm climatology; in the WRB winter storms dominate and most AM events occur during November–February, while in the EOR early summer (May–June) thunderstorms are also prominent. The WRB models performed better than the EOR models at stations 31 and 47 (Figure 7a,b, also station 30 in Figure S5), which have more AM events occurring between December and January and resemble the AM temporal distribution for the pooled WRB data (Figure 1a). The EOR model performed better at stations 54 and 55 (Figure 7c,d, also station 33 in Figure S5), which also have a relatively large number of AM falling between May and June (in addition to the expected winter storms of the Pacific Northwest region) and correspond with the AM temporal distribution for the pooled EOR data (Figure 1b). These results suggest that accounting for the dominate storm mechanisms that influence the AM temporal distribution within the pooled station data of the model may improve predictive performance.
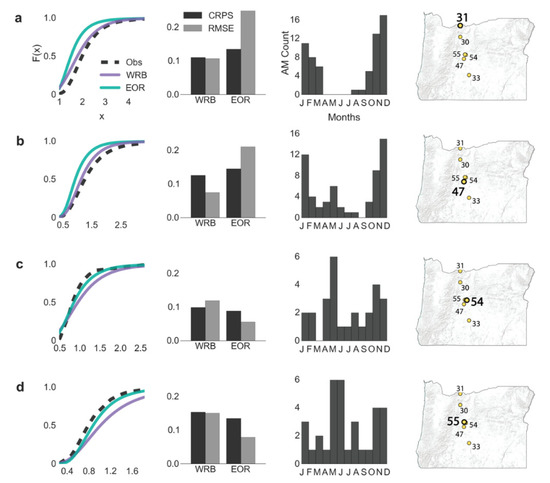
Figure 7.
Comparison of the best model results at the overlapping stations. Each row of plots represents a single station, where row (a) is station 31, row (b) station 47, row (c) station 54, and row (d) station 55, as indicated by the map insets. Each includes, from left to right, the CDF of predicted versus observed annual maxima GEV distributions, CRPS and RMSE of each region’s model, the location’s AM climatology, and the location’s spatial placement within the study region.
Since dominant storm climatology appears to influence model performance among the overlapping stations, we also checked relative model performance at stations that were not included within the overlapping stations (Figure 8). Stations within each region were categorized as “WRB-like AM” if their January and December AM count was greater than their May and June AM count, and “EOR-like AM” if their May and June AM count was greater than or equal to their January and December AM count (Figures S7 and S8). Our results indicate that the median RMSE across EOR-like AM stations is lower (better median performance) than the median RMSE across WRB-like AM stations within the EOR region (Figure 8e). However, the CRPS results are not as conclusive (Figure 7a), which could be due to a bias in CRPS (Figures S9 and S10) introduced by normalizing by length of record. We were unable to duplicate this comparison within the WRB region since all the non-overlapping stations have WRB-like AM distributions (Figure 8c,g). Looking at the difference in performance between the EOR XYZPT2 model (best set of covariates for the WRB) and the EOR XYZPT1 model (best set of covariates for EOR) (Figure S4), we see that using the EOR model that makes use of the same set of covariates that worked best in the WRB region is not sufficient on its own to improve performance for the EOR locations which have a WRB-like AM temporal distribution. The predominance of region-based performance can also be seen when the CDF results of all climatic models (XYZPT1-XYZPT6) for both regions at the overlapping stations are plotted together (Figure S6), showing how the WRB models group together and are clearly different from the EOR model results despite using the same sets of covariates. Additional analysis of the relationship between spatial performance and covariate values was conducted (Figures S9 and S10).
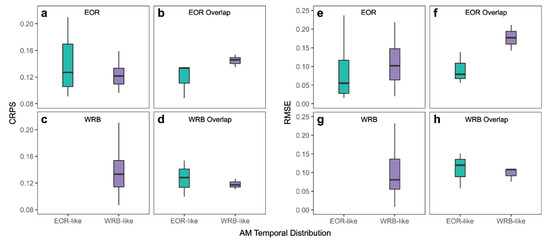
Figure 8.
Comparison of station specific CRPS (a–d) and RMSE (e–h) versus AM temporal distribution by region. EOR (a,e) and WRB (c,g) display the quantiles of station-specific model performance when stations (excluding overlapping stations) are categorized by EOR-like or WRB-like AM temporal distributions. EOR overlap (b,f) and WRB overlap (d,h) display the same performance versus categorization for the overlapping stations only, using the EOR and WRB models’ results, respectively.
4. Conclusions
A limitation of existing precipitation frequency analysis methods is that integrating information on extremes across space (i.e., different observations) is not straightforward. Here, we addressed this through the application of a Bayesian hierarchical model (BHM) framework for the spatial analysis of 24-h precipitation annual maxima (AM) data. The spatial BHM framework utilized in this study includes Bayesian model averaging (BMA) to account for model uncertainty related to the covariates employed, and also allows for analysis of covariate posterior inclusion probability (PIP). To gain further insight into relevant covariates, we analyzed the contribution of the spatial random effects () term to the linear models of the generalized extreme value (GEV) distribution parameters in combination with the PIP results. We explored a wide range of models using physically based information pertaining to geographical and climatological factors that influence precipitation extremes across two regions in Oregon with different dominating rainfall generation mechanisms, and a region of overlap.
The top performing models for each region were determined by comparing mean and median model predictive performance of the LOO-CV results, wherein we compared site-specific predicted versus observed GEV distributions using continuous ranked probability score (CRPS) and root mean squared error (RMSE). Out of the top performing models for each region, one was chosen as the best model based on both performance metrics and model simplicity. Our choice of best model was also checked against a spatial GEV fit of the models. The best model for the Willamette River Basin (WRB) included location, elevation, and mean wet-season precipitation, daily mean temperature, and dewpoint temperature; while the best model for the eastern Oregon (EOR) region included location, elevation, and mean annual precipitation. The improvement in model predictive performance with the inclusion of mean temperature and dewpoint temperature for the WRB is understandable given the variability in climate and topography of the WRB over a much smaller area relative to EOR, in addition to its proximity to the Pacific Ocean.
Including BMA may improve results over non-BMA models as demonstrated by Dyrrdal et al. [37]; however, we found that careful model selection remains an important component of tuning model performance. For example, the most complex model (XYZPT6) containing geographic and monthly climatic information (precipitation, P; dewpoint temperature, Td; and mean daily temperature, T) was among the top performing models for the WRB region, while it performed among the worst in the EOR region despite the use of BMA. However, useful information can be gleaned from the posterior inclusion probability (PIP) results provided through BMA. Across the simpler models, mean wet-season P displayed the highest PIP for μ (GEV location parameter) within both the WRB and EOR. The (GEV inverse scale parameter) PIPs reflect the regional differences in storm climatology of the pooled data, with wet-season P and T and longitude displaying higher PIP for the WRB region, and wet-season P, longitude, and dry-season P displaying higher PIP for the EOR region. Additionally, wet-season T stands out within the WRB PIP results, more so than dewpoint temperature. Elevation has a higher PIP for (GEV shape parameter) within the WRB models, however, apart from model XYZPT6, this was not the case for the EOR models. PIP results of the more complex models generally reflect those of the simpler models, just in higher resolution and with higher PIP across the climatic covariates for both regions. Additionally, the most complex model (XYZPT6) had the lowest overall term contribution relative to the general linear model (GLM) term for the GEV location parameter for both regions, indicating that the inclusion of monthly T and Td information improved location parameter estimates. However, inclusion of monthly T and Td resulted in an increased contribution of the term for the scale parameter in both regions. For the shape parameter, inclusion of monthly T and Td information reduced the median term contribution for the WRB, while it increased the term contribution for the EOR region.
Results from the overlapping stations indicate that the AM temporal distribution within the pooled calibration data may improve model predictive performance for locations with a similar AM temporal distribution, even more so than specific covariate selection. Although the stations in the region of overlap are well outside of the geographical WRB, the WRB model had better skill at the stations that have a similar AM temporal distribution as those within the WRB. The same can be seen for stations with a similar AM temporal distribution as the EOR region, the EOR model performs better at those stations relative to the WRB model. Most likely, this is linked to the storm climatology of the different regions; wherein the WRB is dominated by winter storms from the Pacific Ocean, while the EOR region experiences thunderstorms during the early warm-season and receives less precipitation during the cold-season than the WRB. Based on these results, we suggest exploring the inclusion of AM temporal distribution within the spatial BHM framework further, possibly through the inclusion of relevant covariates that can differentiate the dominate storm for each site.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4441/12/8/2211/s1, Figure S1: Distribution of station performance by model, where models are listed in order (left to right) by increasing complexity, Figure S2: Examples of observed versus simulated distributions for the WRB and EOR models which include PRISM-based covariates. These CDFs are included to give examples of stations were predictive performance was good (locations 13, 87), moderate (locations 60, 84), and poor (locations 12, 47), Figure S3: Maps of CRPS (circle markers) and RMSE (diamond markers) for the top models for each region (model complexity increases from left to right). The outline in the northwestern part of Oregon delineates the Willamette River watershed. Models displayed for the WRB are the simplest of the top performing XYZPT2 (a, c), and the most complex of the top performing XYZPT6 (b, d). Both top performing models are displayed for EOR; XYZPT1 (e, g) and XYZPT3 (f, h), Figure S4: The difference in predictive performance between EOR models XYZPT2 and XYZPT1 at the EOR stations which have WRB-like AM. Using the best performing model for the WRB does not guarantee an improvement in performance for all EOR stations that have a WRB-like AM temporal distribution. A few show a slight improvement (purple), while the performance at others worsens (orange). More factors are involved than simply which set of covariates are used, Figure S5: Performance at all overlapping stations. Example of how a small (hundredths) change in CRPS has a noticeable difference in CDF. Station 54’s EOR result has a CRPS of 0.08 and the simulated CDF is similar to the observed. Whereas, the WRB result has a CRPS of 0.11 and performs poorly relative to the EOR model, Figure S6: CDFs at the overlapping stations for models XYZPT1-XYZPT6 for both the WRB and EOR regions compared with CDF of observed. These models include both geographic and climatic information. The models for each region tend to group together, such that all the models (which include climatic information) from the region that performed best are generally better than those of the other region, Figure S7: AM temporal distribution by station for the WRB study region, excluding the six overlapping stations. Fill color indicates AM type, Fill color indicates AM type, where purple indicate WRB-like AM. None of the non-overlap stations in the WRB have an EOR-like AM, Figure S8: AM temporal distribution by station for the EOR study region, excluding the six overlapping stations. Fill color indicates AM type, where green represents EOR-like AM and purple indicates WRB-like AM, Figure S9: Statistically significant (α = 0.05) Pearson correlation coefficients for the top WRB model’s predictive performance and covariates, as well as mean AM and record length. The moderate negative correlation between CRPS and record length is due to normalizing CRPS by record length. The weak correlation between latitude and RMSE is most likely due to the stations at the northern end of the Coastal Mountains which display poorer model predictive performance across all models. The worst of the aforementioned stations has a relatively short record length and could be the reason for the equally weak negative correlation between RMSE and record length, Figure S10: Statistically significant (α = 0.05) Pearson correlation coefficients for the top EOR model’s predictive performance and covariates, as well as mean AM and record length. The moderate negative correlation between CRPS and record length is due to normalizing CRPS by record length. The EOR region covers a large area that includes stations with WRB-like AM, this could be the reason for the weak correlations between performance, mean annual maximum, and annual precipitation, Table S1: WRB Model Performance, Table S2: EOR Model Performance, Table S3: Spatial GEV Model Fit.
Author Contributions
Conceptualization, C.A.L., B.E.S., J.F.E., and A.A.; methodology, C.A.L., B.E.S., and J.F.E.; validation, B.E.S.; formal analysis, C.A.L. and B.E.S.; investigation, C.A.L. and B.E.S.; resources, A.A. and B.E.S.; data curation, C.A.L.; writing—original draft preparation, C.A.L. and B.E.S.; writing—review and editing, J.F.E., G.K., A.D., and A.A.; visualization, C.A.L.; supervision, B.E.S and A.A.; funding acquisition, B.E.S. and A.A. All authors have read and agreed to the published version of the manuscript.
Funding
C.A.L. was partially supported by USACE Contract Number W912HZ-16-A-0080, and the National Science Foundation Award No. CMMI-1635797. B.E.S. was partially supported by the USACE Risk Management Center and the US Nuclear Regulatory Commission Agreement Number NRC HQ-60-14-I-0022. A.A. was partially supported by the National Science Foundation Award No. CMMI-1635797 and ARO Award No. W911NF-14-1-0684.
Conflicts of Interest
The authors declare no conflict of interest and the funders had no role in the design of the study, analyses, or interpretation of data and results.
References
- Gumbel, E.J. Statistics of Extremes; Columbia University Press: New York, NY, USA, 1958; ISBN 978-0-231-89131-8. [Google Scholar]
- Luke, A.; Vrugt, J.A.; AghaKouchak, A.; Matthew, R.; Sanders, B.F. Predicting nonstationary flood frequencies: Evidence supports an updated stationarity thesis in the United States. Water Resour. Res. 2017, 53, 5469–5694. [Google Scholar] [CrossRef]
- Stedinger, J.R.; Griffis, V.W. Flood Frequency Analysis in the United States: Time to Update. J. Hydrol. Eng. 2008, 13, 199–204. [Google Scholar] [CrossRef]
- Cheng, L.; AghaKouchak, A. Nonstationary Precipitation Intensity-Duration-Frequency Curves for Infrastructure Design in a Changing Climate. Sci. Rep. 2014, 4, 7093. [Google Scholar] [CrossRef]
- Fowler, H.J.; Kilsby, C.G. A regional frequency analysis of United Kingdom extreme rainfall from 1961 to 2000. Int. J. Clim. 2003, 23, 1313–1334. [Google Scholar] [CrossRef]
- Cooley, D.; Nychka, D.; Naveau, P. Bayesian Spatial Modeling of Extreme Precipitation Return Levels. J. Am. Stat. Assoc. 2007, 102, 824–840. [Google Scholar] [CrossRef]
- Gumbel, E.J. Probability-interpretation of the observed return-periods of floods. Eos Trans. Am. Geophys. Union 1941, 22, 836–850. [Google Scholar] [CrossRef]
- Fisher, R.A.; Tippett, L.H.C. Limiting forms of the frequency distribution of the largest or smallest member of a sample. Math. Proc. Camb. Philos. Soc. 1928, 24, 180–190. [Google Scholar] [CrossRef]
- Davison, A.C.; Smith, R.L. Models for Exceedances Over High Thresholds. J. R. Stat. Soc. Ser. B (Methodol.) 1990, 52, 393–425. [Google Scholar] [CrossRef]
- Bonnin, G.; Martin, D.; Lin, B.; Parzybok, T.; Yekta, M.; Riley, D. Precipitation-Frequency Atlas of the United States: NOAA Atlas 14, Volume 1, Version 4; NOAA: Silver Spring, MD, USA, 2006. Available online: https://hdsc.nws.noaa.gov/hdsc/pfds/docs/NA14Vol1.pdf (accessed on 2 May 2017).
- England, J.F., Jr.; Cohn, T.A.; Faber, B.A.; Stedinger, J.R.; Thomas, W.O., Jr.; Veilleux, A.G.; Kiang, J.E.; Mason, R.R., Jr. Guidelines for determining flood flow frequency—Bulletin 17C. In Techniques and Methods; U.S. Geological Survey: Reston, VA, USA, 2018; p. 168. [Google Scholar]
- Jenkinson, A.F. The frequency distribution of the annual maximum (or minimum) values of meteorological elements. Q. J. R. Meteorol. Soc. 1955, 81, 158–171. [Google Scholar] [CrossRef]
- Hosking, J.R.M.; Wallis, J.R. Some statistics useful in regional frequency analysis. Water Resour. Res. 1993, 29, 271–281. [Google Scholar] [CrossRef]
- Coles. An Introduction to Statistical Modeling of Extreme Values, Statistics; Springer: London, UK, 2001; ISBN 978-1-4471-3675-0. [Google Scholar]
- Davison, A.C.; Padoan, S.A.; Ribatet, M. Statistical Modeling of Spatial Extremes. Stat. Sci. 2012, 27, 161–186. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; AghaKouchak, A.; Foufoula-Georgiou, E. A Diagnostic Framework for Understanding Climatology of Tails of Hourly Precipitation Extremes in the United States. Water Resour. Res. 2018, 54, 6725–6738. [Google Scholar] [CrossRef]
- Cooley, D. Extreme value analysis and the study of climate change. Clim. Chang. 2009, 97, 77. [Google Scholar] [CrossRef]
- Renard, B. A Bayesian hierarchical approach to regional frequency analysis. Water Resour. Res. 2011, 7, W11513. [Google Scholar] [CrossRef]
- Banerjee, S.; Carlin, B.P.; Gelfand, A.E. Hierarchical Modeling and Analysis for Spatial Data; Chapman and Hall/CRC: New York, NY, USA, 2014; ISBN 978-0-429-13717-4. [Google Scholar]
- Ribatet, M.; Cooley, D.; Davison, A.C. Bayesian inference from composite likelihoods, with an application to spatial extremes. Stat. Sin. 2012, 813–845. [Google Scholar]
- Wikle, C.K.; Berliner, L.M.; Cressie, N. Hierarchical Bayesian space-time models. Environ. Ecol. Stat. 1998, 5, 117–154. [Google Scholar] [CrossRef]
- Cheng, L.; AghaKouchak, A.; Gilleland, E.; Katz, R.W. Non-stationary extreme value analysis in a changing climate. Clim. Chang. 2014, 127, 353–369. [Google Scholar] [CrossRef]
- Economou, T.; Stephenson, D.B.; Ferro, C.A.T. Spatio-temporal modelling of extreme storms. Ann. Appl. Stat. 2014, 8, 2223–2246. [Google Scholar] [CrossRef]
- Ahn, K.-H.; Palmer, R.; Steinschneider, S. A hierarchical Bayesian model for regionalized seasonal forecasts: Application to low flows in the northeastern United States. Water Resour. Res. 2017, 53, 503–521. [Google Scholar] [CrossRef]
- Coles, S.G.; Tawn, J.A. A Bayesian Analysis of Extreme Rainfall Data. Appl. Stat. 1996, 45, 463. [Google Scholar] [CrossRef]
- Kwon, H.-H.; Brown, C.; Lall, U. Climate informed flood frequency analysis and prediction in Montana using hierarchical Bayesian modeling. Geophys. Res. Lett. 2008, 35, L05404. [Google Scholar] [CrossRef]
- Steinschneider, S.; Lall, U. A hierarchical Bayesian regional model for nonstationary precipitation extremes in Northern California conditioned on tropical moisture exports. Water Resour. Res. 2015, 51, 1472–1492. [Google Scholar] [CrossRef]
- Sang, H.; Gelfand, A.E. Hierarchical modeling for extreme values observed over space and time. Environ. Ecol. Stat. 2008, 16, 407–426. [Google Scholar] [CrossRef]
- Ghosh, S.; Mallick, B.K. A hierarchical Bayesian spatio-temporal model for extreme precipitation events. Environmetrics 2011, 22, 192–204. [Google Scholar] [CrossRef]
- Najafi, M.R.; Moradkhani, H. Analysis of runoff extremes using spatial hierarchical Bayesian modeling. Water Resour. Res. 2013, 49, 6656–6670. [Google Scholar] [CrossRef]
- Najafi, M.R.; Moradkhani, H. A hierarchical Bayesian approach for the analysis of climate change impact on runoff extremes. Hydrol. Process. 2014, 28, 6292–6308. [Google Scholar] [CrossRef]
- Daly, C.; Neilson, R.P.; Phillips, D.L. A Statistical-Topographic Model for Mapping Climatological Precipitation over Mountainous Terrain. J. Appl. Meteor. 1994, 33, 140–158. [Google Scholar] [CrossRef]
- Daly, C.; Taylor, G.; Gibson, W. The PRISM approach to mapping precipitation and temperature. In Proceedings of the 10th Conference on Applied Climatology, Reno, NV, USA, 20–23 October 1997; pp. 10–12. [Google Scholar]
- Daly, C.; Halbleib, M.; Smith, J.I.; Gibson, W.P.; Doggett, M.K.; Taylor, G.H.; Curtis, J.; Pasteris, P.P. Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous United States. Int. J. Clim. 2008, 28, 2031–2064. [Google Scholar] [CrossRef]
- Bracken, C.; Rajagopalan, B.; Cheng, L.; Kleiber, W.; Gangopadhyay, S. Spatial Bayesian hierarchical modeling of precipitation extremes over a large domain. Water Resour. Res. 2016, 52, 6643–6655. [Google Scholar] [CrossRef]
- Lenkoski, A. spatial.gev.bma: Hierarchical Spatial Generalized Extreme Value (GEV) Modeling with Bayesian Model Averaging (BMA), (R package version 1.0) [Computer software manual]. 2014. [Google Scholar]
- Dyrrdal, A.V.; Lenkoski, A.; Thorarinsdottir, T.L.; Stordal, F. Bayesian hierarchical modeling of extreme hourly precipitation in Norway. Environmetrics 2014, 26, 89–106. [Google Scholar] [CrossRef]
- Hersbach, H. Decomposition of the Continuous Ranked Probability Score for Ensemble Prediction Systems. Weather Forecast. 2000, 15, 559–570. [Google Scholar] [CrossRef]
- Gneiting, T.; Raftery, A.E. Strictly Proper Scoring Rules, Prediction, and Estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Redmond, K.T.; Koch, R.W. Surface Climate and Streamflow Variability in the Western United States and Their Relationship to Large-Scale Circulation Indices. Water Resour. Res. 1991, 27, 2381–2399. [Google Scholar] [CrossRef]
- Lee, K.K.; Risley, J.C. Estimates for Ground-Water Recharge, Base Flow, and Stream Reach Gains and Losses in the Willamette River Basin, Oregon; USGS: Portland, OR, USA, 2002. [Google Scholar]
- Melack, J.M.; Dozier, J.; Goldman, C.R.; Greenland, D.; Milner, A.M.; Naiman, R.J. Effects of Climate Change on Inland Waters of the Pacific Coastal Mountains and Western Great Basin of North America. Hydrol. Process. 1997, 11, 971–992. [Google Scholar] [CrossRef]
- Mock, C.J. Climatic Controls and Spatial Variations of Precipitation in the Western United States. J. Clim. 1996, 9, 1111–1125. [Google Scholar] [CrossRef]
- Esri. “Terrain with Labels” [basemap]. “World Terrain Map”. 1 July 2009. Available online: https://server.arcgisonline.com/ArcGIS/rest/services/World_Terrain_Base/MapServer (accessed on 10 April 2018).
- Bond, N.A.; Vecchi, G.A. The Influence of the Madden–Julian Oscillation on Precipitation in Oregon and Washington. Weather Forecast. 2003, 18, 600–613. [Google Scholar] [CrossRef]
- Harris, D.D.; Hubbard, L.E. Magnitude and Frequency of Floods in Eastern Oregon; United States Geological Survey, U.S. Department of the Interior: Portland, OR, USA, 1983.
- Schaefer, M.G.; Barker, B.L.; Taylor, G.H.; Wallis, J.R. Regional Precipitation-Frequency Analysis and Spatial Mapping of 24-Hour Precipitation for Oregon; Oregon Department of Transportation: Salem, OR, USA, 2008.
- Oki, T.; Musiake, K.; Koike, T. Spatial rainfall distribution at a storm event in mountainous regions, estimated by orography and wind direction. Water Resour. Res. 1991, 27, 359–369. [Google Scholar] [CrossRef]
- Javier, J.R.N.; Smith, J.A.; England, J.; Baeck, M.L.; Steiner, M.; Ntelekos, A.A. Climatology of extreme rainfall and flooding from orographic thunderstorm systems in the upper Arkansas River basin. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Zhao, W.; Khalil, M.a.K. The Relationship between Precipitation and Temperature over the Contiguous United States. J. Clim. 1993, 6, 1232–1236. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Shea, D.J. Relationships between precipitation and surface temperature. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Adler, R.F.; Gu, G.; Wang, J.-J.; Huffman, G.J.; Curtis, S.; Bolvin, D. Relationships between global precipitation and surface temperature on interannual and longer timescales (1979–2006). J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).