Event-Based Rainfall Interception Modeling in a Cerrado Riparian Forest—Central Brazil: An Alternative Approach to the IS Method for Parameterization of the Gash Model
Abstract
1. Introduction
2. Materials and Methods
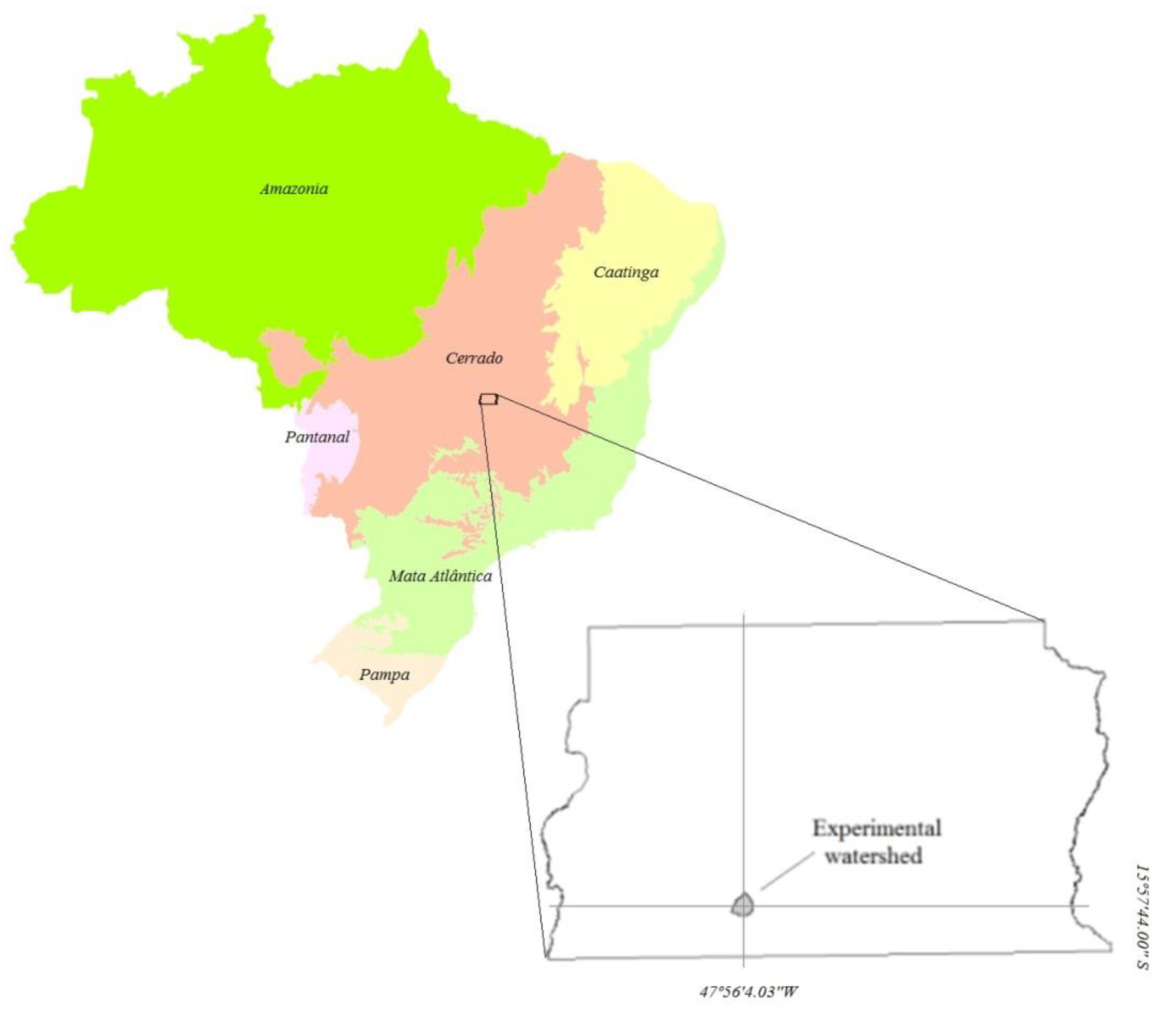
2.1. Site Description and Data Collection
2.2. The Gash Analytical Model
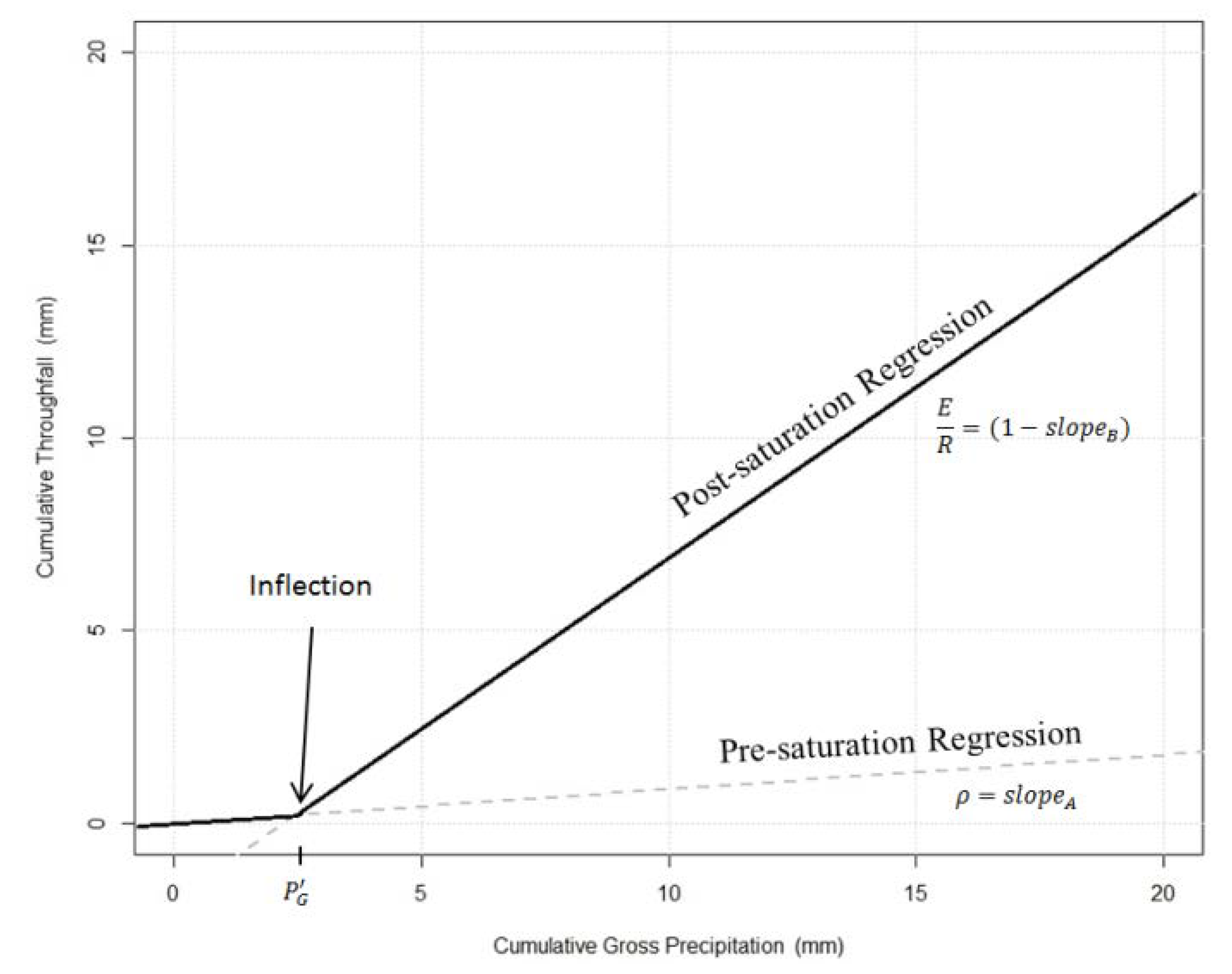
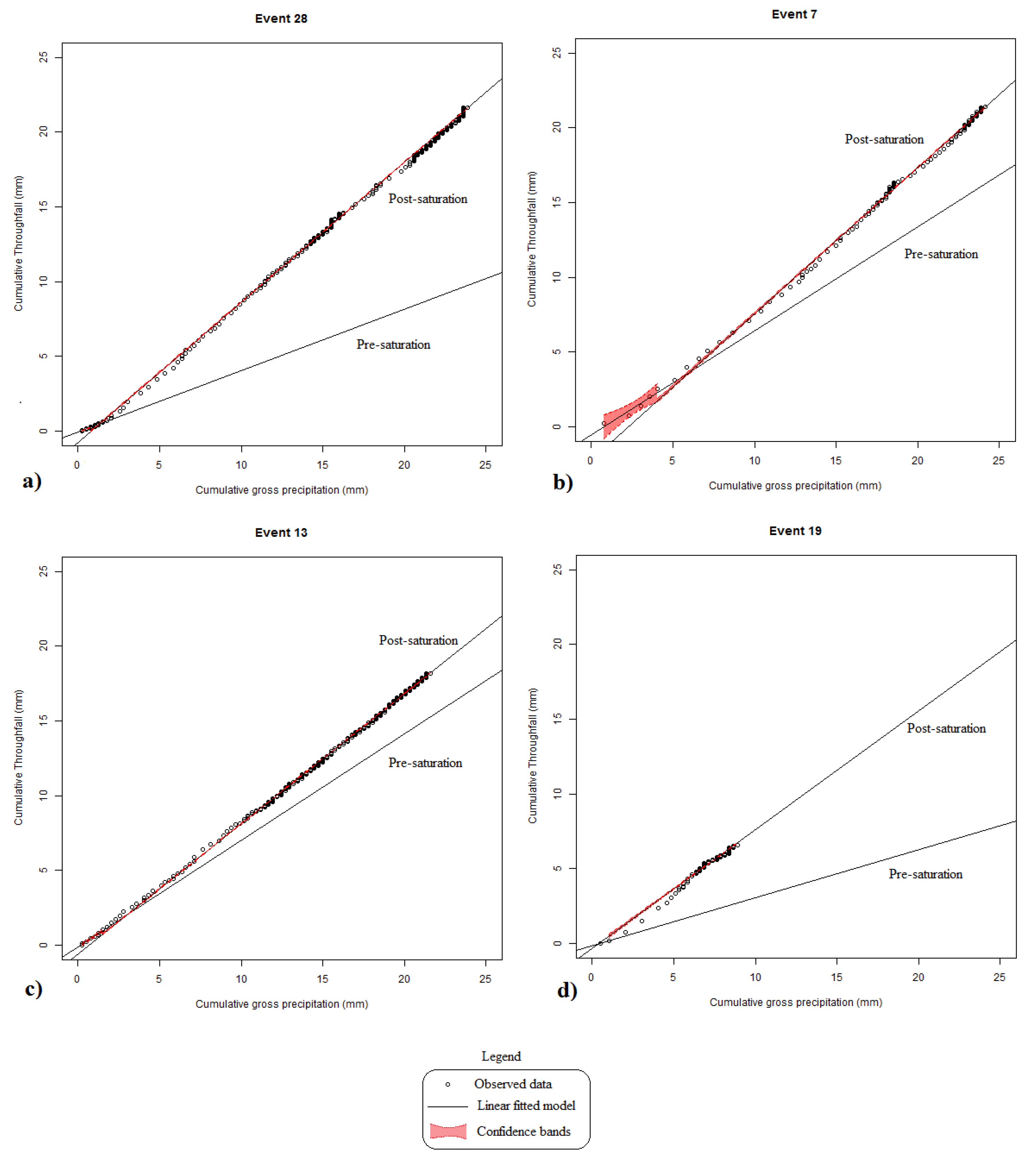
2.3. Model Parameterization—IS Linear Regression
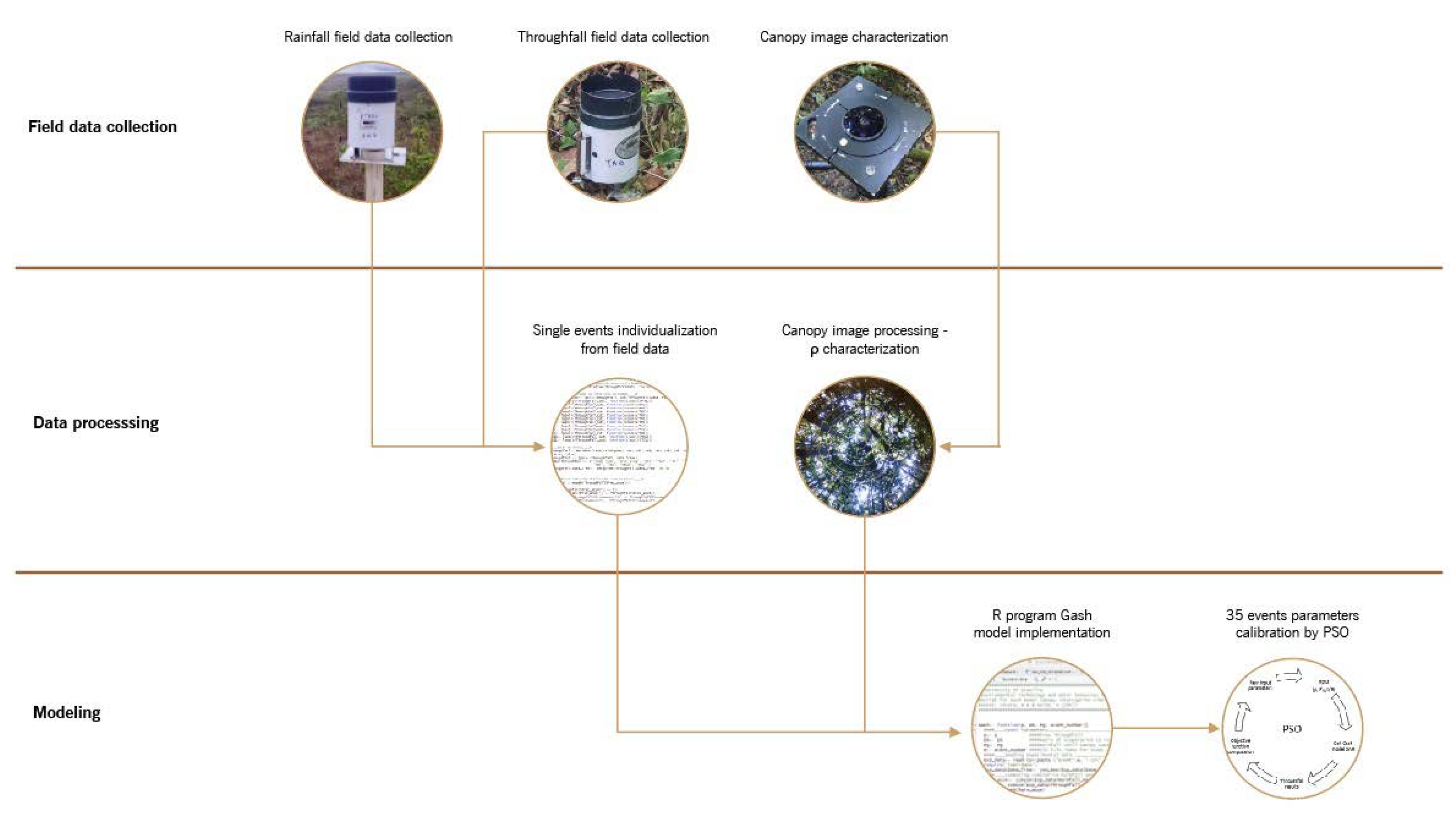
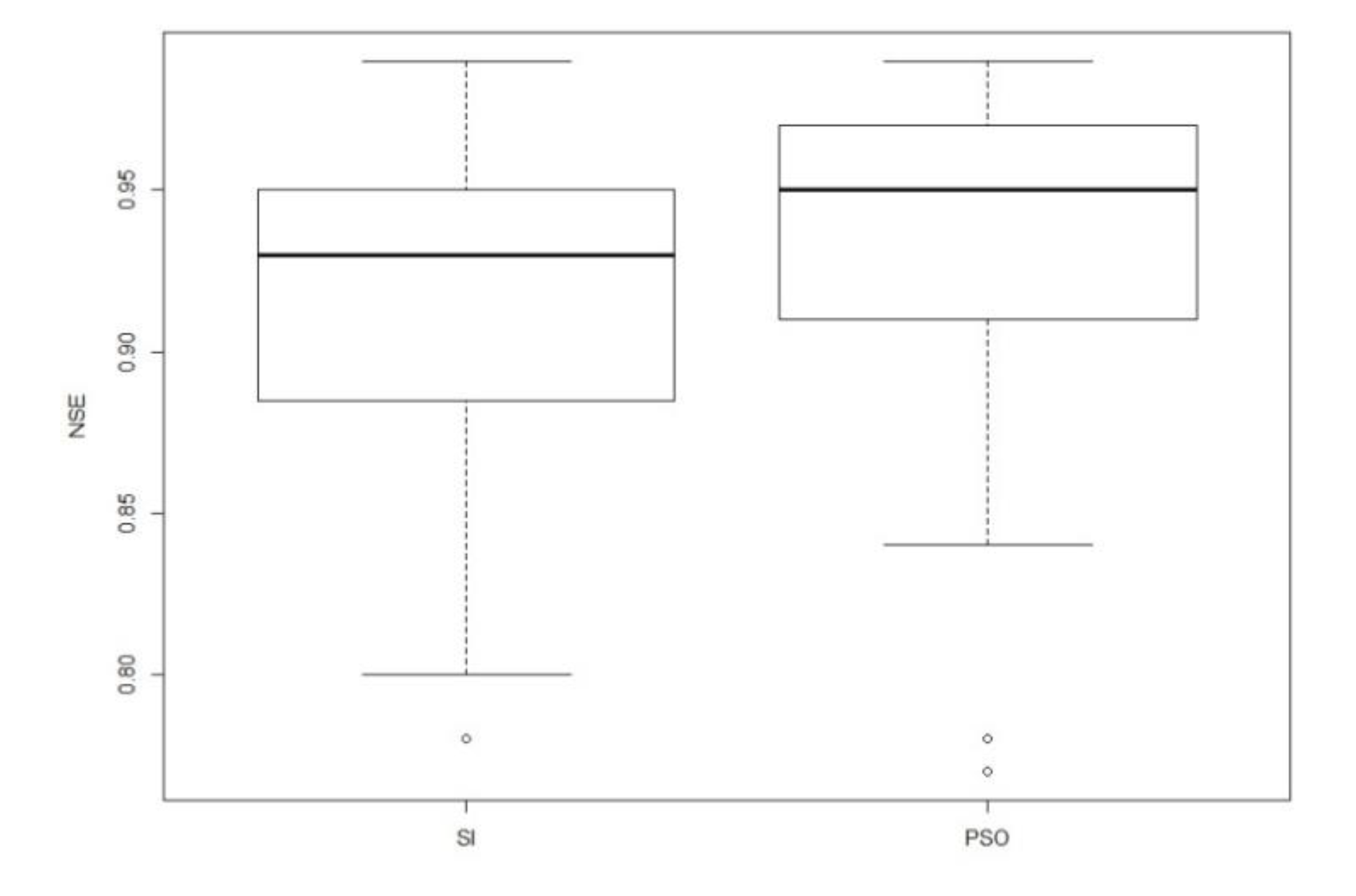
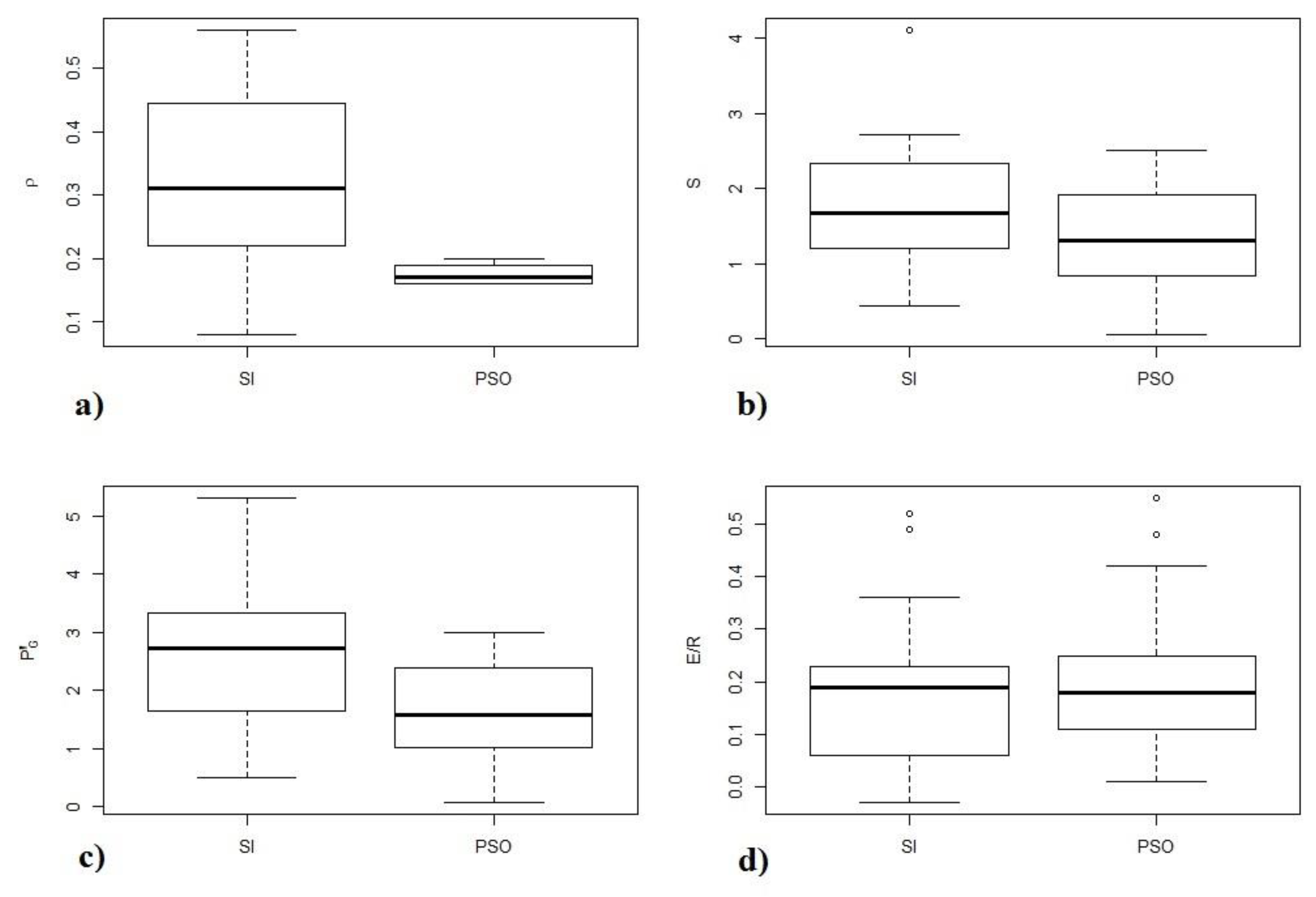
2.4. Gash Model Parameterization—Image-Based and Particle Swarm Optimization—PSO
3. Results
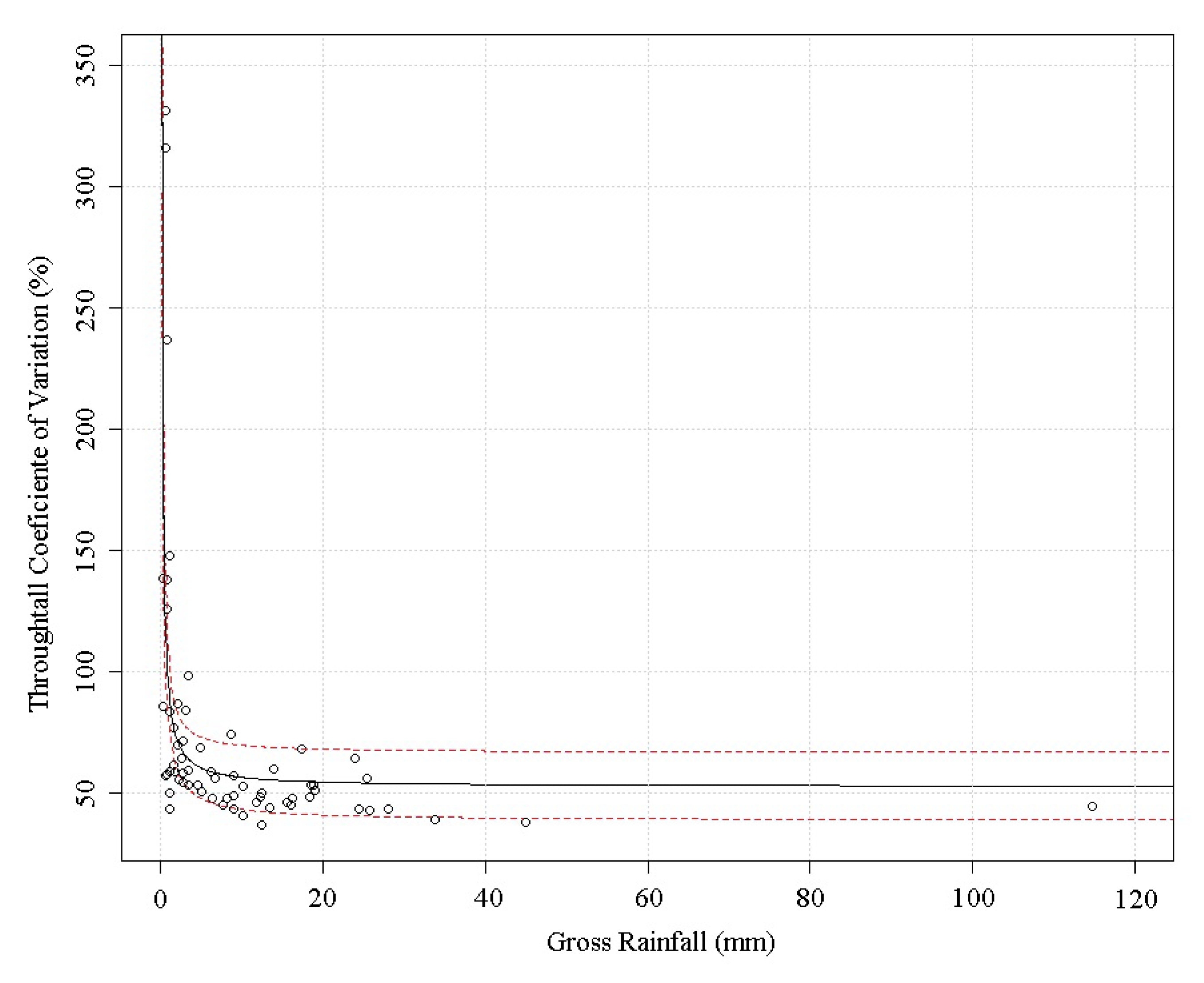
3.1. Sample Variability, Overall Throughfall, and Interception Behavior
3.2. Event-Based Canopy Characterization and Gash Model Application
4. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Véliz-Chávez, C.; Mastachi-Loza, C.A.; González-Sosa, E.; Becerril-Piña, R.; Ramos-Salinas, N.M. Canopy Storage Implications on Interception Loss Modeling. Am. J. Plant Sci. 2014, 5, 3032–3048. [Google Scholar] [CrossRef]
- Helvey, J.D.; Patric, J.H. Design criteria for interception studies. Hydrol. Sci. Bull. Int. Assoc. Hydrol. Sci. 1966, 67, 131–137. [Google Scholar]
- Murakami, S. A proposal for a new forest canopy interception mechanism: Splash droplet evaporation. J. Hydrol. 2006, 319, 72–82. [Google Scholar] [CrossRef]
- Kavian, A.; Alipour, A.; Soleimani, K.; Gholami, L.; Smith, P.; Rodrigo-Comino, J. The increase of rainfall erosivity and initial soil erosion processes due to rainfall acidification. Hydrol. Process. 2019, 33, 261–270. [Google Scholar] [CrossRef]
- Beguería, S.; Angulo-Martínez, M.; Gaspar, L.; Navas, A. Detachment of soil organic carbon by rainfall splash: Experimental assessment on three agricultural soils of Spain. Geoderma 2015, 245–246, 21–30. [Google Scholar] [CrossRef]
- Rutter, A.J.; Kershaw, K.A.; Robins, P.C.; Morton, A.J. A predictive model of rainfall interception in forests, 1. Derivation of the model from observations in a plantation of Corsican pine. Agric. Meteorol. 1971, 9, 367–384. [Google Scholar] [CrossRef]
- Gash, J.H.C. An analytical model of rainfall interception by forests. Q. J. R. Meteorol. Soc. 1979, 105, 43–55. [Google Scholar] [CrossRef]
- Link, T.E.; Unsworth, M.; Marks, D. The dynamics of rainfall interception by a seasonal temperate rainforest. Agric. For. Meteorol. 2004, 124, 171–191. [Google Scholar] [CrossRef]
- Pypker, T.G.; Bond, B.J.; Link, T.E.; Marks, D.; Unsworth, M.H. The importance of canopy structure in controlling the interception loss of rainfall: Examples from a young and an old-growth Douglas-fir forest. Agric. For. Meteorol. 2005, 130, 113–129. [Google Scholar] [CrossRef]
- Brutsaert, W. Hydrology: An Introduction, 5th ed.; Cambridge University Press: Cambridge, UK, 2010; ISBN 0521824796. [Google Scholar]
- MMA—Ministry of Environment O Bioma Cerrado. Available online: http://www.mma.gov.br/biomas/cerrado (accessed on 16 May 2016).
- Giglio, J.N.; Kobiyama, M. Interceptação da Chuva: Uma Revisão com Ênfase no Monitoramento em Florestas Brasileiras. RBRH-Rev. Bras. Recur. Hídricos 2013, 18, 297–317. [Google Scholar] [CrossRef]
- Zimmermann, A.; Zimmermann, B.; Elsenbeer, H. Rainfall redistribution in a tropical forest: Spatial and temporal patterns. Water Resour. Res. 2009, 45, 1–18. [Google Scholar] [CrossRef]
- De Oliveira, M.C.; Felfili, J.M.; da Silva Júnior, M.C. Análise florística e fitossociológica da comunidade arbórea da Mata de Galeria do Capetinga, após vinte anos de passagem de fogo, na Fazenda Água Limpa, Brasília—DF. Heringeriana 2011, 5, 19–31. [Google Scholar]
- Seabra, H.F.; Encinas, J.M.; Felfili, J.M. Análise estrutural da mata ciliar do Córrego Capetinga—DF, habitat de Callithrix jacchus penicillata. Pesqui. Agropecuária Bras. 1991, 26, 11–17. [Google Scholar]
- Crockford, R.H.; Richardson, D.P. Partitioning of rainfall into throughfall, stemslow∠d interception effect of forest type, ground cover and climate. Hydrol. Process. 2000, 14, 2903–2920. [Google Scholar] [CrossRef]
- Lloyd, C.R.; Gash, J.H.C.; Shuttleworth, W.J. The measurement and modelling of rainfall interception by Amazonian rain forest. Agric. For. Meteorol. 1988, 43, 277–294. [Google Scholar] [CrossRef]
- Marin, C.T.; Bouten, W.; Sevink, J. Gross rainfall and its partitioning into throughfall, stemflow and evaporation of intercepted water in four forest ecosystems in western Amazonia. J. Hydrol. 2000, 237, 40–57. [Google Scholar] [CrossRef]
- Zimmermann, B.; Zimmermann, A.; Elsenbeer, H. Sampling procedures for throughfall monitoring: A simulation study. Water Resour. Res. 2010, 46, 1–15. [Google Scholar] [CrossRef]
- Kimmins, J.P. Some Statistical Aspects of Sampling Throughfall Precipitation in Nutrient Cycling Studies in British Columbian Coastal Forests. Ecology 1973, 54, 1008–1019. [Google Scholar] [CrossRef]
- Gash, J.H.; Lloyd, C.R.; Lachaud, G. Estimating sparse forest rainfall interception with an analytical model. J. Hydrol. 1995, 170, 79–86. [Google Scholar] [CrossRef]
- Chen, S.; Chen, C.; Zou, C.B.; Stebler, E.; Zhang, S.; Hou, L.; Wang, D. Application of Gash analytical model and parameterized Fan model to estimate canopy interception of a Chinese red pine forest. J. For. Res. 2013, 18, 335–344. [Google Scholar] [CrossRef]
- Frazer, G.; Canham, C.; Lertzman, K. Gap Light Analyzer (GLA): Imaging software to extract canopy structure and gap light transmission indices from true-colour fisheye photographs. Program 1999, 36. [Google Scholar]
- Zambrano-Bigiarini, M.; Rojas, R. Particle Swarm Optimisation, with Focus on Environmental Models. R Package Version 0.3-4 2013. [Google Scholar] [CrossRef]
- Jackson, I.J. Problems of throughfall and interception assessment under tropical forest. J. Hydrol. 1971, 12, 234–254. [Google Scholar] [CrossRef]
- Vieira, C.P.; Palmier, L.R. Medida e Modelagem da Interceptação da Chuva em uma Área Florestada na Região Metropolitana de Belo Horizonte, Minas Gerais. Rev. Bras. Recur. Hídricos 2006, 11, 101–112. [Google Scholar] [CrossRef]
- Oliveira, P.T.S.; Wendland, E.; Nearing, M.A.; Scott, R.L.; Rosolem, R.; Da Rocha, H.R. The water balance components of undisturbed tropical woodlands in the Brazilian cerrado. Hydrol. Earth Syst. Sci. 2015, 19, 2899–2910. [Google Scholar] [CrossRef]
- Carvalho, F.; da Assunção, H.F.; Scopel, I. Partição Pluviométrica Em Fitofisionomias Do Cerrado. Mercator 2013, 12, 135–147. [Google Scholar] [CrossRef]
- Germer, S.; Elsenbeer, H.; Moraes, J.M. Throughfall and temporal trends of rainfall redistribution in an open tropical rainforest, south-western Amazonia (Rondônia, Brazil). Hydrol. Earth Syst. Sci. Discuss. 2005, 2, 2707–2738. [Google Scholar] [CrossRef]
- Cuartas, L.A.; Tomasella, J.; Nobre, A.D.; Hodnett, M.G.; Waterloo, M.J.; Múnera, J.C. Interception water-partitioning dynamics for a pristine rainforest in Central Amazonia: Marked differences between normal and dry years. Agric. For. Meteorol. 2007, 145, 69–83. [Google Scholar] [CrossRef]
- Dunkerley, D.L. Evaporation of impact water droplets in interception processes: Historical precedence of the hypothesis and a brief literature overview. J. Hydrol. 2009, 376, 599–604. [Google Scholar] [CrossRef]




| Observed Data | IS Method Adjusted Coefficient Statistics | |||||
|---|---|---|---|---|---|---|
| Event | Precipitation (mm) | Throughfall (mm) | ρ | Lower CI | Upper CI | p-Value |
| 1 | 24.38 | 16.28 | 0.21 | 0.04 | 0.38 | 2.99 × 10−2 |
| 2 | 27.94 | 18.94 | 0.25 | 0.19 | 0.31 | 1.90 × 10−5 |
| 3 | 13.21 | 8.7 | 0.12 | 0.04 | 0.2 | 1.29 × 10−2 |
| 4 | 12.45 | 5.54 | 0.08 | 0.03 | 0.14 | 6.59 × 10−3 |
| 5 | 16 | 13.58 | 0.5 | 0.34 | 0.67 | 2.40 × 10−3 |
| 6 | 10.16 | 7.78 | 0.35 | 0.23 | 0.47 | 2.50 × 10−3 |
| 7 | 24.13 | 21.4 | NA | NA | NA | NA |
| 8 | 6.6 | 4.9 | 0.11 | −0.02 | 0.23 | 8.16 × 10−2 |
| 9 | 4.83 | 3.55 | 0.51 | 0.39 | 0.63 | 8.91 × 10−4 |
| 10 | 18.8 | 16.03 | 0.44 | 0.35 | 0.53 | 2.48 × 10−7 |
| 11 | 43.69 | 40.46 | NA | NA | NA | NA |
| 12 | 4.32 | 1.82 | 0.36 | 0.21 | 0.52 | 6.13 × 10−4 |
| 13 | 21.59 | 18.16 | NA | NA | NA | NA |
| 14 | 10.16 | 6.8 | 0.38 | 0.26 | 0.49 | 7.17 × 10−4 |
| 15 | 6.35 | 4.8 | NA | NA | NA | NA |
| 16 | 16.26 | 11.8 | 0.22 | 0.21 | 0.23 | 2.20 × 10−16 |
| 17 | 19.3 | 17 | NA | NA | NA | NA |
| 18 | 4.57 | 2.6 | 0.46 | 0.38 | 0.54 | 9.00 × 10−5 |
| 19 | 8.89 | 6.55 | NA | NA | NA | NA |
| 20 | 17.27 | 12.53 | 0.3 | 0.13 | 0.47 | 1.09 × 10−2 |
| 21 | 33.78 | 30.47 | 0.56 | 0.53 | 0.59 | 2.20 × 10−16 |
| 22 | 16.76 | 12.94 | NA | NA | NA | NA |
| 23 | 15.24 | 9.55 | 0.16 | 0.11 | 0.2 | 1.58 × 10−5 |
| 24 | 13.56 | 10.16 | 0.44 | 0.41 | 0.47 | 2.27 × 10−9 |
| 25 | 12.19 | 7.67 | 0.27 | 0.14 | 0.39 | 6.43 × 10−3 |
| 26 | 10.67 | 7.38 | 0.22 | 0.11 | 0.33 | 7.84 × 10−3 |
| 27 | 9.65 | 6.6 | 0.17 | 0.05 | 0.29 | 2.16 × 10−2 |
| 28 | 23.88 | 21.63 | 0.41 | 0.37 | 0.45 | 2.20 × 10−16 |
| 29 | 6.35 | 3.53 | NA | NA | NA | NA |
| 30 | 8.13 | 5.78 | 0.23 | 0.21 | 0.26 | 2.20 × 10−16 |
| 31 | 13.72 | 9.3 | 0.31 | 0.21 | 0.4 | 2.25 × 10−5 |
| 32 | 115.57 | 93.7 | 0.45 | 0.41 | 0.48 | 2.20 × 10−16 |
| 33 | 14.99 | 13.08 | 0.48 | 0.34 | 0.61 | 4.08 × 10−3 |
| 34 | 8.64 | 4.6 | 0.23 | 0.15 | 0.31 | 1.27 × 10−3 |
| 35 | 6.35 | 4 | 0.47 | 0.44 | 0.5 | 2.20 × 10−16 |
| Observed Data | Individual Storm—IS | Particle Swarm Optimization—PSO | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Event | Precipitation (mm) | Throughfall (mm) | S (mm) | P′G (mm) | E/R | Nash | S (mm) | P′G (mm) | E/R | Nash | ||
| 1 | 24.38 | 16.28 | 0.21 | 2.72 | 3.23 | 0.26 | 0.92 | 0.16 | 2.46 | 2.93 | 0.25 | 0.93 |
| 2 | 27.94 | 18.94 | 0.25 | 1.16 | 1.45 | 0.29 | 0.95 | 0.18 | 1.47 | 1.79 | 0.27 | 0.97 |
| 3 | 13.21 | 8.7 | 0.12 | 2.48 | 2.74 | 0.19 | 0.9 | 0.16 | 2.4 | 2.86 | 0.16 | 0.87 |
| 4 | 12.45 | 5.54 | 0.08 | 1.52 | 1.61 | 0.49 | 0.8 | 0.16 | 1.37 | 1.63 | 0.48 | 0.72 |
| 5 | 16 | 13.58 | 0.5 | 2.25 | 3.53 | −0.03 | 0.97 | 0.2 | 2.39 | 2.97 | 0.01 | 0.98 |
| 6 | 10.16 | 7.78 | 0.35 | 2.35 | 3.39 | −0.01 | 0.95 | 0.2 | 2.41 | 3 | 0.05 | 0.96 |
| 7 | 24.13 | 21.4 | NA | NA | NA | NA | NA | 0.16 | 1.25 | 1.5 | 0.11 | 0.97 |
| 8 | 6.6 | 4.9 | 0.11 | 0.45 | 0.5 | 0.22 | 0.96 | 0.17 | 0.53 | 0.64 | 0.25 | 0.96 |
| 9 | 4.83 | 3.55 | 0.51 | 1.01 | 2.06 | 0.06 | 0.94 | 0.17 | 0.37 | 0.44 | 0.18 | 0.86 |
| 10 | 18.8 | 16.03 | 0.44 | 1.68 | 2.74 | 0.07 | 0.86 | 0.16 | 0.92 | 1.1 | 0.13 | 0.89 |
| 11 | 43.69 | 40.46 | NA | NA | NA | NA | NA | 0.18 | 0.63 | 0.76 | 0.01 | 0.97 |
| 12 | 4.32 | 1.82 | 0.36 | 0.97 | 1.39 | 0.52 | 0.94 | 0.19 | 0.85 | 1.05 | 0.55 | 0.95 |
| 13 | 21.59 | 18.16 | NA | NA | NA | NA | NA | 0.2 | 0.23 | 0.29 | 0.14 | 0.91 |
| 14 | 10.16 | 6.8 | 0.38 | 1.19 | 1.69 | 0.2 | 0.84 | 0.2 | 0.76 | 0.94 | 0.23 | 0.87 |
| 15 | 6.35 | 4.8 | NA | NA | NA | NA | NA | 0.18 | 0.06 | 0.08 | 0.26 | 0.98 |
| 16 | 16.26 | 11.8 | 0.22 | 0.8 | 0.94 | 0.24 | 0.92 | 0.16 | 0.85 | 1.01 | 0.2 | 0.91 |
| 17 | 19.3 | 17 | NA | NA | NA | NA | NA | NA | NA | NA | NA | NA |
| 18 | 4.57 | 2.6 | 0.46 | 1.45 | 2.78 | 0.22 | 0.88 | NA | NA | NA | NA | NA |
| 19 | 8.89 | 6.55 | NA | NA | NA | NA | NA | 0.16 | 1.31 | 1.56 | 0.11 | 0.94 |
| 20 | 17.27 | 12.53 | 0.3 | 2.43 | 3.32 | 0.16 | 0.99 | 0.19 | 2.42 | 2.98 | 0.16 | 0.99 |
| 21 | 33.78 | 30.47 | 0.56 | 2.33 | 5.14 | 0.04 | 0.94 | 0.16 | 2.28 | 2.72 | 0.04 | 0.91 |
| 22 | 16.76 | 12.94 | NA | NA | NA | NA | NA | 0.2 | 0.82 | 1.02 | 0.18 | 0.94 |
| 23 | 15.24 | 9.55 | 0.16 | 2.63 | 3 | 0.26 | 0.89 | 0.17 | 2.09 | 2.52 | 0.35 | 0.88 |
| 24 | 13.56 | 10.16 | 0.44 | 2.6 | 4.45 | 0.04 | 0.95 | 0.16 | 1.92 | 2.29 | 0.18 | 0.97 |
| 25 | 12.19 | 7.67 | 0.27 | 4.11 | 5.31 | 0.04 | 0.94 | 0.16 | 2.51 | 3 | 0.19 | 0.95 |
| 26 | 10.67 | 7.38 | 0.22 | 2.1 | 2.56 | 0.14 | 0.93 | 0.16 | 1.48 | 1.77 | 0.24 | 0.95 |
| 27 | 9.65 | 6.6 | 0.17 | 1.24 | 1.46 | 0.21 | 0.85 | 0.17 | 1.31 | 1.58 | 0.21 | 0.90 |
| 28 | 23.88 | 21.63 | 0.41 | 0.82 | 1.26 | 0.06 | 0.93 | 0.16 | 1.47 | 1.76 | 0.08 | 0.94 |
| 29 | 6.35 | 3.53 | NA | NA | NA | NA | NA | 0.16 | 0.38 | 0.46 | 0.42 | 0.69 |
| 30 | 8.13 | 5.78 | 0.23 | 1.66 | 1.95 | 0.06 | 0.81 | 0.19 | 1.41 | 1.73 | 0.11 | 0.80 |
| 31 | 13.72 | 9.3 | 0.31 | 1.52 | 2.1 | 0.21 | 0.78 | 0.17 | 1.07 | 1.29 | 0.27 | 0.80 |
| 32 | 115.57 | 93.7 | 0.45 | 1.79 | 3.02 | 0.17 | 0.98 | 0.2 | 1.48 | 1.84 | 0.18 | 0.98 |
| 33 | 14.99 | 13.08 | 0.48 | 1.98 | 3.36 | 0 | 0.89 | 0.18 | 1.24 | 1.5 | 0.09 | 0.90 |
| 34 | 8.64 | 4.6 | 0.23 | 1.52 | 1.87 | 0.36 | 0.93 | 0.16 | 1.28 | 1.53 | 0.41 | 0.97 |
| 35 | 6.35 | 4 | 0.47 | 1.82 | 3.61 | 0.2 | 0.99 | 0.2 | 1.92 | 2.39 | 0.21 | 0.98 |
| Parameters | t-Value | df | p-Value | Mean of the Differences |
|---|---|---|---|---|
| 5.412 | 25 | 1.29 × 10−5 | 0.142 | |
| S | 2.864 | 25 | 8.34 × 10−3 | 0.249 |
| P′G | 4.269 | 25 | 2.48 × 10−4 | 0.708 |
| E/R | −3.941 | 25 | 5.77 × 10−4 | −0.040 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Távora, B.E.; Koide, S. Event-Based Rainfall Interception Modeling in a Cerrado Riparian Forest—Central Brazil: An Alternative Approach to the IS Method for Parameterization of the Gash Model. Water 2020, 12, 2128. https://doi.org/10.3390/w12082128
Távora BE, Koide S. Event-Based Rainfall Interception Modeling in a Cerrado Riparian Forest—Central Brazil: An Alternative Approach to the IS Method for Parameterization of the Gash Model. Water. 2020; 12(8):2128. https://doi.org/10.3390/w12082128
Chicago/Turabian StyleTávora, Bruno Esteves, and Sérgio Koide. 2020. "Event-Based Rainfall Interception Modeling in a Cerrado Riparian Forest—Central Brazil: An Alternative Approach to the IS Method for Parameterization of the Gash Model" Water 12, no. 8: 2128. https://doi.org/10.3390/w12082128
APA StyleTávora, B. E., & Koide, S. (2020). Event-Based Rainfall Interception Modeling in a Cerrado Riparian Forest—Central Brazil: An Alternative Approach to the IS Method for Parameterization of the Gash Model. Water, 12(8), 2128. https://doi.org/10.3390/w12082128





