Mekong Delta Runoff Prediction Using Standardized Remotely-Sensed Water Balance Variables
Abstract
1. Introduction
2. Datasets and Their Post-Processing
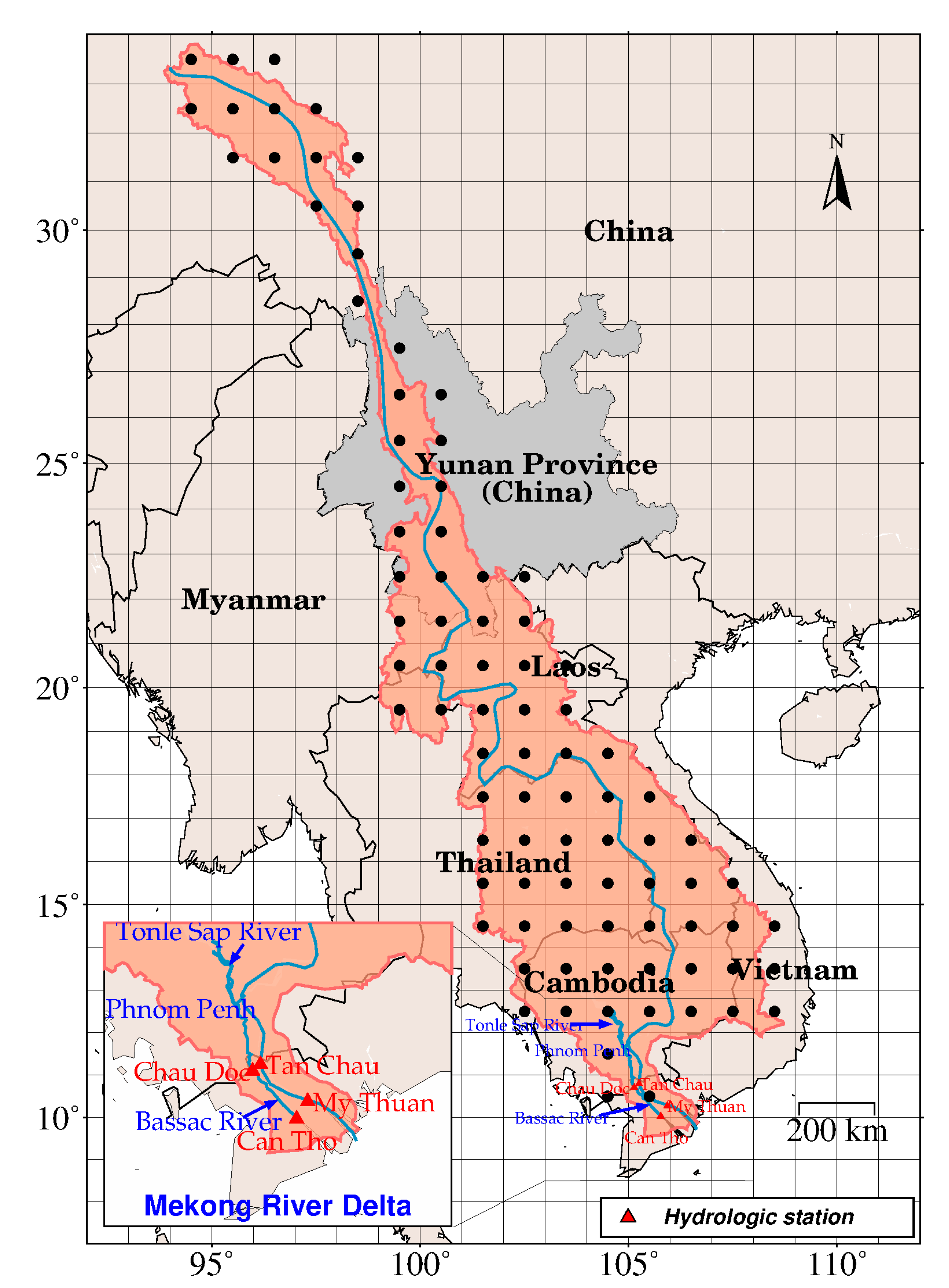
2.1. Ground-Observed Discharge and Passive RS Surface Variables
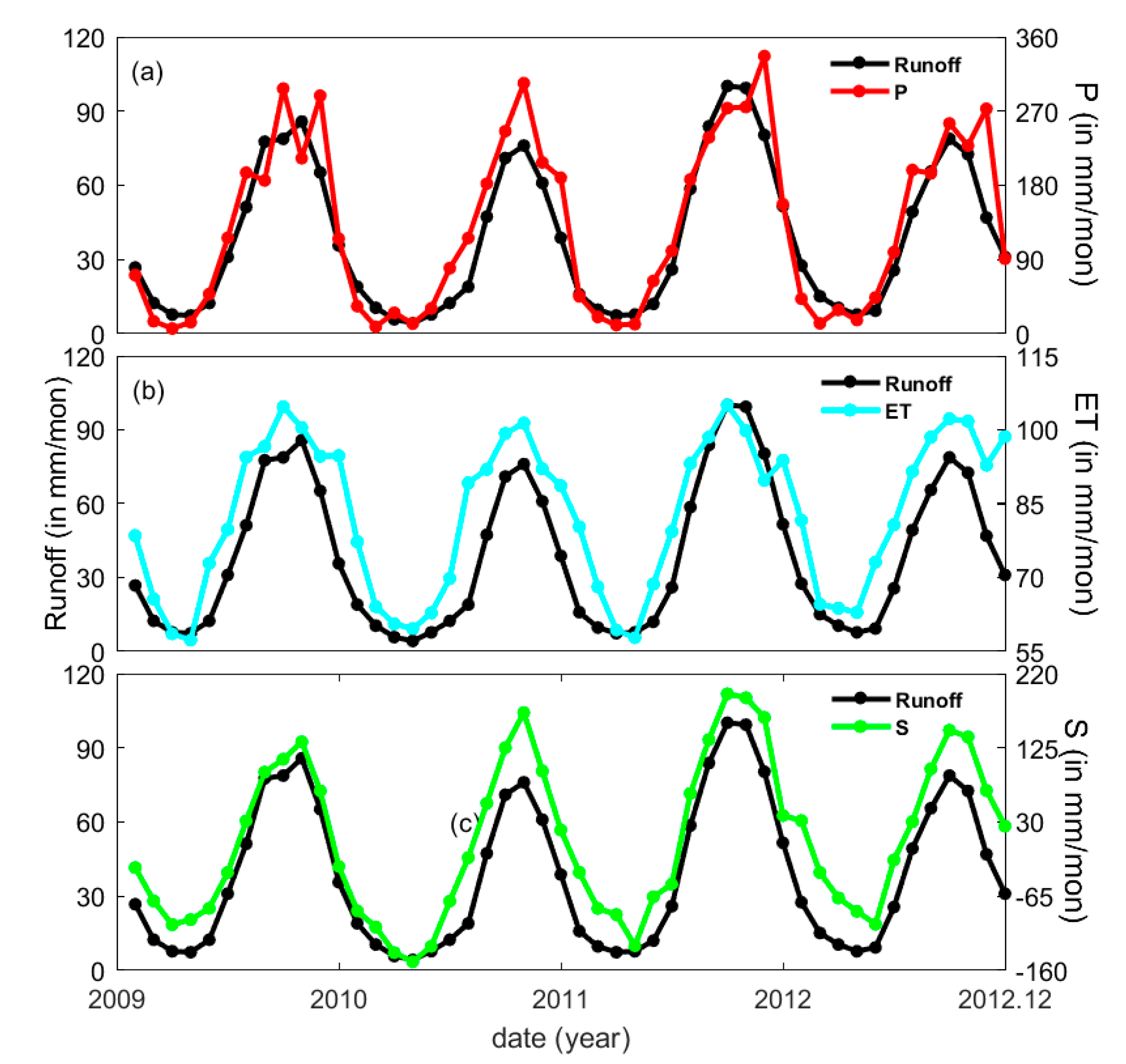
2.2. Water Balance Variables and Their Standardization Based on RS Data
2.2.1. GRACE Terrestrial Water Storage (S) and Its Standardization
2.2.2. MODIS Evapotranspiration (ET) and Its Standardization
2.2.3. TRMM Precipitation (P) and Its Standardization
3. Methodology
3.1. Linear Regression Analysis and Data Standardization
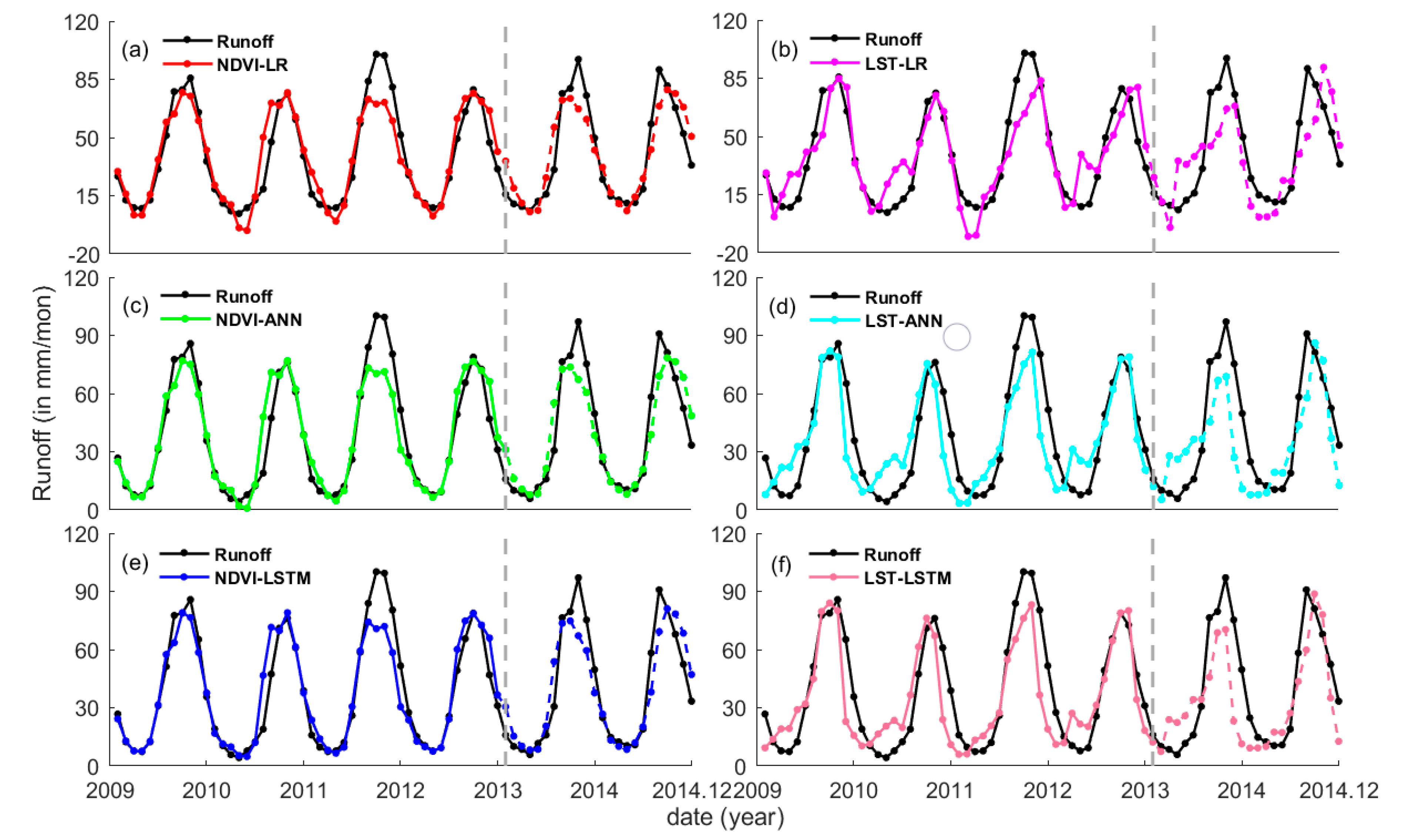
3.2. AI-Based Models
3.3. Assessment Indicators
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vörösmarty, C.; Askew, A.; Grabs, W.; Barry, R.; Birkett, C.; Döll, P.; Goodison, B.; Hall, A.; Jenne, R.; Kitaev, L. Global water data: A newly endangered species. Eos Trans. Am. Geophys. Union 2001, 82, 54–58. [Google Scholar] [CrossRef]
- Sneeuw, N.; Lorenz, C.; Devaraju, B.; Tourian, M.J.; Riegger, J.; Kunstmann, H.; Bardossy, A. Estimating runoff using hydro-geodetic approaches. Surv. Geophys. 2014, 35, 1333–1359. [Google Scholar] [CrossRef]
- Wen, X.; Hu, D.; Cao, B.; Shen, S.; Tang, X. Dynamics change of Honghu lake’s water surface area and its driving force analysis based on remote sensing technique and TOPMODEL model. IOP Conf. Ser. Earth Environ. Sci. 2014, 17, 012130. [Google Scholar] [CrossRef]
- Townsend, P.A.; Walsh, S.J. Modeling floodplain inundation using an integrated GIS with radar and optical remote sensing. Geomorphology 1998, 21, 295–312. [Google Scholar] [CrossRef]
- Yue, W.; Xu, J.; Tan, W. The relationship between land surface temperature and NDVI with remote sensing: Application to shanghai Landsat 7 ETM+ data. Int. J. Remote Sens. 2007, 28, 3205–3226. [Google Scholar] [CrossRef]
- Pan, F.; Nichols, J. Remote sensing of river stage using the cross-sectional inundation area-river stage relationship (IARSR) constructed from digital elevation model data. Hydrol. Process. 2013, 27, 3596–3606. [Google Scholar] [CrossRef]
- Fok, H.S.; He, Q.; Chun, K.P.; Zhou, Z.; Chu, T. Application of ENSO and drought indices for water level reconstruction and prediction: A case study in the lower Mekong river estuary. Water 2018, 10, 58. [Google Scholar] [CrossRef]
- Fok, H.S.; He, Q. Water level reconstruction based on satellite gravimetry in the Yangtze River Basin. ISPRS Int. J. Geo-Inf. 2018, 7, 286. [Google Scholar] [CrossRef]
- Frappart, F.; Minh, K.D.; L’Hermitte, J.; Cazenave, A.; Ramillien, G.; Le Toan, T.; Mognard-Campbell, N. Water volume change in the lower Mekong from satellite altimetry and imagery data. Geophys. J. Int. 2006, 167, 570–584. [Google Scholar] [CrossRef]
- Calmant, S.; Seyler, F.; Cretaux, J.F. Monitoring continental surface waters by satellite altimetry. Surv. Geophys. 2008, 29, 247–269. [Google Scholar] [CrossRef]
- Beven, K.J. Rainfall-Runoff Modelling: The Primer; John Wiley Sons Chichester: Hoboken, NJ, USA, 2001. [Google Scholar]
- Tourian, M.J.; Sneeuw, N.; Bárdossy, A. A quantile function approach to discharge estimation from satellite altimetry (ENVISAT). Water Resour. Res. 2013, 49, 4174–4186. [Google Scholar] [CrossRef]
- Kouraev, A.V.; Zakharova, E.A.; Samain, O.; Mognard, N.M.; Cazenave, A. Ob’river discharge from TOPEX/Poseidon satellite altimetry (1992–2002). Remote Sens. Environ. 2004, 93, 238–245. [Google Scholar] [CrossRef]
- Birkinshaw, S.J.; O’donnell, G.M.; Moore, P.; Kilsby, C.G.; Fowler, H.J.; Berry, P.A.M. Using satellite altimetry data to augment flow estimation techniques on the Mekong River. Hydrol. Process. 2010, 24, 3811–3825. [Google Scholar] [CrossRef]
- Paiva, R.C.D.; Collischonn, W.; Bonnet, M.P.; De Goncalves, L.G.G.; Calmant, S.; Getirana, A.; Santos da Silva, J. Assimilating in situ and radar altimetry data into a large-scale hydrologic-hydrodynamic model for streamflow forecast in the Amazon. Hydrol. Earth Syst. Sci. 2013, 17, 2929–2946. [Google Scholar] [CrossRef]
- Tourian, M.J.; Schwatke, C.; Sneeuw, N. River discharge estimation at daily resolution from satellite altimetry over an entire river basin. J. Hydrol. 2017, 546, 230–247. [Google Scholar] [CrossRef]
- Sulistioadi, Y.B.; Tseng, K.H.; Shum, C.K.; Hidayat, H.; Sumaryono, M.; Suhardiman, A.; Setiawan, F.; Sunarso, S. Satellite radar altimetry for monitoring small rivers and lakes in Indonesia. Hydrol. Earth Syst. Sci. 2015, 19, 341–359. [Google Scholar] [CrossRef]
- Wahr, J.; Swenson, S.; Zlotnicki, V.; Velicogna, I. Time-variable gravity from GRACE: First results. Geophys. Res. Lett. 2004, 31, L11501. [Google Scholar] [CrossRef]
- Crowley, J.W.; Mitrovica, J.X.; Bailey, R.C.; Tamisiea, M.E.; Davis, J.L. Land water storage within the Congo Basin inferred from GRACE satellite gravity data. Geophys. Res. Lett. 2006, 33, L19402. [Google Scholar] [CrossRef]
- Riegger, J.; Tourian, M.J. Characterization of runoff-storage relationships by satellite gravimetry and remote sensing. Water Resour. Res. 2014, 50, 3444–3466. [Google Scholar] [CrossRef]
- Sproles, E.A.; Reager, J.T.; Leibowitz, S.G. GRACE storage-runoff hystereses reveal the dynamics of regional watersheds. Hydrol. Earth Syst. Sci. 2015, 19, 3253–3272. [Google Scholar] [CrossRef]
- Syed, T.H.; Famiglietti, J.S.; Chambers, D.P. GRACE-based estimates of terrestrial freshwater discharge from basin to continental scales. J. Hydrometeorol. 2009, 10, 22–40. [Google Scholar] [CrossRef]
- Ferreira, V.G.; Gong, Z.; He, X.; Zhang, Y.; Andam-Akorful, S.A. Estimating total discharge in the Yangtze River Basin using satellite-based observations. Remote Sens. 2013, 5, 3415–3430. [Google Scholar] [CrossRef]
- Chen, Y.; Fok, H.S.; Ma, Z.; Tenzer, R. An improved remotely-sensed total basin discharge with its seasonal error characterization in the Yangtze River Basin. Sensors 2019, 19, 3386. [Google Scholar] [CrossRef] [PubMed]
- Box, G.E.P.; Jenkins, G.M. Times Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1970. [Google Scholar]
- Hassoun, M.H. Fundamentals of Artificial Neural Networks; MIT press: Cambridge, MA, USA, 1995. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Wang, W.-C.; Chau, K.-W.; Cheng, C.-T.; Qiu, L. A comparison of performance of several artificial intelligence methods for forecasting monthly discharge time series. J. Hydrol. 2009, 374, 294–306. [Google Scholar] [CrossRef]
- Ferreira, V.G.; Montecino, H.C.; Ndehedehe, C.E.; Heck, B.; Gong, Z.; de Freitas, S.R.C.; Westerhaus, M. Space-based observations of crustal deflections for drought characterization in brazil. Sci. Total Environ. 2018, 644, 256–273. [Google Scholar] [CrossRef] [PubMed]
- Jones, P.D.; Hulme, M. Calculating regional climatic time series for temperature and precipitation: Methods and illustrations. Int. J. Climatol. 1996, 16, 361–377. [Google Scholar] [CrossRef]
- Tang, J.; Yin, X.A.; Yang, P.; Yang, Z.F. Assessment of contributions of climatic variation and human activities to streamflow changes in the Lancang River, China. Water Resour. Manag. 2014, 28, 2953–2966. [Google Scholar] [CrossRef]
- Fok, H.S.; Iz, H.B.; Shum, C.K.; Yi, Y.; Andersen, O.; Braun, A.; Chao, Y.; Han, G.; Kuo, C.Y.; Matsumoto, K.; et al. Evaluation of ocean tide models used for Jason-2 altimetry corrections. Mar. Geod. 2010, 33, 285–303. [Google Scholar] [CrossRef]
- Anthony, E.J.; Brunier, G.; Besset, M.; Goichot, M.; Dussouillez, P.; Nguyen, V.L. Linking rapid erosion of the Mekong river delta to human activities. Sci. Rep. 2015, 5, 14745. [Google Scholar] [CrossRef]
- Gugliotta, M.; Saito, Y.; Nguyen, V.L.; Ta, T.K.O.; Tamura, T. Sediment distribution and depositional processes along the fluvial to marine transition zone of the Mekong River delta, Vietnam. Sedimentology 2019, 66, 146–164. [Google Scholar] [CrossRef]
- Kummu, M.; Tes, S.; Yin, S.; Adamson, P.; Józsa, J.; Koponen, J.; Richey, J.; Sarkkula, J. Water balance analysis for the Tonle Sap Lake–floodplain system. Hydrol. Process. 2014, 28, 1722–1733. [Google Scholar] [CrossRef]
- Frappart, F.; Biancamaria, S.; Normandin, C.; Blarel, F.; Bourrel, L.; Aumont, M.; Azemar, P.; Vu, P.L.; Le Toan, T.; Lubac, B.; et al. Influence of recent climatic events on the surface water storage of the Tonle Sap Lake. Sci. Total Environ. 2018, 636, 1520–1533. [Google Scholar] [CrossRef]
- Huang, S.; Krysanova, V.; Zhai, J.; Su, B. Impact of intensive irrigation activities on river discharge under agricultural scenarios in the semi-arid Aksu river basin, northwest China. Water Resour. Manag. 2015, 29, 945–959. [Google Scholar] [CrossRef]
- Zampieri, M.; Carmona Garcia, G.; Dentener, F.; Gumma, M.; Salamon, P.; Seguini, L.; Toreti, A. Surface freshwater limitation explains worst rice production anomaly in India in 2002. Remote Sens. 2018, 10, 244. [Google Scholar] [CrossRef]
- Jung, H.C.; Alsdorf, D.; Moritz, M.; Lee, H.; Vassolo, S. Analysis of the relationship between flooding area and water height in the Logone floodplain. Phys. Chem. Earth Parts A/B/C 2011, 36, 232–240. [Google Scholar] [CrossRef]
- Hirpa, F.A.; Hopson, T.M.; De Groeve, T.; Brakenridge, G.R.; Gebremichael, M.; Restrepo, P.J. Upstream satellite remote sensing for river discharge forecasting: Application to major rivers in South Asia. Remote Sens. Environ. 2013, 131, 140–151. [Google Scholar] [CrossRef]
- Tarpanelli, A.; Amarnath, G.; Brocca, L.; Massari, C.; Moramarco, T. Discharge estimation and forecasting by MODIS and altimetry data in Niger-Benue River. Remote Sens. Environ. 2017, 195, 96–106. [Google Scholar] [CrossRef]
- Li, X.; Liu, J.P.; Saito, Y.; Nguyen, V.L. Recent evolution of the Mekong Delta and the impacts of dams. Earth-Sci. Rev. 2017, 175, 1–17. [Google Scholar] [CrossRef]
- Lu, X.X.; Li, S.; Kummu, M.; Padawangi, R.; Wang, J.J. Observed changes in the water flow at Chiang Saen in the lower Mekong: Impacts of Chinese dams? Quat. Int. 2014, 336, 145–157. [Google Scholar] [CrossRef]
- Cochrane, T.A.; Arias, M.E.; Piman, T. Historical impact of water infrastructure on water levels of the Mekong River and the Tonle Sap system. Hydrol. Earth Syst. Sci. 2014, 18, 4529–4541. [Google Scholar] [CrossRef]
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D. Variations in the Earth’s oblateness during the past 28 years. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Swenson, S.; Chambers, D.; Wahr, J. Estimating geocenter variations from a combination of grace and ocean model output. J. Geophys. Res. 2008, 113, B08410. [Google Scholar] [CrossRef]
- Ramillien, G.; Frappart, F.; Cazenave, A.; Güntner, A. Time variations of land water storage from an inversion of 2 years of GRACE geoids. Earth. Planet. Sci. Lett. 2005, 235, 283–301. [Google Scholar] [CrossRef]
- Swenson, S.; Wahr, J. Post-processing removal of correlated errors in GRACE data. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Liu, Z.; Ostrenga, D.; Teng, W.; Kempler, S. Tropical Rainfall Measuring Mission (TRMM) precipitation data and services for research and applications. Bull. Am. Meteorol. Soc. 2012, 93, 1317–1325. [Google Scholar] [CrossRef]
- Huffman, G.J.; Adler, R.F.; Bolvin, D.T.; Gu, G.; Nelkin, E.J.; Bowman, K.P.; Hong, Y.; Stocker, E.F.; Wolff, D.B. The TRMM Multi-satellite Precipitation Analysis: Quasi-Global, Multi-Year, Combined-Sensor Precipitation Estimates at Fine Scale. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; American Meteorological Society: Boston, MA, USA, 1993. [Google Scholar]
- Kumar, M.N.; Murthy, C.S.; Sai, M.V.R.S.; Roy, P.S. On the use of Standardized Precipitation Index (SPI) for drought intensity assessment. Meteorol. Appl. 2009, 16, 381–389. [Google Scholar] [CrossRef]
- Räsänen, T.A.; Kummu, M. Spatiotemporal influences of ENSO on precipitation and flood pulse in the Mekong River Basin. J. Hydrol. 2013, 476, 154–168. [Google Scholar] [CrossRef]
- Fok, H.S.; Zhou, L.; Liu, Y.; Ma, Z.; Chen, Y. Upstream GPS Vertical displacement and its standardization for mekong river basin surface runoff reconstruction and estimation. Remote Sens. 2020, 12, 18. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSEperformance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Ritter, A.; Muñoz-Carpena, R. Performance evaluation of hydrological models: Statistical significance for reducing subjectivity in goodness-of-fit assessments. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Cheng, K.-S.; Lien, Y.-T.; Wu, Y.-C.; Su, Y.-F. On the criteria of model performance evaluation for real-time flood forecasting. Stoch. Environ. Res. Risk Assess. 2017, 31, 1–24. [Google Scholar] [CrossRef]
- Li, Y.; Wang, W.; Lu, H.; Khem, S.; Yang, K.; Huang, X. Evaluation of three satellite-based precipitation products over the lower mekong river basin using rain gauge observations and hydrological modeling. IEEE J-STARS 2019, 12, 2357–2373. [Google Scholar] [CrossRef]
- Jiang, L.; Islam, S.; Carlson, T.N. Uncertainties in latent heat flux measurement and estimation: Implications for using a simplified approach with remote sensing data. Can. J. Remote Sens. 2004, 30, 769–787. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]


| Station | Data | Variable | a | b (mm/mon) | Standard Deviation (a and b) | |
|---|---|---|---|---|---|---|
| MT–CT station pair | Passive RS | NDVI | 325.6314 | −168.8107 | 23.2843 | 15.2443 |
| LST | −151.9813 | 2279.3453 | 9.9238 | 146.0701 | ||
| RS WBVs | P | 0.3144 | 9.2319 | 0.0257 | 3.5330 | |
| ET | 1.2716 | −53.1952 | 0.0805 | 6.3268 | ||
| S | 0.3467 | 43.5832 | 0.0372 | 2.7332 | ||
| TC–CD station pair | Passive RS | NDVI | 312.2021 | −163.8793 | 18.9117 | 12.3816 |
| LST | −142.5538 | 2136.8119 | 8.9802 | 132.1818 | ||
| RS WBVs | P | 0.3021 | 6.7515 | 0.0215 | 2.9484 | |
| ET | 1.2118 | −52.4742 | 0.0655 | 5.1480 | ||
| S | 0.3317 | 39.7533 | 0.0329 | 2.4186 | ||
| Station | Data | Variable | a | b (mm/mon) | Standard Deviation (a and b) | |
|---|---|---|---|---|---|---|
| MT–CT station pair | Passive RS | NDVI | 396.7570 | −184.0357 | 28.1345 | 16.1888 |
| LST | −199.2218 | 3005.0215 | 18.2062 | 270.7465 | ||
| RS WBVs | P | 0.2835 | 5.8395 | 0.0180 | 2.9624 | |
| ET | 1.7823 | −104.5923 | 0.1470 | 12.3381 | ||
| S | 0.3112 | 40.2074 | 0.0123 | 1.2019 | ||
| TC–CD station pair | Passive RS | NDVI | 379.6232 | −178.0361 | 23.0676 | 13.2733 |
| LST | −188.2365 | 2837.8818 | 16.3860 | 243.6776 | ||
| RS WBVs | P | 0.2680 | 4.0628 | 0.0155 | 2.5513 | |
| ET | 1.7074 | −102.1954 | 0.1244 | 10.4440 | ||
| S | 0.2909 | 36.5738 | 0.0111 | 1.0865 | ||
| Station | Methods | Data/Index | Reconstruction | Prediction | ||||
|---|---|---|---|---|---|---|---|---|
| PCC | NRMSE | NSE | PCC | NRMSE | NSE | |||
| MT–CT pair | Linear Regression | NDVI | 0.900 | 0.116 | 0.810 | 0.934 | 0.120 | 0.853 |
| LST | 0.914 | 0.107 | 0.836 | 0.865 | 0.164 | 0.725 | ||
| P | 0.874 | 0.129 | 0.765 | 0.953 | 0.095 | 0.909 | ||
| ET | 0.919 | 0.105 | 0.844 | 0.920 | 0.124 | 0.844 | ||
| S | 0.809 | 0.156 | 0.654 | 0.940 | 0.107 | 0.884 | ||
| ANN | NDVI | 0.924 | 0.102 | 0.851 | 0.947 | 0.106 | 0.886 | |
| LST | 0.925 | 0.103 | 0.849 | 0.886 | 0.153 | 0.762 | ||
| P | 0.883 | 0.125 | 0.779 | 0.958 | 0.092 | 0.913 | ||
| ET | 0.925 | 0.104 | 0.847 | 0.929 | 0.123 | 0.845 | ||
| S | 0.825 | 0.155 | 0.660 | 0.949 | 0.109 | 0.878 | ||
| LSTM | NDVI | 0.930 | 0.098 | 0.864 | 0.956 | 0.094 | 0.910 | |
| LST | 0.926 | 0.102 | 0.853 | 0.888 | 0.151 | 0.767 | ||
| P | 0.880 | 0.126 | 0.774 | 0.957 | 0.092 | 0.913 | ||
| ET | 0.929 | 0.101 | 0.856 | 0.939 | 0.117 | 0.862 | ||
| S | 0.819 | 0.158 | 0.643 | 0.948 | 0.111 | 0.876 | ||
| Data Standardization | SPI | 0.946 | 0.086 | 0.894 | 0.960 | 0.089 | 0.919 | |
| SETI | 0.935 | 0.095 | 0.871 | 0.946 | 0.103 | 0.892 | ||
| SI | 0.936 | 0.094 | 0.876 | 0.957 | 0.092 | 0.914 | ||
| TC–CD pair | Linear Regression | NDVI | 0.925 | 0.116 | 0.856 | 0.929 | 0.132 | 0.842 |
| LST | 0.920 | 0.120 | 0.846 | 0.847 | 0.182 | 0.699 | ||
| P | 0.901 | 0.133 | 0.811 | 0.935 | 0.118 | 0.873 | ||
| ET | 0.939 | 0.105 | 0.882 | 0.911 | 0.137 | 0.828 | ||
| S | 0.830 | 0.171 | 0.688 | 0.937 | 0.116 | 0.877 | ||
| ANN | NDVI | 0.949 | 0.097 | 0.899 | 0.945 | 0.114 | 0.883 | |
| LST | 0.932 | 0.111 | 0.869 | 0.867 | 0.168 | 0.743 | ||
| P | 0.907 | 0.129 | 0.823 | 0.942 | 0.113 | 0.885 | ||
| ET | 0.945 | 0.101 | 0.890 | 0.925 | 0.129 | 0.850 | ||
| S | 0.849 | 0.169 | 0.696 | 0.949 | 0.115 | 0.879 | ||
| LSTM | NDVI | 0.954 | 0.093 | 0.909 | 0.951 | 0.106 | 0.897 | |
| LST | 0.942 | 0.103 | 0.887 | 0.881 | 0.160 | 0.767 | ||
| P | 0.907 | 0.130 | 0.820 | 0.941 | 0.114 | 0.881 | ||
| ET | 0.949 | 0.098 | 0.898 | 0.931 | 0.125 | 0.859 | ||
| S | 0.844 | 0.172 | 0.684 | 0.947 | 0.115 | 0.880 | ||
| Data Standardization | SPI | 0.958 | 0.088 | 0.917 | 0.960 | 0.094 | 0.919 | |
| SETI | 0.957 | 0.089 | 0.915 | 0.943 | 0.111 | 0.887 | ||
| SI | 0.953 | 0.093 | 0.908 | 0.956 | 0.099 | 0.911 | ||
| Station | Methods | Data/Index | Reconstruction | Prediction | ||||
|---|---|---|---|---|---|---|---|---|
| PCC | NRMSE | NSE | PCC | NRMSE | NSE | |||
| MT–CT pair | Linear Regression | NDVI | 0.901 | 0.115 | 0.812 | 0.914 | 0.129 | 0.831 |
| LST | 0.850 | 0.140 | 0.723 | 0.749 | 0.214 | 0.537 | ||
| P | 0.919 | 0.105 | 0.844 | 0.926 | 0.121 | 0.850 | ||
| ET | 0.873 | 0.130 | 0.762 | 0.837 | 0.174 | 0.692 | ||
| S | 0.966 | 0.069 | 0.933 | 0.960 | 0.092 | 0.915 | ||
| ANN | NDVI | 0.910 | 0.111 | 0.826 | 0.921 | 0.125 | 0.840 | |
| LST | 0.827 | 0.154 | 0.664 | 0.792 | 0.208 | 0.561 | ||
| P | 0.922 | 0.104 | 0.846 | 0.934 | 0.116 | 0.864 | ||
| ET | 0.896 | 0.119 | 0.800 | 0.868 | 0.163 | 0.728 | ||
| S | 0.973 | 0.063 | 0.944 | 0.970 | 0.083 | 0.930 | ||
| LSTM | NDVI | 0.913 | 0.109 | 0.830 | 0.922 | 0.125 | 0.841 | |
| LST | 0.831 | 0.154 | 0.662 | 0.801 | 0.209 | 0.554 | ||
| P | 0.920 | 0.107 | 0.836 | 0.925 | 0.123 | 0.847 | ||
| ET | 0.900 | 0.117 | 0.806 | 0.871 | 0.162 | 0.733 | ||
| S | 0.977 | 0.057 | 0.954 | 0.972 | 0.077 | 0.939 | ||
| Data Standardization | SPI | 0.985 | 0.047 | 0.968 | 0.927 | 0.122 | 0.848 | |
| SETI | 0.940 | 0.090 | 0.884 | 0.942 | 0.114 | 0.867 | ||
| SI | 0.981 | 0.052 | 0.961 | 0.978 | 0.072 | 0.947 | ||
| TC–CD pair | Linear Regression | NDVI | 0.923 | 0.117 | 0.855 | 0.908 | 0.141 | 0.820 |
| LST | 0.861 | 0.156 | 0.742 | 0.755 | 0.222 | 0.552 | ||
| P | 0.931 | 0.112 | 0.867 | 0.925 | 0.128 | 0.851 | ||
| ET | 0.897 | 0.136 | 0.804 | 0.839 | 0.183 | 0.697 | ||
| S | 0.968 | 0.077 | 0.937 | 0.955 | 0.101 | 0.907 | ||
| ANN | NDVI | 0.934 | 0.110 | 0.872 | 0.916 | 0.135 | 0.834 | |
| LST | 0.833 | 0.172 | 0.686 | 0.763 | 0.225 | 0.540 | ||
| P | 0.938 | 0.106 | 0.879 | 0.935 | 0.120 | 0.870 | ||
| ET | 0.921 | 0.120 | 0.846 | 0.870 | 0.167 | 0.747 | ||
| S | 0.974 | 0.070 | 0.948 | 0.964 | 0.092 | 0.924 | ||
| LSTM | NDVI | 0.937 | 0.108 | 0.876 | 0.917 | 0.134 | 0.837 | |
| LST | 0.844 | 0.168 | 0.699 | 0.786 | 0.219 | 0.566 | ||
| P | 0.934 | 0.110 | 0.872 | 0.929 | 0.124 | 0.859 | ||
| ET | 0.926 | 0.116 | 0.856 | 0.875 | 0.167 | 0.747 | ||
| S | 0.976 | 0.067 | 0.952 | 0.966 | 0.089 | 0.929 | ||
| Data Standardization | SPI | 0.986 | 0.052 | 0.971 | 0.932 | 0.124 | 0.861 | |
| SETI | 0.959 | 0.087 | 0.919 | 0.946 | 0.113 | 0.884 | ||
| SI | 0.984 | 0.056 | 0.966 | 0.971 | 0.085 | 0.935 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fok, H.S.; Zhou, L.; Ji, H. Mekong Delta Runoff Prediction Using Standardized Remotely-Sensed Water Balance Variables. Water 2020, 12, 2025. https://doi.org/10.3390/w12072025
Fok HS, Zhou L, Ji H. Mekong Delta Runoff Prediction Using Standardized Remotely-Sensed Water Balance Variables. Water. 2020; 12(7):2025. https://doi.org/10.3390/w12072025
Chicago/Turabian StyleFok, Hok Sum, Linghao Zhou, and Hang Ji. 2020. "Mekong Delta Runoff Prediction Using Standardized Remotely-Sensed Water Balance Variables" Water 12, no. 7: 2025. https://doi.org/10.3390/w12072025
APA StyleFok, H. S., Zhou, L., & Ji, H. (2020). Mekong Delta Runoff Prediction Using Standardized Remotely-Sensed Water Balance Variables. Water, 12(7), 2025. https://doi.org/10.3390/w12072025






