A Prediction Model Based on Deep Belief Network and Least Squares SVR Applied to Cross-Section Water Quality
Abstract
1. Introduction
2. Materials and Methodology
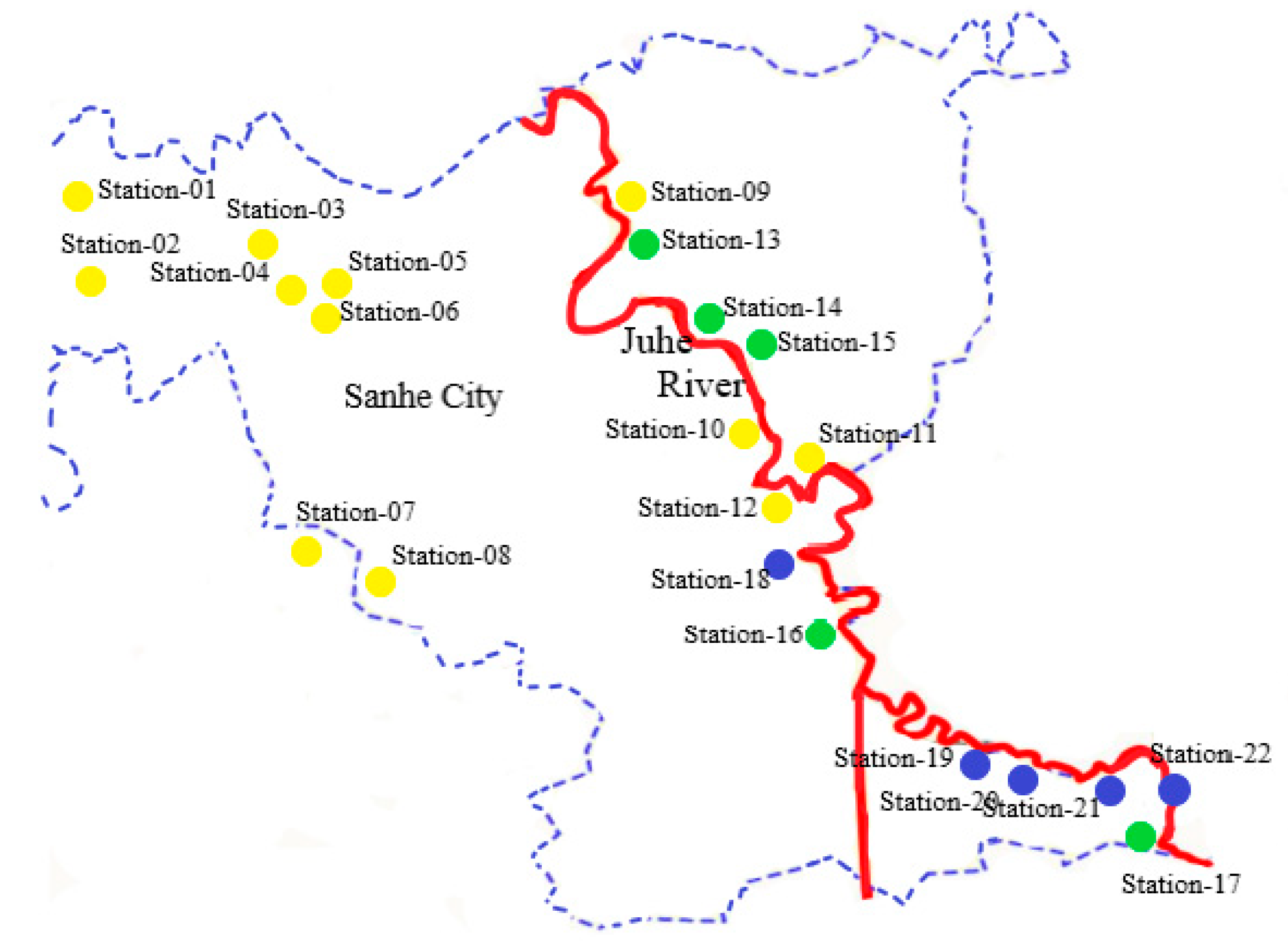
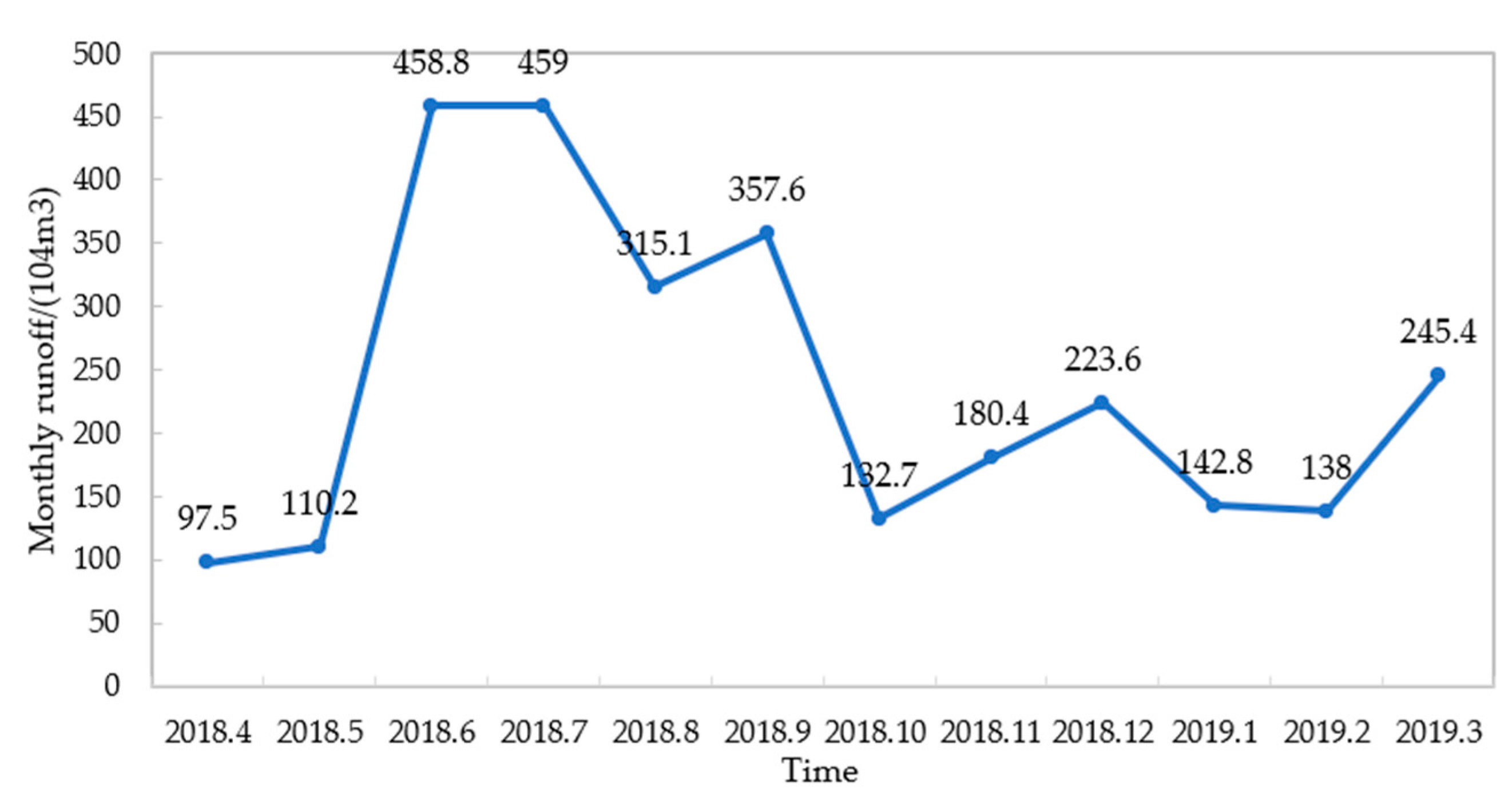
2.1. Study Area and Monitoring Data
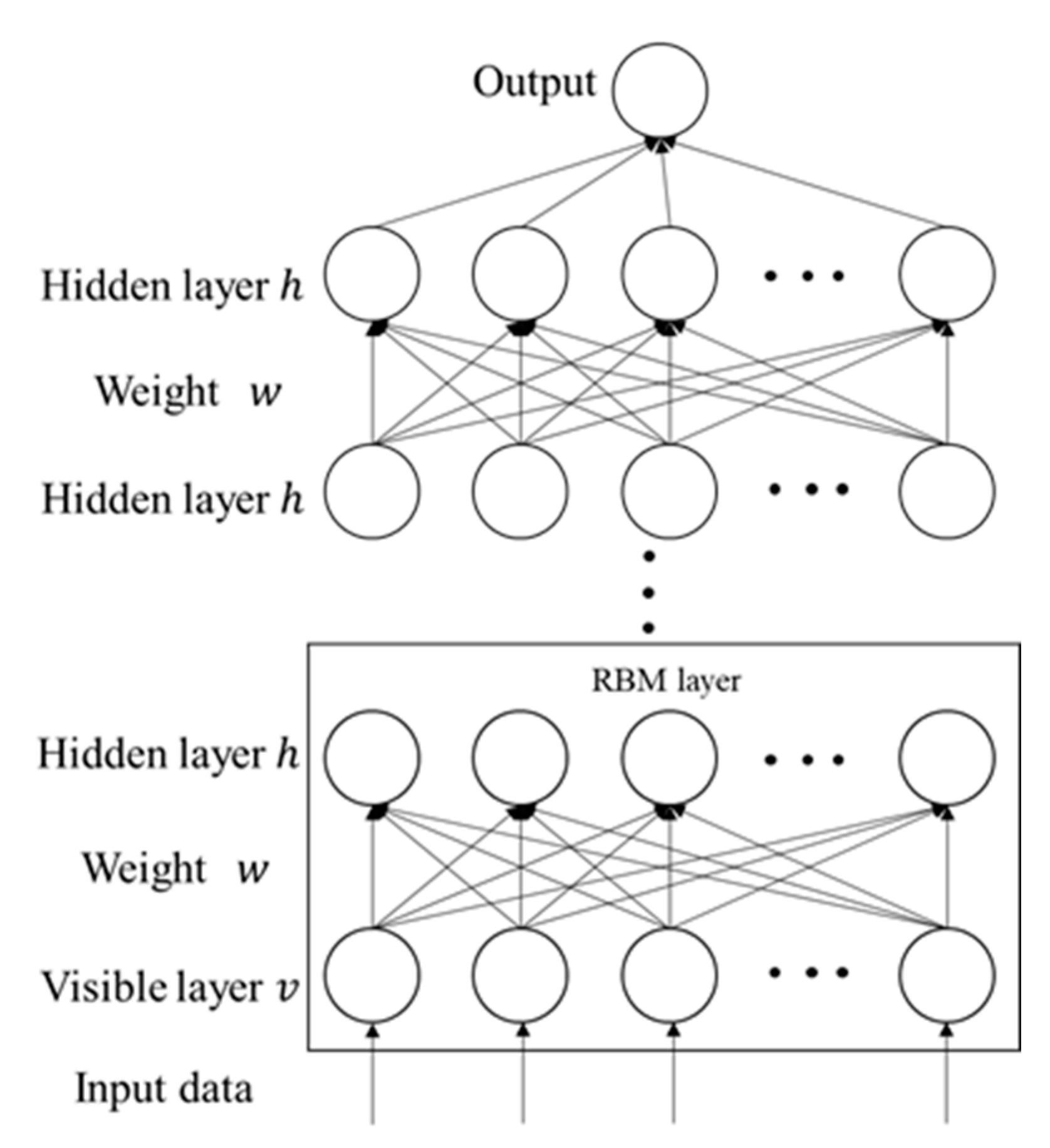
2.2. Feature Extraction Based on DBN Model
2.3. Optimizing DBN Model Using PSO
2.4. Least Squares Support Vector Regression Machine
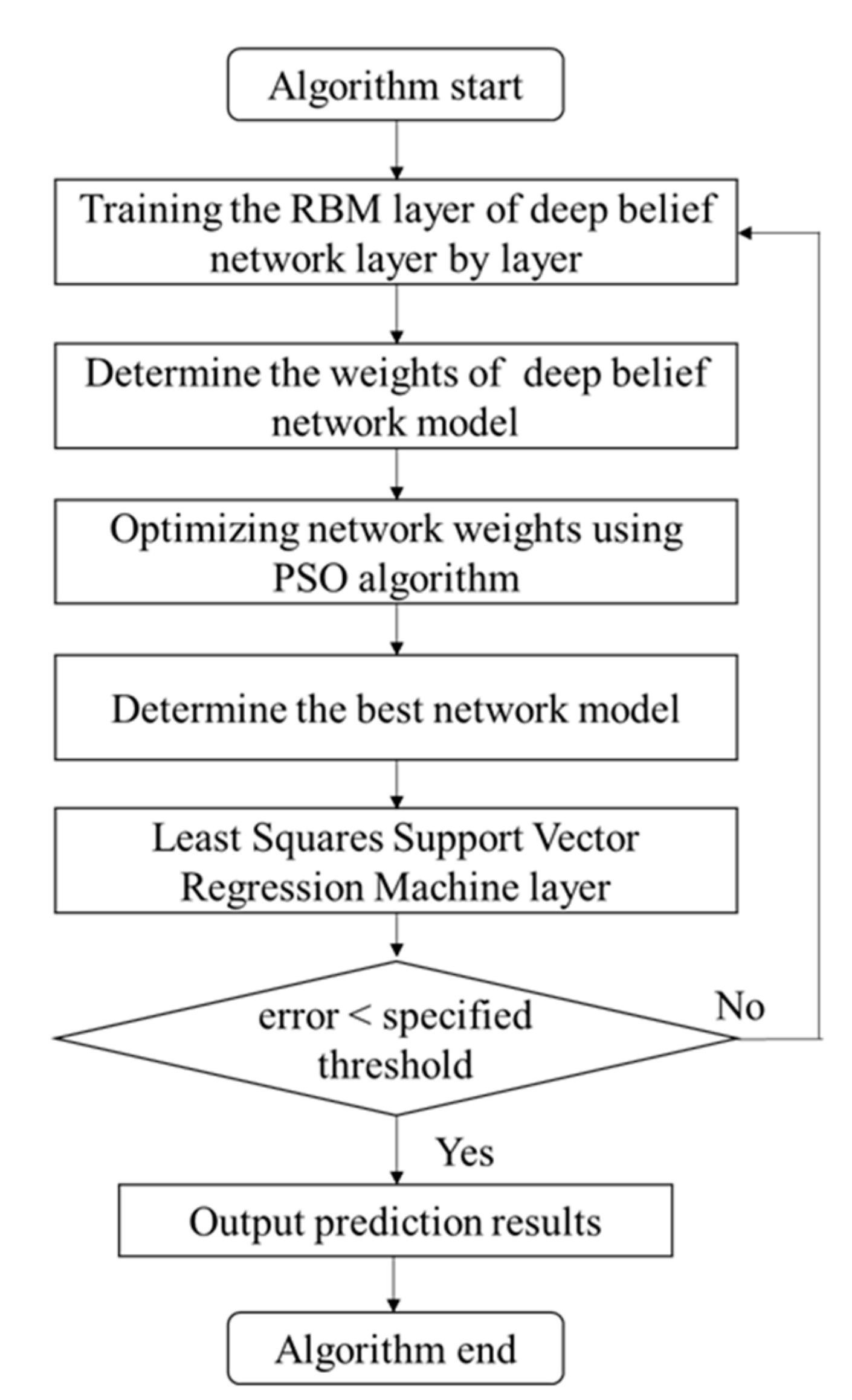
2.5. Prediction Model Based on PSO Optimized DBN Network and LSSVR
- Step 1:
- Determination of DBN model parameters. Initialize the learning rate and the number of iterations. The number of visible layer neurons is determined by the number of input features and the number of hidden layer neurons and the number of hidden layers, as well as the weights and thresholds of each layer, are determined in the training RBM layer by layer. Next, use the CD algorithm to pre-train each layer of RBM, while, regard the output of each lower layer RBM as the input of the higher layer RBM, and then train the higher layer RBM. The data will undergo feature extraction and reduce the dimension, output the feature vector, and obtain the appropriate initial weight of the model after each layer of RBM training. This step is mainly to pre-train each RBM layer of the DBN model.
- Step 2:
- To overcome the shortcoming that the DBN network is easy to fall into local optimum during the learning and training process, utilize the PSO optimization algorithm to dynamically optimize and adjust all RBM model parameters, and find the optimal initial weight of the network model.
- Step 3:
- Determination of LSSVR model parameters. The output of the top-level RBM is used as the input of the LSSVR regression layer to train the LLSVR regression model. When the maximum number of cycles or the error is less than the specified threshold, the LSSVR model training is ended, and the LSSVR prediction model is constructed with the optimal combination parameters.
- Step 4:
- After the LSSVR model training is completed, each layer of the RBM network can only ensure that the weights in its own layer are optimal for the feature vector mapping of this layer, not for the feature vector mapping of the entire DBN and LSSVR combined model. So it is necessary that the top-level LSSVR model propagates from top to bottom to each layer of RBM, and iteratively updates the weights and offsets of the fine-tuned DBN network until the model converges, and the training of the model is completed.
2.6. Evaluation of Performance
3. Results and Discussion
3.1. Data Selection and Preprocessing
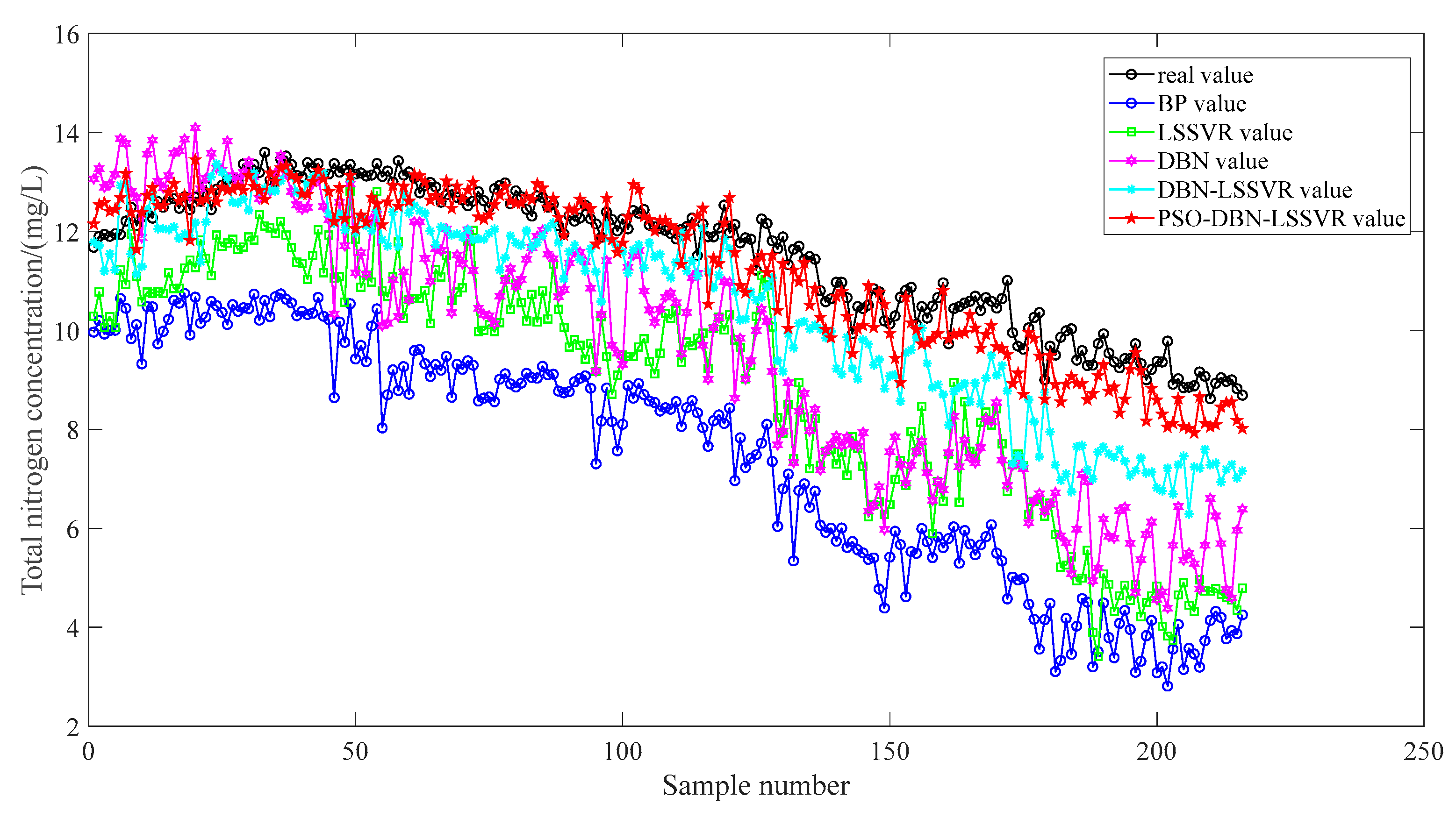
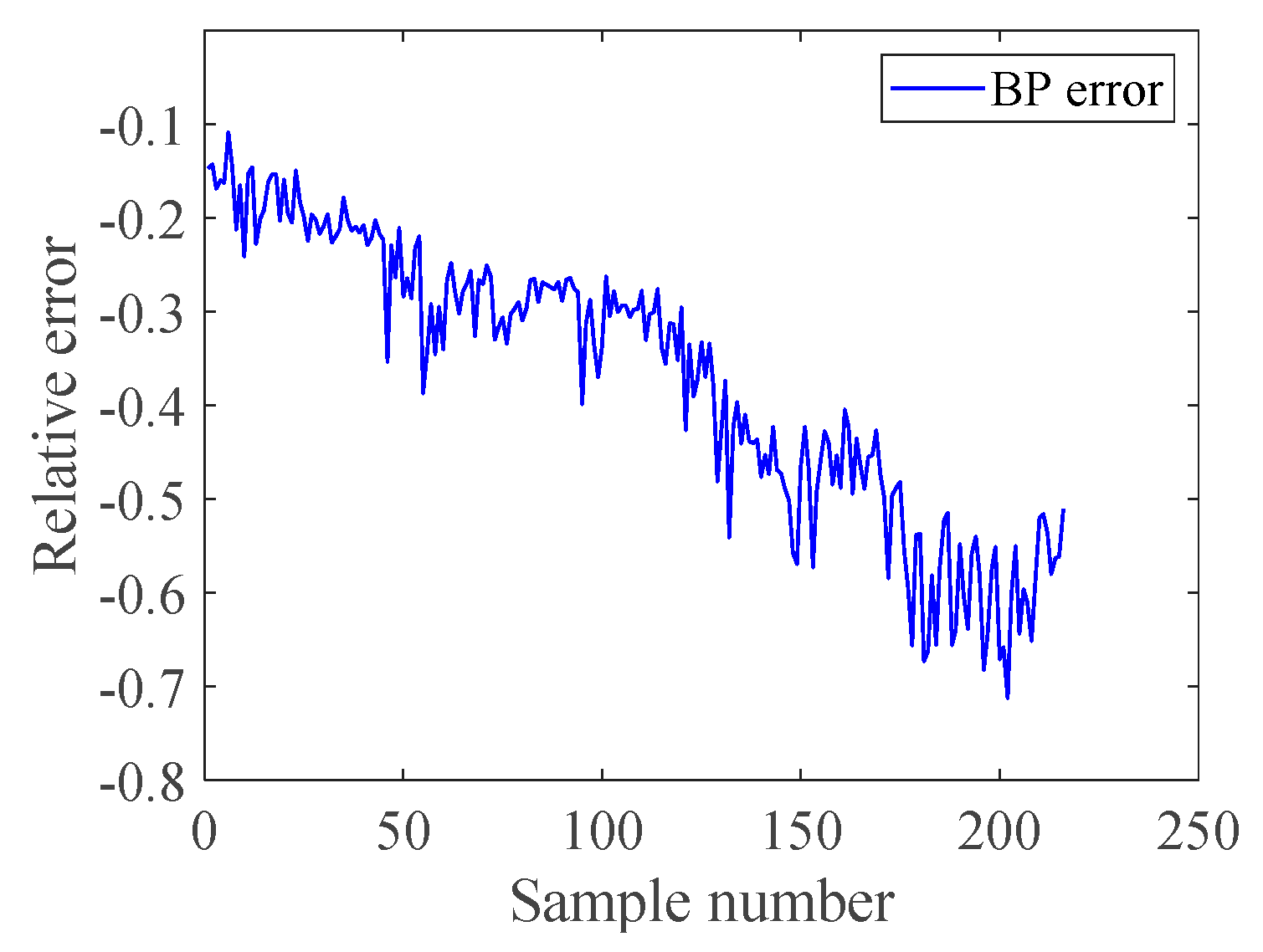
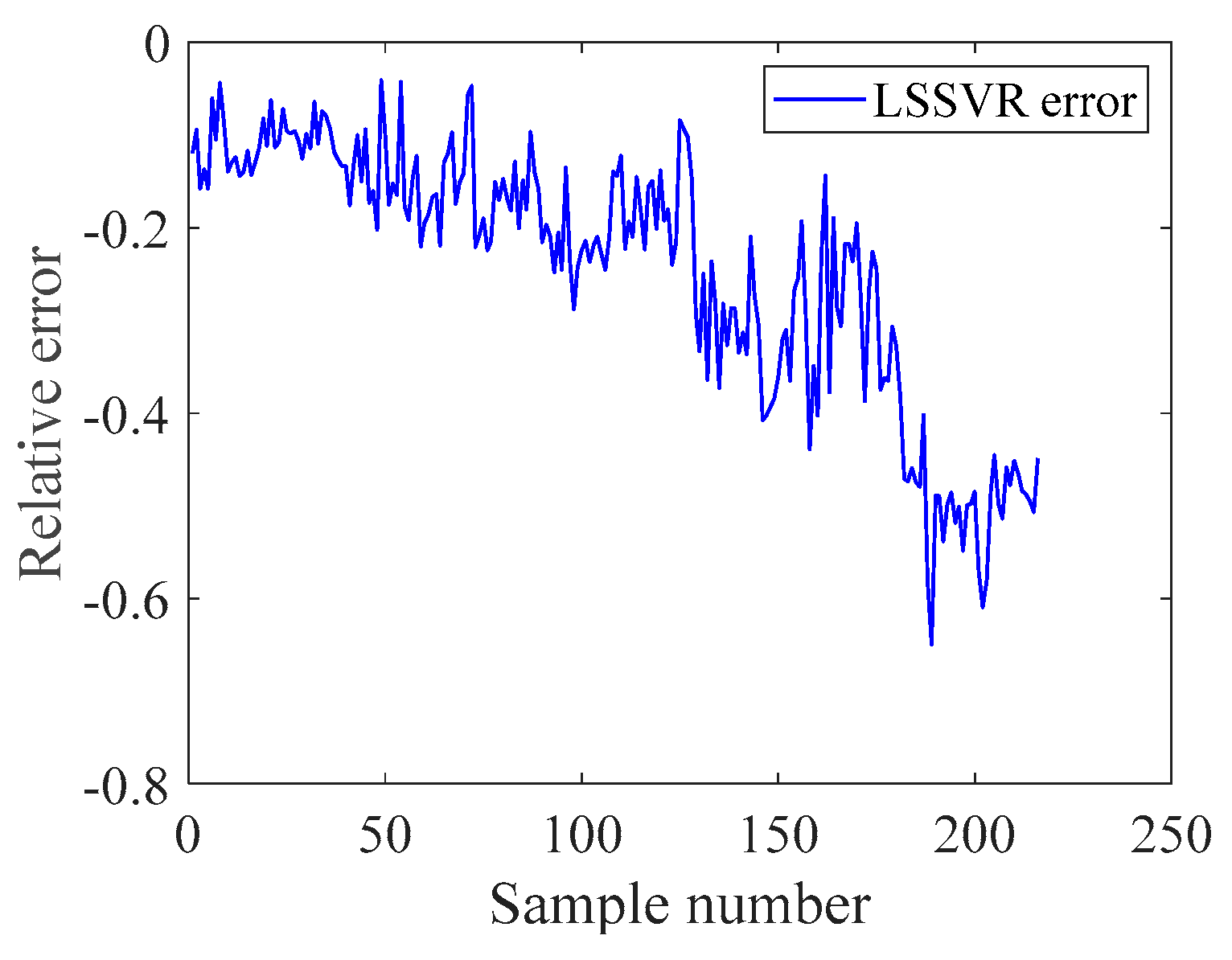
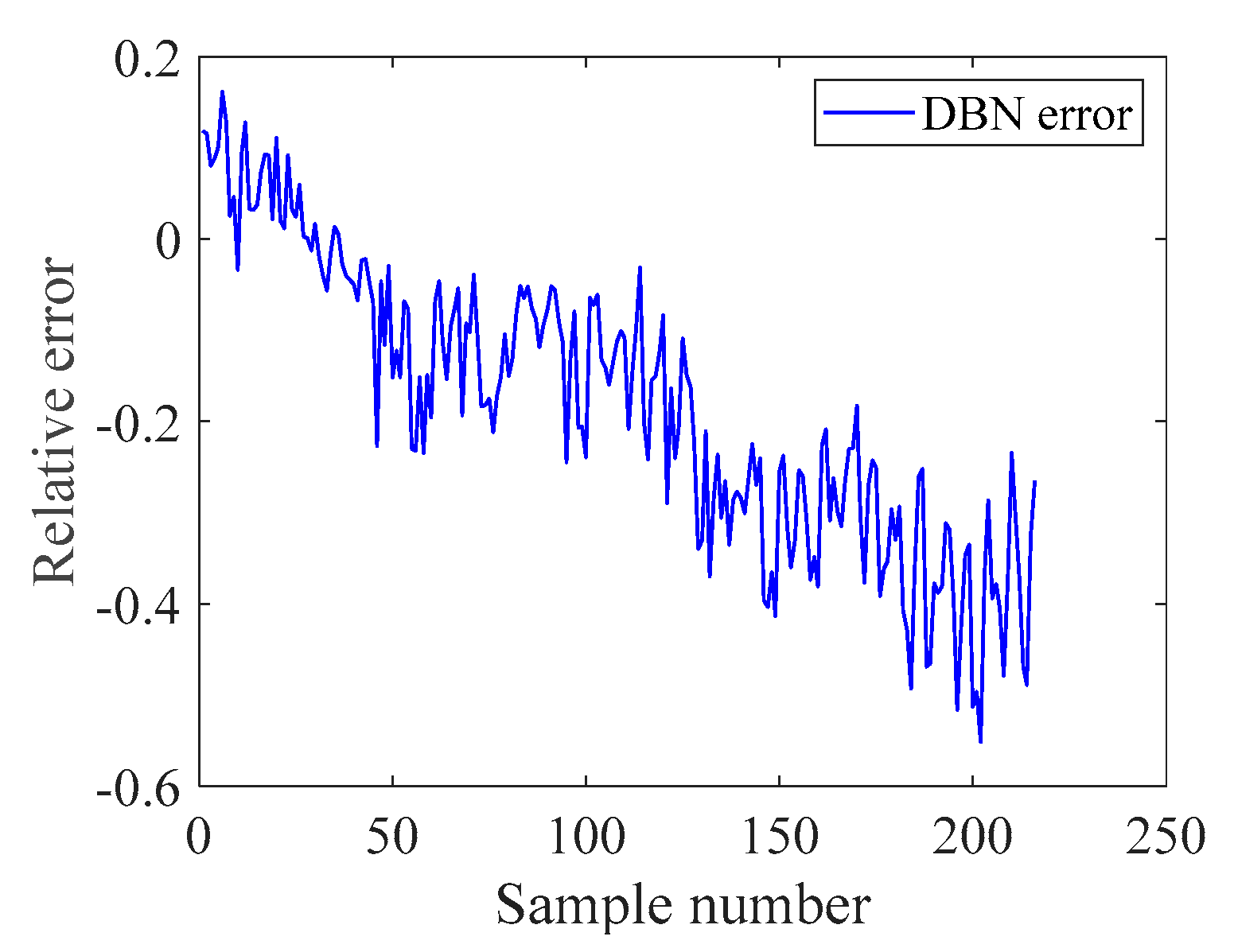
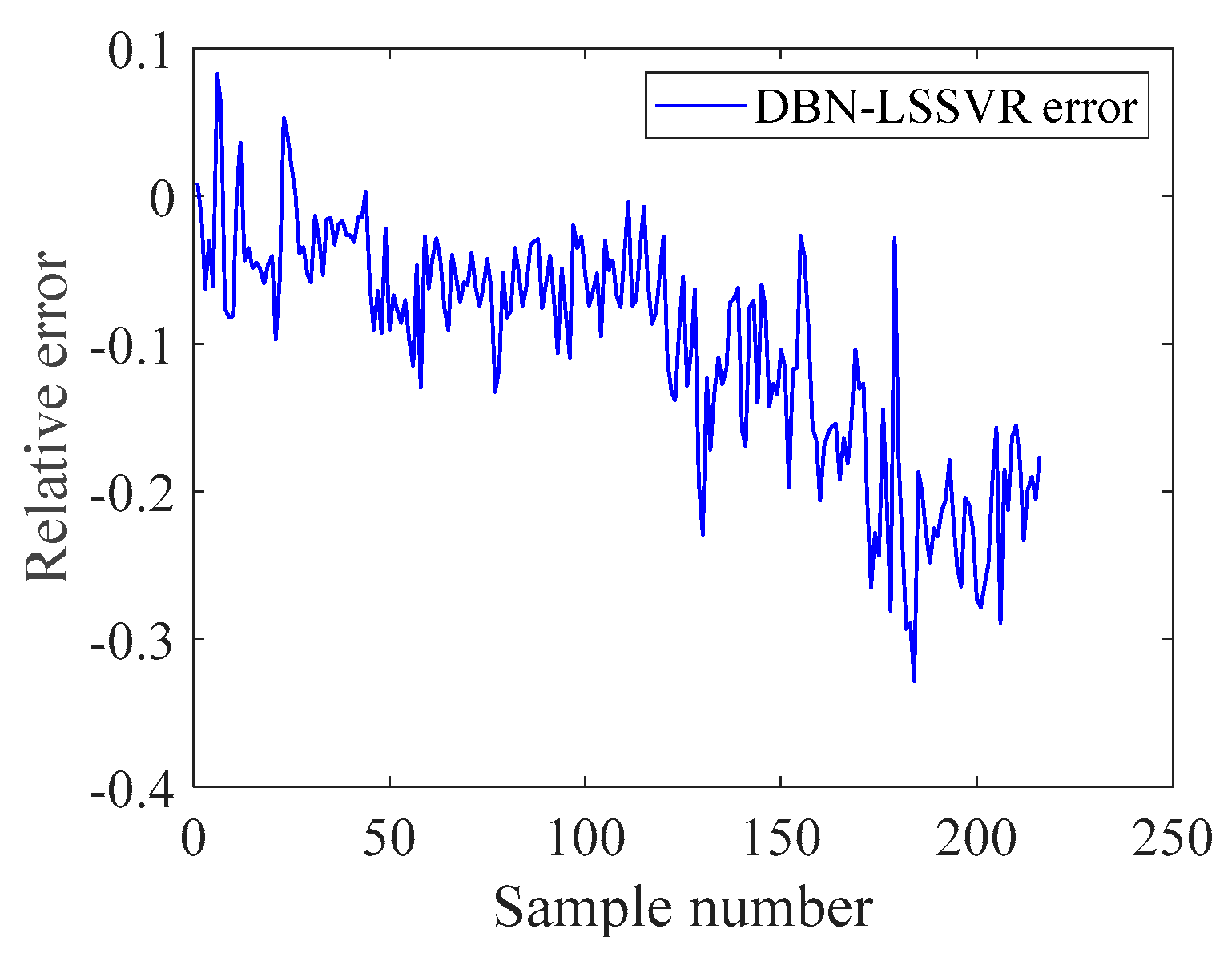
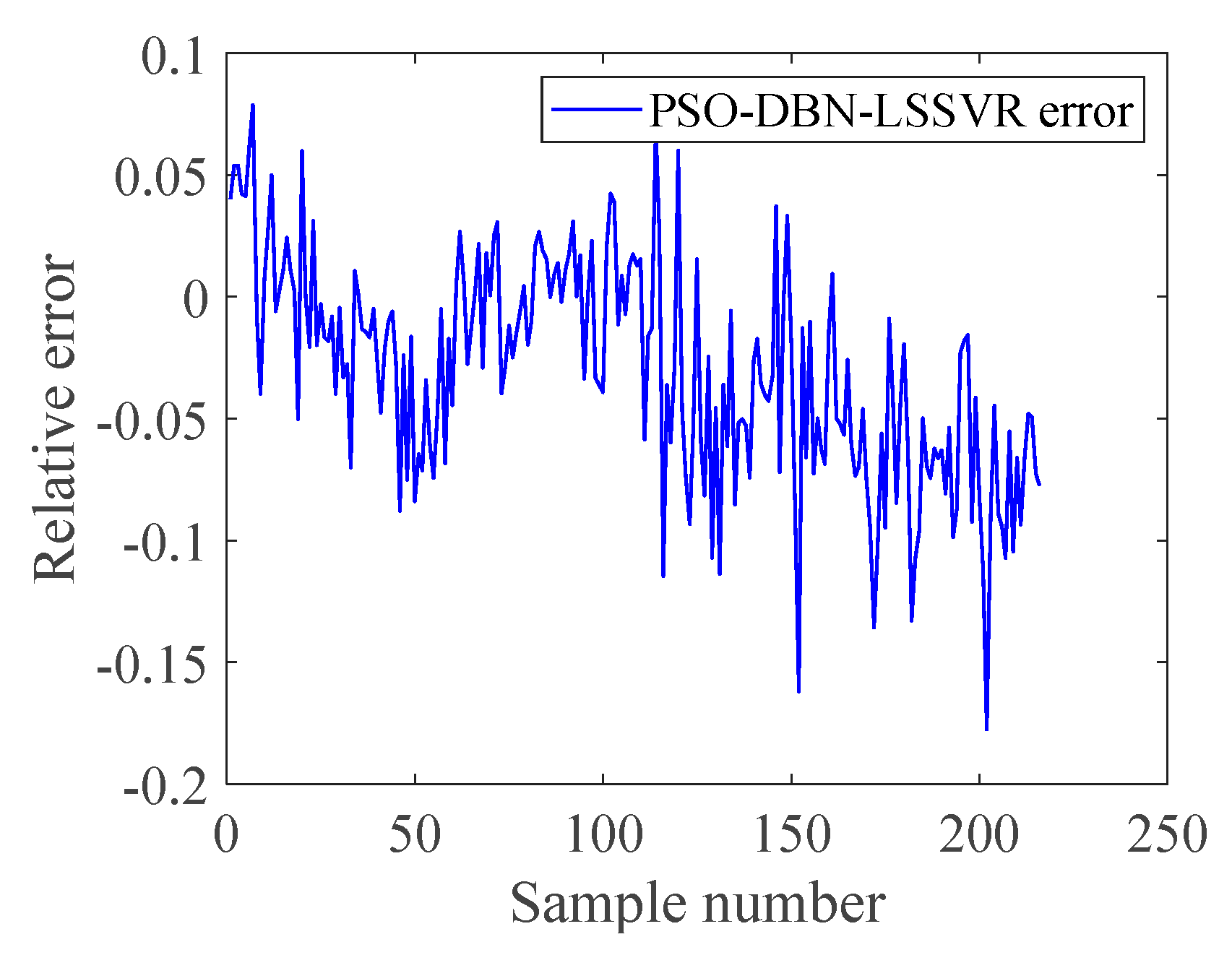
3.2. Results of Experiments
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cabral Pinto, M.M.S.; Ordens, C.M.; de Melo, M.T.C.; Inácio, M.; Almeida, A.; Pinto, E.; da Silva, E.A.F. An inter-disciplinary approach to evaluate human health risks due to long-term exposure to contaminated groundwater near a chemical complex. Exp. Health 2020, 12, 199–214. [Google Scholar] [CrossRef]
- Cabral-Pinto, M.M.S.; Marinho-Reis, A.P.; Almeida, A.; Ordens, C.M.; Silva, M.M.; Freitas, S.; da Silva, E.A.F. Human predisposition to cognitive impairment and its relation with environmental exposure to potentially toxic elements. Environ. Geochem. Health 2018, 40, 1767–1784. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Che, D.L.; Pham, V.T. Application of a Neural Network Technique for Prediction of the Water Quality Index in the Dong Nai River, Vietnam. J. Environ. Sci. Eng. B 2016, 7, 363–370. [Google Scholar]
- Lai, Y.C.; Yang, C.P.; Hsieh, C.Y.; Wu, C.Y.; Kao, C.M. Evaluation of non-point source pollution and river water quality using a multimedia two-model system. J. Hyd. 2011, 409, 583–595. [Google Scholar] [CrossRef]
- Huang, J.; Liu, N.; Wang, M.; Yan, K. Application WASP model on validation of reservoir-drinking water source protection areas delineation. In Proceedings of the 2010 3rd International Conference on Biomedical Engineering and Informatics, Yantai, China, 16–18 October 2010; pp. 3031–3035. [Google Scholar]
- Warren, I.; Bach, H. MIKE21: A modeling system for estuaries, coastal waters and seas. Environ. Soft. 1992, 7, 229–240. [Google Scholar] [CrossRef]
- Hayes, D.F.; Labadie, J.W.; Sanders, T.G. Enhancing water quality in hydropower system operations. Water Resour. Res. 1998, 34, 471–483. [Google Scholar] [CrossRef]
- Tang, G.; Li, J.; Zhu, Z.; Li, Z.; Nerry, F. Two-dimensional water environment numerical simulation research based on EFDC in Mudan River, Northeast China. In Proceedings of the 2015 IEEE European Modelling Symposium (EMS), Madrid, Spain, 6–8 October 2015; pp. 238–243. [Google Scholar]
- Aly, A.H.; Peralta, R.C. Optimal Design of Aquifer Cleanup Systems under Uncertainty Using a Neural Network and a Genetic Algorithm. Water Resour. Res. 1999, 35, 2523–2532. [Google Scholar] [CrossRef]
- Tirabassi, M.A. A statistically based mathematical water quality model for a non-estuarine river system. J. Am. Water Resour. Assoc. 1971, 7, 1221–1237. [Google Scholar] [CrossRef]
- Hu, L.; Zhang, C.; Hu, C.; Jiang, G. Use of grey system for assessment of drinking water quality: A case S study of Jiaozuo city, China. In Proceedings of the IEEE International Conference on Grey Systems and Intelligent Services, Nanjing, China, 10–12 November 2009; pp. 803–808. [Google Scholar]
- Batur, E.; Maktav, D. Assessment of surface water quality by using satellite images fusion based on PCA method in the Lake Gala, Turkey. IEEE Trans. Geosci. Rem. Sens. 2019, 57, 2983–2989. [Google Scholar] [CrossRef]
- Jaloree, S.; Rajput, A.; Sanjeev, G. Decision tree approach to build a model for water quality. Bin. J. Data Min. Net. 2014, 4, 25–28. [Google Scholar]
- Liu, J.T.; Yu, C.; Hu, Z.H.; Zhao, Y.C. Accurate prediction scheme of water quality in smart mariculture with deep Bi-S-SRU learning network. IEEE Access 2020, 8, 24784–24798. [Google Scholar] [CrossRef]
- Khan, K.; See, C.S. Predicting and analyzing water quality using machine learning: A comprehensive model. In Proceedings of the IEEE Long Island Systems Applications and Technology Conference (LISAT), Farmingdale, NY, USA, 29–29 April 2016; pp. 1–6. [Google Scholar]
- Liao, H.; Sun, W. Forecasting and evaluating water quality of Chao Lake based on an improved decision tree method. Proc. Environ. Sci. 2010, 2, 970–979. [Google Scholar] [CrossRef]
- Li, X.; Song, J. A new ANN-Markov chain methodology for water quality prediction. In Proceedings of the International Joint Conference on Neural Networks, Killarney, Ireland, 12–17 July 2015; pp. 1–6. [Google Scholar]
- Ahmed, A.M.; Shah, S.M.A. Application of adaptive neuro-fuzzy inference system (ANFIS) to estimate the biochemical oxygen demand (BOD) of Surma River. J. King. Saud. Univ. Eng. Sci. 2015, 12, 237–243. [Google Scholar] [CrossRef]
- Yan, J.Z.; Xu, Z.B.; Yu, Y.C.; Xu, H.X.; Gao, K.L. Application of a hybrid optimized BP network model to estimate water quality parameters of Beihai Lake in Beijing. Appl. Sci. 2019, 9, 1863. [Google Scholar] [CrossRef]
- Yan, L.; Qian, M. AP-LSSVM modeling for water quality prediction. In Proceedings of the 31st Chinese Control Conference, Hefei, China, 25–27 July 2012; pp. 6928–6932. [Google Scholar]
- Solanki, A.; Aggarwal, H.; Khare, K. Predictive analysis of water quality parameters using deep learning. Int. J. Comput. Appl. 2015, 125, 975–8887. [Google Scholar] [CrossRef]
- Ghesu, F.C. Marginal space deep learning: Efficient architecture for volumetric image parsing. IEEE Trans. Med. Imag. Vol. 2016, 35, 1217–1228. [Google Scholar] [CrossRef]
- Tu, Y.; Du, J.; Lee, C. Speech enhancement based on teacher–student deep learning using improved speech presence probability for noise-robust speech recognition. IEEE/ACM Trans. Audio Speech Lang Process. 2019, 27, 2080–2091. [Google Scholar] [CrossRef]
- Lee, K.P.; Wu, B.H.; Peng, S.L. Deep-learning-based fault detection and diagnosis of air-handling units. Build. Environ. 2019, 157, 24–33. [Google Scholar] [CrossRef]
- Sun, C.; Ma, M.; Zhao, Z.; Tian, S.; Yan, R.; Chen, X. Deep transfer learning based on sparse autoencoder for remaining useful life prediction of tool in manufacturing. IEEE Trans. Ind. Inf. 2019, 15, 2416–2425. [Google Scholar] [CrossRef]
- Mughees, A.; Tao, L. Multiple deep-belief-network-based spectral-spatial classification of hyperspectral images. Tsinghua Sci. Technol. 2019, 24, 183–194. [Google Scholar] [CrossRef]
- Karimi, M.; Majidi, M.; MirSaeedi, H.; Arefi, M.M.; Oskuoee, M. A novel application of deep belief networks in learning partial discharge patterns for classifying corona, surface, and internal discharges. IEEE Trans. Ind. Electron. 2020, 67, 3277–3287. [Google Scholar] [CrossRef]
- Huang, W.; Song, G.; Hong, H.; Xie, K. Deep architecture for traffic flow prediction: Deep belief networks with multitask learning. IEEE Trans. Intell. Trans. Syst. 2014, 15, 2191–2210. [Google Scholar] [CrossRef]
- Zhu, K.; Xun, P.; Li, W.; Li, Z.; Zhou, R. Prediction of passenger flow in urban rail transit based on big data analysis and deep learning. IEEE Access 2019, 7, 142272–142279. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhou, X.; Wan, S.; Choo, K.R. Deep belief network for meteorological time series prediction in the Internet of things. IEEE Int. Things J. 2019, 6, 4369–4376. [Google Scholar] [CrossRef]
- Marir, N.; Wang, H.; Feng, G.; Li, B.; Jia, M. Distributed abnormal behavior detection approach based on deep belief network and ensemble SVM using spark. IEEE Access 2018, 6, 59657–59671. [Google Scholar] [CrossRef]
- Fadlullah, Z.M.; Tang, F.; Mao, B.; Liu, J.; Kato, N. On intelligent traffic control for large-scale heterogeneous networks: A value matrix-based deep learning approach. IEEE Commun. Lett. 2018, 22, 2479–2482. [Google Scholar] [CrossRef]
- Bengio, Y. Learning deep architectures for AI. Found. Trends Mach. Learn. 2009, 2, 1–127. [Google Scholar] [CrossRef]
- Nicolas, L.R.; Yoshua, B. Representational power of restricted boltzmann machines and deep belief networks. Neural Comput. 2008, 20, 1631–1649. [Google Scholar]
- Hinton, G.E. Training products of experts by minimizing contrastive divergence. Neural Comput. 2002, 14, 1771–1800. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Xu, L.Q.; Liu, S.Y. Water quality prediction model based on APSO-WLSSVR. Eng. Sci. 2014, 42, 80–86. [Google Scholar]
| Time | Original Value (mg/L) | BP Value (mg/L) | LSSVR Value (mg/L) | DBN Value (mg/L) | DBN-LSSVR Value (mg/L) | PSO-DBN-LSSVR Value (mg/L) |
|---|---|---|---|---|---|---|
| 2019-02-20 00:00 | 13.22 | 8.6979 | 10.6828 | 10.1474 | 11.7031 | 12.5979 |
| 2019-02-20 04:00 | 13 | 9.1988 | 11.0839 | 11.0232 | 12.3903 | 12.9361 |
| 2019-02-20 08:00 | 13.43 | 8.7839 | 11.7840 | 10.2788 | 11.6919 | 12.5109 |
| 2019-02-20 12:00 | 13.14 | 9.2670 | 10.2441 | 11.1805 | 12.7838 | 12.9132 |
| 2019-02-20 16:00 | 13.2 | 8.7083 | 10.6196 | 10.6156 | 12.3741 | 12.6128 |
| 2019-02-20 20:00 | 13.08 | 9.5872 | 10.6417 | 12.1926 | 12.5264 | 13.1486 |
| 2019-02-21 00:00 | 12.78 | 9.6111 | 10.6462 | 12.1894 | 12.4182 | 13.1224 |
| 2019-02-21 04:00 | 12.92 | 9.3237 | 10.8038 | 11.4544 | 12.3650 | 12.9969 |
| 2019-02-21 08:00 | 12.99 | 9.0675 | 10.1418 | 10.9945 | 12.0069 | 12.6309 |
| 2019-02-21 12:00 | 12.9 | 9.3087 | 11.2319 | 11.6579 | 11.7297 | 12.7271 |
| 2019-02-21 16:00 | 12.59 | 9.1945 | 11.0802 | 11.6121 | 12.0948 | 12.6160 |
| 2019-02-21 20:00 | 12.74 | 9.4751 | 11.5087 | 12.0508 | 12.0435 | 13.0189 |
| 2019-02-22 00:00 | 12.84 | 8.6493 | 10.6011 | 10.3545 | 11.924 | 12.4661 |
| 2019-02-22 04:00 | 12.69 | 9.3122 | 10.7719 | 11.5210 | 11.9509 | 12.9189 |
| 2019-02-22 08:00 | 12.64 | 9.2152 | 10.8572 | 11.3491 | 11.8826 | 12.6472 |
| 2019-02-22 12:00 | 12.52 | 9.3832 | 11.8051 | 12.0268 | 12.0394 | 12.8339 |
| 2019-02-22 16:00 | 12.61 | 9.2937 | 12.0186 | 11.2113 | 11.8317 | 12.9972 |
| 2019-02-22 20:00 | 12.8 | 8.5731 | 9.9736 | 10.4456 | 11.8490 | 12.2926 |
| 2019-02-23 00:00 | 12.62 | 8.6272 | 9.9999 | 10.3224 | 11.8396 | 12.2493 |
| 2019-02-23 04:00 | 12.48 | 8.6526 | 10.1130 | 10.2941 | 11.9544 | 12.3347 |
| 2019-02-23 08:00 | 12.86 | 8.5593 | 9.9745 | 10.1306 | 12.0480 | 12.5404 |
| 2019-02-23 12:00 | 12.93 | 9.0141 | 10.1563 | 10.6933 | 11.2165 | 12.7351 |
| 2019-02-23 16:00 | 12.98 | 9.1184 | 11.0300 | 11.0070 | 11.4718 | 12.9092 |
| 2019-02-23 20:00 | 12.56 | 8.9183 | 10.4243 | 11.2505 | 11.9139 | 12.6163 |
| 2019-02-24 00:00 | 12.82 | 8.8536 | 10.9359 | 10.8929 | 11.7686 | 12.5671 |
| 2019-02-24 04:00 | 12.7 | 8.9303 | 10.5588 | 11.0289 | 11.7201 | 12.5730 |
| 2019-02-24 08:00 | 12.45 | 9.1310 | 10.1881 | 11.4343 | 12.0153 | 12.7089 |
| 2019-02-24 12:00 | 12.31 | 9.0471 | 10.7265 | 11.6779 | 11.6864 | 12.6388 |
| 2019-02-24 16:00 | 12.72 | 9.0342 | 10.1683 | 11.8963 | 11.7758 | 12.9611 |
| 2019-02-24 20:00 | 12.68 | 9.2703 | 10.7973 | 12.0175 | 11.9109 | 12.8765 |
| 2019-02-25 00:00 | 12.49 | 9.1006 | 10.2320 | 11.5420 | 12.0775 | 12.4876 |
| 2019-02-25 04:00 | 12.55 | 9.1129 | 11.3385 | 11.4486 | 12.1674 | 12.6664 |
| 2019-02-25 08:00 | 12.12 | 8.7699 | 10.4254 | 10.6797 | 11.7704 | 12.2886 |
| 2019-02-25 12:00 | 11.95 | 8.7389 | 10.0619 | 10.8228 | 11.0445 | 11.9256 |
| 2019-02-25 16:00 | 12.32 | 8.7616 | 9.6618 | 11.3603 | 11.5961 | 12.4552 |
| 2019-02-25 20:00 | 12.21 | 8.9600 | 9.8102 | 11.5786 | 11.7213 | 12.4258 |
| 2019-02-26 00:00 | 12.27 | 9.0319 | 9.6956 | 11.5797 | 11.4317 | 12.6510 |
| 2019-02-26 04:00 | 12.53 | 9.0776 | 9.4178 | 11.3904 | 11.1997 | 12.5317 |
| 2019-02-26 08:00 | 12.25 | 8.8293 | 9.7401 | 10.8543 | 11.6494 | 12.4592 |
| 2019-02-26 12:00 | 12.15 | 7.3018 | 9.1662 | 9.1761 | 11.1869 | 11.7418 |
| 2019-02-26 16:00 | 11.88 | 8.1665 | 10.2781 | 10.3215 | 10.5819 | 11.8875 |
| 2019-02-26 20:00 | 12.39 | 8.8330 | 9.4702 | 11.4059 | 12.1509 | 12.6760 |
| Model | MAE | MAPE (%) | RMSE | |
|---|---|---|---|---|
| BP | 4.0943 | 36.99 | 4.2746 | 0.2871 |
| LSSVR | 2.8406 | 19.86 | 2.4957 | 0.6142 |
| DBN | 2.6679 | 24.54 | 2.9354 | 0.6454 |
| DBN-LSSVR | 1.1290 | 10.48 | 1.3306 | 0.8714 |
| PSO-DBN-LSSVR | 0.4765 | 4.32 | 0.4877 | 0.9327 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, J.; Gao, Y.; Yu, Y.; Xu, H.; Xu, Z. A Prediction Model Based on Deep Belief Network and Least Squares SVR Applied to Cross-Section Water Quality. Water 2020, 12, 1929. https://doi.org/10.3390/w12071929
Yan J, Gao Y, Yu Y, Xu H, Xu Z. A Prediction Model Based on Deep Belief Network and Least Squares SVR Applied to Cross-Section Water Quality. Water. 2020; 12(7):1929. https://doi.org/10.3390/w12071929
Chicago/Turabian StyleYan, Jianzhuo, Ya Gao, Yongchuan Yu, Hongxia Xu, and Zongbao Xu. 2020. "A Prediction Model Based on Deep Belief Network and Least Squares SVR Applied to Cross-Section Water Quality" Water 12, no. 7: 1929. https://doi.org/10.3390/w12071929
APA StyleYan, J., Gao, Y., Yu, Y., Xu, H., & Xu, Z. (2020). A Prediction Model Based on Deep Belief Network and Least Squares SVR Applied to Cross-Section Water Quality. Water, 12(7), 1929. https://doi.org/10.3390/w12071929






