Utility of Artificial Neural Networks in Modeling Pan Evaporation in Hyper-Arid Climates
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.1.1. Geography, Water Resources and Climate
2.1.2. Available Data
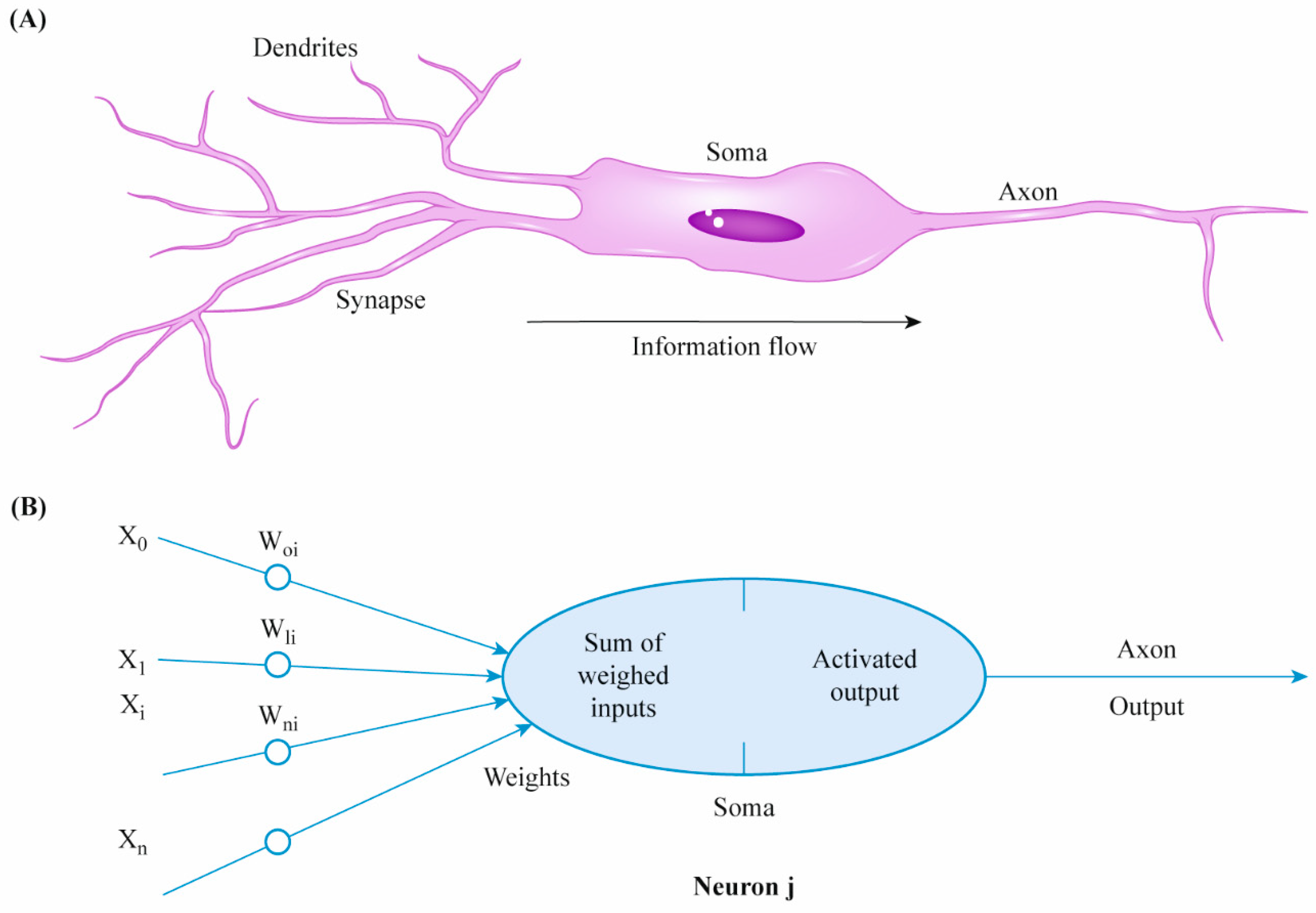
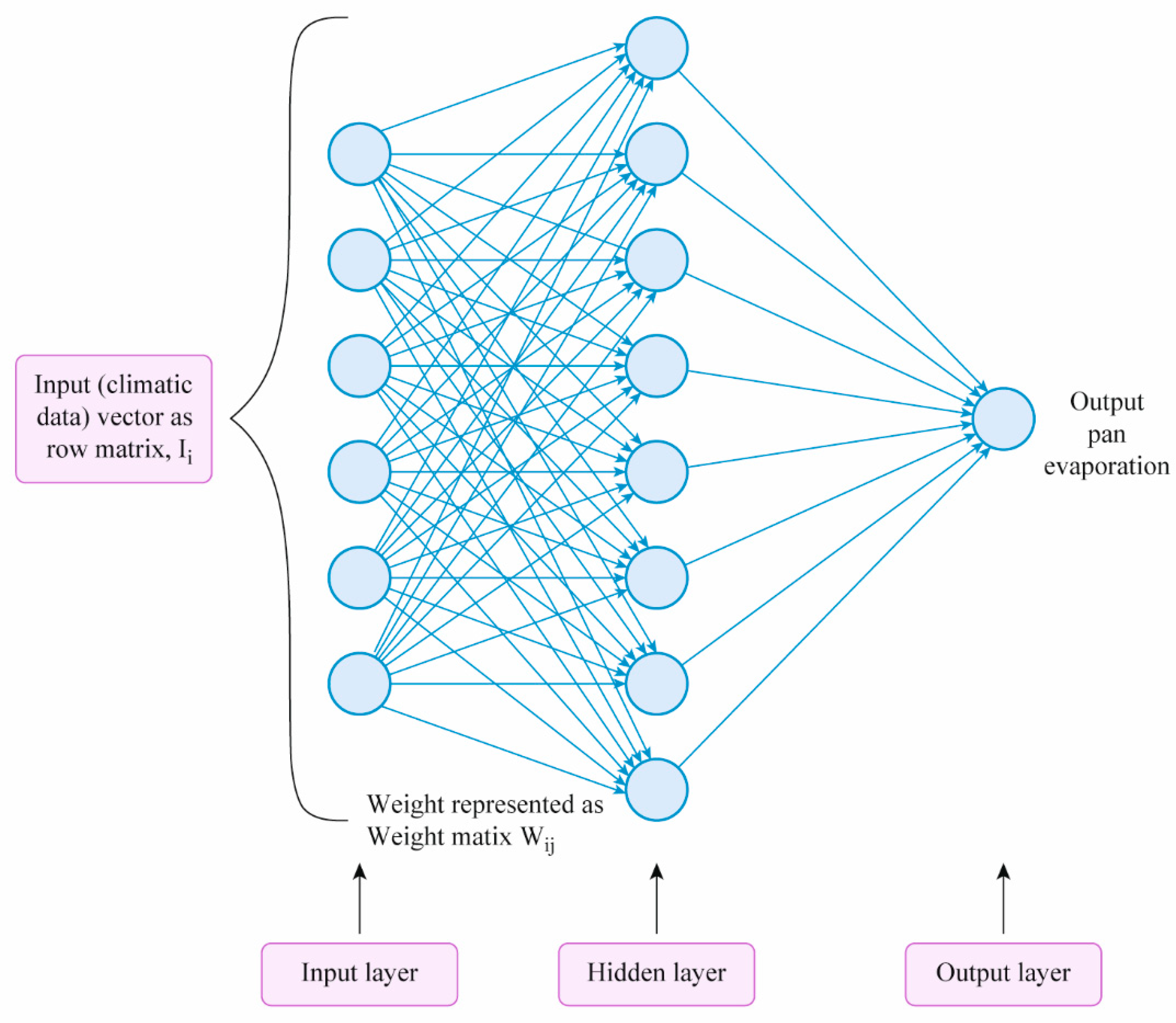
2.2. Artificial Neural Networks
2.2.1. Basic Theory and Architecture
2.2.2. Data Pre-Processing
2.2.3. Training Algorithms
2.3. Sensitivity Analysis
2.4. Validation and Statistical Assessment
3. Results and Discussion
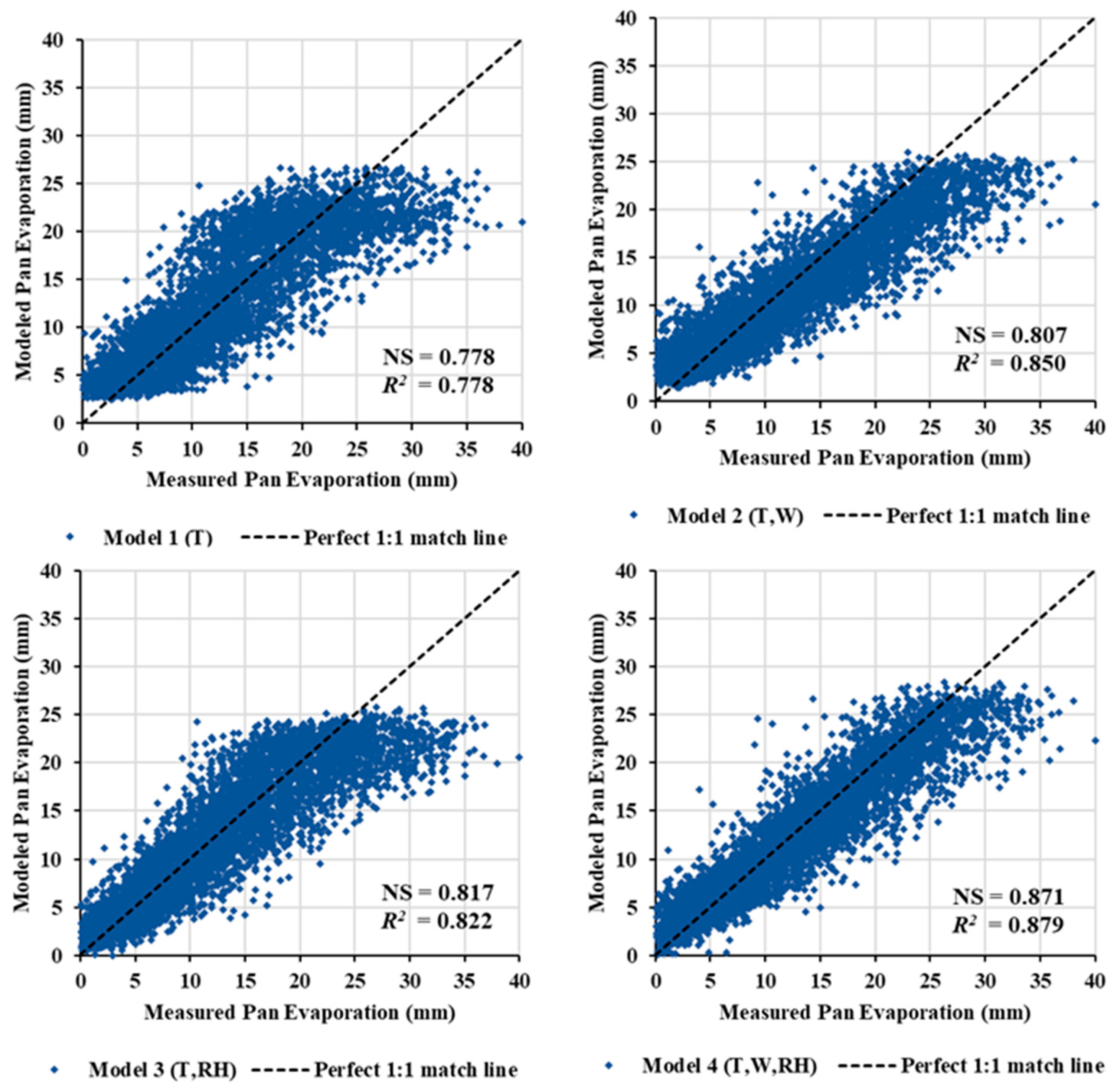
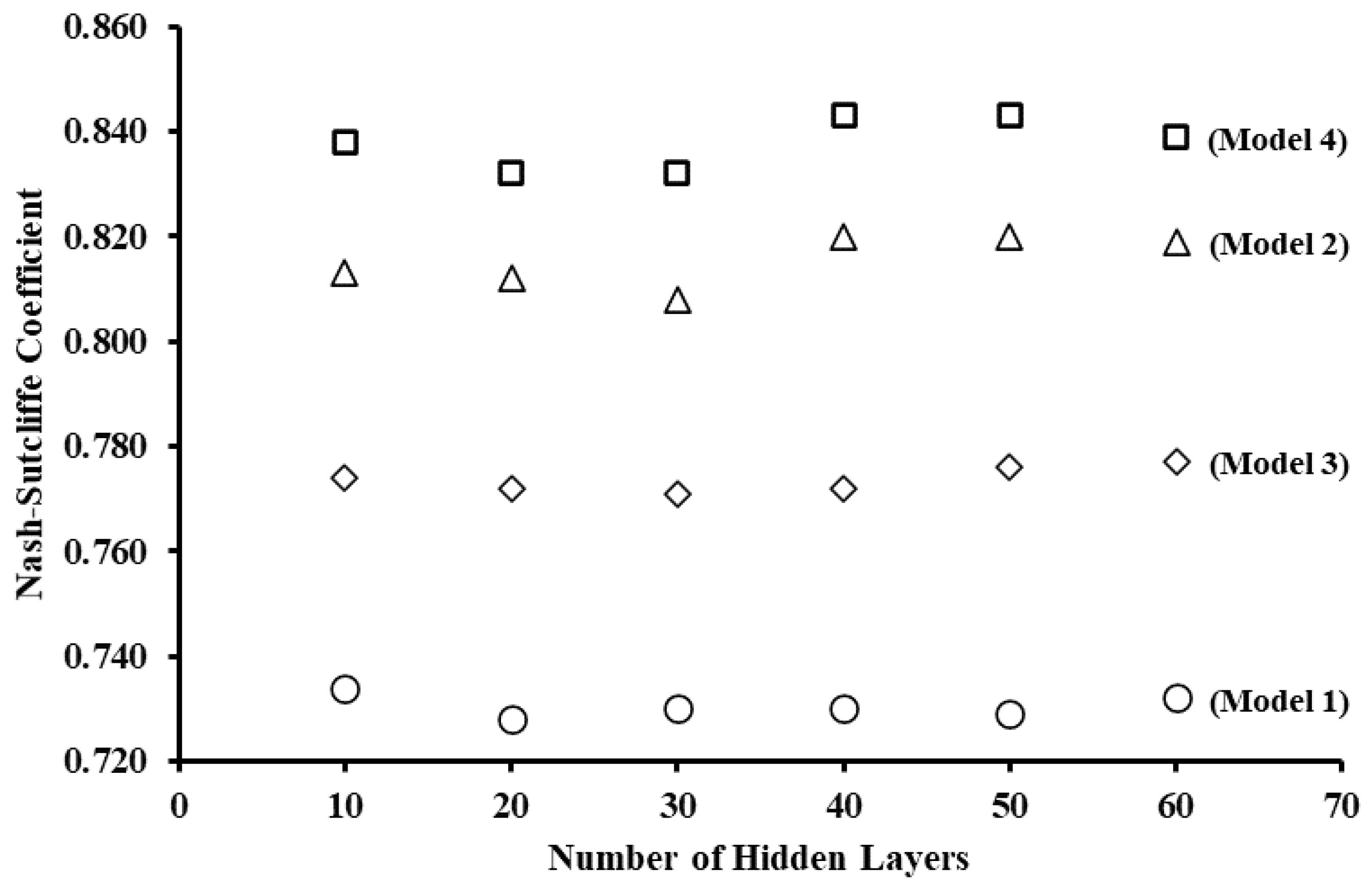
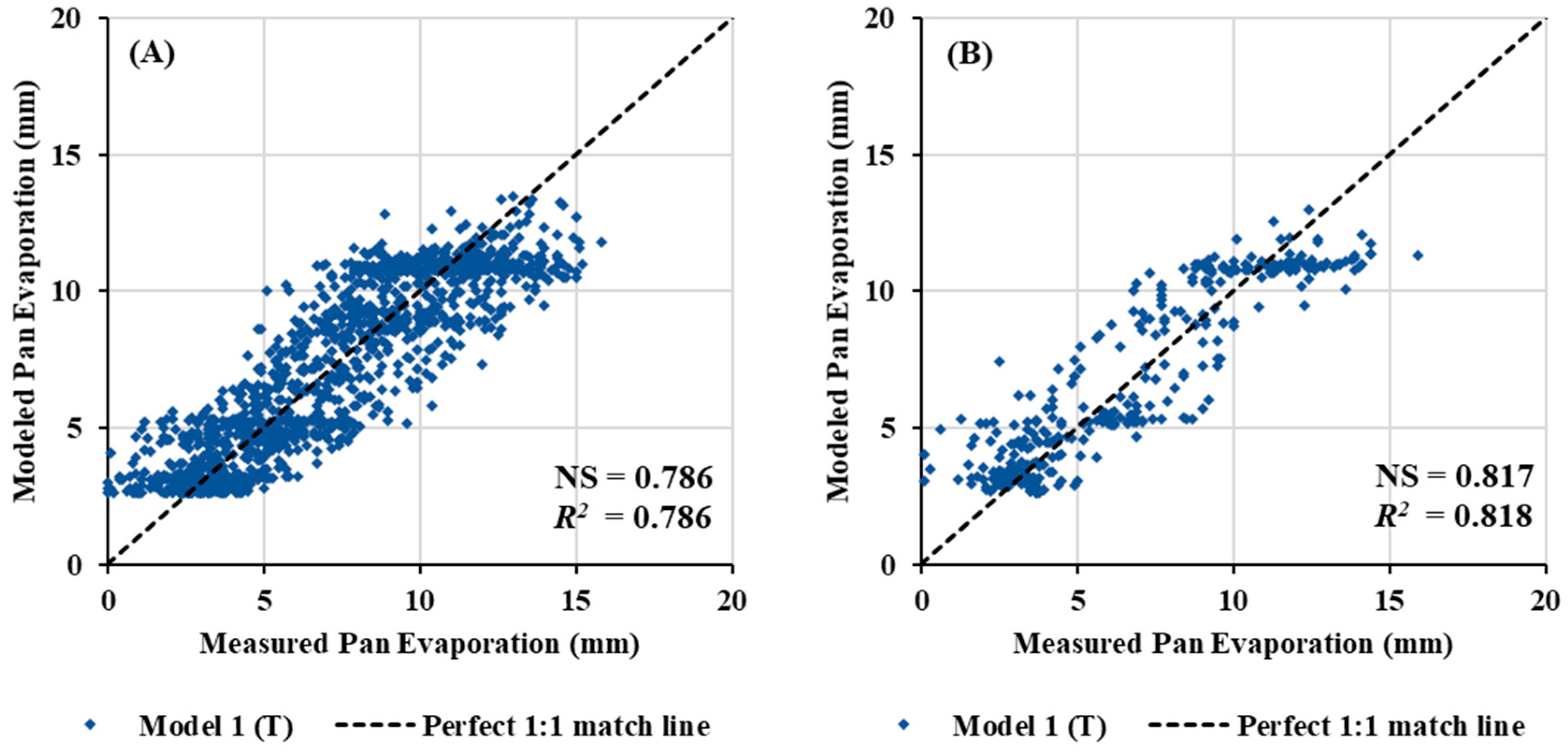
3.1. ANNs Modeling Results
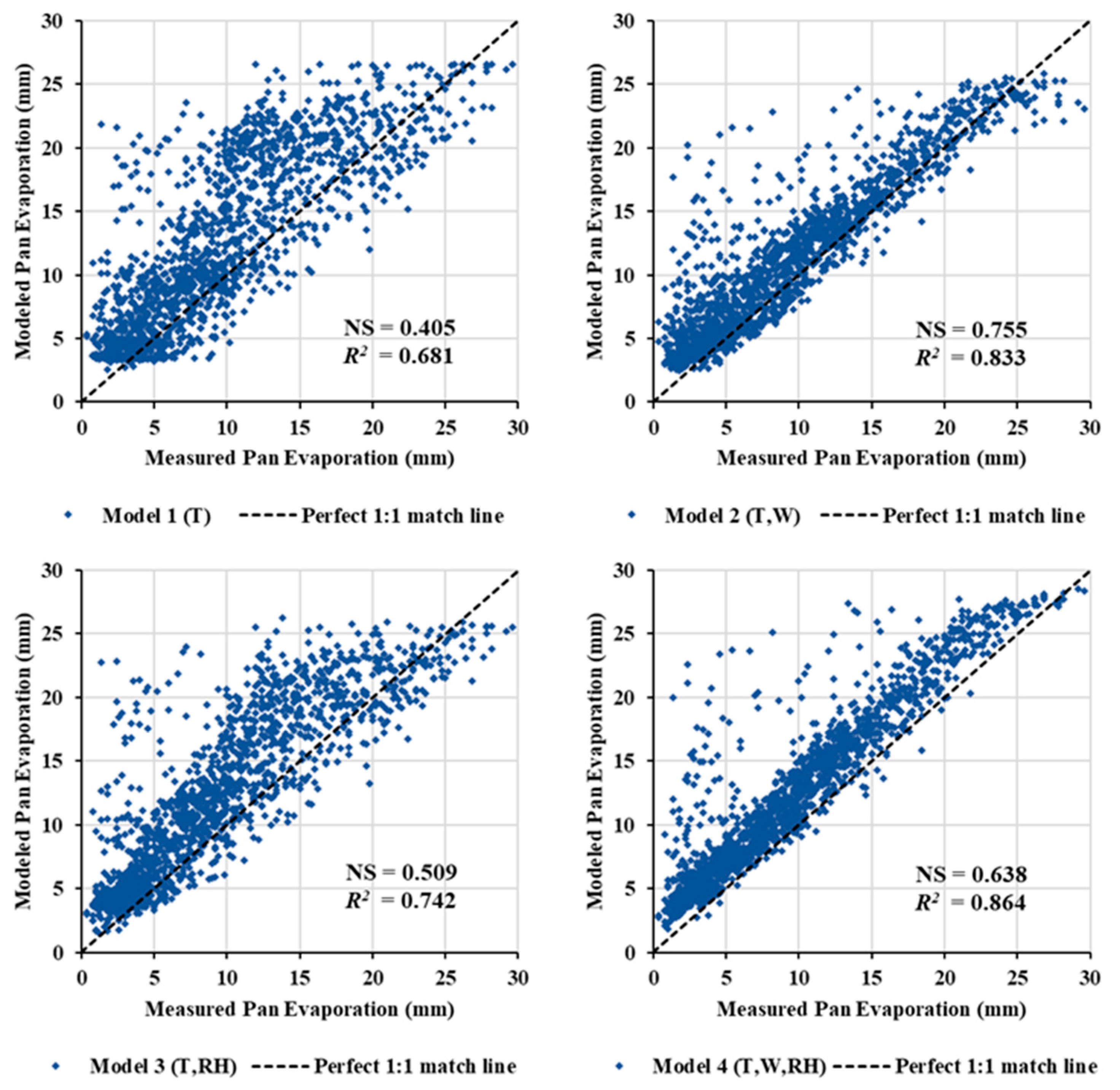
3.2. Model Generalizability
3.3. Agreement with Past Studies
3.4. Comparisons with Conventional Evaporation Estimation Methods
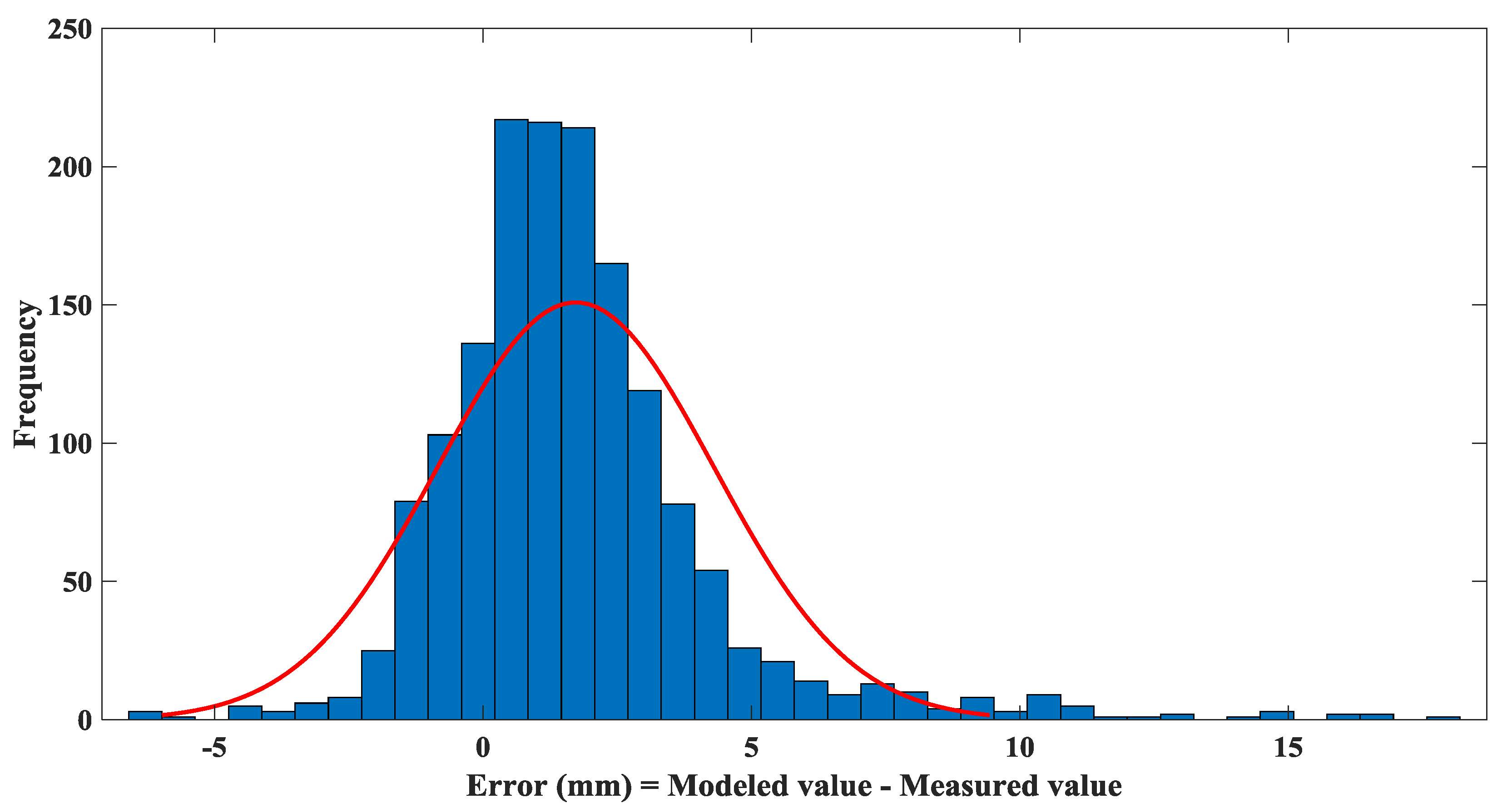
3.5. Model Shortcomings
4. Conclusions
Funding
Conflicts of Interest
References
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988; ISBN 0070108102. [Google Scholar]
- Stanhill, G. Is the Class A evaporation pan still the most practical and accurate meteorological method for determining irrigation water requirements? Agric. For. Meteorol. 2002, 112, 233–236. [Google Scholar] [CrossRef]
- Irmak, S.; Haman, D.Z.; Jones, J.W. Evaluation of class A pan coefficients for estimating reference evapotranspiration in humid location. J. Irrig. Drain. Eng. 2002, 128, 153–159. [Google Scholar] [CrossRef]
- Frevert, D.K.; Hill, R.W.; Braaten, B.C. Estimation of FAO evapotranspiration coefficients. J. Irrig. Drain. Eng. 1983, 109, 265–270. [Google Scholar] [CrossRef]
- Rosenberry, D.O.; Winter, T.C.; Buso, D.C.; Likens, G.E. Comparison of 15 evaporation methods applied to a small mountain lake in the northeastern USA. J. Hydrol. 2007, 340, 149–166. [Google Scholar] [CrossRef]
- Burman, R.D. Intercontinental comparison of evaporation estimates. J. Irrig. Drain. Div. 1976, 102, 109–118. [Google Scholar]
- Rotstayn, L.D.; Roderick, M.L.; Farquhar, G.D. A simple pan-evaporation model for analysis of climate simulations: Evaluation over Australia. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Yang, D. Climatic factors influencing changing pan evaporation across China from 1961 to 2001. J. Hydrol. 2012, 414, 184–193. [Google Scholar] [CrossRef]
- Yang, H.; Li, Z.; Li, M.; Yang, D. Inconsistency in Chinese solar radiation data caused by instrument replacement: Quantification based on pan evaporation observations. J. Geophys. Res. Atmos. 2015, 120, 3191–3198. [Google Scholar] [CrossRef]
- Nourani, V.; Elkiran, G.; Abdullahi, J. Multi-station artificial intelligence based ensemble modeling of reference evapotranspiration using pan evaporation measurements. J. Hydrol. 2019, 577, 123958. [Google Scholar] [CrossRef]
- Qasem, S.N.; Samadianfard, S.; Kheshtgar, S.; Jarhan, S.; Kisi, O.; Shamshirband, S.; Chau, K.-W. Modeling monthly pan evaporation using wavelet support vector regression and wavelet artificial neural networks in arid and humid climates. Eng. Appl. Comput. Fluid Mech. 2019, 13, 177–187. [Google Scholar] [CrossRef] [Green Version]
- Rezaie-Balf, M.; Kisi, O.; Chua, L.H.C. Application of ensemble empirical mode decomposition based on machine learning methodologies in forecasting monthly pan evaporation. Hydrol. Res. 2019, 50, 498–516. [Google Scholar] [CrossRef]
- Bruton, J.M.; McClendon, R.W.; Hoogenboom, G. Estimating daily pan evaporation with artificial neural networks. Trans. ASAE 2000, 43, 491. [Google Scholar] [CrossRef]
- Sudheer, K.P.; Gosain, A.K.; Ramasastri, K.S. Estimating actual evapotranspiration from limited climatic data using neural computing technique. J. Irrig. Drain. Eng. 2003, 129, 214–218. [Google Scholar] [CrossRef]
- Zanetti, S.S.; Sousa, E.F.; Oliveira, V.P.; Almeida, F.T.; Bernardo, S. Estimating evapotranspiration using artificial neural network and minimum climatological data. J. Irrig. Drain. Eng. 2007, 133, 83–89. [Google Scholar] [CrossRef]
- Khoob, A.R. Artificial neural network estimation of reference evapotranspiration from pan evaporation in a semi-arid environment. Irrig. Sci. 2008, 27, 35–39. [Google Scholar] [CrossRef]
- Sudheer, K.P.; Gosain, A.K.; Ramasastri, K.S. A data-driven algorithm for constructing artificial neural network rainfall-runoff models. Hydrol. Process. 2002, 16, 1325–1330. [Google Scholar] [CrossRef]
- Traore, S.; Wang, Y.-M.; Kerh, T. Artificial neural network for modeling reference evapotranspiration complex process in Sudano-Sahelian zone. Agric. Water Manag. 2010, 97, 707–714. [Google Scholar] [CrossRef]
- Kumar, M.; Raghuwanshi, N.S.; Singh, R. Artificial neural networks approach in evapotranspiration modeling: A review. Irrig. Sci. 2011, 29, 11–25. [Google Scholar] [CrossRef]
- Kişi, Ö. Daily pan evaporation modelling using multi-layer perceptrons and radial basis neural networks. Hydrol. Process. Int. J. 2009, 23, 213–223. [Google Scholar] [CrossRef]
- Tabari, H.; Marofi, S.; Sabziparvar, A.-A. Estimation of daily pan evaporation using artificial neural network and multivariate non-linear regression. Irrig. Sci. 2010, 28, 399–406. [Google Scholar] [CrossRef]
- Keskin, M.E.; Terzi, Ö. Artificial neural network models of daily pan evaporation. J. Hydrol. Eng. 2006, 11, 65–70. [Google Scholar] [CrossRef]
- Dou, X.; Yang, Y. Evapotranspiration estimation using four different machine learning approaches in different terrestrial ecosystems. Comput. Electron. Agric. 2018, 148, 95–106. [Google Scholar] [CrossRef]
- Almedeij, J. Modeling rainfall variability over urban areas: A case study for Kuwait. Sci. World J. 2012, 2012. [Google Scholar] [CrossRef] [Green Version]
- Almedeij, J. Modeling pan evaporation for Kuwait by multiple linear regression. Sci. World J. 2012, 2012. [Google Scholar] [CrossRef] [Green Version]
- Almedeij, J. Modeling pan evaporation for kuwait using multiple linear regression and time-series techniques. Am. J. Appl. Sci. 2016, 13, 739–747. [Google Scholar] [CrossRef] [Green Version]
- Almedeij, J. Thornthwaite-Holzman model for a wide range of daily evaporation rates. Int. J. Water 2017, 11, 315–327. [Google Scholar] [CrossRef]
- Dawson, C.W.; Wilby, R. An artificial neural network approach to rainfall-runoff modelling. Hydrol. Sci. J. 1998, 43, 47–66. [Google Scholar] [CrossRef]
- Rao, V.B.; Rao, H. C++, Neural Networks and Fuzzy Logic; Mis Press: New York, NY, USA, 1995; ISBN 1558515526. [Google Scholar]
- Hegazy, T.; Ayed, A. Neural network model for parametric cost estimation of highway projects. J. Constr. Eng. Manag. 1998, 124, 210–218. [Google Scholar] [CrossRef]
- Campolo, M.; Andreussi, P.; Soldati, A. River flood forecasting with a neural network model. Water Resour. Res. 1999, 35, 1191–1197. [Google Scholar] [CrossRef]
- Adeloye, A.J.; De Munari, A. Artificial neural network based generalized storage–yield–reliability models using the Levenberg–Marquardt algorithm. J. Hydrol. 2006, 326, 215–230. [Google Scholar] [CrossRef]
- Hagan, M.T.; Menhaj, M.B. Training feedforward networks with the Marquardt algorithm. IEEE Trans. Neural Netw. 1994, 5, 989–993. [Google Scholar] [CrossRef] [PubMed]
- Khaki, M.; Yusoff, I.; Islami, N. Application of the Artificial Neural Network and Neuro-fuzzy System for Assessment of Groundwater Quality. Clean–Soil Air Water 2015, 43, 551–560. [Google Scholar] [CrossRef]
- Kişi, Ö. Streamflow forecasting using different artificial neural network algorithms. J. Hydrol. Eng. 2007, 12, 532–539. [Google Scholar] [CrossRef]
- Bishop, C.M. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995; ISBN 0198538642. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Alsumaiei, A.A. Monitoring Hydrometeorological Droughts Using a Simplified Precipitation Index. Climate 2020, 8, 19. [Google Scholar] [CrossRef] [Green Version]
- Salem, B.B. Arid Zone Forestry: A Guide for Field Technicians; Food and Agriculture Organization (FAO): Rome, Italy, 1989; ISBN 9251028095. [Google Scholar]
- Piri, J.; Amin, S.; Moghaddamnia, A.; Keshavarz, A.; Han, D.; Remesan, R. Daily pan evaporation modeling in a hot and dry climate. J. Hydrol. Eng. 2009, 14, 803–811. [Google Scholar] [CrossRef]
- Moghaddamnia, A.; Gousheh, M.G.; Piri, J.; Amin, S.; Han, D. Evaporation estimation using artificial neural networks and adaptive neuro-fuzzy inference system techniques. Adv. Water Resour. 2009, 32, 88–97. [Google Scholar] [CrossRef]
- Abusada, S.M. The Essentials of Groundwater Resources of Kuwait. Kuwait Inst. Sci. Res. Rep. No. KISR 1988, 2665. [Google Scholar]
- Brutsaert, W. Evaluation of some practical methods of estimating evapotranspiration in arid climates at low latitudes. Water Resour. Res. 1965, 1, 187–191. [Google Scholar] [CrossRef]
- Linacre, E.T. Estimating US Class A pan evaporation from few climate data. Water Int. 1994, 19, 5–14. [Google Scholar] [CrossRef]
- Shirsath, P.B.; Singh, A.K. A comparative study of daily pan evaporation estimation using ANN, regression and climate based models. Water Resour. Manag. 2010, 24, 1571–1581. [Google Scholar] [CrossRef]



| Meteorological Variable | Mean | Standard Deviation | Minimum | First Quartile | Median | Third Quartile | Maximum |
|---|---|---|---|---|---|---|---|
| Max. Temperature, Tmax (°C) | 34.0 | 10.5 | 9.0 | 24.2 | 35.3 | 44.0 | 51.5 |
| Min. Temperature, Tmin (°C) | 19.6 | 8.8 | −1.6 | 12.1 | 20.4 | 27.4 | 39.7 |
| Avg. Temperature, Tavg (°C) | 27.0 | 9.6 | 5.1 | 18.1 | 27.9 | 36.3 | 44.1 |
| Max. Relative Humidity, RHmax | 56.2 | 27.2 | 9.0 | 30.0 | 55.0 | 82.0 | 100.0 |
| Min. Relative Humidity, RHmin | 18.5 | 15.5 | 0.0 | 7.0 | 12.7 | 25.0 | 95.0 |
| Avg. Relative Humidity, RHavg | 37.4 | 20.2 | 5.5 | 19.0 | 34.2 | 53.5 | 97.5 |
| Avg. Wind Speed, W (m/s) | 4.1 | 1.9 | 0.1 | 2.6 | 3.8 | 5.2 | 11.5 |
| Pan Evaporation, Epan (mm) | 11.2 | 7.6 | 0.1 | 4.8 | 9.6 | 16.3 | 40.0 |
| ANN Model No. | Meteorological Variable Combination |
|---|---|
| Model 1 | Tavg |
| Model 2 | Tavg and W |
| Model 3 | Tavg and RHavg, |
| Model 4 | Tavg, W, and RHavg |
| Model No. | Statistical Metric | Training Period | Validation Period |
|---|---|---|---|
| Model 1 | Pearson correlation | 0.882 | 0.825 |
| R2 | 0.778 | 0.681 | |
| NS | 0.778 | 0.405 | |
| MAE (mm) | 2.771 | 3.609 | |
| Model 2 | Pearson correlation | 0.922 | 0.913 |
| R2 | 0.85 | 0.833 | |
| NS | 0.807 | 0.755 | |
| MAE (mm) | 2.517 | 2.155 | |
| Model 3 | Pearson correlation | 0.907 | 0.862 |
| R2 | 0.822 | 0.742 | |
| NS | 0.817 | 0.509 | |
| MAE (mm) | 2.403 | 3.284 | |
| Model 4 | Pearson correlation | 0.937 | 0.93 |
| R2 | 0.879 | 0.864 | |
| NS | 0.871 | 0.638 | |
| MAE (mm) | 2.017 | 2.920 |
| Model Parameter | Value |
|---|---|
| Input layers | 2 |
| Hidden layers | 10 |
| Output layers | 1 |
| Training algorithms | Levenberg-Marquardt |
| Number of epochs | 8 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsumaiei, A.A. Utility of Artificial Neural Networks in Modeling Pan Evaporation in Hyper-Arid Climates. Water 2020, 12, 1508. https://doi.org/10.3390/w12051508
Alsumaiei AA. Utility of Artificial Neural Networks in Modeling Pan Evaporation in Hyper-Arid Climates. Water. 2020; 12(5):1508. https://doi.org/10.3390/w12051508
Chicago/Turabian StyleAlsumaiei, Abdullah A. 2020. "Utility of Artificial Neural Networks in Modeling Pan Evaporation in Hyper-Arid Climates" Water 12, no. 5: 1508. https://doi.org/10.3390/w12051508





