Real Time Flow Forecasting in a Mountain River Catchment Using Conceptual Models with Simple Error Correction Scheme
Abstract
:1. Introduction
2. Case Study
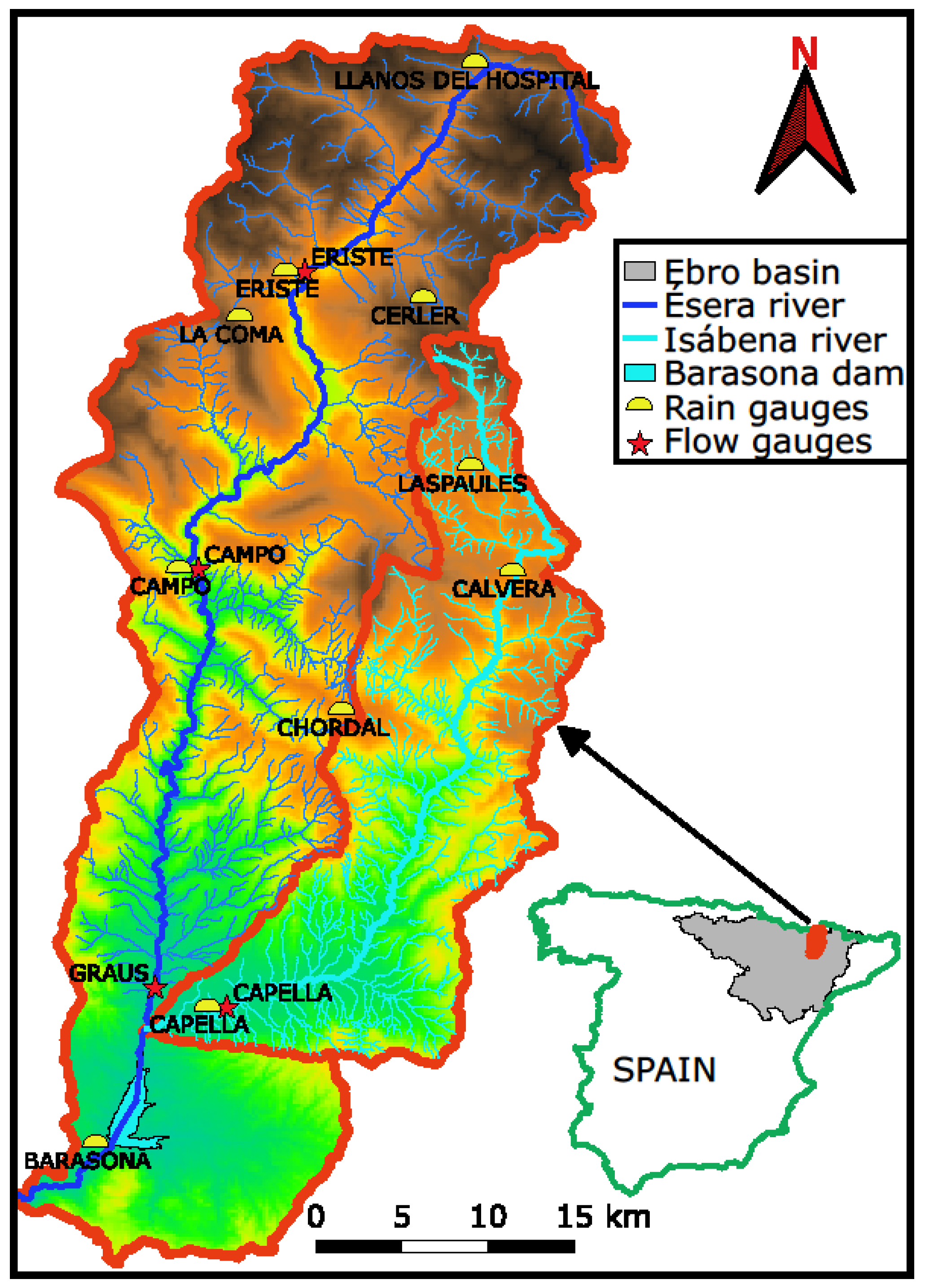
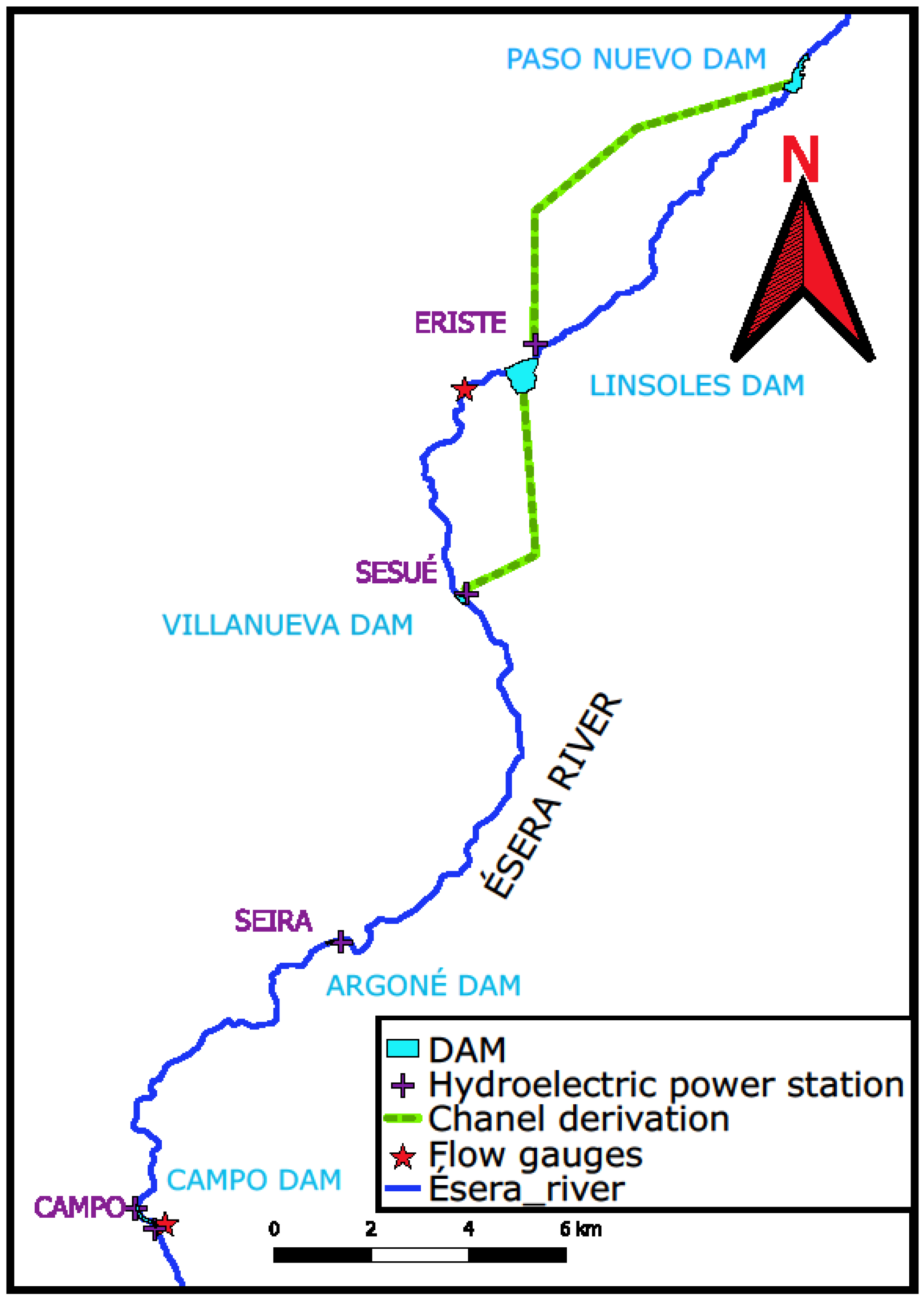
2.1. Catchment Description
2.2. Data Set
3. Real-Time Forecast Modeling
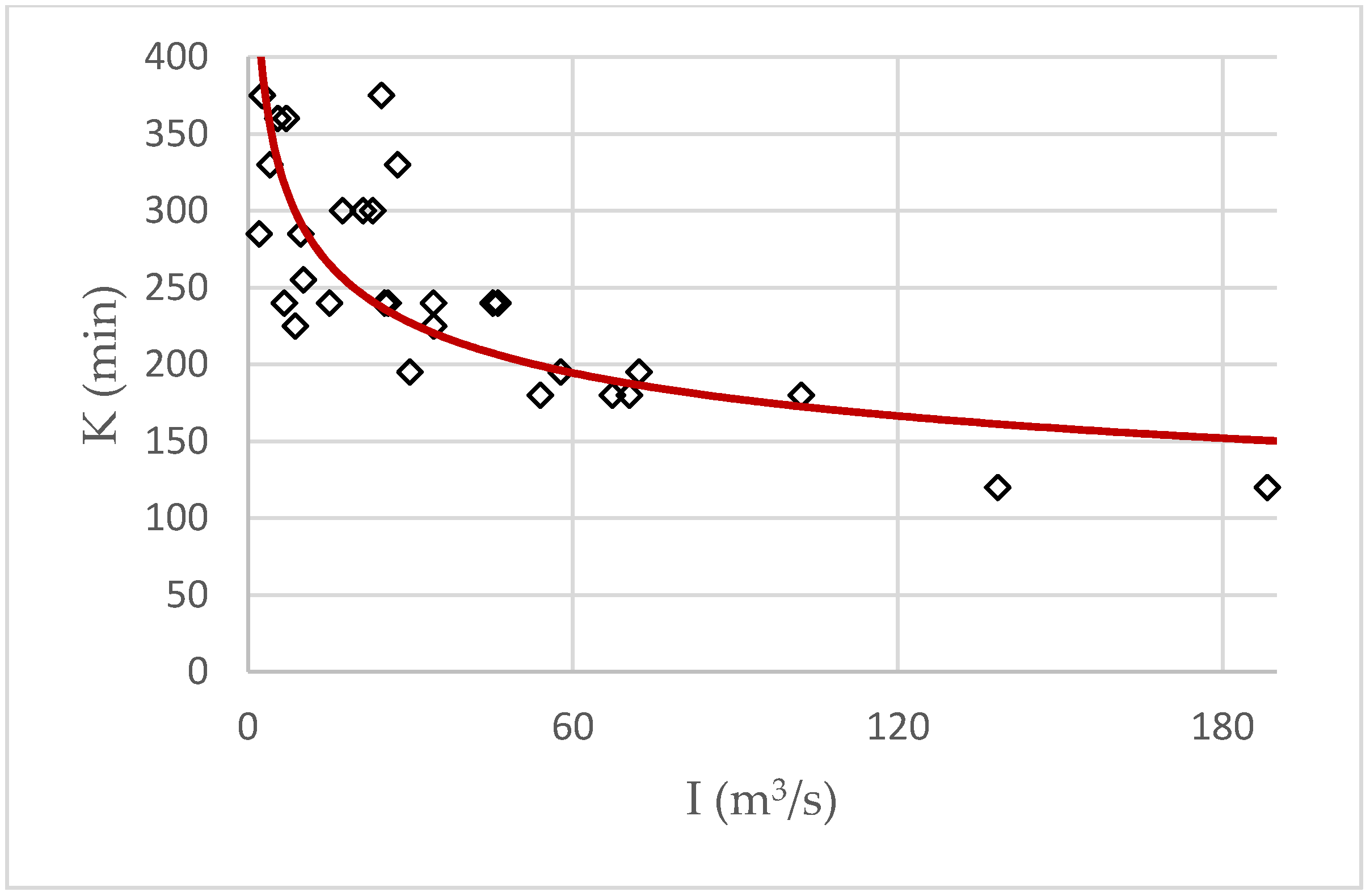
3.1. Model-1 Basic Component
3.2. Model-2 Basic Component
3.3. Error Updating Scheme
3.4. Model Evaluation
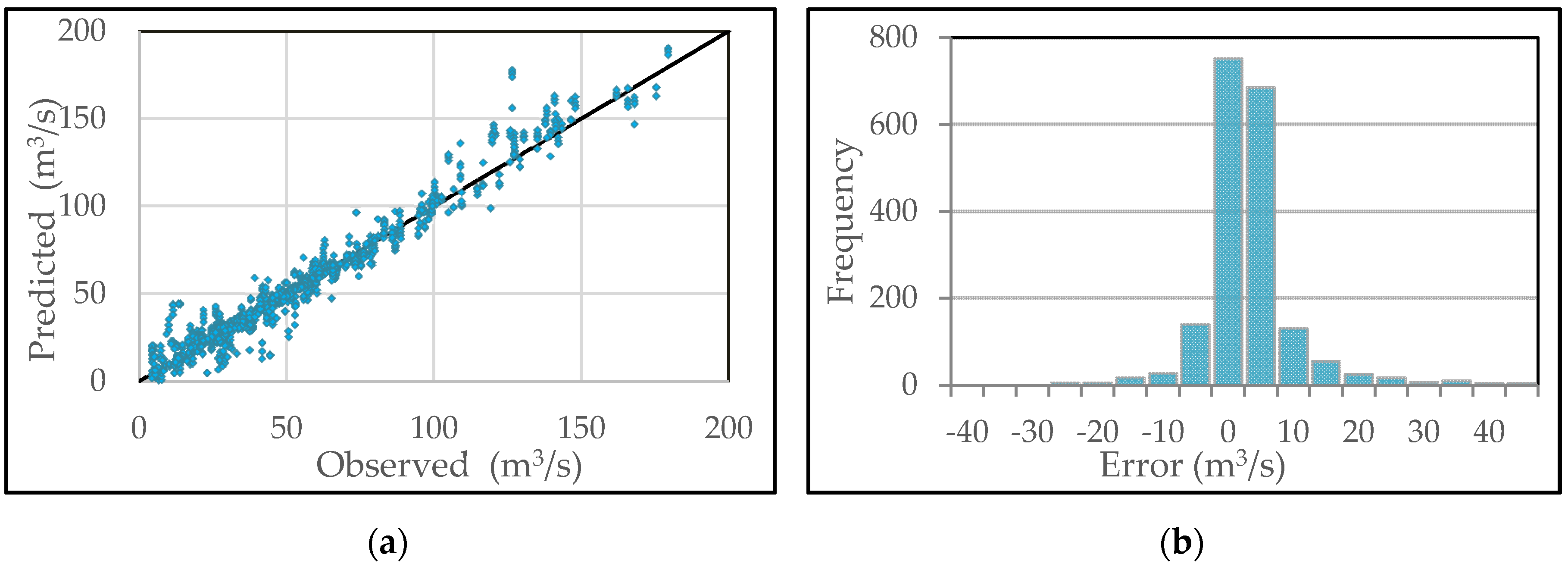
4. Results and Discussion
4.1. Results for Model-1
4.2. Results for Model-2
4.3. Comparison of Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moramarco, T.; Barbetta, S.; Melone, F.; Singh, V.P. A real-time stage Muskingum forecasting model for a site without rating curve. Hydrol. Sci. J. 2006, 51, 66–82. [Google Scholar] [CrossRef]
- Perumal, M.; Moramarco, T.; Barbetta, S.; Melone, F.; Sahoo, B. Real-time flood stage forecasting by Variable Parameter Muskingum Stage hydrograph routing method. Hydrol. Res. 2011, 42, 150–161. [Google Scholar] [CrossRef]
- McCarthy, G. The unit hydrograph and flood routing. In Proceedings of the Conference North Atlantic Divsion, Chapel Hill, NC, USA, 20–25 April 1938. [Google Scholar]
- Clark, C.O. Storage and the Unit Hydrograph. Trans. Am. Soc. Civ. Eng. 1945, 110, 1419–1446. [Google Scholar]
- Te Chow, V. Open-Channel Hydraulics; McGraw-Hill Book Company: New York, NY, USA, 1959; pp. 507–510. [Google Scholar]
- Nash, J.E. The Form of the Instantaneous Unit Hydrograph; International Association of Scientific Hydrology: Wallingford, UK, 1957. [Google Scholar]
- Cunge, J.A. On The Subject Of A Flood Propagation Computation Method (Musklngum Method). J. Hydraul. Res. 1969, 7, 205–230. [Google Scholar] [CrossRef]
- Dooge, J.C.; Strupczewski, W.G.; Napiorkowski, J. Hydrodynamic derivation of storage parameters of the Muskingum model. J. Hydrol. 1982, 54, 371–387. [Google Scholar] [CrossRef]
- Ponce, V.M.; Yevjevich, V. Muskingum-Cunge method with variable parameters. J. Hydraul. Div. 1978, 104, 1663–1667. [Google Scholar] [CrossRef]
- Ponce, V.M.; Theurer, F.D. Accuracy Criteria in Diffusion Routing. J. Hydraul. Eng. 1983, 109, 806–807. [Google Scholar] [CrossRef]
- Kundzewicz, Z.W. Physically based hydrological flood routing methods. Hydrol. Sci. J. 1986, 31, 237–261. [Google Scholar] [CrossRef] [Green Version]
- Singh, V.P. Kinematic Wave Modeling in Water Resources. Surface-Water Hydrology; John Wiley: Chichester, UK, 1996. [Google Scholar]
- Singh, V.P.; Scarlatos, P.D. Analysis of Nonlinear Muskingum Flood Routing. J. Hydraul. Eng. 1987, 113, 61–79. [Google Scholar] [CrossRef]
- Perumal, M. Multilinear Muskingum flood routing method. J. Hydrol. 1992, 133, 259–272. [Google Scholar] [CrossRef]
- Perumal, M. Removing some anomalies of the Muskingum method. Watershed Hydrol. 2003, 6, 180. [Google Scholar]
- Ponce, V.; Changanti, P. Variable-parameter Muskingum-Cunge method revisited. J. Hydrol. 1994, 162, 433–439. [Google Scholar] [CrossRef]
- Tang, X.; Knight, D.W.; Samuels, P. Variable parameter Muskingum-Cunge method for flood routing in a compound channel. J. Hydraul. Res. 1999, 37, 591–614. [Google Scholar] [CrossRef]
- Al-Humoud, J.M.; Esen, I.I. Approximate Methods for the Estimation of Muskingum Flood Routing Parameters. Water Resour. Manag. 2006, 20, 979–990. [Google Scholar] [CrossRef]
- Todini, E. A mass conservative and water storage consistent variable parameter Muskingum-Cunge approach. Hydrol. Earth Syst. Sci. 2007, 11, 1645–1659. [Google Scholar] [CrossRef] [Green Version]
- Brakensiek, D.L. Estimating coefficients for storage flood routing. J. Geophys. Res. Space Phys. 1963, 68, 6471–6474. [Google Scholar] [CrossRef]
- Birkhead, A.; James, C. Muskingum river routing with dynamic bank storage. J. Hydrol. 2002, 264, 113–132. [Google Scholar] [CrossRef]
- Xiaofang, R.; Fanggui, L.; Mei, Y. Discussion of Muskingum method parameter X. Water Sci. Eng. 2008, 1, 16–23. [Google Scholar]
- Perumal, M.; Price, R.K. A fully mass conservative variable parameter McCarthy–Muskingum method: Theory and verification. J. Hydrol. 2013, 502, 89–102. [Google Scholar] [CrossRef]
- O’Donnell, T. A direct three-parameter Muskingum procedure incorporating lateral inflow. Hydrol. Sci. J. 1985, 30, 479–496. [Google Scholar] [CrossRef] [Green Version]
- Kshirsagar, M.; Rajagopalan, B.; Lal, U. Optimal parameter estimation for Muskingum routing with ungauged lateral inflow. J. Hydrol. 1995, 169, 25–35. [Google Scholar] [CrossRef]
- Barbetta, S.; Brocca, L.; Melone, F.; Moramarco, T. On the lateral inflows assessment within a real-time stage monitoring addressed to flood forecasting. In Proceedings of the 4th International Congress on Environmental Modelling and Software, iEMSs 2008, Barcelona, Spain, 7–10 July 2008; Volume 1, pp. 438–445. [Google Scholar]
- Yadav, B.; Perumal, M.; Bárdossy, A. Variable parameter McCarthy–Muskingum routing method considering lateral flow. J. Hydrol. 2015, 523, 489–499. [Google Scholar] [CrossRef]
- Perumal, M. Hydrodynamic derivation of a variable parameter Muskingum method: 1. Theory and solution procedure. Hydrol. Sci. J. 1994, 39, 431–442. [Google Scholar] [CrossRef] [Green Version]
- Perumal, M.; O’Connell, E.; Raju, K.G.R. Field Applications of a Variable-Parameter Muskingum Method. J. Hydrol. Eng. 2001, 6, 196–207. [Google Scholar] [CrossRef]
- Perumal, M.; Sahoo, B. Applicability criteria of the variable parameter Muskingum stage and discharge routing methods. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Gill, M.A. Flood routing by the Muskingum method. J. Hydrol. 1978, 36, 353–363. [Google Scholar] [CrossRef]
- Tung, Y. River Flood Routing by Nonlinear Muskingum Method. J. Hydraul. Eng. 1985, 111, 1447–1460. [Google Scholar] [CrossRef] [Green Version]
- Papamichail, D.M.; Georgiou, P.E. River flood routing by a nonlinear form of the Muskingum method. In Proceedings of the 5th Conference of the Greek Hydrotechnical Association, Larisa, Greece, 3–6 July 1992; pp. 141–149. [Google Scholar]
- Yoon, J.; Padmanabhan, G. Parameter estimation of linear and nonlinear Muskingum models. J. Water Resour. Plan. Manag. 1993, 119, 600–610. [Google Scholar] [CrossRef]
- Mohan, S. Parameter Estimation of Nonlinear Muskingum Models Using Genetic Algorithm. J. Hydraul. Eng. 1997, 123, 137–142. [Google Scholar] [CrossRef]
- Luo, J.; Xie, J. Parameter Estimation for Nonlinear Muskingum Model Based on Immune Clonal Selection Algorithm. J. Hydrol. Eng. 2010, 15, 844–851. [Google Scholar] [CrossRef]
- Kang, L.; Zhang, S. Application of the Elitist-Mutated PSO and an Improved GSA to Estimate Parameters of Linear and Nonlinear Muskingum Flood Routing Models. PLoS ONE 2016, 11, e0147338. [Google Scholar] [CrossRef] [PubMed]
- Geem, Z.W. Parameter Estimation for the Nonlinear Muskingum Model Using the BFGS Technique. J. Irrig. Drain. Eng. 2006, 132, 474–478. [Google Scholar] [CrossRef]
- Chu, H.-J.; Chang, L.-C. Applying Particle Swarm Optimization to Parameter Estimation of the Nonlinear Muskingum Model. J. Hydrol. Eng. 2009, 14, 1024–1027. [Google Scholar] [CrossRef]
- Barati, R. Parameter Estimation of Nonlinear Muskingum Models Using Nelder-Mead Simplex Algorithm. J. Hydrol. Eng. 2011, 16, 946–954. [Google Scholar] [CrossRef]
- Karahan, H.; Gurarslan, G.; Geem, Z.W. Parameter Estimation of the Nonlinear Muskingum Flood-Routing Model Using a Hybrid Harmony Search Algorithm. J. Hydrol. Eng. 2013, 18, 352–360. [Google Scholar] [CrossRef]
- Chen, X.; Chau, K.-W.; Busari, A. A comparative study of population-based optimization algorithms for downstream river flow forecasting by a hybrid neural network model. Eng. Appl. Artif. Intell. 2015, 46, 258–268. [Google Scholar] [CrossRef]
- Latt, Z.Z. Application of Feedforward Artificial Neural Network in Muskingum Flood Routing: A Black-Box Forecasting Approach for a Natural River System. Water Resour. Manag. 2015, 29, 4995–5014. [Google Scholar] [CrossRef]
- Niazkar, M.; Afzali, S.H. Application of New Hybrid Optimization Technique for Parameter Estimation of New Improved Version of Muskingum Model. Water Resour. Manag. 2016, 30, 4713–4730. [Google Scholar] [CrossRef]
- Dong, S.; Su, B.; Zhang, Y. Optimization Estimation of Muskingum Model Parameter Based on Genetic Algorithm. In Recent Advances in Computer Science and Information Engineering; Springer: Berlin/Heidelberg, Germany, 2012; pp. 563–569. [Google Scholar]
- Kucukkoc, I.; Zhang, D.Z. Integrating ant colony and genetic algorithms in the balancing and scheduling of complex assembly lines. Int. J. Adv. Manuf. Technol. 2015, 82, 265–285. [Google Scholar] [CrossRef] [Green Version]
- Bazargan, J.; Norouzi, H. Investigation the Effect of Using Variable Values for the Parameters of the Linear Muskingum Method Using the Particle Swarm Algorithm (PSO). Water Resour. Manag. 2018, 32, 4763–4777. [Google Scholar] [CrossRef]
- Ehteram, M.; Mousavi, S.F.; Karami, H.; Farzin, S.; Singh, V.P.; Chau, K.-W.; El-Shafie, A. Reservoir operation based on evolutionary algorithms and multi-criteria decision-making under climate change and uncertainty. J. Hydroinform. 2018, 20, 332–355. [Google Scholar] [CrossRef]
- Pei, J.; Su, Y.; Zhang, D. Fuzzy energy management strategy for parallel HEV based on pigeon-inspired optimization algorithm. Sci. China Ser. E Technol. Sci. 2016, 60, 425–433. [Google Scholar] [CrossRef]
- Schumm, S.A. Evolution of drainage systems and slopes in badlands at perth amboy, New Jersey. GSA Bull. 1956, 67, 597. [Google Scholar] [CrossRef]
- Fread, D.L. Flow Routing in Handbook of Hydrology; Maidment, D.R., Ed.; McGraw-Hill Inc.: New York, NY, USA, 1993. [Google Scholar]
- McCuen, R.H. Hydrologic Analysis and Design; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Balaz, M.; Danáčová, M.; Szolgay, J. On the use of the Muskingum method for the simulation of flood wave movements. Slovak J. Civ. Eng. 2010, 18, 14–20. [Google Scholar] [CrossRef] [Green Version]
- Franchini, M.; Lamberti, P. A flood routing Muskingum type simulation and forecasting model based on level data alone. Water Resour. Res. 1994, 30, 2183–2196. [Google Scholar] [CrossRef]
- Yadav, P.; Singh, N.; Goel, P.S.; Itabashi-Campbell, R. A framework for reliability prediction during product development process incorporating engineering judgments. Qual. Eng. 2003, 15, 649–662. [Google Scholar] [CrossRef]
- Tayfur, G. Soft Computing in Water Resources Engineering: Artificial Neural Networks, Fuzzy Logic and Genetic Algorithms; WIT Press: Southampton, NY, USA, 2014. [Google Scholar]
- Song, X.-M.; Kong, F.-Z.; Zhu, Z.-X. Application of Muskingum routing method with variable parameters in ungauged basin. Water Sci. Eng 2011, 4, 1–12. [Google Scholar]
- Weinmann, P.E.; Laurenson, E.M. Approximate flood routing methods: A review. J. Hydraul. Div. 1979, 105, 1521–1536. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Kitanidis, P.K.; Bras, R.L. Real-time forecasting with a conceptual hydrologic model: 2. Applications and results. Water Resour. Res. 1980, 16, 1034–1044. [Google Scholar] [CrossRef]
- Franchini, M.; Bernini, A.; Barbetta, S.; Moramarco, T. Forecasting discharges at the downstream end of a river reach through two simple Muskingum based procedures. J. Hydrol. 2011, 399, 335–352. [Google Scholar] [CrossRef]
- Alhumoud, J.M.; Almashan, N. Muskingum Method with Variable Parameter Estimation. Math. Model. Eng. Probl. 2019, 6, 355–362. [Google Scholar] [CrossRef]
- Yang, R.; Hou, B.; Xiao, W.; Liang, C.; Zhang, X.; Li, B.; Yu, H. The applicability of real-time flood forecasting correction techniques coupled with the Muskingum method. Hydrol. Res. 2019, 51, 17–29. [Google Scholar] [CrossRef] [Green Version]
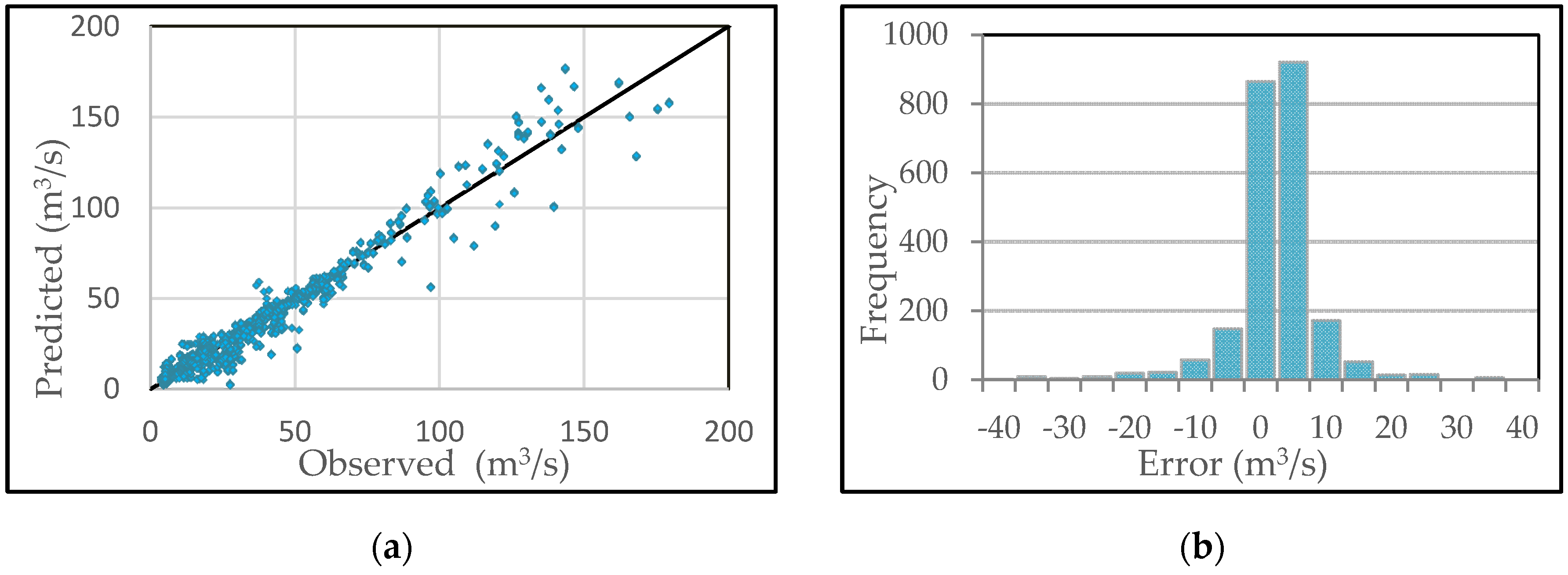
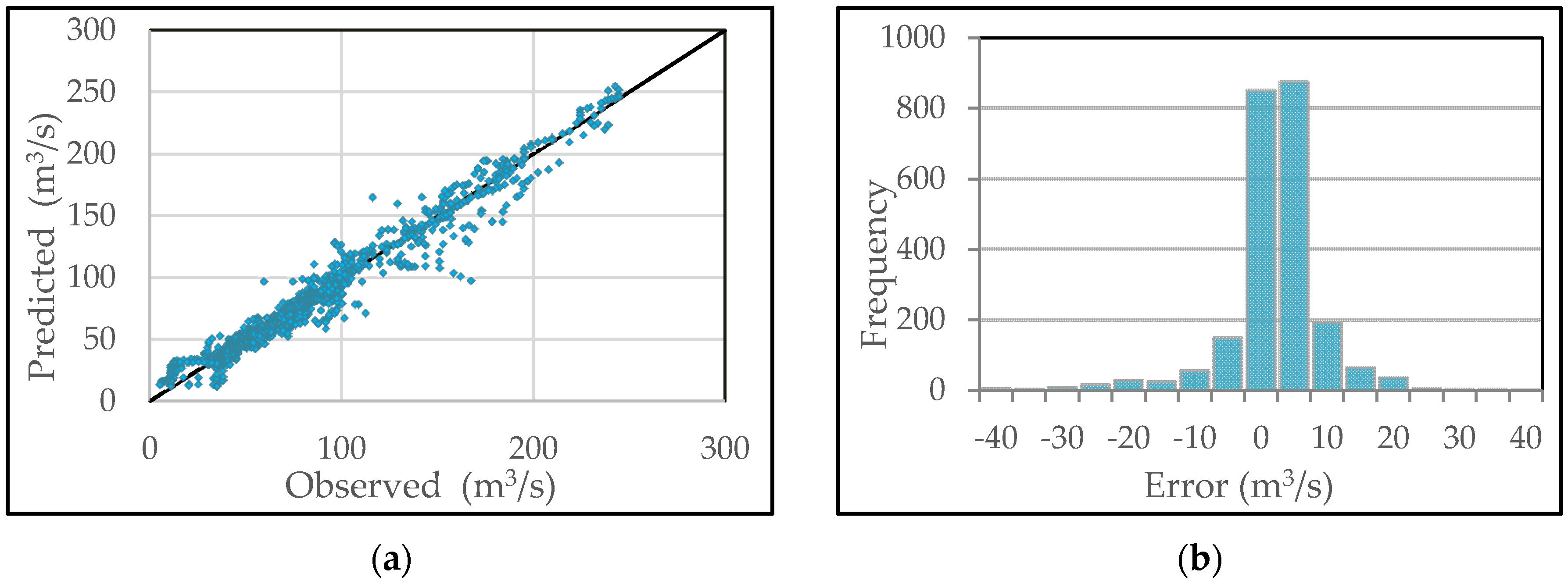
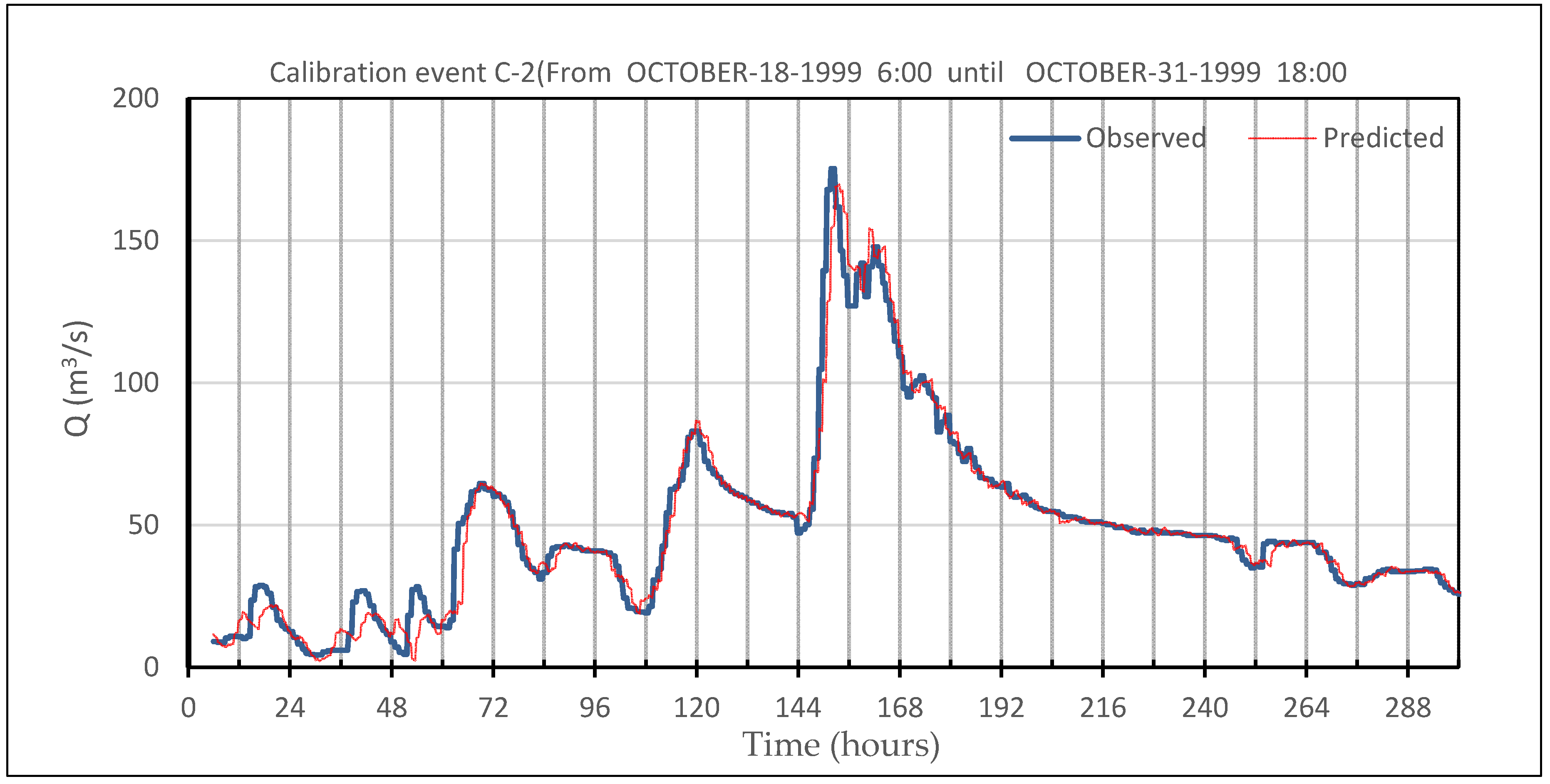
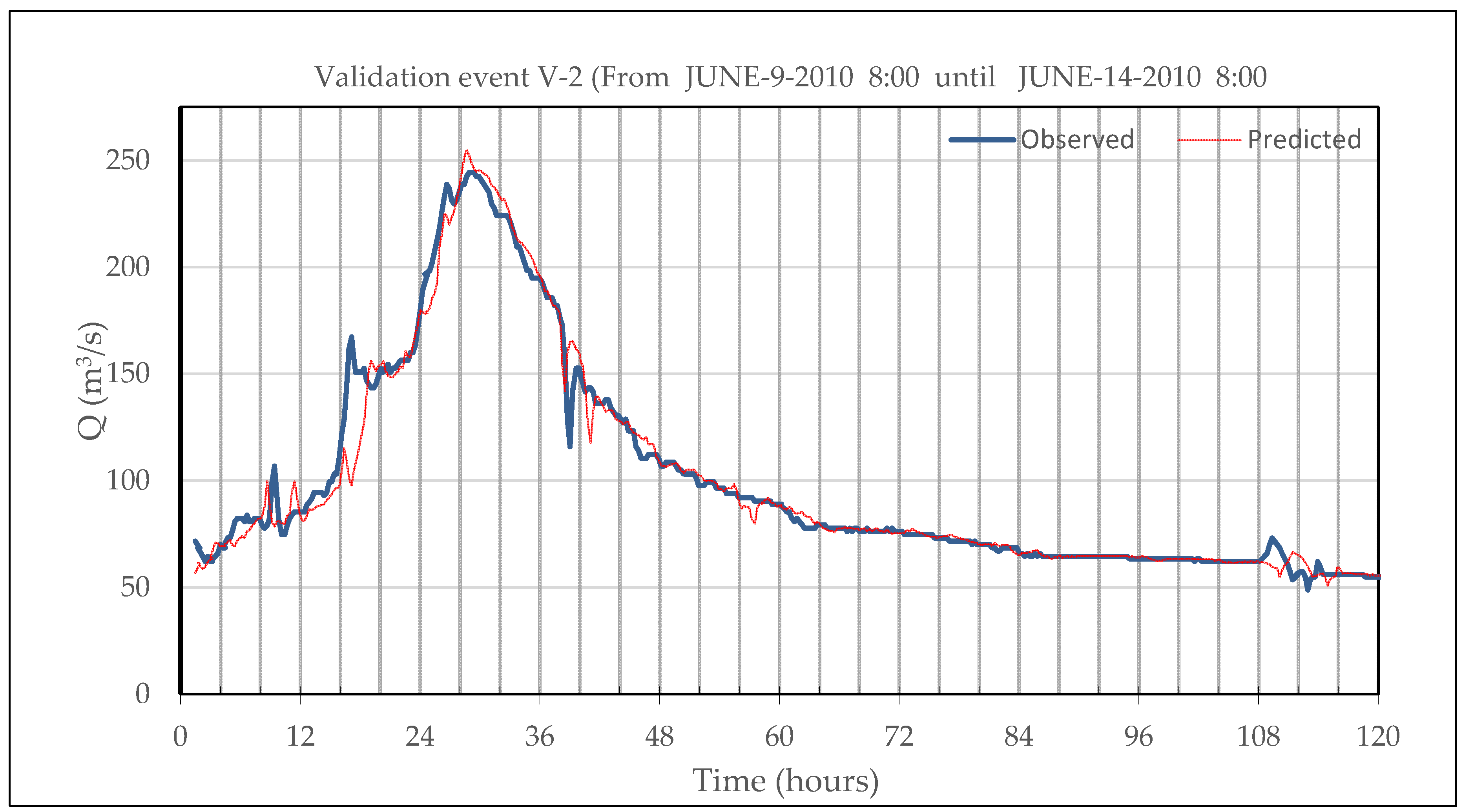




| Event | Initial Date | Qmax Campo (m3/s) | Qmax Graus (m3/s) | Volume Campo (106 m3) | Volume Graus (106 m3) | Time lag (hour) |
|---|---|---|---|---|---|---|
| Calibration Events | ||||||
| C1 | 19 September 1999 | 154.8 | 127.8 | 18.2 | 17.7 | 1.75 |
| C2 | 18 October 1999 | 169.4 | 145.0 | 49.1 | 46.8 | 2.00 |
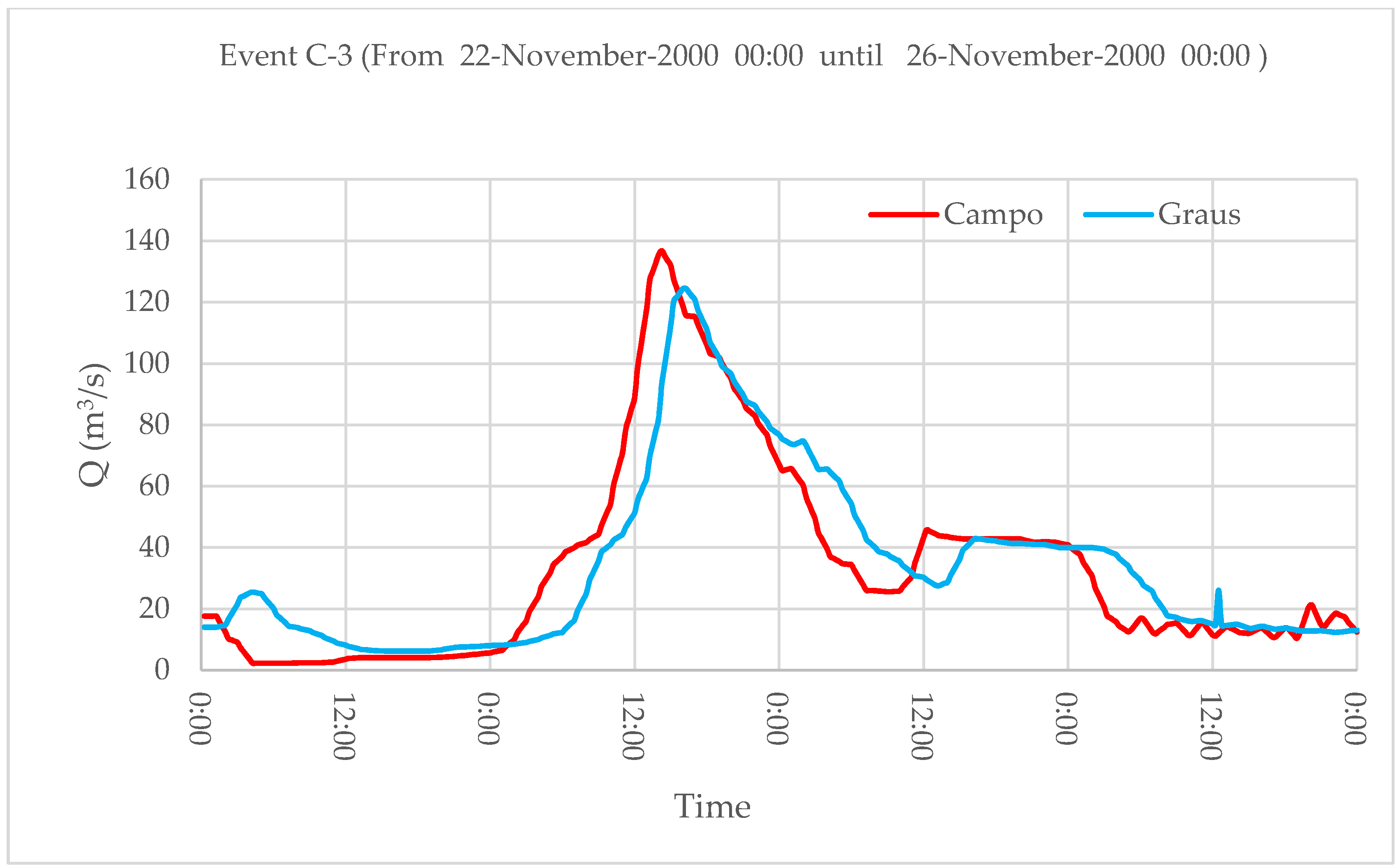
| C3 | 22 November 2000 | 103.7 | 95.7 | 11.0 | 11.1 | 2.50 |
| C4 | 20 October 2004 | 64.8 | 56.8 | 7.7 | 7.0 | 3.25 |
| Validation Events | ||||||
| V1 | 22 September 2006 | 117.5 | 109.7 | 21.1 | 22.8 | 2.25 |
| V2 | 16 October 2006 | 210.5 | 178.7 | 65.4 | 56.6 | 3.25 |
| V3 | 08 June 2010 | 229.1 | 219.8 | 34.7 | 39.4 | 2.75 |
| V4 | 1 November 2011 | 151.7 | 158.1 | 19.8 | 28.3 | 2.50 |
| Lead Time (min) | Calibration | Error Distribution | 5% and 95% Percentiles | |||||
|---|---|---|---|---|---|---|---|---|
| r | NS | PC | Mean (m3/s) | Std. dev. (m3/s) | Err. (m3/s) | |||
| 60 | 0.986 | 0.971 | 0.244 | 1.026 | −0.038 | 5.077 | −7.28 | 7.75 |
| 75 | 0.984 | 0.968 | 0.401 | 1.030 | −0.029 | 5.268 | −7.93 | 7.96 |
| 90 | 0.982 | 0.963 | 0.489 | 1.034 | −0.015 | 5.331 | −7.88 | 8.24 |
| 105 | 0.980 | 0.959 | 0.536 | 1.038 | −0.037 | 5.342 | −8.01 | 8.00 |
| 120 | 0.978 | 0.954 | 0.574 | 1.045 | −0.060 | 5.360 | −8.01 | 7.97 |
| Lead Time (min) | VALIDATION | Error Distribution | 5% and 95% Percentiles | |||||
|---|---|---|---|---|---|---|---|---|
| r | NS | PC | Mean (m3/s) | Std. dev. (m3/s) | Err. (m3/s) | |||
| 60 | 0.987 | 0.974 | 0.205 | 0.996 | −0.110 | 6.777 | −10.29 | 9.29 |
| 75 | 0.987 | 0.974 | 0.387 | 0.997 | −0.104 | 6.911 | −10.40 | 9.45 |
| 90 | 0.986 | 0.973 | 0.491 | 0.998 | −0.108 | 6.963 | −10.46 | 9.41 |
| 105 | 0.986 | 0.972 | 0.557 | 0.999 | −0.110 | 6.986 | −10.58 | 9.37 |
| 120 | 0.985 | 0.970 | 0.601 | 1.001 | −0.121 | 6.996 | −10.59 | 9.37 |
| Average | Maximum | |||||||
|---|---|---|---|---|---|---|---|---|
| Lead Time (min) | h | Absolute Error m3/s | Relative. Error% | Min h sub | Max h over | Absolute Error m3/s | Relative. Error % | |
| Calibration | 120 | 0.972 | −3.581 | −2.822 | 0.955 | 0.986 | −6.77 | −4.54 |
| Validation | 120 | 1.059 | 9.712 | 5.945 | 0.997 | 1.193 | 31.38 | 19.33 |
| Lead Time (min) | Calibration | Error Distribution | 5% and 95% Percentiles | |||||
|---|---|---|---|---|---|---|---|---|
| r | NS | PC | Mean(m3/s) | Std. dev(m3/s) | Err.(m3/s) | |||
| 60 | 0.984 | 0.965 | 0.468 | 0.818 | −0.728 | 6.186 | −10.80 | 5.99 |
| 75 | 0.983 | 0.963 | 0.570 | 1.008 | −0.751 | 6.487 | −11.45 | 6.90 |
| 90 | 0.982 | 0.960 | 0.631 | 1.014 | −0.745 | 6.790 | −11.44 | 7.09 |
| 105 | 0.981 | 0.958 | 0.676 | 1.024 | −0.727 | 7.129 | −11.56 | 7.36 |
| 120 | 0.979 | 0.955 | 0.712 | 0.890 | −0.723 | 7.460 | −12.07 | 7.66 |
| Lead Time (min) | Validation | Error Distribution | 5% and 95% Percentiles | |||||
|---|---|---|---|---|---|---|---|---|
| r | NS | PC | mean(m3/s) | Std. dev(m3/s) | Err.(m3/s) | |||
| 60 | 0.988 | 0.977 | 0.318 | 1.006 | −0.560 | 8.486 | −10.25 | 9.09 |
| 75 | 0.988 | 0.975 | 0.465 | 1.006 | −0.549 | 8.695 | −9.84 | 9.47 |
| 90 | 0.987 | 0.974 | 0.545 | 1.006 | −0.567 | 8.869 | −11.01 | 9.98 |
| 105 | 0.986 | 0.972 | 0.601 | 1.007 | −0.546 | 8.997 | −11.42 | 10.63 |
| 120 | 0.985 | 0.970 | 0.648 | 1.008 | −0.483 | 9.096 | −12.79 | 11.19 |
| Average | Maximum | |||||||
|---|---|---|---|---|---|---|---|---|
| Lead Time (min) | h | Absolute Error m3/s | Relative Error % | Min h sub | Max h over | Absolute Error m3/s | Relative. Error % | |
| Calibration | 120 | 1.031 | 3.630 | 3.060 | 0.958 | 1.114 | 12.68 | 11.44 |
| Validation | 120 | 1.059 | 9.712 | 5.945 | 0.997 | 1.193 | 31.38 | 19.33 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montes, N.; Aranda, J.Á.; García-Bartual, R. Real Time Flow Forecasting in a Mountain River Catchment Using Conceptual Models with Simple Error Correction Scheme. Water 2020, 12, 1484. https://doi.org/10.3390/w12051484
Montes N, Aranda JÁ, García-Bartual R. Real Time Flow Forecasting in a Mountain River Catchment Using Conceptual Models with Simple Error Correction Scheme. Water. 2020; 12(5):1484. https://doi.org/10.3390/w12051484
Chicago/Turabian StyleMontes, Nicolás, José Ángel Aranda, and Rafael García-Bartual. 2020. "Real Time Flow Forecasting in a Mountain River Catchment Using Conceptual Models with Simple Error Correction Scheme" Water 12, no. 5: 1484. https://doi.org/10.3390/w12051484
APA StyleMontes, N., Aranda, J. Á., & García-Bartual, R. (2020). Real Time Flow Forecasting in a Mountain River Catchment Using Conceptual Models with Simple Error Correction Scheme. Water, 12(5), 1484. https://doi.org/10.3390/w12051484






