Application of Soft Computing Models with Input Vectors of Snow Cover Area in Addition to Hydro-Climatic Data to Predict the Sediment Loads
Abstract
1. Introduction
Background
2. Materials and Methods
2.1. Study Area
2.2. Application of Temperature-Index Snow Model for Snow Cover Estimates
2.3. Artificial Neural Networks (ANN)
2.4. Adaptive Neuro-Fuzzy Logic Inference System (ANFIS)
2.5. Multivariate Adaptive Regression Splines (MARS)
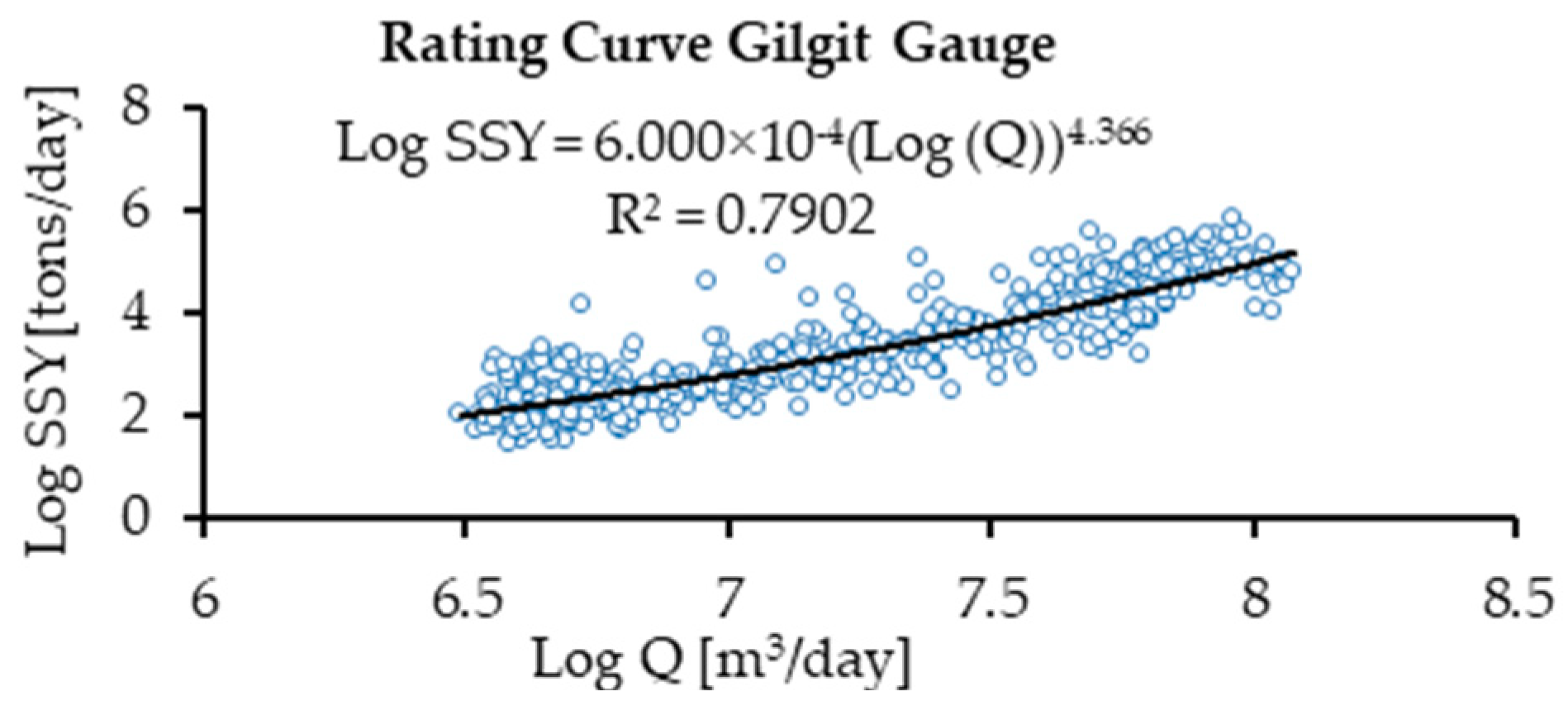
2.6. Sediment Rating Curve (SRC)
2.7. Performance Measurement Metrics for Model Evaluation
2.8. Application of the ANN, ANFIS-GP, ANFIS-SC, ANFIS-FCM, and MARS Models
- (a)
- FlowsS1 = SSCt = f (Qt, β1) + eiS2 = SSCt = f (Qt, Qt−1, β1, β2) + eiS3 = SSCt = f (Qt, Qt−1, Qt−2, β1, β2, β3) + eiS4 = SSCt = f (Qt, Qt−1, Qt−2, Qt−3, β1, β2, β3, β4) + eiS5 = SSCt = f (Qt, Qt−1, Qt−2, Qt−3, Qt−4, β1, β2, β3, β4, β5) + ei
- (b)
- Flows and snow cover areaS6 = SSCt = f (Qt, SCAt, β1, β6) + eiS7 = SSCt = f (Qt, SCAt, SCAt−1, β1, β6, β7) + eiS8 = SSCt = f (Qt, SCAt, SCAt−1, SCAt−2, β1, β6, β7, β8) + ei
- (c)
- Flow, snow cover area, and effective rainfallS9 = SSCt = f (Qt, Rt−1, SCAt, SCAt−4, β1, β9, β6, β10) + ei
- (d)
- Flow, snow cover area, temperature, and evapotranspirationS10 = SSCt = f (Qt, Tt−1, Evapt−1, SCAt, SCAt−4, β1, β11, β12, β6, β10) + ei
- (e)
- Average mean basin air temperatureS11 = SSCt = f (Tt, β13) + eiS12 = SSCt = f (Tt, Tt−1, β13, β11) + eiS13 = SSCt = f (Tt, Tt−1, Tt−2, β13, β11, β14) + eiS14 = SSCt = f (Tt, Tt−1, Tt−2, Tt−3, β13, β11, β14, β15) + eiS15 = SSCt = f (Tt, Tt−1, Tt−2, Tt−3, Tt−4, β13, β11, β14, β15, β16) + ei
3. Results and Discussion
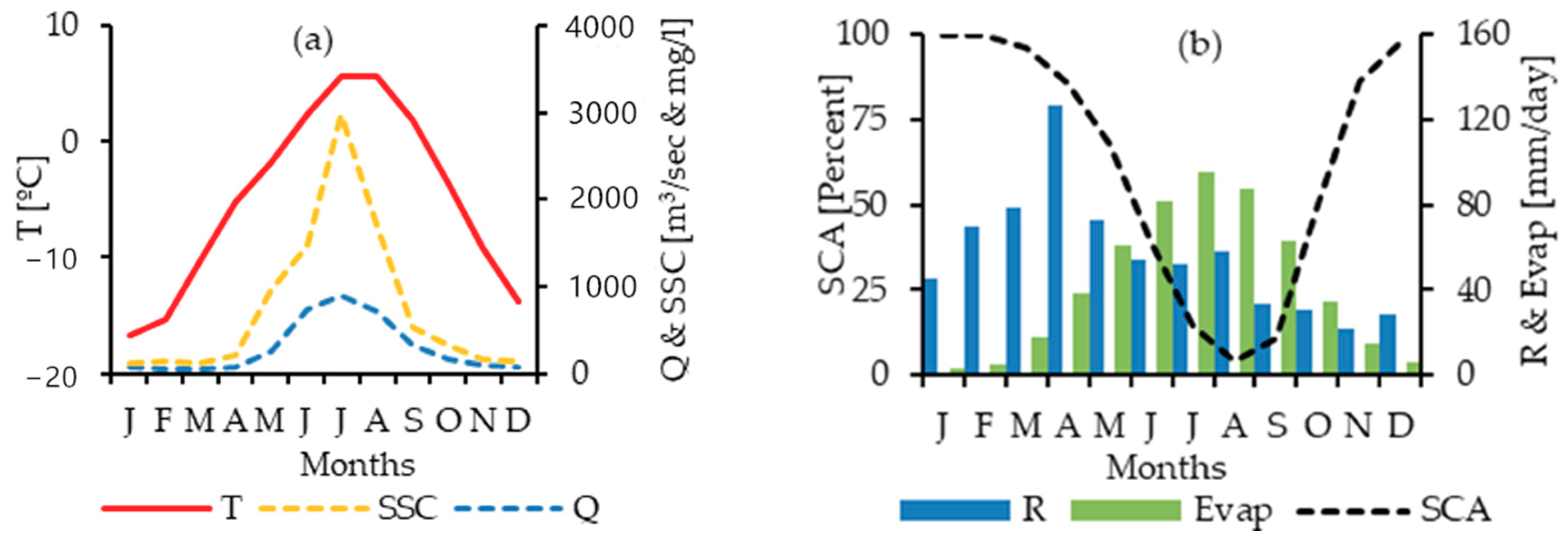
3.1. Simulation of Snow Melts and Snow Cover Area
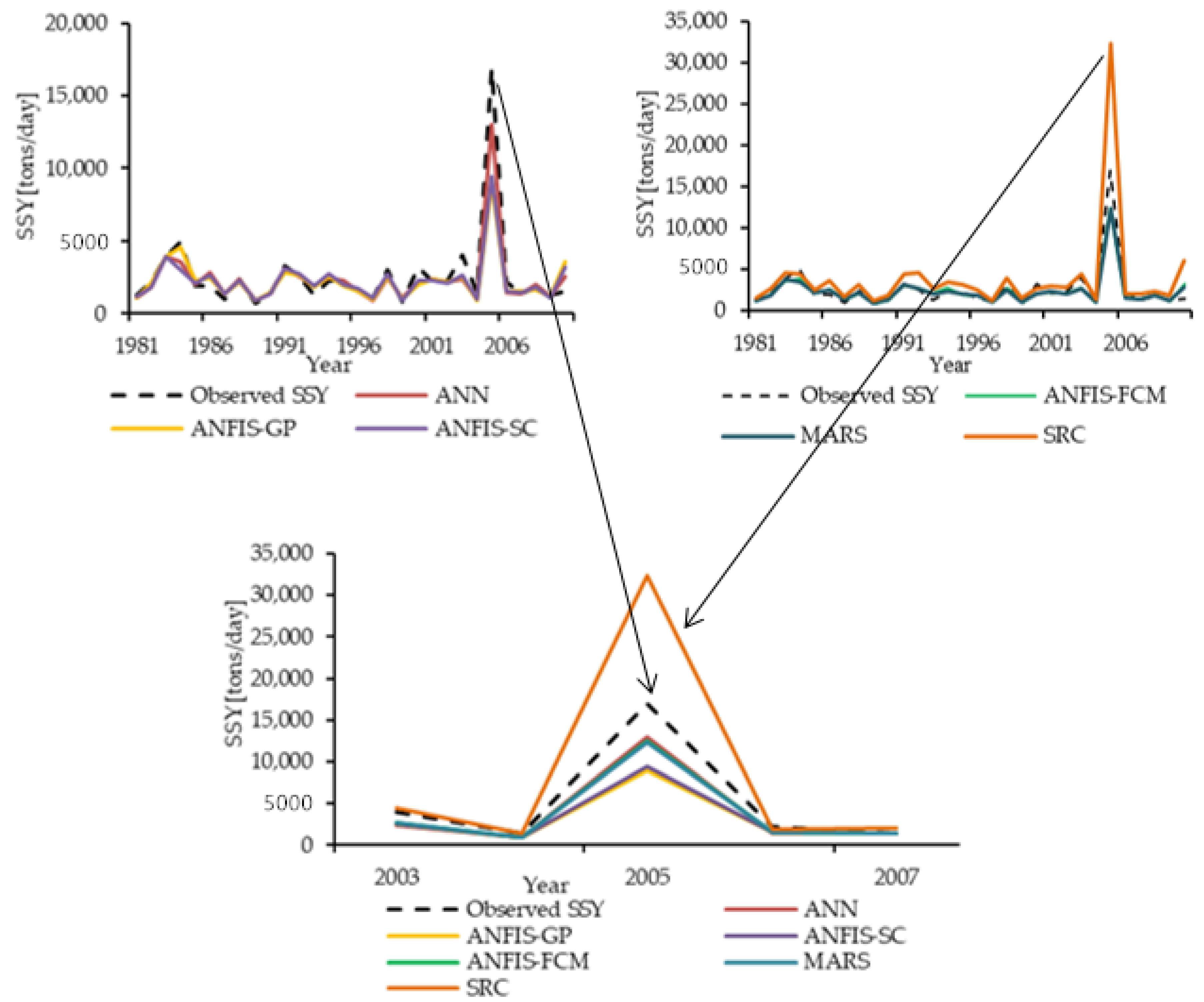
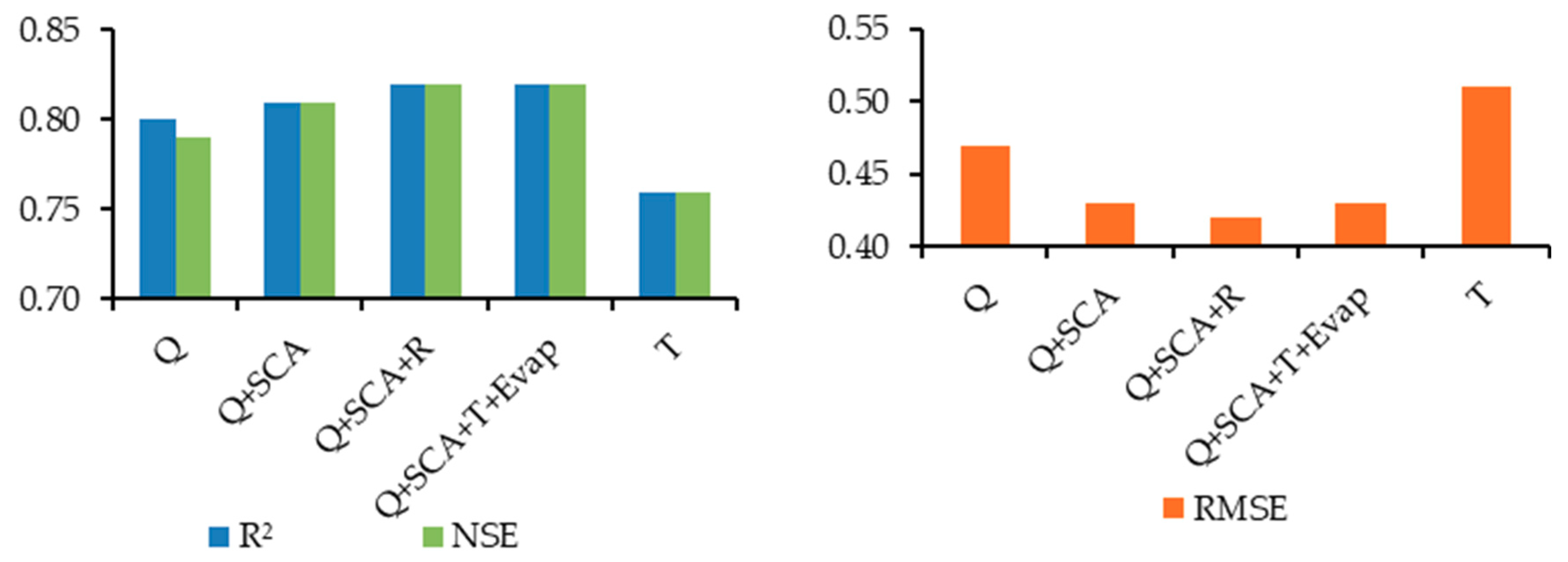
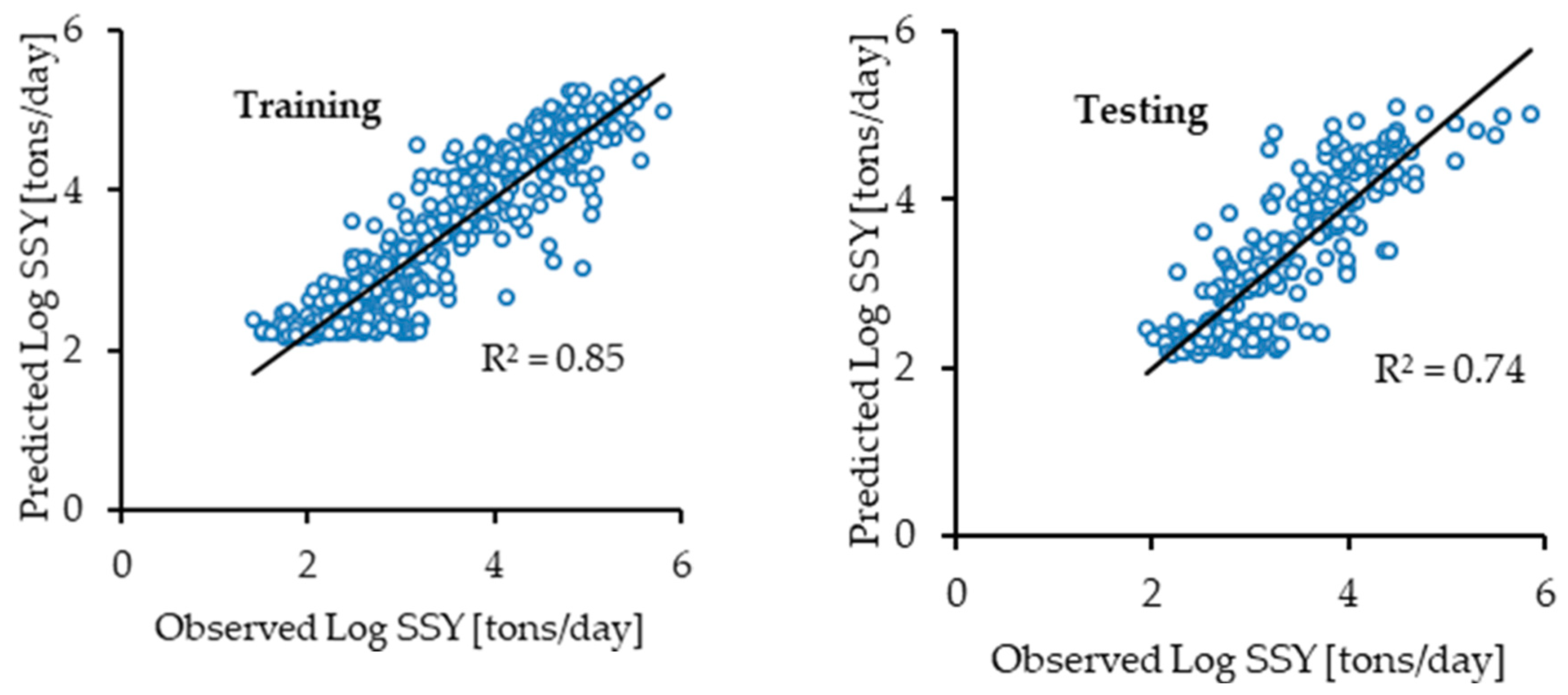
3.2. Comparison of the ANN, ANFIS-GP, ANFIS-SC, ANFIS-FCM, MARS, and SRC Models
3.3. Deveoplement of Multiple Linear Regression Equation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Foster, G.R.; Meyer, L.D. A Closed-Form Soil Erosion Equation for Upland Areas. In Sedimentation Symposium in Honor Prof. H.A. Einstein; Shen, H.W., Ed.; Colorado State University: Fort Collins, CO, USA, 1972; pp. 12.1–12.19. [Google Scholar]
- Knack, I.M.; Shen, H.T. A numerical model for sediment transport and bed change with river ice. J. Hydraul. Res. 2018, 56, 844–856. [Google Scholar] [CrossRef]
- Burrell, B.C.; Beltaos, S. Effects and implications of river ice breakup on suspended-sediment concentrations: A synthesis. In Proceedings of the CGU HS Committee on River Ice Processes and the Environment 20th Workshop on the Hydraulics of Ice-Covered Rivers, Ottawa, ON, Canada, 14–16 May 2019. [Google Scholar]
- Gomez, B. Bedload transport. Earth Sci. Rev. 1991, 31, 89–132. [Google Scholar] [CrossRef]
- Kemp, P.; Sear, D.; Collins, A.; Naden, P.; Jones, I. The impacts of fine sediment on riverine fish. Hydrol. Process. 2011, 25, 1800–1821. [Google Scholar] [CrossRef]
- Yang, C.T.; Marsooli, R.; Aalami, M.T. Evaluation of total load sediment transport formulas using ANN. Int. J. Sediment. Res. 2009, 24, 274–286. [Google Scholar] [CrossRef]
- Bashar, K.E.; ElTahir, E.O.; Fattah, S.A.; Ali, A.S.; Osman, M. Nile Basin Reservoir Sedimentation Prediction and Mitigation; Nile Basin Capacity Building Network: Cairo, Egypt, 2010; Available online: https://www.nbcbn.com/ctrl/images/img/uploads/4427_31104551.pdf (accessed on 21 May 2020).
- Ghernaout, R.; Remini, B. Impact of suspended sediment load on the silting of SMBA reservoir (Algeria). Environ. Earth Sci. 2014, 72, 915–929. [Google Scholar] [CrossRef]
- Wisser, D.; Frolking, S.; Hagen, S.; Bierkens, M.F.P. Beyond peak reservoir storage? A global estimate of declining water storage capacity in large reservoirs. Water Resour. Res. 2013, 49, 5732–5739. [Google Scholar] [CrossRef]
- Khan, N.M.; Tingsanchali, T. Optimization and simulation of reservoir operation with sediment evacuation: A case study of the Tarbela Dam, Pakistan. Hydrol. Process. 2009, 23, 730–747. [Google Scholar] [CrossRef]
- Ackers, J.; Hieatt, M.; Molyneux, J.D. Mangla reservoir, Pakistan–Approaching 50 years of service. Dams Reserv. 2016, 26, 68–83. [Google Scholar] [CrossRef]
- Pakistan Water and Power Development Authority (WAPDA). 5th Hydrographic Survey of Chashma Reservoir; International Sedimentation Research Institute: Lahore, Pakistan, 2012. [Google Scholar]
- King, R.; Stevens, M. Sediment management at Warsak, Pakistan. Int. J. Hydropower Dams 2001, 8, 61–68. [Google Scholar]
- Meadows, A.; Meadows, P.S. The Indus River. Biodiversity, Resources, Humankind; Meadows, A., Meadows, P.S., Eds.; Oxford University Press for the Linnean Society of London: Oxford, UK, 1999; ISBN 0195779053. [Google Scholar]
- Ahmad, N. Water Resources of Pakistan and Their Utilization; Shahid Nazir: Lahore, Pakistan, 1993; Available online: http://catalogue.nust.edu.pk/cgi-bin/koha/opac-detail.pl?biblionumber=695 (accessed on 21 May 2020).
- Pakistan Water Sector Strategy. Executive Summary; Report; Ministry of Water and Power, Office of the Chief Engineering Advisor/Chairman Federal Flood Commission, Govt of Pakistan: Islamabad, Pakistan, 2002; Volume 1.
- Pakistan Water Gateway. The Pakistan Water Situational Analysis. Report; Consultative Process in Pakistan (WCD CPP) Project; Pakistan Water Gateway. 2005. Available online: https://de.scribd.com/document/334572557/Pakistan-Water-Situation-Analysis (accessed on 21 May 2020).
- Faran Ali, K.; de Boer, D.H. Factors controlling specific sediment yield in the upper Indus River basin, northern Pakistan. Hydrol. Process. 2008, 22, 3102–3114. [Google Scholar] [CrossRef]
- Chen, X.Y.; Chau, K.W. A Hybrid Double Feedforward Neural Network for Suspended Sediment Load Estimation. Water Resour. Manag. 2016, 30, 2179–2194. [Google Scholar] [CrossRef]
- Jain, S.K. Development of Integrated Sediment Rating Curves Using ANNs. J. Hydraul. Eng. 2001, 127, 30–37. [Google Scholar] [CrossRef]
- Kerem Cigizoglu, H.; Kisi, Ö. Methods to improve the neural network performance in suspended sediment estimation. J. Hydrol. 2006, 317, 221–238. [Google Scholar] [CrossRef]
- Rajaee, T.; Mirbagheri, S.A.; Zounemat-Kermani, M.; Nourani, V. Daily suspended sediment concentration simulation using ANN and neuro-fuzzy models. Sci. Total Environ. 2009, 407, 4916–4927. [Google Scholar] [CrossRef] [PubMed]
- Melesse, A.M.; Ahmad, S.; McClain, M.E.; Wang, X.; Lim, Y.H. Suspended sediment load prediction of river systems: An artificial neural network approach. Agric. Water Manag. 2011, 98, 855–866. [Google Scholar] [CrossRef]
- Taşar, B.; Kaya, Y.; Varçin, H.; Üneş, F.; Demirci, M. Forecasting of Suspended Sediment in Rivers Using Artificial Neural Networks Approach. Int. J. Adv. Eng. Res. Sci. 2017, 4, 79–84. [Google Scholar] [CrossRef]
- Kumar, D.; Pandey, A.; Sharma, N.; Flügel, W.-A. Modeling Suspended Sediment Using Artificial Neural Networks and TRMM-3B42 Version 7 Rainfall Dataset. J. Hydrol. Eng. 2015, 20. [Google Scholar] [CrossRef]
- Cobaner, M.; Unal, B.; Kisi, O. Suspended sediment concentration estimation by an adaptive neuro-fuzzy and neural network approaches using hydro-meteorological data. J. Hydrol. 2009, 367, 52–61. [Google Scholar] [CrossRef]
- Kisi, O.; Haktanir, T.; Ardiclioglu, M.; Ozturk, O.; Yalcin, E.; Uludag, S. Adaptive neuro-fuzzy computing technique for suspended sediment estimation. Adv. Eng. Softw. 2009, 40, 438–444. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J. River suspended sediment estimation by climatic variables implication: Comparative study among soft computing techniques. Comput. Geosci. 2012, 43, 73–82. [Google Scholar] [CrossRef]
- Emamgholizadeh, S.; Demneh, R. The comparison of artificial intelligence models for the estimation of daily suspended sediment load: A case study on Telar and Kasilian Rivers in Iran. Water Sci. Technol. Water Supply 2018, 19, ws2018062. [Google Scholar] [CrossRef]
- Cimen, M. Estimation of daily suspended sediments using support vector machines. Hydrol. Sci. J. 2008, 53, 656–666. [Google Scholar] [CrossRef]
- Buyukyildiz, M.; Kumcu, S.Y. An Estimation of the Suspended Sediment Load Using Adaptive Network Based Fuzzy Inference System, Support Vector Machine and Artificial Neural Network Models. Water Resour. Manag. 2017, 31, 1343–1359. [Google Scholar] [CrossRef]
- Kakaei Lafdani, E.; Moghaddam Nia, A.; Ahmadi, A. Daily suspended sediment load prediction using artificial neural networks and support vector machines. J. Hydrol. 2013, 478, 50–62. [Google Scholar] [CrossRef]
- Rajaee, T. Wavelet and ANN combination model for prediction of daily suspended sediment load in rivers. Sci. Total Environ. 2011, 409, 2917–2928. [Google Scholar] [CrossRef] [PubMed]
- Olyaie, E.; Banejad, H.; Chau, K.-W.; Melesse, A.M. A comparison of various artificial intelligence approaches performance for estimating suspended sediment load of river systems: A case study in United States. Environ. Monit. Assess. 2015, 187, 189. [Google Scholar] [CrossRef]
- Nourani, V.; Andalib, G. Daily and Monthly Suspended Sediment Load Predictions Using Wavelet Based Artificial Intelligence Approaches. J. Mt. Sci. 2015, 12, 85–100. [Google Scholar] [CrossRef]
- Hild, C.; Bozdogan, H. The use of information-based model evaluation criteria in the GMDH algorithm. Syst. Anal. Model. Simul. 1995, 20, 29–50. [Google Scholar]
- Ivakhnenko, A.G. The Group Method of Data of Handling; A rival of the method of stochastic approximation. Sov. Autom. Control 1968, 1, 43–55. [Google Scholar]
- Rahgoshay, M.; Feiznia, S.; Arian, M.; Hashemi, S.A.A. Simulation of daily suspended sediment load using an improved model of support vector machine and genetic algorithms and particle swarm. Arab J. Geosci. 2019, 12, 447. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A.; Kisi, O.; Shiri, J. Evaluating the performance of four different heuristic approaches with Gamma test for daily suspended sediment concentration modeling. Environ. Sci. Pollut. Res. Int. 2019, 26, 22670–22687. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; Trajkovic, S.; Zounemat-Kermani, M.; Li, B.; Kisi, O. Daily streamflow prediction using optimally pruned extreme learning machine. J. Hydrol. 2019, 577, 123981. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; El-Shafie, A.; Zounemat-Kermani, M.; Kisi, O. Prediction of Suspended Sediment Load Using Data-Driven Models. Water 2019, 11, 2060. [Google Scholar] [CrossRef]
- Vali, A.A.; Moayeri, M.; Ramesht, M.H.; Movahedinia, N.A. Comparative performance analysis of artificial neural networks and regression models for suspended sediment prediction (case study: Eskandari cachment in Zayande Roud basin, Iran). Phys. Geogr. Res. Q. 2010, 42, 21–30. Available online: https://www.sid.ir/en/Journal/ViewPaper.aspx?ID=173113 (accessed on 21 May 2020).
- Chachi, J.; Taheri, S.M.; Pazhand, H.R. Suspended load estimation using L1 -fuzzy regression, L2 -fuzzy regression and MARS-fuzzy regression models. Hydrol. Sci. J. 2016, 61, 1489–1502. [Google Scholar] [CrossRef]
- Janga Reddy, M.; Ghimire, B. Use of Model Tree and Gene Expression Programming to Predict the Suspended Sediment Load in Rivers. J. Intell. Syst. 2009, 18. [Google Scholar] [CrossRef]
- Goyal, M.K. Modeling of Sediment Yield Prediction Using M5 Model Tree Algorithm and Wavelet Regression. Water Resour. Manag. 2014, 28, 1991–2003. [Google Scholar] [CrossRef]
- Senthil Kumar, A.R.; Ojha, C.S.P.; Goyal, M.K.; Singh, R.D.; Swamee, P.K. Modeling of Suspended Sediment Concentration at Kasol in India Using ANN, Fuzzy Logic, and Decision Tree Algorithms. J. Hydrol. Eng. 2012, 17, 394–404. [Google Scholar] [CrossRef]
- Immerzeel, W.W.; Wanders, N.; Lutz, A.F.; Shea, J.M.; Bierkens, M.F.P. Reconciling high-altitude precipitation in the upper Indus basin with glacier mass balances and runoff. Hydrol. Earth Syst. Sci. 2015, 19, 4673–4687. [Google Scholar] [CrossRef]
- Lutz, A.F.; Immerzeel, W.W. HI-AWARE Reference Climate Dataset for the Indus, Ganges and Brahmaputra River Basins; Report of Future Water 146; Future Water: Wageningen, The Netherlands, 2015. [Google Scholar]
- Tahir, A.A.; Chevallier, P.; Arnaud, Y.; Neppel, L.; Ahmad, B. Modeling snowmelt-runoff under climate scenarios in the Hunza River basin, Karakoram Range, Northern Pakistan. J. Hydrol. 2011, 409, 104–117. [Google Scholar] [CrossRef]
- Adnan, M.; Nabi, G.; Saleem Poomee, M.; Ashraf, A. Snowmelt runoff prediction under changing climate in the Himalayan cryosphere: A case of Gilgit River Basin. Geosci. Front. 2017, 8, 941–949. [Google Scholar] [CrossRef]
- Shahin, M.A.; Maier, H.R.; Jaksa, M.B. Data Division for Developing Neural Networks Applied to Geotechnical Engineering. J. Comput. Civ. Eng. 2004, 18, 105–114. [Google Scholar] [CrossRef]
- Pham, B.T.; van Phong, T.; Nguyen, H.D.; Qi, C.; Al-Ansari, N.; Amini, A.; Ho, L.S.; Tuyen, T.T.; Yen, H.P.H.; Ly, H.-B.; et al. A Comparative Study of Kernel Logistic Regression, Radial Basis Function Classifier, Multinomial Naïve Bayes, and Logistic Model Tree for Flash Flood Susceptibility Mapping. Water 2020, 12, 239. [Google Scholar] [CrossRef]
- Hewitt, K. The Karakoram Anomaly? Glacier Expansion and the ‘Elevation Effect,’ Karakoram Himalaya. Mt. Res. Dev. 2005, 25, 332–340. [Google Scholar]
- Hewitt, K. Tributary glacier surges: An exceptional concentration at Panmah Glacier, Karakoram Himalaya. J. Glaciol. 2007, 53, 181–188. [Google Scholar] [CrossRef]
- Winiger, M.; Gumpert, M.; Yamout, H. Karakorum-Hindukush-western Himalaya: Assessing high-altitude water resources. Hydrol. Process. 2005, 19, 2329–2338. [Google Scholar] [CrossRef]
- Hock, R. Temperature index melt modelling in mountain areas. J. Hydrol. 2003, 282, 104–115. [Google Scholar] [CrossRef]
- Costa, A.; Molnar, P.; Stutenbecker, L.; Bakker, M.; Silva, T.A.; Schlunegger, F.; Lane, S.N.; Loizeau, J.-L.; Girardclos, S. Temperature signal in suspended sediment export from an Alpine catchment. Hydrol. Earth Syst. Sci. 2018, 22, 509–528. [Google Scholar] [CrossRef]
- Artificial Neural Networks in Hydrology. I: Preliminary Concepts. J. Hydrol. Eng. 2000, 5, 115–123. [Google Scholar] [CrossRef]
- Artificial Neural Networks in Hydrology. II: Hydrologic Applications. J. Hydrol. Eng. 2000, 5, 124–137. [Google Scholar] [CrossRef]
- Haykin, S.S. Neural Networks. A Comprehensive Foundation/Simon Haykin, 2nd ed.; Prentice Hall: London, UK; Prentice-Hall International: Upper Saddle River, NJ, USA, 1999; ISBN 0132733501. [Google Scholar]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Internal Representations by Error Propagation: Parallel Distributed Processing: Explorations in the Microstructure of Cognition; Rumelhart, D.E., McClelland, J.L., PDP Research Group, Eds.; MIT Press: Cambridge, MA, USA, 1986; Volume 1, pp. 318–362. ISBN 0-262-68053-X. [Google Scholar]
- Minns, A.W.; Hall, M.J. Artificial neural networks as rainfall-runoff models. Hydrol. Sci. J. 1996, 41, 399–417. [Google Scholar] [CrossRef]
- Nourani, V.; Baghanam, A.H.; Adamowski, J.; Gebremichael, M. Using self-organizing maps and wavelet transforms for space–time pre-processing of satellite precipitation and runoff data in neural network-based rainfall–runoff modeling. J. Hydrol. 2013, 476, 228–243. [Google Scholar] [CrossRef]
- Jang, J.-S.R. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Mamdani, E.H.; Assilian, S. An experiment in linguistic synthesis with a fuzzy logic controller. Int. J. Man Mach. Stud. 1975, 7, 1–13. [Google Scholar] [CrossRef]
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Abonyi, J.; Andersen, H.; Nagy, L.; Szeifert, F. Inverse fuzzy-process-model based direct adaptive control. Math. Comput. Simul. 1999, 51, 119–132. [Google Scholar] [CrossRef]
- Yager, R.R.; Filev, D.P. Approximate clustering via the mountain method. IEEE Trans. Syst. Man Cybern. 1994, 24, 1279–1284. [Google Scholar] [CrossRef]
- Chiu, S. Extracting Fuzzy rules from Data for Function Approximation and Pattern Classification. In Fuzzy Information Engineering: A Guided Tour of Applications; John Wiley & Sons: Hoboken, NJ, USA, 1997; pp. 1–10. [Google Scholar]
- Chiu, S. Extracting fuzzy rules for pattern classification by cluster estimation. In Proceedings of the Sixth International Fuzzy Systems Association World Congress, Sao Paulo, Brazl, 1–4 July 1995; Volume II, pp. 273–276. [Google Scholar]
- Chiu, S. Fuzzy Model Identification Based on Cluster Estimation. J. Intell. Fuzzy Syst. 1994, 2, 267–278. [Google Scholar] [CrossRef]
- Cobaner, M. Evapotranspiration estimation by two different neuro-fuzzy inference systems. J. Hydrol. 2011, 398, 292–302. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1988; ISBN 0-13-022278-X. [Google Scholar]
- Tsai, D.-M.; Lin, C.-C. Fuzzy C-means based clustering for linearly and nonlinearly separable data. Pattern Recognit. 2011, 44, 1750–1760. [Google Scholar] [CrossRef]
- Taherdangkoo, M.; Bagheri, M.H. A powerful hybrid clustering method based on modified stem cells and Fuzzy C-means algorithms. Eng. Appl. Artif. Intell. 2013, 26, 1493–1502. [Google Scholar] [CrossRef]
- Zhang, D.-Q.; Chen, S.-C. A novel kernelized fuzzy C-means algorithm with application in medical image segmentation. Artif. Intell. Med. 2004, 32, 37–50. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Statist. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Kisi, O.; Parmar, K.S. Application of least square support vector machine and multivariate adaptive regression spline models in long term prediction of river water pollution. J. Hydrol. 2016, 534, 104–112. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Zounemat-Kermani, M.; Gan, Y. Comparison of six different soft computing methods in modeling evaporation in different climates. Hydrol. Earth Syst. Sci. Discuss. 2016, 1–51. [Google Scholar] [CrossRef]
- Yilmaz, B.; Aras, E.; Nacar, S.; Kankal, M. Estimating suspended sediment load with multivariate adaptive regression spline, teaching-learning based optimization, and artificial bee colony models. Sci. Total Environ. 2018, 639, 826–840. [Google Scholar] [CrossRef]
- Tahir, A.A.; Hakeem, S.A.; Hu, T.; Hayat, H.; Yasir, M. Simulation of snowmelt-runoff under climate change scenarios in a data-scarce mountain environment. Int. J. Digit. Earth 2019, 12, 910–930. [Google Scholar] [CrossRef]
- Hayat, H.; Akbar, T.; Tahir, A.; Hassan, Q.; Dewan, A.; Irshad, M. Simulating Current and Future River-Flows in the Karakoram and Himalayan Regions of Pakistan Using Snowmelt-Runoff Model and RCP Scenarios. Water 2019, 11, 761. [Google Scholar] [CrossRef]
- Lutz, A.F.; Immerzeel, W.W.; Kraaijenbrink, P.D.A.; Shrestha, A.B.; Bierkens, M.F.P. Climate Change Impacts on the Upper Indus Hydrology: Sources, Shifts and Extremes. PLoS ONE 2016, 11, e0165630. [Google Scholar] [CrossRef] [PubMed]
- Adnan, M.; Nabi, G.; Kang, S.; Zhang, G.; Adnan, R.M.; Anjum, M.N.; Iqbal, M.; Ali, A.F. Snowmelt Runoff Modelling under Projected Climate Change Patterns in the Gilgit River Basin of Northern Pakistan. Pol. J. Environ. Stud. 2017, 26, 525–542. [Google Scholar] [CrossRef]
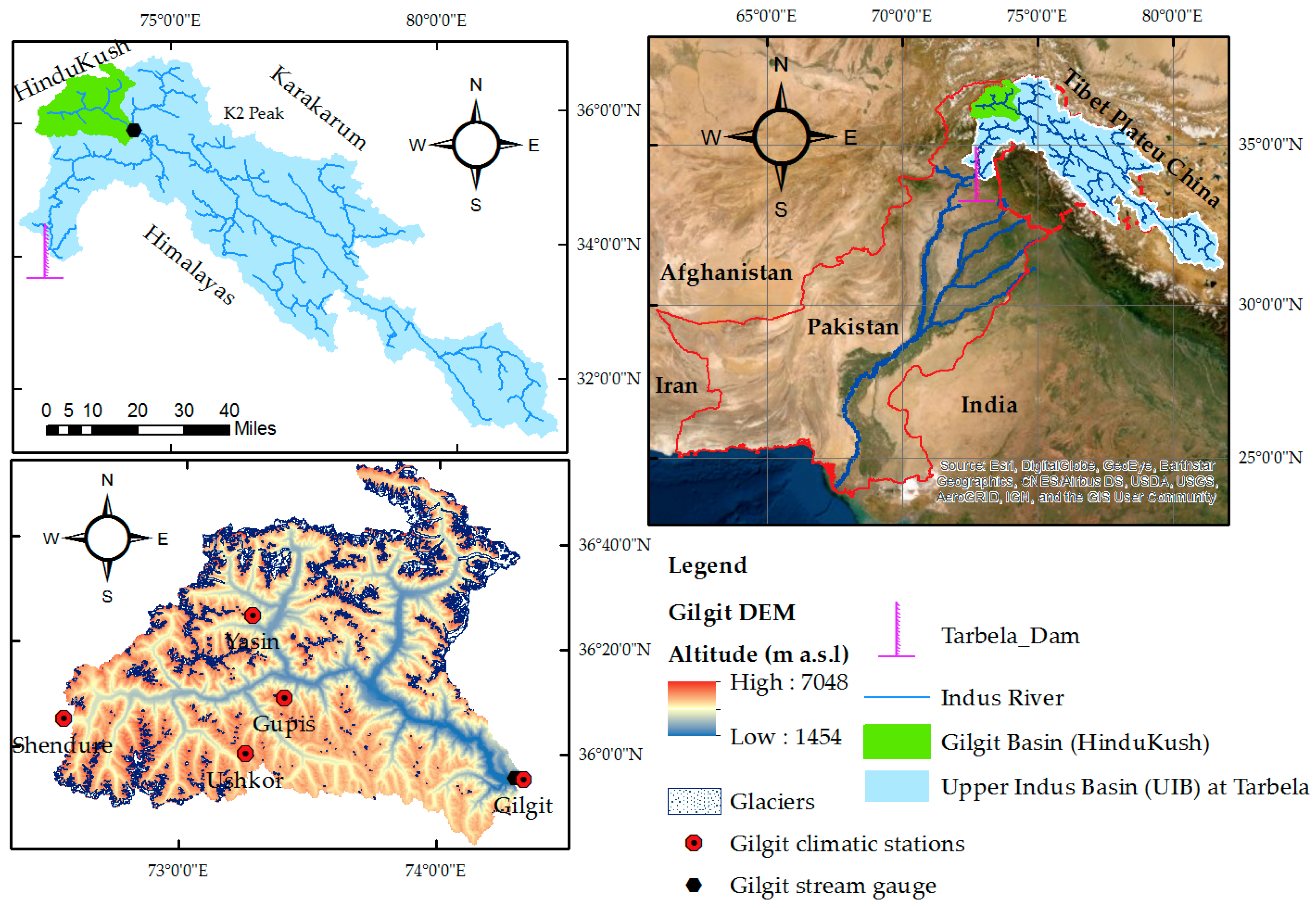


| Variable | Data Source | Period | Source |
|---|---|---|---|
| Q * | Daily mean discharge (m3/sec) | Daily, 1981–2010 | Water and Power Development Authority (WAPDA), Pakistan |
| SSC * | Suspended sediment concentration (mg/L) | Intermittent days per week 1981–2010 | Water and Power Development Authority (WAPDA), Pakistan |
| SCF | Snow cover fractions ranging (0–1) extracted from MODIS satellite data | Weekly, basin avg. 2000–2010 | https://nsidc.org/data/MOD10A2 |
| T | Daily mean, maximum & minimum air temperature (°C) on a 5 × 5 km grid | Daily, basin avg. 1981–2010 | HI-AWARE project [47,48] |
| P | Daily mean rainfall (mm/day) on a 5 × 5 km grid | Daily, basin avg. 1981–2010 | HI-AWARE project [47,48] |
| Evap | Daily mean Evapotranspiration (mm/day) on a 5 × 5 km grid | Daily, basin avg. 1981–2010 | HI-AWARE project [47,48] |
| log Q (m3/day) | log SSY (tons/day) | SCA (fractions) | Tavg (°C) | P (mm) | Evap (mm/day) | |
|---|---|---|---|---|---|---|
| log Q (m3/day) | 1 | |||||
| log SSY (tons/day) | 0.87 | 1 | ||||
| SCA (fractions) | −0.85 | −0.74 | 1 | |||
| Tavg. (°C) | 0.87 | 0.79 | −0.88 | 1 | ||
| P (mm) | 0.16 | 0.15 | 0.09 | 0.1 | 1 | |
| Evap. (mm/day) | 0.86 | 0.81 | −0.82 | 0.93 | 0.06 | 1 |
| ksnow = 4.2 (mm/day/°C) | ||
|---|---|---|
| Calibration Period (2000–2007) | Validation Period (2008–2010) | |
| R2 | 0.90 | 0.90 |
| NSE | 0.72 | 0.70 |
| RMSE | 0.15 | 0.15 |
| Scenarios | Model Inputs | Neurons | Transfer Function | R2 | RMSE | NSE | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Input | Output | Training | Testing | Training | Testing | Training | Testing | |||
| S1 | Qt | 3 | logsig | purelin | 0.76 | 0.81 | 0.48 | 0.42 | 0.76 | 0.8 |
| S2 | Qt, Qt−1 | 3 | logsig | purelin | 0.77 | 0.79 | 0.48 | 0.44 | 0.77 | 0.79 |
| S3 | Qt, Qt−1, Qt−2 | 5 | radbas | purlin | 0.78 | 0.79 | 0.46 | 0.45 | 0.78 | 0.79 |
| S4 | Qt, Qt−1, Qt−2, Qt−3 | 5 | tansig | purelin | 0.80 | 0.80 | 0.44 | 0.47 | 0.80 | 0.79 |
| S5 | Qt, Qt−1, Qt−2, Qt−3, Qt−4 | 7 | logsig | purelin | 0.81 | 0.80 | 0.43 | 0.44 | 0.81 | 0.80 |
| S6 | Qt, SCAt | 5 | tansig | purelin | 0.79 | 0.82 | 0.45 | 0.44 | 0.79 | 0.81 |
| S7 | Qt, SCAt, SCAt−1 | 7 | tansig | tansig | 0.80 | 0.80 | 0.44 | 0.43 | 0.80 | 0.8 |
| S8 | Qt, SCAt, SCAt−1, SCAt−2 | 8 | tansig | tansig | 0.80 | 0.81 | 0.44 | 0.43 | 0.80 | 0.81 |
| S9 | Qt, Rt−1, SCAt, SCAt−4 | 7 | logsig | purelin | 0.80 | 0.82 | 0.44 | 0.42 | 0.80 | 0.82 |
| S10 | Qt, Tt−1, Evapt−1, SCAt, SCAt−4 | 5 | radbas | tansig | 0.81 | 0.82 | 0.42 | 0.43 | 0.81 | 0.81 |
| S11 | Tt | 3 | logsig | purelin | 0.69 | 0.73 | 0.55 | 0.50 | 0.69 | 0.73 |
| S12 | Tt, Tt−1 | 3 | logsig | tansig | 0.69 | 0.74 | 0.54 | 0.51 | 0.69 | 0.73 |
| S13 | Tt, Tt−1, Tt−2 | 6 | tansig | tansig | 0.74 | 0.73 | 0.51 | 0.51 | 0.74 | 0.72 |
| S14 | Tt, Tt−1, Tt−2, Tt−3 | 8 | tansig | tansig | 0.75 | 0.74 | 0.49 | 0.51 | 0.75 | 0.74 |
| S15 | Tt, Tt−1, Tt−2, Tt−3, Tt−4 | 7 | radbas | tansig | 0.74 | 0.76 | 0.49 | 0.51 | 0.74 | 0.76 |
| Scenarios | Model Inputs | Membership Functions | No of Functions | R2 | RMSE | NSE | |||
|---|---|---|---|---|---|---|---|---|---|
| Training | Testing | Training | Testing | Training | Testing | ||||
| S1 | Qt | pimf | 4 | 0.77 | 0.78 | 0.46 | 0.47 | 0.77 | 0.78 |
| S2 | Qt, Qt−1 | pimf | 2 | 0.78 | 0.78 | 0.46 | 0.47 | 0.78 | 0.78 |
| S3 | Qt, Qt−1, Qt−2 | gauss2mf | 2 | 0.79 | 0.77 | 0.45 | 0.49 | 0.79 | 0.77 |
| S4 | Qt, Qt−1, Qt−2, Qt−3 | gbellmf | 2 | 0.81 | 0.75 | 0.43 | 0.50 | 0.81 | 0.75 |
| S5 | Qt, Qt−1, Qt−2, Qt−3, Qt−4 | trimf | 2 | 0.81 | 0.71 | 0.43 | 0.53 | 0.81 | 0.69 |
| S6 | Qt, SCAt | trimf | 2 | 0.79 | 0.77 | 0.45 | 0.45 | 0.79 | 0.77 |
| S7 | Qt, SCAt, SCAt−1 | trimf | 2 | 0.79 | 0.78 | 0.44 | 0.47 | 0.79 | 0.78 |
| S8 | Qt, SCAt, SCAt−1, SCAt−2 | trimf | 2 | 0.82 | 0.76 | 0.42 | 0.47 | 0.82 | 0.75 |
| S9 | Qt, Rt−1, SCAt, SCAt−4 | trimf | 2 | 0.82 | 0.76 | 0.41 | 0.49 | 0.82 | 0.76 |
| S10 | Qt, Tt−1, Evapt−1, SCAt, SCAt−4 | trimf | 2 | 0.85 | 0.72 | 0.38 | 0.52 | 0.85 | 0.72 |
| S11 | Tt | psigmf | 2 | 0.70 | 0.70 | 0.55 | 0.52 | 0.70 | 0.70 |
| S12 | Tt, Tt−1 | pimf | 2 | 0.71 | 0.71 | 0.54 | 0.51 | 0.71 | 0.71 |
| S13 | Tt, Tt−1, Tt−2 | trimf | 2 | 0.71 | 0.73 | 0.52 | 0.52 | 0.71 | 0.73 |
| S14 | Tt, Tt−1, Tt−2, Tt−3 | trapmf | 2 | 0.72 | 0.72 | 0.51 | 0.53 | 0.72 | 0.72 |
| S15 | Tt, Tt−1, Tt−2, Tt−3, Tt−4 | trimf | 2 | 0.77 | 0.60 | 0.46 | 0.65 | 0.77 | 0.59 |
| Scenarios | Model Inputs | Radii | R2 | RMSE | NSE | |||
|---|---|---|---|---|---|---|---|---|
| Training | Testing | Training | Testing | Training | Testing | |||
| S1 | Qt | 0.50 | 0.77 | 0.78 | 0.46 | 0.47 | 0.77 | 0.78 |
| S2 | Qt, Qt−1 | 0.70 | 0.77 | 0.78 | 0.46 | 0.47 | 0.77 | 0.78 |
| S3 | Qt, Qt−1, Qt−2 | 0.70 | 0.77 | 0.78 | 0.46 | 0.47 | 0.77 | 0.78 |
| S4 | Qt, Qt−1, Qt−2, Qt−3 | 0.70 | 0.78 | 0.78 | 0.45 | 0.47 | 0.78 | 0.78 |
| S5 | Qt, Qt−1, Qt−2, Qt−3, Qt−4 | 0.80 | 0.78 | 0.78 | 0.45 | 0.47 | 0.78 | 0.78 |
| S6 | Qt, SCAt | 0.60 | 0.78 | 0.78 | 0.45 | 0.47 | 0.78 | 0.78 |
| S7 | Qt, SCAt, SCAt−1 | 0.80 | 0.78 | 0.78 | 0.45 | 0.47 | 0.78 | 0.78 |
| S8 | Qt, SCAt, SCAt−1, SCAt−2 | 0.70 | 0.79 | 0.77 | 0.44 | 0.48 | 0.79 | 0.77 |
| S9 | Qt, Rt−1, SCAt, SCAt−4 | 0.60 | 0.79 | 0.78 | 0.45 | 0.47 | 0.79 | 0.78 |
| S10 | Qt, Tt−1, Evapt−1, SCAt, SCAt−4 | 0.90 | 0.80 | 0.79 | 0.43 | 0.46 | 0.80 | 0.79 |
| S11 | Tt | 0.50 | 0.70 | 0.70 | 0.53 | 0.55 | 0.70 | 0.70 |
| S12 | Tt, Tt−1 | 0.60 | 0.71 | 0.70 | 0.52 | 0.55 | 0.71 | 0.70 |
| S13 | Tt, Tt−1, Tt−2 | 0.80 | 0.72 | 0.72 | 0.51 | 0.53 | 0.72 | 0.72 |
| S14 | Tt, Tt−1, Tt−2, Tt−3 | 0.80 | 0.72 | 0.71 | 0.51 | 0.54 | 0.72 | 0.71 |
| S15 | Tt, Tt−1, Tt−2, Tt−3, Tt−4 | 0.70 | 0.72 | 0.73 | 0.51 | 0.52 | 0.72 | 0.73 |
| Scenarios | Model Inputs | No of Clusters | R2 | RMSE | NSE | |||
|---|---|---|---|---|---|---|---|---|
| Training | Testing | Training | Testing | Training | Testing | |||
| S1 | Qt | 2 | 0.77 | 0.78 | 0.46 | 0.47 | 0.77 | 0.78 |
| S2 | Qt, Qt−1 | 4 | 0.77 | 0.78 | 0.46 | 0.47 | 0.77 | 0.78 |
| S3 | Qt, Qt−1, Qt−2 | 2 | 0.77 | 0.78 | 0.46 | 0.47 | 0.78 | 0.78 |
| S4 | Qt, Qt−1, Qt−2, Qt−3 | 2 | 0.77 | 0.78 | 0.46 | 0.48 | 0.77 | 0.78 |
| S5 | Qt, Qt−1, Qt−2, Qt−3, Qt−4 | 2 | 0.77 | 0.78 | 0.46 | 0.48 | 0.77 | 0.77 |
| S6 | Qt, SCAt | 2 | 0.78 | 0.78 | 0.45 | 0.47 | 0.78 | 0.78 |
| S7 | Qt, SCAt, SCAt−1 | 2 | 0.78 | 0.78 | 0.45 | 0.47 | 0.78 | 0.78 |
| S8 | Qt, SCAt, SCAt−1, SCAt−2 | 2 | 0.78 | 0.77 | 0.45 | 0.48 | 0.80 | 0.78 |
| S9 | Qt, Rt−1, SCAt, SCAt−4 | 2 | 0.79 | 0.78 | 0.44 | 0.47 | 0.79 | 0.78 |
| S10 | Qt, Tt−1, Evapt−1, SCAt, SCAt−4 | 2 | 0.80 | 0.78 | 0.43 | 0.47 | 0.80 | 0.78 |
| S11 | Tt | 3 | 0.70 | 0.70 | 0.53 | 0.55 | 0.70 | 0.70 |
| S12 | Tt, Tt−1 | 2 | 0.71 | 0.70 | 0.53 | 0.55 | 0.71 | 0.70 |
| S13 | Tt, Tt−1, Tt−2 | 4 | 0.72 | 0.71 | 0.51 | 0.54 | 0.72 | 0.71 |
| S14 | Tt, Tt−1, Tt−2, Tt−3 | 6 | 0.76 | 0.72 | 0.48 | 0.53 | 0.76 | 0.72 |
| S15 | Tt, Tt−1, Tt−2, Tt−3, Tt−4 | 2 | 0.72 | 0.70 | 0.51 | 0.55 | 0.72 | 0.70 |
| Scenarios | Model Inputs | Basis Function | R2 | RMSE | NSE | |||
|---|---|---|---|---|---|---|---|---|
| Training | Testing | Training | Testing | Training | Testing | |||
| S1 | Qt | 5 | 0.77 | 0.78 | 0.47 | 0.47 | 0.77 | 0.78 |
| S2 | Qt, Qt−1 | 15 | 0.77 | 0.78 | 0.47 | 0.47 | 0.77 | 0.78 |
| S3 | Qt, Qt−1, Qt−2 | 15 | 0.77 | 0.78 | 0.47 | 0.47 | 0.77 | 0.78 |
| S4 | Qt, Qt−1, Qt−2, Qt−3 | 15 | 0.77 | 0.78 | 0.47 | 0.47 | 0.77 | 0.78 |
| S5 | Qt, Qt−1, Qt−2, Qt−3, Qt−4 | 15 | 0.78 | 0.78 | 0.47 | 0.47 | 0.77 | 0.78 |
| S6 | Qt, SCAt | 15 | 0.77 | 0.78 | 0.46 | 0.48 | 0.78 | 0.77 |
| S7 | Qt, SCAt, SCAt−1 | 20 | 0.77 | 0.77 | 0.46 | 0.48 | 0.77 | 0.77 |
| S8 | Qt, SCAt, SCAt−1, SCAt−2 | 15 | 0.77 | 0.77 | 0.46 | 0.48 | 0.77 | 0.77 |
| S9 | Qt, Rt−1, SCAt, SCAt−4 | 25 | 0.78 | 0.77 | 0.45 | 0.48 | 0.78 | 0.77 |
| S10 | Qt, Tt−1, Evapt−1, SCAt, SCAt−4 | 10 | 0.79 | 0.79 | 0.45 | 0.46 | 0.79 | 0.79 |
| S11 | Tt | 20 | 0.69 | 0.70 | 0.54 | 0.55 | 0.69 | 0.70 |
| S12 | Tt, Tt−1 | 15 | 0.70 | 0.70 | 0.53 | 0.55 | 0.70 | 0.70 |
| S13 | Tt, Tt−1, Tt−2 | 10 | 0.71 | 0.71 | 0.52 | 0.55 | 0.71 | 0.70 |
| S14 | Tt, Tt−1, Tt−2, Tt−3 | 10 | 0.72 | 0.71 | 0.52 | 0.54 | 0.72 | 0.71 |
| S15 | Tt, Tt−1, Tt−2, Tt−3, Tt−4 | 20 | 0.72 | 0.71 | 0.51 | 0.54 | 0.72 | 0.71 |
| Models | Training Period | Testing Period | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE | NSE | R2 | RMSE | NSE | |
| SRC | 0.81 | 0.49 | 0.75 | 0.71 | 0.60 | 0.66 |
| ANN | 0.81 | 0.42 | 0.81 | 0.82 | 0.43 | 0.81 |
| ANFIS-GP | 0.79 | 0.44 | 0.79 | 0.78 | 0.47 | 0.78 |
| ANFIS-SC | 0.80 | 0.43 | 0.80 | 0.79 | 0.46 | 0.79 |
| ANFIS-FCM | 0.80 | 0.43 | 0.80 | 0.78 | 0.47 | 0.78 |
| MARS | 0.79 | 0.45 | 0.79 | 0.79 | 0.46 | 0.79 |
| Year | Peaks > 3200 (tons/day) | ANN (tons/day) | ANFIS-GP (tons/day) | ANFIS-SC (tons/day) | ANFIS-FCM (tons/day) | MARS (tons/day) | SRC (tons/day) |
|---|---|---|---|---|---|---|---|
| 1983 | 3901 | 3934 (99.15) | 3884 (99.56) | 3886 (99.62) | 3613 (92.62) | 3826 (98.07) | 4654 (80.69) |
| 1984 | 4955 | 3542 (71.48) | 4543 (91.68) | 3033 (61.21) | 3789 (76.46) | 3385 (68.31) | 4375 (88.29) |
| 1991 | 3256 | 3088 (94.84) | 2804 (86.11) | 3128 (96.06) | 3093 (94.99) | 3105 (95.36) | 4468 (62.77) |
| 2003 | 4057 | 2372 (58.46) | 2514 (61.96) | 2616 (64.48) | 2790 (68.77) | 2674 (65.91) | 4400 (91.54) |
| 2005 | 16,898 | 12,993 (76.89) | 8949 (52.95) | 9480 (56.10) | 12,458 (73.72) | 12,365 (73.17) | 32,385 (8.35) |
| Mean (Relative Accuracy %) | 6613 | 5186 (80.17) | 4539 (78.45) | 4429 (75.49) | 5149 (81.31) | 5071 (80.16) | 10,056 (66.33) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hussan, W.U.; Khurram Shahzad, M.; Seidel, F.; Nestmann, F. Application of Soft Computing Models with Input Vectors of Snow Cover Area in Addition to Hydro-Climatic Data to Predict the Sediment Loads. Water 2020, 12, 1481. https://doi.org/10.3390/w12051481
Hussan WU, Khurram Shahzad M, Seidel F, Nestmann F. Application of Soft Computing Models with Input Vectors of Snow Cover Area in Addition to Hydro-Climatic Data to Predict the Sediment Loads. Water. 2020; 12(5):1481. https://doi.org/10.3390/w12051481
Chicago/Turabian StyleHussan, Waqas Ul, Muhammad Khurram Shahzad, Frank Seidel, and Franz Nestmann. 2020. "Application of Soft Computing Models with Input Vectors of Snow Cover Area in Addition to Hydro-Climatic Data to Predict the Sediment Loads" Water 12, no. 5: 1481. https://doi.org/10.3390/w12051481
APA StyleHussan, W. U., Khurram Shahzad, M., Seidel, F., & Nestmann, F. (2020). Application of Soft Computing Models with Input Vectors of Snow Cover Area in Addition to Hydro-Climatic Data to Predict the Sediment Loads. Water, 12(5), 1481. https://doi.org/10.3390/w12051481




