Possibility of Using Selected Rainfall-Runoff Models for Determining the Design Hydrograph in Mountainous Catchments: A Case Study in Poland
Abstract
:1. Introduction
2. Materials and Methods
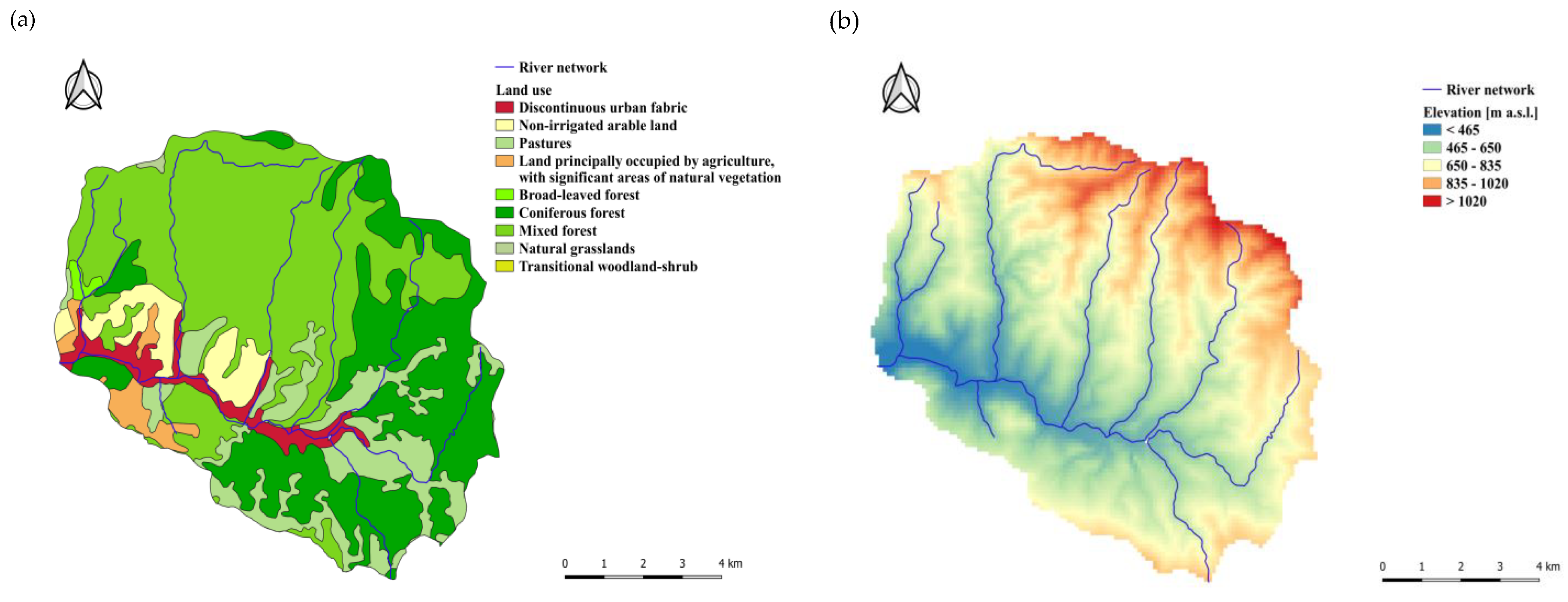
2.1. Research Area Characteristic
2.2. Hydrometeorological Data Verification
- n—number of elements in the time series.
- Var*(S)—corrected variance;
- n—the real number of observation;
- —effective number of observations calculated as:
- k—next group with repeating elements;
- ρk—value of the next significant autocorrelation coefficient.
2.3. Calculation of Maximum Annual Rainfall and Flows with Specific Occurrence Frequency
- xp—quantile of the theoretical log-normal distribution;
- ε—lower string limit;
- erf(2(1 − p) − 1)—Gauss error function.
2.4. Determination of the Design Hydrograph
- to—wave fall time (h);
- ts—wave rise time (h);
- Pe—excess rainfall (mm);
- P—total rainfall (mm);
- S—maximum potential catchment retention (mm).
- TL—delay time (h);
- Ct—factor related to catchment retention (-);
- L—maximum distance along the watercourse from the outlet cross-section to the drainage divide (km);
- Lc—distance along the main watercourse from the outlet cross-section to the centroid of the catchment (km).
- Qp—peak flow of the unit hydrograph (m3·s−1·mm);
- Cp—empirical coefficient resulting from the simplification of the hydrograph to triangular shape (-);
- A—catchment area (km2).
- qp—peak flow of the unit hydrograph (m3·s−1·mm);
- c—conversion factor (c = 0.208) (-);
- Tp—flood rise time, (h), calculated as:
- D—duration of excess rainfall (h);
- TLAG—lag time in the SCS-UH method, (h), calculated as:
- L—maximum length of the runoff path (km);
- CN—Curve Number value (-);
- I—average catchment slope (%).
- q0—infiltration indicator;
- tp—ponding time;
- Ks—saturated hydraulic conductivity;
- I—cumulative infiltration;
- Δθ—change in soil-water content between the initial value and the field saturated soil-water content;
- ΔH—difference between the pressure head at the soil surface and the matric pressure head at the moving wetting front.
- Lc, Lh—hillslope and channel flow paths, functions of DEM cell x, respectively;
- Vc, Vh—runoff velocity for hillslope cells and flow channel cells.
- A—catchment area (km2);
- T—duration of rainfall (h);
- Pn(t)—excess rainfall determined by the CN4GA method (mm/h).
2.5. Assessment of Quality of Analysed Hydrological Models
- Qm,max—maximum flow with a certain frequency of occurrence, calculated using rainfall-runoff models (m3·s−1);
- Qs,max—maximum flow with a specified frequency of occurrence, calculated using the log-normal distribution on observed data (m3·s−1).
3. Results
3.1. Hydrometeorological Data Verification
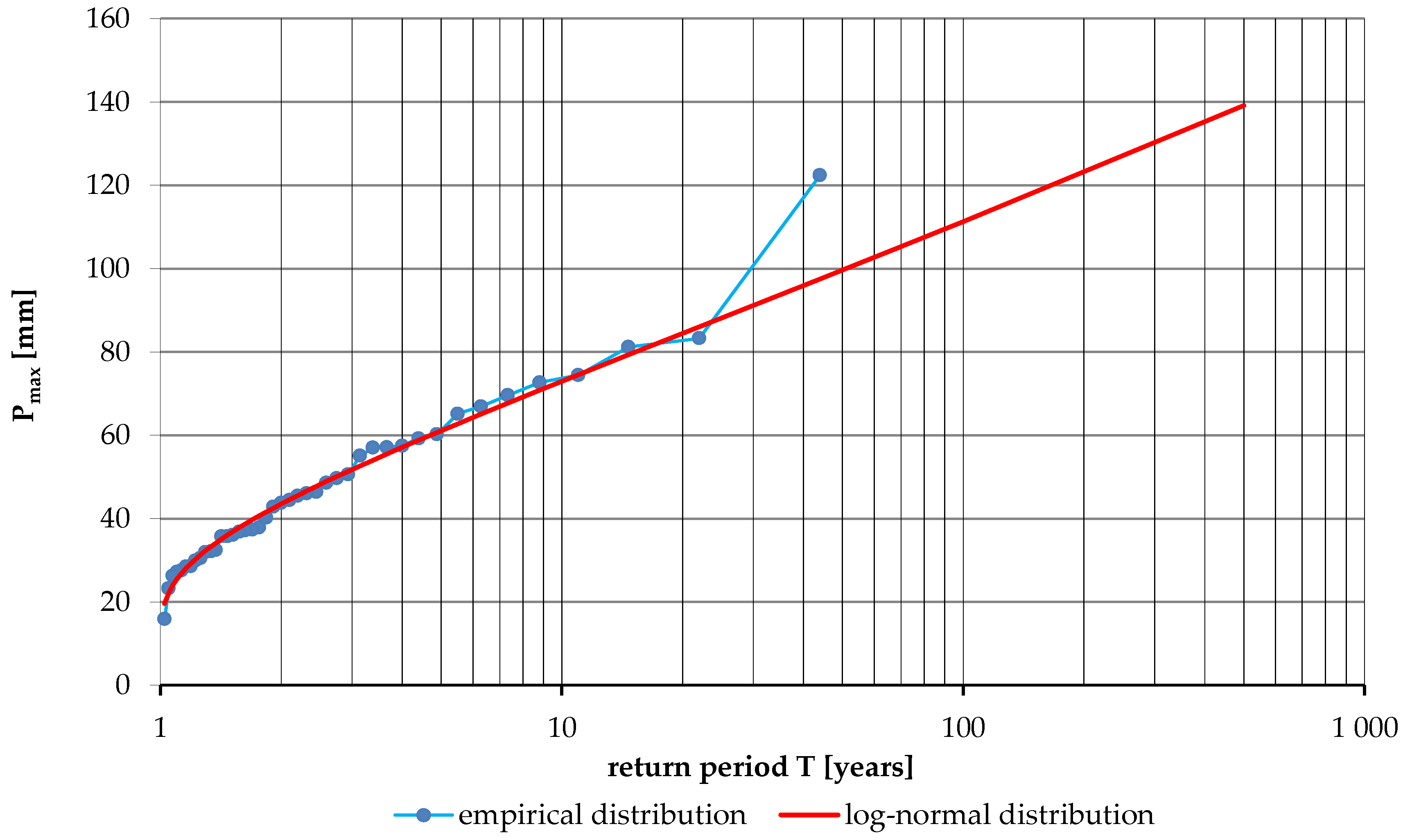
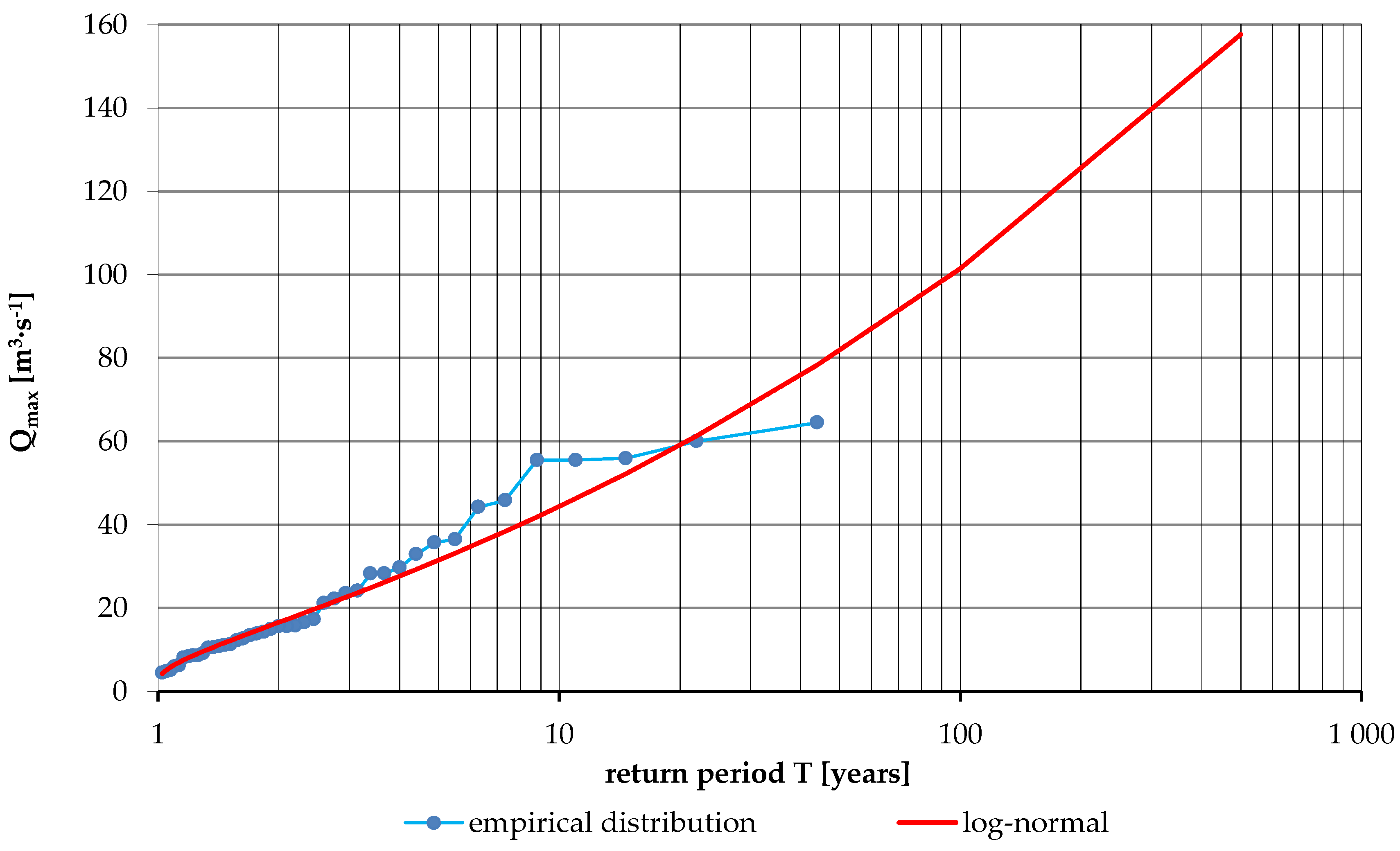
3.2. Determination of Rainfall and Peak Flows at a Specific Occurrence Frequency
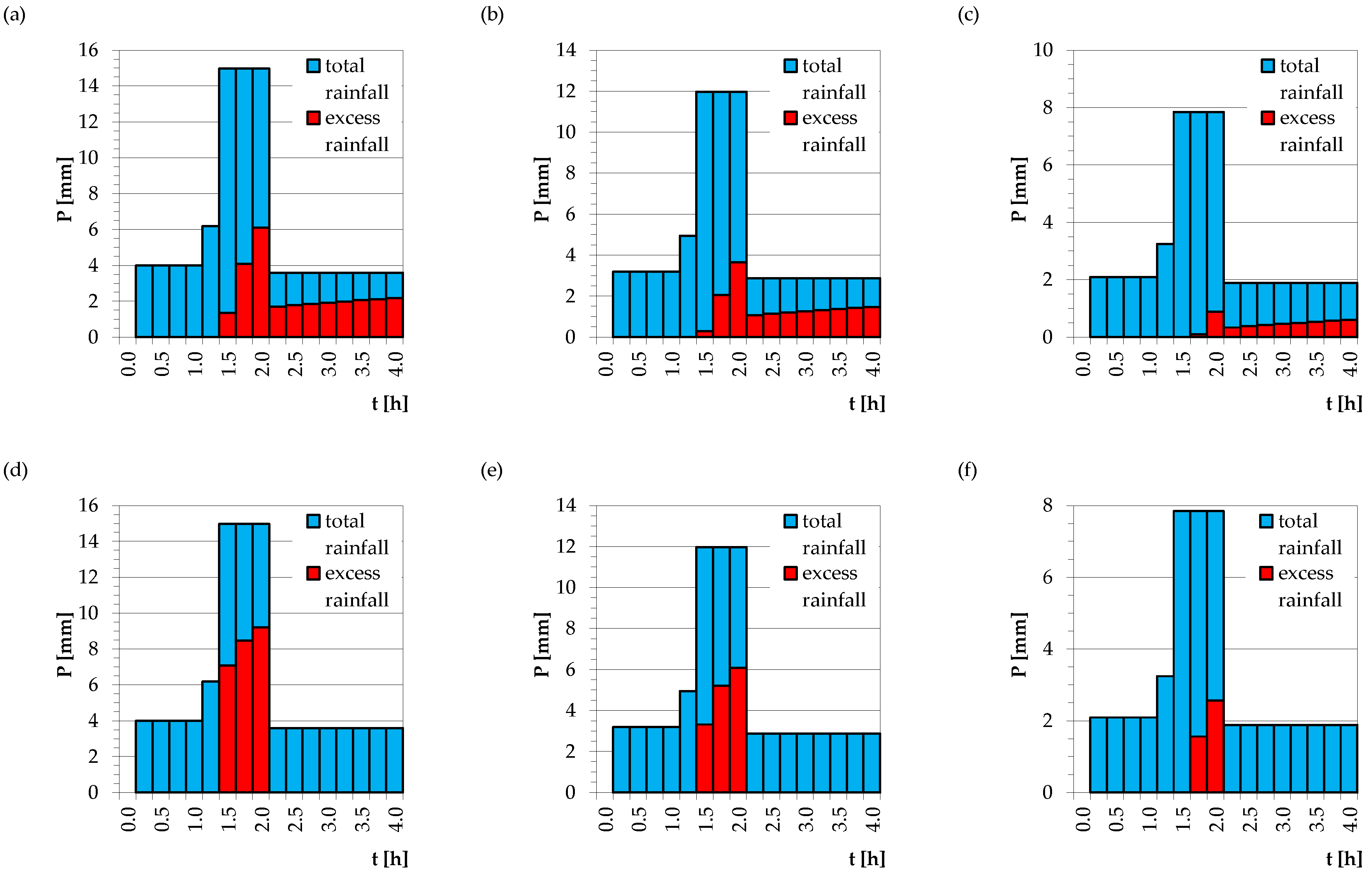
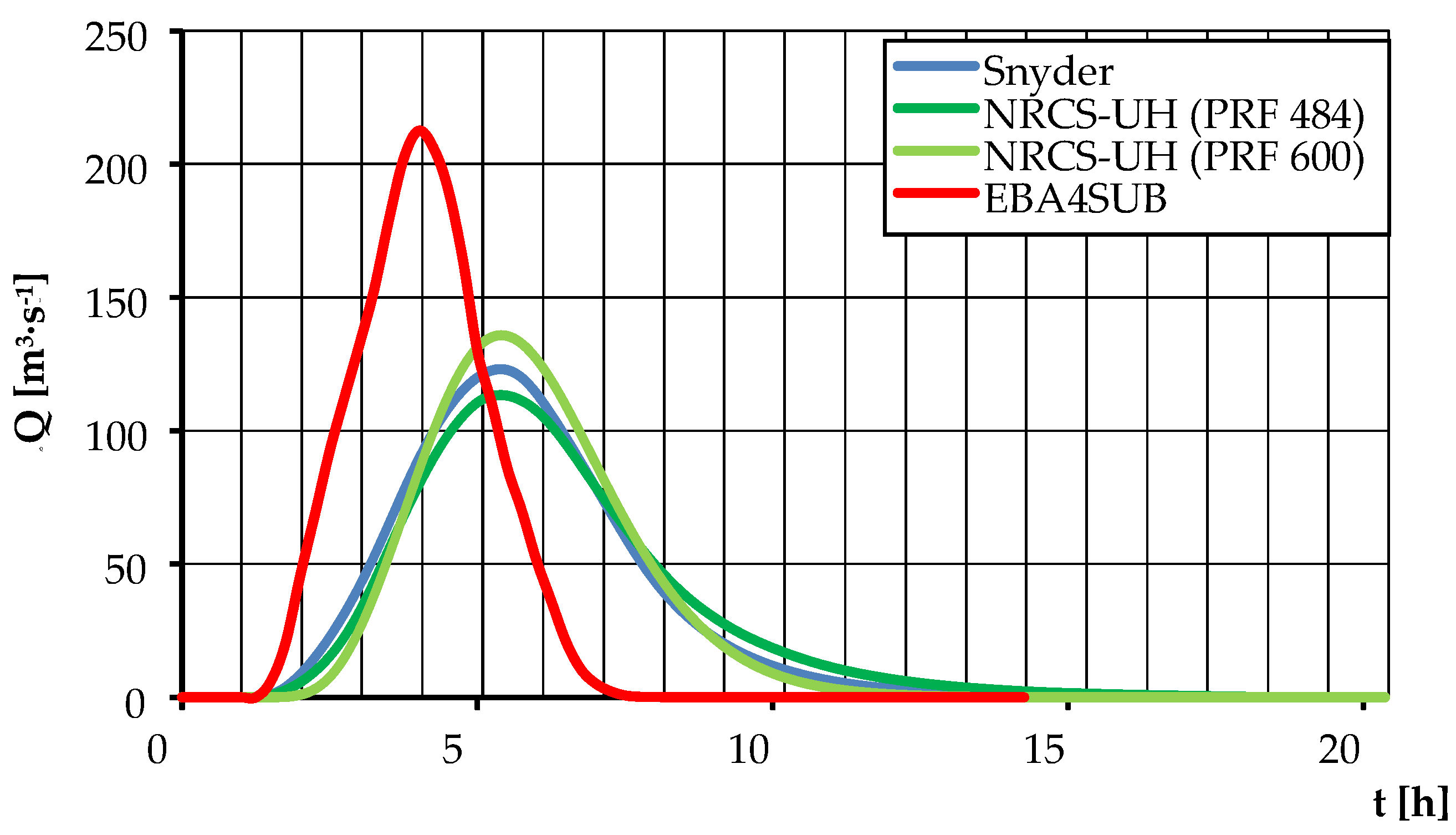
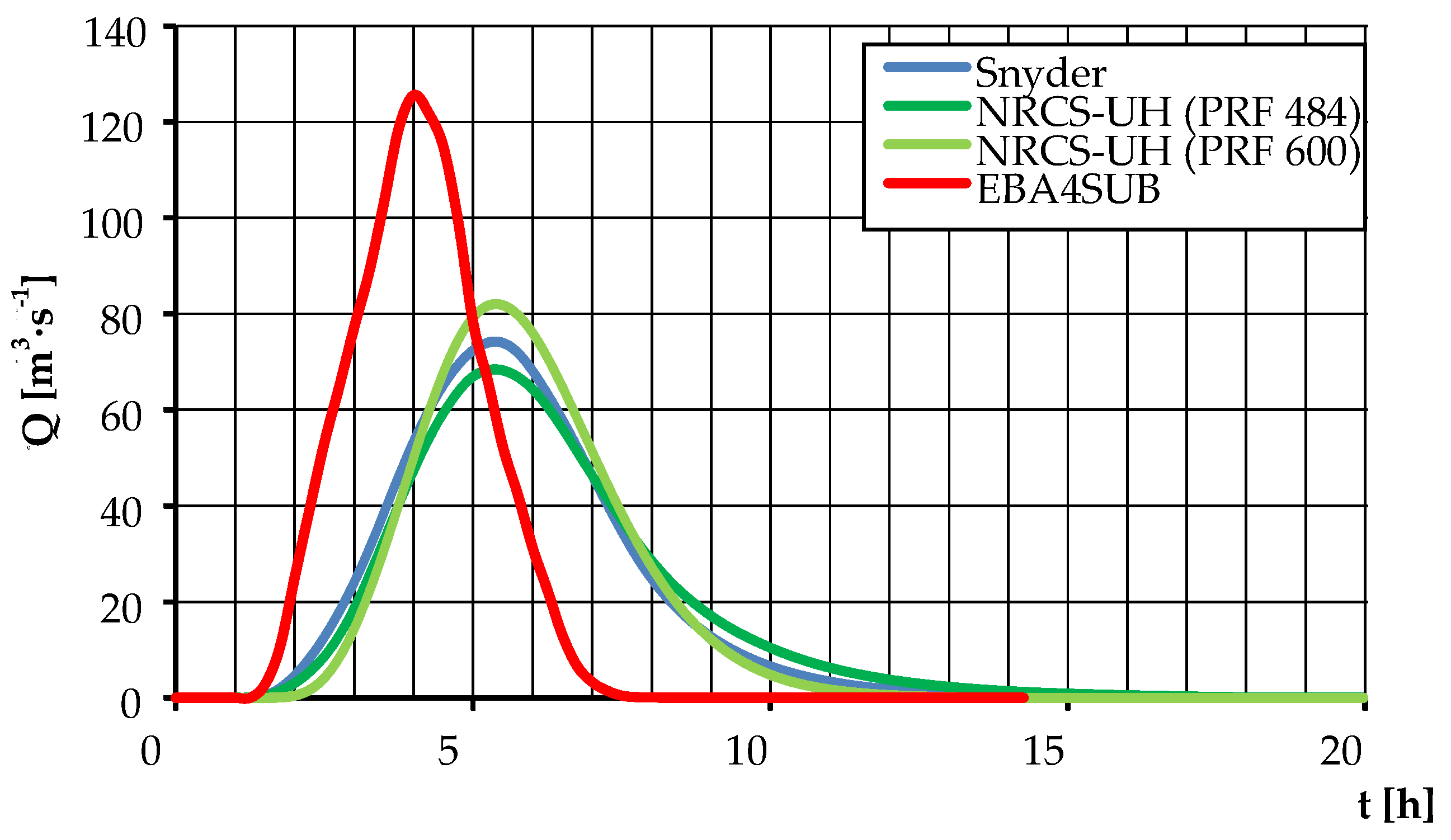
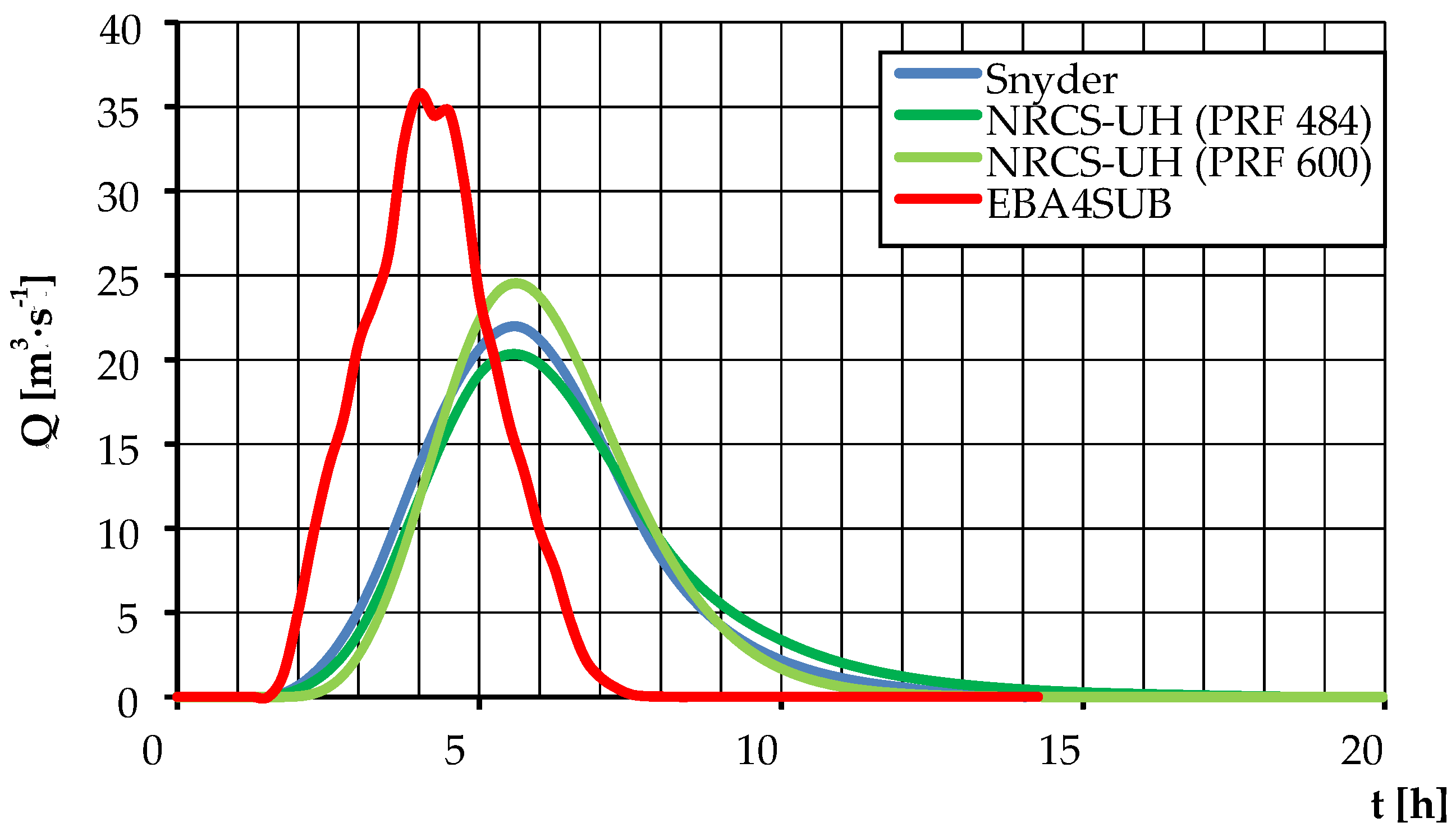
3.3. Determination of Design Hydrographs Employing the Selected Rainfall-Runoff Models
3.4. Evaluation of the Quality of Analysed Hydrological Models
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Cerdà Bolinches, A.; Lucas Borja, M.E.; Úbeda, X.; Martínez Murillo, J.F.; Keesstra, S. Pinus halepensis M. versus Quercus ilex subsp. Rotundifolia L. runoff and soil erosion at pedon scale under natural rainfall in Eastern Spain three decades after a forest fire. For. Ecol. Manag. 2018, 400, 447–456. [Google Scholar] [CrossRef] [Green Version]
- Van Eck, C.M.; Nunes, J.P.; Vieira, D.C.; Keesstra, S.; Keizer, J.J. Physically-Based modelling of the post-fire runoff response of a forest catchment in central Portugal: Using field versus remote sensing based estimates of vegetation recovery. Land Degrad. Dev. 2016, 27, 1535–1544. [Google Scholar] [CrossRef]
- Banach, W. Determination of synthetic flood hydrograph in ungauged catchments. Infrastruct. Ecol. Rural Areas 2011, 12, 147–156. [Google Scholar]
- Salami, A.W.; Bilewu, S.O.; Ibitoye, A.B.; Ayanshola, A.M. Runoff hydrographs using Snyder and SCS unit hydrograph methods: A case study of selected rivers in south west Nigeria. J. Ecol. Eng. 2017, 18, 25–34. [Google Scholar] [CrossRef] [Green Version]
- Gądek, W. Assessment of limingraph data usefulness for determining the hypothetical flood waves with the Cracow method. J. Water Land Dev. 2014, 21, 71–78. [Google Scholar] [CrossRef] [Green Version]
- Gądek, W.; Środula, A. The evaluation of the design flood hydrographs determined with the Hydroproject method in the gauged catchments. Infrastruct. Ecol. Rural Areas 2014, 4, 29–47. [Google Scholar]
- Pietrusiewicz, I.; Cupak, A.; Wałęga, A.; Michalec, B. The use of NRCS synthetic unit hydrograph and Wackerman conceptual model in the simulation of a flood wave in uncontrolled catchment. J. Water Land Dev. 2014, 23, 53–59. [Google Scholar] [CrossRef] [Green Version]
- Wypych, A.; Ustrnul, Z.; Henek, E. Meteorological hazards—Visualization system of national protection against extreme hazards for Poland. Meteorol. Hydrol. Water Manag. 2014, 2, 37–42. [Google Scholar] [CrossRef]
- Karabová, B.; Sikorska, A.; Banasik, K.; Kohnová, S. Parameters determination of a conceptual rainfall-runoff model for a small catchment in Carpathians. Ann. Wars. Univ. Life Sci. SGGW 2012, 44, 155–162. [Google Scholar]
- Wałęga, A.; Młyński, D. Seasonality of median monthly discharge in selected Carpathian rivers of the upper Vistula basin. Carpath. J. Earth Environ. Sci. 2017, 12, 617–628. [Google Scholar]
- Tolentino, P.L.M.; Poortinga, A.; Kanamaru, H.; Keesstra, S.; Maroulis, J.; David, C.P.C.; Ritsema, C.J. Projected impact of climate change on hydrological regimes in the Philippines. PLoS ONE 2016, 11, e0163941. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Wang, S.; Bai, X.; Shu, D.; Tian, Y. Runoff response to climate change and human activities in a typical karst watershed, SW China. PLoS ONE 2018, 13, e0193073. [Google Scholar] [CrossRef] [PubMed]
- Blair, A.; Sanger, D.; White, D.; Holland, A.F.; Vandiver, L.; Bowker, C.; White, S. Quantifying and simulating stormwater runoff in watersheds. Hydrol. Process. 2012, 28, 559–569. [Google Scholar] [CrossRef]
- Banasik, K.; Rutkowska, A.; Kohnová, S. Retention and Curve Number variability in a small agricultural catchment: The probabilistic approach. Water 2014, 6, 1118–1133. [Google Scholar] [CrossRef]
- Kowalik, T.; Wałęga, A. Estimation of CN Parameter for small agricultural watersheds using asymptotic functions. Water 2015, 7, 939–955. [Google Scholar] [CrossRef] [Green Version]
- Wałega, A.; Książek, L. Influence of rainfall data on the uncertainty of flood simulation. Soil Water Res. 2016, 11, 277–284. [Google Scholar] [CrossRef] [Green Version]
- Grimaldi, S.; Petroselli, A. Do we still need the Rational Formula? An alternative empirical procedure for peak discharge estimation in small and ungauged basins. Hydrol. Sci. J. 2015, 60, 67–77. [Google Scholar] [CrossRef]
- Piscopia, R.; Petroselli, A.; Grimaldi, S. A software package for the prediction of design flood hydrograph in small and ungauged basins. J. Agric. Eng. 2015, 432, 74–84. [Google Scholar]
- Petroselli, A.; Grimaldi, S. Design hydrograph estimation in small and fully ungauged basin: A preliminary assessment of the EBA4SUB framework. J. Flood Risk Manag. 2018, 11, 197–2010. [Google Scholar] [CrossRef]
- Sun, S.; Barraud, S.; Branger, F.; Braud, I.; Castebrunet, H. Urban hydrology trend analysis based on rainfall and runoff data analysis and conceptual model calibration. Hydrol. Process. 2017, 31, 1349–1359. [Google Scholar] [CrossRef] [Green Version]
- Operacz, A.; Wałęga, A.; Cupak, A.; Tomaszewska, B. The comparison of environmental flow assessment—The barrier for investment in Poland or river protection? J. Clean. Prod. 2018, 193, 575–592. [Google Scholar] [CrossRef]
- Viglione, A.; Blöschl, G. On the role of storm duration in the mapping of rainfall to flood return period. Hydrol. Earth Syst. Sci. Discuss. 2008, 5, 3419–3447. [Google Scholar] [CrossRef]
- Hogg, R.V.; Craig, A.T. Introduction to Mathematical Statistics; Macmilan Publishing Co.: New York, NY, USA, 1978. [Google Scholar]
- Grimaldi, S.; Petroselli, A.; Tauro, F.; Porfiri, M. Time of concentration: A paradox in modern hydrology. Hydrol. Sci. J. 2012, 57, 217–228. [Google Scholar] [CrossRef] [Green Version]
- Wałęga, A.; Drożdżal, E.; Piórecki, M.; Radoń, R. Some problems of hydrology modelling of outflow from ungauged catchments with aspect of flood maps design. Acta Sci. Pol. Form. Circumiectus 2012, 11, 57–68. (In Polish) [Google Scholar]
- Wałęga, A. The importance of calibration parameters on the accuracy of the floods description in the Snyder’s model. J. Water Land Dev. 2016, 28, 19–25. [Google Scholar] [CrossRef]
- Soulis, K.X.; Dercas, N. Development of a GIS-based Spatially Distributed Continuous Hydrological Model and its First Application. Water Int. 2007, 32, 177–192. [Google Scholar] [CrossRef]
- Soulis, K.X.; Valiantzas, J.D. Identification of the SCS-CN Parameter Spatial Distribution Using Rainfall-Runoff Data in Heterogeneous Watersheds. Water Res. Man. 2013, 27, 1737–1749. [Google Scholar] [CrossRef]
- Xiao, B.; Wang, Q.; Fan, J.; Han, F.; Dai, Q. Application of the SCS-CN Model to Runoff Estimation in a Small Watershed with High Spatial Heterogeneity. Pedosphere 2011, 26, 738–749. [Google Scholar] [CrossRef]
- Soulis, K.X.; Valiantzas, J.D. SCS-CN parameter determination using rainfall-runoff data in heterogeneous watersheds—The two-CN system approach. Hydrol. Earth Syst. Sci. 2012, 16, 1001–1015. [Google Scholar] [CrossRef] [Green Version]
- Soulis, K.X. Estimation of SCS Curve Number variation following forest fires. Hydrol. Sci. J. 2018, 63, 1332–1346. [Google Scholar] [CrossRef]
- Wałęga, A.; Salata, T. Influence of land cover data sources on estimation of direct runoff according to SCS-CN and modified SME methods. Catena 2019, 172, 232–242. [Google Scholar] [CrossRef]
- Singh, P.K.; Mishra, S.K.; Jain, M.K. A review of the synthetic unit hydrograph: From the empirical UH to advanced geomorphological methods. Hydrol. Sci. J. 2014, 59, 239–261. [Google Scholar] [CrossRef]
- Sudhakar, B.S.; Anupam, K.S.; Akshay, A.J. Snyder unit hydrograph and GIS for estimation of flood for un-gauged catchments in lower Tapi basin, India. Hydrol. Curr. Res. 2015, 6, 1–10. [Google Scholar]
- Federova, D.; Kovář, P.; Gregar, J.; Jelínková, A.; Novotná, J. The use of Snyder synthetic hydrograph for simulation of overland flow in small ungauged and gauged catchments. Soil Water Res. 2018, 13, 185–192. [Google Scholar]
- Amatya, D.M.; Cupak, A.; Wałęga, A. Influence of time concentration on variation of runoff from a small urbanized watershed. GLL 2015, 2, 7–19. [Google Scholar]
- Grimaldi, S.; Petroselli, A.; Romano, N. Curve-Number/Green–Ampt mixed procedure for streamflow predictions in ungauged basins: Parameter sensitivity analysis. Hydrol. Process. 2013, 27, 1265–1275. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Nardi, F.; Alonso, G. Flow time estimation with variable hillslope velocity in ungauged basins. Adv. Water Resour. 2010, 33, 1216–1223. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H. A new metric of absolute percentage error for intermittent demand forecast. Int. J. Forecast 2016, 32, 669–679. [Google Scholar] [CrossRef]
- Niedźwiedź, T.; Łupikasza, E.; Pińskwar, I.; Kundzewicz, Z.W.; Stoffel, M.; Małarzewski, Ł. Climatological background of floods at the northern foothills of the Tatra Mountains. Theor. Appl. Climatol. 2014, 119, 273–284. [Google Scholar] [CrossRef] [Green Version]
- Młyński, D.; Cebulska, M.; Wałęga, A. Trends, variability, and seasonality of Maximum annual daily precipitation in the upper Vistula basin, Poland. Atmosphere 2018, 9, 313. [Google Scholar] [CrossRef] [Green Version]
- Kundzewicz, Z.W.; Stoffel, M.; Kaczka, R.J.; Wyżga, B.; Niedźwiedź, T.; Pińskwar, I.; Ruiz-Villanueva, V.; Łupikasza, E.; Czajka, B.; Ballesteros-Canovas, J.A. Floods at the Northern Foothills of the Tatra Mountains—A Polish–Swiss Research Project. Acta Geophys. 2014, 62, 620–641. [Google Scholar] [CrossRef]
- Wałęga, A.; Młyński, D.; Bogdał, A.; Kowalik, T. Analysis of the course and frequency of high water stages in selected catchments of the Upper Vistula basin in the south of Poland. Water 2016, 8, 394. [Google Scholar] [CrossRef]
- Młyński, D.; Petroselli, A.; Wałęga, A. Flood frequency analysis by an event-based rainfall-runoff model in selected catchments of southern Poland. Soil Water Res. 2018, 13, 170–176. [Google Scholar]
- Kundzewicz, Z.W.; Pińskwar, I.; Choryński, A.; Wyżga, B. Floods still pose a hazard. Aura 2017, 3, 3–9. (In Polish) [Google Scholar]
- Młyński, D.; Wałęga, A.; Stachura, T.; Kaczor, G. A new empirical approach to calculating flood frequency in ungauged catchments: A case study of the upper Vistula basin, Poland. Water 2019, 11, 601. [Google Scholar] [CrossRef] [Green Version]
- Młyński, D.; Wałęga, A.; Petroselli, A.; Tauro, F.; Cebulska, M. Estimating maximum daily precipitation in the upper Vistula basin, Poland. Atmosphere 2019, 10, 43. [Google Scholar] [CrossRef] [Green Version]
- Kuczera, G. Robust flood frequency models. Water Resour. Res. 1982, 18, 315–324. [Google Scholar] [CrossRef]
- Strupczewski, W.G.; Singh, V.P.; Mitosek, H.T. Non-stationary approach to at site flood frequency modeling. III. Flood analysis for Polish rivers. J. Hydrol. 2001, 248, 152–167. [Google Scholar] [CrossRef]
- Wałęga, A.; Rutkowska, A. Usefulness of the modified NRCS-CN method for the assessment of direct runoff in a mountain catchment. Acta Geophys. 2015, 63, 1423–1446. [Google Scholar] [CrossRef] [Green Version]
- Soulis, K.X.; Valiantzas, J.D.; Dercas, N.; Londra, P.A. Investigation of the direct runoff generation mechanism for the analysis of the SCS-CN method applicability to a partial area experimental watershed. Hydrol. Earth Syst. Sci. 2009, 13, 605–615. [Google Scholar] [CrossRef] [Green Version]
- Walega, A.; Amatya, D.M.; Caldwell, P.; Marion, D.; Panda, S. Assessment of storm direct runoff and peak flow rates using improved SCS-CN models for selected forested watersheds in the Southeastern United States. J. Hydrol. Reg. Stud. 2020, 27, 1–18. [Google Scholar] [CrossRef]
- Maidment, D.W.; Hoogerwerf, T.N. Parameter Sensitivity in Hydrologic Modeling. Technical Report; The University of Texas: Austin, TX, USA, 2002. [Google Scholar]
- Wałęga, A. An attempt to establish regional dependecies for the parameter calculation of the Snyder’s syntetic unit hydrograph. Infrastruct. Ecol. Rural Areas 2012, 2, 5–16. [Google Scholar]
- Ignacio, J.A.F.; Cruz, G.T.; Nardi, F.; Henry, S. Assessing the effectiveness of a social vulnerability index in predicting heterogeneity in the impacts of natural hazards: Case study of the Tropical Storm Washi flood in the Philippines. Vienna Yearb. Popul. Res. 2015, 13, 91–129. [Google Scholar]
- Cerdà, A.; Rodrigo-Comino, J.; Novara, A.; Brevik, E.C.; Vaezi, A.R.; Pulido, M.; Gimenez-Morera, A.; Keesstra, S.D. Long-term impact of rainfed agricultural land abandonment on soil erosion in the Western Mediterranean basin. Prog. Phys. Geogr. 2018, 42, 202–219. [Google Scholar]
- Keesstra, S.D. Impact of natural reforestation on floodplain sedimentation in the Dragonja basin, SW Slovenia. Earth Surf. Process. Landf. 2007, 32, 49–65. [Google Scholar] [CrossRef]
- Recanatesi, F.; Petroselli, A.; Ripa, M.N.; Leone, A. Assessment of stormwater runoff management practices and BMPs under soil sealing: A study case in a peri-urban watershed of the metropolitan area of Rome (Italy). J. Environ. Manag. 2017, 201, 6–18. [Google Scholar] [CrossRef]

| Characteristic | Zc | pc | Varc | n/n * | Z | p | Var |
|---|---|---|---|---|---|---|---|
| Pmax | 1.582 | 0.114 | 7721.554 | 0.846 | 1.455 | 0.146 | 9129.333 |
| Qmax | 1.143 | 0.253 | 9766.667 | 1.000 | 1.143 | 0.253 | 9766.667 |
| Return Period | Tc (h) | CN | P (mm) | Pnet (mm) |
|---|---|---|---|---|
| 500 | 4 | 68.1 | 95.8 | 24.7 |
| 100 | 76.6 | 14.6 | ||
| 10 | 50.2 | 4.1 |
| Characteristic | Snyder | NRCS-UH | EBA4SUB | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 500 | 100 | 10 | 500 | 100 | 10 | 500 | 100 | 10 | |
| Qmax [m3·s−1] | 122.909 | 74.191 | 21.975 | 113.235 * | 68.424 * | 20.329 * | 212.531 | 125.602 | 35.779 |
| 135.483 ** | 82.059 ** | 24.529 ** | |||||||
| V [mln m3] | 2.291 | 1.377 | 0.403 | 2.291 | 1.377 | 0.403 | 2.078 | 1.226 | 0.346 |
| t [h] | 15.250 | 15.250 | 15.000 | 21.750 * | 21.750 * | 21.500 * | 6.800 | 6.800 | 6.500 |
| 16.000 ** | 15.750 ** | 15.500 ** | |||||||
| α [–] | 2.100 | 1.952 | 1.905 | 3.150 * | 3.000 * | 2.950 * | 1.545 | 1.545 | 1.500 |
| 2.095 ** | 2.095 ** | 2.150 ** | |||||||
| Model | MAPE [%] | ||
|---|---|---|---|
| 500 | 100 | 10 | |
| Snyder | 22.0 | 26.9 | 50.5 |
| NRCS-UH (PRF 484) | 28.2 | 32.6 | 54.2 |
| NRCS-UH (PRF 600) | 14.1 | 19.1 | 44.7 |
| EBA4SUB | −34.8 | −23.8 | 19.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Młyński, D.; Wałęga, A.; Książek, L.; Florek, J.; Petroselli, A. Possibility of Using Selected Rainfall-Runoff Models for Determining the Design Hydrograph in Mountainous Catchments: A Case Study in Poland. Water 2020, 12, 1450. https://doi.org/10.3390/w12051450
Młyński D, Wałęga A, Książek L, Florek J, Petroselli A. Possibility of Using Selected Rainfall-Runoff Models for Determining the Design Hydrograph in Mountainous Catchments: A Case Study in Poland. Water. 2020; 12(5):1450. https://doi.org/10.3390/w12051450
Chicago/Turabian StyleMłyński, Dariusz, Andrzej Wałęga, Leszek Książek, Jacek Florek, and Andrea Petroselli. 2020. "Possibility of Using Selected Rainfall-Runoff Models for Determining the Design Hydrograph in Mountainous Catchments: A Case Study in Poland" Water 12, no. 5: 1450. https://doi.org/10.3390/w12051450






