Optimal In-Stream Structure Design through Considering Nitrogen Removal in Hyporheic Zone
Abstract
:1. Introduction
2. Materials and Methods
2.1. Numerical Model
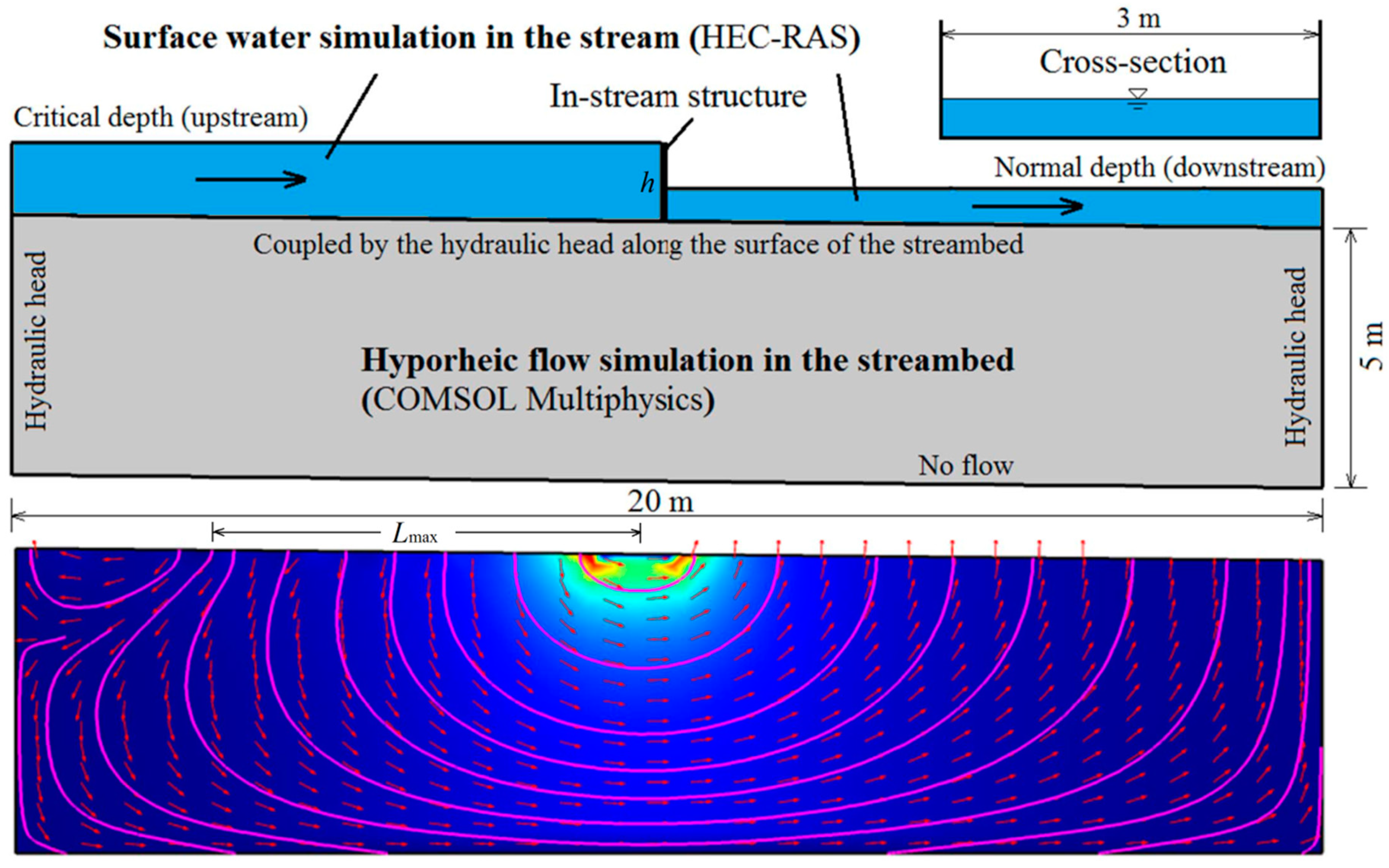
2.1.1. Hydrologic Engineering Center’s River Analysis System (HEC-RAS) for Surface Water Simulation
2.1.2. COMSOL Multiphysics for Hyporheic Flow Simulation
2.1.3. Nitrogen Transport/Removal Calculation
2.1.4. Modeling Scenarios
2.2. Optimal In-Stream Structure Design
2.2.1. Framework
2.2.2. Relevant Indicators
2.2.3. Objective Function
2.3. Validation and Sensitivity Analysis Methods
3. Results and Discussion
3.1. Regression Equations
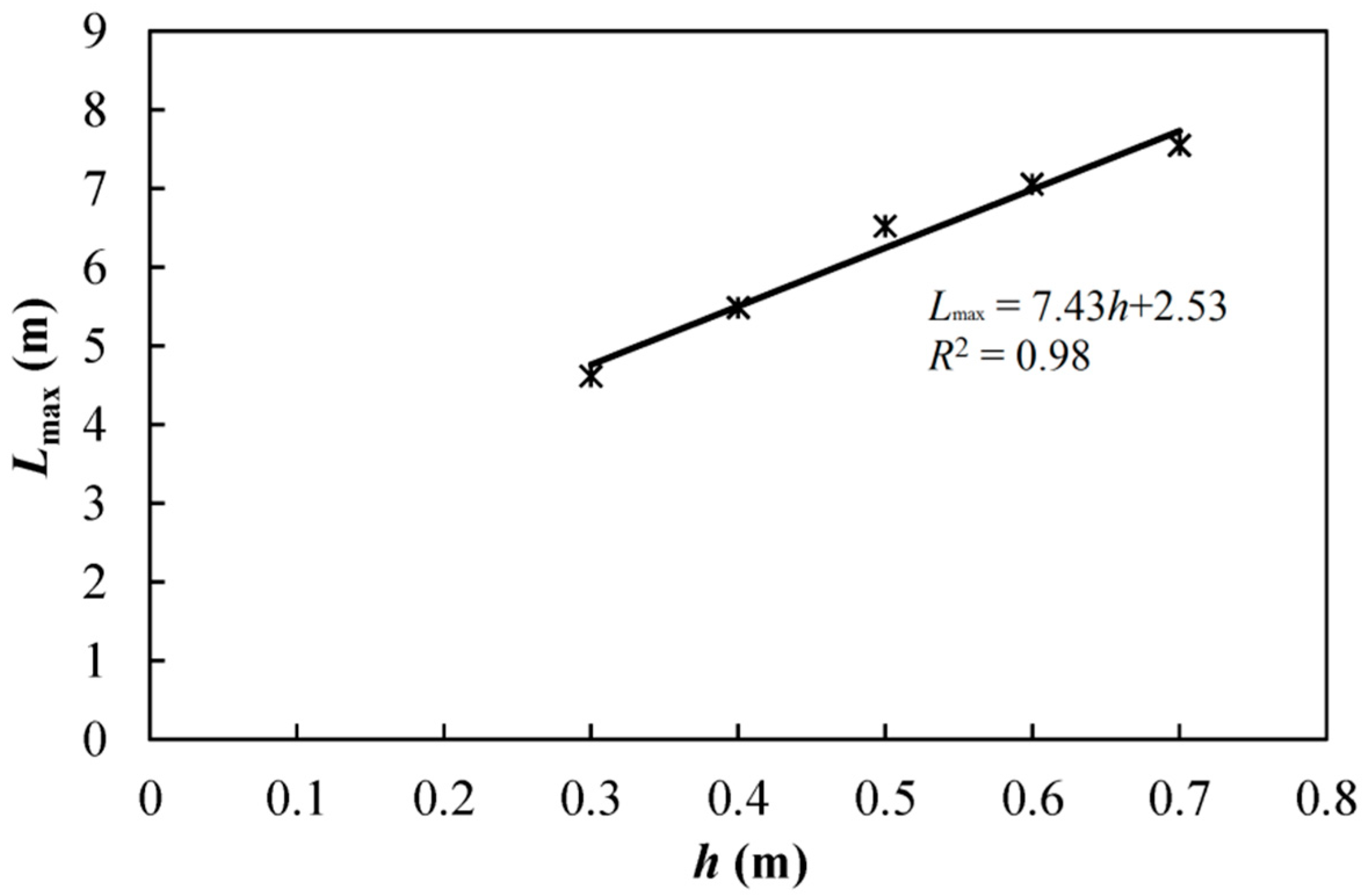
3.1.1. The Maximum Upstream Distance in the Subsurface Flow Influenced by the Weir (Lmax)
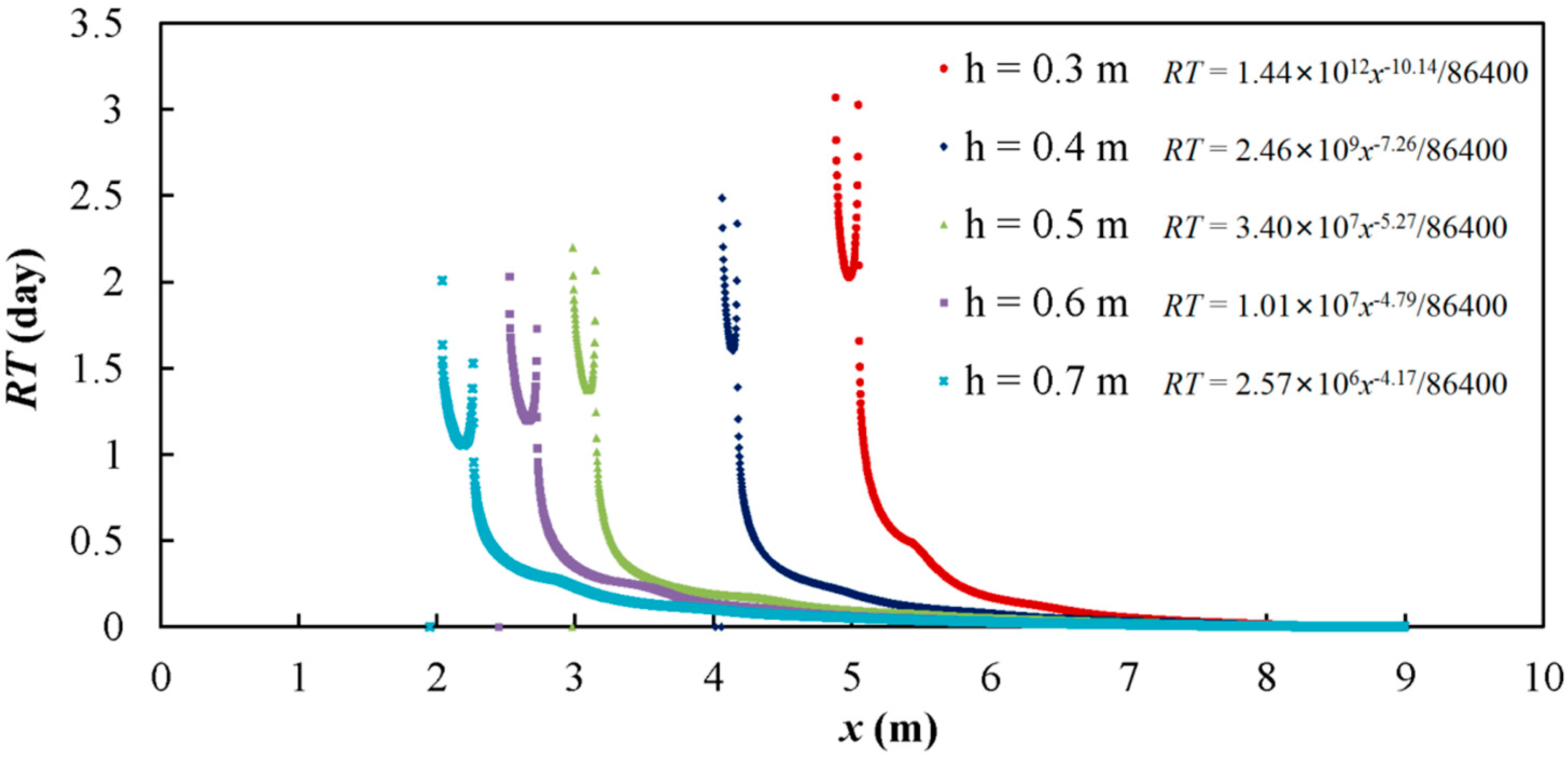
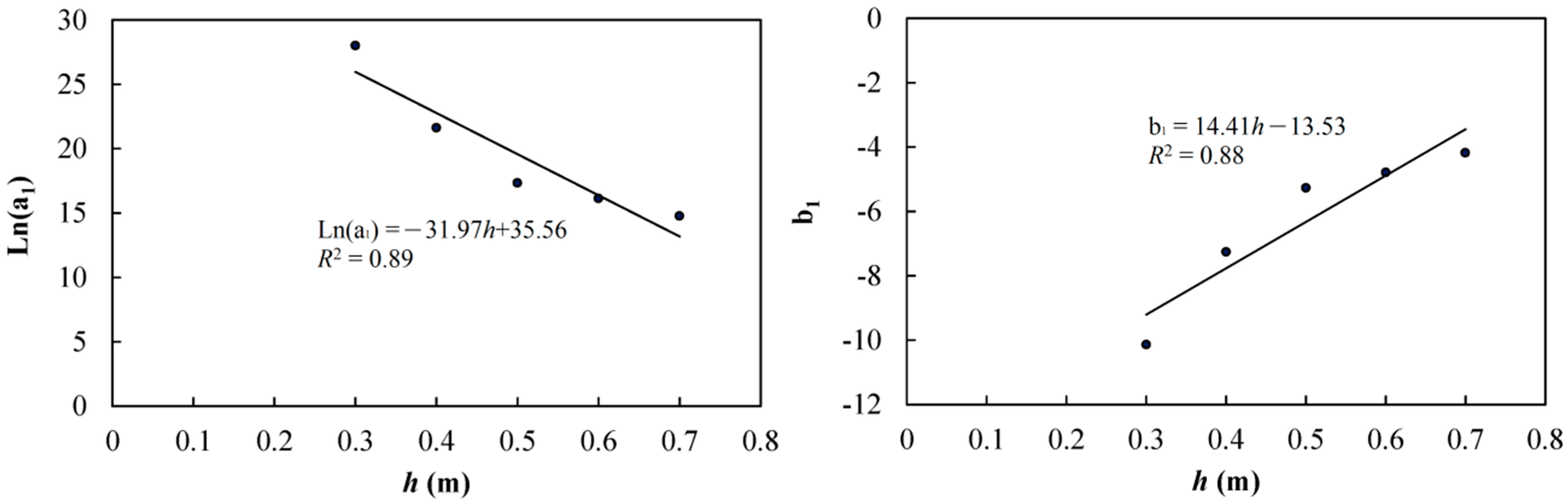
3.1.2. Residence Time (RT)
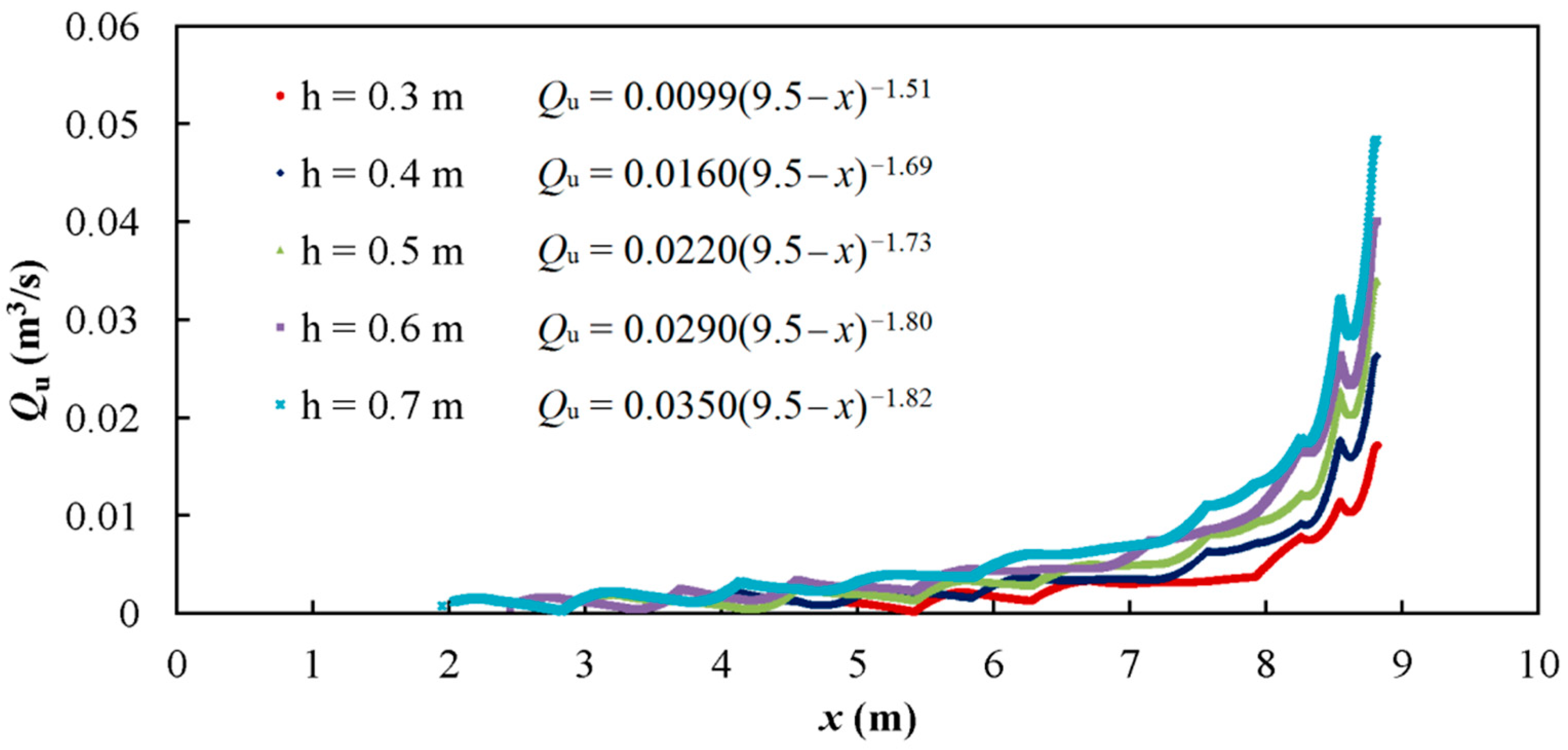
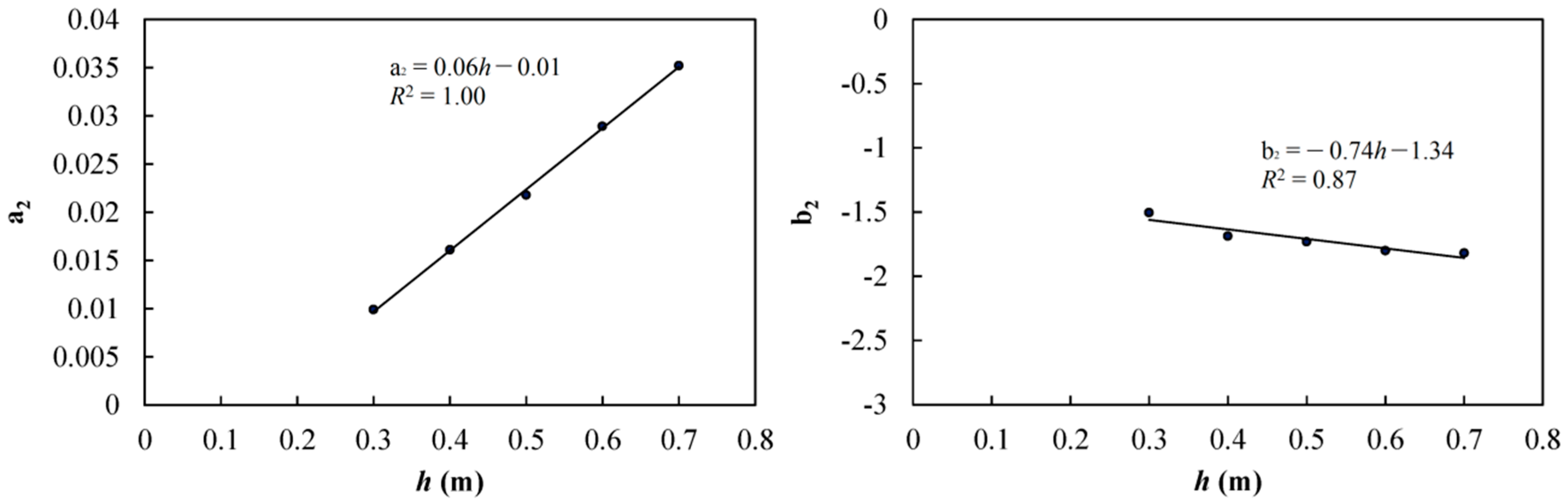
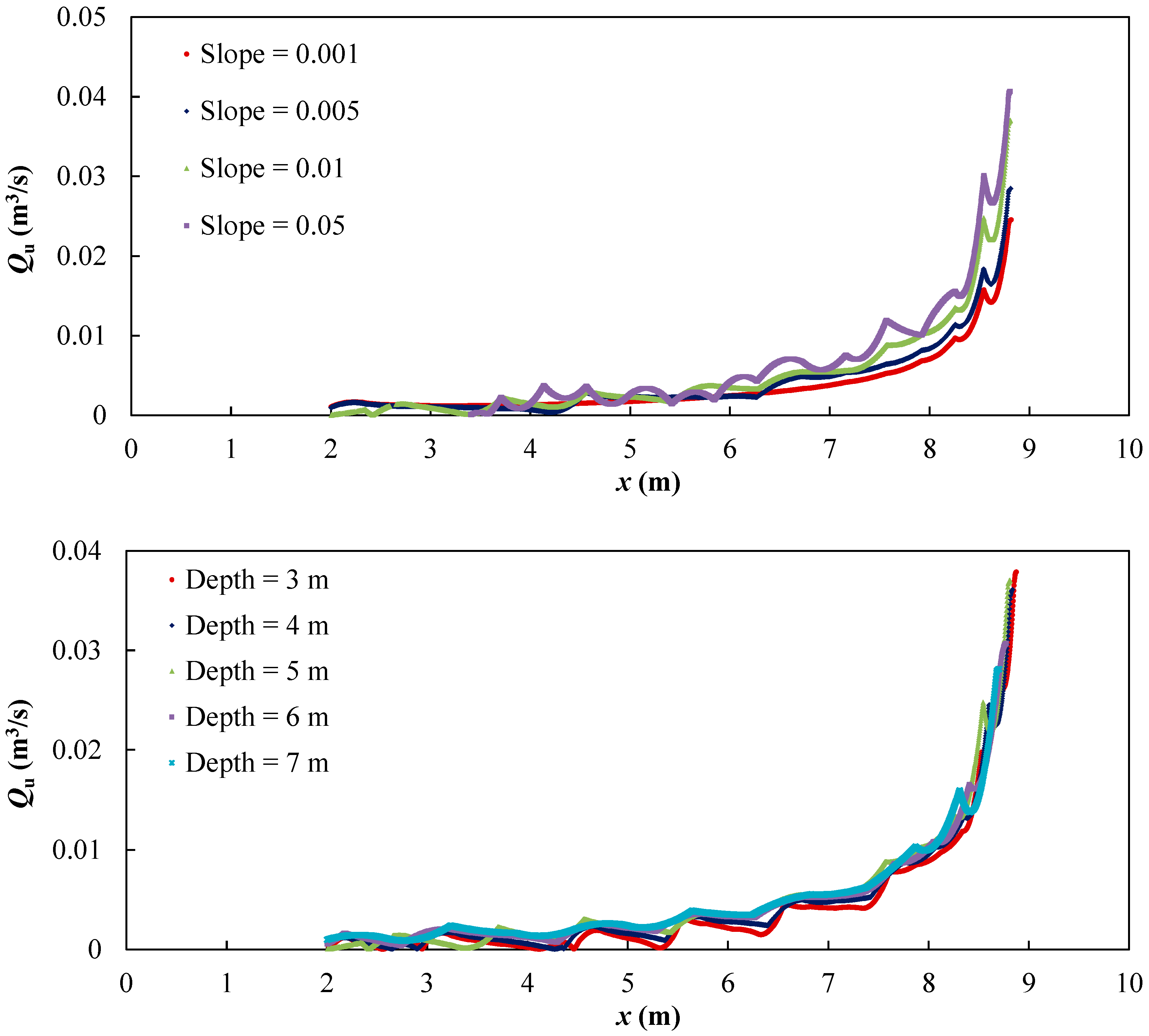
3.1.3. Hyporheic Flux in the Upstream (Qu)
3.2. Objective Function Calculation
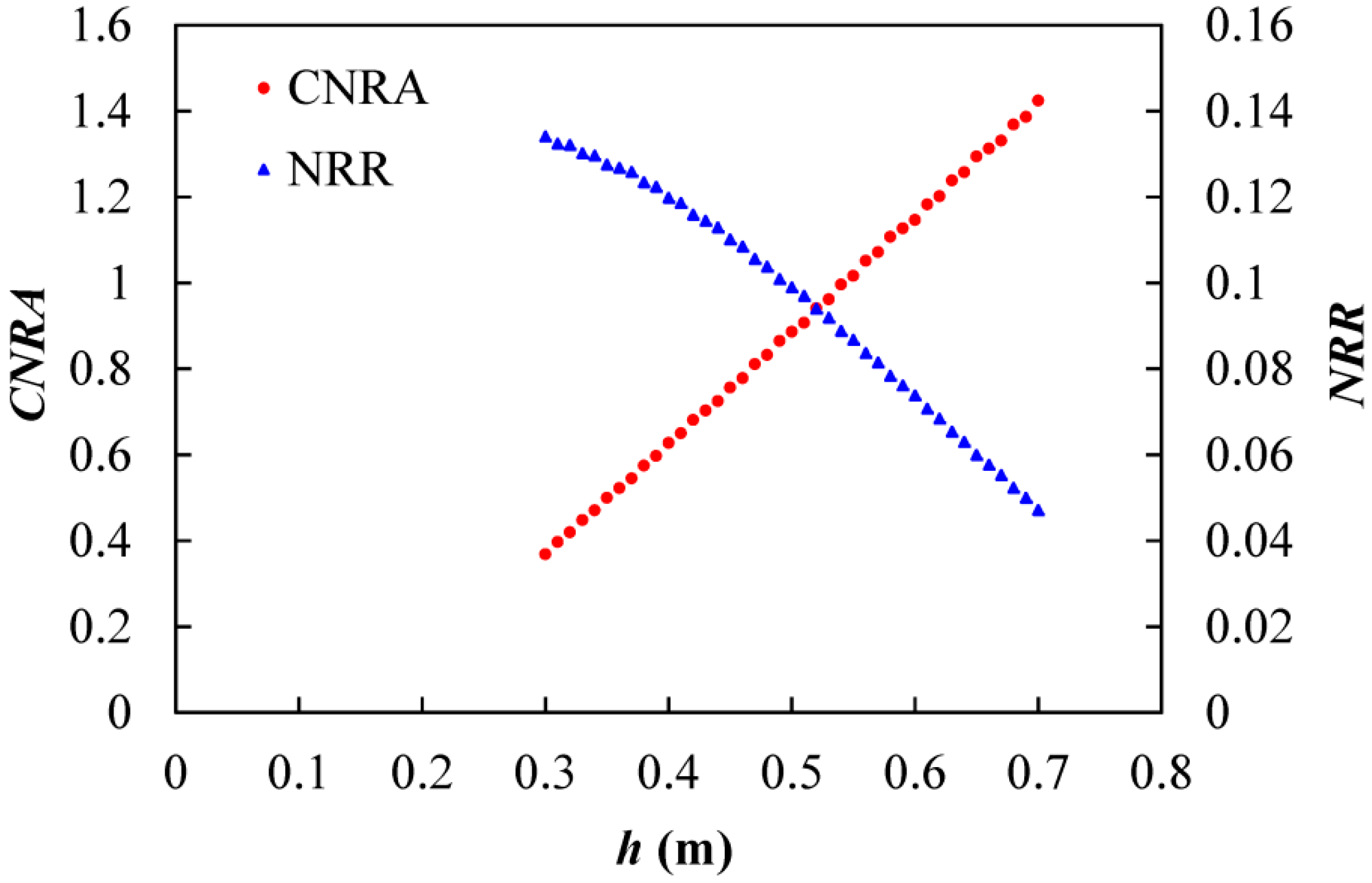
3.2.1. Cumulative Nitrogen Removal Amount (CNRA) and Nitrogen Removal Ratio (NRR)
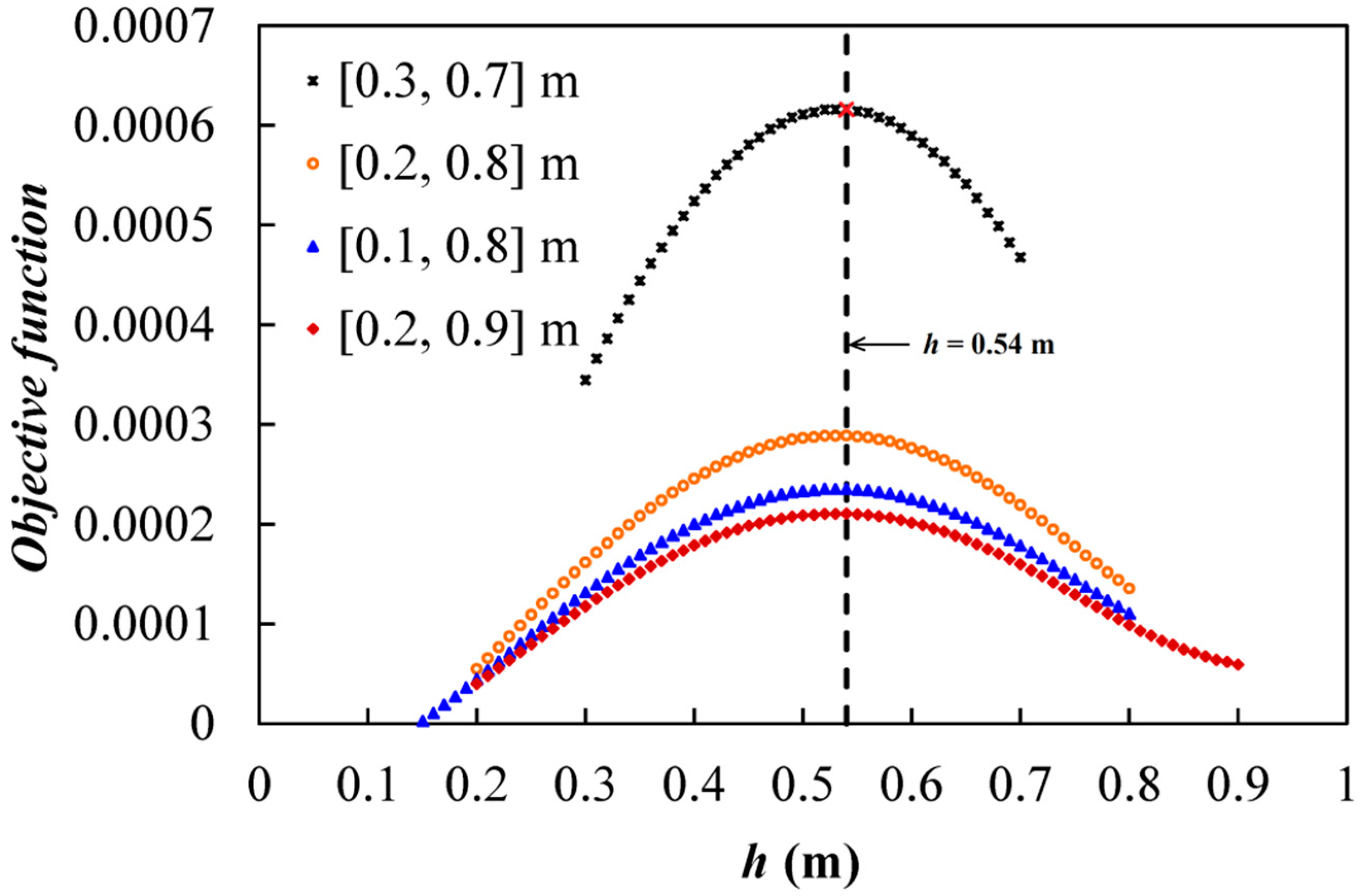
3.2.2. Optimal Height of the Weir
3.2.3. Validation
3.3. Sensitivity Analysis
3.4. Limitations and Future Studies
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Boulton, A.J.; Findlay, S.; Marmonier, P.; Stanley, E.H.; Valett, H.M. The functional significance of the hyporheic zone in streams and rivers. Annu. Rev. Ecol. Syst. 1998, 29, 59–81. [Google Scholar] [CrossRef] [Green Version]
- Soulsby, C.; Malcolm, I.; Youngson, A. Hydrochemistry of the hyporheic zone in salmon spawning gravels: A preliminary assessment in a degraded agricultural stream. River Res. Appl. 2001, 17, 651–665. [Google Scholar] [CrossRef]
- Peterson, E.W.; Sickbert, T.B.; Moore, S.L. High frequency stream bed mobility of a low-gradient agricultural stream with implications on the hyporheic zone. Hydrol. Process. 2008, 22, 4239–4248. [Google Scholar] [CrossRef]
- Hester, E.T.; Gooseff, M.N. Moving beyond the banks: Hyporheic restoration is fundamental to restoring ecological services and functions of streams. Environ. Sci. Technol. 2010, 44, 1521–1525. [Google Scholar] [CrossRef]
- Peralta-Maraver, I.; Reiss, J.; Robertson, A.L. Interplay of hydrology. Community ecology and pollutant attenuation in the hyporheic zone. Sci. Total Environ. 2018, 610, 267–275. [Google Scholar] [CrossRef] [Green Version]
- Liu, S.N.; Chui, T.F.M. Impacts of streambed heterogeneity and anisotropy on residence time of hyporheic zone. Groundwater 2018, 56, 425–436. [Google Scholar] [CrossRef]
- Liu, S.N.; Chui, T.F.M. Impacts of different rainfall patterns on hyporheic zone under transient conditions. J. Hydrol. 2018, 561, 598–608. [Google Scholar] [CrossRef]
- Montgomery, D.R.; Buffington, J.M.; Peterson, N.P.; Schuett-Hames, D.; Quinn, T.P. Stream-bed scour. Egg burial depths, and the influence of salmonid spawning on bed surface mobility and embryo survival. Can. J. Fish. Aquat. Sci. 1996, 53, 1061–1070. [Google Scholar] [CrossRef]
- Bilby, R.E.; Fransen, B.R.; Bisson, P.A. Incorporation of nitrogen and carbon from spawning coho salmon into the trophic system of small streams: Evidence from stable isotopes. Can. J. Fish. Aquat. Sci. 1996, 53, 164–173. [Google Scholar] [CrossRef]
- Harvey, J.W.; Böhlke, J.K.; Voytek, M.A.; Scott, D.; Tobias, C.R. Hyporheic zone denitrification: Controls on effective reaction depth and contribution to whole-stream mass balance. Water Resour. Res. 2013, 49, 6298–6316. [Google Scholar] [CrossRef]
- Sheibley, R.W.; Jackman, A.P.; Duff, J.H.; Triska, F.J. Numerical modeling of coupled nitrification–denitrification in sediment perfusion cores from the hyporheic zone of the Shingobee River, MN. Adv. Water Resour. 2003, 26, 977–987. [Google Scholar] [CrossRef]
- Zarnetske, J.P.; Haggerty, R.; Wondzell, S.M.; Baker, M.A. Labile dissolved organic carbon supply limits hyporheic denitrification. J. Geophys. Res. Biogeosci. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Meghdadi, A.; Javar, N. Evaluation of nitrate sources and the percent contribution of bacterial denitrification in hyporheic zone using isotope fractionation technique and multi-linear regression analysis. J. Environ. Manag. 2018, 222, 54–65. [Google Scholar] [CrossRef] [PubMed]
- Crispell, J.K.; Endreny, T.A. Hyporheic exchange flow around constructed in-channel structures and implications for restoration design. Hydrol. Process. 2009, 23, 1158–1168. [Google Scholar] [CrossRef]
- Hester, E.T.; Doyle, M.W. In-stream geomorphic structures as drivers of hyporheic exchange. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Hester, E.T.; Doyle, M.W.; Poole, G.C. The influence of in-stream structures on summer water temperatures via induced hyporheic exchange. Limnol. Oceanogr. 2009, 54, 355–367. [Google Scholar] [CrossRef]
- Hester, E.T.; Gooseff, M.N. Hyporheic Restoration in Streams and Rivers, in Stream Restoration in Dynamic Fluvial Systems; American Geophysical Union: Washington, DC, USA, 2013. [Google Scholar] [CrossRef]
- Hester, E.T.; Hammond, B.; Scott, D.T. Effects of inset floodplains and hyporheic exchange induced by in-stream structures on nitrate removal in a headwater stream. Ecol. Eng. 2016, 97, 452–464. [Google Scholar] [CrossRef] [Green Version]
- Ward, A.S.; Gooseff, M.N.; Johnson, P.A. How can subsurface modifications to hydraulic conductivity be designed as stream restoration structures? Analysis of Vaux’s conceptual models to enhance hyporheic exchange. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Kasahara, T.; Hill, A.R. Effects of riffle step restoration on hyporheic zone chemistry in N-rich lowland streams. Can. J. Fish. Aquat. Sci. 2006, 63, 120–133. [Google Scholar] [CrossRef]
- Lautz, L.; Fanelli, R. Seasonal biogeochemical hotspots in the streambed around restoration structures. Biogeochemistry 2008, 91, 85–104. [Google Scholar] [CrossRef]
- Fanelli, R.M.; Lautz, L.K. Patterns of water. heat, and solute flux through streambeds around small dams. Groundwater 2008, 46, 671–687. [Google Scholar] [CrossRef] [PubMed]
- Grant, S.B.; Stolzenbach, K.; Azizian, M.; Stewardson, M.J.; Boano, F.; Bardini, L. First-order contaminant removal in the hyporheic zone of streams: Physical insights from a simple analytical model. Environ. Sci. Technol. 2014, 48, 11369–11378. [Google Scholar] [CrossRef] [Green Version]
- Lammers, R.W.; Bledsoe, B.P. What role does stream restoration play in nutrient management? Environ. Sci. Technol. 2017, 47, 335–371. [Google Scholar] [CrossRef]
- Patrick, W.; Reddy, K. Nitrification-denitrification reactions in flooded soils and water bottoms: Dependence on oxygen supply and ammonium diffusion. J. Environ. Qual. 1976, 5, 469–472. [Google Scholar] [CrossRef]
- Hill, A.R. Nitrate removal in stream riparian zones. J. Environ. Qual. 1996, 25, 743–755. [Google Scholar] [CrossRef]
- Ward, B. Nitrification and denitrification: Probing the nitrogen cycle in aquatic environments. Microb. Ecol. 1996, 32, 247–261. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Zhu, G. Biological nitrogen removal with nitrification and denitrification via nitrite pathway. Appl. Microbiol. Biotechnol. 2006, 73, 15–26. [Google Scholar] [CrossRef]
- Liu, S.N.; Chui, T.F.M. Numerical modelling for evaluation of the nitrogen removal rate in hyporheic zone and its implication to stream management. Hydrol. Process. 2019, 33, 3084–3097. [Google Scholar] [CrossRef]
- Roley, S.S.; Tank, J.L.; Williams, M.A. Hydrologic connectivity increases denitrification in the hyporheic zone and restored floodplains of an agricultural stream. J. Geophys. Res. Biogeosci. 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Gordon, R.P.; Lautz, L.K.; Daniluk, T.L. Spatial patterns of hyporheic exchange and biogeochemical cycling around cross-vane restoration structures: Implications for stream restoration design. Water Resour. Res. 2013, 49, 2040–2055. [Google Scholar] [CrossRef]
- Hydrologic Engineering Center (HEC). HEC-RAS River Analysis System User’s Manual; US Army Corps of Engineers (USACE): Washington, DC, USA, 2016.
- HEC. HEC-RAS River Analysis System Hydraulic Reference Manual; US Army Corps of Engineers (USACE): Washington, DC, USA, 2016.
- Brinkman, H.C. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl. Sci. Res. 1949, 1, 27–34. [Google Scholar] [CrossRef]
- Sawyer, C.N. Chemistry for Environmental Engineering and Science; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Cardenas, M.B. Surface water-groundwater interface geomorphology leads to scaling of residence times. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Haggerty, R.; Wondzell, S.M.; Johnson, M.A. Power-law residence time distribution in the hyporheic zone of a 2nd-order mountain stream. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef] [Green Version]
| Variables to be Held Constant | Variable to be Changed |
|---|---|
| Slope = 0.01 River discharge = 1 m3/s Depth to bedrock = 5 m | Height of the weir = 0.3, 0.4, 0.5, 0.6, and 0.7 m |
| h (m) | h = 0.3 | h = 0.4 | h = 0.5 | h = 0.6 | h = 0.7 |
|---|---|---|---|---|---|
| a1 | 1.44 × 1012 | 2.46 × 109 | 3.40 × 107 | 1.01 × 107 | 2.57 × 106 |
| Ln(a1) | 28.00 | 21.62 | 17.34 | 16.13 | 14.76 |
| b1 | −10.14 | −7.26 | −5.27 | −4.79 | −4.17 |
| R2 | 0.97 | 0.94 | 0.91 | 0.93 | 0.92 |
| h (m) | h = 0.3 | h = 0.4 | h = 0.5 | h = 0.6 | h = 0.7 |
|---|---|---|---|---|---|
| a2 | 0.0099 | 0.016 | 0.022 | 0.029 | 0.035 |
| b2 | −1.51 | −1.69 | −1.73 | −1.80 | −1.82 |
| R2 | 0.83 | 0.71 | 0.79 | 0.78 | 0.84 |
| h (m) | h = 0.5 | h = 0.54 | h = 0.6 |
|---|---|---|---|
| CNRA | 2.81 | 3.15 | 3.43 |
| NRR | 14.2% | 20% | 14.5% |
| CNRA·NRR | 0.40 | 0.63 | 0.50 |
| h (m) | h = 0.5 | h = 0.53 | h = 0.54 | h = 0.55 | h = 0.6 |
|---|---|---|---|---|---|
| RTmax (day) | 2.98 | 2.96 | 2.89 | 2.58 | 2.33 |
| M1den (mol) | 1.07 × 10−5 | 1.08 × 10−5 | 1.12 × 10−5 | 9.77 × 10−6 | 7.94 × 10−6 |
| M2den (mol) | 1.09 × 10−5 | 1.10 × 10−5 | 1.17 × 10−5 | 1.15 × 10−5 | 1.01 × 10−5 |
| M1den (mol) | River Discharge (m3/s) | |||
|---|---|---|---|---|
| 0.5 | 1.0 | 1.5 | ||
| Height of the in-stream structure (m) | 0.53 | 1.01 × 10−5 | 1.08 × 10−5 | 9.70 × 10−6 |
| 0.54 | 9.43 × 10−6 | 1.12 × 10−5 | 1.04 × 10−5 | |
| 0.55 | 8.08 × 10−6 | 9.77 × 10−6 | 1.06 × 10−5 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, S.; Chui, T.F.M. Optimal In-Stream Structure Design through Considering Nitrogen Removal in Hyporheic Zone. Water 2020, 12, 1399. https://doi.org/10.3390/w12051399
Liu S, Chui TFM. Optimal In-Stream Structure Design through Considering Nitrogen Removal in Hyporheic Zone. Water. 2020; 12(5):1399. https://doi.org/10.3390/w12051399
Chicago/Turabian StyleLiu, Suning, and Ting Fong May Chui. 2020. "Optimal In-Stream Structure Design through Considering Nitrogen Removal in Hyporheic Zone" Water 12, no. 5: 1399. https://doi.org/10.3390/w12051399
APA StyleLiu, S., & Chui, T. F. M. (2020). Optimal In-Stream Structure Design through Considering Nitrogen Removal in Hyporheic Zone. Water, 12(5), 1399. https://doi.org/10.3390/w12051399





